Heat and Mass Transfer in a Viscous Nanofluid Containing a Gyrotactic Micro-Organism Over a Stretching Cylinder
Abstract
:1. Introduction
2. Governing Equations
3. Spectral Relaxation Method and Comparison
- By using the velocity equation can transformed in terms of .
- Supposing that are familiar since past iterations (symbolized by ) form an iteration scheme for by supposing that only linear terms in are to be calculated at the present iteration level (indicated by ) and all dissimilar expressions are supposed to be familiar from the past iteration. Further, nonlinear terms in are calculated at the past iteration.
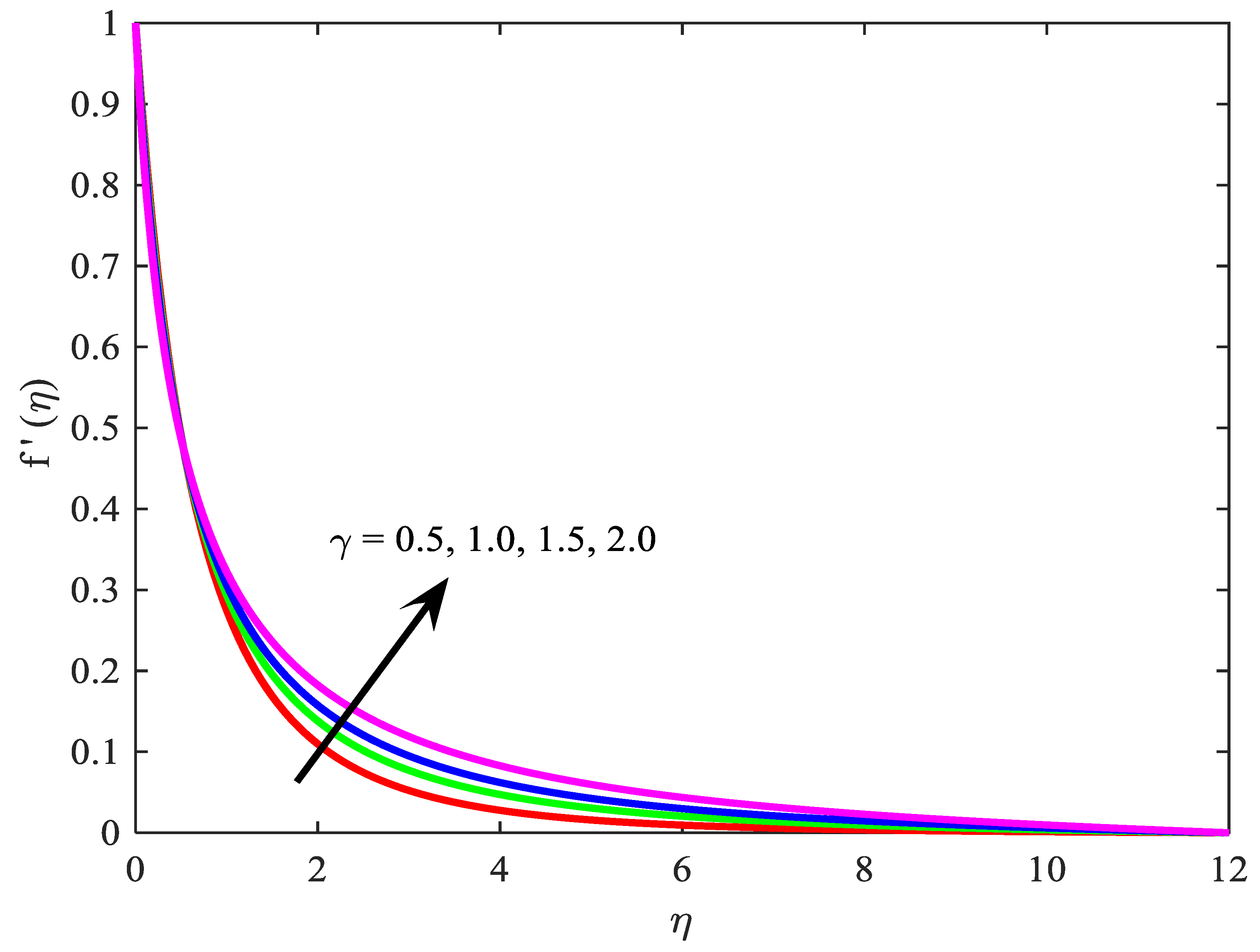
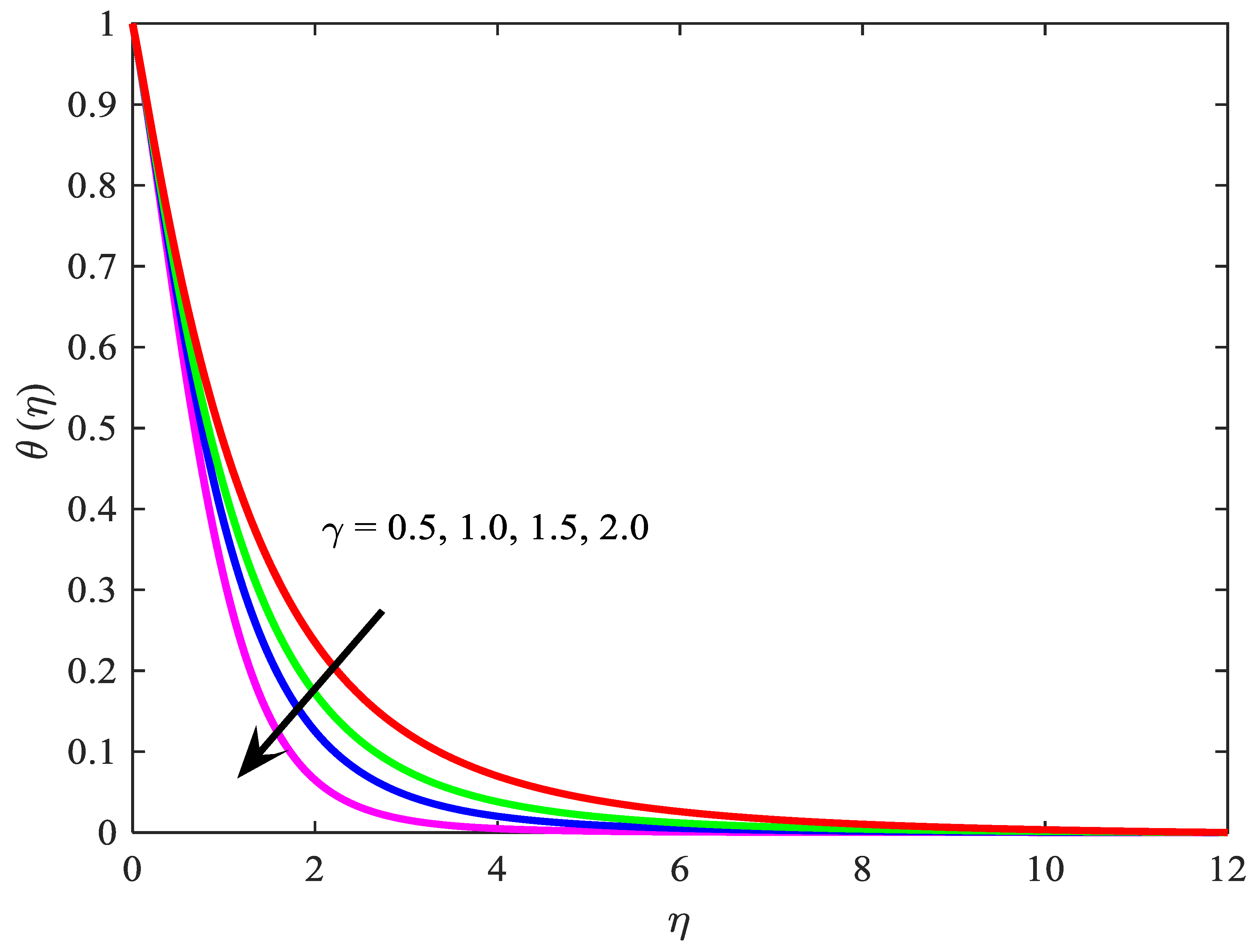
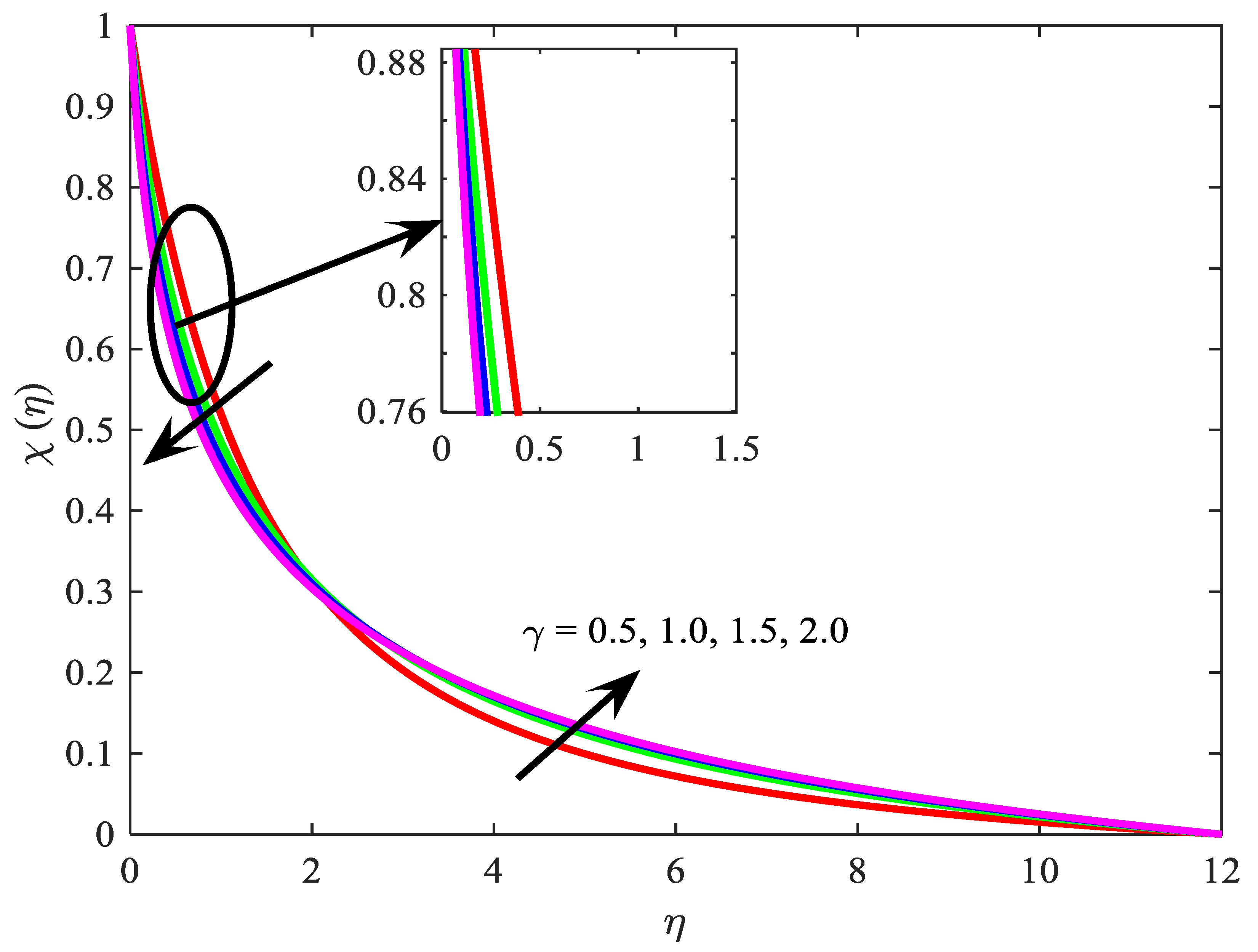
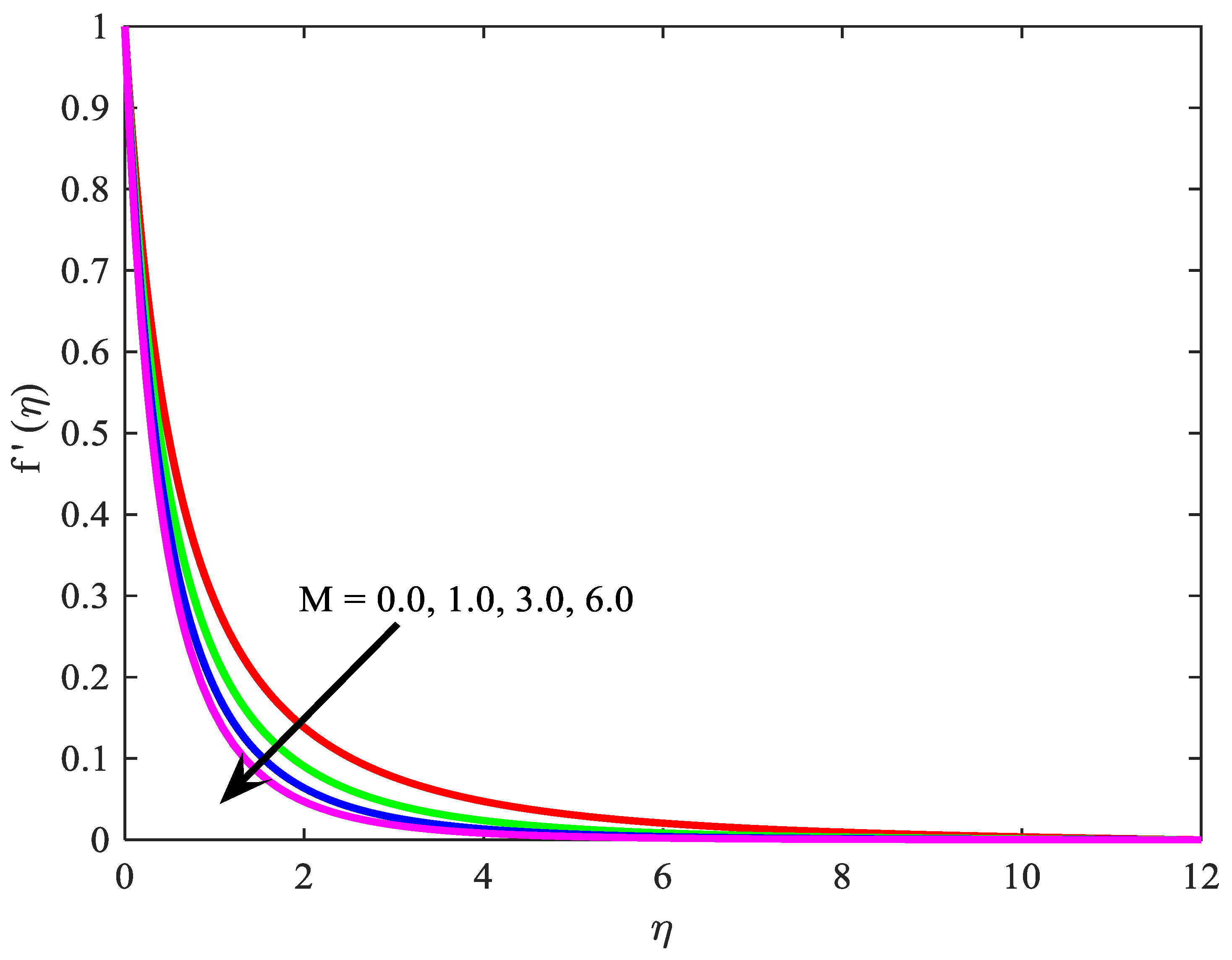
4. Discussions
5. Conclusions
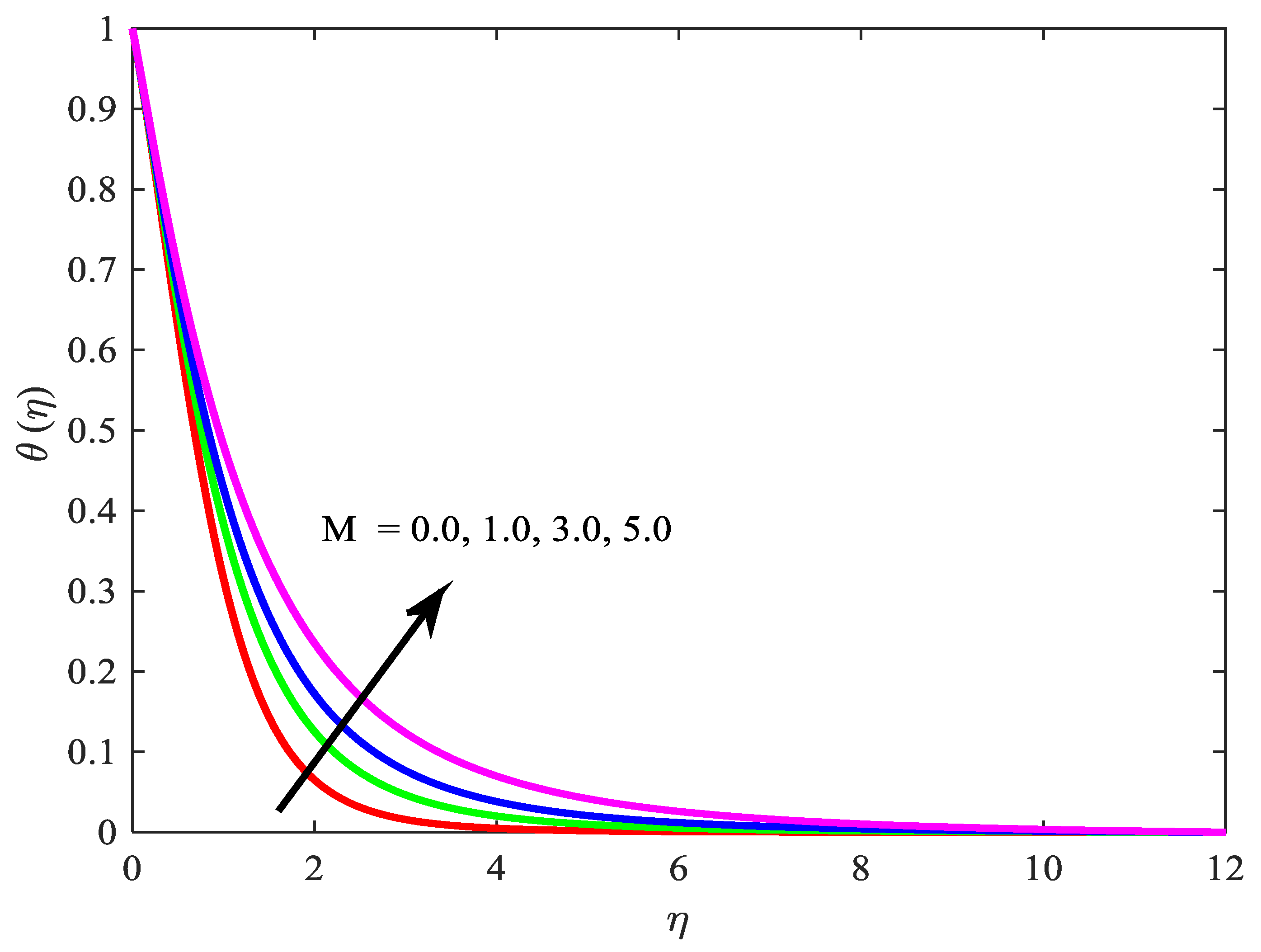
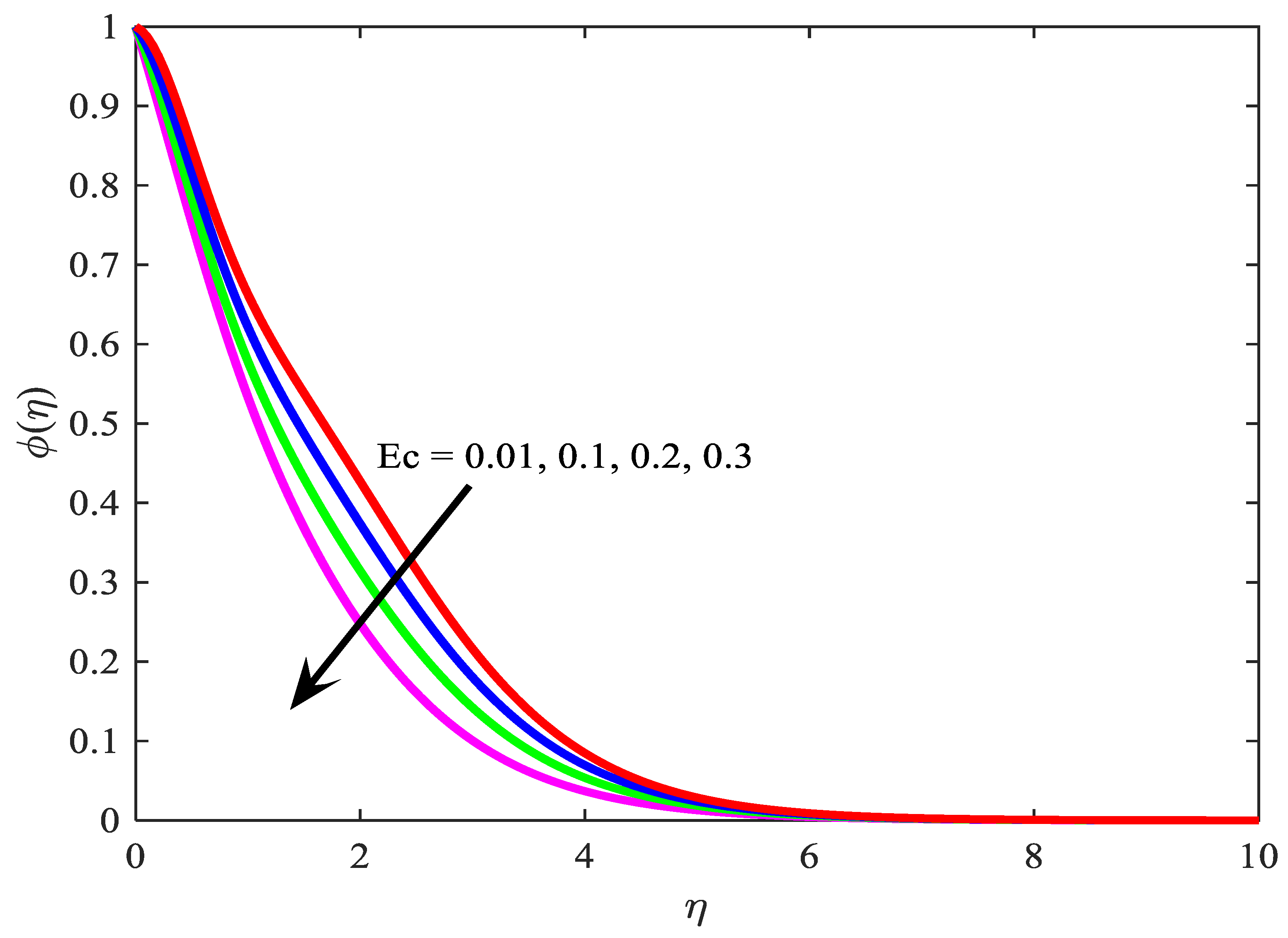
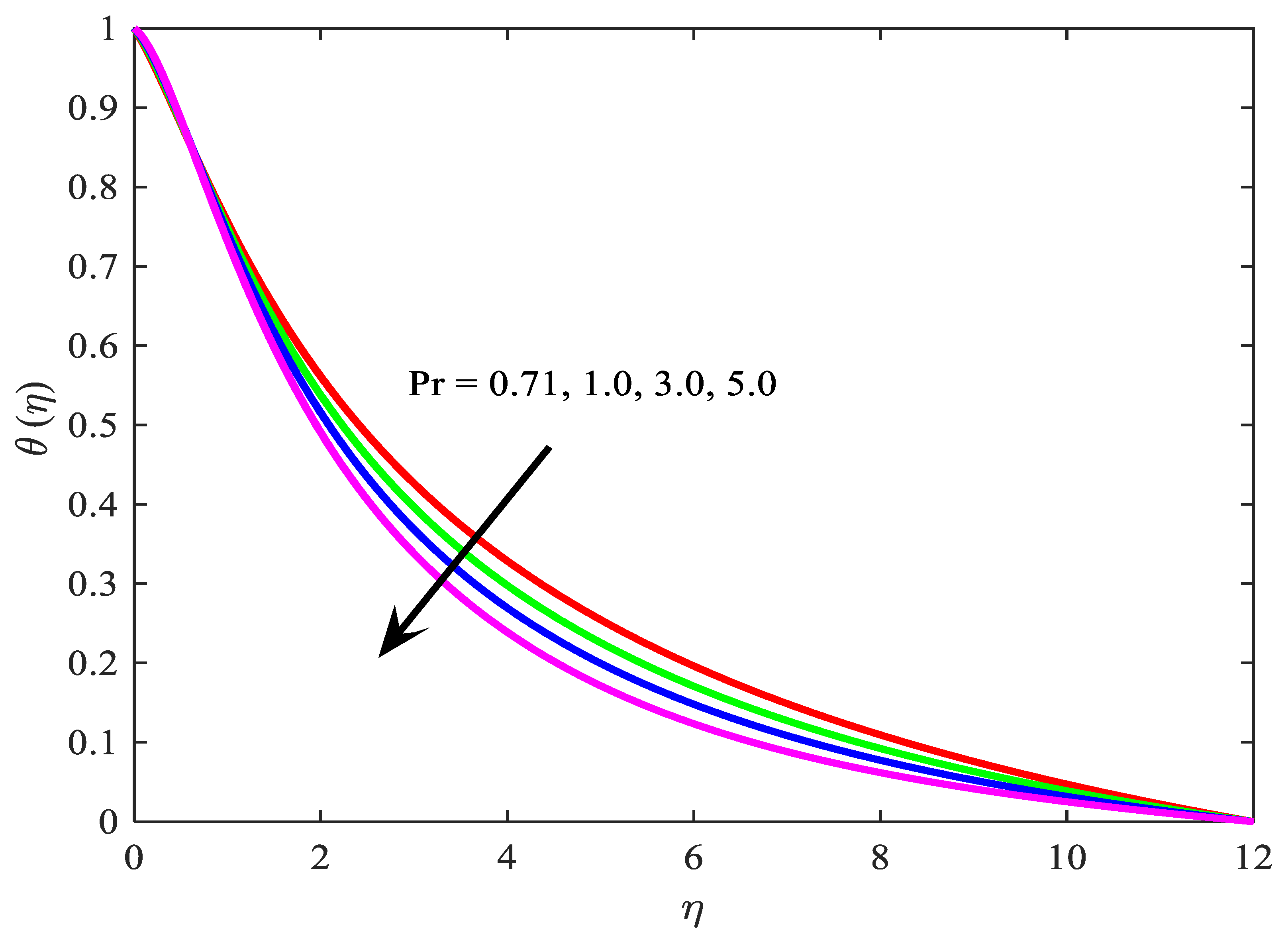
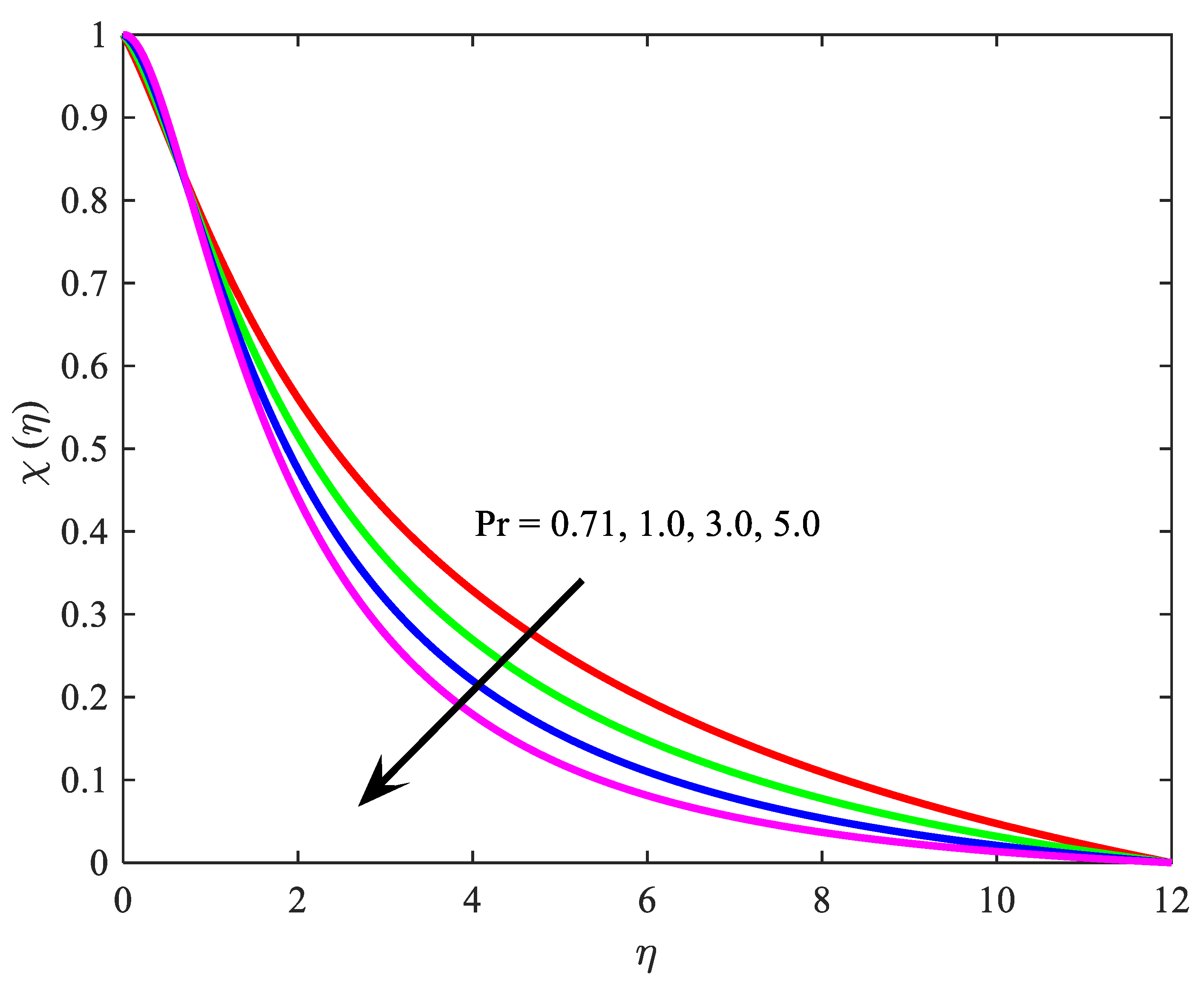
- enhance the temperature field ;
- decreases the velocity profile ;
- reduce the temperature field ;
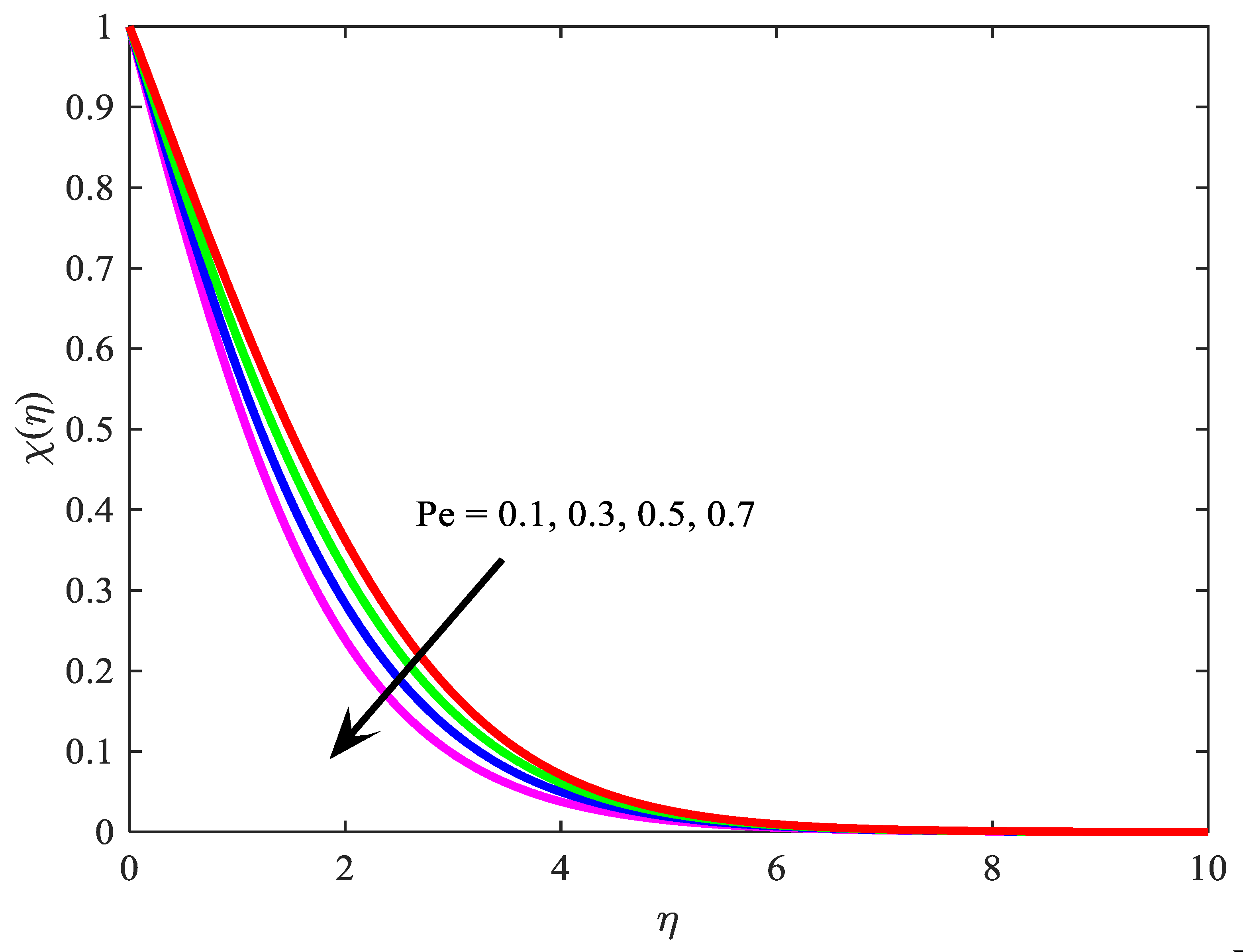
- The wall thickness of the motile microorganism is a declining function of ;
- The density of the motile microorganism is an enhancing function of ;
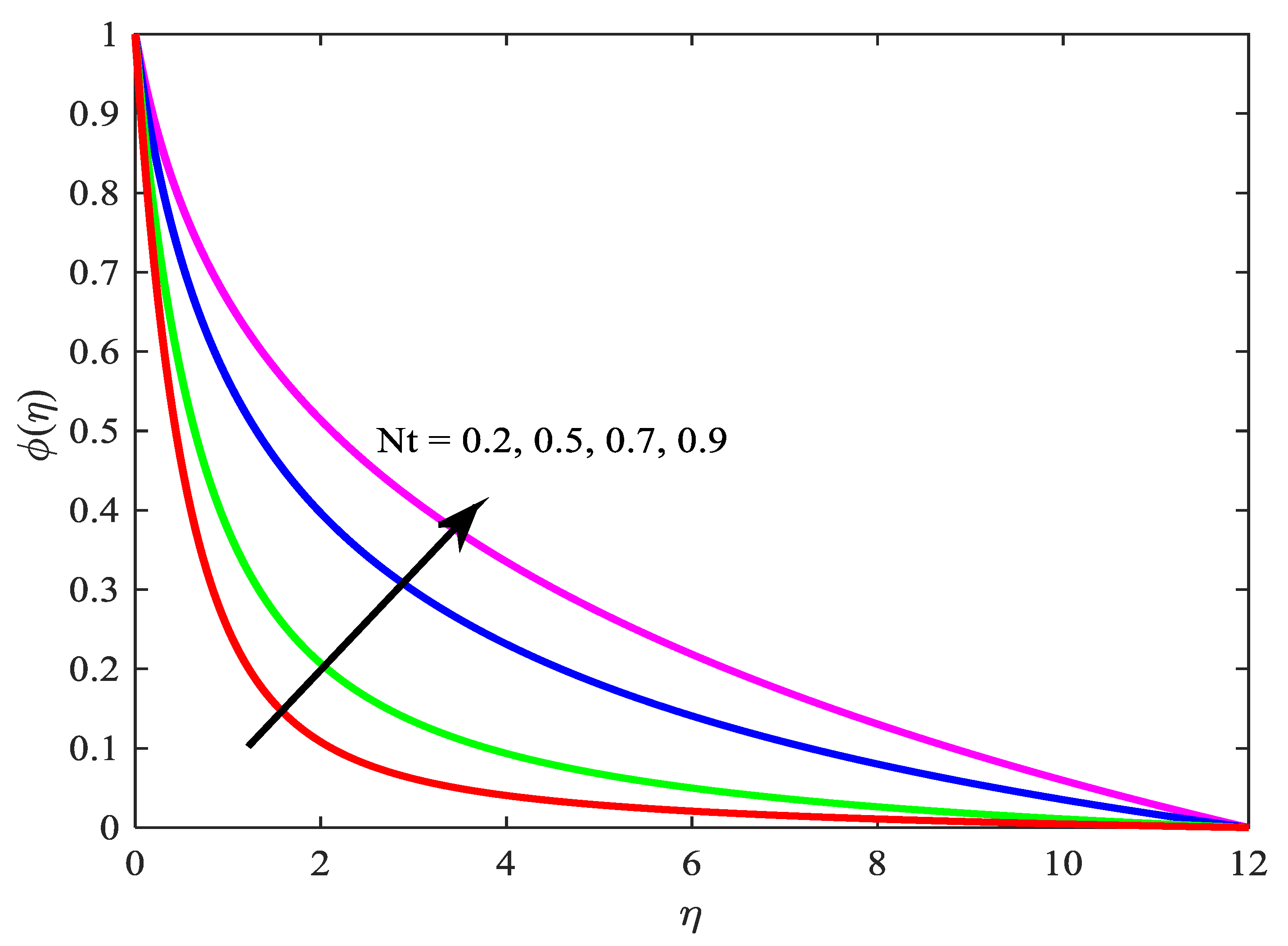
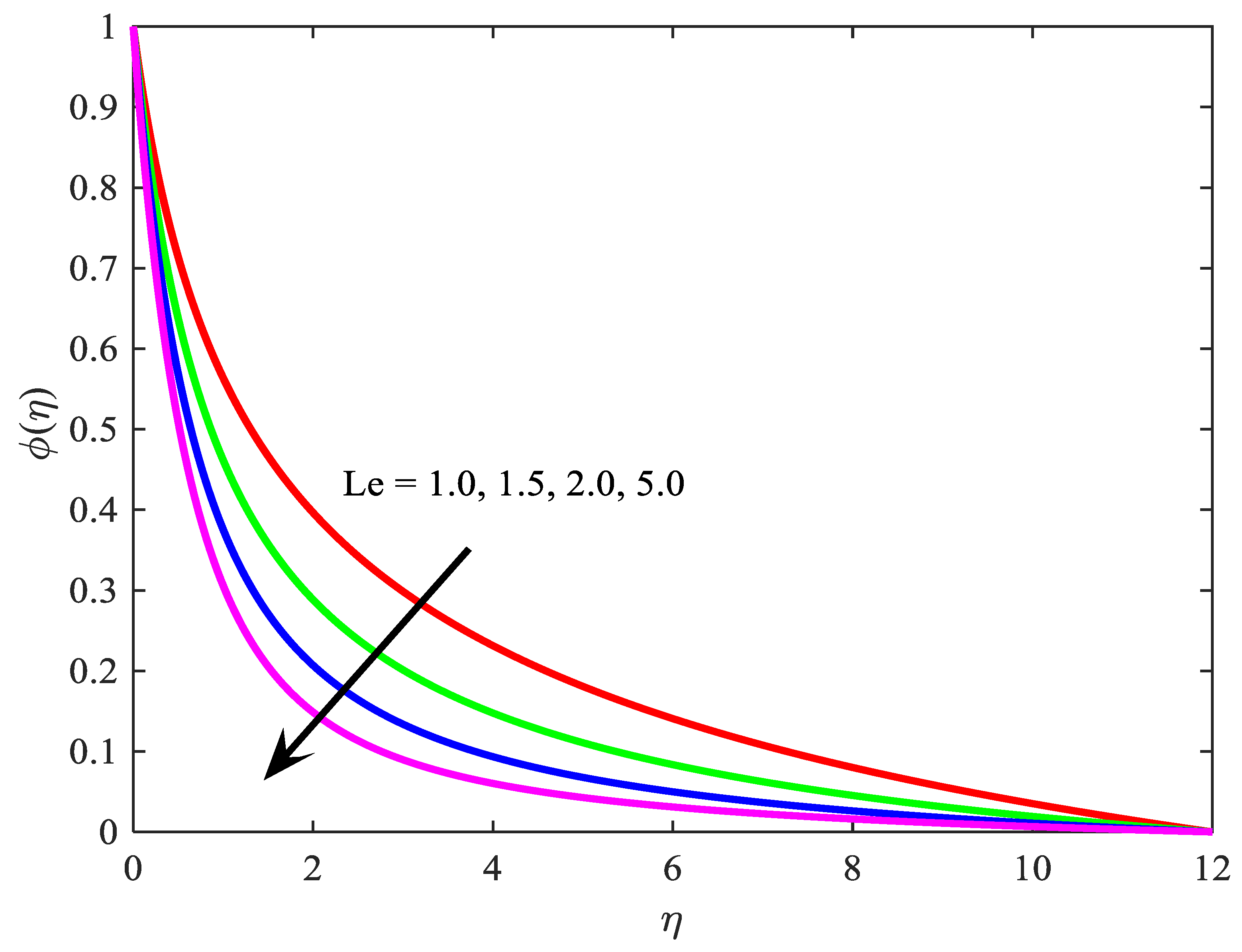
- regulate the concentration profile;
- The concentration field increases with the rise of and decreases with the increase of .
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Radius of the cylinder | |
| Magnetic field of strength | |
| Concentration | |
| Skin friction coefficient | |
| Concentration at the surface | |
| Concentration in the free stream | |
| Specific heat at constant pressure | |
| Brownian diffusion coefficient | |
| Diffusivity of the microorganism | |
| Thermophoresis coefficient | |
| Eckert number | |
| Bioconvection Lewis number | |
| Lewis number | |
| Characteristic length. | |
| Magnetic field parameter | |
| Brownian motion parameter | |
| Thermophoresis parameter | |
| Density number of the motile microorganism | |
| Local Nusselt number | |
| Density of the motile microorganism | |
| Constant motile microorganism | |
| Peclet number | |
| Prandtl number | |
| Surface motile microorganism flux. | |
| Surface mass flux | |
| Surface heat flux | |
| Reynolds number | |
| Local Sherwood number | |
| Indicates the temperature | |
| Constant temperature | |
| Velocity parts along directions | |
| Constant | |
| Axial route having velocity | |
| Constant maximum cell swimming speed | |
| Velocity parts along directions | |
| Greek letters | |
| Bioconvection parameter | |
| Electrical conductivity | |
| Thermal diffusivity | |
| Effective heat capacitance | |
| Kinematic viscosity | |
| Curvature parameter | |
| Surface shear stress | |
References
- Schlichting, H.; Gersten, K.; Krause, E.; Oertel, H. Boundary-Layer Theory; McGraw-Hill: New York, NY, USA, 1960; Volume 7. [Google Scholar]
- Sakiadis, B.C. Boundarylayer behavior on continuous solid surfaces: I. Boundarylayer equations for two dimensional and axi-symmetric flow. AIChE J. 1961, 7, 26–28. [Google Scholar] [CrossRef]
- Sakiadis, B.C. Boundary-layer behavior on continuous solid surfaces: II. The boundary layer on a continuous flat surface. AIChE J. 1961, 7, 221–225. [Google Scholar] [CrossRef]
- Crane, L.J. Flow past a stretching plate. Z. Angew. Math. Phys. 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Dutta, B.; Roy, P.; Gupta, A. Temperature field in flow over a stretching sheet with uniform heat flux. Int. Commun. Heat Mass Transf. 1985, 12, 89–94. [Google Scholar] [CrossRef]
- Chen, C.-K.; Char, M.-I. Heat transfer of a continuous, stretching surface with suction or blowing. J. Math. Anal. Appl. 1988, 135, 568–580. [Google Scholar] [CrossRef] [Green Version]
- Gupta, P.S.; Gupta, A.S. Heat and mass transfer on a stretching sheet with suction or blowing. Can. J. Chem. Eng. 1977, 55, 744–746. [Google Scholar] [CrossRef]
- Hayat, T.; Javed, T.; Abbas, Z. Slip flow and heat transfer of a second grade fluid past a stretching sheet through a porous space. Int. J. Heat Mass Transf. 2008, 51, 4528–4534. [Google Scholar] [CrossRef]
- Hayat, T.; Abbas, Z.; Sajid, M. Series solution for the upper-convected Maxwell fluid over a porous stretching plate. Phys. Lett. A 2006, 358, 396–403. [Google Scholar] [CrossRef]
- Xu, H.; Liao, S.J. Analytic solutions of magnetohydrodynamic flows of non- Newtonian fluids caused by an impulsively stretching plate. J. Non-Newton Fluid Mech. 2005, 159, 46–55. [Google Scholar] [CrossRef]
- Cortell, R. Flow and heat transfer of a fluid through a porous medium over a stretching surface with internal heat generation/absorption and suction/blowing. Fluid Dyn. Res. 2005, 37, 231–245. [Google Scholar] [CrossRef]
- Cortell, R. Effects of viscous dissipation and work done by deformation on the MHD flow and heat transfer of a viscoelastic fluid over a stretching sheet. Phys. Lett. A 2006, 357, 298–305. [Google Scholar] [CrossRef]
- Datta, P.; Anilkumar, D.; Roy, S.; Mahanti, N.C. Effect of non-uniform slot injection (suction) on a forced flow over a slender cylinder. Int. J. Heat Mass Transf. 2006, 49, 2366–2371. [Google Scholar] [CrossRef]
- Elbarbary, E.M.E.; Elgazery, N.S. Flow and heat transfer of a micropolar fluid in an axi-symmetric stagnation flow on a cylinder with variable properties and suction (numerical study). Acta Mech. 2005, 76, 213–229. [Google Scholar] [CrossRef]
- Wang, C.Y. Fluid flow due to a stretching cylinder. Phys. Fluids 1988, 31, 466. [Google Scholar] [CrossRef]
- Ishak, A.; Nazar, R.; Pop, I. Magnetohydrodynamic (MHD) flow and heat transfer due to a stretching cylinder. Energy Convers. Manag. 2008, 49, 3265–3269. [Google Scholar] [CrossRef]
- Ishak, A.; Nazar, R.; Pop, I. Uniform suction/blowing effect on flow and heat transfer due to a stretching cylinder. Appl. Math. Model. 2008, 32, 2059–2066. [Google Scholar] [CrossRef]
- Butt, A.S.; Ali, A.; Mehmood, A. Numerical investigation of magnetic field effects on entropy generation in viscous flow over a stretching cylinder embedded in a porous medium. Energy 2016, 99, 237–249. [Google Scholar] [CrossRef]
- Choi, S.U.S.; Zhang, Z.G.; Yu, W.; Lockwood, F.E.; Grulke, E.A. Anomalous thermal conductivity enhancement in nanotube suspensions. Appl. Phys. Lett. 2001, 79, 2252–2254. [Google Scholar] [CrossRef]
- Masuda, H.; Ebata, A.; Teramae, K. Alteration of thermal conductivity and viscosity of liquid by dispersing ultra-fine particles. Dispersion of Al2O3, SiO2 and TiO2 ultra-fine particles. Jpn. Soc. Thermophys. Prop. 1993, 7, 227–233. [Google Scholar] [CrossRef]
- Platt, J.R. “Bioconvection Patterns” in Cultures of Free-Swimming organisms. Science 1961, 133, 1766–1767. [Google Scholar] [CrossRef]
- Kuznetsov, A. Bio-thermal convection induced by two different species of microorganisms. Int. Commun. Heat Mass Transf. 2011, 38, 548–553. [Google Scholar] [CrossRef]
- Kuznetsov, A. The onset of thermo-bioconvection in a shallow fluid saturated porous layer heated from below in a suspension of oxytactic microorganisms. Eur. J. Mech. B Fluids 2006, 25, 223–233. [Google Scholar] [CrossRef]
- Nield, D.A.; Kuznetsov, A.V. The onset of bio-thermal convection in a suspension of gyrotactic microorganisms in a fluid layer: Oscillatory convection. Int. J. Therm. Sci. 2006, 45, 990–997. [Google Scholar] [CrossRef]
- Avramenko, A.A.; Kuznetsov, A.V. Stability of a suspension of gyrotactic microorganisms in superimposed fluid and porous layers. Int. Commun. Heat Mass Transf. 2004, 31, 1057–1066. [Google Scholar] [CrossRef]
- Alloui, Z.; Nguyen, T.H.; Bilgen, E. Numerical investigation of thermo-bioconvection in a suspension of gravitactic microorganisms. Int. Commun. Heat Mass Transf. 2007, 50, 1435–1441. [Google Scholar] [CrossRef]
- Mahdy, A. Gyrotactic Microorganisms Mixed Convection Nanofluid Flow along an Isothermal Vertical Wedge in Porous Media. Int. Sch. Sci. Res. Innov. 2017, 11, 829–839. [Google Scholar]
- Tham, L.; Nazar, R.; Pop, I. Steady Mixed Convection Flow on a Horizontal Circular Cylinder Embedded in a Porous Medium Filled by a Nanofluid Containing Gyrotactic Micro-Organisms. J. Heat Transf. 2013, 135, 102601. [Google Scholar] [CrossRef]
- Kuznetsov, A. The onset of nanofluid bioconvection in a suspension containing both nanoparticles and gyrotactic microorganisms. Int. Commun. Heat Mass Transf. 2010, 37, 1421–1425. [Google Scholar] [CrossRef]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Dinarvand, S.; Hosseini, R.; Pop, I. Unsteady convective heat and mass transfer of a nanofluid in Howarth’s stagnation point by Buongiorno’s model. Int. J. Numer. Methods Heat Fluid Flow 2015, 25, 1176–1197. [Google Scholar] [CrossRef]
- Dinarvand, S.; Abbassi, A.; Hosseini, R.; Pop, I. Homotopy analysis method for mixed convective boundary layer flow of a nanofluid over a vertical circular cylinder. Therm. Sci. 2015, 19, 549–561. [Google Scholar] [CrossRef]
- Babu, M.J.; Sandeep, N. Effect of nonlinear thermal radiation on non-aligned bio-convective stagnation point flow of a magnetic-nanofluid over a stretching sheet. Alex. Eng. J. 2016, 55, 1931–1939. [Google Scholar] [CrossRef] [Green Version]
- Khan, W.; Pop, I.; Khan, W. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
- Wang, C.Y. Free Convection on a Vertical Stretching Surface. ZAMM 1989, 69, 418–420. [Google Scholar] [CrossRef]
- Mukhopadhyay, S. MHD boundary layerslip flow along a stretching cylinder. Ain Shams Eng. J. 2013, 4, 317–324. [Google Scholar] [CrossRef]
- Motsa, S.S. A new spectral relaxation method for similarity variable nonlinear boundary layer flow systems. Chem. Eng. Commun. 2014, 201, 241–256. [Google Scholar] [CrossRef]
- Motsa, S.S.; Makukula, Z.G. On spectral relaxation method approach for steady von Kármán flow of a Reiner-Rivlin fluid with Joule heating, viscous dissipation and suction/injection. Cent. Eur. J. Phys. 2013, 11, 363–374. [Google Scholar] [CrossRef]
- Shateyi, S. A new numerical approach to MHD flow of a maxwelfluid past a vertical stretching sheet in the presence of thermophoresis and chemical reaction. Bound. Value Probl. 2013, 2013, 196. [Google Scholar] [CrossRef]
- Shateyi, S.; Makinde, O.D. Hydromagnetic stagnation-point flow towards a radially stretching convectively heated disk. Math. Probl. Eng. 2013, 2013, 616947. [Google Scholar] [CrossRef]
- Shateyi, S.; Marewo, G.T. A new numerical approach of MHD flow with heat and mass transfer for the UCM fluid over a stretching surface in the presence of thermal radiation. Math. Probl. Eng. 2013, 2013, 670205. [Google Scholar] [CrossRef]
- Motsa, S.S.; Dlamini, P.G.; Khumalo, M. Solving hyperchaotic systems using the spectral relaxation method. Abstr. Appl. Anal. 2012, 2012, 203461. [Google Scholar] [CrossRef]
- Motsa, S.S.; Dlamini, P.; Khumalo, M. A new multistage spectral relaxation method for solving chaotic initial value systems. Nonlinear Dyn. 2013, 72, 265–283. [Google Scholar] [CrossRef]
- SaberiNik, H.; Rebelo, P. Multistage spectral relaxation method for solving the hyperchaotic complex systems. Sci. World J. 2014, 2014, 943293. [Google Scholar]
- Motsa, S.S.; Dlamini, P.G.; Khumalo, M. Spectral relaxation method and spectral quasilinearization method for solving unsteady boundary layer flow problems. Adv. Math. Phys. 2014, 2014, 341964. [Google Scholar] [CrossRef]
- Awad, F.G.; Motsa, S.; Khumalo, M. Heat and mass transfer in unsteady rotating fluid flow with binary chemical reaction and activation energy. PLoS ONE 2014, 9, e107622. [Google Scholar] [CrossRef] [PubMed]
- Haroun, N.A.; Sibanda, P.; Mondal, S.; Motsa, S.S. On unsteady MHD mixed convection in a nanofluid due to a stretching/shrinking surface with suction/injection using the spectral relaxation method. Bound. Value Probl. 2015, 24, 1–17. [Google Scholar] [CrossRef]
- Elbashbeshy, E.; Emam, T.G.; El-Azab, M.S.; Abdelgaber, K.M. Slip effects on flow, heat, and mass transfer of nanofluid over stretching horizontal cylinder in the presence of suction/injection. Therm. Sci. 2014, 135. [Google Scholar] [CrossRef]



















| Pr | Present Study | Khan and Pop [34] | Wang [35] | Elbashbeshy et al. [39] |
|---|---|---|---|---|
| 0.2 | 0.16911012 | 0.1691 | 0.1697 | 0.1690886 |
| 0.7 | 0.45391616 | 0.4539 | 0.4539 | 0.4539161 |
| 2 | 0.91135768 | 0.9114 | 0.9114 | 0.9113577 |
| 7 | 1.89540305 | 1.8954 | 1.8954 | 1.8954033 |
| 20 | 3.35390414 | 3.3539 | 3.3539 | 3.3539042 |
| 70 | 6.46218077 | 6.4622 | 6.4622 | 6.4621996 |
| 0.5 1 2 3 | 1 | 5 | 0.3 | 0.5 | 0.2 | 5 | 0.2 | 0.2 | 0.01 | 1.62649308 1.82111645 2.17941349 2.51241569 | 2.42810268 2.67528648 3.03778670 3.23014786 | 0.85568261 0.81591240 0.79123180 0.83834565 | 0.77721513 0.91919885 1.17739872 1.43491309 |
| 1 | 0 1 2 | 0.71 | 0.5 | 0.5 | 0.1 | 5 | 0.5 | 0.2 | 0.2 | 1.35577051 2.82111645 2.15890400 | 1.08610352 0.71283719 0.32331590 | 1.71241497 1.63058296 1.59635412 | 1.34116551 1.28080156 1.25335316 |
| 1 | 1 | 0.71 1 5 7 | 0.5 | 0.5 | 0.2 | 5 | 0.5 | 0.2 | 0.1 | 1.82111645 1.82111645 1.82111645 1.82111645 | 0.99942787 1.08600254 1.12591585 0.87986583 | 1.39642364 1.37153874 1.40748237 1.51248713 | 1.12678471 1.13654847 1.52920649 1.77773396 |
| 1 | 1 | 0.71 | 0.3 0.5 0.7 | 0.5 | 0.1 | 5 | 0.5 | 0.2 | 0.2 | 1.82111645 1.82111645 1.82111645 | 0.71283719 0.71283719 0.71283719 | 1.63058296 1.63058296 1.63058296 | 1.19404622 1.28080156 1.35483099 |
| 0.5 | 1 | 0.71 | 0.5 | 0.25 0.5 1.2 | 0.2 | 5 | 0.5 | 0.2 | 0.1 | 1.62649308 1.62649308 1.62649308 | 0.40047131 0.62834887 1.18153356 | 1.39670138 1.43755939 1.47036457 | 0.97004499 0.98733892 0.99954647 |
| 0.5 | 1 | 0.71 | 0.3 | 0.5 | 0.2 0.5 1.2 | 5 | 0.5 | 0.2 | 0.1 | 1.62649308 1.62649308 1.62649308 | 0.81885213 0.72661881 0.55314537 | 1.37025917 1.07378725 0.63142889 | 0.87739871 0.73600200 0.49242417 |
| 1 | 1 | 0.71 | 0.5 | 0.5 | 0.1 | 1 1.5 2 5 | 0.5 | 0.2 | 0.2 | 1.82111645 1.82111645 1.82111645 1.82111645 | 0.71283719 0.71283719 0.71283719 0.71283719 | 0.67841111 0.81415772 0.94753387 1.63058296 | 0.64189010 0.73312212 0.81755282 1.19404622 |
| 1 | 1 | 5 | 0.5 | 0.5 | 0.1 | 5 | 0.5 0.6 0.7 | 0.2 | 0.1 | 1.82111645 1.82111645 1.82111645 | 1.67403063 1.67403063 1.67403063 | 1.47926112 1.47926112 1.47926112 | 1.55544165 1.63930009 1.7210218 |
| 1 | 1 | 0.71 | 0.5 | 0.5 | 0.1 | 5 | 0.5 | 0.2 0.4 0.6 | 0.2 | 1.82111645 1.82111645 1.82111645 | 1.04300428 1.04300428 1.04300428 | 1.56883842 1.56883842 1.56883842 | 1.23920758 1.49489645 1.69489645 |
| 1 | 1 | 6.17 | 0.5 | 0.5 | 0.2 | 5 | 0.5 | 0.2 | 0.01 0.1 0.2 | 1.82111645 1.82111645 1.82111645 | 2.80350693 0.99256106 0.53315880 | 0.77232258 1.46526840 1.64145133 | 1.19996973 1.67326495 1.79135562 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferdows, M.; Reddy, M.G.; Alzahrani, F.; Sun, S. Heat and Mass Transfer in a Viscous Nanofluid Containing a Gyrotactic Micro-Organism Over a Stretching Cylinder. Symmetry 2019, 11, 1131. https://doi.org/10.3390/sym11091131
Ferdows M, Reddy MG, Alzahrani F, Sun S. Heat and Mass Transfer in a Viscous Nanofluid Containing a Gyrotactic Micro-Organism Over a Stretching Cylinder. Symmetry. 2019; 11(9):1131. https://doi.org/10.3390/sym11091131
Chicago/Turabian StyleFerdows, Mohammad, M. Gnaneswara Reddy, Faris Alzahrani, and Shuyu Sun. 2019. "Heat and Mass Transfer in a Viscous Nanofluid Containing a Gyrotactic Micro-Organism Over a Stretching Cylinder" Symmetry 11, no. 9: 1131. https://doi.org/10.3390/sym11091131
APA StyleFerdows, M., Reddy, M. G., Alzahrani, F., & Sun, S. (2019). Heat and Mass Transfer in a Viscous Nanofluid Containing a Gyrotactic Micro-Organism Over a Stretching Cylinder. Symmetry, 11(9), 1131. https://doi.org/10.3390/sym11091131





