Abstract
With the fast development of the Internet of Things (IoT) technology, normal people and organizations can produce massive data every day. Due to a lack of data mining expertise and computation resources, most of them choose to use data mining services. Unfortunately, directly sending query data to the cloud may violate their privacy. In this work, we mainly consider designing a scheme that enables the cloud to provide an efficient privacy-preserving decision tree evaluation service for resource-constrained clients in the IoT. To design such a scheme, a new secure comparison protocol based on additive secret sharing technology is proposed in a two-cloud model. Then we introduce our privacy-preserving decision tree evaluation scheme which is designed by the secret sharing technology and additively homomorphic cryptosystem. In this scheme, the cloud learns nothing of the query data and classification results, and the client has no idea of the tree. Moreover, this scheme also supports offline users. Theoretical analyses and experimental results show that our scheme is very efficient. Compared with the state-of-art work, both the communication and computational overheads of the newly designed scheme are smaller when dealing with deep but sparse trees.
1. Introduction
Recently, ubiquitous mobile devices equipped with various powerful embedded sensors (e.g., GPS, camera, digital compass, and gyroscope) have become an important part of our daily life. Moreover, the increasingly powerful wireless network technology has made communications between different mobile devices easier than before. The progress of these technologies gives rise to the concept of the Internet of Things (IoT). It is forecasted that there will be around 50 billion devices connected to the Internet by 2020 [1]. These devices in the IoT can generate volumes of data. The generated data can be used to find potential trends or making decisions on current events. Building a data mining model from the data generated from IoT has revolutionized our society in many ways, such as healthcare, social networks, and consumer electronics. For instance, the data generated from the wearable devices, such as heart rate, temperature, and oxygen saturation, along the data contributed from the hospitals, can be collected to build a data mining model for providing an online diagnosis.
Nowadays, several big Internet Giants, such as Amazon [2], Google [3] and Microsoft [4], all offer this kind of data mining service for users. These companies can collect the data from IoT and then use them to train a predictive model. With such a kind of service, resource-constrained users in the IoT can easily get the predictive results without data mining expertise and massive data training computations.
In the real world setting, to use these data mining services, clients in the IoT usually are required to reveal query data and classification results to the data mining service provider. On one hand, the query data and the classification results contain very sensitive information for the client. Directly leaking this information to the untrusted cloud platform may violate the client’s privacy. One direct way to solve this problem is to let the cloud send the model to clients. However, the data mining model is trained with great efforts. The cloud also rejects directly revealing such a valuable asset to clients. What is more important is that data mining model leakage could violate the laws and regulations in some areas, for instance, the Health Insurance Portability and Accountability Act (HIPAA). To address such problems, one navie solution is to let the client encrypt their query before sending it to the cloud service provider. However, the normal cryptosystem cannot support various computations on the ciphertext. The fully homomorphic cryptosystem which supports polynomial calculations on the ciphertext is a potential option. However, since the inefficiency of the fully homomorphic cryptosystem, it could definitely bring large computation costs for the client in IoT which usually has low-power computation and communication ability. In addition, as we know, the building of a data mining model involves a lot of non-linear arithmetic, which cannot be calculated directly from the fully homomorphic cryptosystem. Therefore, how to efficiently provide a privacy-preserving data mining service to clients remains a big challenge.
There are a lot of security and privacy issues in the IoT [5,6,7,8]. The data security and privacy issues during the evaluation of the decision tree are mainly considered in our work. Decision tree is a widely used data mining model, such as text classification [9], remote diagnosis [10,11] and credit-risk assessment [12]. Such a model consists of a set of internal nodes, which are called decision nodes and several leaf nodes which are associated with classification labels. Most of the works previously proposed have considered privacy problems existing in the decision tree training [13,14]. In recent years, privacy issues during the evaluation of decision tree model have attracted many researchers [15,16,17,18]. Most of the works about privacy-preserving decision tree evaluation schemes are designed on a client-server model. In these schemes, the cloud usually owns a decision tree and the client inputs an encrypted query. After several rounds of communication with each other, the client can obtain the classification result. These schemes cannot support offline users meaning that all the clients should connect with the cloud and calculate some intermediate data to assist the cloud to fulfill the evaluation. More importantly, these schemes cloud leak the tree depth or the node numbers to the client. Most recently, Liang et al. [19] proposed a model which can support the offline users. However, the computation cost grows exponentially with the number of the nodes. Obviously, such a scheme cannot be adopted for large-scale trees. Zheng et al. [20] proposed a work where the model is outsourced to the cloud from the model provider, e.g., a hospital, and the cloud with this outsourced model can provide decision tree evaluation service. Zheng et al.’s scheme is designed based on the two-cloud model. The scheme proposed is more efficient than most of the recent works. But, we also note that this proposed scheme just works on fully complete binary trees. The computation and communication overheads of their schemes grow exponentially with the depth of the tree. When dealing with a tree with high depth but fewer nodes, the provider should add many meaningless dummy nodes, which may cause large computation and communication costs for the cloud. Unlike Liang et al.’s scheme, this scheme also leaks the depth of the tree to the client too.
1.1. Motivation
As stated before, most of the proposed works about the privacy-preserving decision tree evaluation scheme either could arouse large computation or communication costs for users or cannot provide efficient service for the client, especially when dealing with large but sparse trees. Therefore, we intend to propose a decision tree evaluation scheme that can give the cloud the ability to provide an efficient but highly secure classification service for the resource-constrained client in the IoT. In such a privacy-preserving decision tree evaluation scenario, we mainly consider two kinds of privacy and security issues. First, we should protect the query data and its prediction label from the cloud server as well as the outside unauthorized entities. Moreover, clients using the prediction service cannot infer anything about the decision tree during the evaluation. Besides privacy and security issues, efficiency is also supposed to be well considered. IoT devices usually have limited computation and communication ability. The less computation the client needs, the better for the client. Besides, for the system’s scalability, our scheme also needs to support off-line clients.
1.2. Our Contributions
To address the mentioned issues, we designed a decision tree evaluation scheme that can protect the model and data security in this work. The main contributions are listed in the following:
- We newly design a secure comparison protocol that can return additive shares of the comparison result on additively secret shared inputs. Compared with the Huang et al.’s work [21] and Zheng et al.’s work [20], the number of additive multiplications required can be reduced from and to l respectively, where l is the bit-length of a feature vector’s element. Compared with Liu et al.’s work [22], which is based on additive secret sharing and additively homomorphic cryptosystem, the proposed work is more secure and efficient.
- With the additive secret sharing technology and an asymmetrically homomorphic cryptosystem, i.e., Paillier cryptosystem [23], the privacy-preserving decision tree scheme based on the two-cloud model is proposed in this work. The scheme is tested on several widely used real-world datasets. The experimental results show that compared with the most recent work, i.e., Zheng et al.’s work [20], our scheme is more efficient when dealing with deeper trees. Particularly, the communication cost of our scheme is just 1/709 of Zheng et al.’s work [20].
- We show that our scheme can fully protect the privacy of the client. At the same time, during the evaluation process, the client also learns nothing of the decision tree. Additionally, since there are two clouds involved, we can also prove the model is not leaked to the other cloud except the number of the decision node.
1.3. Organization
The organization of this work is presented as follows. The preliminary background on the decision tree, additive secret sharing technology, and Paillier encryption system are given in Section 2. In Section 3, we give a system model and design goals of our scheme. Our privacy-preserving method for decision tree evaluation service is presented in Section 4. Next, we analyze the security and performance of our scheme in Section 5 and Section 6 respectively. Then, the related works are introduced in Section 7. Finally, we conclude our work and present our future works in Section 8.
2. Preliminaries
Some basic concepts of the decision tree and cryptographic knowledge are introduced in this section. We also present the key notations used in Table 1.

Table 1.
Notation Used.
2.1. Decision Tree
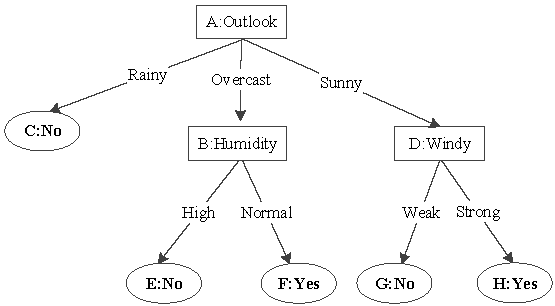
The decision tree is a well-known data mining algorithm, which has many well-known applications. We present an example of a decision tree in Figure 1. In such a tree T, we assume that the number of the internal nodes is m. These internal nodes are also called as decision nodes. Besides, the nodes with classification labels are called leaf nodes. The longest path’s length of T is called the depth of tree T. Note that a decision tree is usually not binary. However, we can easily transform a tree into a binary one [16]. For each internal node of T, it has a threshold , where . Moreover, the vector feature is represent as . There is a boolean function which is associated with a tree node, i.e., . The function’s value decides the path of classification of this tree. For example, we can let “1” denote the left child of this node and “0” denote the right child [15]. When it comes to the leaf node, the corresponding label of this node is the prediction result of .
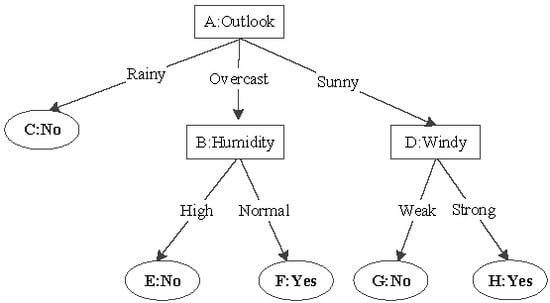
Figure 1.
A Decision Tree Model.
2.2. Additive Secret Sharing
Shamir proposed the additive secret sharing technology [24] which is a typical secure multi-party computation scheme [25]. In this scheme, we split an integer into two additive shares, which can be represented as . Besides, we use , to represent party A’s and B’s shares of x. The Rec is adopted to represent the reconstruction function, i.e., (mod P). Since all the calculations are made with the ring , “mod” P will be omitted for simpilicty.
2.2.1. Addition of Additive Shares
To calculate the addition of two additive shares and , party A and B just need to make some local computations, i.e, , . Note that no interaction is required between the two parties.
2.2.2. Multiplication of Additive Shares
To calculate the multiplication of two additive shares, the Beaver triples [26] are needed. First, the two parties should share pre-computed triples which can be denoted as . The Beaver triples can be generated by the two parties by Oblivious Transfer [27] or distributed from a trusted third party [21]. Suppose that the to be multiplied integers are x and y. After running this secure multiplication protocol, the two parties obtain . More details about the multiplication of additive shares can be found in references [21,22].
2.3. Paillier Cryptosystem
Paillier cryptosystem is an asymmetric cryptosystem which is also additively homomorphic [23]. The plaintext space of Paillier cryptosystem is while the ciphertext domain is . In this work, is used to represent the ciphertext of x encrypted by the Paillier cryptosystem. As we have stated before, the Paillier cryptosystem is additively homomorphic, with the following properties:
- Homomorphic Addition: If we have two ciphertext, e.g., , , encrypted by the same public key, we can easily compute .
- Scalar Multiplication: If given the ciphertext and a constant integer c, we could easily compute . Particularly, if c is , we can easily obtain that , where .
More details of the security proof of Paillier cryptosystem are shown in reference [23].
3. System Model and Design Goals
The system model and design goals are introduced as followed.
3.1. System Model
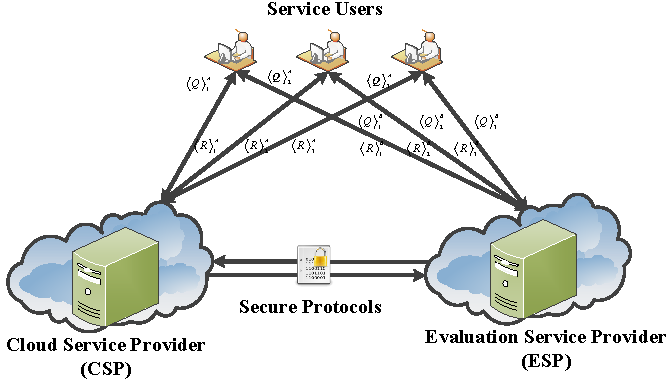
In this work, our scheme is designed on a widely-used two-cloud model, including a Cloud Service Provider (CSP) and an Evaluation Service Provider (ESP). Details of the system model are given in Figure 2 [28].
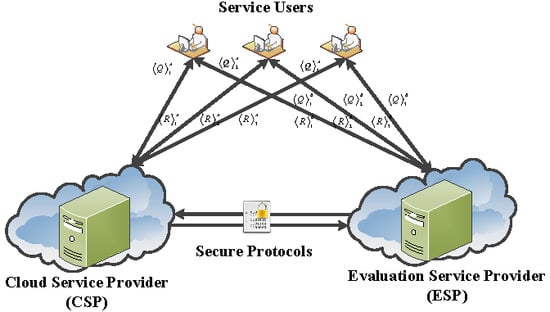
Figure 2.
System model [28].
- Service Users: The Service User (SU) in our system wants to use a decision tree evaluation service in a privacy-preserving way. The SU splits the query vector into two additive shares before sending them to two clouds respectively.
- Cloud Service Provider: Assume that a trained decision tree model belongs to Cloud Service Provider. The CSP provides a decision tree classification service to SU. Since only one of the shares is sent to it, CSP needs to cooperate with the Evaluation Service Provider to fulfill the evaluation.
- Evaluation Service Provider: In our system, the ESP’s mission is to cooperate with the CSP to give the SU the evaluation result of the decision tree model in a privacy-preserving way. Besides, ESP generates the public/private key pair of the Paillier cryptosystem and reveals the public key to CSP.
In this system, the decision tree model just belongs to CSP. This is a practical assumption in reality. For instance, the CSP could be a famous cloud service provider, such as Google, who is able to collect data from massive data owners and then train a decision tree model for remote diagnosis. Since it wants to provide an efficient and highly secure decision tree prediction service, an ESP is also essential in this scheme. Namely, there exist two main reasons. First, since CSP just owns parts of query data, it cannot make the decision tree evaluation all by himself. In addition, in the two-cloud model, the SUs usually can stay offline during the evaluation process while the single server model usually cannot [5,6,28,29,30,31].
3.2. Threat Model
Here, we assume all parties in our scheme are semi-honest, which is also known as honest-but-curious, which means that they strictly follow the rules of designed protocols, and at the same time they may attempt to get other additional information. Besides, we also stress that two clouds cannot collude with each other. This is a basic assumption in secure multiparty computation. In addition, there is an active adversary in such a scheme. Such an adversary attempts to infer the query data of the SU, details of the decision tree model owned by CSP and the classification results as well. We assume has the following capabilities:
- may eavesdrop the communication channel between CSP and ESP.
- may compromise ESP.
The adversary is restricted from comprising (1) CSP and ESP simultaneously, and (2) the communication channels between SU and the cloud.
3.3. Design Goals
Our scheme’s design goals are listed as follows:
- Data Protection. For this decision tree evaluation scheme, data security and privacy issues are the most important ones to be solved. As we know, the outsourced data and the calculated classification result contain sensitive information that should be kept secret to the cloud, including CSP and ESP. Besides, for the CSP, the decision tree model is its assert, which also should not be leaked to ESP and the SUs. Moreover, all such information should be confidential to the active adversary .
- Classification Result’s Accuracy. The classification result should be the same as the non-privacy- preserving one.
- Efficiency. In this scheme, we insist that the two clouds should finish the evaluation process as fast as they can and return the classification labels to SUs quickly. Thus, the computation and communication costs of the clouds should be small enough.
- Offline SUs. As we know, SUs in the IoT usually do not have strong computation power and large storage space. Therefore, we should minimize the computation and communication burdens for the SUs. Thus, once sending the query to CSP and ESP, SUs should stay offline until obtaining results. We also should note that many clients are using this decision tree evaluation service. Thus, for the scalability of the system, this scheme is supposed to support offline SUs.
4. Privacy-Preserving Decision Tree Evaluation
Before introducing this privacy-preserving decision tree evaluation scheme, we first present our secure comparison, which serves as the basis of this scheme. In this work, the party A is CSP while the party B is ESP.
4.1. Secure Comparison Algorithm
As we have stated, the comparison is one of the most important parts of our decision tree evalutation scheme. Assume that CSP has a private input x, while CSP also additively shares a set of with ESP, where , and is the bit-composition of y. Let’s assume that bit lenghts of x and y are both l. After running this Secure Comparison (SC) algorithm, CSP and ESP get the additvely shared comparison result .
First, CSP makes a bit-decomposition of x as . Then, CSP and ESP can locally calculate , where mod 2, and mod 2. Then compute , . After that, CSP randomly picks an from , and sets . CSP and ESP can locally calculate for each . Moreover, , . CSP randomly chooses an from , and runs a Mul with ESP on to get . ESP randomly picks an from , and calculates . ESP sends to CSP. CSP runs a Rec to reconstruct . Then, ESP runs a permutaiton on all the and sends them to CSP. Receiving them, CSP removes the blinded . If there is at least one 0 of , set . Otherwise, set . Note that the comparison result r is equal to . Therefore, CSP and ESP run the Mul on and to obtain . The specific details of our SC are shown in Algorithm 1.
| Algorithm 1 Secure Comparison (SC) |
|
Correctness. We stress that our SC is a kind of variant of DGK comparison [32], but is not a naive secret shared version of the DGK comparison. In DGK, the sender calculates the ciphertext of , and then blinds it with a random integer . The receiver decrypts the received data. If one of them is 0, set . In this algorithm, no encryption is needed. More importantly, in this SC, we use to simulate . The naive way to calculate is to calculate . If so, for each , the two servers need to run a multiplication protocol. If using such a naive method, the two clouds need to run l times , which can cause many computation and communication costs. To avoid these communication and computation costs, in this SC, we let the two clouds calculate instead. Here, if and only if . Otherwise, or . We also should note that only when matters the value of . Even though not every , is equal to whenever . Since, , when , CSP and ESP cooperate with each other to run the Mul to obtain shares of the result. More correctness proof of our SC can be easily verifed according to DGK comparison [32].
Discussion. There already exist several protocols about privacy-preserving comparison of two additive shared integers [20,21,22,32]. First, we should note that the setting of these comparisons is different from ours. In their setting, the two integers x and y are additively shared by the two-party. In ours, one of the integers belongs to one party, and the other is shared by the two parties. Moreover, for the Huang et al.’s work [21], there are Mul needed, while ours just need Mul. Zheng et al.’s Secure decision node evaluation, is designed to get the additively shared comparison result. The basic idea is similar to Huang et al.’s SC [21], but is less efficient, which needs almost Mul. Note that, Mul is the most time-consuming part of ours and Huang et al.’s [21], meaning that ours SC is more efficient. Liu et al.’s work [22] is based on a variant Paillier cryptosystem [33] and additive secret share technology. Since encryption and decryption are much time-consuming than fixed numbers multiplication and addition. Obviously, this SC is more efficient than [22] for integers with short bits. In addition, in reference [22], the is sent to ESP. Note that since are not randomly chosen from , they cannot perfectly disguise . Thus, the secure comparison algorithm in [22] is not perfectly secure which just achieves statistical security [34].
4.2. Privacy-Preserving Decision Tree Evaluation
There are two stages in our privacy-preserving decision tree evaluation scheme, i.e., query vector issuing and secure decision tree evaluation. During the execution, the SU can be offline and cannot infer anything about the decision tree. Simultaneously, the clouds cannot get anything about the query vector and the final classification results. We also note that the decision tree just belongs to CSP. In this section, we propose two privacy-preserving decision tree evaluation schemes. One of them leaks the number of the nodes of the tree to the ESP, which achieves the same security level as previous works [15,16,17]. The other one can provide a higher security level, which can protect the number of tree nodes with statistical security.
4.2.1. Query Request Issuing
One of the cloud should send the modular P to SU, which is used to split and reconstruct integers. Note that, . Receiving P from CSP, SUs split their query data vectors into additive shares. For a query vector , the SU first makes a bit decomposition on every , and then splits every into two additive shares. Specifically, the SU picks random integers from where . After that, the SU sets , and . Then, the SU respectively sends to the CSP and to the ESP. In this scheme, the cannot eavesdrop communication channels between the cloud and SUs.
4.2.2. Secure Decision Tree Evaluation
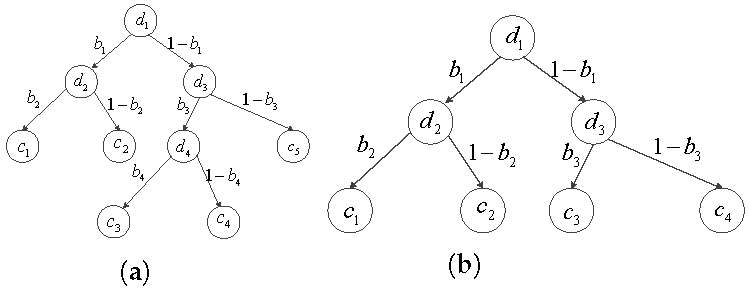
Once receiving the query from the SU, the clouds run a Secure Decision Tree Evaluation (SDTE) protocol and return shares of the classification result to SU. Our SDTE follows the similar idea from Tai et al., who propose to express a decision tree into a set of linear equations of path cost [17]. For every leaf node in the tree, we calculate the sum of the boolean results along the path from the root to the leaf as the path cost . We present an example of the path costs of the tree in Figure 3a, i.e., , , , and . Note that is the comparison result between the decision node and the corresponding attribute data in the query, which is 0 or 1. Therefore, for one specific query, there is only one is 0.
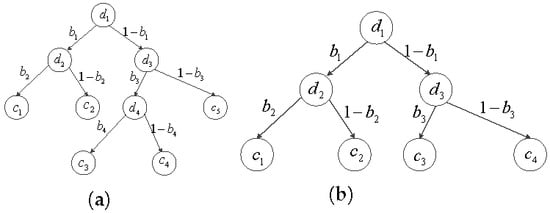
Figure 3.
Binary Decision Tree. (a) Binary Tree. (b) Complete Binary Tree.
SDTEI. Before running this SDTEI, ESP generates the public/private key pair of Paillier and then reveals the public key to CSP. First, we introduce a SDTEI algorithm, which can protect the query data and classification result well but leak the number of nodes to ESP. In the following, n denotes the length of the query vector, m denotes the number of the decision nodes in the tree, represents the number of the leaf nodes in the tree. For each tree node, CSP and ESP compare it with its corresponding query vector element. Specifically, they run the SC to get additive shares of the comparison result. Then, ESP encrypts the shares he holds and sends the encrypted shares to CSP. Receiving the encrypted shares, CSP calculates every path’s edge cost and blinds it with a random number. Note that there are only one of the path’s value is zero. Then, CSP runs a permutation function on them and sends them to ESP. ESP decrypts the data received. ESP generates a vector . If the decrypted result is 0, ESP sets its corresponding . Otherwise, set it as . Then, ESP encrypts the and sends it to CSP. CSP runs the reverse permutation function on these . Next, CSP calculates . After that, CSP sends to the SU and to ESP. ESP decrypts as and then sends it to SU. Receiving and , SU can run Rec to get the classification result.
Step 1 (CSP & ESP): For each node of tree T, a SC is run by CSP and ESP on the threshold with its corresponding feature in the query vector to get the comparison result . We can see that from SC, the comparison results are kept confidential to both CSP and ESP.
Step 2 (ESP): For each , ESP encrypts it as through Pailler cryptosystem, and then sends it to CSP.
Step 3 (CSP): For each , CSP encrypts as through Pailler cryptosystem. Then, CSP calculates . Since the path cost of each node just contains the addition of the comparison result, the CSP can easily get all the . After that, CSP randomly chooses from , where , and calculates the path cost . Next, CSP runs a permutation function on these before sending them to ESP.
Step 4 (ESP): Receiving all the , ESP decrypts them all. If the decrypted result is 0, ESP sets . Otherwise, ESP sets . Then, ESP encrypts all the and sends them to CSP.
Step 5 (CSP): CSP runs a on these . Next, CSP calculates . CSP randomly picks a from , and calculates . After that, CSP sends to the SU and to ESP.
Step 6 (ESP): ESP decrypts as and then sends it to SU.
Step 7 (SU): Receiving both and , SU calculates mod P as the classification result.
Remark 1. For a fully binary tree, there is only a path cost is 0 [17]. Therefore, in the Step 4, when one of the decrypted result is 0, ESP can stop the decryption and set the other . In Step 5, . Since there is only one is 1 and the others is 0, c is the corresponding classification label.
Remark 2. For a fully binary tree, we observe that the relationship between the number of the leaf nodes, i.e, and the number of the decision node is . Since in Step 1, the ESP already infers m through counting the number of the SC, the number of dose not leak more information in Step 4.
Remark 3. In Zheng [20] et al.’s work, the two clouds blind the path cost along with the classification labels together and send them to the SU. Therefore, in their scheme, the SU needs to calculate more blinded path costs to recover the classification result. Moreover, the depth of the tree can be inferred by the SU through counting the number of the leaf nodes (Note that, in their scheme, the tree is transformed to a fully complete binary tree, where .). However, in our scheme, the SU just runs Rec once, and the SU learns nothing about the tree model.
SDTEII. We note the in our SDTEI algorithm, the ESP can infer the number of the nodes, i.e., m, in the tree through counting the number of the SC runs. To avoid such an information leakage, CSP can also add a proportional dummy node in the tree to disguise the information of m. Receiving all the from ESP, CSP can delete the dummy node’s comparison result easily. Moreover, in Step 3, the CSP also needs to add the dummy path cost to disguise the number of leaf nodes. And in Step 5, CSP deletes the dummy path costs. Since the number of the dummy nodes is hard to decide for each evaluation, our SDTEII achieves a statistically secure for the protection of m.
5. Security Analysis
Security analysis of the proposed cryptographic building blocks is made first and then we analyze the security of our scheme.
5.1. Security of Cryptographic Blocks
In this section, we give the details of the security analysis of the proposed SC. Before that, we first introduce security definition under the semi-honest model [35].
Definition 1
(Security in the Semi-Honest Model [35]). A protocol can be represented as π. We use (resp. ) to represent the input (resp. ouput) of the protocol of party . Moreover, let and represent ’s execution image and simulated image of the protocol π repsectively. Therefore, a protocol π is secure if the distribution of the simulated image and its execution image are computationally indistinguishable (More details are shown in [35]).
From the description of Definition 1, we can conclude that a cryptographic protocol is secure, if and only if its simulated execution image and its corresponding execution image are computationally indistinguishable. Note that, the data exchanged and the information calculated when the protocol is run are also included in the execution image of this cryptographic protocol. The following lemmas may also be adopted to prove the proposed protocols’ security. We refer the reader to find more proof details of Lemmas 1 and 2 in reference [21].
To prove the security of our protocols, the following lemmas may also be adopted.
Lemma 1
([21]). If a protocol’s sub-protocols are all perfectly simulatable, this protocol is perfectly simulatable.
Lemma 2.
If a variable is added by a uniformly random integer from , we can conclude that is not only independent from x but also uniformly random.
Theorem 1.
Proof.
Since the security of the Mul has been proved in [26], in the following we just prove that the security of the steps shown from line 1 to line 7.
Here, we use to denote the execution image of CSP, i.e, , where . Moreover, the is a random number picked from . We assume that where all the elements are picked randomly from except , where is a random number picked from and is randomly picked from . Note that, are intermediate integers computed by Add or Mul, which are computationally indistinguishable from . Besides, both and are uniformly picked from . Therefore, and are computationally indistinguishable. According to the above analysis, we could conclude that is indistinguishable from .
In a similar way, we can prove that is computationally indistinguishable from .
Since we have proved the security of the steps shown from line 1 to line 7 in SC, and the Mul is secure as well. Thus, we can draw a conclusion that the proposed SC is secure under the semi-honest model according to Lemma 1. □
5.2. Security of Privacy-Preserving Decision Tree Evaluation Scheme
Theorem 2.
The designed privacy-preserving decision tree evaluation scheme is secure, and also can protect the query data and classification result secure from an outside active adversary.
Proof.
Followed the similar idea shown in Section 5.1, we can easily prove the security of our SDTE algorithm under the semi-honest model. Note that, the calculations SU made in query request issuing stage and Step 7 in SDTE are locally, thus this part is obliviously secure.
In Step 1, the CSP and ESP cooperate to run the SC to get the additive shares of comparison results between the threshold with the feature elements. As we know, the security of SC has been proven in Theorem 1. In Step 2, the ESP just encrypts several integers with Paillier cryptosystem and sends the ciphertext to CSP. Since the Paillier cryptosystem is semantically secure, the ciphertext is indistinguishable from random numbers in . Therefore, the simulated image is indistinguishable from its actual execution image. Similarly, we can prove the security of Step 3, 4, 5, 6. Therefore, according to Lemma 1, we could draw a conclusion the proposed SDTE algorithm is secure under the assumption of the semi-honest model.
Next, we can show that our scheme is secure under the threat model in Section 3.2. For an active adversary , the data obtained from eavesdropping the communication channel between CSP and ESP are all partial shares. These data are either random numbers or the addition results of random numbers. According to Lemma 2, they are both uniformly random to . Thus, we can conclude that our scheme is secure under the threat model in Section 3.2. □
6. Performance Analysis and Comparison
In this section, we first test the SC and then the whole scheme on five real-world UCI machine learning datasets. After that, we compare our work with the most related works in this area.
6.1. Experiment Analysis
We test our scheme on two personal computers which run Ubuntu 16.04 with Intel Core i5-8300H CPU 2.30 GHz six-core processor and 8 GB RAM memory. These two machines act as the CSP and ESP respectively. The system is written by C code by GNU MP library [36].
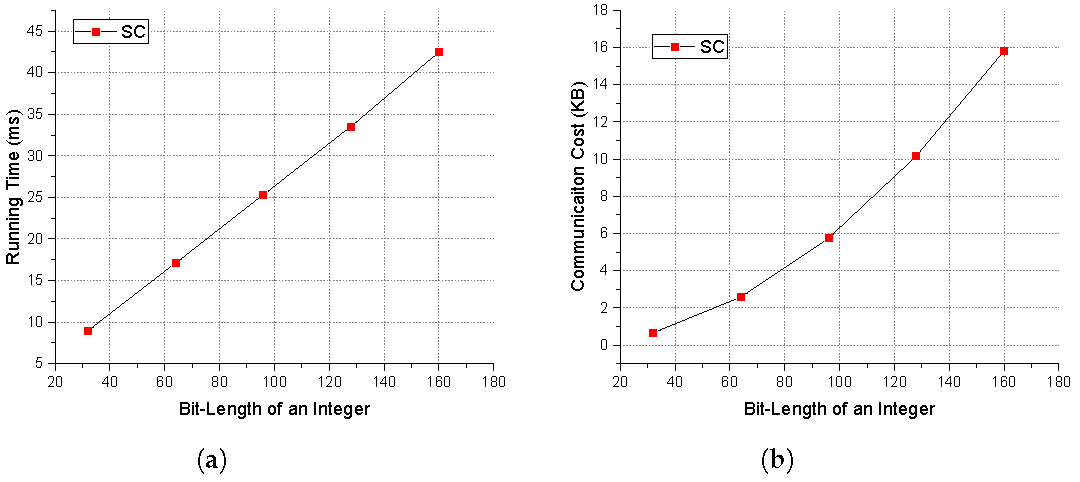
Firstly, we test our SC with varied bit length. From Figure 4, we can see that both the communication and computation costs grow with the increase of the bit length. Moreover, we also conduct several experiments about our scheme on five widely-used datasets from UCI repository (UC Irvine Machine Learning Repository [37]), i.e., breast-cancer, heat-disease, housing, credit-screening, and spambase. The application domain of these datasets contains credit rating and breast cancer diagnosis. To start with, we use standard Matlab tools (classregtree and TreeBagger) on these dataset to train a model. The performance of the SUs in our scheme is the same as the clients in Zheng et al.’s [20], since they all just spit the data into additive shares. Therefore, we mainly test the performance of two clouds in our designed scheme. The details of our experimental results are shown in Table 2. Here, n is the dimension of a query vector, d is the depth of a tree and m is the number of nodes in a tree. In our experiment, we set the bit length of an integer is 64. Note that the same experimental datasets are used compared with the works in reference [16,20,22]. We show the specific results in Table 2.
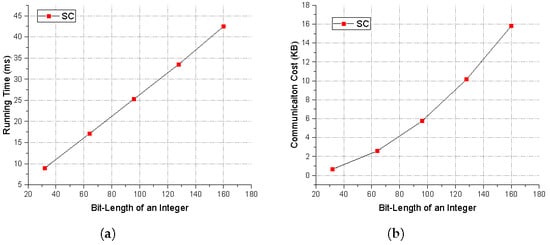
Figure 4.
SC Performance Test. (a) Running Time. (b) Communication Cost.

Table 2.
Performance on Real-World Dataset (1000-Times for Average).
6.2. Performance Comparison and Analysis
From experimental results presented in Table 2, we could clearly see both communication and computational overheads of ours are much smaller than Wu et al.’s work [16]. Compared with the most recent work, i.e., Zheng et al.’s work [20], our scheme’s computation and communication costs of small datasets are larger. However, when scaled up the large dataset, i.e., spambase, both the computation and communication costs of ours are less than theirs. Specifically, the computational cost of ours is nearly 1/11 of theirs, and the communication cost is almost 1/709 of theirs. The reason behind it is that the communication and computation costs of their work are exponential with the depth of the tree, while ours grows linearly with the number of the nodes in the tree. When dealing with the sparse but deep tree, too many dummy nodes are added in Zheng et al.’s scheme.
From the above experimental analysis, we can conclude there are mainly two factors that influence the performance of our scheme, i.e, the number of nodes m in a tree and the bit length of an integer l. In the real world setting, most of the time l can be smaller than 64. Moreover, since m comparison can be paralleled, the performance of our designed scheme can be further greatly improved.
6.3. Comparative Analysis
A detailed comparison between our designed scheme with most related works about privacy-preserving decision tree evaluation is made in this section. Based on fully homomorphic cryptosystem (FHE), Bost et al. [15] recently presented one privacy-preserving decision tree evaluation scheme. Such a scheme is not efficient because of the heavy computation cost of FHE. Wu et al. [16] improved Bost et al.’s work, by using additive homomorphic cryptosystem (AHE) and Oblivious Transfer (OT). Tai et al. further improved Wu et al.’s work, where an exponential number of encryptions of the depth of the tree is not avoided. Joye et al. [38], Tueno et al. [18] followed the similar idea to improve the efficiency. With the help of secret sharing technology (SS), Cock et al. [39] designed one privacy-preserving decision tree scheme. This work is efficient, but a trusted third party is needed. However, all the work proposed cannot protect the tree model well. Either the m or d is leaked to the client. Moreover, these methods cannot support offline users. Most recently, Liang et al. [19] and Liu et al. [22] use searchable symmetric encryption (SSE) and SS, AHE respectively to design new privacy-preserving decision tree evaluation schemes. Unfortunately, the running time grows exponentially with m in [19]. As in the scheme in [39], a trusted third party is also needed in [22]. Zheng et al. designed a decision tree evaluation scheme on the two-cloud model, based on additive secret sharing technology, which is quite similar to ours. In their scheme, the depth of the tree model is not protected. Both their computation and communication costs grow exponentially with d.
We propose two kinds of secure decision tree evaluation schemes. One of the methods leaks the number of decision nodes, and the other one can protect it with statistical security. For these works supporting offline users, i.e., [19,20], the computation cost of the servers or clouds is exponential with either with d or m, meaning that the performance of these works decreases quickly when dealing with deep trees or large trees. Moreover, we have shown that the building blocks in [22] is not secure enough compared with our work. The computation and communication costs of our SDTEI and SDTEII just grow linearly with the number of decision nodes m. We also note that our SDTEI also leaks the number of nodes of the tree. However, in our scheme, this information is just leaked to ESP, not to the SU. This is different from the scheme in [20], where d is leaked to the cloud and the SU simultaneously. We make a more detailed comparison which is shown in Table 3.

Table 3.
Comparison Summary.
7. Related Work
This work is related to the Secure Multiparty Computation (SMC) [25] and privacy-preserving data mining [14]. With SMC, several parties can cooperate with each other to compute a function without revealing their private inputs. We also note that in SMC, no trusted third party is needed for secure computation. This kind of technology has been widely used in many secure outsourced computation areas [31,40,41]. Recently, SMC and homomorphic cryptosystem [23] have been adopted to build privacy-preserving data mining classifiers [15,20,42]. This work mainly focus on the privacy-preserving data mining issues, particularly decision trees, for the IoT.
The data security and privacy issues about decision trees were first proposed by [13,14]. These earlier researches just focus on privacy-preserving decision tree training. Brickell et al. first consider the privacy-preserving decision tree evaluation issues [43]. They proposed a remote diagnosis system, which adopts both the Garble Circuit (GC) and Homomorphic Encryption (HE).
Recently, Bost et al. [15] creatively proposed to represent a decision tree as a polynomial, and its calculation result is the classification label. Based on such an idea, they designed a privacy-preserving decision tree evaluation scheme through fully homomorphic encryption (FHE). Unfortunately, since the FHE is not that efficient, their scheme cannot be scaled up to a large dataset. Wu et al. [16] proposed another privacy-preserving decision tree evaluation scheme that adopts the more efficient additive homomorphic encryption (AHE) technology. In their scheme, at the end of the execution, clients are required to run an Oblivious Transfer (OT) to obtain prediction results. Tai et al. [17] further improved the efficiency of Wu et al.’s work. In Tai et al.’s designed scheme, linear functions are used to represent the costs of the decision tree, which voids the computation of a high-degree polynomial. Based on the additive secret sharing (SS) technology, Cock et al. [39] designed one efficient privacy-preserving decision tree evaluation scheme in a commodity-based model. When worked on relatively small trees, it is efficient but cannot deal with large trees efficiently. Joye et al. [38] designed a scheme also based on [16]’s basic idea. In their scheme, a new secure comparison protocol is proposed. They also improved the total number of comparisons needed in the evaluation process. Most recently, through denoting decision trees as arrays, Tueno et al. [18] designed one decision tree evaluation system, achieving the sub-linear complexity of trees’ sizes. Nevertheless, the works mentioned above cannot fully protect the tree model’s information. For instance, either the depth or the number of nodes or even both of them is revealed. In addition, offline clients are not supported in any of the above works. Frequent computation and communication with the server are needed for clients in these schemes, which is not useful for the resource-constrained users in IoT.
Most recently, Liang et al. [19] and Liu et al. [22] respectively proposed new privacy-preserving decision tree evaluation schemes, which can fully protect the user’s and cloud’s privacy. However, the computation cost of scheme in [19] grows exponentially with m. Liu et al.’s SC cannot achieve perfect security to ESP. Moreover, in their scheme, a third party is needed for the distribution of the keys. Zheng et al. [20] proposed a similar decision tree evaluation scheme on the two-cloud model, based on additive secret sharing technology. Their setting is a little different from ours. In their setting, the decision tree model is outsourced by some providers. Even though their scheme can provide offline users, the tree model is not well protected, i.e., the depth of the tree is leaked to the cloud and the client. Moreover, when scaled up to large trees, their computation and communication costs are larger than ours. In this work, we propose two kinds of secure decision tree evaluation schemes. One of them leaks the number of decision nodes to ESP while the other one can protect this information with statistical security. Moreover, in our proposed scheme, service users can be offline during the evaluation which can greatly reduce computation and communication overheads of them, which is important for the IoT users.
8. Conclusions and Future Work
In this paper, we designed an efficient but highly secure decision tree evaluation scheme for the cloud, which is based on additive secret sharing technology and Paillier cryptosystem. Our scheme is built on a widely-used two-cloud model but without a trust third party. During the evaluation process, service users can be offline. After the evaluation, clouds infer nothing of the client query and the prediction results, and at the same time service, users cannot infer anything about the tree. According to the experimental results on building blocks and the real-world dataset, we can conclude that our scheme is quite efficient.
In this work, we mainly focus on the privacy issues in the decision tree evaluation. In our future work, we will try to further improve the efficiency of decision tree evaluation on a large dataset. In addition, the decision tree training is a more challenging job. We will try to design a privacy-preserving decision tree training scheme on the cloud without help from the client. Moreover, in the future, we will also try to extend the building blocks designed to include more privacy-preserving data mining algorithms, such as the random forest.
Author Contributions
Conceptualization, L.L. and J.S.; methodology, L.L., J.S.; software, J.C.; validation, B.Z. and Q.W.; formal analysis, Q.W. and Y.L.; writing—original draft preparation, L.L.; writing—review and editing, Q.W. and Y.L., funding acquisition, B.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by National Key Research and Development Program of China (No. 2018YFB0204301), the National Natural Science Foundation of China (No. 61702541, No. 61702105, No.61806216, No. 61972412, No. 61872087, No. 61822202, No. 61872089), the Young Elite Scientists Sponsorship Program by CAST (2017QNRC001), the Science and Technology Research Plan Program by NUDT (Grant No. ZK17-03-46, No. ZK19-38).
Conflicts of Interest
The authors declare no conflict of interest regarding the publication of this manuscript.
References
- Mahdavinejad, M.S.; Rezvan, M.; Barekatain, M.; Adibi, P.; Barnaghi, P.; Sheth, A.P. Machine learning for Internet of Things data analysis: A survey. Digit. Commun. Netw. 2018, 4, 161–175. [Google Scholar] [CrossRef]
- Amazon Machine Learning Service. Available online: https://aws.amazon.com/cn/machine-learning/ (accessed on 16 December 2019).
- Google Cloud, A.I. Available online: https://cloud.google.com/products/ai/ (accessed on 16 December 2019).
- Microsoft AI Service. Available online: https://www.microsoft.com/en-us/ai/ai-platform (accessed on 16 December 2019).
- Li, J.; Chen, R.; Su, J.; Huang, X.; Wang, X. ME-TLS: Middlebox-Enhanced TLS for Internet-of-things Devices. IEEE Internet Things J. 2019. [Google Scholar] [CrossRef]
- Zhao, B.; Liu, P.; Wang, X.; You, I. Toward efficient authentication for space-air-ground integrated Internet of things. Int. J. Distrib. Sens. Netw. 2019, 15. [Google Scholar] [CrossRef]
- Yang, Z.; Chen, R.; Li, C.; Qu, L.; Yang, G. On the Security of LWE Cryptosystem against Subversion Attacks. Comput. J. 2019. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, R.; Liu, C.; Wang, B.; Wang, Y. Available online: https://doi.org/10.1007/s00779-018-01193-x (accessed on 02 January 2019).
- Rago, A.; Marcos, C.; Diazpace, J.A. Using semantic roles to improve text classification in the requirements domain. Lang. Resour. Eval. 2018, 52, 801–837. [Google Scholar] [CrossRef]
- Singh, A.; Guttag, J.V. A comparison of non-symmetric entropy-based classification trees and support vector machine for cardiovascular risk stratification. In Proceedings of the 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–3 September 2011; pp. 79–82. [Google Scholar]
- Azar, A.T.; Elmetwally, S.M. Decision tree classifiers for automated medical diagnosis. Neural Comput. Appl. 2013, 23, 2387–2403. [Google Scholar] [CrossRef]
- Koh, H.C.; Tan, W.C.; Goh, C.P. Available online: https://ijbi.org/ijbi/article/view/5 (accessed on 12 November 2019).
- Lindell, Y.; Pinkas, B. Privacy preserving data mining. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 20–24 August 2000; pp. 36–54. [Google Scholar]
- Agrawal, R.; Srikant, R. Privacy-preserving data mining. In ACM Sigmod Record; ACM: New York, NY, USA, 2000; Volume 29, pp. 439–450. [Google Scholar]
- Bost, R.; Popa, R.A.; Tu, S.; Goldwasser, S. Machine learning classification over encrypted data. In Proceedings of the NDSS, San Diego, CA, USA, 8–11 February 2015; Volume 4324, p. 4325. [Google Scholar]
- Wu, D.J.; Feng, T.; Naehrig, M.; Lauter, K. Privately evaluating decision trees and random forests. Proc. Priv. Enhancing Technol. 2016, 2016, 335–355. [Google Scholar] [CrossRef]
- Tai, R.K.; Ma, J.P.; Zhao, Y.; Chow, S.S. Privacy-Preserving Decision Trees Evaluation via Linear Functions. In Proceedings of the European Symposium on Research in Computer Security, Oslo, Norway, 11–15 September 2017; pp. 494–512. [Google Scholar]
- Tueno, A.; Kerschbaum, F.; Katzenbeisser, S. Private evaluation of decision trees using sublinear cost. Proc. Priv. Enhancing Technol. 2019, 2019, 266–286. [Google Scholar] [CrossRef]
- Liang, J.; Qin, Z.; Xiao, S.; Ou, L.; Lin, X. Efficient and Secure Decision Tree Classification for Cloud-Assisted Online Diagnosis Services. IEEE Trans. Dependable Secur. Comput. 2019. [Google Scholar] [CrossRef]
- Zheng, Y.; Duan, H.; Wang, C. Towards Secure and Efficient Outsourcing of Machine Learning Classification. In Proceedings of the European Symposium on Research in Computer Security, Luxembourg, 23–27 September 2019; pp. 22–40. [Google Scholar]
- Huang, K.; Liu, X.; Fu, S.; Guo, D.; Xu, M. A Lightweight Privacy-Preserving CNN Feature Extraction Framework for Mobile Sensing. IEEE Trans. Dependable Secur. Comput. 2019. [Google Scholar] [CrossRef]
- Liu, L.; Su, J.; Chen, R.; Chen, J.; Sun, G.; Li, J. Secure and Fast Decision Tree Evaluation on Outsourced Cloud Data. In Proceedings of the Second International Conference on Machine Learning for Cyber Security, Xi’an, China, 19–21 September 2019; pp. 1–17. [Google Scholar]
- Paillier, P. Public-key cryptosystems based on composite degree residuosity classes. In International Conference on the Theory and Applications of Cryptographic Techniques; Springer: Berlin/Heidelberg, Germany, 1999; Volume 99, pp. 223–238. [Google Scholar]
- Shamir, A. How to share a secret. Commun. ACM 1979, 22, 612–613. [Google Scholar] [CrossRef]
- Yao, A.C.C. How to generate and exchange secrets. In Proceedings of the 27th Annual Symposium on Foundations of Computer Science (sfcs 1986), Toronto, ON, Canada, 27–29 October 1986; pp. 162–167. [Google Scholar]
- Beaver, D. Efficient multiparty protocols using circuit randomization. In Proceedings of the Annual International Cryptology Conference, Santa Barbara, CA, USA, 11–15 August 1991; pp. 420–432. [Google Scholar]
- Ohrimenko, O.; Schuster, F.; Fournet, C.; Mehta, A.; Nowozin, S.; Vaswani, K.; Costa, M. Oblivious Multi-Party Machine Learning on Trusted Processors. In Proceedings of the USENIX Security Symposium, Austin, TX, USA, 10–12 August 2016; pp. 619–636. [Google Scholar]
- Liu, L.; Su, J.; Liu, X.; Chen, R.; Huang, K.; Deng, R.H.; Wang, X. Towards Highly Secure Yet Efficient KNN Classification Scheme on Outsourced Cloud Data. IEEE Internet Things J. 2019, 6, 9841–9852. [Google Scholar] [CrossRef]
- Liu, X.; Choo, R.; Deng, R.; Lu, R.; Weng, J. Efficient and privacy-preserving outsourced calculation of rational numbers. IEEE Trans. Dependable Secur. Comput. 2016, 15, 27–39. [Google Scholar] [CrossRef]
- Liu, L.; Su, J.; Chen, R.; Liu, X.; Wang, X.; Chen, S.; Leung, H. Privacy-preserving mining of association rule on outsourced cloud data from multiple parties. In Proceedings of the Australasian Conference on Information Security and Privacy, Wollongong, NSW, Australia, 11–13 July 2018; pp. 431–451. [Google Scholar]
- Luo, Y.; Jia, X.; Fu, S.; Xu, M. pRide: Privacy-Preserving Ride Matching Over Road Networks for Online Ride-Hailing Service. IEEE Trans. Inf. Forensics Secur. 2018, 14, 1791–1802. [Google Scholar] [CrossRef]
- Damgård, I.; Fitzi, M.; Kiltz, E.; Nielsen, J.B.; Toft, T. Unconditionally secure constant-rounds multi-party computation for equality, comparison, bits and exponentiation. In Proceedings of the Theory of Cryptography Conference, New York, NY, USA, 4–7 March 2006; pp. 285–304. [Google Scholar]
- Hazay, C.; Mikkelsen, G.L.; Rabin, T.; Toft, T.; Nicolosi, A.A. Efficient RSA Key Generation and Threshold Paillier in the Two-Party Setting. J. Cryptol. 2019, 32, 265–323. [Google Scholar] [CrossRef]
- Veugen, T. Improving the DGK comparison protocol. In Proceedings of the 2012 IEEE International Workshop on Information Forensics and Security (WIFS), Tenerife, Spain, 2–5 December 2012; pp. 49–54. [Google Scholar]
- Goldreich, O. Foundations of Cryptography: Volume 2, Basic Applications; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- GNU MP Library. Available online: https://gmplib.org/ (accessed on 16 December 2016).
- UC Irvine Machine Learning Respository. Available online: https://archive.ics.uci.edu/ml/index.php (accessed on 16 December 2019).
- Joye, M.; Salehi, F. Private yet efficient decision tree evaluation. In Proceedings of the IFIP Annual Conference on Data and Applications Security and Privacy, Bergamo, Italy, 16–18 July 2018; pp. 243–259. [Google Scholar]
- De Cock, M.; Dowsley, R.; Horst, C.; Katti, R.; Nascimento, A.; Poon, W.S.; Truex, S. Efficient and private scoring of decision trees, support vector machines and logistic regression models based on pre-computation. IEEE Trans. Dependable Secur. Comput. 2017, 16, 217–230. [Google Scholar] [CrossRef]
- Luo, Y.; Xu, M.; Huang, K.; Wang, D.; Fu, S. Efficient auditing for shared data in the cloud with secure user revocation and computations outsourcing. Comput. Secur. 2018, 73, 492–506. [Google Scholar] [CrossRef]
- Karapiperis, D.; Verykios, V.S. An LSH-based blocking approach with a homomorphic matching technique for privacy-preserving record linkage. IEEE Trans. Knowl. Data Eng. 2014, 27, 909–921. [Google Scholar] [CrossRef]
- Dritsas, E.; Kanavos, A.; Trigka, M.; Sioutas, S.; Tsakalidis, A. Storage Efficient Trajectory Clustering and k-NN for Robust Privacy Preservation Spatio-Temporal Databases. Algorithms 2019, 12, 266. [Google Scholar] [CrossRef]
- Brickell, J.; Porter, D.E.; Shmatikov, V.; Witchel, E. Privacy-preserving remote diagnostics. In Proceedings of the 14th ACM Conference on Computer and Communications Security, Alexandria, VA, USA, 28–31 October 2007; pp. 498–507. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).