Symmetries in Teleportation Assisted by N-Channels under Indefinite Causal Order and Post-Measurement

Abstract

Quantum teleportation has had notorious advances in the last decade, being successfully deployed in the experimental domain. In other terrains, the understanding of indefinite causal order has demonstrated a valuable enhancement in quantum communication to correct channel imperfections. In this work, we address the symmetries underlying imperfect teleportation when it is assisted by indefinite causal order to correct the use of noisy entangled resources. In the strategy being presented, indefinite causal order introduces a control state to address the causal ordering. Then, by using post-selection, it fulfills the teleportation enhancement to recover the teleported state by constructive interference. By analysing primarily sequential teleportation under definite causal order, we perform a comparison basis for notable outcomes derived from indefinite causal order. After, the analysis is conducted by increasing the number of teleportation processes, thus suggesting additional alternatives to exploit the most valuable outcomes in the process by adding weak measurement as a complementary strategy. Finally, we discuss the current affordability for an experimental implementation.

1. Introduction

Quantum communication has always looked for improvements and new outstanding approaches. Particularly, it has been shown that certain enhancements in information transmission can be reached through the superposition of quantum communication channels. That enhancement has shown that the interference of causal orders using sequential extreme imperfect depolarizing channels surprisingly produces a transparent quantum channel due to constructive superposition in the components of the state being transmitted [1]. Since that discovery, a growing interest in indefinite causal order has emerged boosting a deep study of this topic. Experimental implementations have been proposed in order to find, to understand, and to control their advantages [2].

1.1. Background of Indefinite Causal Order in Communication

In quantum communication with extremely noisy channels, only limited information can be transmitted. If we continue applying such quantum channels sequentially, no information becomes transmitted, obtaining the so-called depolarizing quantum channel. Despite, it has been shown that when such channels are applied in a superposition of causal orders, we can still transmit information, and notably, the quality of information transmitted becomes improved while more channels are applied under this scheme. Concretely for the case of two quantum channels, some works considering controllable strengths of depolarization have shown that combining a superposition of causal orders, it is still possible to transmit information (instead of worsening it as it obviously happens for the simpler sequential case) [1,3]. The success of the causal orders superposition has been experimentally verified for two channels transmitting information [4].

Following such a trend in communication, it has been found the possibility to extrapolate the increasing number of causal orders superposed (with more than two channels) by developing a combinatoric approach to the problem [5,6]. As a matter of fact, it has been shown that the amount of information transmitted, in comparison with the two-channel scenario, increases for the three-channels scenario [5]. Therefore, it has been concluded that the amount of classical information transmitted becomes higher if the number of causal orders increases.

Some notorious approaches regarding the indefiniteness of causal orders have been explored, exhibiting the capability to transmit information in a more efficient way. It highlights the importance to extend this approach on teleportation, as a genuine communication process [7,8].

1.2. Approaches to Teleportation under Causal Order Schemes

Information can be transmitted from one party to another as a quantum state if it is prepared in combination with an Einstein–Podolsky–Rosen state [9]. Such a quantum communication process is called quantum teleportation. It plays an important role related to quantum information and quantum communication. Teleportation algorithm for one single qubit is performed using one entangled Bell state and one channel for classical communication in order to achieve it [10]. Symmetries in the conformation of such quantum entangled state automatically transfer a state into another party if post-measurement is applied. The same algorithm has also been useful to teleport states of larger systems if they are composed of two-level systems [11]. The teleportation algorithm has been widely studied and new approaches have been discovered, as well as variants on the algorithm in order to make it either more efficient in terms of the quantum resources used [12] or more adaptive to some specific quantum systems [13,14,15]. Additionally, several successful tests have been experimentally performed in order to prove the feasibility of teleportation when the distance increases [16,17,18]. Tests with larger multidimensional states rather than qubits have been performed successfully [19]. Recently, a new approach has shown that the assistance of indefinite causal order in teleportation improves its performance when imperfect entangled resources become involved [7], which is equivalent to a quantum noisy communication channel.

Teleportation assisted by indefinite causal order and measurement has been introduced in [7] by pointing out that teleportation is a quantum channel itself (here, entanglement distribution is assumed to be performed through a transparent communication channel). The last proposal has been criticized in [20] arguing the entanglement distribution in teleportation is a critical aspect not being considered there (due to the large distances and communication issues involved). Instead, as in [7], the most recent work [20] interestingly has analysed the use of indefinite causal order in the form of a quantum switch for the entanglement distribution process as a part of the teleportation algorithm, thus making an analysis to quantify the performance gained by such a switch. Nevertheless, nowadays teleportation has been achieved through kilometers in the free space or through optical fiber, with still high fidelities [21] without considerable deformation in the entangled resource other than that the introduced in its imperfect generation. Thus, we believe both approaches are still valuable in the quest of understanding creative ways to implement indefinite causal order in teleportation. Both approaches show interesting features in the quantification of indefinite causal order issues applied to teleportation.

In [7], the quantum teleportation uses imperfect singlets showing that despite those noisy singlets make impossible a faithful teleportation, there is still a stochastic possibility of teleporting perfectly the state by applying indefinite causal order as the superposition of two teleportation channels. Such teleportation process has been conducted considering two identical teleportation channels with the same imperfect entangled resources, but in a superposition of causal orders through an evenly quantum control system. Finally, the outcome is measured on a specific basis in order to improve the fidelity of the teleportation process in the best possible way by recovering the symmetrical composition of the teleported state. Following this analysis and considering the same two imperfect channels but with an arbitrary initialized quantum control system, it has been also found the possibility to get again the highest possible transmission by post-selecting the appropriate outputs under alternative scenarios [22]: a proper selection of the post-measurement state on the control system, thus extending the interesting outcomes obtained in [7]. In addition, it has been shown that for the less noisy cases, the effect becomes still limited [7].

In teleportation, the traditional algorithm [9] is entirely represented as a quantum channel T in Figure 1a. In order to carry out the teleportation, it is necessary an entangled resource shown as $|\chi \rangle$. When this resource is the Bell state $|{\beta }_{00}\rangle =\frac{1}{\sqrt{2}}(|00\rangle +|11\rangle )$, a perfect teleportation is then achieved, but if such state is imperfect (it can be generally expressed as a mixture of all Bell states), teleportation process does not work properly. In Figure 1b, an alternative (but still equivalent) circuit is presented assuming that Bell states measurements could be performed. In such a case, no gates are required, due to teleportation is just reached due to the non-locality of the entangled resource $|{\beta }_{00}\rangle$ (or imperfectly, $|\chi \rangle$). This fact will be useful at the end of the article for a tentative experimental proposal.

Still, applying a sequence of two imperfect teleportation channels, the outcome worsens. In [7], it has been shown that for the worst deformed case of $|\chi \rangle$, the fidelity of single teleportation goes down. However, if two teleportation channels are used in an indefinite causal order with the superposition ruled by a quantum control system, surprisingly the previous worst-case arises with fidelity equal to 1. The analysis has been extended in [22] considering a wider kind of measurements required in the original approach. In this sense, the use of indefinite causal order improves the teleportation process. Thus, it is possible to correct this lack of fidelity working with the worst entangled state by applying indefinite causal order, together, with some appropriate selection in the control used and in the measurement performed, making possible to reach perfect teleportation.

In the current work, we deal with an extended version of the algorithm presented in [7,22] by using several sequential channels in order to benchmark the outcomes obtained by increasing the number of channels [5]. Section 2 develops the case of sequential channels in a definite causal order as a comparison basis. Section 3 develops the same situation but considering an indefinite causal order superposition using N channels. Section 4 uses the last formalism with more than two teleportation channels under indefinite causal order widening the spectrum of analysis. Section 5 revisits the problem but implementing additionally weak measurement proposing an improved procedure. Finally, Section 6 discusses the affordability of a possible experimental implementation for two teleportation channels under indefinite causal order using the current experimental developments. The last section gives the conclusions and future work to extend our findings.

2. Teleportation Algorithm as a Quantum Channel and $N$-Redundant Teleportation Problem

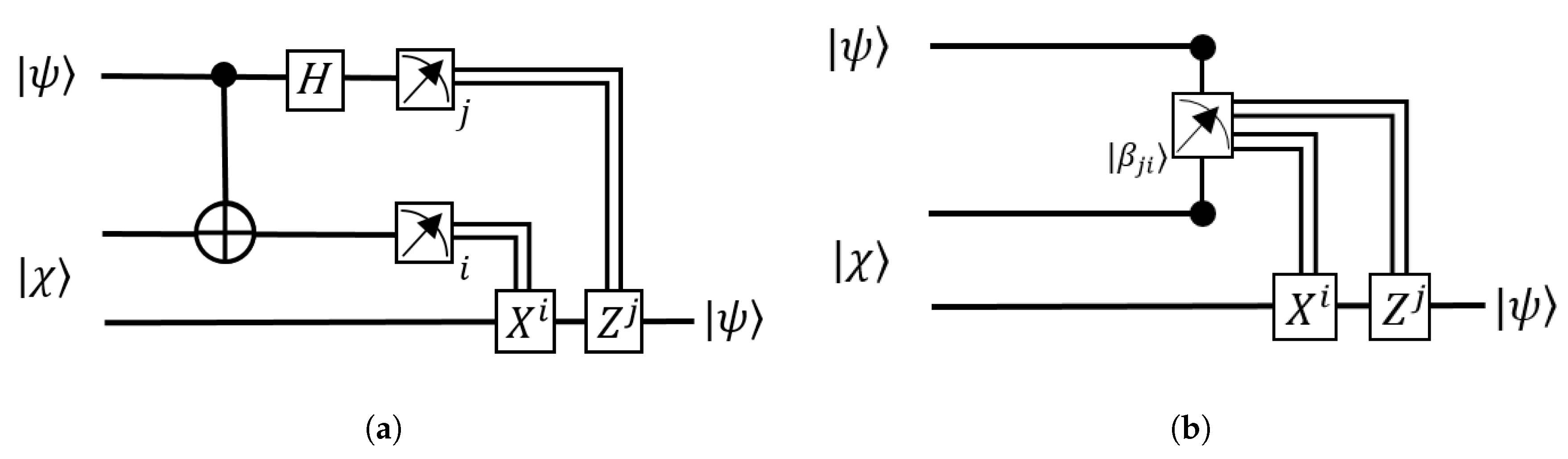
2.1. Quantum Teleportation as a Quantum Channel

Traditional quantum teleportation algorithm developed originally in [10] has become a central procedure in quantum information theory. This process uses an entangled resource in the form of the Bell state $|{\beta }_{00}\rangle =\frac{1}{\sqrt{2}}(|00\rangle +|11\rangle )$. Experimentally, such an entangled state becomes difficult to create and to sustain. For this reason, it could arrive imperfect to the process. Thus, considering a general variation of this resource in the form of the general state $\left|\chi \right.〉={\sum }_{i=0}^3\sqrt{p_i}\left|{\beta }_i\right.〉$, where $\left|{\beta }_i\right.〉$ is a short notation for the Bell basis $\left|{\beta }_0\right.〉= \left|{\beta }_{00}\right.〉$, $\left|{\beta }_1\right.〉= \left|{\beta }_{01}\right.〉$, $\left|{\beta }_2\right.〉= \left|{\beta }_{11}\right.〉$ and $\left|{\beta }_3\right.〉= \left|{\beta }_{10}\right.〉$. The traditional teleportation algorithm running under this resource (instead the perfect case with $p_0=1$ and $p_1=p_2=p_3=0$) becomes a quantum channel whose output expression in terms of Kraus operators is given by [23]:

$$\begin{array}{c}\hfill \Lambda \left[\rho \right]=\sum _{i=0}^3{p}_i{\tilde{\sigma }}_i\rho {\tilde{\sigma }}_i^{†}=\sum _{i=0}^3{p}_i{\sigma }_i\rho {\sigma }_i\end{array}$$

(1)

with ${\tilde{\sigma }}_i={\sigma }_i$ if $i=0,1,3$ and ${\tilde{\sigma }}_2=i{\sigma }_2$. $\rho =\left|\psi \right.〉\left.〈\psi \right|$ is the state to teleportate (in the current work we will restrict the analysis to pure state cases, despite our outcomes can be extended to mixed states [8]). This formula, regarding teleportation algorithm as a communication channel will be discussed at the end of the article in terms of possible and current available experimental developments for its implementation. It means Kraus operators are $K_i=\sqrt{p_i}{\sigma }_i$. In the terms stated before, we are interested to assess the corresponding fidelity of the process as function of the $p_i$ values under several schemes. It has the form of a Pauli channel [24] and it has been recently studied to characterize its properties under indefinite causal order and measurement [8] exhibiting notable properties and symmetries of communication enhancement as function of the parameters $p_i$. In the current approach, the set $\{p_i|i=0,1,2,3\}$ plays an additional role because it is associated with the quantum resource $|\chi \rangle$.

In the current article, we will use the fidelity to measure the channel performance:

$$\begin{array}{c}\hfill \mathcal{F}\left(\rho ,\Lambda \left[\rho \right]\right)={\left[\mathrm{Tr}\left(\sqrt{\sqrt{\rho }\Lambda \left[\rho \right]\sqrt{\rho }}\right)\right]}^2,\end{array}$$

(2)

because we will restrict to the case when $\rho$ is a pure state $\rho =|\psi \rangle \langle \psi |$, then $\sqrt{\rho }=\rho$. Those facts still give the easier formula: $\mathcal{F}\left(\rho ,\Lambda \left[\rho \right]\right)=\langle \psi |\Lambda [\rho ]|\psi \rangle =\mathrm{Tr}(\rho \Lambda [\rho \left]\right)$. Then, in the following, we will express the fidelity briefly as ${\mathcal{F}}_{\Lambda }\equiv \mathcal{F}\left(\rho ,\Lambda \left[\rho \right]\right)$.

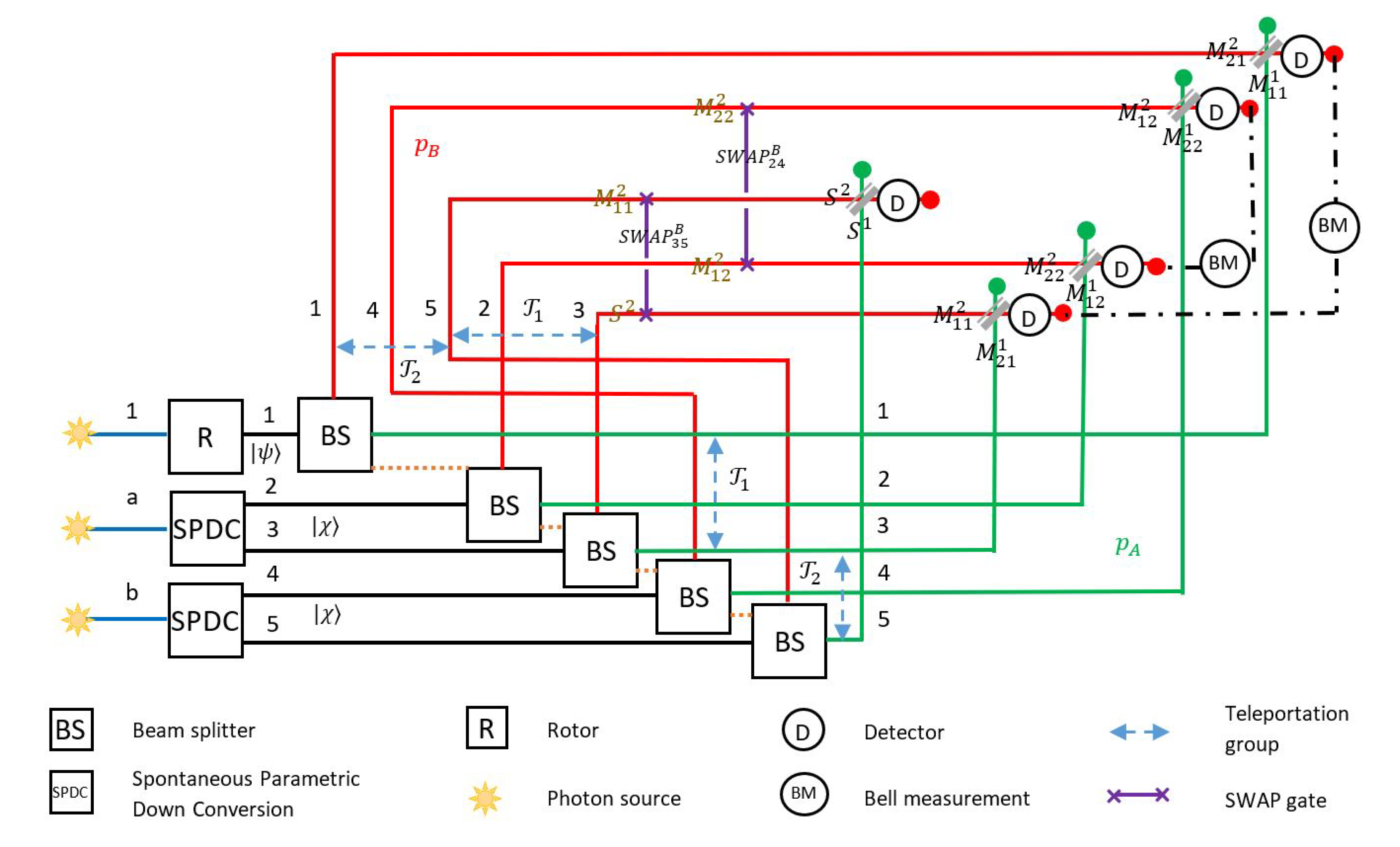
2.2. N-Redundant Quantum Teleportation

In this section, we will study the effect on the fidelity of imperfect teleportation as it was previously depicted. For such reason, we first consider a set of identical and redundant N teleportation channels in a definite causal order as a composition of the depicted channel in (1). In addition, we consider for the sake of simplicity that each channel is identical to others in the redundant application:

$$({◯}_N\Lambda )\left[\rho \right]\equiv \Lambda [\Lambda [\dots \Lambda \left[\rho \right]\dots ]]=\sum _{i_1,\dots ,i_n=0}^3{p}_{i_1}\cdots p_{i_n}{\sigma }_{i_N}\cdots {\sigma }_{i_1}\rho {\sigma }_{i_1}\cdots {\sigma }_{i_N}.$$

(3)

If $p_1=p_2=p_3\equiv p$, with $0\le p\le \frac{1}{3}$ for simplicity (to avoid the increasing parameters involved), we have gotten the expressions for the corresponding fidelity ${\mathcal{F}}_{{◯}_N\Lambda }\equiv \mathrm{Tr}\left(\rho ({◯}_N\Lambda )\left[\rho \right]\right)$ for the first five cases of redundant sequential applications of teleportation (assuming $\rho$ is a pure state), getting:

$$\begin{array}{ccc}\hfill {\mathcal{F}}_{{◯}_1\Lambda }& =& 1-2p\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill {\mathcal{F}}_{{◯}_2\Lambda }& =& 1-4p+8p^2\hfill \end{array}$$

(5)

$$\begin{array}{ccc}\hfill {\mathcal{F}}_{{◯}_3\Lambda }& =& 1-6p+24p^2-32p^3\hfill \end{array}$$

(6)

$$\begin{array}{ccc}\hfill {\mathcal{F}}_{{◯}_4\Lambda }& =& 1-8p+48p^2-128p^3+128p^4\hfill \end{array}$$

(7)

$$\begin{array}{ccc}\hfill {\mathcal{F}}_{{◯}_5\Lambda }& =& 1-10p+80p^2-320p^3+640p^4-512p^5.\hfill \end{array}$$

(8)

Interestingly, those outcomes are independent from the state to teleport (a consequence from the symmetric simplification $p_1=p_2=p_3=p$ and the algebraic properties of Pauli operators). Such cases can be computationally developed to get last outcomes (and other for larger cases). Figure 2 exhibits the behavior of such applications as function of p. The gray zone sets the middle point ${\mathcal{F}}_{{◯}_1\Lambda }=\frac{2}{3}$ of fidelity ${\mathcal{F}}_{{◯}_1\Lambda }\in [\frac{1}{3},1]$ for the case $N=1$ as a reference (as it was remarked in [7]). The single case $N=1$ sets the expected outcome about the effect of p on ${\mathcal{F}}_{{◯}_1\Lambda }$ giving the worst value for $p=\frac{1}{3}$. For $N>1$, the outcome becomes as it could be expected, each application of a new teleportation worsens the output state teleported. Despite this, there are certain recoveries for $p=\frac{1}{3}$, useful only for the lowest values of N. A convergent value ${\mathcal{F}}_{N\to \infty }=\frac{1}{2}$ appears (it corresponds to the behavior of total depolarization for the channel, ${\rho }_{\mathrm{out}}\equiv ({◯}_N\Lambda )\left[\rho \right]=\frac{{\sigma }_0}{2}$). The cases $p=\frac{1}{4}$ coincide for all N because for $N=1$ the total depolarized state $\frac{{\sigma }_0}{2}$ is obtained, then any further application of the teleportation cannot worsen the outcome.

3. Quantum Teleportation Assisted by Indefinite Causal Order with $N$ Channels

In this section, we will consider a generalization of some variants of the process under indefinite causal order as they are presented in [7,22] by considering N channels in a superposition of causal orders. By applying N channels in a superposition of causal orders, we could have $N!$ combinations with different orders. Thus, we will need a control state with such number of dimensions ($|0\rangle$ sets for the normal sequential order of gates $T_1,T_2,...,T_N$) to rule the application of each causal order:

$${\rho }_c=(\sum _{i=0}^{N!-1}\sqrt{q_i}|i{\rangle }_c)(\sum _{j=0}^{N!-1}\sqrt{q_j}\langle j{|}_c)=\sum _{i,j=0}^{N!-1}\sqrt{q_i{q}_j}|i{\rangle }_c\langle j|.$$

(9)

For a definite causal order of teleportation channels $T_{i_1},T_{i_2},...,T_{i_N}$ given by the element ${\pi }_k\in {\Sigma }_N$ in the symmetric group of permutations ${\Sigma }_N$ from the ordered case, it has the effect:

$$\begin{array}{c}\hfill {\pi }_k=\left(\begin{array}{cccc}{T}_{i_1}& T_{i_2}& \cdots & T_{i_N}\\ T_{i_{j_1}}& T_{i_{j_2}}& \cdots & T_{i_{j_N}}\end{array}\right)\to {\pi }_k(K_{i_1}{K}_{i_2}\cdots K_{i_N})=K_{i_{j_1}}{K}_{i_{j_2}}\cdots K_{i_{j_N}},\end{array}$$

(10)

and symbolically corresponding to the control state ${|k\rangle }_c$. Then, the corresponding Kraus operators $W_{i_1,i_2,...,i_N}$ are:

$$W_{i_1,i_2,...,i_N}=\sum _{k=0}^{N!-1}{\pi }_k(K_{i_1}{K}_{i_2}...K_{i_N})\otimes {|k\rangle }_c\langle k|,$$

(11)

where in the following, we will drop the tensor product symbol ⊗ in the sake of simplicity. Thus, the output for $N\text{-}$channels in superposition is given by:

$$\begin{array}{ccc}\hfill {\Lambda }^N\left[\rho \otimes {\rho }_c\right]& =& \sum _{i_1,i_2,\dots ,i_N}{W}_{i_1,i_2,\dots ,i_N}\rho \otimes {\rho }_c{\left(W_{i_1,i_2,\dots ,i_N}\right)}^{†}\hfill \\ & =& \sum _{i_1,i_2,\dots ,i_N}\left(\sum _k{\pi }_k\left(K_{i_1}{K}_{i_2}\dots K_{i_N}\right)|k\rangle \langle k|\right)\rho \otimes {\rho }_c{\left(\sum _{k^{\prime }}{\pi }_{k^{\prime }}\left(K_{i_1}{K}_{i_2}\dots K_{i_N}\right)|k^{\prime }\rangle \langle k^{\prime }|\right)}^{†}\hfill \end{array}$$

(12)

$$\begin{array}{ccc}& =& \sum _{i_1,i_2,\dots ,i_N}{p}_{i_1}\cdots p_{i_N}\left(\sum _k{\pi }_k\left({\sigma }_{i_1}\cdots {\sigma }_{i_N}\right)|k\rangle \langle k|\right)\rho \otimes {\rho }_c\left(\sum _{k^{\prime }}{\pi }_{k^{\prime }}^{†}\left({\sigma }_{i_1}\cdots {\sigma }_{i_N}\right)|k^{\prime }\rangle \langle k^{\prime }|\right)\hfill \\ & =& \sum _{\begin{array}{c}{i}_1,i_2,\dots ,i_N\\ k,k^{\prime }\end{array}}{p}_{i_1}\cdots p_{i_N}\sqrt{q_k{q}_{k^{\prime }}}|k\rangle \langle k^{\prime }|\otimes {\pi }_k\left({\sigma }_{i_1}\cdots {\sigma }_{i_N}\right)\rho {\pi }_{k^{\prime }}^{†}\left({\sigma }_{i_1}\cdots {\sigma }_{i_N}\right).\hfill \end{array}$$

(13)

Still, we can use the last formula to reach a simpler expression using combinatorics and then the properties of Pauli operators. In fact, noting that the sum in (14) includes all different values given to each $i_1,i_2,\dots ,i_N$, after they are permuted as distinguishable objects by ${\pi }_k$ and ${\pi }_{k^{\prime }}$, it can be transformed into:

$$\begin{array}{c}\hfill \sum _{i_1=0}^3\sum _{i_2=0}^3...\sum _{i_N=0}^3⟶\sum _{t_1=0}^N\sum _{t_2=0}^{N-t_1}\sum _{t_3=0}^{N-t_1-t_2}\sum _{p=1}^{N^{\prime }},\end{array}$$

(14)

where $t_j$ is the number of scripts in $i_1,i_2,...,i_N$ equal to $j=0,1,2,3$ ($t_0=N-t_1-t_2-t_3$). Sum over p runs on the distinguishable arrangements obtained with a fix number $t_j$ of operators ${\sigma }_j$ departing from ${\sigma }_0^{t_0}{\sigma }_1^{t_1}{\sigma }_2^{t_2}{\sigma }_3^{t_3}$ by means of a certain permutation ${\pi }_{k_p^{t_1,t_2,t_3}}$. Then, the permutations among identical operators in each one of the four types ${\sigma }_0,{\sigma }_1,{\sigma }_2,{\sigma }_3$ are indistinguishable. There, $N^{\prime }=\frac{N!}{t_0!t_1!t_2!t_3!}$. In such case, Formula (14) can be written as:

$$\begin{array}{ccc}\hfill {\Lambda }^N\left[\rho \otimes {\rho }_c\right]& =& \sum _k\sum _{k^{\prime }}\sqrt{q_k{q}_{k^{\prime }}}|k\rangle \langle k^{\prime }|\sum _{t_1=0}^N\sum _{t_2=0}^{N-t_1}\sum _{t_3=0}^{N-t_1-t_2}\prod _{j=0}^3{p}_j^{t_j}\otimes \hfill \\ & & \sum _{p=1}^{N^{\prime }}{\pi }_k\left({\pi }_{k_p^{t_1,t_2,t_3}}\left({\sigma }_0^{t_0}{\sigma }_1^{t_1}{\sigma }_2^{t_2}{\sigma }_3^{t_3}\right)\right)\rho {\left({\pi }_{k^{\prime }}\left({\pi }_{k_p^{t_1,t_2,t_3}}\left({\sigma }_0^{t_0}{\sigma }_1^{t_1}{\sigma }_2^{t_2}{\sigma }_3^{t_3}\right)\right)\right)}^{†},\hfill \end{array}$$

(15)

providing an easier formula for ${\Lambda }^N\left[\rho \otimes {\rho }_c\right]$ in terms of a definite number of sums and with the teleported state separated from the control state. From the properties of Pauli operators algebra, it is clear that both permutation terms besides $\rho$ in (15) becomes equal until a sign. In addition, each one becomes in the set $\{{\sigma }_j|j=0,1,2,3\}$. Thus, (15) becomes a mixed state obtained as a linear combination of syndromes ${\sigma }_j\rho {\sigma }_j,j=0,1,2,3$ and normally entangled with the control state.

Following to [7], then we select an adequate basis to perform a measurement on the control state: $\mathcal{B}=\{|{\psi }_{M_i}\rangle |i=1,2,...,N!\}$. Such a measurement post-selects the original symmetry of the teleported state mixed with the control and the imperfect entangled state. In such a basis, we hope to find a privileged state $|{\psi }_m\rangle \in \mathcal{B}$ to stochastically maximize the fidelity with probability ${\mathcal{P}}_m$ (assuming $\rho$ is a pure state). ${\mathcal{P}}_m$ sets the probability of success of the process. If the measurement of control does not conduct to $|{\psi }_m\rangle$, then other undesired teleportation outcome will be obtained. Then, if the desired outcome is not obtained, we disregard the output state. The fidelity and the success probability are:

$$\begin{array}{ccc}\hfill {\mathcal{F}}_N& =& \frac{\mathrm{Tr}(\rho \langle {\psi }_m|{\Lambda }^N\left[\rho \otimes {\rho }_c\right]|{\psi }_m\rangle )}{{\mathcal{P}}_m}\hfill \end{array}$$

(16)

$$\begin{array}{ccc}\hfill {\mathcal{P}}_m& =& \mathrm{Tr}(\langle {\psi }_m|{\Lambda }^N\left[\rho \otimes {\rho }_c\right]|{\psi }_m\rangle ).\hfill \end{array}$$

(17)

The process is depicted by Figure 3, where $N!$ causal orders are considered to arrive to the pictorial representation of a complete superposition of causal orders on the right. Each causal order corresponds to one definite order in the application of channels $T_i$ ruled by the control state ${\rho }_c$ above it.

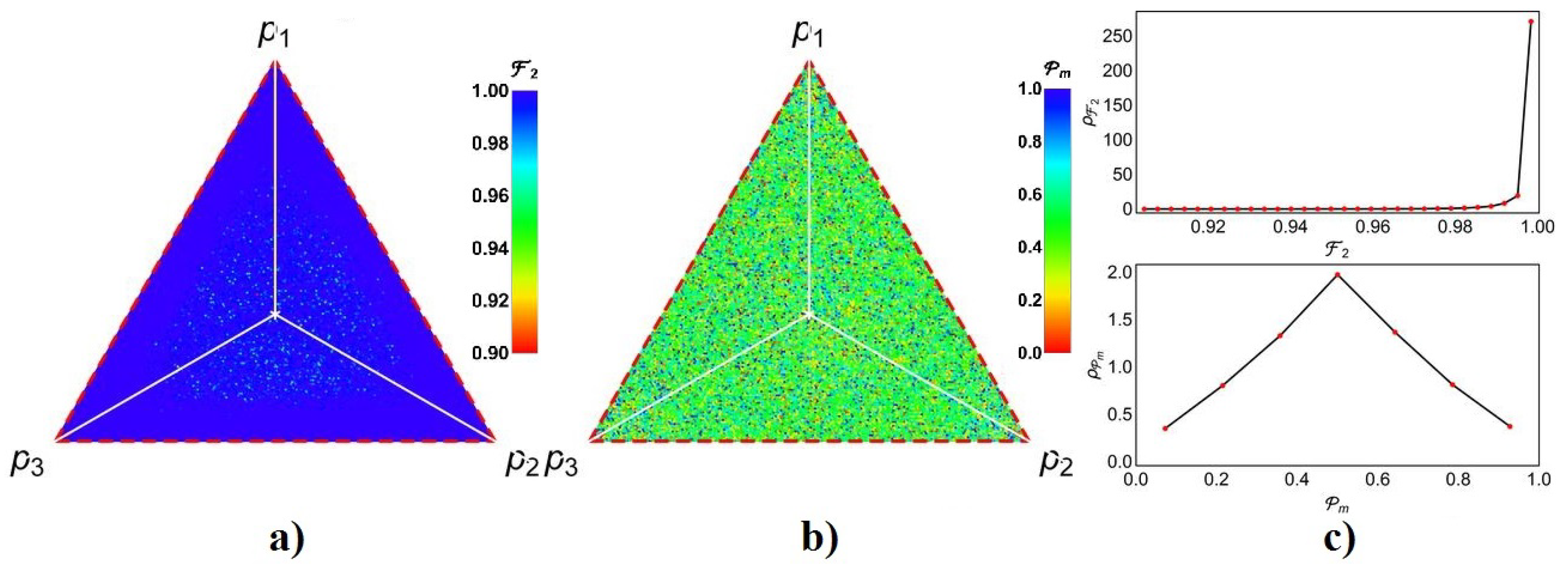
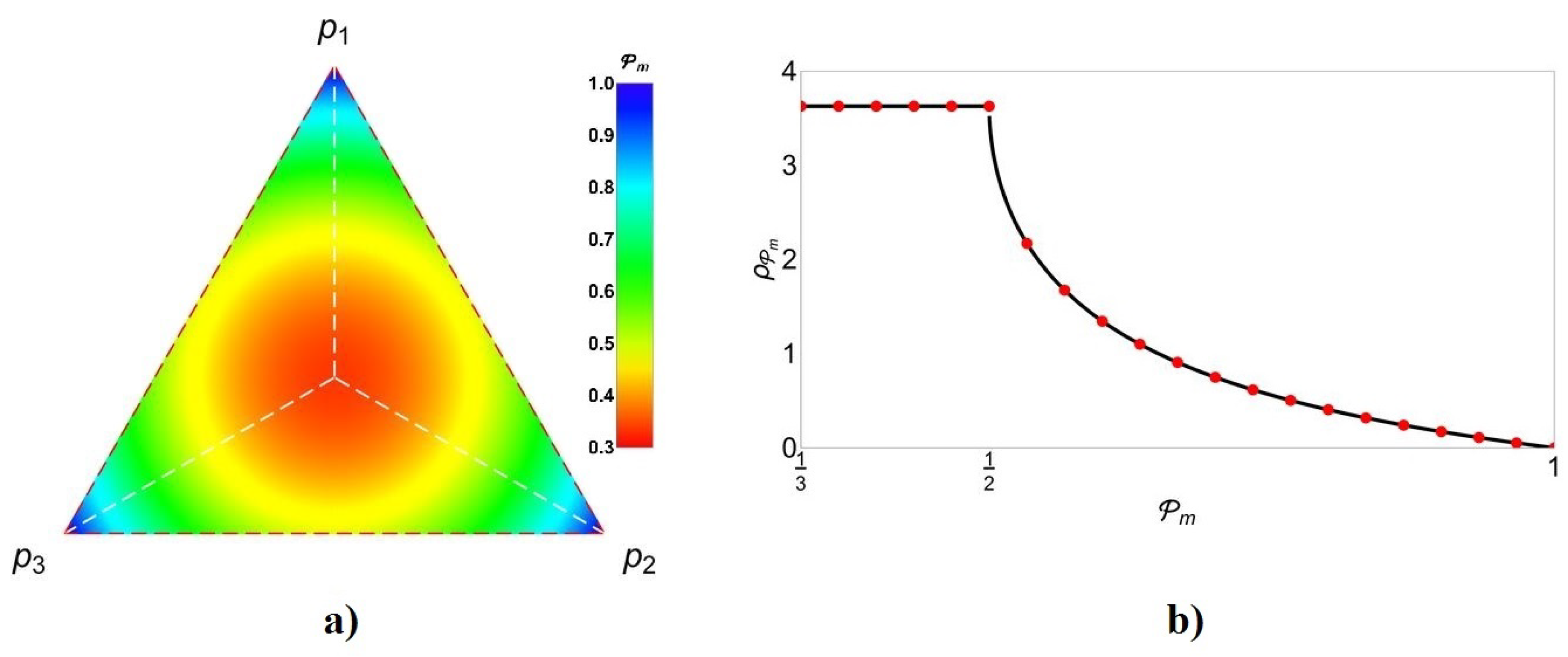
4. Analysis of Quantum Teleportation Assisted by the First Indefinite Causal Orders

In the following section, we deal with the analysis for the increasing number of teleportation channels after to remark some outcomes for the case $N=2$ guiding the further analysis.

4.1. Teleportation with $N=2$ Teleportation Channels in an Indefinite Causal Order Superposition

For the case $N=2$, it has been obtained in [22] that (16) reduces to:

$${\mathcal{F}}_2=\frac{{\sum }_{i,j=0}^3{p}_i{p}_j\left((\frac{1}{2}+(q_0-\frac{1}{2})cos\theta )\mathrm{Tr}\left(\rho {\sigma }_i{\sigma }_j\rho {\sigma }_j{\sigma }_i\right)+\sqrt{q_0{q}_1}sin\theta cos\varphi \mathrm{Tr}\left(\rho {\sigma }_i{\sigma }_j\rho {\sigma }_i{\sigma }_j\right)\right)}{{\sum }_{i,j=0}^3{p}_i{p}_j\left((\frac{1}{2}+(q_0-\frac{1}{2})cos\theta )\mathrm{Tr}\left({\sigma }_i{\sigma }_j\rho {\sigma }_j{\sigma }_i\right)+\sqrt{q_0{q}_1}sin\theta cos\varphi \mathrm{Tr}\left({\sigma }_i{\sigma }_j\rho {\sigma }_i{\sigma }_j\right)\right)},$$

(18)

then, a measurement on the control is made on the basis $\mathcal{B}=\{\left|{\psi }_m\right.〉=cos\frac{\theta }{2}\left|0\right.〉+sin\frac{\theta }{2}{e}^{i\varphi }\left|1\right.〉,\left|{\psi }_m^{\perp }\right.〉=sin\frac{\theta }{2}\left|0\right.〉-cos\frac{\theta }{2}{e}^{-i\varphi }\left|1\right.〉\}$, being $|{\psi }_m\rangle$ the supposed state maximizing ${\mathcal{F}}_2$. The corresponding probability to get that outcome becomes:

$$\begin{array}{ccc}\hfill {\mathcal{P}}_m& =& \sum _{i,j=0}^3{p}_i{p}_j\left((\frac{1}{2}+(q_0-\frac{1}{2})cos\theta )\mathrm{Tr}\left({\sigma }_i{\sigma }_j\rho {\sigma }_j{\sigma }_i\right)+\sqrt{q_0{q}_1}sin\theta cos\varphi \mathrm{Tr}\left({\sigma }_i{\sigma }_j\rho {\sigma }_i{\sigma }_j\right)\right).\hfill \end{array}$$

(19)

Last formulas, (18) and (19) become reduced for pure states $\rho =\left|\psi \right.〉\left.〈\psi \right|,\left|\psi \right.〉=\alpha |0\rangle +\beta |1\rangle$ and $p_0=1-3p,p_1=p_2=p_3=p$ by considering the identities:

$$\begin{array}{ccc}\hfill \sum _{i,j=0}^3{p}_i{p}_j\mathrm{Tr}\left(\rho {\sigma }_i{\sigma }_j\rho {\sigma }_j{\sigma }_i\right)& =& 1-4p+8p^2\hfill \end{array}$$

(20)

$$\begin{array}{ccc}\hfill \sum _{i,j=0}^3{p}_i{p}_j\mathrm{Tr}\left({\sigma }_i{\sigma }_j\rho {\sigma }_j{\sigma }_i\right)& =& 1\hfill \end{array}$$

(21)

$$\begin{array}{ccc}\hfill \sum _{i,j=0}^3{p}_i{p}_j\mathrm{Tr}\left(\rho {\sigma }_i{\sigma }_j\rho {\sigma }_i{\sigma }_j\right)& =& {(1-2p)}^2\hfill \end{array}$$

(22)

$$\begin{array}{ccc}\hfill \sum _{i,j=0}^3{p}_i{p}_j\mathrm{Tr}\left({\sigma }_i{\sigma }_j\rho {\sigma }_i{\sigma }_j\right)& =& 1-12p^2.\hfill \end{array}$$

(23)

Note that the combination of the two first formulas gives the sequential case in (5). The other two terms correspond to the interference terms. First and third formulas can be demonstrated noting that:

$$\begin{array}{ccc}\hfill \rho & =& \frac{1}{2}({\sigma }_0+\widehat{n}·\overrightarrow{\sigma })\hfill \\ \hfill & \mathrm{with}:& \widehat{n}={(|\alpha |}^2-{|\beta |}^2,\alpha {\beta }^{*}+{\alpha }^{*}\beta ,i(\alpha {\beta }^{*}-{\alpha }^{*}\beta )),\hfill \\ & & \overrightarrow{\sigma }=({\sigma }_1,{\sigma }_2,{\sigma }_3).\hfill \end{array}$$

(24)

This fact is not exclusive of the case $N=2$. Due to the Pauli operators algebra and the regarding they are traceless (while, $\mathrm{Tr}\left({\sigma }_0\right)=2$), introducing (24) in (16) and (17), we note for ${\mathcal{P}}_m$ that only the terms containing ${\sigma }_0$ become different from zero. For ${\mathcal{F}}_N$, only the quadratic terms in ${\sigma }_0$ and $\widehat{n}·\overrightarrow{\sigma }$ become different from zero. For the terms quadratic in $\widehat{n}·\overrightarrow{\sigma }$, the additional condition $p_i=p_j\forall i\ne j(i,j\ne 0)$ is required in order to reduce the terms containing ${\sigma }_{\alpha }{\sigma }_{\beta }$ to the magnitude of $\widehat{n}$, thus removing all reference of the teleported state.

In [7], it has been demonstrated that for $|{\psi }_m\rangle =|+\rangle$ the worst deformed state $|\chi \rangle$ with $p=\frac{1}{3}$ still lets a perfect teleportation with probability ${\mathcal{P}}_m=\frac{1}{3}$. In fact, Figure 4 summarizes the findings for the fidelity considering the two families of measurements with $|-\rangle$ (dashed orange lines) and $|+\rangle$ (dashed blue lines). The sequential case with $N=2$ is reported as a continuous line black together with the single teleportation channel $N=1$ (continuous red line). Dashed blue and orange lines go folded from $q_0=0,1$ (two channels in definite causal order) nearest to the two sequential channels case in black to the outermost lines for $q_0=\frac{1}{2}$ (the evenly distributed control state) reaching $\mathcal{F}=1$ in $p=0,\frac{1}{3}$ (blue for $|{\psi }_m\rangle =|+\rangle$) and $\mathcal{F}=\frac{1}{3},\forall p$ (orange for $|{\psi }_m\rangle =|-\rangle$).

For the case $N=2$, [22] has shown that for different values of $q_0=\frac{1}{2}$, other measurements $\left|{\psi }_m\right.〉=cos\frac{\theta }{2}\left|0\right.〉+sin\frac{\theta }{2}{e}^{i\varphi }\left|1\right.〉$ are possible in order to achieve $\mathcal{F}=1$ when $p=\frac{1}{3}$ giving $\varphi =0$ and $\theta$ distributed as in the Figure 5 as function of $q_0$. Thus, the best fidelities ${\mathcal{F}}_2$ depend entirely from p (see the color-scale besides in Figure 5) but the corresponding values of ${\mathcal{P}}_m$ go down far from $q_0=\frac{1}{2}$ ($\theta =\frac{\pi }{2}$). The red dotted line is the threshold setting the minimum fidelity reached in the optimal case for $p=\frac{3-\sqrt{3}}{6}$, ${\mathcal{F}}_2=\frac{1}{\sqrt{3}}$ [22]. Thus, we conclude that for $p=p_1=p_2=p_3$, the best state for the control is $q_0=\frac{1}{2}$ in order to maximize ${\mathcal{P}}_m$, despite only for $p=\frac{1}{3}$ and $p\to 0$ it is possible to approach ${\mathcal{F}}_2\to 1$. The last outstanding outcome for $p=\frac{1}{3}$ is a consequence of the two-folded interference introduced by the indefinite causal order together with the post-selection induced by the measurement which filters only constructive interference among the terms belonging to the original state.

Fidelity (18) can be still analysed for independent values of $p_1,p_2,p_3$. Figure 6 shows a numerical analysis to search the best possible fidelity (achieved for certain teleported state) ${max}_{|{\psi }_m\rangle ,q_0}\left({\mathcal{F}}_2\right)$ for all possible $|{\psi }_m\rangle$ and $0\le q_0\le 1$. The value of fidelity ${\mathcal{F}}_2$ is represented in color in agreement with the color-scale bar besides. Figure 6a shows a cut from the entire plot showing the inner core where fidelity goes down (three parts are symmetric). The higher values of fidelity on the faces of polyhedron suggest that better solutions can be reached for other cases with unequal values of $p_i,i=1,2,3$, particularly for the frontal face $p_0=0$ completely colored in blue in Figure 6. The case $p_1=p_2=p_3\equiv p$ falls in the central red dashed division crossing the clearer core reflecting the outcome in Figure 4, where not good values of ${\mathcal{F}}_2$ are inevitably obtained far from $p=0$ and $p=\frac{1}{3}$. In addition, complementary information for such cases is given by ${\mathcal{P}}_m$ in Figure 6b, the probability to reach the corresponding higher fidelity in each process assisted by an intermediate optimal measurement on the control qubit. The plot depicts disperse outcomes barely around of ${\mathcal{P}}_m\approx 0.5$. Note that the computer process to obtain Figure 6a,b requires optimization on lots of parameters, thus requiring a considerable time of processing. The region $(p_1,p_2,p_3)$ was divided in ${10}^7$ points to perform such optimization. After, each point is reported as a colored sphere to fill the space in order to give a representation in color about the continuity of ${\mathcal{F}}_2$ and ${\mathcal{P}}_m$. Such an approach gives a certain impression of blurring in the figures, but they are reported with the best precision available under numerical processing. Particularly, Figure 6b is a collage of colored dots due to ${\mathcal{P}}_m$ is reported on an average basis, due the optimization was made on ${\mathcal{F}}_2$ on the left. By performing a numerical statistics of our outcomes for each ${\mathcal{P}}_m$, we get an approximation to its statistical distribution ${\rho }_{{\mathcal{P}}_m}$ included in the upper inset in Figure 6b. This distribution shows symmetric behavior around of ${\mathcal{P}}_m=0.5$ as it could be expected for the numerical optimization.

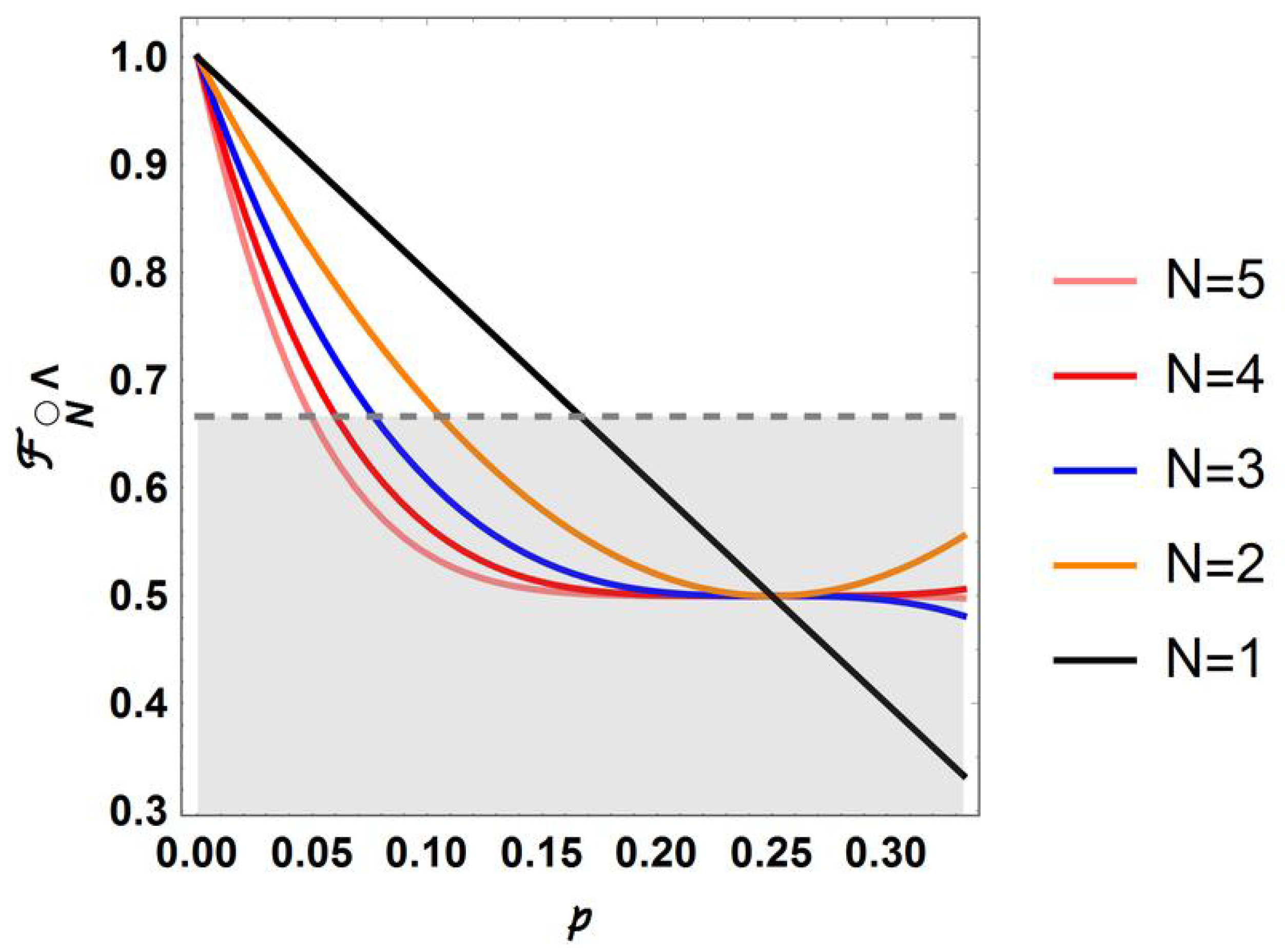
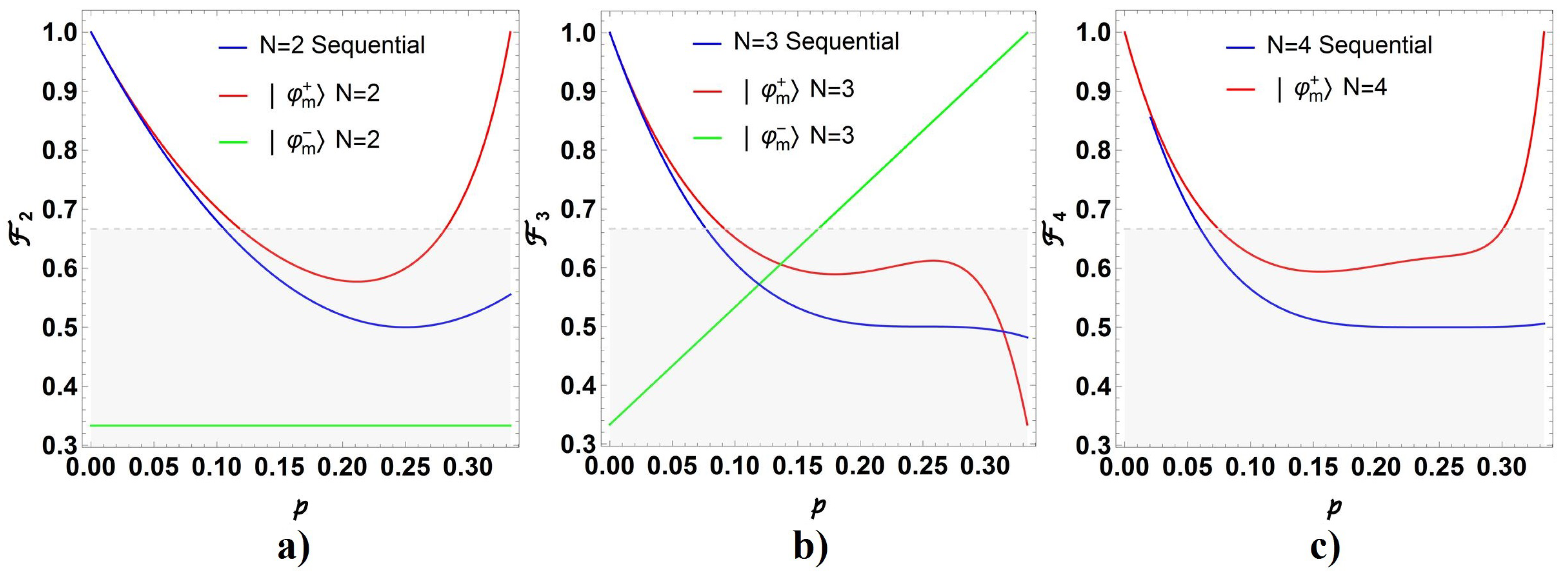
4.2. Teleportation with an Increasing Number of Teleportation Channels in an iNdefinite Causal Order Superposition

Formula (15) exhibits the superposition of terms finally involving the states $\rho ,{\sigma }_1\rho {\sigma }_1,{\sigma }_2\rho {\sigma }_2$ and ${\sigma }_3\rho {\sigma }_3$ while they become entangled with the control state ${\rho }_c$. In the next sections, we deal with two cases of interest for the use of the teleportation algorithm under indefinite causal order.

4.2.1. Case $p_1=p_2=p_3\equiv p$

First, we will address with the case $p=p_1=p_2=p_3$ widely used in the literature for simplicity. In [7], it has been suggested that for $|{\psi }_m\rangle$ having one of the following forms:

$$\begin{array}{c}\hfill |{\phi }_m^{\pm }\rangle \equiv \frac{1}{\sqrt{N!}}\sum _{i=0}^{N!-1}{(\pm 1)}^{\sigma \left({\pi }_i\right)}|i\rangle .\end{array}$$

(25)

The teleportation fidelity becomes optimal. There, $\sigma$ is the signature of the parity of each order $|i\rangle$. By considering (15) together with (25) and the control state with $q_k=\frac{1}{N!}\forall k=0,1,...,N!-1$:

$$\begin{array}{ccc}\hfill \langle {\phi }_m^{\pm }|{\Lambda }^N\left[\rho \otimes {\rho }_c\right]|{\phi }_m^{\pm }\rangle & =& \sum _k\sum _{k^{\prime }}\frac{1}{N{!}^2}{(\pm 1)}^{\sigma \left({\pi }_k\right)+\sigma \left({\pi }_{k^{\prime }}\right)}\sum _{t_1=0}^N\sum _{t_2=0}^{N-t_1}\sum _{t_3=0}^{N-t_1-t_2}\prod _{j=0}^3{p}_j^{t_j}·\hfill \\ & & \sum _{p=1}^{N^{\prime }}{\pi }_k\left({\pi }_{k_p^{t_1,t_2,t_3}}\left({\sigma }_0^{t_0}{\sigma }_1^{t_1}{\sigma }_2^{t_2}{\sigma }_3^{t_3}\right)\right)\rho {\left({\pi }_{k^{\prime }}\left({\pi }_{k_p^{t_1,t_2,t_3}}\left({\sigma }_0^{t_0}{\sigma }_1^{t_1}{\sigma }_2^{t_2}{\sigma }_3^{t_3}\right)\right)\right)}^{†}.\hfill \end{array}$$

(26)

Then, we have developed the Formulas (14) and (16) with $|{\psi }_m\rangle =|{\phi }_m^{\pm }\rangle$ in (25) to get both ${\mathcal{F}}_N$ and ${\mathcal{P}}_N$ for $N=2,3,4$. Those formulas have been plotted (they are not reported here because their complexity, despite they are included in the Appendix A), the outcomes are shown in Figure 7 showing that a perfect fidelity ${\mathcal{F}}_N=1$ for $p=\frac{1}{3}$ is achieved when $|{\phi }_m^{\pm }\rangle$ meets with the same parity to N (p is indicated in the color-scale besides). Despite, for $p=\frac{1}{3}$ the success probabilities ${\mathcal{P}}_m$ decrease while N increases. For $|{\phi }^{-}\rangle$ and $N=4$, we get ${\mathcal{P}}_m=0$, thus ${\mathcal{F}}_4$ becomes undefined in such a case. While $p\in [0,\frac{1}{6}]$ the best election is the single teleportation channel, for $p\in [\frac{1}{6},\frac{1}{3}]$, the assistance of the causal order becomes an alternative to enhance the fidelity of teleportation, particularly with $N=2$ channels.

Figure 8 again compares the fidelity ${\mathcal{F}}_N$ versus p for both measurements with the corresponding sequential case showing the alternated optimization of ${\mathcal{F}}_N$ as function of the parity of N and $|{\phi }_m^{\pm }\rangle$. Despite, the outcomes in Figure 6 suggest analysing the behavior of ${\mathcal{F}}_N$ for independent values of $p_1,p_2,p_3$.

4.2.2. Case $p_j\ll 1$, $j=1,2,3$

In some practical cases, the expected values for the entangled resource $|\chi \rangle$ vary slightly from a perfect entangled state: $p_j\ll 1$ for $j=1,2,3$. Thus, the outcome described through Formula (15) becomes in this case (developing to first order for $p_j,j=1,2,3$ the factor ${\prod }_{j=0}^3{p}_j^{t_j}$ there):

$${\Lambda }^N[\rho \otimes {\rho }_c]\approx \left[\left(1-N\sum _{j=1}^3{p}_j\right)\rho +N\sum _{j=1}^3{p}_j{\sigma }_j\rho {\sigma }_j\right]\otimes {\rho }_c\equiv {\rho }_{out}\otimes {\rho }_c.$$

(27)

Note that under this approximation, ${\rho }_c$ becomes unaltered and separated from the system state. Thus, the optimal way to teleport the state implies to measure the control state considering $|{\psi }_m\rangle ={\sum }_k\sqrt{q_k}|k\rangle$. In the following, we assume such an optimal measurement made on the control state.

For the particular case where $p_j=\frac{1}{4N}$ with $j=1,2,3$, last formula can be written as:

$${\Lambda }^N[\rho \otimes {\rho }_c]\approx \frac{1}{2}{\sigma }_0\otimes {\rho }_c.$$

(28)

Obtaining the totally depolarized state $\frac{1}{2}{\sigma }_0$. Notice that it is only applicable for very large values of N (due to the assumption $p_j\ll 1,j=1,2,3$). This aspect is advised in the Figure 7 where the fidelity drops more rapidly to $\frac{1}{2}$ when N grows around of $p=0$.

In general, the probability and fidelity given in (27) will become respectively (developing to first order in $p_j,j=1,2,3$):

$$\begin{array}{ccc}\hfill {\mathcal{P}}_m& \approx & \mathrm{Tr}\left[{\rho }_{out}\right]=1\hfill \end{array}$$

(29)

$$\begin{array}{ccc}\hfill {\mathcal{F}}_N& \approx & \frac{\mathrm{Tr}\left[\rho {\rho }_{out}\right]}{{\mathcal{P}}_m}=1-N\sum _{j=1}^3{p}_j(1-n_j^2)\equiv 1-N{p}_{\mathrm{ts}}\sum _{j=1}^3{\alpha }_j(1-n_j^2)\equiv 1-N{p}_{\mathrm{ts}}{\mathsf{\Delta }}_{\theta ,\varphi }^{{\alpha }_1,{\alpha }_2,{\alpha }_3},\hfill \end{array}$$

(30)

where $\rho$ was written as in (24). We are introduced the reduced parameters ${\alpha }_j\in [0,1]$ and the threshold probability $p_{\mathrm{ts}}\ll 1$ to limit the validity of the current approximation ($p_j=p_{\mathrm{ts}}{\alpha }_j\ll 1$, $j=1,2,3$). We note in any case that the increasing of N worsens the fidelity. Note each term in the sum in (30) is non-negative, thus the fidelity becomes commonly reduced. Because only one of $n_j^2,j=1,2,3$ could be one at the time, then it is necessary in addition that two $p_j$ become zero to get ${\mathcal{F}}_N=1$. Otherwise, ${\mathcal{F}}_N<1$ with a notable decreasing if N is large. The outcome in (29) exhibits a combination of the three error-syndromes ${\sigma }_1\rho {\sigma }_1,{\sigma }_2\rho {\sigma }_2,{\sigma }_3\rho {\sigma }_3$ reflected through the terms ${\alpha }_j(1-n_j^2)$ as function of ${\alpha }_j$. Thus, for each syndrome ${\sigma }_j\rho {\sigma }_j$ the best states being teleported are those closer to the eigenstates of ${\sigma }_j$, otherwise while several ${\alpha }_j\ne 0$ the teleportation capacity is widely reduced.

Considering $\rho =|\psi \rangle \langle \psi |$ with $\left|\psi \right.〉=cos\frac{\theta }{2}\left|0\right.〉+sin\frac{\theta }{2}{e}^{i\varphi }\left|1\right.〉$ on the Bloch sphere: $n_1=sin\theta cos\varphi ,n_2=sin\theta sin\varphi ,n_3=cos\theta$. Then, we analyze each syndrome and its impact on the fidelity through the quantity ${\mathsf{\Delta }}_{\theta ,\varphi }^{{\alpha }_1,{\alpha }_2,{\alpha }_3}$. As lower it becomes, higher becomes ${\mathcal{F}}_N$. Figure 9a shows the simple behavior of ${\mathsf{\Delta }}_{\theta ,\varphi }^{{\alpha }_1,{\alpha }_2,{\alpha }_3}$ for each state on the Bloch sphere under each syndrome: $p_1=1,p_2=p_3=0$; $p_2=1,p_1=p_3=0$; and $p_3=1,p_1=p_2=0$ in such order. We have denoted as $|0_j\rangle$ and $|1_j\rangle$ to the eigenstates of ${\sigma }_j,j=1,2,3$ (or $j=x,y,z$). Note the behavior commented in the previous paragraph.

Despite, the most interesting issue is centered in the fact that the entanglement resource $|\chi \rangle$ is normally unknown but with a tiny variation of $|{\beta }_0\rangle$ through the deformation parameters $p_1,p_2,p_3$. By calculating the average and the standard deviation of ${\mathsf{\Delta }}_{\theta ,\varphi }^{{\alpha }_1,{\alpha }_2,{\alpha }_3}$ on the parameters ${\alpha }_1,{\alpha }_2,{\alpha }_3\in [0,1]$:

$$\begin{array}{ccc}\hfill {\mu }_{{\mathsf{\Delta }}_{\theta ,\varphi }^{{\alpha }_1,{\alpha }_2,{\alpha }_3}}& =& {\int }_0^1{\int }_0^1{\int }_0^1{\mathsf{\Delta }}_{\theta ,\varphi }^{{\alpha }_1,{\alpha }_2,{\alpha }_3}\mathrm{d}{\alpha }_1\mathrm{d}{\alpha }_2\mathrm{d}{\alpha }_3=1\to {\mu }_{{\mathcal{F}}_N}=1-N{p}_{\mathrm{ts}}\hfill \\ \hfill {\sigma }_{{\mathsf{\Delta }}_{\theta ,\varphi }^{{\alpha }_1,{\alpha }_2,{\alpha }_3}}& =& \sqrt{{\mu }_{{\left({\mathsf{\Delta }}_{\theta ,\varphi }^{{\alpha }_1,{\alpha }_2,{\alpha }_3}\right)}^2}-{({\mu }_{{\mathsf{\Delta }}_{\theta ,\varphi }^{{\alpha }_1,{\alpha }_2,{\alpha }_3}})}^2}\hfill \end{array}$$

(31)

$$\begin{array}{ccc}& =& \frac{1}{8\sqrt{6}}\sqrt{53+{sin}^4\left(\theta \right)cos\left(4\varphi \right)+4cos\left(2\theta \right)+7cos\left(4\theta \right)}\in [\frac{1}{3},\frac{1}{\sqrt{6}}]\hfill \end{array}$$

(32)

$$\begin{array}{ccc}& \to & {\sigma }_{{\mathcal{F}}_N}=N{p}_{\mathrm{ts}}{\sigma }_{{\mathsf{\Delta }}_{\theta ,\varphi }^{{\alpha }_1,{\alpha }_2,{\alpha }_3}}.\hfill \end{array}$$

(33)

We note that the average value of fidelity ${\mathcal{F}}_N=1-N{p}_{\mathrm{ts}}$ becomes independent from the state being teleported. While, the dispersion for ${\mathsf{\Delta }}_{\theta ,\varphi }^{{\alpha }_1,{\alpha }_2,{\alpha }_3}$ on the values $p_1,p_2,p_3$ depends from the teleported state and it becomes lowest for the eigenstates of ${\sigma }_1,{\sigma }_2,{\sigma }_3$. In fact, the exact result for the case of $N=1$ is precisely (30) with such value in (1): ${\mathcal{F}}_1=1-{\sum }_{j=1}^3{p}_j(1-n_j^2)$, thus the values in (33) are scaled from it by a factor N. The reason is easily noticed, the ${\rho }_{\mathrm{out}}$ in (27) obtained by linearization from (3) coincides with the sequential case (3) under linearization, so both cases exactly meet under the current limit. It implies that indefinite causal order procedure in teleportation becomes unpractical in this limit.

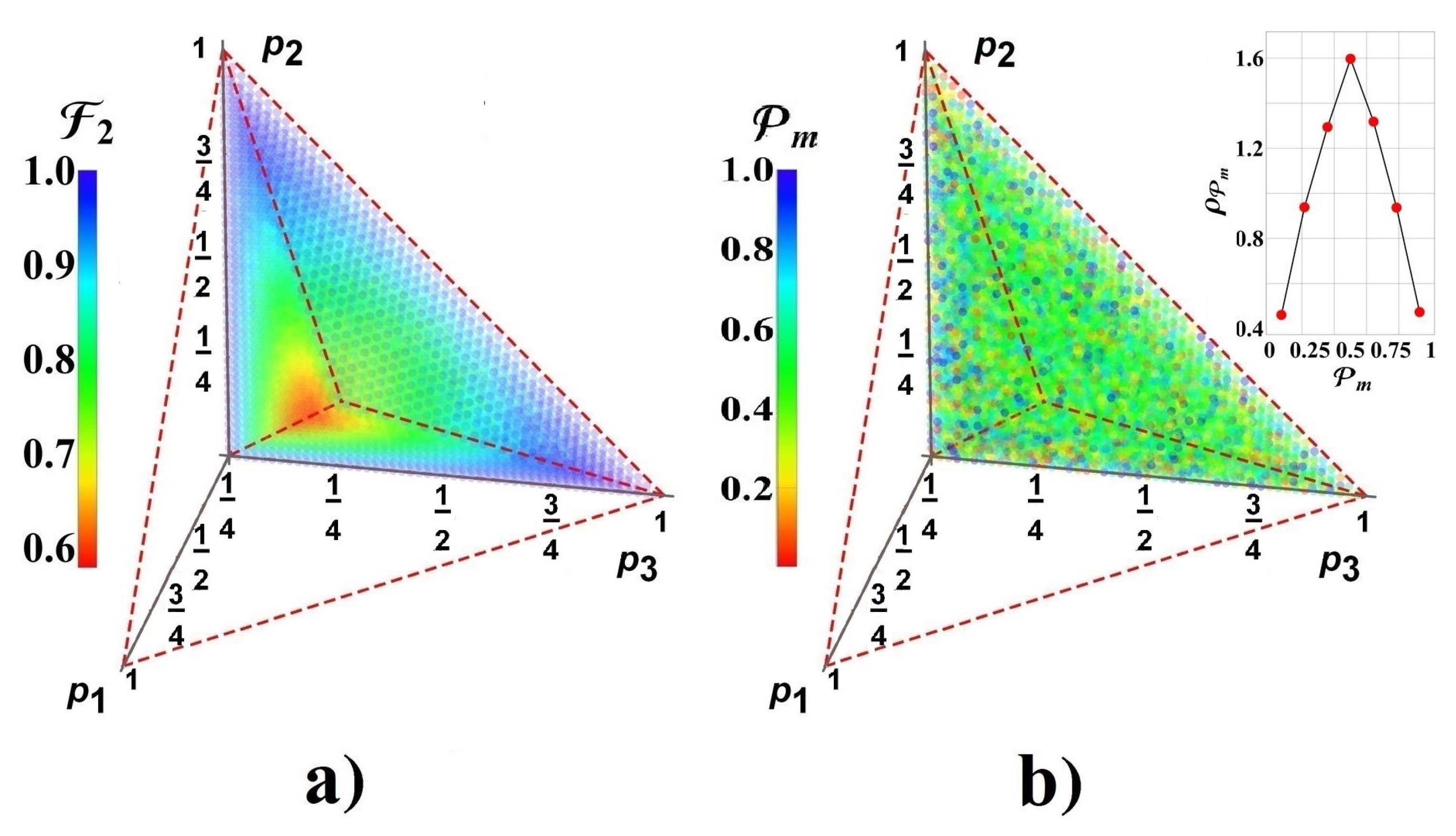
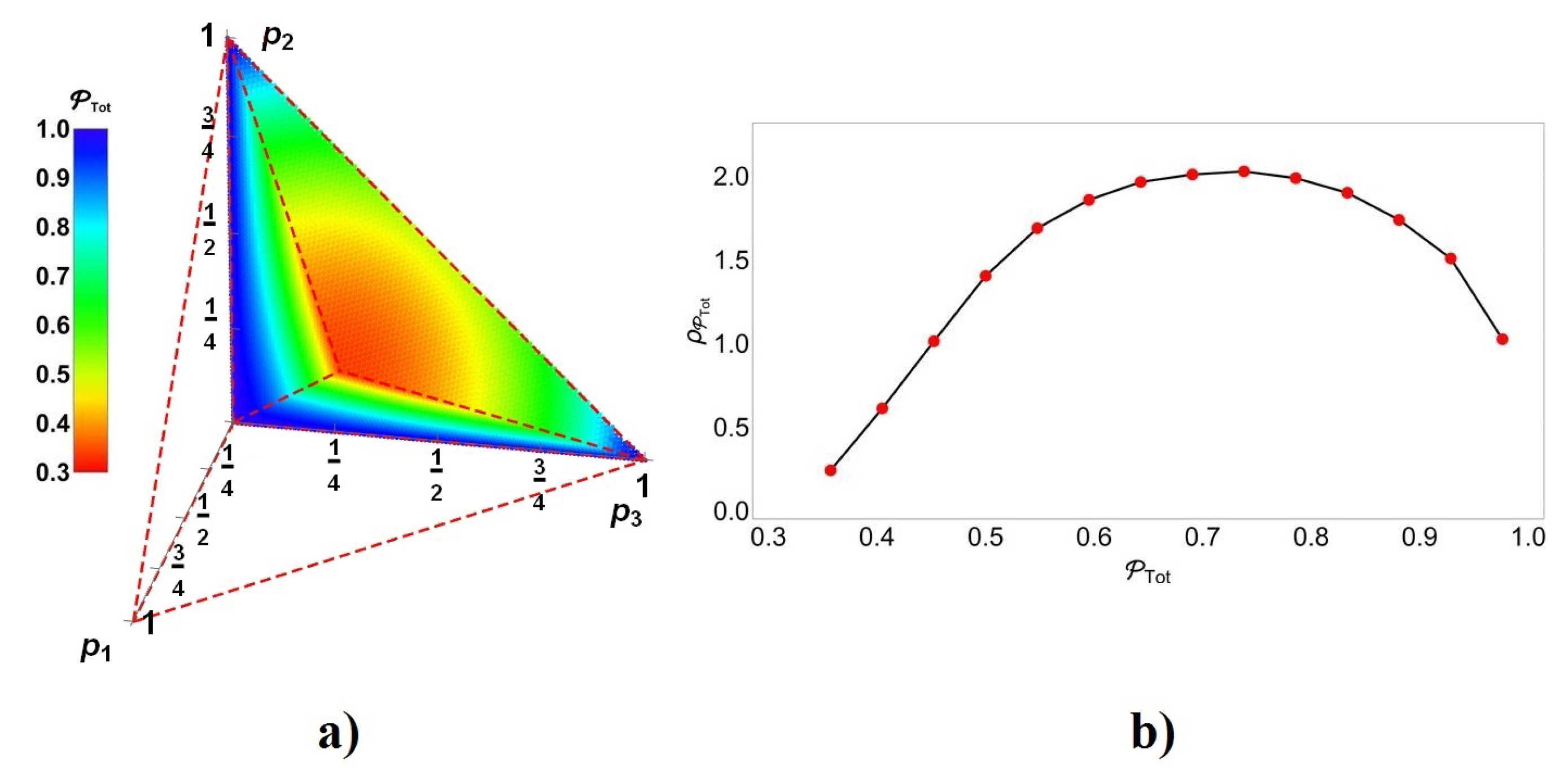
4.3. Notable Behavior on the Frontal Face of Parametric Region: Case $p_0=0$

The behavior of ${\mathcal{F}}_2$ on the frontal face ($p_0=0$) in Figure 6 can be now better advised in Figure 10. There, we have calculated numerically (for ${10}^5$ states covering the frontal face), the best fidelity obtained using two teleportation channels under indefinite causal order by taking the optimal measurement on the control state together with the best state able to be teleported. Thus, it represents naively the best possible scenario.

In the last process, for each $|\chi \rangle$ on the frontal face, we have additionally taken a sample of ${10}^2$ sets of values for $q_0\in [0,1]$ (the initialization value for the control state for $N=2$), $\theta \in [0,\pi ],\varphi \in [0,2\pi ]$ for $|{\psi }_{\mathrm{m}}\rangle$ and ${\theta }_0\in [0,\pi ],{\varphi }_0\in [0,2\pi ]$ for the teleported state $|\psi \rangle =cos\frac{{\theta }_0}{2}\left|0\right.〉+sin\frac{{\theta }_0}{2}{e}^{i{\varphi }_0}\left|1\right.〉$. Each value is used as initial condition to find a local maximum for the fidelity ${\mathcal{F}}_2$. Then, those values are used to predict the global maximum of ${\mathcal{F}}_2$ for each point on the frontal face. Figure 10a shows the best fidelity on the face together with the statistical distribution of the fidelities on the frontal face in the upper image of Figure 10c, which suggests that ${\mathcal{F}}_2=1$ could be obtained on the face always (the little dispersion with lower values of ${\mathcal{F}}_2\in [0.9,1]$ are due to the numerical procedure followed). The same follows for ${\mathcal{P}}_m$ (Figure 10b,c lower) but denoting that such probabilities of success are centrally distributed around $\frac{1}{2}$ (note they are not the best probabilities because the process is centred on maximize ${\mathcal{F}}_2)$. As in Figure 6, images in Figure 10 appear blurred due to the limited number of points considered because the time processing.

Nevertheless, the last fact is in reality a blind strategy. A more critical view of Formulas (18) and (19) and referring to [22] which numerically suggests that $q_0={sin}^2\frac{\theta }{2}=\frac{1}{2}(1-cos\theta ),\varphi =0$ is related with the optimal case for the case $p=p_1=p_2=p_3=\frac{1}{3}$. In fact, in such case, last formulas become reduced to:

$$\begin{array}{ccc}\hfill {\mathcal{F}}_2& =& \frac{{\sum }_{i,j=0}^3{p}_i{p}_j\left(\mathrm{Tr}\left(\rho {\sigma }_i{\sigma }_j\rho {\sigma }_j{\sigma }_i\right)+\mathrm{Tr}\left(\rho {\sigma }_i{\sigma }_j\rho {\sigma }_i{\sigma }_j\right)\right)}{{\sum }_{i,j=0}^3{p}_i{p}_j\left(\mathrm{Tr}\left({\sigma }_i{\sigma }_j\rho {\sigma }_j{\sigma }_i\right)+\mathrm{Tr}\left({\sigma }_i{\sigma }_j\rho {\sigma }_i{\sigma }_j\right)\right)}\hfill \end{array}$$

(34)

$$\begin{array}{ccc}\hfill {\mathcal{P}}_m& =& \frac{{sin}^2\theta }{2}\sum _{i,j=0}^3{p}_i{p}_j\left(\mathrm{Tr}\left({\sigma }_i{\sigma }_j\rho {\sigma }_j{\sigma }_i\right)+\mathrm{Tr}\left({\sigma }_i{\sigma }_j\rho {\sigma }_i{\sigma }_j\right)\right).\hfill \end{array}$$

(35)

Last formula explains the reason because the case $\theta =\frac{\pi }{2}$ is optimal for ${\mathcal{P}}_m$. Moreover, on the frontal face $p_0=0$ (then $i,j=1,2,3$), then (34) and (35) clearly become (by splitting the cases $i=j$ from $i\ne j$, noting for the last case ${\sigma }_i{\sigma }_j=-{\sigma }_j{\sigma }_i$ and the fact that we are dealing with pure states):

$$\begin{array}{ccc}\hfill {\mathcal{F}}_2& =& 1\hfill \end{array}$$

(36)

$$\begin{array}{ccc}\hfill {\mathcal{P}}_m& =& {sin}^2\theta \sum _{i=1}^3{p}_i^2,\mathrm{with}:\sum _{i=1}^3{p}_i=1.\hfill \end{array}$$

(37)

Thus, the last conditions make the teleportation optimal not only for $p=p_1=p_2=p_3=\frac{1}{3}$ but also for the entire cases on the frontal face, being independent from the teleported state. Nevertheless, the probability of success depends entirely from the values of $p_i$ (considering only the best case $\theta =\frac{\pi }{2}$). Figure 11 shows the distribution of ${\mathcal{P}}_m$ on the frontal face (in some cases we will denote this probability by ${\mathcal{P}}_{m,N=2}^{\mathrm{ff},\left\{p_i\right\}}$ to state $\theta =\frac{\pi }{2},p_0=0$ and $p_i$ arbitrary but fulfilling $p_1+p_2+p_3=1$), which ranges on $[\frac{1}{3},1]$. In fact, the case $p=p_1=p_2=p_3=\frac{1}{3}$ corresponds to the worst case for ${\mathcal{P}}_m$ in the center of the face. We have constructed the norm on the frontal face to report such distribution. The mean ${\mu }_{{\mathcal{P}}_m}=\frac{1}{2}$ and the standard deviation ${\sigma }_{{\mathcal{P}}_m}\approx 0.13$ were calculated using such distribution.

In order to solve the cases for $N>2$ by including further teleportation channels under indefinite causal order, last analysis suggests for arbitrary N that the procurement of an analytical formula for (15) is in order at least for the case $p_0=0$, implying $t_0=0$:

$$\begin{array}{ccc}\hfill {\Lambda }^N\left[\rho \otimes {\rho }_c\right]& =& \sum _k\sum _{k^{\prime }}\sqrt{q_k{q}_{k^{\prime }}}|k\rangle \langle k^{\prime }|\sum _{t_1=0}^N\sum _{t_2=0}^{N-t_1}\prod _{j=1}^3{p}_j^{t_j}\otimes \hfill \\ & & \sum _{p=1}^{N^{\prime }}{\pi }_k\left({\pi }_{k_p^{t_1,t_2,t_3}}\left({\sigma }_1^{t_1}{\sigma }_2^{t_2}{\sigma }_3^{t_3}\right)\right)\rho {\left({\pi }_{k^{\prime }}\left({\pi }_{k_p^{t_1,t_2,t_3}}\left({\sigma }_1^{t_1}{\sigma }_2^{t_2}{\sigma }_3^{t_3}\right)\right)\right)}^{†}\hfill \end{array}$$

(38)

$$\begin{array}{ccc}& =& \sum _k\sum _{k^{\prime }}\sqrt{q_k{q}_{k^{\prime }}}|k\rangle \langle k^{\prime }|\sum _{t_1=0}^N\sum _{t_2=0}^{N-t_1}\prod _{j=1}^3{p}_j^{t_j}\otimes \sum _{p=1}^{N^{\prime }}{\Sigma }_{k_p}^k{\Sigma }_{k_p}^{k^{\prime }}\left({\sigma }_1^{t_1}{\sigma }_2^{t_2}{\sigma }_3^{t_3}\right)\rho {\left({\sigma }_1^{t_1}{\sigma }_2^{t_2}{\sigma }_3^{t_3}\right)}^{†}\hfill \end{array}$$

(39)

and $t_3=N-t_1-t_2$. As it was previously mentioned, factors generated by ${\pi }_k$ and ${\pi }_{k^{\prime }}$ are equal until a sign. In addition, they always evolve to ${\sigma }_0,{\sigma }_1,{\sigma }_2$ or ${\sigma }_3$ (easily depending on the parity of $t_1,t_2,t_3$). Thus, those factors and their signs state the introduction of syndromes on $\rho$ together with interference among them and the different orders. Such interference could be manipulated through the parameters $q_k,p_j$.

Even so, this formula is not easy to address in order to get a simpler closed result because the sign ${\Sigma }_{k_p}^k,{\Sigma }_{k_p}^{k^{\prime }}$ introduced in the permutation with respect ${\sigma }_1^{t_1}{\sigma }_2^{t_2}{\sigma }_3^{t_3}$ cannot be advised easily (see a parallel analysis in [8]). Nevertheless, we can still to analyse computationally the cases for the lowest values of N (analytical cases addressed by computer aided methods due to the factorial increasing number of terms). Thus, formulas for ${\mathcal{P}}_{m,N}^{\mathrm{ff},\left\{p_i^{\prime }\right\}}$ and $\mathcal{F}$ for N larger than two have been obtained using a computational treatment. The formulas obtained in the analysis are reported in Appendix B. As in our previous discussion for the case $p_1=p_2=p_3=p$ in the Section 4.2.1, $\mathcal{F}=1$ is obtained for all cases on the frontal face if the measurement in the indefinite causal order becomes $|{\phi }_m^{+}\rangle$ for $N=2,4$ and $|{\phi }_m^{-}\rangle$ for $N=3$ independently of the teleported state. Again, it is a consequence of the order interference due to the indefinite causal order together the post-selection induced by the measurement. For complementary cases using other measurement outcomes, we get $\mathcal{F}\not\equiv 1$ depending from $p_1,p_2,p_3$ or still undefined, and additionally depending from the teleported state (see Appendix B).

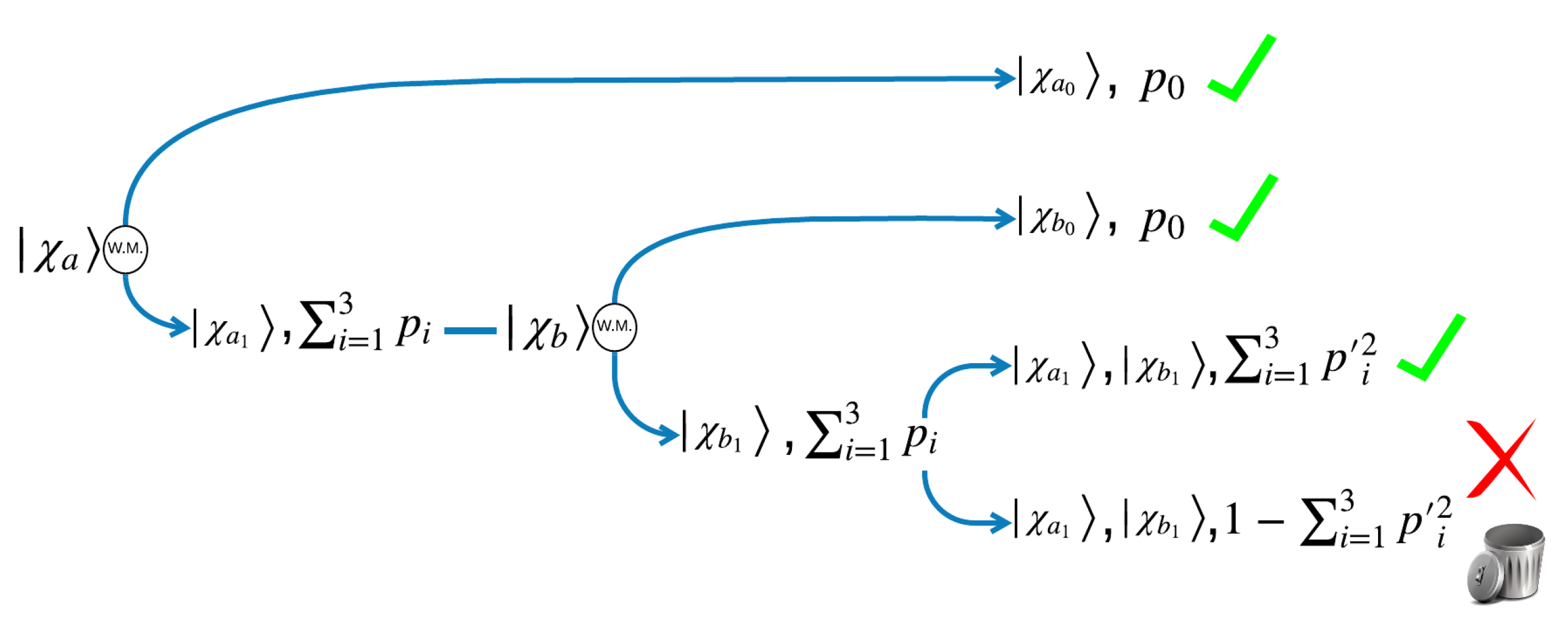
5. An Alternative Procedure Introducing Weak Measurement

In spite of the previous outcomes, we guess the indefinite causal order could not work properly at any point inside of region depicted in the Figure 6. Nevertheless, due to the outcomes in [7] for the case $p=p_1=p_2=p_3$ and those exhibited in the Figure 6, the teleportation process assisted by indefinite causal order (at least for two channels) becomes optimal on $p_0=0$ and $p_0=1$ (the origin and the frontal face in Figure 6a). Then, we propose an alternative strategy beginning with a weak measurement on the entangled resource.

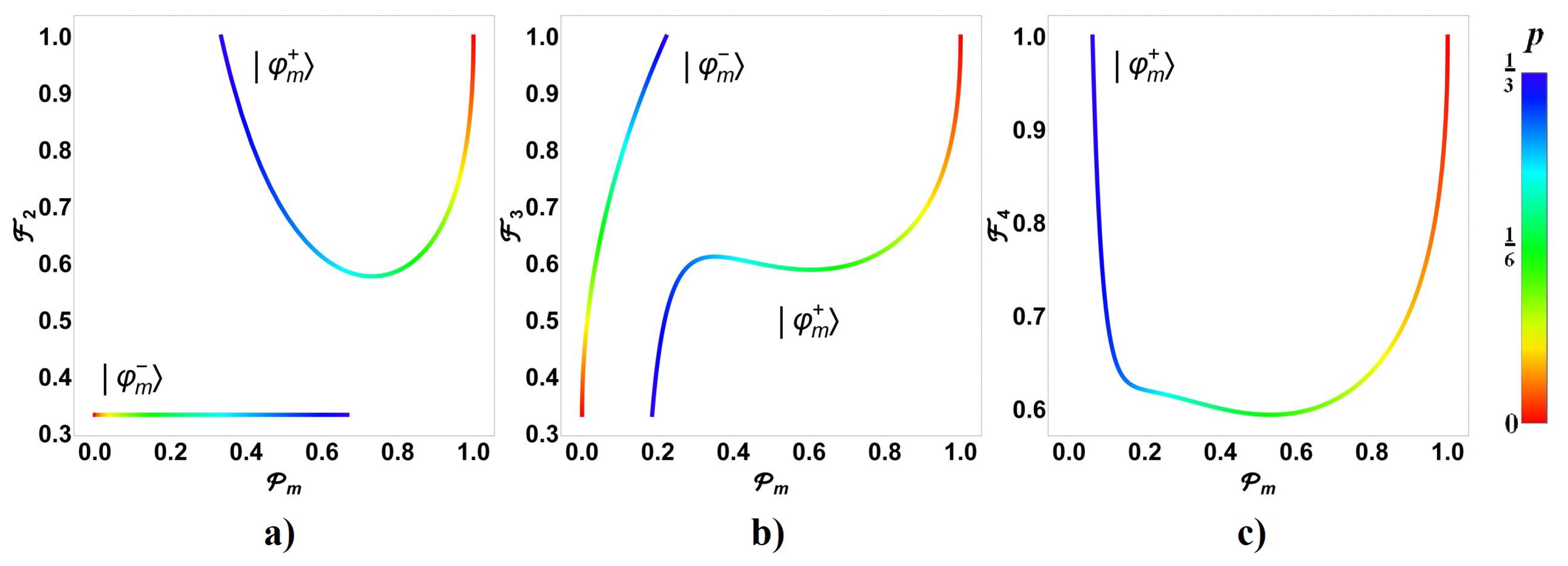
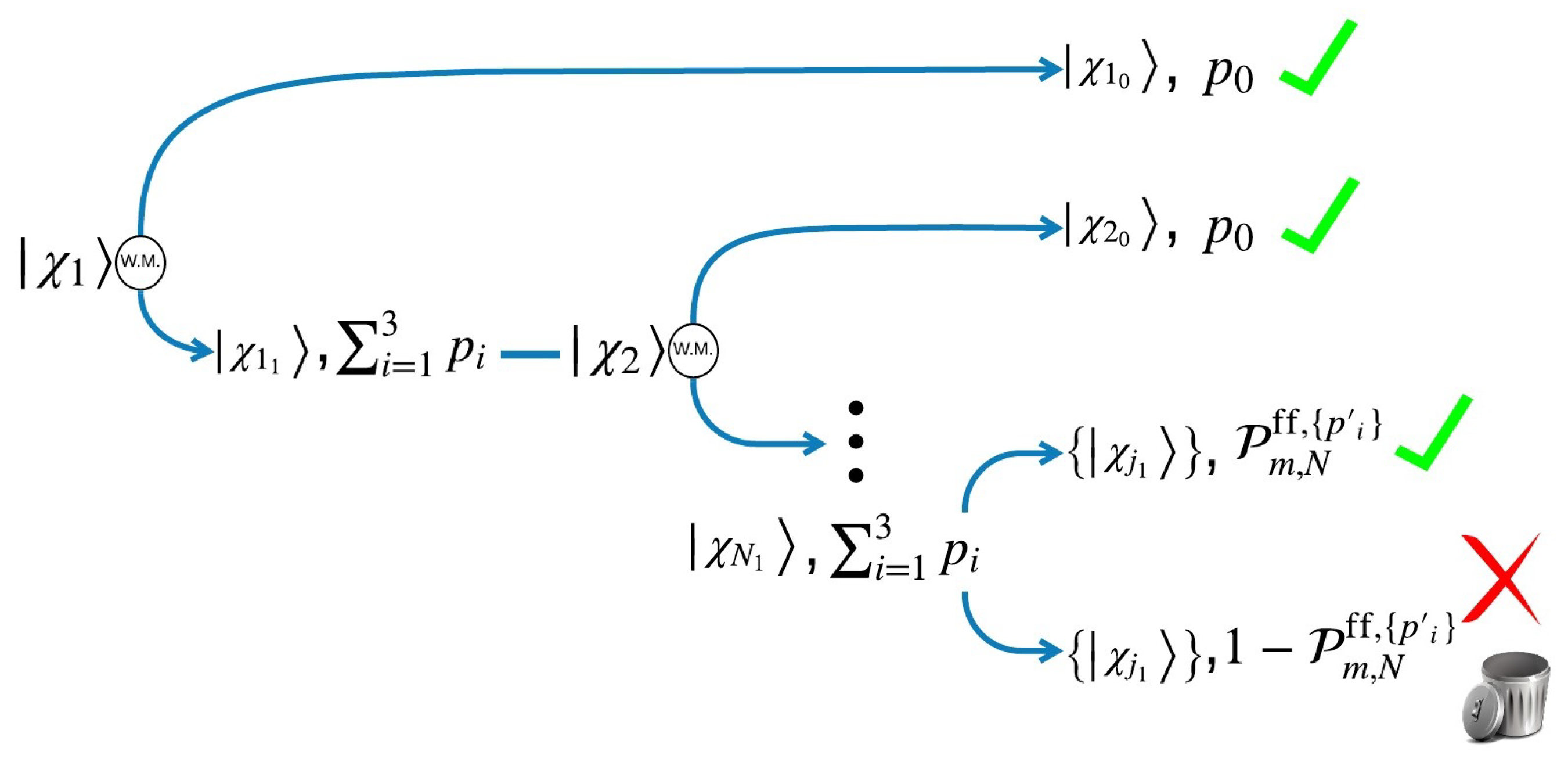
5.1. General Case for $N=2$ Assisted by a Weak Measurement

By considering first the following weak measurements on $|\chi \rangle$, we get the post-measurement states and their probabilities of occurrence:

$$\begin{array}{ccc}\hfill P_0& =& |{\beta }_0\rangle \langle {\beta }_0|\to |{\chi }_0\rangle =(P_0|\chi \rangle {)}_{\mathrm{norm}}=|{\beta }_0\rangle ,{\tilde{p}}_0=p_0\hfill \end{array}$$

(40)

$$\begin{array}{ccc}\hfill P_1& =& \mathbb{I}-P_0\to |{\chi }_1\rangle =(P_1|\chi \rangle {)}_{\mathrm{norm}}=\sum _{i=1}^3\sqrt{\frac{p_i}{{\tilde{p}}_1}}|{\beta }_i\rangle \equiv \sum _{i=1}^3\sqrt{p_i^{\prime }}|{\beta }_i\rangle ,{\tilde{p}}_1=\sum _{i=1}^3{p}_i\hfill \end{array}$$

(41)

which projects the entangled state on one of the two states $|{\chi }_0\rangle$ or $|{\chi }_1\rangle$ with probabilities ${\tilde{p}}_0$ or ${\tilde{p}}_1$ respectively. Each state is located on the origin or otherwise on the frontal face of the region in Figure 6. Then, if $|{\chi }_0\rangle$ is obtained, the teleportation process can go as in the Figure 1, otherwise, if $|{\chi }_1\rangle$ is obtained, we can try the teleportation assisted by indefinite causal order (at this point the reader could note that clearly, we need two entangled resources). We will come back to discuss the weak measurement strategy widely in the last section).

The entire process is depicted in the Figure 12, a schematic diagram of the process as it was originally proposed by [7]. Given certain state to teleport, we use certain entangled resource $|{\chi }_a\rangle$. It goes through the weak measurement in (40) to get $|{{\chi }_a}_0\rangle =|{\beta }_0\rangle$ with probability $p_0$. Then we perform a single teleportation. Instead, by obtaining $|{{\chi }_a}_1\rangle$ with probability $1-p_0$, then we prepare a second entangled resource $|{\chi }_b\rangle$ repeating with it the same procedure, if after of the weak measurement $|{{\chi }_b}_0\rangle = |{\beta }_0\rangle$ is obtained with probability $p_0$, we disregard $|{{\chi }_a}_1\rangle$ proceeding with a single teleportation using such state. Otherwise, if $|{{\chi }_b}_1\rangle$ is obtained, we perform a two-channel teleportation assisted by indefinite causal order using the states previously obtained. There, the teleportation will become successful with probability ${p^{\prime }}_1^2+{p^{\prime }}_2^2+{p^{\prime }}_3^2$, otherwise it becomes unsuccessful and we need disregard the process. Thus, the global probability of success is (there, ${\mathcal{P}}_{m,N=2}^{\mathrm{ff}}$ corresponds to (37) with $\theta =\frac{\pi }{2},\varphi =0$, renaming $p_i$ as $p_i^{\prime }$, with $p_1^{\prime }+p_2^{\prime }+p_3^{\prime }=1$):

$$\begin{array}{ccc}\hfill {\mathcal{P}}_{\mathrm{Tot}}& =& p_0+(1-p_0)p_0+{(1-p_0)}^2{\mathcal{P}}_{m,N=2}^{\mathrm{ff},\left\{p_i^{\prime }\right\}}\hfill \\ & =& p_0+(1-p_0)p_0+{(1-p_0)}^2\sum _{i=1}^3{p^{\prime }}_i^2=1-2(p_1{p}_2+p_2{p}_3+p_3{p}_1)\hfill \end{array}$$

(42)

The last function has been represented in the plots of Figure 13. For each initial set $(p_1,p_2,p_3)$ of the entangled resources (assumed identical), ${\mathcal{P}}_{\mathrm{Tot}}$ is plotted in color in agreement with the bar besides in the Figure 13a. One-third of the plot has shown, due to its symmetry, to exhibit its inner structure. The corresponding statistical distribution is obtained numerically in the Figure 13b by uniformly sampling the space in the figure on the left. The mean value of ${\mathcal{P}}_{\mathrm{Tot}}$ becomes 0.70 and their standard deviation 0.16.

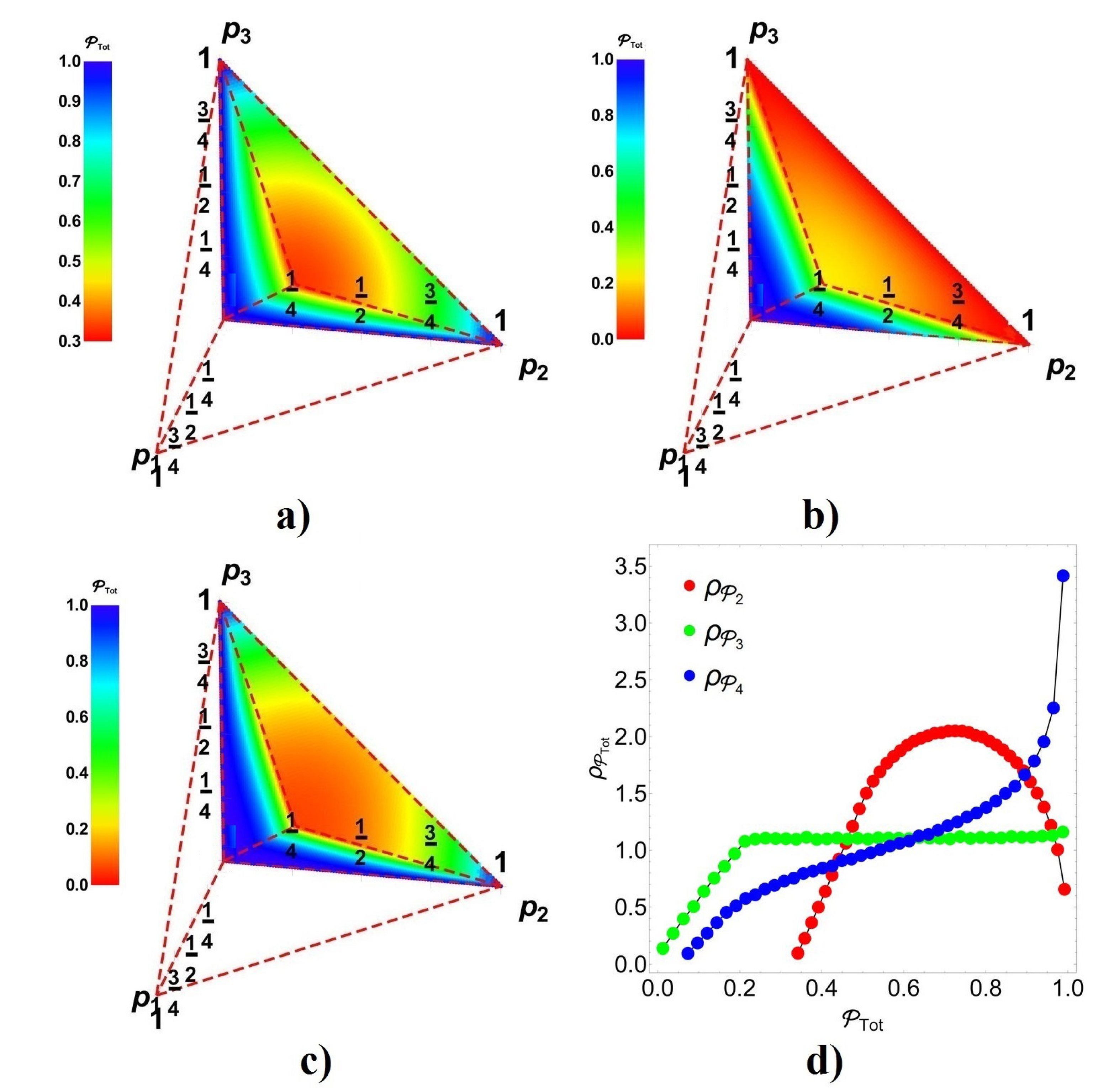
5.2. Cases for $N\ge 2$ Assisted by a Weak Measurement

For $N\ge 2$, the procedure follows as in the previous section by introducing N imperfect entangled resources, $|{\chi }_i\rangle$ (assumed identical for simplicity) but in each step, we decide if after of the weak measurement, the state $|{{\chi }_j}_0\rangle = |{\beta }_0\rangle$ is used to perform a single teleportation or if we continue the process of weak measurement N times on identical entangled resources $|{\chi }_j\rangle$ to finally get $|{{\chi }_N}_1\rangle ={\sum }_{i=1}^3{p}_i^{\prime }|{\beta }_i\rangle$ as in the Figure 12. The corresponding situation is now depicted for the general case in the Figure 14. In this case, the global probability of success becomes:

$$\begin{array}{c}\hfill {{\mathcal{P}}_{\mathrm{Tot}}}_N=\sum _{j=1}^N{p}_0{(1-p_0)}^{j-1}+{(1-p_0)}^N{\mathcal{P}}_{m,N}^{\mathrm{ff},\left\{p_i^{\prime }\right\}}.\end{array}$$

(43)

Inserting the formulas for ${\mathcal{P}}_{m,N}^{\mathrm{ff},\left\{p_i^{\prime }\right\}}$ in Appendix B (specialized for the frontal face $p_0=0$ and changing $p_i$ by $p_i^{\prime }$). Then, we can get the outcomes for global probability ${{\mathcal{P}}_{\mathrm{Tot}}}_N$ for the last cases with $\mathcal{F}=1$:

$$\begin{array}{ccc}\hfill {{\mathcal{P}}_{\mathrm{Tot}}}_2& =& 1-2(p_1{p}_2+p_1{p}_3+p_2{p}_3)\hfill \end{array}$$

(44)

$$\begin{array}{ccc}\hfill {{\mathcal{P}}_{\mathrm{Tot}}}_3& =& 1-(p_1^3+p_2^3+p_3^3)-3(p_1^2(p_2+p_3)+p_2^2(p_1+p_3)+p_3^2(p_1+p_2))\hfill \\ \hfill {{\mathcal{P}}_{\mathrm{Tot}}}_4& =& 1-4(p_1^3(p_2+p_3)+p_2^3(p_1+p_3)+p_3^3(p_1+p_2))\hfill \end{array}$$

(45)

$$\begin{array}{ccc}& & -12p_1{p}_2{p}_3(p_1+p_2+p_3)-\frac{16}{3}(p_1^2{p}_3^2+p_2^2{p}_3^2+p_1^2{p}_2^2).\hfill \end{array}$$

(46)

Now, we can visualize last outcomes for ${\mathcal{P}}_{\mathrm{Tot}}$ in Figure 15. Again, all the entangled states used for the teleportation process are assumed to be identical by simplicity. Figure 15a–c depict the probability ${{\mathcal{P}}_{\mathrm{Tot}}}_N$ to reach $\mathcal{F}=1$ in the entire process represented in color. Each color bar shows the entire range of values for such probabilities on the graphs. According to the color, the blue zone represents the region where ${\mathcal{P}}_{\mathrm{Tot}}\to 1$, observing for the case $N=4$ a larger blue area, suggesting still the goodness of increase the number of teleportation channels under indefinite causal order combined with post-measurement.

Figure 15d depicts a numerical analysis of statistical distribution for the cases $N=2,3,4$. Note that for $N=3$, all greater values for the probability occur almost evenly. For the case $N=4$, it is observed a larger amount of success probabilities than failure probabilities compared with $N=3$. Despite, ${\mu }_{{{\mathcal{P}}_{\mathrm{Tot}}}_2}\approx 0.702,{\sigma }_{{{\mathcal{P}}_{\mathrm{Tot}}}_2}\approx 0.158$ and ${\mu }_{{{\mathcal{P}}_{\mathrm{Tot}}}_4}\approx 0.667,{\sigma }_{{{\mathcal{P}}_{\mathrm{Tot}}}_4}\approx 0.249$ (because for $N=2$ there are a large distribution for medium success probabilities). In any case, the most successful outcomes of teleportation appears for $N=4$.

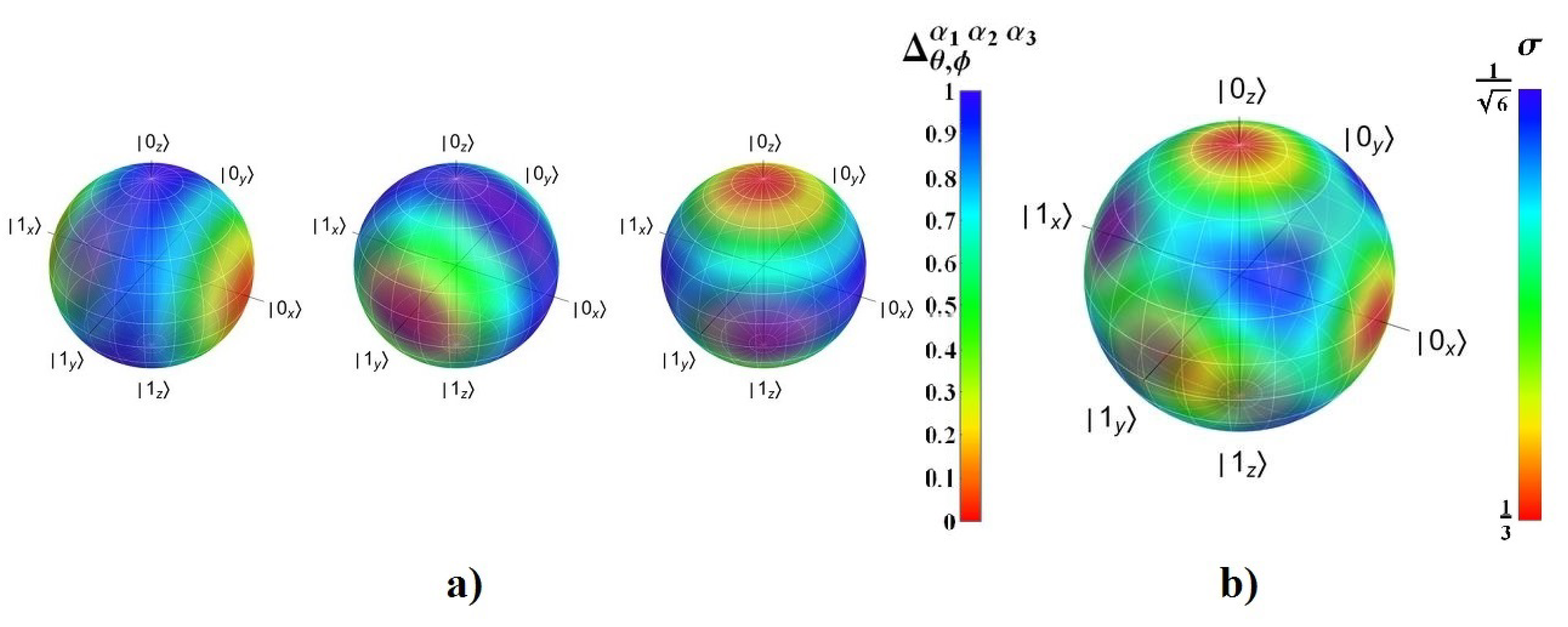
6. Experimental Deployment of Teleportation with Indefinite Causal Order

In this section, we comment on some main experimental developments for a possible deployment of indefinite causal order in teleportation. We begin with the procedure to set the weak measurement used in Section 5.1. Afterwards, we set some elements and experimental developments to propose the implementation of the theoretical proposal before presented.

6.1. Implementation of Weak Measurement to Project $|\chi \rangle$

In Section 5.1, we stated the implementation of a weak measurement to project $|\chi \rangle$ conveniently onto $|{\chi }_0\rangle =|{\beta }_0\rangle$ or $|{\chi }_1\rangle ={\sum }_{i=1}^3{p}_i^{\prime }|{\beta }_i\rangle$. Despite, in the experimental approach, there are certain differences due to the resources been used. In this section, we present how to afford the weak measurement stated in (40). We use an ancilla qubit $|0_a\rangle$ to do the measurement minimizing the impact on $|\chi \rangle$ as is desired. In this implementation, we will use as a central resource the Toffoli gate. In order to prepare the $|\chi \rangle$ stated properly for such measurement, we combine it with the ancilla. Then, we send the combined system into the circuit presented in Figure 16a. This circuit employs the Toffoli gate ${\mathcal{T}}_{1,2,a}$ on channels $1,2$ for $|\chi \rangle$ and a for $|0_a\rangle$ together with the $C^{1}No{t}_2$ gate (already developed for ions [25,26] and photons [27]). In fact, it is well-known that Toffoli gate can be performed using $CNOT$ gates and single-qubit gates [14] o by means of the Sleator–Weinfurter construction [28], despite other more efficient developments are known for ions [29] and photons [30]. Some single-qubit gates as Hadamard ($\mathcal{H}$) and Not ($\mathcal{X}$) are also used. In the following development, we write $|\chi \rangle ={\sum }_{i=0}^3\sqrt{p_i^{*}}|{\beta }_i\rangle$ as the imperfect entangled resource (be aware that * not means complex conjugation). Thus, all necessary quantum gates have been experimentally developed in our days at least in quantum optics.

A direct calculation shows that this circuit performs the following transformation on $|{\psi }_0\rangle =|\chi \rangle \otimes |0_a\rangle$ into:

$$\begin{array}{ccc}\hfill |{\psi }_1\rangle & =& \sqrt{p_0}|{\beta }_0\rangle \otimes |1_a\rangle +\left(\sqrt{p_1}|{\beta }_1\rangle +\sqrt{p_2}|{\beta }_2\rangle +\sqrt{p_3}|{\beta }_3\rangle \right)\otimes |0_a\rangle \hfill \end{array}$$

(47)

$$\begin{array}{ccc}& \mathrm{with}:& \sqrt{2p_0}=\sqrt{p_0^{*}}-\sqrt{p_3^{*}},\sqrt{2p_1}=\sqrt{p_1^{*}}-\sqrt{p_2^{*}},\hfill \\ & & \sqrt{2p_2}=\sqrt{p_0^{*}}+\sqrt{p_3^{*}},\sqrt{2p_3}=\sqrt{p_1^{*}}+\sqrt{p_2^{*}}\hfill \end{array}$$

(48)

Just before of the projective measurement on the qubit a shown in the Figure 16a. Clearly, after measurement, two possible outcomes arise in the qubit a, $|1_a\rangle ,|0_a\rangle$ while on qubits $1,2$ the outcomes are $|{\chi }_0\rangle =|{\beta }_0\rangle$, $|{\chi }_1\rangle ={\sum }_{i=1}^3\sqrt{p_i^{\prime }}|{\beta }_i\rangle$ respectively as in the Section 5.1, thus completing the weak measurement. The only difference with respect our previous development is that those coefficients are not the original $\left\{p_i^{*}\right\}$. Despite this, in the event that such coefficients are unknown, this fact is not important, the really outstanding outcome is that this procedure projects the state into the perfect Bell state to perform the teleportation $|{\beta }_0\rangle$ or otherwise on the frontal face if this resource is planned to be used under indefinite causal order and measurement (as it was previously depicted in the procedure of Section 5.1). Anyway, Figure 16b shows the contour plots of $p_1^{*}$ (red), $p_2^{*}$ (green) and $p_3^{*}$ (blue) in the region $(p_1,p_2,p_3)$ as a reference of the involved geometric transformations.

6.2. An Insight View about Teleportation Implementing Indefinite Causal Orders Experimentally with Light

Formula (1) regards the teleportation algorithm as a quantum communication channel. Despite this formula being a useful simplification for the theoretical analysis, it expresses the teleportation channel with the input and output through the same system, which is not precisely the real experimental situation. Then, as it was true for the original implementation of the original teleportation proposal [9] in [31], the deployment should be modified to have a correct approach to the theory. In this section we discuss an insight view into the experimental deployment together with indefinite causal order based on current techniques and experimental developments.

A possible implementation with light should to consider an initial state with at least three initial photons exhibiting each one at least a pair of quantum variables as polarization, frequency or spatial localization ($\mathbf{k}$-vector state) among others (as in the original experimental teleportation proposal [31]): $|{\psi }_0\rangle ={|v\rangle }_1\otimes {|v\rangle }_a\otimes {|v\rangle }_b$, using polarization in the vertical direction as instance. Those photons should then be converted into five photons by splitting the last two into entangled pairs using Spontaneous Parametric Down Conversion (SPDC) [32] as instance, while the first state is arbitrarily rotated by a quartz polarization rotator (QPR) [33] -to generate the state to teleportate-: $|{\psi }_1\rangle =(\alpha {|v\rangle }_1+\beta {|h\rangle }_1)\otimes \frac{1}{\sqrt{2}}({|v\rangle }_2{|h\rangle }_3+{|h\rangle }_2{|v\rangle }_3)\otimes \frac{1}{\sqrt{2}}({|v\rangle }_4{|h\rangle }_5+{|h\rangle }_4{|v\rangle }_5)$. After, five photons should be sent together into two alternative directions (through a dichroic beamsplitter—a splitting wavelength dependent—instead a polarization beamsplitter) coincidentally, not independently (it means five photons will travel through corresponding paths labeled by $p_A$ or $p_B$). This beamsplitter (BS) works as our control state superposing the two path states (the two causal orders further). Last effect should be solved based on the frequency of original photons which should be quantum generated to let a quantum splitting of all beams (or otherwise based on the previous generation of a $GHZ$ state [34]). This necessary beamsplitter is still a cutting-edge technology. Such spatial quantization introduces an additional quantum variable thus converting the initial state into (removing the tensor product symbols for the sake of simplicity):

$$\begin{array}{c}\hfill |{\psi }_2\rangle =\frac{1}{\sqrt{8}}((\alpha {|v\rangle }_1+\beta {|h\rangle }_1){|p_A\rangle }_1({|v\rangle }_2{|h\rangle }_3+{|h\rangle }_2{|v\rangle }_3){|p_A\rangle }_2{|p_A\rangle }_3({|v\rangle }_4{|h\rangle }_5+{|h\rangle }_4{|v\rangle }_5){|p_A\rangle }_4{|p_A\rangle }_5\\ \hfill +(\alpha {|v\rangle }_1+\beta {|h\rangle }_1){|p_B\rangle }_1({|v\rangle }_2{|h\rangle }_3+{|h\rangle }_2{|v\rangle }_3){|p_B\rangle }_2{|p_B\rangle }_3({|v\rangle }_4{|h\rangle }_5+{|h\rangle }_4{|v\rangle }_5){|p_B\rangle }_4{|p_B\rangle }_5)\end{array}$$

(49)

If additionally we introduce certain optical distortion in the SPDC, we get imperfect entangled states then changing each $\frac{1}{\sqrt{2}}({|v\rangle }_i{|h\rangle }_j+{|h\rangle }_i{|v\rangle }_j)$ by ${|\chi \rangle }_{ij}$. In the following, we will change $v,h$ by $0,1$ respectively for simplicity.

Note that teleportation is, in a certain sense, automatically generated due to the non-locality of the resource $|{\beta }_0\rangle$ (or imperfectly by $|\chi \rangle$), then collapsed on four adequate outcomes involving an additional correction as a function of those outcomes using classical communication (Figure 1a). In addition, for two sequential teleportation channels, the process can be achieved by post-measurement at the end of both processes. Nevertheless, the implementation of indefinite causal order in teleportation introduces additional challenges due to the connectivity of paths and measurements. In the process, it will be required the implementation of the $SWAP$ gate, which has already been experimentally performed in optics [35,36].

Thus, Figure 17 depicts a possible implementation for two teleportation processes assisted by indefinite causal order. The first photon goes to the QRP and then the five photons go through the coordinated BS. The proposed process can be then followed in the Figure 17 with paths labeled by $p_A$ in green and $p_B$ in red. For simplicity, teleportation processes are assumed to perform measurements on the Bell states basis as in Figure 1b, thus avoiding the use of H and $CNOT$ gates in the analysis. Due to the above construction (post-measurement and measurement assumed on the Bell basis), almost no gates are present in the process, just two $SWAP$ gates stating the causal connections. At the end of each path, a semi-transparent mirror should mix again the paths (but not the polarization) by pairs into the basis ${|\pm \rangle }_i=\frac{1}{2}({|p_A\rangle }_i\pm {|p_B\rangle }_i)$ for each photon i, in order to erase the information of the path followed. We labeled each path (or the information being carried on it) by $M_{ij}^k$ (in case that photon carries the information of one of the complementary systems not containing the output of teleportation) remarking the path type followed $k=A,B,+,-$; the final belonging teleportation process $i=1,2$; and the number of the sequential qubit to be measured there: $j=1$ for the former input and $j=2$ for the correspondent to the first qubit of the original entangled resource. Instead, the final outputs are labeled by $S^k$ ($k=A,B,+,-$). By following the color, the reader should easily identify each path considering additionally the effect of the intermediate use of $SWAP$ gates which is discussed below.

By ignoring first the $SWAP$ gates in the Figure 17, we can realize that the circuit has not any effect. We have indicated each optical element described before. The dotted line connecting the $BS$’s denotes the not independent functioning, all together should send the five photons on the green paths or on the red ones. States $|\psi \rangle$ and $|\chi \rangle$ are remarked on photons 1 and $2,3,4,5$ respectively. Each path (green or red) is labeled from 1 to 5 in agreement with the photon carried out. Blue arrow remarks the group of photons involved in each teleportation process ${\mathcal{T}}_1$ or ${\mathcal{T}}_2$ on each path (the first subscript in $M_{ij}^k$): $1,2,3$ and $3,4,5$ respectively for the green paths, and $1,4,5$ and $5,2,3$ respectively for the red ones. On each path, we reported the associated label for each system $S^k$ or $M_{ij}^k$ as it was depicted before. Note that brown labels correspond to the information being carried before of $SWAP$ gates, while black labels are the final states reported there at the end of the path but before of the recombining in the semi-transparent mirrors. The reason for the $SWAP$ gate between the paths 3 and 5 should be clear, we need to get the teleportation outputs on the same photon to generate the superposition of information. The $SWAP$ gate on the red paths 2 and 4 exchanges the information on those paths in order to generate the superposition at the end among path information $M_{ij}^1$ and $M_{i^{\prime }j}^2$ with $i\ne i^{\prime }$, $j=1,2$ thus mixing both. Note that the set of states in $M_{ij}^k$ are those to be measured in the teleportation process (here in the Bell basis by pairs) in order to correct the output states. The reader should advise this process does not reproduce exactly that depicted by (1) because such formula assumes the measurements are internal operations generating a mixed state coming from the corresponding projections and corrections. In this approach, we have the possibility to measure only four qubits instead of eight. Despite, we will note this procedure still reproduces some of the main previous features analyzed. At the end of the process, each semi-transparent mirror (diagonal in grey) mixes the information on the states ${|\pm \rangle }_i$ for each photon i on the red and green edges (with information $M_{ij}^{\pm }$ or $S^{\pm }$ respectively -red and green-, not represented in the Figure 17). On the red edges, a detector first decides if the photon exits through them (they are the projective measurement on $|{\phi }_m^{\pm }\rangle$ states in our development). In addition, a Bell measurement is then performed on each pair $1,3$ and $2,4$ in order to inquire the information codified in the output $S^{+}$.

A direct but large calculation to expand (49) then applying the $SWAP$ gates and projecting on ${|+\rangle }_i,i=1,...,5$ was performed. Finally, this output was written in terms of $|{\beta }_i{\rangle }_{1,3}\otimes {|{\beta }_j\rangle }_{2,4},i,j=0,...,3$ to ease the identification of final successful measurements. If $p_0=1$ or $p_0=0$, upon the measurement of $|{\beta }_i{\rangle }_{1,3}\otimes {|{\beta }_j\rangle }_{2,4}$ and then the application of ${\sigma }_i{\sigma }_j$ as correction, the output $S^{+}$ becomes $|\psi \rangle$ faithfully in the following cases:

• If $p_0=1$ for all $i,j=0,\dots ,3$ cases with a global successful probability of $\frac{1}{16}$.
• If $p_0=0$ for the cases $i=0,\dots ,3$ and $j=2$ with a global successful probability of $\frac{{(p_1-p_2+p_3)}^2}{64}$.

This clearly resembles our main outcomes. For the second case, other measurement outcomes give imperfect teleportation thus rearranging the success probabilities with respect of those in our theoretical development. Thus, alternative experimental proposals should be developed to approach them into the ideal case considered in our theoretical results.

7. Conclusions

Quantum teleportation has an important role in quantum processing for the transmission of quantum information, nevertheless, there are possible issues on the entangled resource assisting the teleportation process mainly related to its maintenance and precise generation. It introduces imprecision in the teleported state. In this work, the implementation of indefinite causal order has been studied in order to propose an improved scheme to tackle such imprecision on the entangled state when it is combined with the measurement of the control assessing it.

The analysis for the redundant case where quantum channels are simply applied sequentially (assumed as identical) shows that the number N of channels applied, rapidly decreases the fidelity converging to the maximal depolarization of the teleported state thus obtaining ${\mathcal{F}}_{N\to \infty }=\frac{1}{2}$. By modifying the process under indefinite causal order for two or more teleportation channels as it was proposed by [7] and later discussed in [22], we advise advantages on the quantum fidelity of the teleported state for the first values N of sequential teleportation channels. From the outcomes, a categorization was performed to analyze the effects on the entangled state, thus obtaining a surprising enhancement for the most imperfect entangled resource, $p_0=0$ with the absence of the ideal entangled resource $|{\beta }_0\rangle$, and still for near regions of it with $p_0\approx 0$ when N increases. Notably, in the first case, it is possible to obtain a perfect teleportation process with ${\mathcal{F}}_N=1$. However, when N increases, the principal downside is the reduction of the probability of successful measurement ${\mathcal{P}}_m$, which decreases drastically as N increases.

In order to improve the global probability of success, we have proposed the combined use of weak measurement to first projecting the entangled resource to either $p_0=1$ with $p_1,p_2,p_3=0$ or $p_1+p_2+p_3=1$ with $p_0=0$, where the indefinite causal order generates the most notable enhancements. In such cases, $\mathcal{F}=1$ is obtained always and ${\mathcal{P}}_m$ is improved. Those notable processes are possible as for pure as for mixed states [8]. A remarkable aspect is that for such a notable case the outcome is independent of the teleported state.

Finally, a more detailed process for the weak measurement (first barely discussed in the initial presentation) is after detailed and oriented to the practical implementation in terms of the current experimental developments for light and matter. The development of a Toffoli gate is advised as central in the implementation. In addition, an introductory analysis for a possible experimental implementation has been included for the teleportation process under indefinite causal order using two teleportation channels. Such an approach is still imperfect and not optimal. Despite this, it reproduces the main features found in our development. In the proposal, recent experiments and technological developments in optics become central, particularly the implementation of the $SWAP$ gate and the generation of $|GHZ\rangle$ states. A valuable aspect being noticed is the use of post-measurement in the teleportation process. Additional theoretical and experimental developments should still improve the vast possibilities of indefinite causal order in the teleportation research field.