Soliton Behaviours for the Conformable Space–Time Fractional Complex Ginzburg–Landau Equation in Optical Fibers
Abstract
:1. Introduction
2. Conformable Fractional Derivative
3. Mathematical Analysis and Equations
3.1. Description of the Method
3.2. Travelling Wave Reduction for Equation (1)
4. Solitons with Kerr Law Nonlinearity
5. Solitons with Power Law Nonlinearity
6. Solitons with Dual-Power Law Nonlinearity
6.1. First Type of Optical Soliton Solution
6.2. Second Type of Optical Soliton Solution
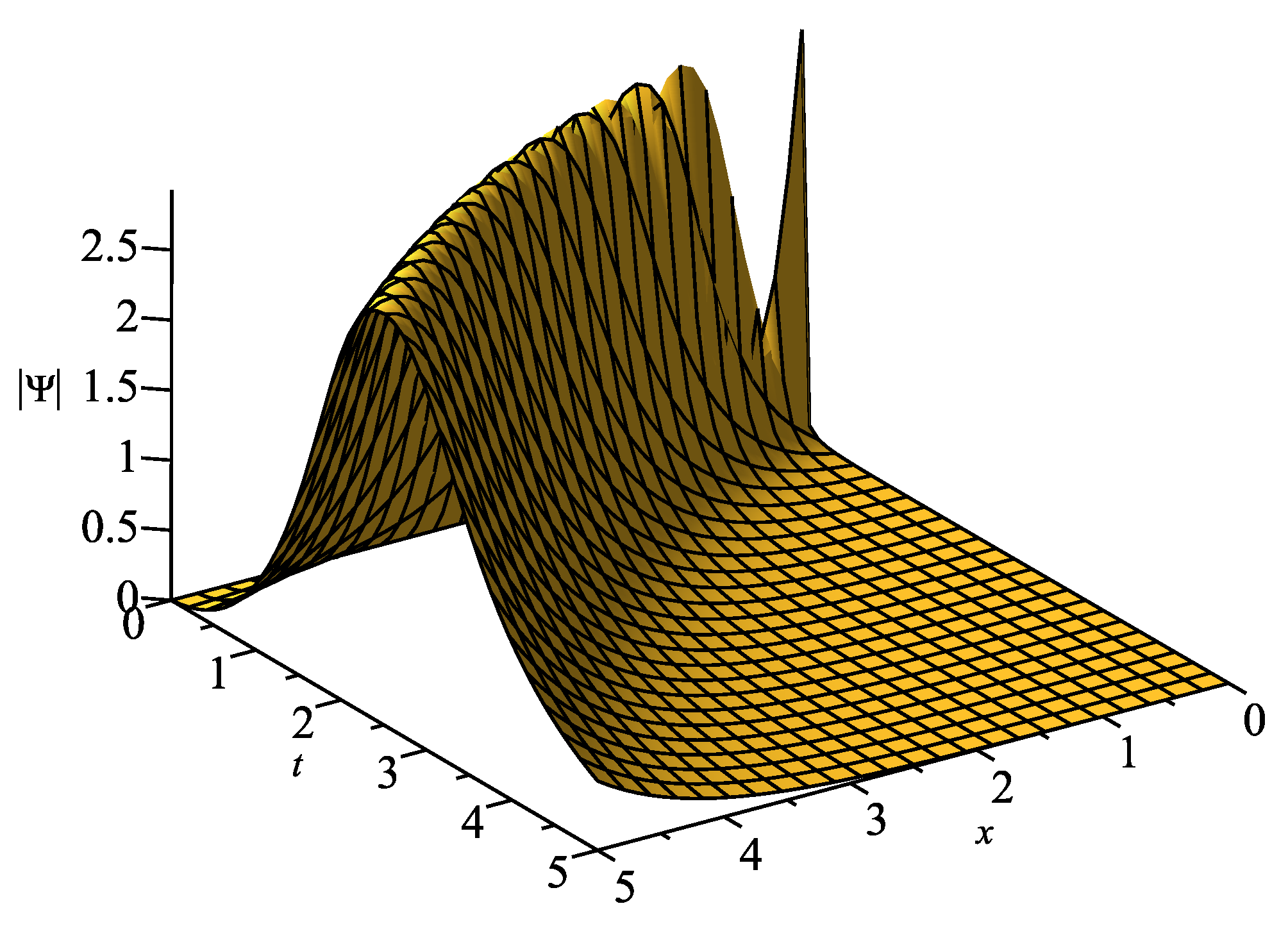
7. Interpreting Graphical Representations
8. Discussion and Conclusions
Funding
Conflicts of Interest
References
- Porsezian, K.; Nakkeeran, K. Optical solitons in presence of Kerr dispersion and self-frequency shift. Phys. Rev. Lett. 1996, 76, 3955. [Google Scholar] [CrossRef]
- Gedalin, M.; Scott, T.; Band, Y. Optical solitary waves in the higher order nonlinear Schrödinger equation. Phys. Rev. Lett. 1997, 78, 448. [Google Scholar] [CrossRef] [Green Version]
- Radhakrishnan, R.; Kundu, A.; Lakshmanan, M. Coupled nonlinear Schrödinger equations with cubic-quintic nonlinearity: Integrability and soliton interaction in non-Kerr media. Phys. Rev. E 1999, 60, 3314. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hong, W.P. Optical solitary wave solutions for the higher order nonlinear Schrödinger equation with cubic-quintic non-Kerr terms. Opt. Commun. 2001, 194, 217–223. [Google Scholar] [CrossRef]
- Biswas, A.; Konar, S. Introduction to non-Kerr Law Optical Solitons; Chapman and Hall/CRC: London, UK, 2006. [Google Scholar]
- Biswas, A.; Mirzazadeh, M.; Savescu, M.; Milovic, D.; Khan, K.R.; Mahmood, M.F.; Belic, M. Singular solitons in optical metamaterials by ansatz method and simplest equation approach. J. Mod. Opt. 2014, 61, 1550–1555. [Google Scholar] [CrossRef]
- Zayed, E.; Alurrfi, K. New extended auxiliary equation method and its applications to nonlinear Schrödinger-type equations. Optik 2016, 127, 9131–9151. [Google Scholar] [CrossRef]
- Arnous, A.H.; Ullah, M.Z.; Moshokoa, S.P.; Zhou, Q.; Triki, H.; Mirzazadeh, M.; Biswas, A. Optical solitons in birefringent fibers with modified simple equation method. Optik 2017, 130, 996–1003. [Google Scholar] [CrossRef]
- Al-Ghafri, K. Soliton-type solutions for two models in mathematical physics. Waves Random Complex Media 2018, 28, 261–269. [Google Scholar] [CrossRef]
- Biswas, A.; Ekici, M.; Sonmezoglu, A.; Zhou, Q.; Moshokoa, S.P.; Belic, M. Chirped solitons in optical metamaterials with parabolic law nonlinearity by extended trial function method. Optik 2018, 160, 92–99. [Google Scholar] [CrossRef]
- Foroutan, M.; Manafian, J.; Ranjbaran, A. Solitons in optical metamaterials with anti-cubic law of nonlinearity by generalized G′/G-expansion method. Optik 2018, 162, 86–94. [Google Scholar] [CrossRef]
- Biswas, A.; Rezazadeh, H.; Mirzazadeh, M.; Eslami, M.; Ekici, M.; Zhou, Q.; Moshokoa, S.P.; Belic, M. Optical soliton perturbation with Fokas–Lenells equation using three exotic and efficient integration schemes. Optik 2018, 165, 288–294. [Google Scholar] [CrossRef]
- Al-Ghafri, K.S. Solitary wave solutions of two KdV-type equations. Open Phys. 2018, 16, 311–318. [Google Scholar] [CrossRef]
- Al-Ghafri, K.; Krishnan, E.; Biswas, A.; Ekici, M. Optical solitons having anti-cubic nonlinearity with a couple of exotic integration schemes. Optik 2018, 172, 794–800. [Google Scholar] [CrossRef]
- Biswas, A.; Arshed, S. Application of semi-inverse variational principle to cubic-quartic optical solitons with kerr and power law nonlinearity. Optik 2018, 172, 847–850. [Google Scholar] [CrossRef]
- Kader, A.A.; Latif, M.A.; Zhou, Q. Exact optical solitons in metamaterials with anti-cubic law of nonlinearity by Lie group method. Opt. Quantum Electron. 2019, 51, 30. [Google Scholar] [CrossRef]
- Krishnan, E.; Biswas, A.; Zhou, Q.; Alfiras, M. Optical soliton perturbation with Fokas–Lenells equation by mapping methods. Optik 2019, 178, 104–110. [Google Scholar] [CrossRef]
- Zayed, E.M.; Alngar, M.E.; Al-Nowehy, A.G. On solving the nonlinear Schrödinger equation with an anti-cubic nonlinearity in presence of Hamiltonian perturbation terms. Optik 2019, 178, 488–508. [Google Scholar] [CrossRef]
- Al-Ghafri, K. Different Physical Structures of Solutions for a Generalized Resonant Dispersive Nonlinear Schrödinger Equation with Power Law Nonlinearity. J. Appl. Math. 2019, 2019. [Google Scholar] [CrossRef]
- Al-Ghafri, K.; Rezazadeh, H. Solitons and other solutions of (3 + 1)-dimensional space–time fractional modified KdV–Zakharov–Kuznetsov equation. Appl. Math. Nonlinear Sci. 2019, 4, 289–304. [Google Scholar] [CrossRef] [Green Version]
- Oliveira, D.S.; de Oliveira, E.C. On a Caputo-type fractional derivative. Adv. Pure Appl. Math. 2019, 10, 81–91. [Google Scholar] [CrossRef]
- Atanacković, T.M.; Pilipović, S.; Zorica, D. Properties of the Caputo-Fabrizio fractional derivative and its distributional settings. Fract. Calc. Appl. Anal. 2018, 21, 29–44. [Google Scholar] [CrossRef] [Green Version]
- Ortigueira, M.D. Fractional Calculus for Scientists and Engineers; Springer Science & Business Media: Berlin, Germany, 2011; Volume 84. [Google Scholar]
- Jacobs, B.A. A new Grünwald-Letnikov derivative derived from a second-order scheme. Abstr. Appl. Anal. 2015, 2015, 952057. [Google Scholar] [CrossRef] [Green Version]
- Khalil, R.; Al Horani, M.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Tasbozan, O.; Kurt, A.; Tozar, A. New optical solutions of complex Ginzburg–Landau equation arising in semiconductor lasers. Appl. Phys. B 2019, 125, 104. [Google Scholar] [CrossRef]
- Sulaiman, T.A.; Baskonus, H.M.; Bulut, H. Optical solitons and other solutions to the conformable space–time fractional complex Ginzburg–Landau equation under Kerr law nonlinearity. Pramana 2018, 91, 58. [Google Scholar] [CrossRef]
- Mirzazadeh, M.; Ekici, M.; Sonmezoglu, A.; Eslami, M.; Zhou, Q.; Kara, A.H.; Milovic, D.; Majid, F.B.; Biswas, A.; Belić, M. Optical solitons with complex Ginzburg–Landau equation. Nonlinear Dyn. 2016, 85, 1979–2016. [Google Scholar] [CrossRef]
- Arnous, A.H.; Seadawy, A.R.; Alqahtani, R.T.; Biswas, A. Optical solitons with complex Ginzburg–Landau equation by modified simple equation method. Optik 2017, 144, 475–480. [Google Scholar] [CrossRef]
- Inc, M.; Aliyu, A.I.; Yusuf, A.; Baleanu, D. Optical solitons for complex Ginzburg–Landau model in nonlinear optics. Optik 2018, 158, 368–375. [Google Scholar] [CrossRef]
- Arshed, S. Soliton solutions of fractional complex Ginzburg–Landau equation with Kerr law and non-Kerr law media. Optik 2018, 160, 322–332. [Google Scholar] [CrossRef]
- Biswas, A.; Yildirim, Y.; Yasar, E.; Triki, H.; Alshomrani, A.S.; Ullah, M.Z.; Zhou, Q.; Moshokoa, S.P.; Belic, M. Optical soliton perturbation with complex Ginzburg–Landau equation using trial solution approach. Optik 2018, 160, 44–60. [Google Scholar] [CrossRef]
- Rezazadeh, H. New solitons solutions of the complex Ginzburg-Landau equation with Kerr law nonlinearity. Optik 2018, 167, 218–227. [Google Scholar] [CrossRef]
- Raza, N. Exact periodic and explicit solutions of the conformable time fractional Ginzburg Landau equation. Opt. Quantum Electron. 2018, 50, 154. [Google Scholar] [CrossRef]
- Biswas, A. Chirp-free bright optical solitons and conservation laws for complex Ginzburg-Landau equation with three nonlinear forms. Optik 2018, 174, 207–215. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, S.; Wei, L.; Guan, B. Exact solutions to complex Ginzburg–Landau equation. Pramana 2018, 91, 29. [Google Scholar] [CrossRef]
- Ahmed, I.; Seadawy, A.R.; Lu, D. Combined multi-waves rational solutions for complex Ginzburg–Landau equation with Kerr law of nonlinearity. Mod. Phys. Lett. A 2019, 34, 1950019. [Google Scholar] [CrossRef]
- Arshed, S.; Biswas, A.; Mallawi, F.; Belic, M.R. Optical solitons with complex Ginzburg–Landau equation having three nonlinear forms. Phys. Lett. A 2019, 383, 126026. [Google Scholar] [CrossRef]
- Lawden, D.F. Elliptic Functions and Applications; Springer-Verlag: New York, NY, USA, 1989; Volume 80. [Google Scholar]
- Chen, Y.; Yan, Z. The Weierstrass elliptic function expansion method and its applications in nonlinear wave equations. Chaos Solitons Fractals 2006, 29, 948–964. [Google Scholar] [CrossRef] [Green Version]



© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Ghafri, K.S. Soliton Behaviours for the Conformable Space–Time Fractional Complex Ginzburg–Landau Equation in Optical Fibers. Symmetry 2020, 12, 219. https://doi.org/10.3390/sym12020219
Al-Ghafri KS. Soliton Behaviours for the Conformable Space–Time Fractional Complex Ginzburg–Landau Equation in Optical Fibers. Symmetry. 2020; 12(2):219. https://doi.org/10.3390/sym12020219
Chicago/Turabian StyleAl-Ghafri, Khalil S. 2020. "Soliton Behaviours for the Conformable Space–Time Fractional Complex Ginzburg–Landau Equation in Optical Fibers" Symmetry 12, no. 2: 219. https://doi.org/10.3390/sym12020219
APA StyleAl-Ghafri, K. S. (2020). Soliton Behaviours for the Conformable Space–Time Fractional Complex Ginzburg–Landau Equation in Optical Fibers. Symmetry, 12(2), 219. https://doi.org/10.3390/sym12020219





