Approximate Solutions of the LRS Bianchi Type-I Cosmological Model

Abstract

In this current study, we explore the modified homogeneous cosmological model in the background of LRS Bianchi type-I space–time. For this purpose, we employ the Homotopy Perturbation Method (HPM). HPM is an analytical-based method. Further, we calculated the main field equations of the cosmological model LRS Bianchi type-I space–time. Furthermore, we discuss the necessary calculations of HPM. Therefore, we investigate the analytical solution of our problem by adopting HPM. In this response, we discuss five different values of parameter n. We also give a brief discussion about solutions. The main purpose of this study is to apply the application of HPM in the cosmological field.

1. Introduction

It is fact that the analytical treatment of cosmological models is a challenging task. Finding the exact solutions is seldom problematic and it is not considered easy. This is identified with the major non-linearity of the fundamental conditions in cosmology. This issue turns out to be exceptionally troublesome. In this response, different approximate and analytically schemes are employed to find exact and approximate solutions of different cosmological problems, for example, weak-field scheme in General Relativity (GR) [1,2,3,4], the slow-roll calculation in inflationary cosmology, etc. Significantly, over the span of such approximations, one needs to overlook a few terms in the equations, while osing the universality of the calculated solutions. The fundamental equation used is known as the Friedmann equation. Meanwhile, this equation is important to numerous cosmological models [5,6,7,8].

The HPM was introduced by the Chinese mathematician named He [9] in 1999 to solve differential and integral equations. The essential idea of this method was to introduce a homotopy parameter p, where $p\in [0,1]$. When $p=0$ the system of differential or integral equations reduces to a simplified form. As p increases to 1, the system goes to a sequence of deformation, the solution of each of which is close to that at the previous stage of the deformation, the system takes the original form of the equation at $p=1$ and final stage of deformation gives the desired solutions. Therefore, this method has been broadly considered over several years and effectively employed by various researchers [10,11,12,13,14,15,16,17]. It is recognized that HPM is a combination of homotopy in topology and classic perturbation techniques. The HPM has a huge preferred position in that it gives an analytical approximate solution for a wide scope of nonlinear problems in applied sciences. The HPM is used to solve fractional differential equations (FDE), nonlinear differential equations, nonlinear integral equations, and differences differential equations. It has been shown that HPM permits to solve the nonlinear problems very easily, most effectively, and accurately. The HPM provides a solution generally with one or two iterations with high accuracy. The HPM has a very rapid convergence of the solution series in most cases considered so far in literature. In this current study, we discuss this method in cosmology in the scope of the locally rotational symmetric Bianchi type-I model [18] to find the solutions.

By considering the HPM approach we shall explore the approximate solutions of modified cosmological problems in the background of LRS Bianchi type-I space–time. The plan of our this current study is as follows: In Section 2 we shall calculate the cosmological problem for LRS Bianchi type-I space–time with the help of Einstein fields equations for LRS Bianchi type-I model. In Section 3, we shall present the basic calculations of HPM with all its necessary conditions. In Section 4, we shall explore some approximate solutions for five different values of parameter n. At the end, we shall summarise our main results and achievements.

2. Cosmological Model

The Basic setup for Einstein’s field equations [19,20] with a extra term $\mathsf{\Lambda }{g}_{\alpha \beta }$, is defined as

$$R_{\alpha \beta }-\frac{1}{2}{g}_{\alpha \beta }R-\mathsf{\Lambda }{g}_{\alpha \beta }=8\pi T_{\alpha \beta }$$

(1)

where $R_{\alpha \beta }$, defines the Ricci tensor, R denotes a Ricci scalar, $g_{\alpha \beta }$ reveals a metric of a space–time, and $T_{\alpha \beta }$, is energy–momentum tensor. The geometry of a LRS Bianchi type-I space–time can be given as

$$d{s}^2=d{t}^2-A^2\left(t\right)d{x}^2-B^2\left(t\right)(d{y}^2+d{z}^2).$$

(2)

In the response of matter profile the energy-momentum tensor is presented as

$$T_{\alpha \beta }=(\rho +p)u_{\alpha }{u}_{\beta }-p{g}_{\alpha \beta }.$$

(3)

where $u_{\mu }=\sqrt{g_{00}}(1,0,0,0)$ is the four-velocity in co-moving coordinates. Using the Equations (2) and (3) in Equation (1), we get the following fields equations for LRS Bianchi type-I space–time.

$$\begin{array}{c}\frac{{\dot{B}}^2}{B^2}+\frac{2\dot{A}\dot{B}}{AB}=8\pi \rho +\mathsf{\Lambda }\hfill \end{array}$$

(4)

$$\begin{array}{c}\frac{2\ddot{B}}{B}+\frac{{\dot{B}}^2}{B^2}=-8\pi p+\mathsf{\Lambda }\hfill \end{array}$$

(5)

$$\begin{array}{c}\frac{\ddot{A}}{A}+\frac{\ddot{B}}{B}+\frac{\dot{A}\dot{B}}{AB}=-8\pi p-\mathsf{\Lambda }\hfill \end{array}$$

(6)

On adding Equations (5) and (6) we have the following calculated expression

$$\frac{\ddot{A}}{A}+\frac{{\dot{B}}^2}{B^2}+\frac{3\ddot{B}}{B}+\frac{\dot{A}\dot{B}}{AB}=-16\pi p$$

(7)

From Equations (1) and (7) we get the following modified continuity equation

$$\dot{\rho }+(\rho +p)\left(\frac{\dot{A}}{A}+\frac{2\dot{B}}{B}\right)=0$$

(8)

By plugging the $A=l{B}^n$ in Equation (8) we get the following equation

$$\dot{\rho }+(\rho +p)\left(\frac{n\dot{B}}{B}+\frac{2\dot{B}}{B}\right)=0\Rightarrow \frac{\dot{\rho }}{\rho }+\left(1+\frac{p}{\rho }\right)\left(\frac{n\dot{B}}{B}+\frac{2\dot{B}}{B}\right)=0$$

(9)

Here, we fix $l=1$ for simplicity purpose. The above Equation (9), can be expressed as

$$\frac{\dot{\rho }}{\rho }+(1+w_m)\left(\frac{n\dot{B}}{B}+\frac{2\dot{B}}{B}\right)=0$$

(10)

where $w_m=\frac{p}{\rho }$, is equation of state parameter. When $w_m=0,i.e.,p=0$, it is known as dust case. On the integration, we get the below relation

$$ln\left(\rho \right)+(1+w_m)(nln\left(B\right)+2ln\left(B\right))=ln{\rho }_0$$

(11)

where $ln{\rho }_0$, is assumed a constant of integration. It can be written as.

$$ln\left(\rho \right)=ln{\rho }_0{\left(B^{n+2}\right)}^{-(1+w_m)}\Rightarrow \rho ={\rho }_0{\left(B^{n+2}\right)}^{-(1+w_m)}$$

(12)

Using above equation in Equation (1) we have the following calculation

$$\frac{{\dot{B}}^2}{B^2}+\frac{\dot{A}\dot{B}}{AB}=8\pi \left({\rho }_0{\left(B^{n+2}\right)}^{-(1+w_m)}+\mathsf{\Lambda }\right)$$

(13)

On simplifying the above Equation (13), we have the following final expression

$${\dot{B}}^2=\frac{8\pi {\rho }_0\left({\left(B^{n+2}\right)}^{-(1+w_m)}{B}^2\right)}{1+n}+\frac{8\pi B^2\mathsf{\Lambda }}{1+n}$$

(14)

The above equation can be re-written as

$${\dot{B}}^2=H_{\mathsf{\Lambda }}^2\left(\frac{{\rho }_0}{\mathsf{\Lambda }}{B}^{-(n+n{w}_m+2w_m)}+B^2\right)$$

(15)

where $H_{\mathsf{\Lambda }}^2=\frac{8\pi \mathsf{\Lambda }}{1+n}$. On reshaping the above Equation (15), we have

$$\frac{{\dot{B}}^2}{H_{\mathsf{\Lambda }}^2}={\mathsf{\Omega }}_{m\mathsf{\Lambda }}{B}^{-(n+n{w}_m+2w_m)}+B^2$$

(16)

where ${\mathsf{\Omega }}_{m\mathsf{\Lambda }}=\frac{{\rho }_0}{\mathsf{\Lambda }}$. By plugging the dimensionless cosmic time $\tau =H_{\mathsf{\Lambda }}t$, we can rewrite the Equation (16) as

$$B^{\prime 2}={\mathsf{\Omega }}_{m\mathsf{\Lambda }}{B}^{-(n+n{w}_m+2w_m)}+B^2$$

(17)

where the prime denotes the derivative with respect to cosmic parameter $\tau$.

3. Basic Formulation of HPM

For the briefly discussion of the HPM. We assume the following non-linear differential equation:

$$A\left(u\right)-f\left(r\right)=0,r\in \mathsf{\Omega }$$

(18)

with boundary conditions

$$B(u,\frac{\partial u}{\partial n})=0,r\in \Gamma$$

(19)

where $A\left(u\right)$ denotes the differential operator, $B(u,\frac{\partial u}{\partial n})$ represents the boundary condition, $f\left(r\right)$ reveals the analytical function, and $\Gamma$ is the boundary of the domain $\mathsf{\Omega }$. The operator A can be written into two parts which are mention as L and N, where L is used for linear part and N is utilizing for nonlinear part. Finally, the above equation can be written as

$$L\left(u\right)+N\left(u\right)-f\left(r\right)=0$$

(20)

according to the HP scheme, we construct a following Homotopy $v(r,p):\mathsf{\Omega }\times [0,1]⟶R$, which reveals as

$$H(v,p)=(1-p)\times [L\left(v\right)-L\left(u_0\right)]+p\times [A\left(v\right)-f\left(r\right)]=0p\in [0,1]$$

(21)

where $p\in [0,1]$ is an embedding parameter and $u_0)$ is an initial approximation of Equation (20). The above equation implies as

$$H(v,o)=L\left(v\right)-L\left(u_0\right)=0H(v,1)=A\left(v\right)-f\left(r\right)=0$$

(22)

The process of taking the values of p from zero to 1, implies that the homotopy $v(r,p)$ changing from $u_0\left(r\right)$ to $u\left(r\right)$. This is called deformation, and also $L\left(v\right)-L\left(u_0\right)$ and $A\left(v\right)-f\left(r\right)$ are called Homotopic relations in topology. According to the HPM, we can first used the embedding parameter p as a small parameter and assume that the solution of the Equation (20) can be written as a power series in p

$$v=v_0+p{v}_1+p^2{v}_2+\cdots$$

(23)

With setting $p=1$ the approximate solution can be obtained as

$$u=li{m}_{p\to 1}v=v_0+v_1+v_2+\cdots$$

(24)

4. Application of HPM

In this section, we will discuss the applications of HPM on a cosmological model which is presented in Equation (17), with equation of state parameter $w_m$. Many researchers have put a lot of efforts to deal the universe in the background of different kinds of matters. According to the different sources of matter, which can be discussed by employing the equation of state parameter, i.e., $w_m=\frac{p}{\rho }$, where p and $\rho$ mention the pressure and density function, respectively. The different values of equation of state parameter, i.e., $w_m=0,\frac{1}{3},\&1$ describe the dust, stiff, and radiation nature of matter source, respectively. On the other hand $w_m=-1$ represents the vacuum case, $w_m\in (-1,\frac{-1}{3})$ provides the quintessence era, and $w_m<-1$ demonstrates the phantom region. For simplicity, we shall take dust case i.e., $w_m=0$, the Equation (17), gets the following form

$$B^n{B}^{\prime 2}={\mathsf{\Omega }}_{m\mathsf{\Lambda }}+B^n{B}^2$$

(25)

In the above Equation (25), the parameter n, has some important role. In this study, we shall explore the HPM base solution of Equation (25), by plugging the five different values of parameter n, i.e., $n=1,n=2,n=3,n=4,$ and $n=5$. The main objective of this study to explore solutions of cosmological model. The exact solution of this current cosmological models is difficult in a proper way, so that is why we shall employ the HPM method. The HPM provided the analytical solutions.

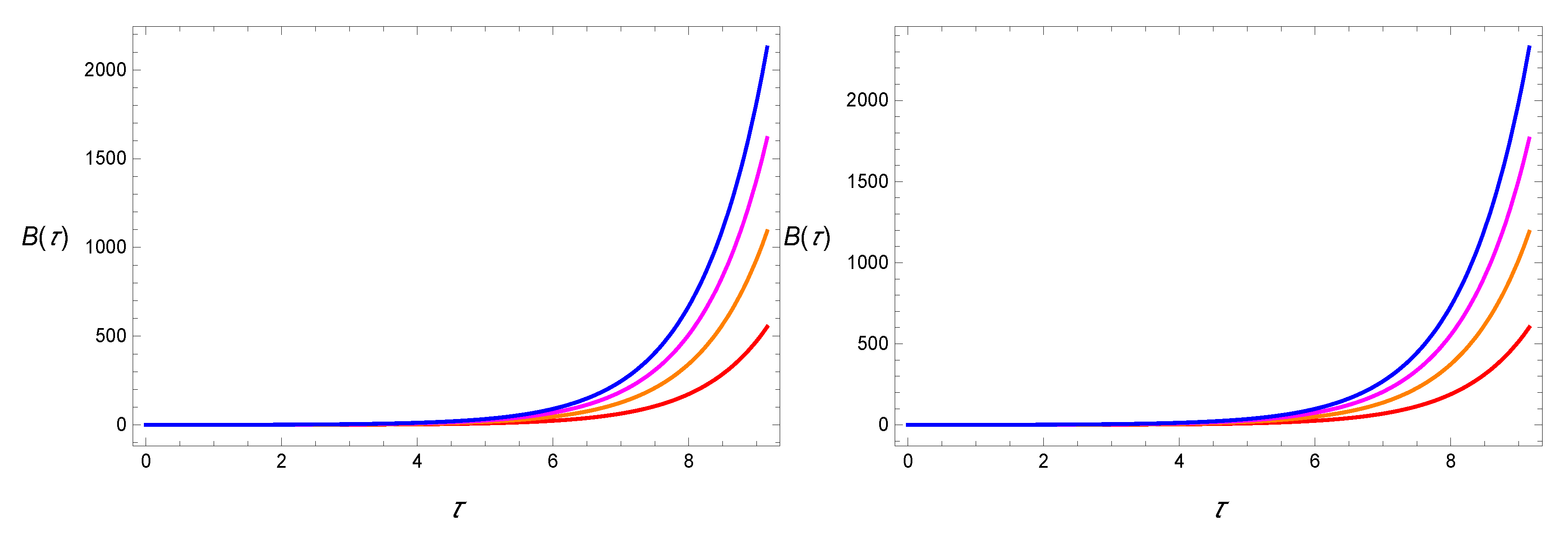
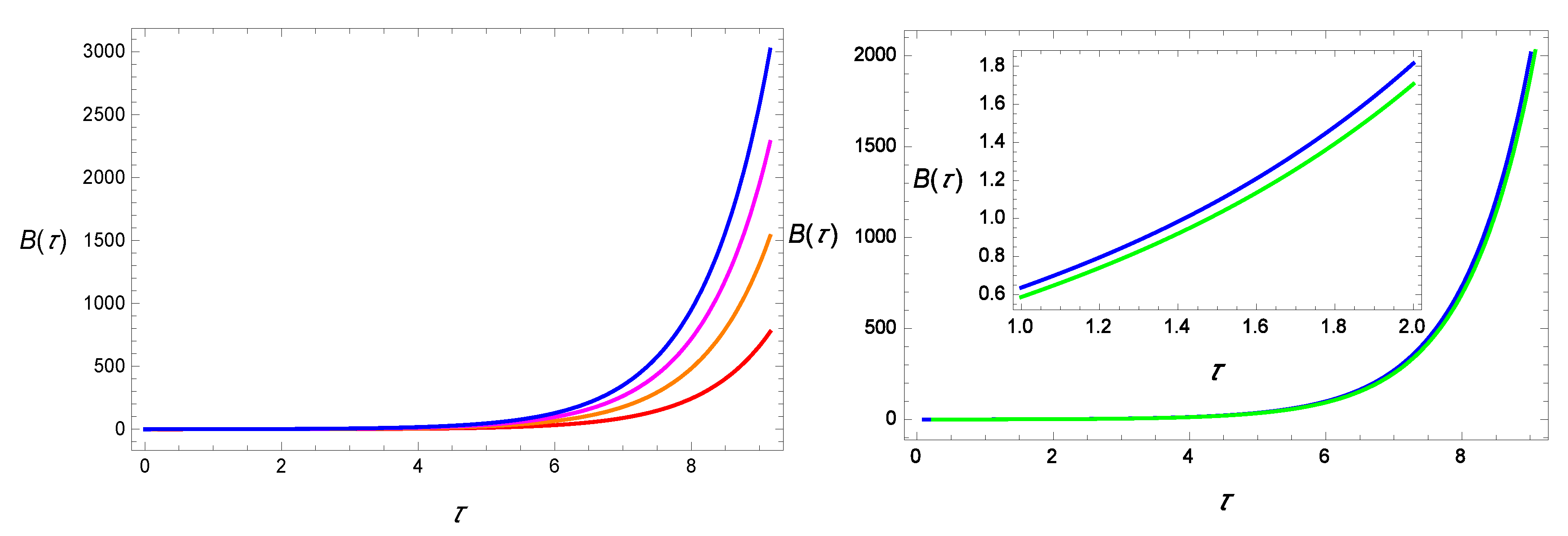
4.1. Solution for $n=1$

From above Equation (25) we have the following non-linear differential equation after putting the values of parameter $n=1$ as

$$B{B}^{\prime 2}={\mathsf{\Omega }}_{m\mathsf{\Lambda }}+B^3.$$

(26)

Now, by employing the HPM scheme, we have the following Homotopy

$$B{B}^{\prime 2}-B^3-p{\mathsf{\Omega }}_{m\mathsf{\Lambda }}=0p\in [0,1],$$

we have

$$B\left(t\right)=B_0\left(t\right)+p{B}_1\left(t\right)+p^2{B}_2\left(t\right)+p^3{B}_3\left(t\right)+\cdots$$

Here, we assumed the initial condition $B_0\left(0\right)=const=\tilde{B}$ and $B_i\left(0\right)=0$ where $i\ge 1$. The Equation (26) becomes after equating the powers of p.

$$\begin{array}{ccc}{p}^0\hfill & :& -B_0^3\left(t\right)+B_0\left(t\right)B_0^{\prime 2}\left(t\right)=0,B_0\left(0\right)=\tilde{B}\hfill \end{array}$$

(27)

$$\begin{array}{ccc}{p}^1\hfill & :& -{\mathsf{\Omega }}_{m\mathsf{\Lambda }}-3B_0^2\left(t\right)B_1\left(t\right)+B_1\left(t\right)B_0^{\prime 2}\left(t\right)+2B_0\left(t\right)B_0^{\prime }\left(t\right)B_1^{\prime }\left(t\right)=0,B_1\left(0\right)=0\hfill \end{array}$$

(28)

$$\begin{array}{ccc}{p}^2\hfill & :& -3B_0\left(t\right)B_1^2\left(t\right)-3B_0^2\left(t\right)B_2\left(t\right)+B_2\left(t\right)B_0^{\prime 2}\left(t\right)+2B_1\left(t\right)B_0^{\prime }\left(t\right)B_1^{\prime }\left(t\right)+B_0\left(t\right)B_1^{\prime 2}\left(t\right)+\hfill \\ & & 2B_0\left(t\right)B_0^{\prime }\left(t\right)B_2^{\prime }\left(t\right)=0,B_2\left(0\right)=0\hfill \\ \cdots \hfill & \cdots & \cdots \hfill \end{array}$$

(29)

On solving the differential Equations (27)–(29), we get the following solutions

$$\begin{array}{ccc}{B}_0\left(t\right)\hfill & =& \tilde{B}{e}^t\hfill \end{array}$$

(30)

$$\begin{array}{ccc}{B}_1\left(t\right)\hfill & =& -\frac{6{\tilde{B}}_0^3{e}^t+e^{-2t}{\mathsf{\Omega }}_{m\mathsf{\Lambda }}-e^t{\mathsf{\Omega }}_{m\mathsf{\Lambda }}}{6{\tilde{B}}_0^2}\hfill \end{array}$$

(31)

$$\begin{array}{ccc}{B}_2\left(t\right)\hfill & =& \frac{e^{-5t}(-1+e^{3t}){\mathsf{\Omega }}_{m\mathsf{\Lambda }}(48{\tilde{B}}_0^3{e}^{3t}+{\mathsf{\Omega }}_{m\mathsf{\Lambda }}-7e^{3t}{\mathsf{\Omega }}_{m\mathsf{\Lambda }})}{144{\tilde{B}}_0^5}\hfill \end{array}$$

(32)

Adding Equations (30)–(32) we get the final $B\left(t\right)$

$$B\left(t\right)=\frac{e^{-5t}(-1+e^{3t}){\mathsf{\Omega }}_{m\mathsf{\Lambda }}(72{\tilde{B}}_0^3{e}^{3t}+{\mathsf{\Omega }}_{m\mathsf{\Lambda }}-7e^{3t}{\mathsf{\Omega }}_{m\mathsf{\Lambda }})}{144{\tilde{B}}_0^5}$$

(33)

This is a approximate solution for $n=1$. In this calculated approximate solutions the parameter ${\mathsf{\Omega }}_{m\mathsf{\Lambda }}$, has some crucial role. The different can be seen from the left penal of the Figure 1, under the different values of parameter ${\mathsf{\Omega }}_{m\mathsf{\Lambda }}$. The increases and positive trend shows that our HPM solutions are physically acceptable.

4.2. Solution for $n=2$

From Equation (25) we get the non-linear differential equation by taking $n=2$ as

$$B^2{B}^{\prime 2}={\mathsf{\Omega }}_{m\mathsf{\Lambda }}+B^4.$$

(34)

By HPM scheme

$$B^2{B}^{\prime 2}-B^4-p{\mathsf{\Omega }}_{m\mathsf{\Lambda }}=0p\in [0,1],$$

consider

$$B\left(t\right)=B_0\left(t\right)+p{B}_1\left(t\right)+p^2{B}_2\left(t\right)+p^3{B}_3\left(t\right)+\cdots$$

We considered the initial condition $B_0\left(0\right)=const=\tilde{B}$ and $B_i\left(0\right)=0$ where $i\ge 1$. The Equation (34) becomes with equating the powers of p.

$$\begin{array}{ccc}{p}^0\hfill & :& -B_0^4\left(t\right)+B_0^2\left(t\right)B_0^{\prime 2}\left(t\right)=0,B_0\left(0\right)=\tilde{B}\hfill \end{array}$$

(35)

$$\begin{array}{ccc}{p}^1\hfill & :& -{\mathsf{\Omega }}_{m\mathsf{\Lambda }}-4B_0^3\left(t\right)B_1\left(t\right)+2B_0{B}_1\left(t\right)B_0^{\prime 2}\left(t\right)+2B_0^2\left(t\right)B_0^{\prime }\left(t\right)B_1^{\prime }\left(t\right)=0,B_1\left(0\right)=0\hfill \end{array}$$

(36)

$$\begin{array}{ccc}{p}^2\hfill & :& -6B_0^2\left(t\right)B_1^2\left(t\right)-4B_0^3\left(t\right)B_2\left(t\right)+B_1^2\left(t\right)B_0^{\prime 2}\left(t\right)+2B_0{B}_2\left(t\right)B_0^{\prime 2}\left(t\right)+4B_0{B}_1{B}_0^{{}^{\prime }}{B}_1^{\prime }\left(t\right)+\hfill \\ & & B_0^2{B}_1^{\prime 2}\left(t\right)+2B_0^2\left(t\right)B_0^{{}^{\prime }}\left(t\right)B_2^{\prime }\left(t\right)=0,B_2\left(0\right)=0\hfill \\ \cdots \hfill & \cdots & \cdots \hfill \end{array}$$

(37)

On solving the Equations (35)–(37), we have

$$\begin{array}{ccc}{B}_0\left(t\right)\hfill & =& \tilde{B}{e}^t\hfill \end{array}$$

(38)

$$\begin{array}{ccc}{B}_1\left(t\right)\hfill & =& -\frac{8{\tilde{B}}_0^4{e}^t+e^{-3t}{\mathsf{\Omega }}_{m\mathsf{\Lambda }}-e^t{\mathsf{\Omega }}_{m\mathsf{\Lambda }}}{8{\tilde{B}}_0^3}\hfill \end{array}$$

(39)

$$\begin{array}{ccc}{B}_2\left(t\right)\hfill & =& \frac{e^{-7t}(-1+e^{4t}){\mathsf{\Omega }}_{m\mathsf{\Lambda }}(48{\tilde{B}}_0^4{e}^{4t}+{\mathsf{\Omega }}_{m\mathsf{\Lambda }}-5e^{4t}{\mathsf{\Omega }}_{m\mathsf{\Lambda }})}{128{\tilde{B}}_0^7}\hfill \end{array}$$

(40)

From Equations (38)–(40)

$$B\left(t\right)=\frac{e^{-7t}(-1+e^{4t}){\mathsf{\Omega }}_{m\mathsf{\Lambda }}(64{\tilde{B}}_0^4{e}^{4t}+{\mathsf{\Omega }}_{m\mathsf{\Lambda }}-5e^{4t}{\mathsf{\Omega }}_{m\mathsf{\Lambda }})}{128{\tilde{B}}_0^7}$$

(41)

This is a approximate solution for $n=2$. The different developments can be seen from the right penal of the Figure 1, under the different values of parameter ${\mathsf{\Omega }}_{m\mathsf{\Lambda }}$. The positively increasing behavior shows that our HPM solutions are physically considerable.

4.3. Solution for $n=3$

By Equation (25) we have the following non-linear differential equation for $n=3$ as

$$B^3{B}^{\prime 2}={\mathsf{\Omega }}_{m\mathsf{\Lambda }}+B^5$$

(42)

By employing HPM scheme

$$B^3{B}^{\prime 2}-B^5-p{\mathsf{\Omega }}_{m\mathsf{\Lambda }}=0p\in [0,1],$$

we have

$$B\left(t\right)=B_0\left(t\right)+p{B}_1\left(t\right)+p^2{B}_2\left(t\right)+p^3{B}_3\left(t\right)+\cdots$$

The initial condition $B_0\left(0\right)$ can be freely picked. Here we set $B_0\left(0\right)=const=\tilde{B}$ and $B_i\left(0\right)=0$ where $i\ge 1$. The Equation (42), has following HPM setup

$$\begin{array}{ccc}{p}^0\hfill & :& -B_0^5\left(t\right)+B_0^3\left(t\right)B_0^{\prime 2}\left(t\right)=0,B_0\left(0\right)=\tilde{B}\hfill \end{array}$$

(43)

$$\begin{array}{ccc}{p}^1\hfill & :& -{\mathsf{\Omega }}_{m\mathsf{\Lambda }}-5B_0^5\left(t\right)B_1\left(t\right)+3B_0^2{B}_1\left(t\right)B_0^{\prime 2}\left(t\right)+2B_0^3\left(t\right)B_0^{\prime }\left(t\right)B_1^{\prime }\left(t\right)=0,B_1\left(0\right)=0\hfill \end{array}$$

(44)

$$\begin{array}{ccc}{p}^2\hfill & :& -10B_0^3\left(t\right)B_1^2\left(t\right)-5B_0^4\left(t\right)B_2\left(t\right)+3B_0{B}_1^2\left(t\right)B_0^{\prime 2}\left(t\right)+3B_0^2{B}_2\left(t\right)B_0^{\prime 2}\left(t\right)+6B_0^2{B}_1{B}_0^{{}^{\prime }}{B}_1^{\prime }\left(t\right)+\hfill \\ & & B_0^3{B}_1^{\prime 2}\left(t\right)+2B_0^3\left(t\right)B_0^{\prime }\left(t\right)B_2^{\prime }\left(t\right)=0,B_2\left(0\right)=0\hfill \\ \cdots \hfill & \cdots & \cdots \hfill \end{array}$$

(45)

Now we solve the Equations (43)–(45), we get

$$\begin{array}{ccc}{B}_0\left(t\right)\hfill & =& \tilde{B}{e}^t\hfill \end{array}$$

(46)

$$\begin{array}{ccc}{B}_1\left(t\right)\hfill & =& -\frac{10{\tilde{B}}_0^5{e}^t-4e^{-4t}{\mathsf{\Omega }}_{m\mathsf{\Lambda }}-e^t{\mathsf{\Omega }}_{m\mathsf{\Lambda }}}{10{\tilde{B}}_0^4}\hfill \end{array}$$

(47)

$$\begin{array}{ccc}{B}_2\left(t\right)\hfill & =& \frac{e^{-9t}(-1+e^{5t}){\mathsf{\Omega }}_{m\mathsf{\Lambda }}(160{\tilde{B}}_0^5{e}^{5t}+{\mathsf{\Omega }}_{m\mathsf{\Lambda }}+(3-13e^{5t}){\mathsf{\Omega }}_{m\mathsf{\Lambda }})}{400{\tilde{B}}_0^9}\hfill \end{array}$$

(48)

Adding Equations (46)–(48), we get.

$$B\left(t\right)=\frac{e^{-9t}(-1+e^{5t}){\mathsf{\Omega }}_{m\mathsf{\Lambda }}(200{\tilde{B}}_0^5{e}^{5t}+{\mathsf{\Omega }}_{m\mathsf{\Lambda }}+(3-13e^{5t}){\mathsf{\Omega }}_{m\mathsf{\Lambda }})}{400{\tilde{B}}_0^9}$$

(49)

The approximate solution for $n=3$. In this approximate solutions the parameter ${\mathsf{\Omega }}_{m\mathsf{\Lambda }}$, has some important role. The different developments can be seen from the left penal of the Figure 2, under the different values of parameter ${\mathsf{\Omega }}_{m\mathsf{\Lambda }}$. The increasing attribute shows that our HPM solutions are physically acceptable.

4.4. Solution for $n=4$

From above equation Equation (25) we have the following non-linear differential equation after putting the values of parameter $n=4$ as

$$B^4{B}^{{}^{\prime 2}}={\mathsf{\Omega }}_{m\mathsf{\Lambda }}+B^6$$

(50)

Now, by using HPM scheme

$$\begin{array}{ccc}{p}^0\hfill & :& -B_0^6\left(t\right)+B_0^4\left(t\right)B_0^{\prime 2}\left(t\right)=0,B_0\left(0\right)=\tilde{B}\hfill \end{array}$$

(51)

$$\begin{array}{ccc}{p}^1\hfill & :& -{\mathsf{\Omega }}_{m\mathsf{\Lambda }}-6B_0^5\left(t\right)B_1\left(t\right)+4B_0^3{B}_1\left(t\right)B_0^{\prime 2}\left(t\right)+2B_0^4\left(t\right)B_0^{\prime }\left(t\right)B_1^{\prime }\left(t\right)=0,B_1\left(0\right)=0\hfill \end{array}$$

(52)

$$\begin{array}{ccc}{p}^2\hfill & :& -15B_0^4\left(t\right)B_1^2\left(t\right)-6B_0^5\left(t\right)B_2\left(t\right)+6B_0^2{B}_1^2\left(t\right)B_0^{\prime 2}\left(t\right)+4B_0^3{B}_2\left(t\right)B_0^{\prime 2}\left(t\right)+8B_0^3{B}_1{B}_0^{\prime }{B}_1^{\prime }\left(t\right)+\hfill \\ & & B_0^4{B}_1^{\prime 2}\left(t\right)+2B_0^4\left(t\right)B_0^{\prime }\left(t\right)B_2^{\prime }\left(t\right)=0,B_2\left(0\right)=0\hfill \\ \cdots \hfill & \cdots & \cdots \hfill \end{array}$$

(53)

In solving the Equations (51)–(53),

$$\begin{array}{ccc}{B}_0\left(t\right)\hfill & =& \tilde{B}{e}^t\hfill \end{array}$$

(54)

$$\begin{array}{ccc}{B}_1\left(t\right)\hfill & =& -\frac{12{\tilde{B}}_0^6{e}^t+e^{-5t}{\mathsf{\Omega }}_{m\mathsf{\Lambda }}-e^t{\mathsf{\Omega }}_{m\mathsf{\Lambda }}}{12{\tilde{B}}_0^5}\hfill \end{array}$$

(55)

$$\begin{array}{ccc}{B}_2\left(t\right)\hfill & =& \frac{e^{-11t}(-1+e^{6t}){\mathsf{\Omega }}_{m\mathsf{\Lambda }}(60{\tilde{B}}_0^6{e}^{6t}+{\mathsf{\Omega }}_{m\mathsf{\Lambda }}-4e^{6t}{\mathsf{\Omega }}_{m\mathsf{\Lambda }})}{144{\tilde{B}}_0^{11}}\hfill \end{array}$$

(56)

By Equations (54)–(56),

$$B\left(t\right)=\frac{e^{-11t}(-1+e^{6t}){\mathsf{\Omega }}_{m\mathsf{\Lambda }}(72{\tilde{B}}_0^6{e}^{6t}+{\mathsf{\Omega }}_{m\mathsf{\Lambda }}-4e^{6t}{\mathsf{\Omega }}_{m\mathsf{\Lambda }})}{144{\tilde{B}}_0^{11}}$$

(57)

This is a approximate solutions for $n=4$, its graphically representation can be seen from the right side of the Figure 2.

4.5. Solution for $n=5$

By Equation (25) with parameter $n=5$ we have the following non-linear equation

$$B^5{B}^{{}^{\prime 2}}={\mathsf{\Omega }}_{m\mathsf{\Lambda }}+B^7$$

(58)

By employing HPM technique.

$$\begin{array}{ccc}{p}^0\hfill & :& -B_0^7\left(t\right)+B_0^5\left(t\right)B_0^{\prime 2}\left(t\right)=0,B_0\left(0\right)=\tilde{B}\hfill \end{array}$$

(59)

$$\begin{array}{ccc}{p}^1\hfill & :& -{\mathsf{\Omega }}_{m\mathsf{\Lambda }}-7B_0^6\left(t\right)B_1\left(t\right)+5B_0^4{B}_1\left(t\right)B_0^{\prime 2}\left(t\right)+2B_0^5\left(t\right)B_0^{\prime }\left(t\right)B_1^{\prime }\left(t\right)=0,B_1\left(0\right)=0\hfill \end{array}$$

(60)

$$\begin{array}{ccc}{p}^2\hfill & :& -21B_0^5\left(t\right)B_1^2\left(t\right)-7B_0^6\left(t\right)B_2\left(t\right)+10B_0^3{B}_1^2\left(t\right)B_0^{\prime 2}\left(t\right)+5B_0^4{B}_2\left(t\right)B_0^{\prime 2}\left(t\right)+10B_0^4{B}_1{B}_0^{\prime }{B}_1^{\prime }\left(t\right)+\hfill \\ & & B_0^5{B}_1^{\prime 2}\left(t\right)+2B_0^5\left(t\right)B_0^{\prime }\left(t\right)B_2^{\prime }\left(t\right)=0,B_2\left(0\right)=0\hfill \\ \cdots \hfill & \cdots & \cdots \hfill \end{array}$$

(61)

Now we solve the problems by Equations (59)–(61), we get

$$\begin{array}{ccc}{B}_0\left(t\right)\hfill & =& \tilde{B}{e}^t\hfill \end{array}$$

(62)

$$\begin{array}{ccc}{B}_1\left(t\right)\hfill & =& -\frac{14{\tilde{B}}_0^7{e}^t+e^{-6t}{\mathsf{\Omega }}_{m\mathsf{\Lambda }}-e^t{\mathsf{\Omega }}_{m\mathsf{\Lambda }}}{14{\tilde{B}}_0^6}\hfill \end{array}$$

(63)

$$\begin{array}{ccc}{B}_2\left(t\right)\hfill & =& \frac{e^{-13t}(-1+e^{7t}){\mathsf{\Omega }}_{m\mathsf{\Lambda }}(336{\tilde{B}}_0^7{e}^{7t}+{\mathsf{\Omega }}_{m\mathsf{\Lambda }}+(5-19e^{7t}){\mathsf{\Omega }}_{m\mathsf{\Lambda }})}{784{\tilde{B}}_0^{13}}\hfill \end{array}$$

(64)

Adding Equations (62)–(64), we get.

$$B\left(t\right)=\frac{e^{-13t}(-1+e^{7t}){\mathsf{\Omega }}_{m\mathsf{\Lambda }}(392{\tilde{B}}_0^7{e}^{7t}+{\mathsf{\Omega }}_{m\mathsf{\Lambda }}+(5-19e^{7t}){\mathsf{\Omega }}_{m\mathsf{\Lambda }})}{784{\tilde{B}}_0^{13}}$$

(65)

The approximate solution for $n=5$. In this approximate solution, parameter ${\mathsf{\Omega }}_{m\mathsf{\Lambda }}$ has some important role. The different developments can be seen from the Figure 3, under the different values of parameter ${\mathsf{\Omega }}_{m\mathsf{\Lambda }}$.

4.6. Special Case

In this special case, we discuss the comparative study in the background of an exact solution of Equation (26) and HPM solution by Equation (33) with ${\mathsf{\Omega }}_{m\mathsf{\Lambda }}=0.4$. The exact solution of Equation (26) is calculated as

$$B\left(t\right)=\frac{e^{-C_1-t}{\left(e^{3C_1+3t}-{\mathsf{\Omega }}_{m\mathsf{\Lambda }}\right)}^{2/3}}{2^{2/3}},$$

where $C_1$ is a constant of integration. The comparison analysis of exact solution and HPM based solution can be seen from the right penal of from the Figure 3. We have also estimated the quantitative values of the exact solution for $n=1$, which was possible to calculate and have shown these values in

Table 1. Estimated values for HPM and exact solutions.

$\mathit{H}\mathit{P}\mathit{M}({\mathsf{\Omega }}_{\mathit{m}\mathsf{\Lambda }}=0.4)$ and $\mathit{Exact}({\mathsf{\Omega }}_{\mathit{m}\mathsf{\Lambda }}=0.4)$
$\mathit{t}$	HPM	Exact
0.3	0.198989	0.100976
0.8	0.499301	0.451041
1.3	0.885666	0.827151
1.8	1.483150	1.393510
2.3	2.453730	2.308390
2.8	4.048630	3.809900
3.3	6.676200	6.282930
3.8	11.00760	10.35930
4.3	18.14860	17.07990
4.8	29.92210	28.16000
5.3	49.33320	46.42800
5.8	81.33670	76.54680
6.3	134.1020	126.2040
6.8	221.0960	208.0760
7.3	364.5260	343.0590
7.8	601.0010	565.6090
8.3	990.8840	932.5310
8.8	1633.690	1537.480
9.3	2693.500	2534.880
9.8	4440.830	4179.320

.

5. Conclusions

In this article, we have studied the LRS Bianchi type-I space–time and calculated the fields equations. We have also calculated a cosmological model, which was presented in Equation (17). Further, we have developed an HPM scheme for a nonlinear differential equation. Furthermore, we have tried to find the solutions for the spatially modified cosmological model for LRS Bianchi type-I space–time, when the exact solution could not be found due to nonlinearity. In this response, we have examined the five different values of parameter n, i., $n=1,n=2,n=3,n=4,$ and $n=5$. We have also explored our solution for the four different values of parameter ${\mathsf{\Omega }}_{m\mathsf{\Lambda }}$, i.e., ${\mathsf{\Omega }}_{m\mathsf{\Lambda }}=0.10,{\mathsf{\Omega }}_{m\mathsf{\Lambda }}=0.20,{\mathsf{\Omega }}_{m\mathsf{\Lambda }}=0.30,$ and ${\mathsf{\Omega }}_{m\mathsf{\Lambda }}=0.40$. Our obtained solutions can be seen from the Figure 1, Figure 2 and Figure 3 for five different cases. The variational development revealed that parameter n, has some special and important role in this study. Further, it is also noticed from Figure 1, Figure 2 and Figure 3 that parameter ${\mathsf{\Omega }}_{m\mathsf{\Lambda }}$ also has a crucial role in this modified cosmological problem. The increased values of parameter ${\mathsf{\Omega }}_{m\mathsf{\Lambda }}$ described the increased nature of our obtaining solutions. In our view, the results of the current study revealed that the HPM is very effective and simple for obtaining approximate solutions of the modified Friedmann equation in cosmology. Our purpose of this study is showing the applications of HMP in the cosmology field. In this study, we have obtained physically acceptable solutions with a positive nature, which support the study of HPM.