Probing Time-Dependent Fundamental Constants with Nucleosynthesis in Population III Stars
Abstract
:1. Introduction
2. Methods
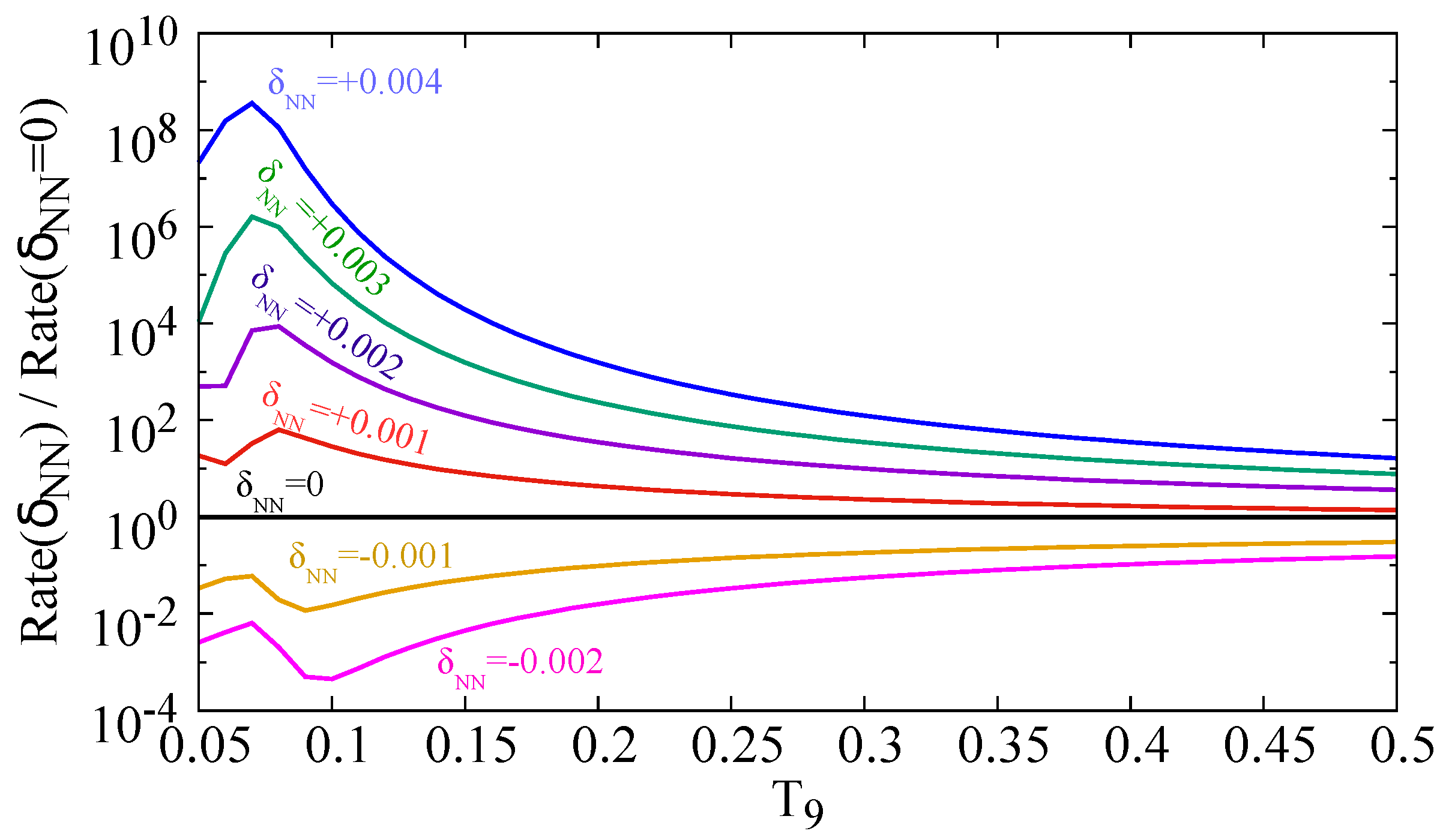
2.1. Triple- Reaction
2.2. Stellar Models
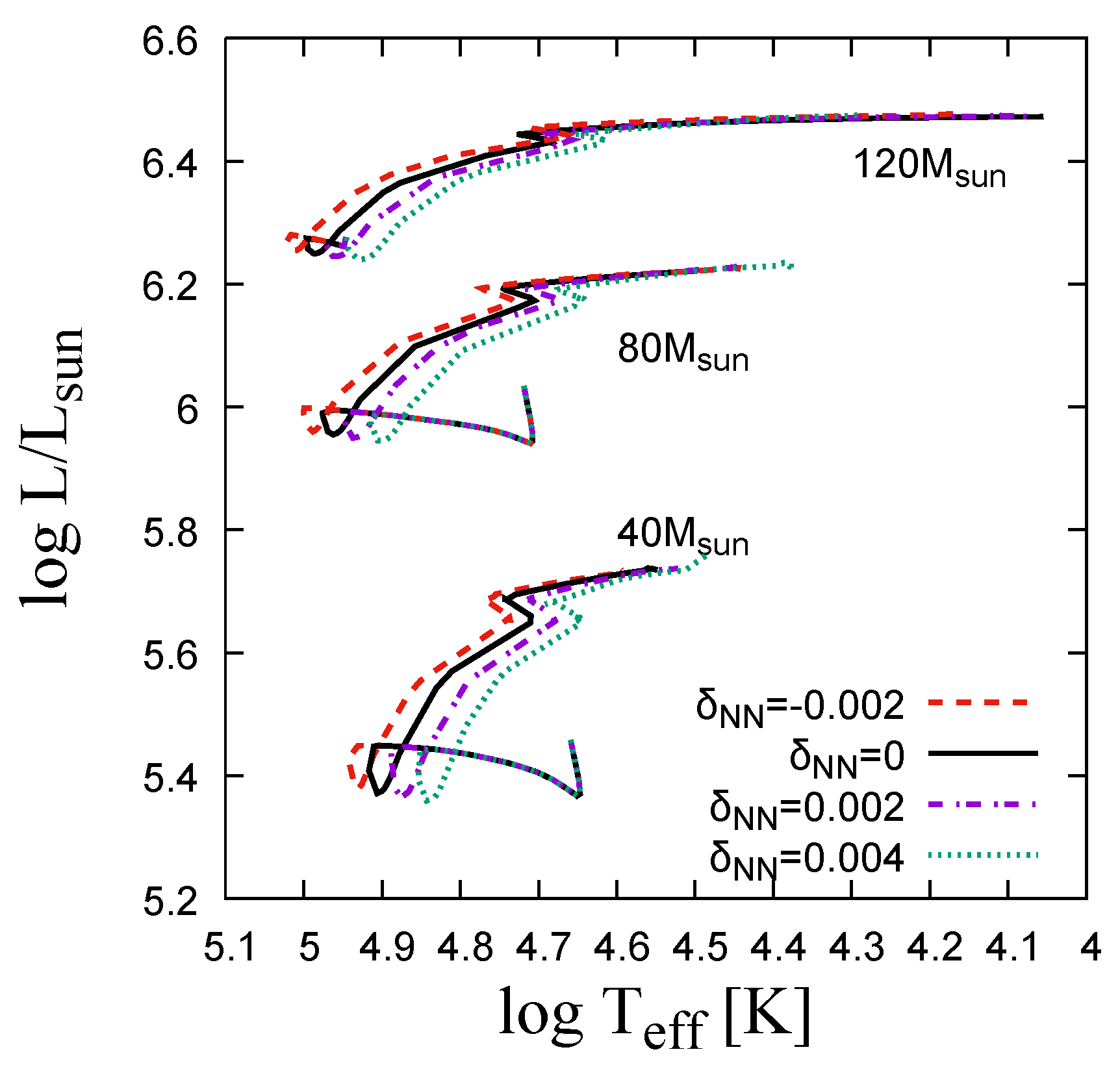
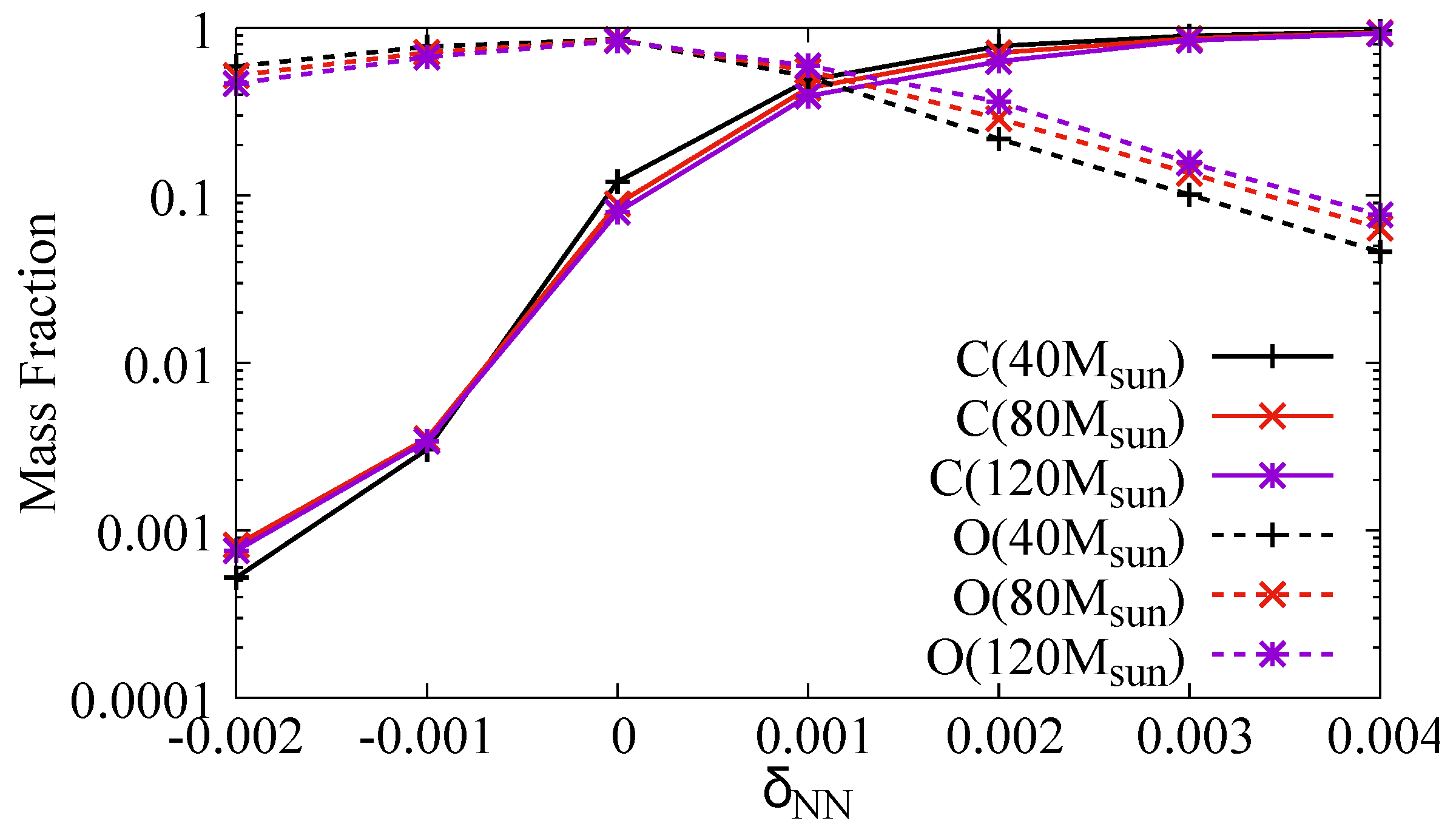
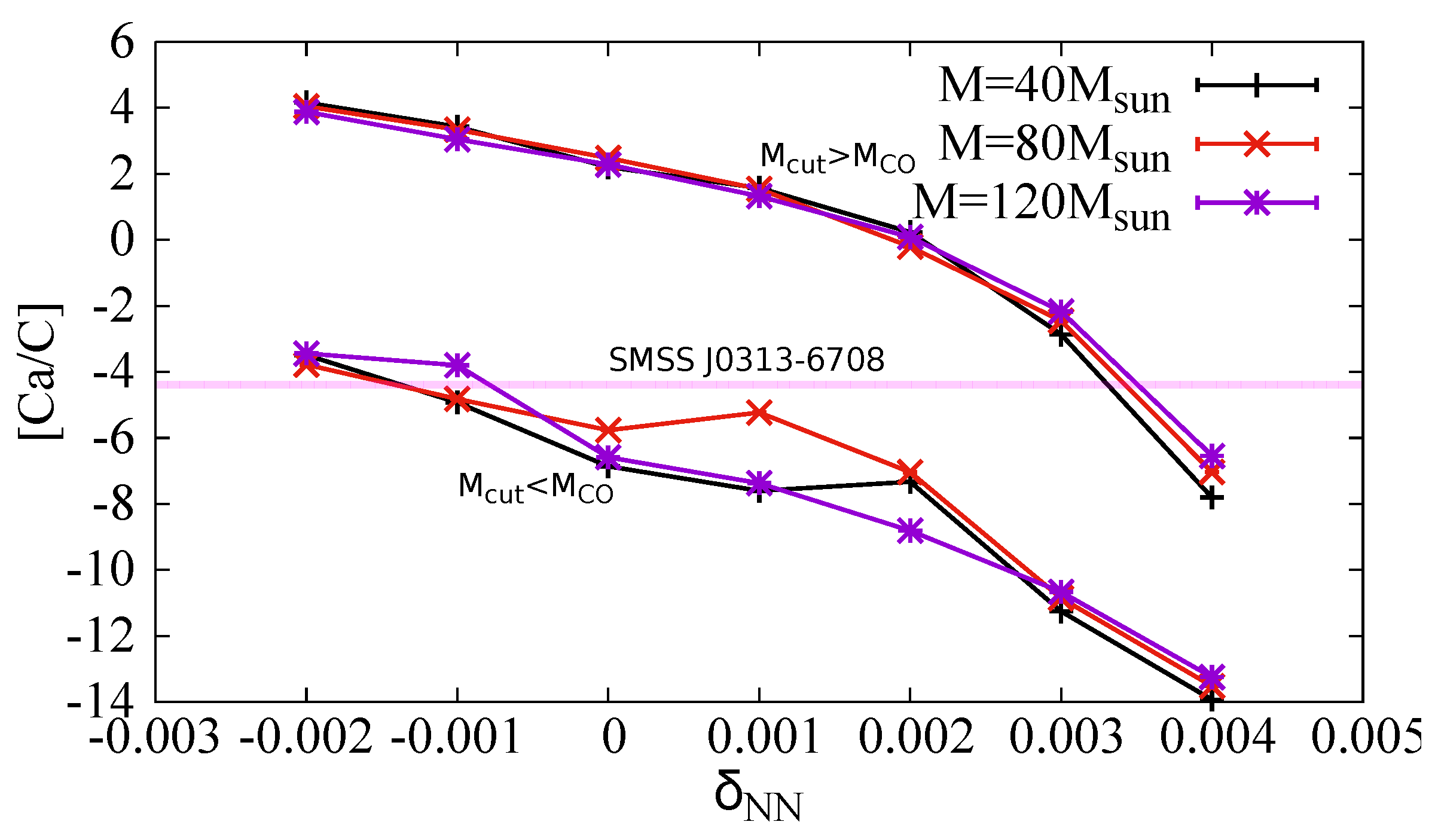
3. Results
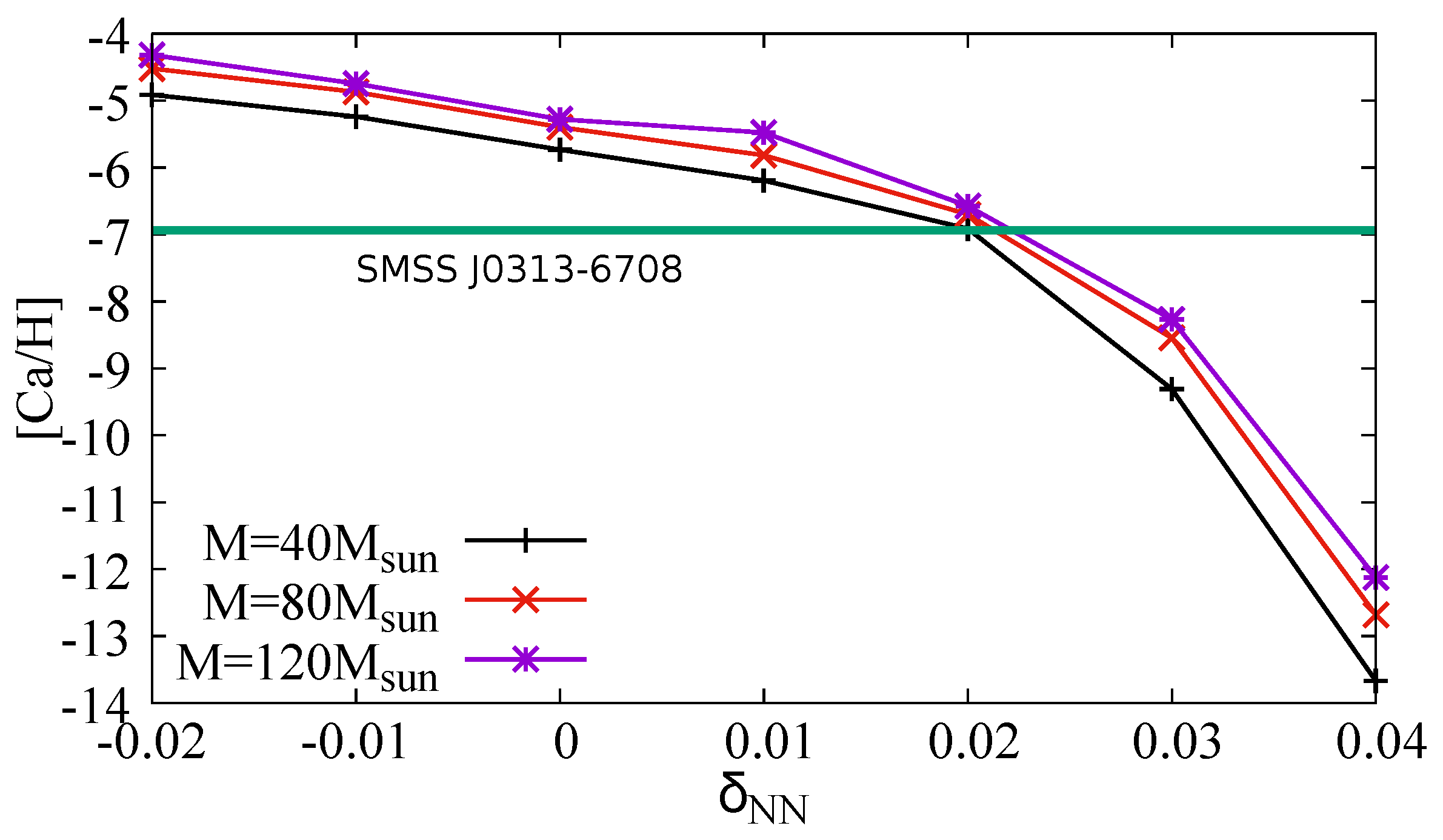
3.1. Evolution and Nucleosynthesis of Population III Stars with
3.2. Compositions of the Ejecta and Chemical Abundances in the Most Iron-Poor Star
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MESA | Modules for Experiments in Stellar Astrophysics |
| N–N | nucleon–nucleon |
| BBN | Big Bang nucleosynthesis |
References
- Dirac, P.A.M. The Cosmological Constants. Nature 1937, 139, 323. [Google Scholar] [CrossRef]
- Martins, C.J.A.P. The status of varying constants: A review of the physics, searches and implications. Rep. Prog. Phys. 2017, 80, 126902. [Google Scholar] [CrossRef] [PubMed]
- Uzan, J.P. Varying Constants, Gravitation and Cosmology. Living Rev. Relativ. 2011, 14, 2. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chiba, T. The Constancy of the Constants of Nature: Updates. Prog. Theor. Phys. 2011, 126, 993–1019. [Google Scholar] [CrossRef] [Green Version]
- Damour, T.; Polyakov, A.M. The string dilation and a least coupling principle. Nucl. Phys. B 1994, 423, 532–558. [Google Scholar] [CrossRef] [Green Version]
- Huang, L.; Adams, F.C.; Grohs, E. Sensitivity of carbon and oxygen yields to the triple-alpha resonance in massive stars. Astropart. Phys. 2019, 105, 13–24. [Google Scholar] [CrossRef] [Green Version]
- Ekström, S.; Coc, A.; Descouvemont, P.; Meynet, G.; Olive, K.A.; Uzan, J.P.; Vangioni, E. Effects of the variation of fundamental constants on Population III stellar evolution. Astron. Astrophys. 2010, 514, A62. [Google Scholar] [CrossRef] [Green Version]
- degl’Innocenti, S.; Fiorentini, G.; Raffelt, G.G.; Ricci, B.; Weiss, A. Time-variation of Newton’s constant and the age of globular clusters. Astron. Astrophys. 1996, 312, 345–352. [Google Scholar]
- Demarque, P.; Krauss, L.M.; Guenther, D.B.; Nydam, D. The Sun as a Probe of Varying G. Astrophys. J. 1994, 437, 870. [Google Scholar] [CrossRef]
- Keller, S.C.; Bessell, M.S.; Frebel, A.; Casey, A.R.; Asplund, M.; Jacobson, H.R.; Lind, K.; Norris, J.E.; Yong, D.; Heger, A.; et al. A single low-energy, iron-poor supernova as the source of metals in the star SMSS J031300.36-670839.3. Nature 2014, 506, 463–466. [Google Scholar] [CrossRef]
- Nordlander, T.; Amarsi, A.M.; Lind, K.; Asplund, M.; Barklem, P.S.; Casey, A.R.; Collet, R.; Leenaarts, J. 3D NLTE analysis of the most iron-deficient star, SMSS0313-6708. Astron. Astrophys. 2017, 597, A6. [Google Scholar] [CrossRef] [Green Version]
- Komiya, Y.; Suda, T.; Fujimoto, M.Y. The Most Iron-deficient Stars as the Polluted Population III Stars. Astrophys. J. 2015, 808, L47. [Google Scholar] [CrossRef]
- Ishigaki, M.N.; Tominaga, N.; Kobayashi, C.; Nomoto, K. Faint Population III Supernovae as the Origin of the Most Iron-poor Stars. Astrophys. J. 2014, 792, L32. [Google Scholar] [CrossRef] [Green Version]
- Mori, K.; Nomoto, K.; Ishigaki, M.N. Calcium Production in Population III Stars and Constraints on the Origin of the Most Metal-poor Stars. 2019. in preparation. [Google Scholar]
- Bessell, M.S.; Collet, R.; Keller, S.C.; Frebel, A.; Heger, A.; Casey, A.R.; Masseron, T.; Asplund, M.; Jacobson, H.R.; Lind, K.; et al. Nucleosynthesis in a Primordial Supernova: Carbon and Oxygen Abundances in SMSS J031300.36-670839.3. Astrophys. J. 2015, 806, L16. [Google Scholar] [CrossRef] [Green Version]
- Hoyle, F. On Nuclear Reactions Occuring in Very Hot STARS.I. the Synthesis of Elements from Carbon to Nickel. Astrophys. J. Suppl. Ser. 1954, 1, 121. [Google Scholar] [CrossRef]
- Cook, C.W.; Fowler, W.A.; Lauritsen, C.C.; Lauritsen, T. B12, C12, and the Red Giants. Phys. Rev. 1957, 107, 508–515. [Google Scholar] [CrossRef]
- Dunbar, D.N.F.; Pixley, R.E.; Wenzel, W.A.; Whaling, W. The 7.68-Mev State in C12. Phys. Rev. 1953, 92, 649–650. [Google Scholar] [CrossRef]
- Korennov, S.; Descouvemont, P. A microscopic three-cluster model in the hyperspherical formalism. Nucl. Phys. A 2004, 740, 249–267. [Google Scholar] [CrossRef]
- Thompson, D.; Lemere, M.; Tang, Y. Systematic investigation of scattering problems with the resonating-group method. Nucl. Phys. A 1977, 286, 53–66. [Google Scholar] [CrossRef]
- Nomoto, K.; Thielemann, F.K.; Miyaji, S. The triple alpha reaction at low temperatures in accreting white dwarfs and neutron stars. Astron. Astrophys. 1985, 149, 239–245. [Google Scholar]
- Angulo, C.; Arnould, M.; Rayet, M.; Descouvemont, P.; Baye, D.; Leclercq-Willain, C.; Coc, A.; Barhoumi, S.; Aguer, P.; Rolfs, C.; et al. A compilation of charged-particle induced thermonuclear reaction rates. Nucl. Phys. A 1999, 656, 3–183. [Google Scholar] [CrossRef]
- Iliadis, C. Nuclear Physics of Stars; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar] [CrossRef]
- Kelley, J.; Purcell, J.; Sheu, C. Energy levels of light nuclei A = 12. Nucl. Phys. A 2017, 968, 71–253. [Google Scholar] [CrossRef] [Green Version]
- Tilley, D.; Kelley, J.; Godwin, J.; Millener, D.; Purcell, J.; Sheu, C.; Weller, H. Energy levels of light nuclei A = 8, 9, 10. Nucl. Phys. A 2004, 745, 155–362. [Google Scholar] [CrossRef]
- Paxton, B.; Smolec, R.; Schwab, J.; Gautschy, A.; Bildsten, L.; Cantiello, M.; Dotter, A.; Farmer, R.; Goldberg, J.A.; Jermyn, A.S.; et al. Modules for Experiments in Stellar Astrophysics (MESA): Pulsating Variable Stars, Rotation, Convective Boundaries, and Energy Conservation. Astrophys. J. Suppl. Ser. 2019, 243, 10. [Google Scholar] [CrossRef]
- Paxton, B.; Schwab, J.; Bauer, E.B.; Bildsten, L.; Blinnikov, S.; Duffell, P.; Farmer, R.; Goldberg, J.A.; Marchant, P.; Sorokina, E.; et al. Modules for Experiments in Stellar Astrophysics (MESA): Convective Boundaries, Element Diffusion, and Massive Star Explosions. Astrophys. J. Suppl. Ser. 2018, 234, 34. [Google Scholar] [CrossRef]
- Paxton, B.; Marchant, P.; Schwab, J.; Bauer, E.B.; Bildsten, L.; Cantiello, M.; Dessart, L.; Farmer, R.; Hu, H.; Langer, N.; et al. Modules for Experiments in Stellar Astrophysics (MESA): Binaries, Pulsations, and Explosions. Astrophys. J. Suppl. Ser. 2015, 220, 15. [Google Scholar] [CrossRef]
- Paxton, B.; Cantiello, M.; Arras, P.; Bildsten, L.; Brown, E.F.; Dotter, A.; Mankovich, C.; Montgomery, M.H.; Stello, D.; Timmes, F.X.; et al. Modules for Experiments in Stellar Astrophysics (MESA): Planets, Oscillations, Rotation, and Massive Stars. Astrophys. J. Suppl. Ser. 2013, 208, 4. [Google Scholar] [CrossRef] [Green Version]
- Paxton, B.; Bildsten, L.; Dotter, A.; Herwig, F.; Lesaffre, P.; Timmes, F. Modules for Experiments in Stellar Astrophysics (MESA). Astrophys. J. Suppl. Ser. 2011, 192, 3. [Google Scholar] [CrossRef]
- Pitrou, C.; Coc, A.; Uzan, J.P.; Vangioni, E. Precision big bang nucleosynthesis with improved Helium-4 predictions. Phys. Rep. 2018, 754, 1–66. [Google Scholar] [CrossRef] [Green Version]
- Girardi, L.; Bressan, A.; Bertelli, G.; Chiosi, C. Evolutionary tracks and isochrones for low- and intermediate-mass stars: From 0.15 to 7 Msun, and from Z = 0.0004 to 0.03. Astron. Astrophys. Suppl. 2000, 141, 371–383. [Google Scholar] [CrossRef] [Green Version]
- Heger, A.; Woosley, S.E. Nucleosynthesis and Evolution of Massive Metal-free Stars. Astrophys. J. 2010, 724, 341–373. [Google Scholar] [CrossRef] [Green Version]
- Ohkubo, T.; Nomoto, K.; Umeda, H.; Yoshida, N.; Tsuruta, S. Evolution of Very Massive Population III Stars with Mass Accretion from Pre-main Sequence to Collapse. Astrophys. J. 2009, 706, 1184–1193. [Google Scholar] [CrossRef] [Green Version]
- Heger, A.; Woosley, S.E. The Nucleosynthetic Signature of Population III. Astrophys. J. 2002, 567, 532–543. [Google Scholar] [CrossRef]
- Marigo, P.; Girardi, L.; Chiosi, C.; Wood, P.R. Zero-metallicity stars. I. Evolution at constant mass. Astron. Astrophys. 2001, 371, 152–173. [Google Scholar] [CrossRef]
- Cassisi, S.; Castellani, V. An Evolutionary Scenario for Primeval Stellar Populations. Astrophys. J. Suppl. Ser. 1993, 88, 509. [Google Scholar] [CrossRef]
- Tur, C.; Heger, A.; Austin, S.M. On the Sensitivity of Massive Star Nucleosynthesis and Evolution to Solar Abundances and to Uncertainties in Helium-Burning Reaction Rates. Astrophys. J. 2007, 671, 821–827. [Google Scholar] [CrossRef] [Green Version]
- Schlattl, H.; Heger, A.; Oberhummer, H.; Rauscher, T.; Csótó, A. Sensitivity of the C and O production on the 3α rate. Astrophys. Space Sci. 2004, 291, 27–56. [Google Scholar] [CrossRef] [Green Version]
- Flambaum, V.V.; Wiringa, R.B. Dependence of nuclear binding on hadronic mass variation. Phys. Rev. C 2007, 76, 054002. [Google Scholar] [CrossRef] [Green Version]
- Wiringa, R.B.; Stoks, V.G.J.; Schiavilla, R. Accurate nucleon-nucleon potential with charge-independence breaking. Phys. Rev. C 1995, 51, 38–51. [Google Scholar] [CrossRef] [Green Version]
- Pudliner, B.S.; Pandharipande, V.R.; Carlson, J.; Wiringa, R.B. Quantum Monte Carlo Calculations of A≤6 Nuclei. Phys. Rev. Lett. 1995, 74, 4396–4399. [Google Scholar] [CrossRef] [Green Version]
- Mori, K.; Kusakabe, M. Roles of 7Be(n,p)7Li resonances in big bang nucleosynthesis with time-dependent quark mass and a possible Li reduction. Phys. Rev. D 2019, 99, 083013. [Google Scholar] [CrossRef] [Green Version]
- Cheoun, M.K.; Kajino, T.; Kusakabe, M.; Mathews, G.J. Time-dependent quark masses and big bang nucleosynthesis revisited. Phys. Rev. D 2011, 84, 043001. [Google Scholar] [CrossRef] [Green Version]
- Bedaque, P.F.; Luu, T.; Platter, L. Quark mass variation constraints from Big Bang nucleosynthesis. Phys. Rev. C 2011, 83, 045803. [Google Scholar] [CrossRef]
- Berengut, J.; Flambaum, V.; Dmitriev, V. Effect of quark mass variation on big bang nucleosynthesis. Phys. Lett. B 2010, 683, 114–118. [Google Scholar] [CrossRef] [Green Version]
- Coc, A.; Nunes, N.J.; Olive, K.A.; Uzan, J.P.; Vangioni, E. Coupled variations of fundamental couplings and primordial nucleosynthesis. Phys. Rev. D 2007, 76, 023511. [Google Scholar] [CrossRef] [Green Version]
- Murphy, M.T.; Malec, A.L.; Prochaska, J.X. Precise limits on cosmological variability of the fine-structure constant with zinc and chromium quasar absorption lines. Mon. Not. R. Astron. Soc. 2016, 461, 2461–2479. [Google Scholar] [CrossRef]
- Oberhummer, H.; Csótó, A.; Schlattl, H. Stellar Production Rates of Carbon and Its Abundance in the Universe. Science 2000, 289, 88–90. [Google Scholar] [CrossRef] [Green Version]
- Machleidt, R.; Entem, D. Chiral effective field theory and nuclear forces. Phys. Rep. 2011, 503, 1–75. [Google Scholar] [CrossRef] [Green Version]
- Skidmore, W.; TMT International Science Development Teams & TMT Science Advisory Committee. Thirty Meter Telescope Detailed Science Case: 2015. Res. Astron. Astrophys. 2015, 15, 1945. [Google Scholar] [CrossRef] [Green Version]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mori, K.; Nomoto, K. Probing Time-Dependent Fundamental Constants with Nucleosynthesis in Population III Stars. Symmetry 2020, 12, 404. https://doi.org/10.3390/sym12030404
Mori K, Nomoto K. Probing Time-Dependent Fundamental Constants with Nucleosynthesis in Population III Stars. Symmetry. 2020; 12(3):404. https://doi.org/10.3390/sym12030404
Chicago/Turabian StyleMori, Kanji, and Ken’ichi Nomoto. 2020. "Probing Time-Dependent Fundamental Constants with Nucleosynthesis in Population III Stars" Symmetry 12, no. 3: 404. https://doi.org/10.3390/sym12030404
APA StyleMori, K., & Nomoto, K. (2020). Probing Time-Dependent Fundamental Constants with Nucleosynthesis in Population III Stars. Symmetry, 12(3), 404. https://doi.org/10.3390/sym12030404




