Abstract
We consider the reduced constrained linear Cosserat continuum, a particular type of a Cosserat medium, for three different material behaviors or symmetries: the isotropic elastic case, a special type of elastic transversely isotropic case, and the isotropic viscoelastic case. Such continua, in which stresses do not work on rates of microrotation gradients, behave as acoustic metamaterials for the (pure) shear waves and also for one branch of the mixed wave in the considered anisotropic material case. In elastic media, those waves do not propagate for frequencies exceeding a certain threshold, whence these media exhibit a single negative acoustic metamaterial behavior in this range. In the isotropic viscoelastic case, dissipation destroys the bandgap and favors wave propagation. This curious effect is, probably, due to the fact that the bandgap is associated not with the dissipation, but with the wave localization which can be destroyed by the viscosity. The dispersion curve is now decreasing in some part of the former bandgap, above a certain frequency, whence the medium is a double negative acoustic metamaterial. We prove the existence of a boundary wavenumber in the viscoelastic case and estimate its value. Below the characteristic frequency corresponding to the boundary of the elastic bandgap, the wave attenuation (logarithmic decrement) is a growing function of the viscous dissipation parameter. Above this frequency, the attenuation decreases as the viscosity increases.
1. Introduction
Three-dimensional solid continua, in which both translational and rotational motions of body points are considered, and respectively characterized by displacement field and microrotation vector field , were introduced by the Cosserat brothers [1]. Their theory then sank into oblivion for about 50 years before it was systematically revisited by [2]. Among recent books on the subject, one can mention [3].
The present study focusses on acoustic or seismic wave propagation in reduced Cosserat continua, a special class of Cosserat media in which internal stresses do not work on the microrotation gradient velocity. This entails special symmetry conditions on the strain energy, which depends on the Cosserat deformation tensor but not on the wryness tensor. Possible strain measures for continua with rotational degrees of freedom with various types of symmetry are discussed in [4,5,6]. Such models may be applied to granular materials [7,8,9,10], media with high contrasts, geomaterials [11,12,13,14,15,16], in which non-classical wave propagation is observed [17]. One of the first applications of an elastic reduced isotropic Cosserat model to wave propagation in granular materials was suggested in [7].
Media with effective negative parameters (density and/or the relevant elastic modulus), as regards wave propagation, are called acoustic metamaterials [18]. This phenomenon takes place in a certain frequency domain. If both elastic and inertial effective frequency-dependent parameters are negative, one has a double negative acoustic metamaterial. It exhibits negative refraction, i.e., a decreasing dispersion curve. If only one of the effective frequency-dependent parameters is negative, this is a single negative acoustic metamaterial, i.e., the dispersion graph for the corresponding harmonic wave has a band gap [19]. These media can be used, for instance, to control wave beams, energy fluxes, or to conceal objects, rendered acoustically undetectable.
We can consider more general elastic continua, in which the strain energy depends on a certain vector field but not on its gradient. In reduced Cosserat media this is the microrotation vector. One can intuitively view a reduced complex continuum as a hosting continuum, with all elastic connections present, including isolated resonators that are not directly coupled to one another.
Such reduced generalized elastic media were shown to behave as acoustic metamaterials [20]. In particular, reduced elastic Cosserat media are single negative acoustic metamaterials, for which harmonic shear waves are evanescent in a certain frequency domain. Lots of works consider acoustic metamaterials with internal (often rotational) degrees of freedom, on the discrete and continuum level [21,22,23,24,25,26,27].
The possible interpretation of a time-dispersive material as an “extended” material with hidden internal degrees of freedom is suggested, for instance, in [28]. Viscosity may drastically change the wave properties of an elastic metamaterial [13], destroying the bandgap and, in some cases, leading to a decreasing dispersion curve in some range. Relaxed linear micromorphic metamaterials (with band gaps) are discussed in [29,30], where a certain kinematical constraint is accepted, as well as in the full constrained Cosserat medium [31]. Other materials with microstructure having band gaps are investigated in [32,33], the latter one being an example of a hosting continuum enhanced by distributed resonators, discussed in [20]. In linear constrained Cosserat media the microrotation is identically equal to the vortex deformation (macrorotation) of the neighbourhood . These models are popular in the scientific community [34,35], possibly they could be used for the description of blocky media.
Specialists in the rotational seismology, a science which has developed during the past decades, agree that rotational degrees of freedom of blocks and heterogeneities in the geomedium must be taken into account [36,37,38]. However, there is a strong discussion on the most appropriate model. There are works that insist taking into account only the macro-rotation of the medium, see, for instance, [39]. To satisfy the principle of material objectivity, in this case, it is necessary to accept the kinematical hypothesis that the macro-rotation is equal to the micro-rotation, i.e., to consider the constrained Cosserat theory. On the other hand, the presence of slow waves [40] is an argument in favor of reduced Cosserat continuum or another acoustic metamaterial as an appropriate model.
In this work, we have considered elastic and viscoelastic models which combine features of the constrained Cosserat medium and reduced Cosserat medium. The viscoelastic model is taken in its simplest isotropic variant, which can be found in [41] for the full linear Cosserat medium; we consider a particular case, when it is reduced (i.e., couple stresses are zero) and constrained (i.e., a kinematical hypothesis “microrotation equals macrorotation” is accepted). The investigation of wave propagation in such media (elastic isotropic, elastic with anisotropic coupling and viscoelastic isotropic) will give some information for experimentalists to judge if it is an adequate theory for a real granular or blocky medium. We have chosen this model also since it has a very few parameters and therefore we can clearly see in this case how the viscosity can change the wave propagation in a rotational metamaterial.
2. Model and Basic Laws
We consider a linear micropolar medium each point of which is characterized by an infinitesimal translational displacement and an infinitesimal microrotation vector . In the linear medium, actual and initial configurations coincide as well as nabla operators in both of them. Since we consider a reduced Cosserat medium, we suppose that no stresses work on , see [7,42]. Since we consider a constrained Cosserat medium, we accept a kinematical hypothesis
as in [31]. Each body point of the medium possesses density and density of the tensor of inertia . We will shortly recall here dynamic laws for a constrained reduced Cosserat medium of any type, which can be found in [13], and write down its final form for the general case.
Balance of force in its local form looks as follows:
where is the stress tensor, is the density of the external body force, is the time derivative. We can write this law, representing as
Here and are the symmetric and antisymmetric parts of , respectively, and , being a certain basis, is the identity tensor. Then (2) takes form
Balance of moment in its local form is
where is the density of the external body moment.
Substituting the kinematical hypothesis (1) into the balance of moment, we obtain
Then we substitute this expression into the balance of force (4) and obtain
Note that if obeys the equations of a local theory, we still obtain a local theory, although with a sophisticated dynamical term that has mixed spatial–temporal derivatives. This is contrary to the case of the constrained full Cosserat medium, where the kinematical constraint yields in equivalent second gradient theory. This difference is related to the fact that the strain energy in the reduced model does not depend on .
The law of balance of energy looks as
(heat transfer is not considered). Equation (7) is valid for any type of the linear constrained reduced Cosserat medium. Symmetric part of the stress is determined by the constitutive equations.
We see that antisymmetric part of is determined by balance of moment (6) and not by a constitutive equation. This is due to the fact that in the linear non-constrained model works on the strain rate . Indeed, if is the mass density of the strain energy for a linear non-constrained reduced model, then [42]
Note that
Constitutive equations for the non-constrained elastic medium are obtained from the law of balance of energy both for the symmetric and antisymmetric part of . In the constrained model, , therefore cannot be obtained from this law, but it is determined by the dynamic law (6).
2.1. Constitutive Equations for the Linear Elastic Constrained Reduced Cosserat Media
We will consider the elastic medium in adiabatic or isothermal processes. The second law of thermodynamics is satisfied identically for this case. Since the medium is linear, U a quadratic form of :
the same as for the classical medium, where is the elastic tensor of the fourth rank. As in the classical elasticity, it satisfies the symmetry conditions . The law of balance of energy (8) thus gives us the constitutive equation
However, since we have rotational degrees of freedom and the kinematical constraint , the medium is not classical, and but determined from dynamic Equation (6). Concrete form of is determined by the symmetry of the material: its group of symmetry includes the group of symmetry of the medium, according to the Curie–Neumann’s principle [43].
We can also obtain the same equations in terms of modified strain energy with Lagrange multipliers. Consider zero external loads. Indeed, Lagrange equations for the continuum look as
where is a generalised vector consisting of generalised co-ordinates (components of and in our case), Lagrangian density , being the density of the kinetic energy, the density of the strain energy of the continuum. This is true in case when there are no kinematical constraints. When they exist, we have to use the density of the modified strain energy instead of U. In our (linear) case
U is defined by (11), and
where is a Lagrange multiplier, an antisymmetric tensor of the second rank, vector . In fact, has a physical sense of .
Note that
2.2. Isotropic Elastic Model
First we choose an isotropic homogeneous elastic model. Then the elastic tensor is also isotropic and looks as
where are elastic Lamé constants. Then the constitutive equation for the symmetric part of the stress tensor takes form
Substituting this expression to the dynamic law (7), and considering zero external loads and spherical density of the inertia tensor , we obtain equations in displacements:
Let us look for the plane wave solution: . Then we obtain
Denote , where . We can rewrite this equation as
Compression plane wave is separated and it is not influenced by the rotational degrees of freedom. Indeed, if , we obtain the classical dispersion relation for the longitudinal wave:
Denote (this will be a certain characteristic frequency of the medium), (wave velocity). The dispersion relation for the shear–rotational wave (), given by (26), is
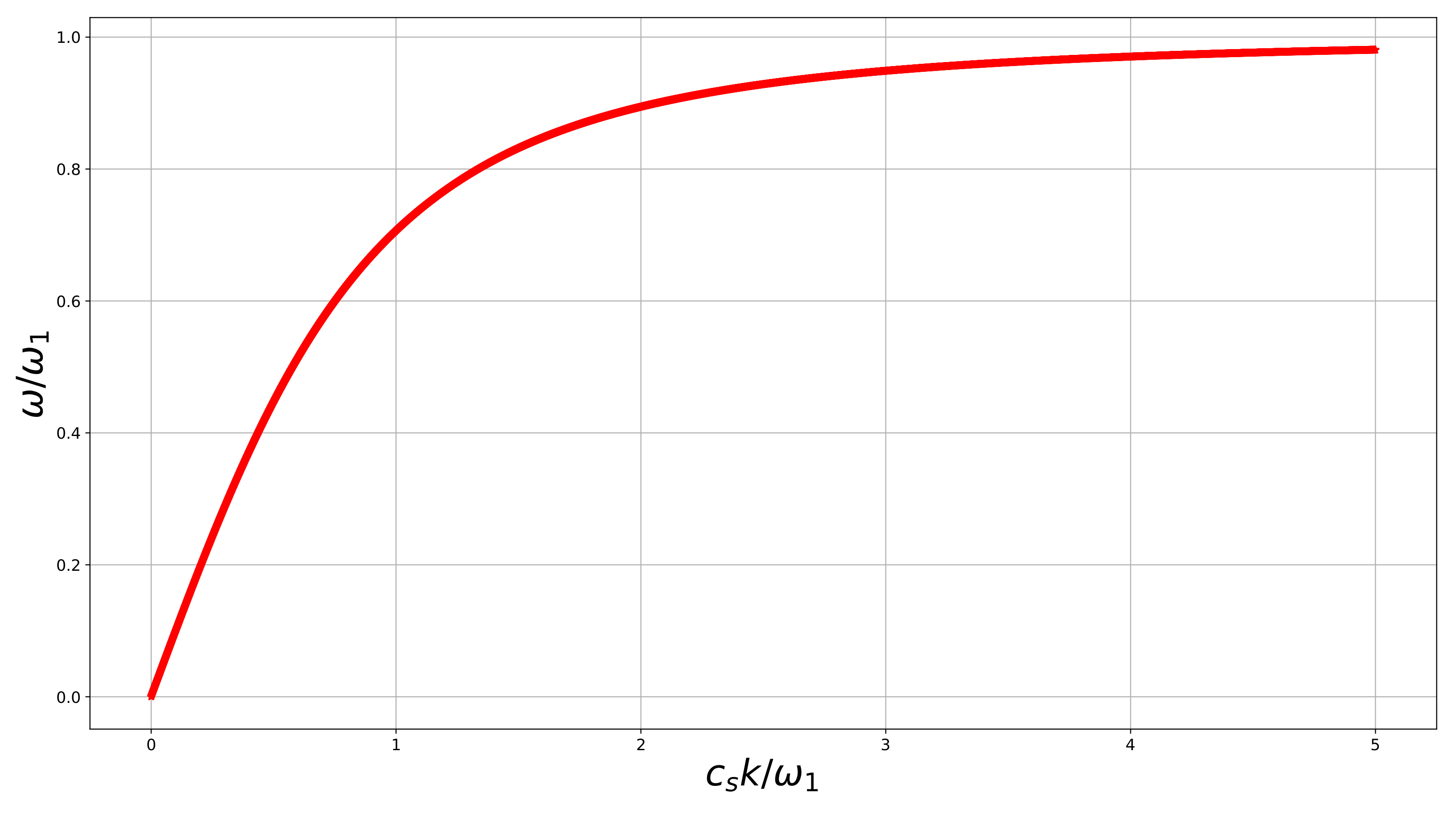
We see that at low frequency this dispersion branch starts as the classical shear wave, but for higher frequencies dispersion becomes more pronounced, and the curve has a horizontal asymptote (boundary frequency). Above this frequency, no shear wave propagates (see Figure 1).
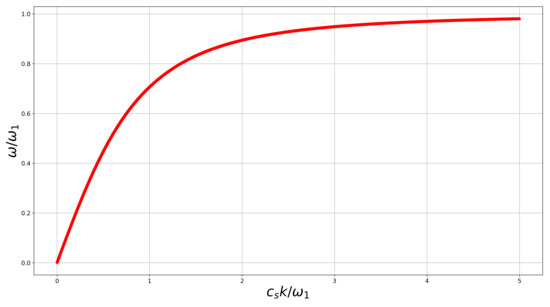
Figure 1.
Dispersion graph for the plane shear–rotational wave in the 3D infinite elastic isotropic linear reduced constrained Cosserat medium. Parameters: . Infinite band gap above .
In the reduced non-constrained linear isotropic elastic Cosserat medium (see [42]) we do not accept kinematical hypothesis (1). Instead of that there exist a rotational elastic constant , and the strain energy has an additional term . In this case there are two branches of this curve with a bandgap between them. The low branch for the non-constrained model is analogous to the curve presented in Figure 1, but instead of for the constrained medium we have a boundary frequency . The upper branch for the non-constrained medium starts at a cut-off frequency . When the resistance to the strain tends to infinity (), the cut-off frequency tends to infinity also, and the boundary frequency tends to , i.e., we obtain the dispersion graph for the constrained linear isotropic elastic reduced Cosserat medium. This is to expect. This also tells us that the theory under consideration could be possibly applicable for blocky media.
2.3. Elastic Model with the Simplest Anisotropic Coupling Term (Axial Symmetry with Axis )
Now consider the influence of anisotropy on the wave propagation. The anisotropic term of most interest would be a coupling between shear and compressional deformations, a feature which is present in granular-like materials. Such a coupling does not exist in isotropic theories. We consider a simplest variant of such an anisotropic medium: a transversally isotropic medium with the unit vector of the axis of isotropy , where the anisotropy is only present in this coupling and has a particular form, coupling volumetric and shear deformations. Namely, let the density of the strain energy be
where is the strain energy for the isotropic case. The constitutive equations are
Substituting them into dynamic law (7), considering zero external loads , and spherical symmetry for the tensor of inertia (), we obtain dynamic equations in displacements:
Looking for the plane wave propagation , we obtain the spectral problem:
Denote , then , where . Then the spectral problem can be rewritten as:
Due to the specific type of coupling there exist a purely shear wave, the same as in the isotropic case, if . The last and the first term in (33) then vanish and the corresponding dispersion relation the same form (28) as in the isotropic case. However, the compression wave, generally speaking, does not exist, it is coupled to the shear wave, with the exception of some special directions of wave propagation.
2.3.1. Special Directions of Wave Propagation
Consider waves propagating along or orthogonal to the axis of isotropy . In both cases the last term in parentheses in (33) disappears, since either if , or . The spectral problem for compression and shear wave can be decoupled, as in the isotropic case, and we have the same dispersion relations, with the only difference that for the wave velocity for the compressional wave is influenced by the anisotropic constant, the dispersion relation looks as
Thus, if or , anisotropic term for the shear wave disappears, and its dispersion relation is the same as for the isotropic medium, longitudinal wave is non-dispersive, with constant velocity ,
2.3.2. Mixed Wave
If neither nor , longitudinal wave and shear wave with not parallel to do not exist. Waves become mixed. Separating the “isotropic-like” shear wave, we obtain from (33) the dispersion relation for the mixed wave:
where
It can be rewritten as
We can find eigenvectors for the mixed wave from this relation and Equation (33). Omitting some calculations, we give the result:
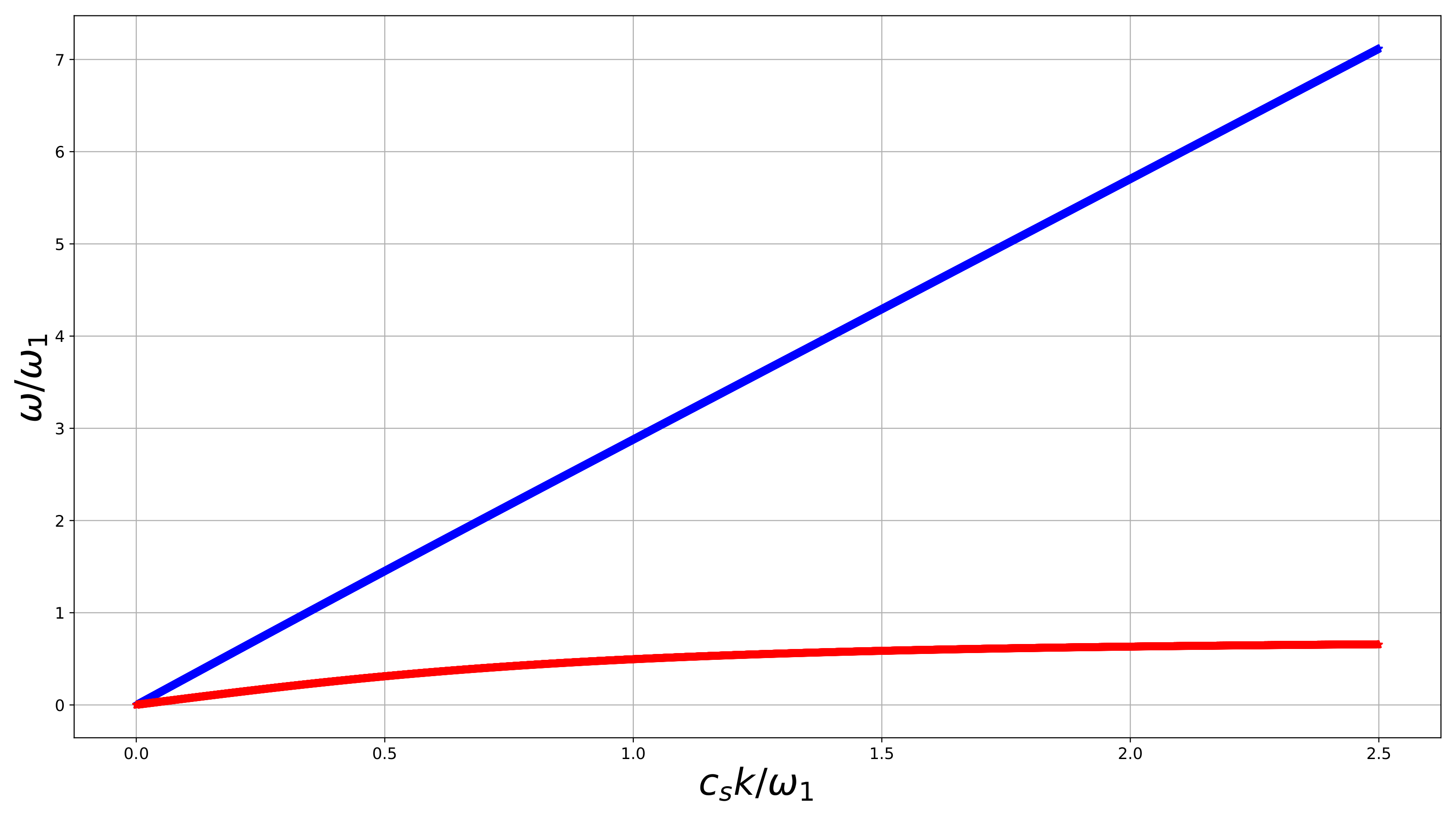
An example of dispersion curves is given in Figure 2. Both curves are dispersive but for the upper one we hardly notice this.
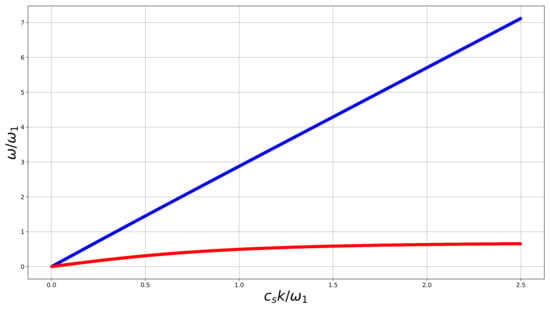
Figure 2.
Dispersion curves for the constrained anisotropic elastic linear reduced Cosserat medium, . Both curves are dispersive but for the upper branch we hardly notice this.
The branch with “+” of Equation (38) at large k tends to , and at small k
These two velocities are relatively close if we require the strain energy to be positively definite. For instance, for the parameters shown in Figure 2, if we take , we obtain the velocity at low frequencies approximately equal to 2.92, and at large frequencies approximately 2.83.
The lower (“−”) branch of Equation (38) has a horizontal asymptote , analogously to the isotropic case, where (for instance, for parameters in Figure 2), and it is highly dispersive. At low frequencies it behaves as
and its velocity is less than .
Summary for the Elastic Models
We see that for the linear elastic constrained reduced Cosserat media (isotropic and special transversally isotropic with a coupling between volumetric and shear deformations)
- there is an infinite bandgap above the boundary frequency for the shear waves in both models and above a lower frequency , which depends also on the anisotropy and propagation direction, for the slower mixed wave in the considered anisotropic case.
- compression wave in the isotropic case is classical, non-dispersive
- the upper branch of the mixed wave in the considered anisotropic case is weakly dispersive and has no band gap; its effective moduli, in particular, depend on the direction of the wave propagation and anisotropy parameter
2.4. Isotropic Viscoelastic Model
Let us consider how viscosity in case of the simplest viscoelastic model will influence the wave propagation. For the reduced isotropic Cosserat medium it yields in drastic change [13]. As we discussed before, for any constrained linear reduced Cosserat medium is determined from the constitutive equations. We choose an isotropic homogeneous viscoelastic Kelvin–Voight model
This constitutive equation satisfies the 2nd law of thermodynamics if . Consider zero external body loads and spherical tensor of inertia, as in previous sections. This equation together with the balance of force (7) lets us to write down equations in displacements:
2.4.1. Plane Shear Wave
Taking the divergence of (43), we see that as in the purely elastic isotropic case, considered in Section 2.2, compression wave is not influenced by rotational degrees of freedom. It is separated from the shear wave. We will not discuss it here, since it is the same as in the classical viscoelasticity.
We look for the plane wave solution of (43): and consider the case of the shear wave (). Shear wave obeys the following equation in the Fourier domain:
It gives us the following dispersion relation:
Let us investigate how the viscosity will influence the band gap which exists in the elastic case. Let us denote
There is one positive root for , since :
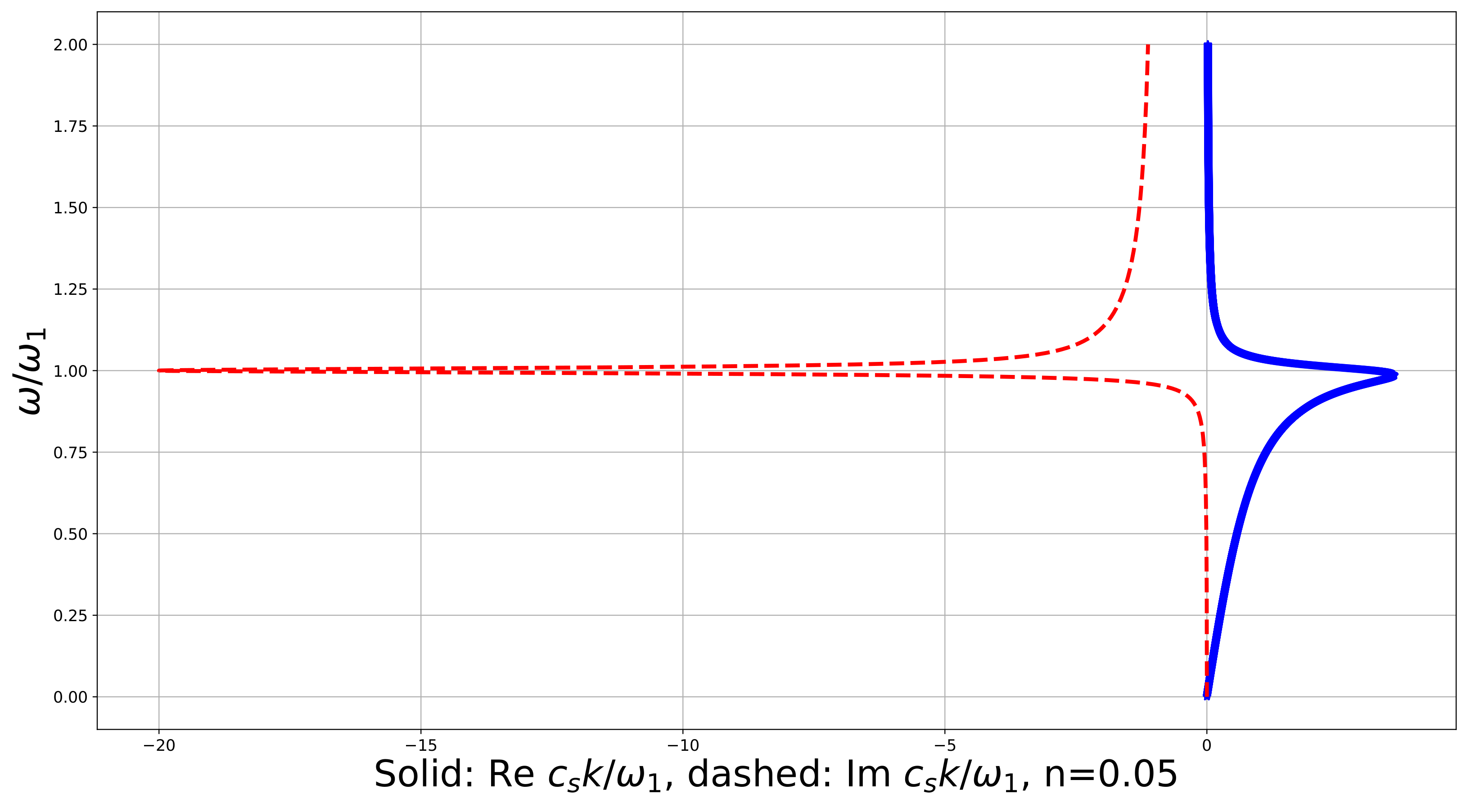
Figure 3 shows us an example of numerical graphs for the dispersion relation:
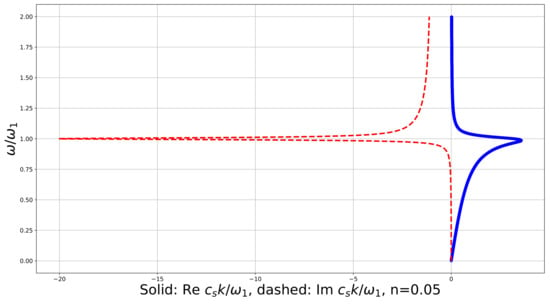
Figure 3.
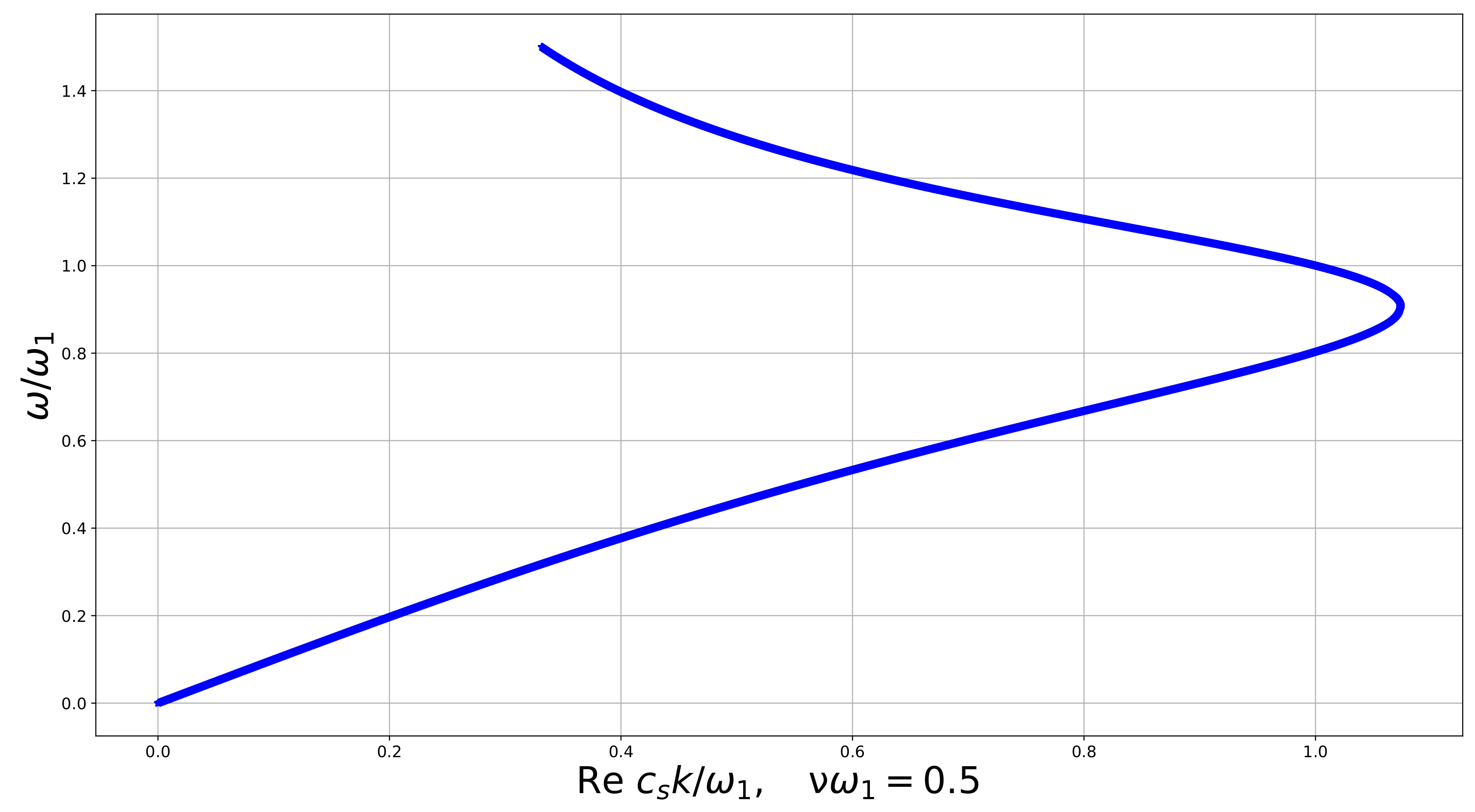
Dispersion curve for the linear constrained reduced viscoelastic isotropic Cosserat medium, vs. , .
In this figure we see that both and first increase with , then they reach their maximal values (not at the same frequency), and after this decrease with . This is a quite untypical behavior. For all parameters checked numerically has one maximum, and has one maximum for n which is small enough. Approximately at the extremum for the imaginary part of the wavenumber disappears.
2.4.2. Dispersion Relation Properties of the Viscoelastic Model
Asymptotics for Various Domains of Frequencies
Let us consider the properties of the dispersion relation (49). First, we can see from this equation, that in the viscoelastic reduced linear isotropic constrained Cosserat continuum there are no band gaps. Indeed, there is one positive root for , given (up to multiplication by a constant ) by Equation (49) for any frequencies. Consider its asymptotics at low frequencies. At we obtain almost classical shear wave. Indeed, (45) in this limit gives us
In the vicinity of the boundary frequency ()
So we see that if dispersion curve decreases at . The decreasing part of the dispersion curve corresponds to the behavior of a double negative acoustic metamaterial. At it increases at this point, and at it has a maximum .
At large frequencies our medium is always a double negative acoustic metamaterial, since the dispersion curve decreases: if (), then
We see that Figure 3 confirms this asymptotics.
Detailed Analysis of the Real Part of the Wavenumber. Influence of the Dissipation Parameter n on Its Behaviour
We see that is a differentiable function, increasing at small and decreasing at large . Therefore, it has at least one maximum and it is limited by a certain value. We will estimate this value from above. Note that
Estimating from above each term in the right part of this equation (see Appendix A), we obtain
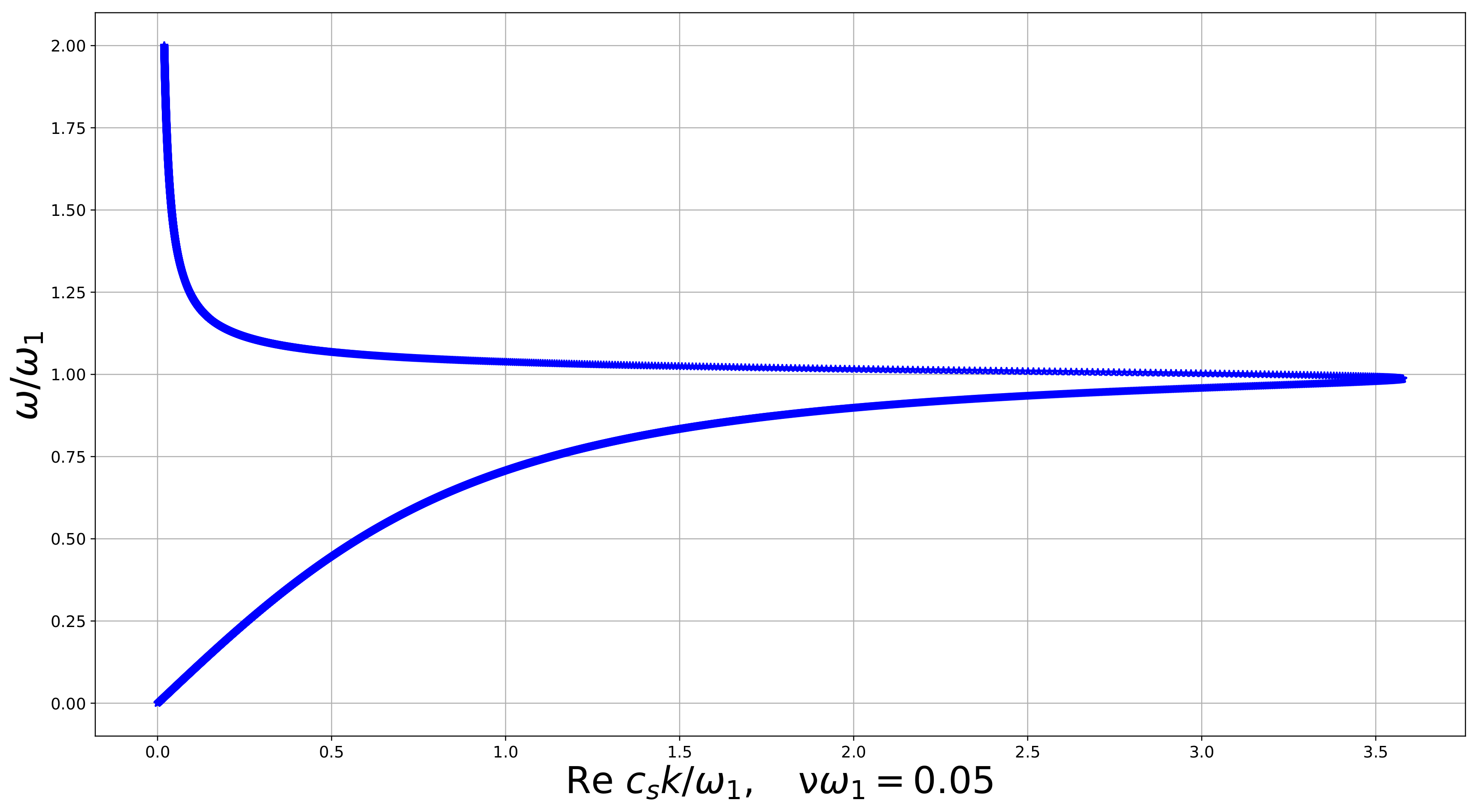
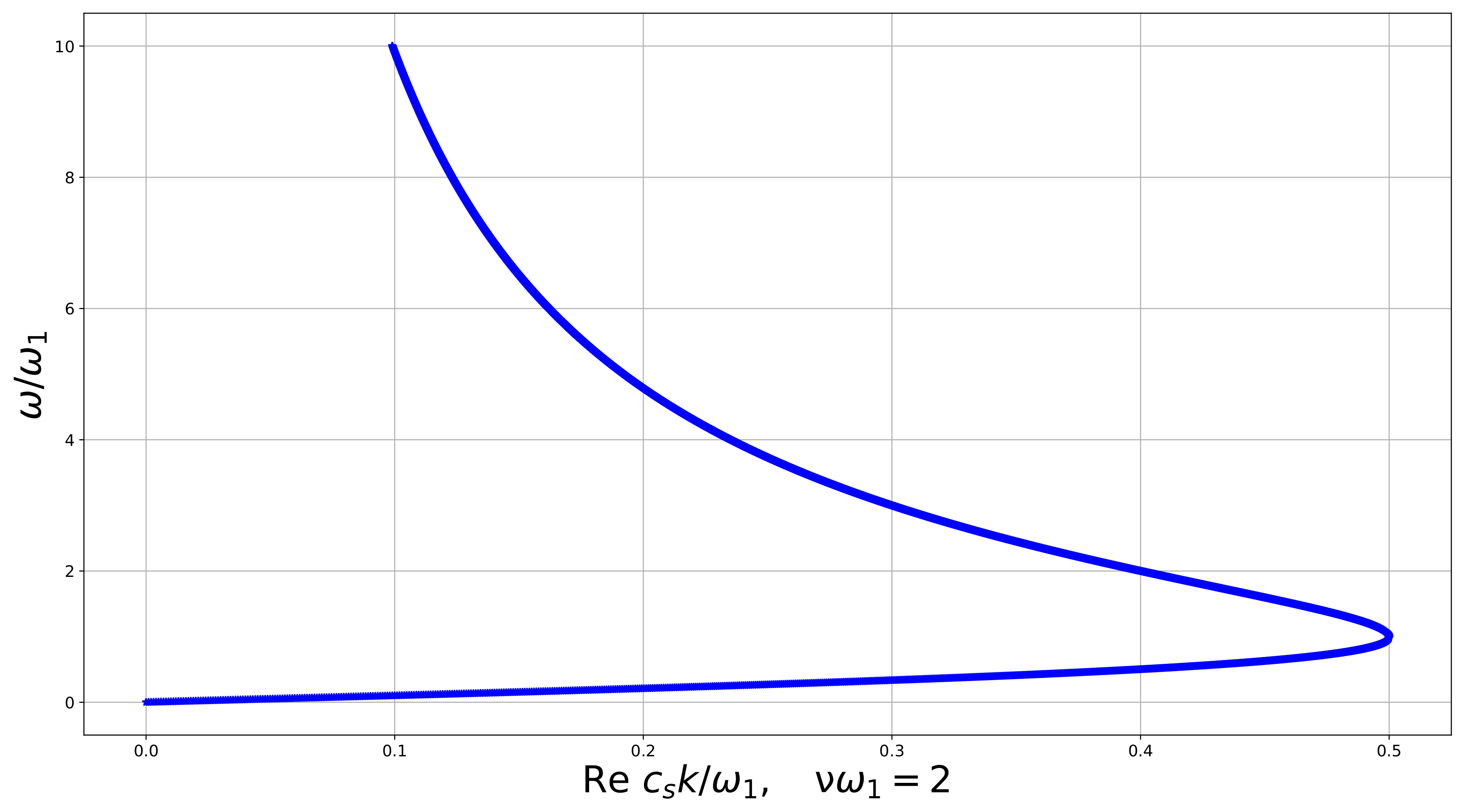
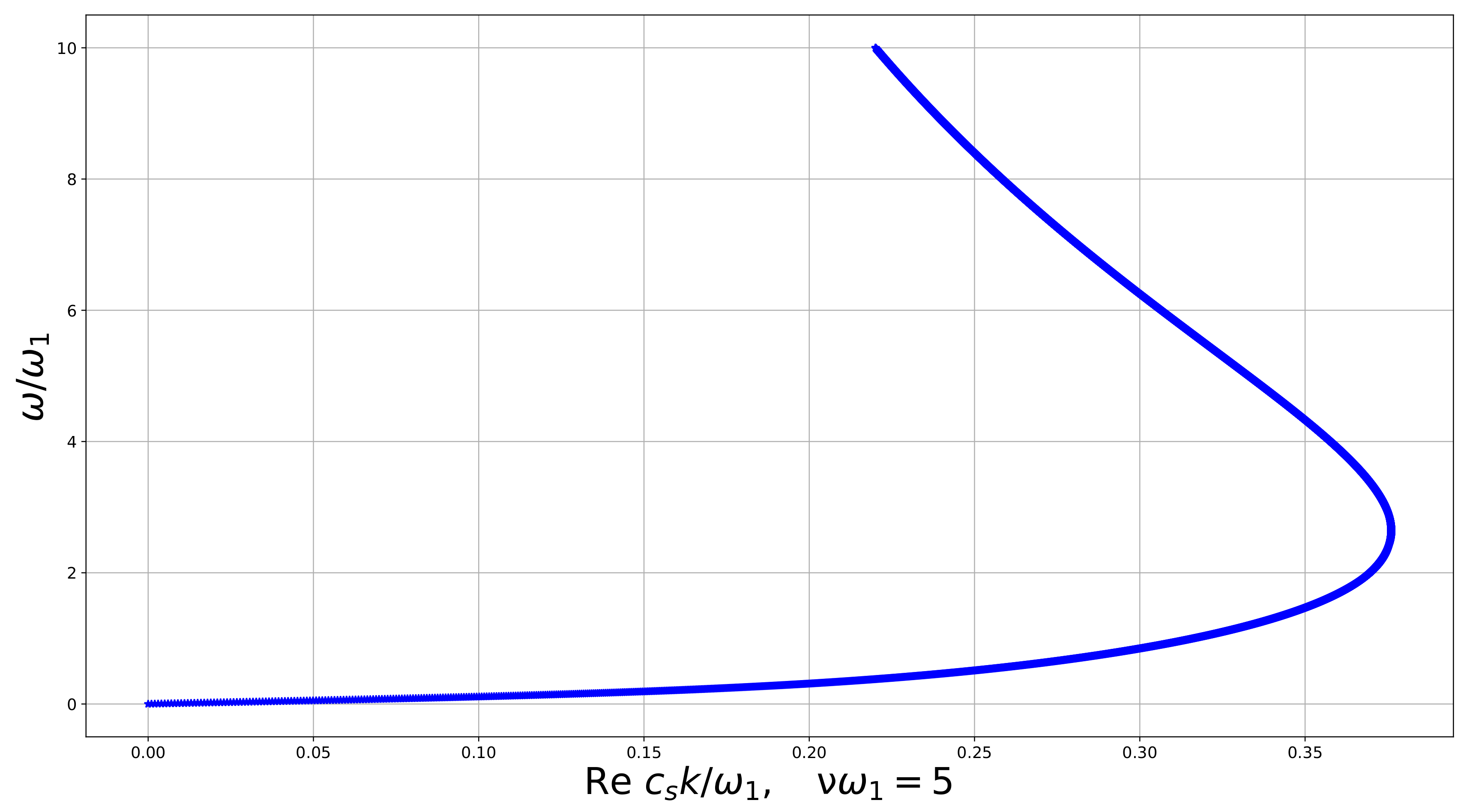
In all numerical examples K increases with until a certain value where it has a maximum and then decreases, tending to 0 at large , as it follows from the analytics obtained above. Numerical examples of the dispersion curve for the real part of the wave number (Figure 4, Figure 5, Figure 6 and Figure 7) show us how it changes when the dissipation parameter n increases. We see that , corresponding to the minimal wavelength, decreases with n. The medium exhibits features of a double negative acoustic metamaterial above , which can be controlled via the dissipation. However, is not a monotone function of n. Numerical examples show us that first, it decreases from 1 as n increases, and then increases, overpassing 1 again at .
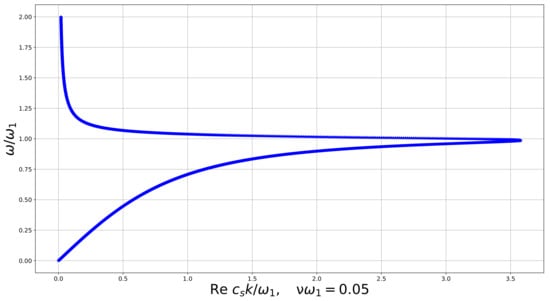
Figure 4.
Dispersion curve for the linear constrained reduced viscoelastic isotropic Cosserat medium, vs. , .
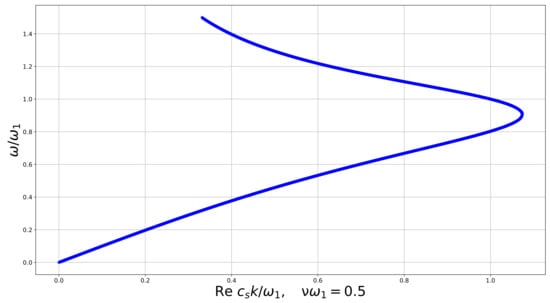
Figure 5.
Dispersion curve for the linear constrained reduced viscoelastic isotropic Cosserat medium, vs. , .
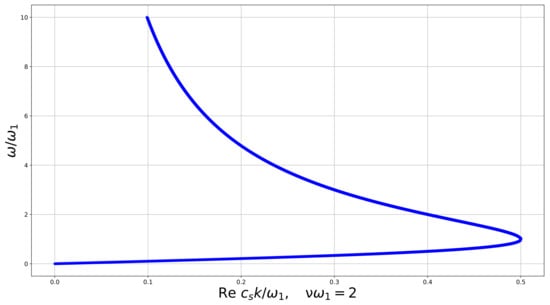
Figure 6.
Dispersion curve for the linear constrained reduced viscoelastic isotropic Cosserat medium, vs. , .
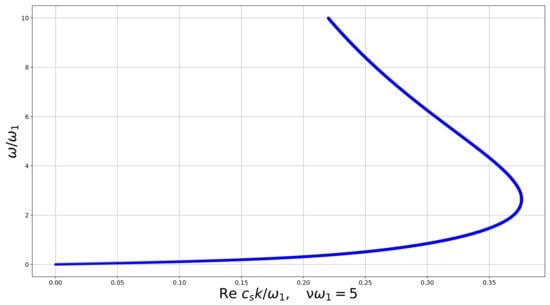
Figure 7.
Dispersion curve for the linear constrained reduced viscoelastic isotropic Cosserat medium, vs. , .
We can analytically find how the value of at a given changes if we change the dissipation parameter n. If we differentiate Equation (54) with respect to and find its extremuma, we obtain that
- at , i.e., in the zone where the shear wave in the elastic medium propagates, as well as at , the value of decreases when n increases;
- at , i.e., in the zone where the shear wave in the elastic medium does not exist, for a given first increases as n increases, then reaches its maximal value at and then decreases as n increases. The corresponding maximal value of is given by
Logarithmic Decrement
It is curious that the logarithmic decrement
at high frequencies behaves as , i.e., the larger dissipation is, the better wave passes. This peculiar property is related to the fact that the band gap in the elastic medium was related not to the dissipation, but to the localization, which appears to be broken by presence of viscosity.
At low frequencies, on the contrary, it is equal to , i.e., it is proportional to the dissipation. At , the same parameter at which K reaches its maximal value at the characteristic frequency , asymptotics for logarithmic decrease at small and large frequencies coincide.
Near the characteristic frequency , i.e., when , , the logarithmic decrement tends to . It means that above this frequency the dissipation favors the shear wave propagation and below it attenuates the wave.
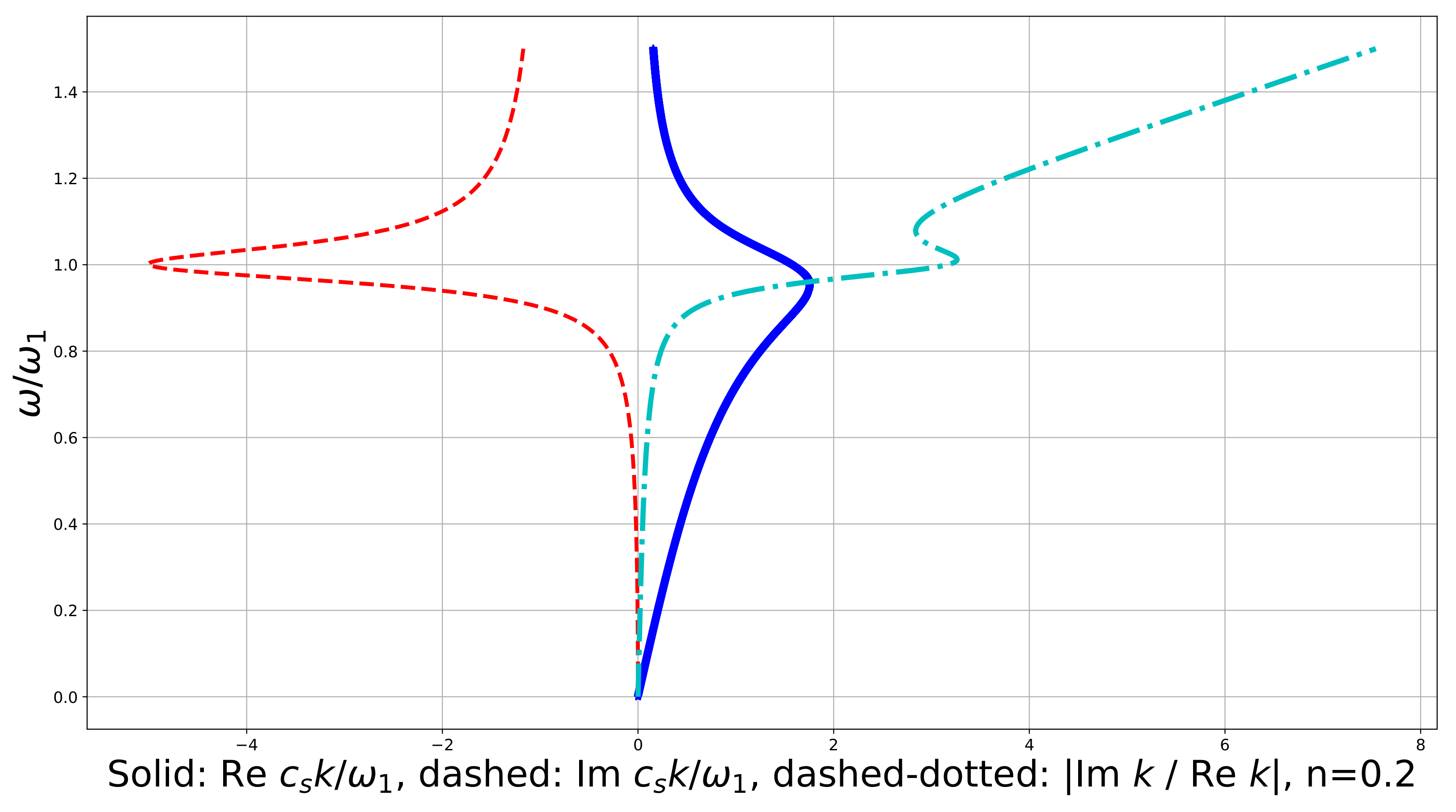
If we differentiate (57) with respect to n, we find that it is a monotone function of n at (increasing with n) and at (decreasing with n), and it does not depend on n at (equals ). Numerical examples show a non-monotonic behavior of the logarithmic decrement as a function of frequency for relatively small n near the characteristic frequency (see Figure 8).
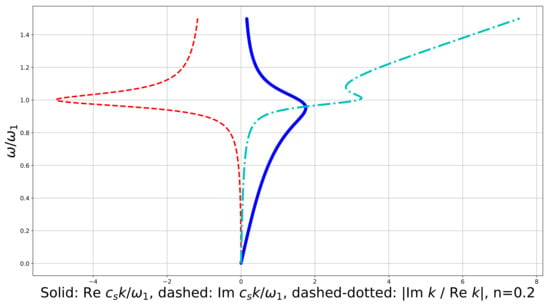
Figure 8.
Dispersion curve for the shear plane wave in the linear constrained reduced viscoelastic isotropic Cosserat medium, vs: (solid), (dashed), logarithmic decrement divided by (dashed-dotted), .
Summary for the Viscoelastic Case
- P-wave is classical due to the isotropy of the model
- Viscoelasticity makes a bandgap for the shear wave to disappear and creates a decreasing part of the dispersion curve
- In the former bandgap (existing for elastic case) viscosity favors the shear wave propagation and below it attenuates the wave
- There exists a boundary wavelength, i.e., a minimal wavelength for propagating waves
3. Discussion
We see that the constrained reduced Cosserat medium in its elastic variant has properties which are similar to the non-constrained reduced Cosserat continuum. It is also a single negative acoustic metamaterial, but the bandgaps for the shear waves in both considered elastic constrained models and for the slower mixed wave in the considered anisotropic case are limited only from below (see Figure 1, Figure 2). The isotropic variant can be obtained as a limit case from the reduced non-constrained isotropic Cosserat model, if we consider in the latter an infinite elastic resistance to the strain . The anisotropic model is not the limit case for an anisotropic reduced non-constrained Cosserat theory with a coupling term between volumetric and rotational deformations, considered in [44]. We cannot introduce a similar coupling because of the kinematical hypothesis which we accept in the constrained model. Indeed, in the non-constrained case, it was a term coupling and . Therefore, it is not strange that one of the branches in the constrained medium is very little dispersive and has no bandgap, unlike the non-constrained continuum. However, both slower waves have some similar to the non-constrained model features (boundary frequencies), due to the fact that both media are reduced, whence some waves cannot propagate.
The constrained reduced viscoelastic Cosserat model demonstrates drastical change in the wave behavior comparing to the elastic case (Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8). We have seen similar effects in the non-constrained theory [13], but in the model considered here, due to its simplicity, it has been possible to analytically investigate the influence of the dissipation in reduced micropolar continua in more detail. We see that in the viscoelastic constrained isotropic reduced Cosserat medium the bandgap does not exist anymore, but it converts, partially or completely, into a decreasing part of the dispersion curve. Thus the medium, which was in a certain domain of frequencies a single negative acoustic metamaterial in the elastic case, becomes a double negative acoustic metamaterial in the viscoelastic case, though, generally speaking, in another domain of frequencies.
At high frequencies, the real part of the wavenumber tends to zero, and the group velocity to infinity. The imaginary part tends to at high frequencies (see Figure 3 and Figure 8). This corresponds to a very fast backward wave whose amplitude decreases in space as . These waves become infinitely fast as their wavelength tends to infinity. This peculiar behavior, in our opinion, is related to the existence of the kinematical hypothesis, which introduces a rigid constraint into the medium.
The real part of the wavenumber is limited by a certain value for all frequencies. In all numerical examples has only one maximum (Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8). It does not coincide with the extremum for the imaginary part, when the latter one exists (Figure 3 and Figure 8). Let us discuss the physical meaning of this. All the plane waves existing in the medium have a wavelength that is larger than a certain minimal value, reached at a specific frequency. Above this frequency we have a decreasing part of dispersion curve (a zone of anomalous dispersion), i.e., the medium is a double negative acoustic metamaterial. Thus, introducing the viscosity, we change the type of acoustic metamaterial. For each wavelength larger than this boundary-value, two plane waves co-exist in the continuum. One of them, a forward wave, whose phase velocity has the same sign as the group velocity, has a lower frequency. Another one, with a higher frequency, is a backward wave: its direction of propagation of wave energy, determined by the group velocity, is opposite to the phase velocity. The longer waves are, the faster is the backward wave, and the forward wave is closer to the classical shear wave.
The frequency which separates two zones, of anomalous and normal dispersion, depends on the dissipation parameter, but, as we can suppose from the numerical experiment, cannot be made arbitrarily small in comparison to the characteristic frequency for the undamped medium. The group velocity at this point is infinite. Some authors believe that such a point on a dispersion graph corresponds to instabilities in the real medium [45]. Numerical examples (Figure 4, Figure 5, Figure 6 and Figure 7) show that this frequency depends on the dissipation parameter n in a non-monotonous way.
Logarithmic decrement has, generally speaking, a complex frequency-dependent behavior (Figure 8), but we know that it decreases with dissipation n for frequencies above the characteristic one (i.e., in the former band gap) and increases with n below it. This, probably, can be explained as follows: in the elastic medium the existence of the bandgap was related not to the dissipation, but to the localization, and the viscosity breaks condition for its existence. At low and high frequencies the logarithmic decrement is proportional to the frequency, but in the middle, it may have (or not have) extremuma, depending on the parameters.
One can observe similar effects also in media of other types. For instance, non-polar dielectrics, if to neglect dissipation, have a bandgap. Dispersion in the low-frequency transparency window is the same as in the elastic constrained reduced isotropic Cosserat medium. The high-frequency transparency window is the same as for the non-constrained elastic reduced isotropic Cosserat medium, but it is absent in our case. When dissipation is taken into account, the bandgap is not present anymore, but a zone of anomalous dispersion appears [45].
In classical viscoelastic metamaterials, considered in [46], viscosity produces similar effects: “transmission is generally worsened in passing bands, while it is enhanced inside locally resonant band gaps”. The metamaterial considered in the work mentioned above is a periodic structure of circular metal bars coated with rubber, embedded into a viscoelastic matrix. It is difficult to make a precise comparison with our case, since we do not consider in this work a discrete structure of metamaterial, as it is done in [46]. A similar model is investigated in [47]. It is also concluded that viscosity contracts existing band gaps, and elasticity enhances them. An important difference with the constrained reduced Cosserat medium is that in our case the dissipation destroys completely the bandgap existing in the elastic case, while for the case considered in these two works band gaps are still present in the viscoelastic case. Perhaps the reason is that the considered discrete structure is much more complex than the reduced Cosserat model.
We could expect that these kinds of models may be useful for the description of blocky media and for design of artificial acoustic metamaterials with desired properties.
4. Materials and Methods
This is a theoretical work with methods based upon fundamental laws of continuum mechanics of complex media in their local form, direct tensor calculus and Fourier transform. Numerical graphs are plotted with help of scripts in python which can be found in Appendix B. Numerical results validate analytical formulae for the obtained dispersion curves.
We describe all the material types considered above and their properties in Table 1.

Table 1.
Linear reduced Cosserat constrained media and their wave properties.
5. Conclusions
We considered three types of linear constrained reduced Cosserat media: elastic isotropic, elastic with specific transversely isotropic coupling between volumetric and shear deformations, and viscoelastic isotropic.
Elastic models present an infinite bandgap above a certain characteristic frequency for some type of waves: shear plane wave and, in case of anisotropic theory, also one of the mixed waves. Therefore they should be classified as single negative acoustic metamaterials. They have also a branch without a bandgap, non-dispersive (in the isotropic case, compressional wave) and weakly dispersive (model with anisotropic coupling, the upper branch of the mixed wave). In the anisotropic case dispersion curves essentially depend on the propagation direction.
The isotropic viscoelastic model possesses a classical compressional wave, but the shear wave changes drastically. The bandgap disappears. At high frequencies, we observe a decreasing dispersion curve in some frequency range (i.e., the medium is a double negative acoustic metamaterial in this domain), with a diverging group velocity as the frequency increases. Depending on dissipation, this frequency domain may cover a part of the former band gap or extend to the whole former bandgap and occupy also some domain below . Above the characteristic frequency the logarithmic decrement decreases as the dissipation increases (the viscosity favors wave propagation), and below it, the logarithmic decrement increases with the viscosity increases (which attenuates the wave in this case). Viscous dissipation appears to destroy the wave localization, related to the existence of the bandgap in the elastic case. Shear waves with a wavelength shorter than a certain threshold cannot propagate in this medium. One may thus control the properties of the acoustic metamaterial by means of viscosity.
In the future, we plan to analyze in more detail the influence of small and large dissipation in the linear isotropic reduced constrained viscoelastic Cosserat medium, to consider a purely viscous case, possibly to combine viscosity with anisotropic coupling and also to continue the investigation of waves in viscoelastic non-constrained reduced Cosserat continua.
Author Contributions
Conceptualization, E.F.G., A.V.P. and F.d.; formal analysis, E.F.G.; investigation, E.F.G.; methodology, E.F.G.; software, E.F.G.; Validation, A.V.P. and F.d.; writing—original draft, E.F.G.; writing—review and editing, A.V.P. and F.d. All authors have read and agree to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors are grateful to Rafael Abreu for bringing their attention to the dynamics of viscoelastic Cosserat acoustic metamaterials and to Ivan Giorgio and Jean-Noël Roux for their valuable remarks.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Estimation of the Minimal Wavelength
Let us estimate from above each term in the right part of Equation (54). First, take into account that reaches its minimal value
and
Then the first term can be estimated as
To estimate the second term in the right part of (54) we calculate the derivative of its square with respect to and find the extremum:
if . The maximal value of is equal to . For this derivative cannot equal zero for positive . For this value the term being estimated is a monotone function changing from 0 at to 1 at .
Therefore, Equation (54) gives us
Appendix B. Numerical Scripts
Script for plotting dispersion graphs for the elastic constrained reduced isotropic and anisotropic Cosserat medium:
import numpy as np
import matplotlib.pyplot as plt
import cmath as~cm
# assign~values
# omega0=1, cs=1, since we have adimensionalised the equations
cp = 2.01 # cp^2 = (lambda + 2 mu)/rho, cp --- compression wave velocity
# in the isotropic case
cn = 2 # cn^2=N/rho. For~isotropic medium it is 0.
c = 0.707 # c = cos(k,n) --- cosine of angle between the axis of isotropy
# and direction of wave propagation
cpnsq = cp**2+2*cn**2*c**2
N = 10000 # number of elements to evaluate
k_values = np.linspace(0.0,1,N) # wave number
real_omegasqp = np.zeros(N) # square of the adimensionalised
# frequency, upper part of the dispersion branch.
real_omegasqm = np.zeros(N) # square of the adimensionalised
# frequency, lower part of the dispersion~branch
real_omegap = np.zeros(N) # adimensionalised frequency,
# upper part of the dispersion branch. For~isotropic case
# it becomes a compressional wave
real_omegam = np.zeros(N) # adimensionalised frequency,
# lower part of the dispersion branch. For~isotropic case
# it is a shear~wave
#-----------
# MAIN CODE
#-----------
for o_index in range(N):
k = k_values[o_index]
# omega1/csalphad=1, we adimensionalised the equations
omegasqp = 0.5*k**2*(cpnsq+1/(1+k**2)
+cm.sqrt((cpnsq-1/(1+k**2))**2+4*cn**4*c**2*(1-c**2)/(1+k**2)))
omegasqm = 0.5*k**2*(cpnsq+1/(1+k**2)
-cm.sqrt((cpnsq-1/(1+k**2))**2+4*cn**4*c**2*(1-c**2)/(1+k**2)))
real_omegasqp[o_index] = np.real(omegasqp)
real_omegasqm[o_index] = np.real(omegasqm)
omegap = cm.sqrt(omegasqp)
real_omegap[o_index] = np.real(omegap)
omegam = cm.sqrt(omegasqm)
real_omegam[o_index] = np.real(omegam)
#----------------
# plot solutions
#----------------
font = {’size’: 12}
plt.rc(’font’, **font)
plt.figure(num=1,figsize=(12,6),dpi=100) # define plot size in inches
# (width, height) & resolution(DPI)
plt.subplot(111)
plt.plot(k_values,real_omegap, ’b*’,linewidth=1)
plt.plot(k_values,real_omegam,’r*’,linewidth=1)
plt.xlabel(’$c_s k/\omega_1$’, size=28)
plt.ylabel(’$\omega/\omega_1$’,size=28)
plt.grid(True)
plt.show()
Script for plotting the dispersion graphs for the viscoelastic reduced isotropic Cosserat medium:
import numpy as np
import matplotlib.pyplot as plt
import cmath as~cm
# viscoelastic isotropic constrained reduced Cosserat medium,
# dispersion curves and logarithmic~decrement
# assign values
n = 0.2
# omega1=1, cs=1, since we have adimensionalised the~equations
N = 10000 # number of elements to evaluate
x_values = np.linspace(0.0,1.5,N) # x = omega / omega_1
real_tgphi = np.zeros(N) # tgphi = Re k / Im k
real_kdsq = np.zeros(N) # kdsq = (Re k c_s / omega_1)^2
real_kd = np.zeros(N) # kd = Re k c_s / omega_1
real_kverif = np.zeros(N) # kverif = Im k c_s / omega_1
#-----------
# MAIN CODE
#-----------
for o_index in range(N):
x = x_values[o_index]
kdsq = x**2*((1-x**2)+cm.sqrt((1-x**2)**2+n**2*x**2))/(2*((1-x**2)**2+n**2*x**2))
real_kdsq[o_index] = np.real(kdsq)
kd = cm.sqrt(kdsq)
real_kd[o_index] = np.real(kd)
kverif = -n*x**3/(2*kd*(1-x**2)**2+n**2*x**2)
real_kverif[o_index] = np.real(kverif)
tgphi = kverif/kd
real_tgphi[o_index] = np.real(tgphi)
#----------------
# plot solutions
#----------------
font = {’size’: 12}
plt.rc(’font’, **font)
plt.figure(num=1,figsize=(12,6),dpi=100) # define plot size in inches
(width, height) & resolution(DPI)
plt.subplot(111)
plt.plot(real_kd, x_values, ’b*’,linewidth=1)
plt.plot(real_kverif,x_values,’r--’,linewidth=3)
plt.plot(-real_tgphi,x_values,’c-.’,linewidth=4)
plt.xlabel(’Solid: Re $c_s k/\omega_1$, dashed: Im $c_s k/\omega_1$,
dashed-dotted: |Im $k$ / Re $k$|, n=’+str(n), size=28)
#plt.xlabel(’Re $c_s k/\omega_1,\quad$’+chr(957)+’$\omega_1=$’+str(n), size=28)
#plt.xlabel(’Im $c_s k/\omega_0$’, color=’red’, size=16)
plt.ylabel(’$\omega/\omega_1$’,size=28)
#plt.ylabel(Blue: ’Re $k$, red: Im $k$’,size=16)
plt.grid(True)
plt.show()
The 7th line from below in the last script contains the following text (which too large to print as it is in python):
plt.xlabel(’Solid: Re $c_s k/\omega_1$, dashed: Im $c_s k/\omega_1$,
dashed-dotted: |Im $k$ / Re $k$|, n=’+str(n), size=28)
References
- Cosserat, E.; Cosserat, F. Théorie Des Corps déformables; A. Hermann et fils: Paris, France, 1909. (In French) [Google Scholar]
- Kafadar, C.; Eringen, A. Micropolar media—I: The classical theory. Int. J. Eng. Sci. 1971, 9, 271–305. [Google Scholar] [CrossRef]
- Eremeyev, V.; Lebedev, L.; Altenbach, H. Foundations of Micropolar Mechanics; Springer: Heidelberg, Germany, 2013. [Google Scholar]
- Eremeyev, V. On the material symmetry group for micromorphic media with applications to granular materials. Mech. Res. Commun. 2018, 94, 8–12. [Google Scholar] [CrossRef]
- Eremeyev, V.; Pietraszkiewicz, W. Material symmetry group and constitutive equations of micropolar anisotropic elastic solids. Math. Mech. Solids 2016, 21, 210–221. [Google Scholar] [CrossRef]
- Eremeyev, V.; Pietraszkiewicz, W. Material symmetry group of the non-linear polar-elastic continuum. Int. J. Solids Struct. 2012, 49, 1993–2005. [Google Scholar] [CrossRef]
- Schwartz, L.; Johnson, D.; Feng, S. Vibrational modes in granular materials. Phys. Rev. Lett. 1984, 52, 831. [Google Scholar] [CrossRef]
- Misra, A.; Poorsolhjouy, P. Identification of higher-order elastic constants for grain assemblies based upon granular micromechanics. Math. Mech. Complex Syst. 2015, 3, 285–308. [Google Scholar] [CrossRef]
- Poorsolhjouy, P.; Misra, A. Granular micromechanics based continuum model for grain rotations and grain rotation waves. J. Mech. Phys. Solids 2019, 129, 244–260. [Google Scholar] [CrossRef]
- Turco, E. In-plane shear loading of granular membranes modeled as a Lagrangian assembly of rotating elastic particles. Mech. Res. Commun. 2018, 92, 61–66. [Google Scholar] [CrossRef]
- Abreu, R.; Thomas, C.; Durand, S. Effect of observed micropolar motions on wave propagation in deep Earth minerals. Phys. Earth Planet. Int. 2018, 276, 215–225. [Google Scholar] [CrossRef]
- Giorgio, I.; De Angelo, M.; Turco, E.; Misra, A. A Biot–Cosserat two-dimensional elastic nonlinear model for a micromorphic medium. Contin. Mech. Thermodyn. 2019. [Google Scholar] [CrossRef]
- Grekova, E.F.; Abreu, R. Isotropic linear viscoelastic reduced Cosserat medium: An acoustic metamaterial and a first step to model geomedium. In New Achievements in Continuum Mechanics and Thermodynamics; Springer: Cham, Switzerland, 2019; pp. 165–185. [Google Scholar]
- Sadovskii, V.; Sadovskaya, O. Modeling of elastic waves in a blocky medium based on equations of the Cosserat continuum. Wave Motion 2015, 52, 138–150. [Google Scholar] [CrossRef]
- Giorgio, I.; Andreaus, U.; Dell’Isola, F.; Lekszycki, T. Viscous second gradient porous materials for bones reconstructed with bio-resorbable grafts. Extrem. Mech. Lett. 2017, 13, 141–147. [Google Scholar] [CrossRef]
- Madeo, A.; George, D.; Lekszycki, T.; Nierenberger, M.; Rémond, Y. A second gradient continuum model accounting for some effects of micro-structure on reconstructed bone remodelling. C. R. Mécanique 2012, 340, 575–589. [Google Scholar] [CrossRef]
- Sato, H.; Fehler, M.; Maeda, T. Seismic Wave Propagation and Scattering in the Heterogeneous Earth; Springer: Berlin/Heidelberg, Germany, 2012; Volume 496. [Google Scholar]
- Kaina, N.; Lemoult, F.; Fink, M.; Lerosey, G. Negative refractive index and acoustic superlens from multiple scattering in single negative metamaterials. Nature 2015, 525, 77–81. [Google Scholar] [CrossRef]
- Haberman, M.R.; Guild, M.D. Acoustic metamaterials. Phys. Today 2016, 69, 42–48. [Google Scholar] [CrossRef]
- Grekova, E.F. Reduced enhanced elastic continua as acoustic metamaterials. In Dynamical Processes in Generalized Continua and Structures; Springer: Cham, Switzerland, 2019; pp. 253–268. [Google Scholar]
- Chesnais, C.; Boutin, C.; Hans, S. Effects of the local resonance on the wave propagation in periodic frame structures: Generalized Newtonian mechanics. J. Acoust. Soc. Am. 2012, 132, 2873–2886. [Google Scholar] [CrossRef]
- Vasiliev, A.A.; Pavlov, I.S. Auxetic properties of hiral hexagonal Cosserat lattices composed of finite–sized particles. Physica Status Solidi (b) 2019. [Google Scholar] [CrossRef]
- Erofeev, V.I.; Pavlov, I.S.; Porubov, A.V.; Vasiliev, A.A. Dispersion properties of a closed-packed lattice consisting of round particles. In Generalized Models and Non-Classical Approaches in Complex Materials 2; Springer: Cham, Switzerland, 2018; pp. 101–117. [Google Scholar]
- dell’Isola, F.; Giorgio, I.; Andreaus, U. Elastic pantographic 2D lattices: A numerical analysis on the static response and wave propagation. Proc. Est. Acad. Sci. 2015, 64, 219. [Google Scholar] [CrossRef]
- Barchiesi, E.; Spagnuolo, M.; Placidi, L. Mechanical metamaterials: A state of the art. Math. Mech. Solids 2019, 24, 212–234. [Google Scholar] [CrossRef]
- Del Vescovo, D.; Giorgio, I. Dynamic problems for metamaterials: Review of existing models and ideas for further research. Int. J. Eng. Sci. 2014, 80, 153–172. [Google Scholar] [CrossRef]
- Dell’Isola, F.; Seppecher, P.; Alibert, J.J.; Lekszycki, T.; Grygoruk, R.; Pawlikowski, M.; Steigmann, D.; Giorgio, I.; Andreaus, U.; Turco, E.; et al. Pantographic metamaterials: An example of mathematically driven design and of its technological challenges. Contin. Mech. Thermodyn. 2019, 31, 851–884. [Google Scholar] [CrossRef]
- Figotin, A.; Schenker, J. Hamiltonian structure for dispersive and dissipative dynamical systems. J. Stat. Phys. 2007, 128, 969–1056. [Google Scholar] [CrossRef]
- Madeo, A.; Neff, P.; Ghiba, I.D.; Placidi, L.; Rosi, G. Band gaps in the relaxed linear micromorphic continuum. ZAMM-J. Appl. Math. Mech./Z. Angew. Math. Und Mech. 2015, 95, 880–887. [Google Scholar] [CrossRef]
- Münch, I.; Neff, P.; Madeo, A.; Ghiba, I.D. The modified indeterminate couple stress model: Why Yang et al.’s arguments motivating a symmetric couple stress tensor contain a gap and why the couple stress tensor may be chosen symmetric nevertheless. ZAMM-J. Appl. Math. Mech./Z. Angew. Math. Und Mech. 2017, 97, 1524–1554. [Google Scholar] [CrossRef]
- Mindlin, R.; Tiersten, H. Effects of Couple-Stresses in Linear Elasticity; Technical Report; Columbia University: New York, NY, USA, 1962. [Google Scholar]
- Misra, A.; Poorsolhjouy, P. Granular micromechanics based micromorphic model predicts frequency band gaps. Contin. Mech. Thermodyn. 2016, 28, 215–234. [Google Scholar] [CrossRef]
- El Sherbiny, M.G.; Placidi, L. Discrete and continuous aspects of some metamaterial elastic structures with band gaps. Arch. Appl. Mech. 2018, 88, 1725–1742. [Google Scholar] [CrossRef]
- Minagawa, S.; Arakawa, K.; Yamada, M. Diamond crystals as Cosserat continua with constrained rotation. Phys. Status Solidi (a) 1980, 57, 713–718. [Google Scholar] [CrossRef]
- Gourgiotis, P.A.; Bigoni, D. The dynamics of folding instability in a constrained Cosserat medium. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2017, 375, 20160159. [Google Scholar] [CrossRef]
- Lee, W.H.; Igel, H.; Trifunac, M.D. Recent advances in rotational seismology. Seismol. Res. Lett. 2009, 80, 479–490. [Google Scholar] [CrossRef]
- Abreu, R.; Kamm, J.; Reiß, A.S. Micropolar modelling of rotational waves in seismology. Geophys. J. Int. 2017, 210, 1021–1046. [Google Scholar] [CrossRef]
- Karachevtseva, I.; Pasternak, E.; Dyskin, A. Wave propagation in geomaterials in the presence of rotation-induced negative stiffness. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 23–28 April 2017; Volume 19, p. 17404. [Google Scholar]
- Teisseyre, R.; Suchcicki, J.; Teisseyre, K.P.; Wiszniowski, J.; Palangio, P. Seismic rotation waves: Basic elements of theory and recording. Ann. Geophys. 2003, 46, 671–685. [Google Scholar]
- Dyskin, A.; Pasternak, E. Slow waves in blocky rock mass. In Proceedings of the 9th Australasian Congress on Applied Mechanics (ACAM9), Sydney, Australia, 27–29 November 2017; p. 226. [Google Scholar]
- Eringen, A. Linear theory of micropolar viscoelasticity. Int. J. Eng. Sci. 1967, 5, 191–204. [Google Scholar] [CrossRef]
- Grekova, E.; Kulesh, M.; Herman, G. Waves in linear elastic media with microrotations, part 2: Isotropic reduced Cosserat model. Bull. Seismol. Soc. Am. 2009, 99, 1423–1428. [Google Scholar] [CrossRef]
- Curie, P. Sur la symétrie dans les phénomènes physiques, symétrie d’un champ électrique et d’un champ magnétique. Journal de physique théorique et appliquée 1894, 3, 393–415. (In French) [Google Scholar] [CrossRef]
- Grekova, E.F. Plane waves in the linear elastic reduced Cosserat medium with a finite axially symmetric coupling between volumetric and rotational strains. Math. Mech. Solids 2016, 21, 73–93. [Google Scholar] [CrossRef]
- Ostrovskii, L.; Potapov, A. Introduction to the Theory of Modulated Waves; Fizmatlit: Moscow, Russia, 2003. (In Russian) [Google Scholar]
- Wang, Y.F.; Wang, Y.S.; Laude, V. Wave propagation in two-dimensional viscoelastic metamaterials. Phys. Rev. B 2015, 92, 104110. [Google Scholar] [CrossRef]
- Frazier, M.J.; Hussein, M.I. Viscous-to-viscoelastic transition in phononic crystal and metamaterial band structures. J. Acoust. Soc. Am. 2015, 138, 3169–3180. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).