A New Experimental Method for Determining the Thickness of Thin Surface Layers of Intensive Plastic Deformation Using Electron Backscatter Diffraction Data

Abstract

It is, in general, essential to investigate correlations between the microstructure and properties of materials. Plastic deformation often localizes within thin layers. As a result, many material properties within such layers are very different from the properties in bulk. The present paper proposes a new method for determining the thickness of a thin surface layer of intensive plastic deformation in metallic materials. For various types of materials, such layers are often generated near frictional interfaces. The method is based on data obtained by Electron Backscatter Diffraction. The results obtained are compared with those obtained by an alternative method based on microhardness measurements. The new method allows for determining the layer thickness of several microns in specimens after grinding. In contrast, the measurement of microhardness does not reveal the presence of this layer. The grain-based and kernel-based types of algorithms are also adopted for determining the thickness of the layer. Data processed by the strain contouring and kernel average misorientation algorithms are given to illustrate this method. It is shown that these algorithms do not clearly detect the boundary between the layer of intensive plastic deformation and the bulk. As a result, these algorithms are unable to determine the thickness of the layer with high accuracy.

1. Introduction

The gradient of material properties near a surface has a significant effect on the performance of structures and machine parts at service conditions (for example, on tribological properties [1,2,3,4,5]) and subsequent technological processes (for example, on diffusion bonding [6]). This gradient can be induced using various techniques (for example, dry friction [6,7,8,9,10,11] and deformation processes [12,13,14,15,16,17]). Independently from how the gradient has been induced, it is necessary to have an accurate experimental method for determining the thickness of the layer of intensive plastic deformation. This method may depend on the material. Currently, two methods are most widely used. One of these methods is based on the measurement of microhardness [6,7,8,14,15] and the other on the evolution of the microstructure of material (grain shape, phase distribution, etc.) [5,9,10,11,13,15,16,17,18]. The former assumes that the hardness of the material increases with plastic deformation. Therefore, tracking the change in the normal to a surface as in the original manuscript one can evaluate the gradient of plastic deformation. This distribution of hardness, supplemented with a criterion for separating the layer of intensive plastic deformation from the bulk, allows for determining the thickness of the layer. It is impossible to propose the criterion above in an unambiguous way. One possible criterion has been proposed in [15]. The latter method is based on the fact that the shape of grains and subgrains, or the phase composition, changes during plastic deformation in comparison with the initial state [19]. As in the case of the previous method, it is necessary to use a criterion for determining the thickness of intensive plastic deformations. Two criteria have been proposed in the literature [16,17]. In [17], the criterion has been introduced for carbon steel. It is based on the coefficient of anisotropy that characterizes the shape of pearlite grains. In [16], the criterion has been introduced for C45E steel. It is based on the thickness of elongated ferrite grains.

It is rather difficult to apply methods based on the evolution of the microstructure if, for example, grains are initially elongated. The determination of the thickness of layers of intensive plastic deformation by microindentation is, in general, a reasonably accurate method. The difficulty here is that this method is not applicable if the thickness of a layer of intensive plastic deformation is very small (say, several microns), since it is practically impossible to measure hardness at the specimen edge. The issues above can be resolved using the electron backscatter diffraction technique (EBSD). This technique is widely used as an effective method of studying the structure, phase composition, and texture, for example [19,20,21,22,23]. In particular, data on the misorientation of the crystal lattice in neighboring regions are used for determining the recrystallized and deformed structure in [19,20], determining the density of geometrically necessary dislocations and subgrain boundaries in [21], and evaluating residual stresses and regions subjected to plastic and elastic deformations in [22,23]. This study aims to extend the area of applications of the EBSD technique to determine the thickness of layers of intensive plastic deformation, as an alternative to the methods mentioned above, based on the evolution of microstructure and the measurement of microhardness.

2. Material and Process of Deformation

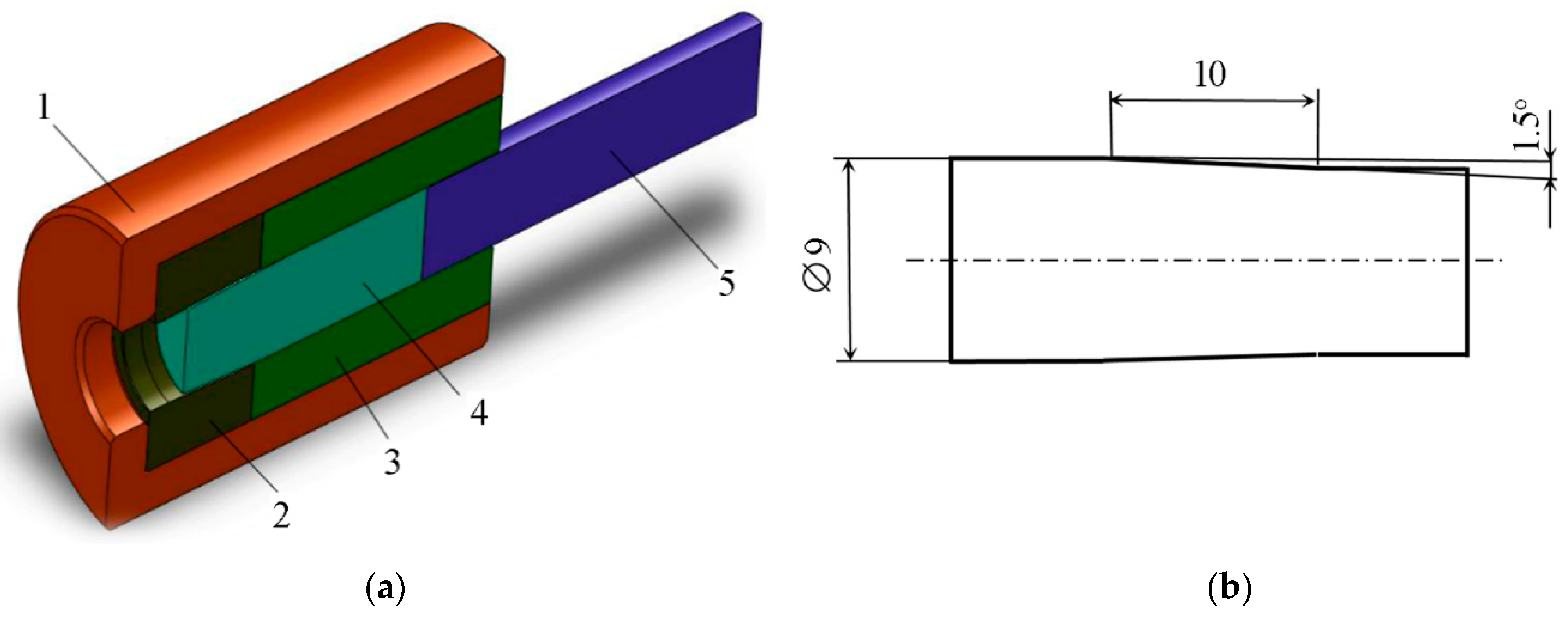
Cylindrical specimens were pushed through an unpolished steel die with a cone half-angle of 1.5 degrees for generating a layer of intensive plastic deformation in the vicinity of the friction surface. The experiment was carried out at room temperature with no lubricant. As a result, favorable conditions were achieved for the occurrence of intense shear deformation near the friction surface. The initial diameter of specimens was 9 mm, and the diameter after testing was 8.48 mm. Figure 1a illustrates the experimental set-up, and Figure 1b shows the dimensions of specimens in millimeters after the process of deformation.

The material of the specimens was the aluminum alloy AMg6. Its chemical composition (92.3 Al, 6.47 Mg, 0.25 Fe, 0.14 Si, 0.026 Cu, 0.63 Mn, 0.04 Ti, 0.08 Zn, 0.0017 Be, wt%) was determined with a SPECTROMAXx analyzer. Before the test, the specimens were annealed in a vacuum at 350 °C for 15 h. The initial microstructure of the material was studied by the electron backscatter diffraction technique (EBSD) on a Vega II Tescan raster electron microscope with an Oxford HKL Nordlys F+ EBSD analysis attachment. The accelerating voltage whilst obtaining electron backscatter patterns was 20 kV. The specimens for the EBSD analysis were, first, mechanically grinded on abrasive papers impregnated by SiC with a stepwise decreasing grain size of 80 and 40 µm, and then subjected to mechanical polishing by a diamond suspension with a stepwise decreasing abrasive particle size of 9 and 1 µm. Further, there was another step of polishing, this time by a colloidal oxide suspension with a particle size of 0.05 µm. Grinding and polishing by abrasive papers and diamond suspensions were carried out for a few minutes at each step. Polishing by a colloidal oxide suspension was carried out for about 15 min. Then, the specimens were subjected to electropolishing in an electrolyte composed of 90% CH₃COOH + 10% HClO₄ cooled to 8 °C. The average polishing time was 4 s at a voltage of 40 V and a current density of 0.3 A/mm².

It was believed that the grains had a misorientation of more than 15° and that the misorientation of the subgrains ranged between 2° and 15° [24,25,26,27]. Indentation and hardness measurements were performed by a Hysitron TI 900 versatile complex designed for nanomechanical testing with the use of a Berkovich indenter. The indenter tip curvature radius was 50 nm. The hardness $H$ was determined according to ISO 14577-1:2002 using the formula $H=\frac{F_{\max }}{A_p}$. Here, $F_{\max }$ is the maximum load and $A_p$ is the projected (cross-sectional) area of contact between the indenter and the test piece, which is determined from the force-displacement curve.

3. New Method and Results

An inhomogeneous distribution of dislocations is observed in crystals after plastic deformation; with an excess of dislocations of one sign, dislocation cells and sub-boundaries arising during deformation lead to microscopic inhomogeneity, thus causing local misorientation [18,28,29]. Under small deformations, the misorientation of adjacent microregions is small. However, the misorientation increases with deformation. This can lead to a significant rotation of different metal material regions relative to each other and, as a consequence, to their fragmentation [10]. Thus, the misorientation of the regions can characterize local zones (regions) that have undergone plastic deformation, and it can be used to determine such zones. The thickness of the deformed subsurface layer in the material can be determined by changes in a quantity that characterizes changes in the portion of all the boundaries (low-angle and high-angle ones), in comparison with the initial undeformed state. Before introducing the quantity to be used in the present paper, it is important to show how the length of the boundaries changes from the edge into the bulk in undeformed specimens (Figure 2) and in specimens after pushing through an unpolished steel die with a cone half-angle of 1.5° (Figure 3). Figure 2a and Figure 3a show band contrast maps superimposed on a crystal orientation map made in Euler angles. In these figures, the gray lines correspond to low-angle boundaries, with a misorientation of 2° to 15°, and the black lines correspond to high-angle boundaries, with a misorientation of more than 15°. In Figure 2a and Figure 3a, the black spots inside grains correspond to the areas with indefinite crystallographic orientation and, generally, they are dispersoids, which may be Al₃Mg₂, Al₆Mn, Mg₂Si, or AlFeSiMn. In Figure 2b, the red lines show the deviation of M_j from its mean value with a confidence probability of 95%.

The white vertical lines in Figure 2a and Figure 3a bound the region in which we determined the total length $L$ of all the boundaries with a misorientation angle $\Theta \ge 1^{\text{o}}$. We considered boundaries with the misorientation angle $\Theta \ge 1^{\text{o}}$, since, if $\Theta <1^{\text{o}}$, the misorientation angle did not affect the deformed layer thickness; this may be due to the sensitivity of the equipment and the settings used for scanning the sections. The thickness of each i-th region, for which the total length of all the boundaries $L$ was determined, was 4 µm, and the length was 300 µm. The scanning step for obtaining the initial electron backscatter pattern (EBSP) was 0.4 µm. Figure 2b and Figure 3b show the dependences of the parameter $L$ for each region on the distance $d$ from the specimen surface edge. Figure 2b shows that, for the undeformed specimen, the parameter $L$ is independent of the distance from the specimen edge. At the same time, for the deformed specimen, the dependence $L-d$ has a falling part, which then turns into a steady one, as shown in Figure 3b. Thus, comparing Figure 2b and Figure 3b, we can unambiguously conclude that pushing the specimen through the die leads to the formation of new boundaries in the microstructure of the specimen near its surface.

To determine the thickness of the layer in which deformation took place, we introduce a dimensionless parameter $K$, calculated in each i-th region by the formula $K_i=\frac{L_i-L_{}^{in}}{L_{}^{in}}$. Here, $L_i$ is the total length of the boundaries with the misorientation angle $\Theta \ge 1^{\text{o}}$ for each i-th region; $L_{}^{in}$ is the average value of the total length of all the boundaries of the undeformed specimen, which is calculated as $L^{in}=\frac{1}{N}{\displaystyle \sum _{j=1}^N{M}_j}$, where $M_j$ is the total length of all the boundaries for each j-th region of the undeformed specimen and $N$ is the number of regions. In the calculation of $L_{}^{in}$, each j-th region must have the same geometric dimensions as each i-th region in the calculation of $K_i$. Figure 3c shows the dependence of the parameter $K_i$ on the distance from the specimen edge. This figure shows that the values of $K_i$ fluctuate near zero, starting from the value of $d$ equal to 146 µm. This can be interpreted as follows: at a distance from the specimen edge exceeding 146 µm, there is no plastic deformation resulting from the specimen pushing through the die. Since the initial experimental data have a spread of values in the regions $i=1,\dots ,N$, it is advisable to determine the boundary (depth) of the deformed region, taking into account the spread of the experimental data. This boundary is indicated by a red horizontal line in Figure 3c. It was determined by changing the parameter $K_i$ of the original specimen, for which it was found that the limit of $K_i$ deviation from the mean value is 0.93 with a confidence probability of 95%. Thus, the depth of the deformed layer of the examined specimen, after pushing, is at least 133 µm with 95% confidence. In order to verify the adequacy of the obtained results, we determine the depth of the deformed layer of the same specimen, after pushing, using the data on the variation of hardness $H$ with the distance $d$ from the specimen edge.

The hardness was measured along the line directed from the specimen edge to the specimen bulk with the indents spaced 6 µm apart (Figure 4a). The first indent was placed at a distance of 3 µm from the edge. The load was 5 mN, and the loading time and unloading time were 10 s each. Figure 4b shows the average data obtained from the five experiments described above. This figure shows a red line, below which there are hardness values corresponding to the undeformed state of the alloy with a 95% probability. Based on Figure 4b, it can be determined that the depth of the deformed layer is at least 110 µm with a 95% probability. Comparing the depth of the deformed layer obtained by the two independent methods, we can conclude that they yield similar results and that, therefore, the proposed method for determining the depth of the deformed layer by EBSD data can be applied on a par with the method based on hardness measurement. An additional advantage over the method based on indentation is the ability to analyze the distorted layer in different sections of the specimen, inside the column of a dual beam electron microscope, with the function of ion etching by removing the required thickness in the material and subsequent accumulation of data on changes in the crystal lattice orientation.

As an additional example of the benefits of using this technique, we show an EBSD image of the AlMg6 alloy specimen after grinding without annealing, as shown in Figure 5, as well as the dependence of $K_i$ on the distance $d$ from the specimen edge, and we showed similar data on hardness $H$. This specimen was first annealed at 350 °C for 15 h and then ground. The scanning step was 0.1 µm for the initial EBSP. It is obvious from Figure 5b that the thickness of the distorted layer during grinding was at least 6 µm with a confidence probability of 95%. The thickness of the distorted layer could not be detected on the basis of microindentation data (see Figure 5c).

Standard EBSD data processing techniques can be applied to the determination of the distorted layer in the material. These techniques can be qualitatively divided into two types: one, the grain-based method, is based on the approach associated with assigning a certain value to a grain, which is obtained from the analysis of misorientations within the grain, and the other, the kernel-based method, is based on the approach that consists of assigning a certain value to each indexed point, depending on neighboring orientations. The former approach includes such well-known algorithms as grain average misorientation (GAM), grain orientation spread (GOS), grain reference orientation deviation (GROD), and strain contouring (in Channel 5) [30,31,32]. The main drawback for using the measurement of distorted layer thickness is the need to specify the minimum value of high-angle boundary misorientation, which is taken arbitrarily, without any explanation, in most studies. The kernel-based approach is devoid of this drawback, and it is often used to determine the zones of plastic deformation. This approach includes such algorithms as kernel average misorientation (KAM), local average misorientation (LAM), and local spread (LS) [30,31,33]. For the first two algorithms, the main drawback is the effect of the scan step. The LS algorithm does not have this disadvantage [25]; however, as in the KAM and LAM algorithms, the results depend on using the distance of the order of the neighbors and the critical angle of misorientation between the kernel point (point $A$ in Figure 6) and the neighbors (points 1, ..., 4 in Figure 6). Figure 6a shows how the average misorientation at point $A$ is determined under the condition that the misorientation of all the neighbors of point $A$ is below critical ${\Theta }_{lim}$. In Figure 6b, points 1 and 2 have a misorientation with respect to point $A$ above critical; therefore, they are not used in the calculation of the average misorientation value. Another drawback of kernel-based algorithms, which may occur in determining the thickness of a deformed layer, is the difficulty of detecting the boundary between a deformed and undeformed material layer. This will be shown in what follows.

As an example, for the specimens considered in this paper, Figure 7 and Figure 8 show the results of the processed EBSD data with the use of the grain-based and kernel-based algorithms. We consider that the strain contouring algorithm is the most suitable of all grain-based algorithms for detecting a deformed layer. In Figure 7, for the EBSD data considered in this paper, we show band contrast maps superimposed on maps constructed using the strain contouring algorithm in the Channel 5 software, as follows [32]. The maximum misorientation between two points was determined for each grain. Then, the obtained maximum misorientation was placed in the center of the grain. After that, the maximum misorientation of all grains was contoured using a Gaussian filter. For the level of “strains” to be assessed, there is a scale in the images of Figure 7, with the blue color corresponding to the minimum level of misorientation and the red color corresponding to the maximum. In each image of Figure 7b,c, there is a white vertical line corresponding to the boundary of the distorted layer determined by the algorithm proposed in this paper; in Figure 7c, there also is a red line, which corresponds to the boundary of the distorted layer determined by microindentation. Studying the maps of “strains” in Figure 7, we can conclude that the strain contouring algorithm shows the presence of local regions of “strains” inside large grains. In this case, for the material pushed through a die, the size of the subsurface layer, which can be taken as distorted, is much smaller (see Figure 7c) than the size of the distorted layer determined by the other two methods.

Figure 8 shows the results of processing the EBSD data with the use of the kernel average misorientation algorithm. When we constructed these maps, first-order neighbors were used, and the maximum misorientation angle between the kernel point and the neighbor was 1.5°. In this figure, as in Figure 7, the red vertical line corresponds to the boundary of the deformed layer determined by the results of microindentation, and the white line corresponds to the method proposed in this paper. Comparing the results obtained by the KAM algorithm with those obtained by the strain contouring algorithm, you can see that neither algorithm allows us to clearly define the boundary between the deformed and undeformed layers.

4. Conclusions

A new method for determining the thickness of thin surface layers of intensive plastic deformation has been proposed and, then, applied to the process of pushing cylindrical specimens made of AlMg6 through a conical die. The results obtained have been compared with the results of the standard method for determining the layer thickness based on indentation. The new method has determined the layer thickness is equal to 133 µm, and the method based on indentation has determined the layer thickness is equal to 110 µm. These discrepancies can be explained by the fact that the data on the crystal lattice misorientation for the AlMg6 alloy obtained using EBSD are more sensitive to plastic deformation. The proof of this suggestion can be found in the results on determining the thickness of the layer of intensive plastic deformation in specimens after grinding. In this case, the new method has determined that the thickness of the layer of intensive plastic deformation is equal to 6 µm. In contrast, the results of indentation have not allowed for the layer to be detected.

The results obtained by the new method have been compared with the EBSD data processed with the use of the standard grain-based and kernel-based algorithms. The results have shown that these types of algorithms do not allow one to clearly determine the boundary between the thin layer of intensive plastic deformation and the bulk. Therefore, they are not capable of finding the accurate thickness of the layer.

A limitation of the new method for determining the thickness of layers of intensive plastic deformation lies in obtaining high-quality electron backscatter patterns (EBSPs) that are necessary for identifying lattice orientations. This problem occurs if the actual thickness of layers is of nano- and submicron levels and for layers with a highly fragmented microstructure. However, in some cases, the Transmission Kikuchi diffraction method, which has a spatial resolution of less than 10 nm, can be used for getting high-quality EBSPs.