Analysis of Key Elements of Truss Structures Based on the Tangent Stiffness Method

Abstract

In recent years, the topic of progressive structural collapse has received more attention around the world, and the study of element importance is the key to studying progressive collapse resistance. However, there are many elements in truss structures, making it difficult to predict their importance. The global stiffness matrix contains the specific information of the structure and singularity of the matrix can reflect the safety status of the structure, so it is useful to evaluate the key elements based on the global stiffness matrix for truss structures. In this paper, according to the tangent stiffness-based method for the element importance, the square pyramid grid was chosen as an example, and the distribution rules of key elements under different support conditions, stiffness distributions, and geometric parameters were studied. Then, three common symmetric grid forms, i.e., diagonal square pyramid grids, biorthogonal lattice grids, and biorthogonal diagonal lattice grids, were selected to investigate their importance indices of elements. The principle in this work can be utilized in progressive collapse analysis and safety assessment for spatial truss structures.

1. Introduction

In recent years, the topic of progressive structural collapse has received more and more attention around the world. Mashhadiali and Kheyroddin [1] studied the progressive collapse with diagrid and hexagrid building models. Kang and Tan [2,3] carried out an experimental study on the resistance and failure mode of concrete frames with column removal, which showed that the horizontal forces on the progressive collapse resistance should be considered. Weng et al. [4] provided a set of damage assessment criteria for RC frames subject to progressive collapse. There were more experimental and numerical studies on frames with column removal to study the resistance against progressive collapse [5,6,7]. Mohamed and Khattab [8] examined the progressive collapse response of steel structures, where the moment-resisting frame was only constructed in the perimeter of a regular steel frame.

It should be noted that the analysis of frame structures accounts for a large proportion of previous studies. Compared with frame structures, investigation on the progressive collapse resistance of spatial truss structures is relatively rare and lacks depth. The existing research is mainly focused on the preliminary stage of collapse accident and theoretical analysis. The spatial truss structures are usually used in large public places and serious damage will be caused by the occurrence of collapse. It is necessary to study the ability of the resistance against the progressive collapse of truss structures. Kim and Park [9] studied a truss which includes steel columns and open-web truss girders rigidly connected to form effective seismic load-resisting systems. The behavior of a metallic truss under progressive damage was investigated, and a possible strategy to sustain damage with random removal of one truss element was defined [10]. Zhao et al. [11] presented an experimental study on the dynamic progressive collapse behavior of planar trusses. A 3D finite element model of a double-layer space grid structure was built to investigate the structural behavior, and several collapse scenarios were studied using the alternative method [12].

The widely used method for analysis of the progressive collapse of structures is the alternative load path method that can determine whether the structure may undergo progressive collapse with the removal of failed elements. The structural robustness can indicate the performance of the structure against the effects of emergencies and progressive collapse. Assessing the importance of elements is the basis for studying structural robustness. The importance indices of elements can reflect the influence of individual member failures on global structural performance caused by sudden events under conventional loads. Based on the robustness, some theories and methods for element importance have been proposed successfully using new evaluation indices.

Ye et al. [13] established the element importance index based on the generalized structural stiffness of frame structures. The load pattern and load transferred path are discussed. Jiang and Chen [14] proposed a method for identifying the sensitive and key elements and studied the robustness of the steel truss roof using both nonlinear static and dynamic analysis while their procedure is complex. An evaluation index for how well-formed a node is, based on the displacement and strain energy under a unit force, was performed by Zhu and Ye [15]. Some researchers proposed an energy-based structural damage index to judge whether the progressive collapse of a steel frame structure occurs. Furthermore, they developed a probabilistic assessment method for a steel frame with a column removal subject to catastrophic events [16,17]. Gordini et al. [18] investigated the effect of length imperfection in the bearing capacity of double-layer domes space structures probabilistically and studied the structure’s reliability using the Monte Carlo simulation method. Cai et al. [19] proposed two structural performance indices based on eigenvalues of the stiffness matrix to predict element importance of truss structures. Li et al. [20] proposed a new method to quantify robustness and considered the dynamic effects and the internal force redistribution within a frame structure. A suitable method for evaluating single-layer grid structures by incremental dynamic analysis using a quantitative evaluation index called the collapse margin ratio was established by Tian et al. [21]. Yan et al. [22] proposed a method to identify the critical members of single-layer lattice domes using an index which implicitly estimates the relative vulnerability to node buckling with a removed member.

During the resistance analysis for the progressive collapse of spatial truss structures, it is impossible to analyze each initial failure because of the number of elements. Researchers often rely on their own experience to subjectively select the key elements for analysis in advance. However, this selection method lacks a theoretical basis. Therefore, it is essential to develop a scientific approach to choose the key elements during the study. Group theory is usually used on structures with a large number of elements [23,24,25,26,27,28]. The method is effective for structures with symmetric or periodic properties, which are prevalent structural forms in practical engineering. The global tangent stiffness matrix contains the specific information of the structure, whose singularity can reflect the safety status of the structure, so it is reasonable to judge the importance of the element based on the global stiffness matrix [19]. This paper follows the idea of group theory and divides the elements into groups to improve computational efficiency. Then, according to the tangent stiffness-based method for the element importance, the square pyramid grid was chosen to study the distribution rules of key elements under different support conditions, stiffness distributions, and geometric parameters. Then, topology of some common grids was investigated. Three kinds of grid structures—diagonal square pyramid grids, biorthogonal lattice grids, and biorthogonal diagonal lattice grids—were selected to study their importance indices of elements and the distribution of key elements.

2. Stiffness-Based Evaluation Method for Element Importance

Combining the idea of sensitivity [29], the importance indices of elements based on the tangent stiffness in this paper are defined as:

$${\alpha }_i=\frac{{\gamma }_0-{\gamma }_i{}^f}{{\gamma }_0}$$

(1)

where ${\gamma }_0{}^f$ is the determinant of the tangent stiffness of undamaged structures, and ${\gamma }_i{}^f$ is the determinant of the tangent stiffness of the structure after the failure of the element i. The α_i is in the range of [0,1]. When the index is equal to 1.0, the element is regarded to be the most important. Conversely, the element with the index zero will not change the tangent stiffness of the truss structure.

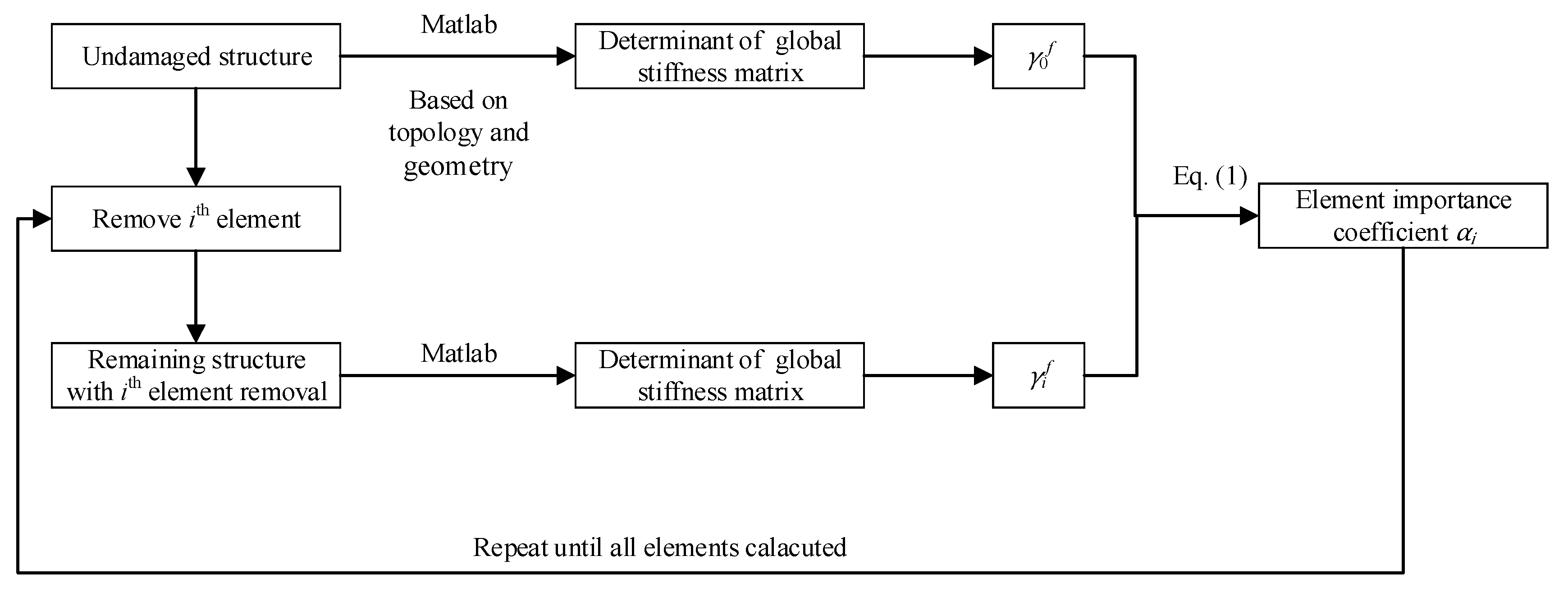
Before predicting the key elements of the grid structure, the grid structure needs to be modeled and calculated. Combined with the tangent stiffness-based method and using MATLAB for programming, the general steps of the program, shown in Figure 1, are as follows.

(a)

According to the symmetry of the truss structures, the simulated model is obtained.

(b)

The stiffness matrix of the undamaged structures is calculated based on the topology and geometry of the truss, the cross-sections and the material behavior of the elements, and the boundary of the structures.

(c)

The Newton–Raphson method is used to get the determinant of the tangent stiffness of the undamaged structures under external loads.

(d)

Delete the ith element, and obtain the determinant of the tangent stiffness of the structure after the failure of the element i.

(e)

Calculate the element importance index of element i based on Equation (1).

(f)

Repeat (d) and (e) to obtain element importance indices of all elements.

3. Analysis of a Square Pyramid Grid

A square pyramid grid, shown in Figure 2, has been chosen to study the distribution of the key elements. The number of grids in both directions is 8 × 8, the length of the grids is 2.5 m, and the height of the grids is 1.5 m. Each node of the upper chord is subjected to a load P in the vertical direction. The upper perimeter nodes are fixed. Moreover, elements are made of steel with elastic modulus 2.1 × 10¹¹ N/m². The elements of the upper chords and lower chords are steel pipes with 60 mm in diameter and 4 mm in thickness. For the diagonal web bars, steel pipes of 51 mm in diameter and 4 mm in thickness are used.

3.1. Effect of the Support Condition

There are two kinds of support conditions. The upper perimeter nodes are all fixed, or only one of the opposite upper boundary nodes are fixed. The load is applied to each upper node in the vertical direction, and the structure is still axisymmetric, shown in Figure 3. The element importance index of the structure under the vertical load of 20 kN on each node is shown in

Table 1. Element importance index under different support conditions.

Element Number	Opposite Boundary Fixed Support	All Boundary Fixed Support	Percent Change (%)	Element Number	Opposite Boundary Fixed Support	All Boundary Fixed Support	Percent Change (%)
9	0.999	0.6308	36.86	167	0.82	0.8004	2.39
10	0.8649	0.7127	17.60	168	0.8	0.7816	2.30
12	0.781	0.7506	3.89	201	0.9381	0.8009	14.63
17	0.999	0.6478	35.16	202	0.901	0.7377	18.12
18	0.8737	0.7258	16.93	203	0.8864	0.7215	18.60
20	0.7986	0.7591	4.95	208	0.8648	0.8517	1.51
33	0.999	0.6506	34.87	210	0.8052	0.7695	4.43
36	0.8035	0.7601	5.40	215	0.8609	0.8569	0.46
76	0.8279	----	----	222	0.86	0.8579	0.24
89	0.6542	0.6478	0.98	224	0.7888	0.7816	0.91
92	0.762	0.7591	0.38	257	0.6498	0.5041	22.42
105	0.6517	0.6506	0.17	291	0.862	0.5347	37.97
108	0.7608	0.7601	0.09	296	0.7448	0.7244	2.74
145	0.8156	0.8009	1.80	325	0.7445	0.6958	6.54
146	0.7479	0.7377	1.36	329	0.7291	0.7061	3.15
147	0.7286	0.7215	0.97	334	0.7197	0.7103	1.31
152	0.8738	0.8517	2.53	355	0.8676	0.5185	40.24
153	0.8118	0.7889	2.82	360	0.7405	0.7191	2.89
154	0.7888	0.7695	2.45	368	0.7249	0.7158	1.26
166	0.8767	0.8579	2.14

.

According to Table 1, we can see that:

(a) The release of the support constraint increases the importance of most elements, which are near the unfixed support. The importance indices of M9, M10, M18, etc. have changed significantly. After the constraints at both ends of M76 are removed, M76 is no longer an isolated chord; cooperative work with the overall structure can reflect its importance.

(b) The importance indices of M9, M17, and M33 are very high. When M17 fails, the remaining chords at the left end node are geometrically coplanar, forming a first-order infinitely small mechanism. The stiffness perpendicular to the plane is mainly provided by the geometric stiffness. The failure of these chords significantly reduces the stiffness in this direction. Their importance index is close, but not equal, to 1.

(c) The distribution of important elements changes with support conditions. The most important lower chord changes from M166 to M201 (both are near the support and perpendicular to the support side), and the most important web changes from M296 to M355 (change from the support corner to the middle unfixed side).

3.2. Effect of the Element Stiffness

The cross sections of the lower chords have been changed to Φ 60 mm × 3 mm (537 mm²), Φ 60 mm × 4 mm (704 mm²), Φ 63 mm × 5 mm (911 mm²) in turn, to compare their element importance. The upper surrounding nodes are all fixed with the other boundary conditions unchanged. The nodal load is 20 kN in the vertical direction. The element number is shown in Figure 3, and the result is given in

Table 2. Important indices of partial elements under different element stiffness.

Element Number	φ60 × 3	φ60 × 4	φ63 × 5
9	0.6333	0.6294	0.6262
18	0.7281	0.7248	0.7222
36	0.7627	0.7592	0.7563
100	0.7627	0.7591	0.7562
160	0.7666	0.7971	0.8244
166	0.8295	0.8573	0.8808
201	0.7611	0.8002	0.8332
257	0.5245	0.5023	0.4829
296	0.7334	0.7234	0.7148
360	0.7287	0.7181	0.7092

.

According to Table 2, the change in the cross-sectional area can represent the variation in the stiffness of the element, where the importance of the element decreases as the element stiffness increases. As the cross-section stiffness of the lower chord increases, the importance of the lower chord increases while the importance of the web and upper chord decreases. The level of change in the element importance of the lower chord is the most obvious, followed by that of the web, and that of the upper chord is the smallest.

4. Effect of the Geometric Parameters

4.1. Number of the Grids

Parametric analysis on the number of grids has been conducted, including 6 × 6, 6 × 8, 6 × 10, 8 × 8, 8 × 10, and 10 × 10. The upper surrounding nodes are all fixed while keeping other conditions unchanged. The distribution characteristic of the most important elements of the upper chords, the lower chords, and the webs are discussed, as shown in Figure 4. Because the grid structure is axisymmetric in both directions, only a quarter of the structure is demonstrated. Moreover, thick blue lines, thick black lines, and thick red lines represent key elements in the upper chords, lower chords, and web members, respectively.

It can be seen from Figure 4 that the positions of key elements in the web remain unchanged and not affected by the number of grids. When the plane of the grid is square, the numbers of the most important upper and lower chords are both two chords. When the plane of the grid is rectangular, the most important upper chord is located at the most central position along the horizontal direction, and the most important lower chord is located near the axis of symmetry in the vertical direction. Although the number of grids affects element importance indices, it does not significantly change the corresponding positions. When the grids are determined, the locations of key elements are determined.

4.2. Sizes of the Grids

We have now tuned the grid sizes to 2.5 m × 1.5 m, 2.5 m × 2.0 m, 2.5 m × 2.5 m, and 2.5 m × 3.0 m in turn for comparison. The upper surrounding nodes are all fixed with the other conditions remaining the same. The same external load is applied in the vertical direction, and the corresponding analysis results are given in

Table 3. Importance index of partial elements under different sizes of the grids.

Element Number	2.5 m × 1.5 m	2.5 m × 2.0 m	2.5 m × 2.5 m	2.5 m × 3.0 m
9	0.6021	0.6144	0.6294	0.6460
36	0.7362	0.7470	0.7592	0.7716
100	0.8355	0.7996	0.7591	0.7187
108	0.8356	0.7996	0.7592	0.7188
160	0.7636	0.7794	0.7971	0.8154
166	0.8274	0.8417	0.8573	0.8731
222	0.9506	0.9068	0.8573	0.8074
224	0.9012	0.8384	0.7808	0.7301
296	0.6870	0.7060	0.7234	0.7385
360	0.6850	0.7016	0.7181	0.7333

.

According to Table 3, the importance indices of elements are more sensitive to adjustment in grid size, especially M222 and M224. When the grid is square, the importance indices of the lower chords M166 and M222 are both the highest. When the horizontal grid size reduces, the importance index of the lower chord M222 in the horizontal direction increases, becoming the most important element. In contrast, the importance index of the chord M166 decreases. The adjustment of linear stiffness of elements can be achieved by changing the grid size. Therefore, it can be concluded that the importance of the element increases with linear stiffness.

5. Effects of the Topology of the Grid Structures

In this subsection, grid structures with different topologies are investigated. Three kinds of symmetric grid structures—diagonal square pyramid grid structures, biorthogonal lattice grid structures, and biorthogonal diagonal lattice grid structures—are studied for their importance indices of elements, shown in Figure 5, Figure 6 and Figure 7. The grid size of all of the upper chords is 1.2 m × 1.2 m. Eight nodes are distributed over horizontal and vertical members, and the heights of the grids are 1.0 m. The upper surrounding nodes are assumed to be fixed, subject to uniform vertical load. The elastic modulus of each element is 2.1 × 10¹¹ N/m². For a diagonal square pyramid grid, the cross-section 89 mm × 4 mm (1068 mm²) is for upper chords, 102 mm × 7 mm (2089 mm²) is for lower chords, and 89 mm × 5 mm (1319 mm²) is for webs. For a biorthogonal lattice grid structure and a biorthogonal diagonal lattice grid structure, the cross-section 60 mm × 4 mm (704 mm²) is for upper chords, the cross-section 60 mm × 4 mm (704 mm²) is for lower chords, and the cross-section 51 mm × 4 mm (591 mm²) is for web members. The symmetrical area of the grids, the number of elements, and the distribution of key elements are all shown in Figure 5, Figure 6 and Figure 7. The importance indices of some elements are shown in

Table 4. Importance index of partial elements in a diagonal square pyramid grid structure.

Element Number	Load (kN)				Element Number	Load (kN)
	0	5	10	15		0	5	10	15
9	0.5947	0.5962	0.5976	0.5991	365	0.7884	0.7892	0.7899	0.7907
65	0.6516	0.6529	0.6541	0.6554	413	0.8824	0.8829	0.8834	0.8839
92	0.8543	0.8548	0.8552	0.8556	461	0.6472	0.6484	0.6496	0.6509
155	0.8536	0.8541	0.8546	0.8550	485	0.7884	0.7892	0.7900	0.7907
220	0.8538	0.8543	0.8547	0.8552	488	0.9612	0.9613	0.9614	0.9615
292	0.9072	0.9076	0.9079	0.9083	542	0.9603	0.9606	0.9608	0.9611
306	0.9136	0.9140	0.9145	0.9149	550	0.9611	0.9614	0.9617	0.9619
308	0.8566	0.8573	0.8581	0.8589	616	0.9604	0.9606	0.9608	0.9609

,

Table 5. Importance indices of partial elements in a biorthogonal lattice grid structure.

Element Number	Load (kN)				Element Number	Load (kN)
	0	5	10	15		0	5	10	15
11	0.7939	0.7953	0.7968	0.7982	229	0.9473	0.9479	0.9485	0.9490
31	0.8311	0.8323	0.8335	0.8346	237	0.9501	0.9506	0.9512	0.9517
81	0.7816	0.7831	0.7846	0.7861	243	0.9446	0.9452	0.9458	0.9464
90	0.8033	0.8047	0.8060	0.8074	244	0.9487	0.9492	0.9498	0.9503
107	0.8195	0.8207	0.8220	0.8232	250	0.9448	0.9453	0.9458	0.9463
108	0.8313	0.8325	0.8337	0.8348	253	1.0000	0.9983	0.9984	0.9985
145	0.8919	0.8927	0.8934	0.8942	278	0.7160	0.7180	0.7199	0.7219
159	0.7973	0.7987	0.8001	0.8014	283	0.7836	0.7852	0.7868	0.7883
193	0.9034	0.9040	0.9047	0.9053	287	0.7839	0.7855	0.7871	0.7887
199	0.9043	0.9050	0.9056	0.9062	291	0.7894	0.7910	0.7925	0.7940
205	0.9031	0.9038	0.9045	0.9052	341	0.7619	0.7636	0.7653	0.7670
207	0.8192	0.8205	0.8218	0.8230	357	0.7768	0.7784	0.7800	0.7815

and

Table 6. Importance index of partial elements in a biorthogonal diagonal lattice grid structure.

Element Number	Load (kN)				Element Number	Load (kN)
	0	5	10	15		0	5	10	15
1	0.8176	0.8207	0.8238	0.8267	382	0.9561	0.9572	0.9583	0.9593
22	0.7881	0.7917	0.7952	0.7985	390	0.9417	0.9428	0.9439	0.9449
25	0.8550	0.8574	0.8597	0.8620	408	0.9545	0.9559	0.9571	0.9585
113	0.7853	0.7889	0.7924	0.7958	411	1.0000	0.9984	0.9986	0.9989
122	0.8505	0.8529	0.8554	0.8577	503	0.8268	0.8296	0.8324	0.8351
225	0.8816	0.8836	0.8855	0.8874	534	0.7843	0.7880	0.7917	0.7952
237	0.8974	0.8991	0.9008	0.9024	536	0.7746	0.7784	0.7822	0.7858
275	0.8264	0.8293	0.8322	0.8350	552	0.6889	0.6941	0.6992	0.7042
345	0.8953	0.8970	0.8987	0.9003	559	0.7275	0.7321	0.7366	0.7409
369	0.9390	0.9400	0.9411	0.9421	573	0.7821	0.7858	0.7894	0.7929

.

From the results in Table 4, Table 5 and Table 6, it can be seen that the load hardly affects the importance indices of elements. The importance index under no load can be directly used in the analysis of the key elements of the grid truss structure. Usually, the sequence of key elements for three kinds of grids structure is vertical webs, lower chords, upper chords, and diagonal chords. In the upper chords, the more important elements are all concentrated in the center of the upper chord plane. In the lower chords, the more important elements are all located around the lower chord plane, whose redundancy is lower. For the diagonal square pyramid grid structure, the importance indices of other elements are relatively higher, except for the elements near the support in the webs. The importance index of the webs is higher than that of the other chords. For the biorthogonal lattice grid structure and the biorthogonal diagonal lattice grid structure, the importance indices of vertical webs are generally very high, reaching above 0.94, due to their low redundancy in the vertical direction. In the vertical direction, the vertical web members are both the main contributor to stiffness and the main path for transferring loads.

6. Conclusions

In this paper, according to the evaluation method of the important elements based on stiffness, the importance indices of elements were calculated using the MATLAB program. The square pyramid grid structure was taken as the original structure, and the characteristics of the key elements of the structure with different support conditions, stiffness distribution, and geometric parameters were studied. Then, the grid structures with different topologies were investigated. Three kinds of grid structures—diagonal square pyramid grids, biorthogonal lattice grids, and biorthogonal diagonal lattice grids—were investigated for their importance indices of elements.

For different types of grid structures, if the periphery of the upper chords is restrained, the distribution positions of key elements of the upper and lower chords remain unchanged. In the upper chords, the higher important elements are concentrated at the center of the upper chord plane. In the lower chords, the higher important elements are located around the lower chord plane.

After releasing the restraints at the support, the importance indices of most elements near the released support will increase, which means that structural design requires special consideration of these elements. It is significant for the influence of the element section stiffness and the grid size on the importance indices of the elements. The change of these two parameters is essentially a change in the linear stiffness of the element. When the key elements are located, it is useful to increase linear stiffness to decrease importance indices. Moreover, the number of grids affects the importance of the elements but does not change the distribution position of key elements. Once the forms of grids are determined, the locations of key elements are determined. These elements should be designed particularly.

This work can be extended in two directions. The applicability of the method to the complex spatial truss structures without symmetry and periodicity should be discussed. Then, the computational cost will be regarded as an important target to optimize the method. The other is the threat assessment. The possibility of an external threat and initial failure should be investigated. The probabilistic approaches and Monte Carlo simulation will be introduced. Moreover, experiments will be performed to verify the proposed method.