The Split Equality Fixed Point Problem of Demicontractive Operators with Numerical Example and Application
Abstract
:1. Introduction
2. Preliminaries
- (i)
- contractive if there can be found with the property
- (ii)
- nonexpansive if
- (iii)
- quasi-nonexpansive if
- (iv)
- directed (firmly quasi-nonexpansive) if
- (v)
- σ-demicontractive if there can be found a constant such thatwhich is the same as
- (vi)
- quasi-pseudo-contractive if
3. Main Results
| Algorithm 1.Let , and be arbitrarily given. |
| The algorithm becomes Step 1. If Step 2. Define and , |
- (a)
- and are demiclosed at 0;
- (b)
- ;
- (c)
- and ;
- (d)
- (I)
- The split common fixed point problem is generalized to the SEFP problem; the nonexpansive mappings are extended to the demicontractive operators;
- (II)
- The weak convergence in ([21], Theorem 3.1) is extended to the strong convergence.
4. Numerical Example
5. Application
| Algorithm 2.Let , be arbitrarily given. |
| The algorithm becomes Step 1. If Step 2. Define and , |
- (1)
- .
- (2)
- If is demiclosed at 0, then so is .
- (3)
- Additionally, if T is quasi-pseudo-contractive, K is quasi-nonexpansive.
- (a)
- and are demiclosed at 0;
- (b)
- ;
- (c)
- and ;
- (d)
6. Conclusions
- (1)
- Theorem 1 mainly enlarge the ones in ([21], Theorem 3.1) and ([22], Theorem 14) from the following issues: (i) we extend the weak convergence result ([21], Theorem 3.1) for the SCFP (1) involving nonexpansive mappings to the strong convergent result for the SEFP (2) involving demicontractive operators; we improve and extend the weak convergence result ([22], Theorem 14) to the strong convergence result and remove the Lipschitz continuous conditions of the operators S and T; the proof of the strong convergence in Theorem 1 is different from the technique used to prove the weak convergence used in ([21], Theorem 3.1) and ([22], Theorem 14) because we use viscosity approximation methods.
- (2)
- Theorem 2 improves and extends ([35], Theorem 3.2) from the following points of view: (i) we remove the conditions of semi-compactness on the operators S and T, and still obtain a strong convergence result by using viscosity approximation methods; (ii) the choice in proving the convergence of Algorithm 3.1 in [35] requires the computation of the related operator norms, which is a complicated task to be accomplished. Thus, our choice (26) of the step sizes is more efficient and desirable.
- (3)
- We give a numerical example to demonstrate the usefulness and convergence of our algorithm.
Author Contributions
Funding
Conflicts of Interest
References
- Censor, Y.; Elfving, T. A multiprojection algorithm using Bregman projections in a product space. Numer. Algorithms 1994, 8, 221–239. [Google Scholar] [CrossRef]
- Qin, X.; Petruşel, A.; Yao, J.-C. CQ iterative algorithms for fixed points of nonexpansive mappings and split feasibility problems in Hilbert spaces. J. Nonlinear Convex Anal. 2018, 19, 157–165. [Google Scholar]
- Cho, S.Y.; Qin, X.; Yao, J.-C.; Yao, Y. Viscosity approximation splitting methods for monotone and nonexpansive operators in Hilbert spaces. J. Nonlinear Convex Anal. 2018, 19, 251–264. [Google Scholar]
- Takahashi, W.; Wen, C.F.; Yao, J.-C. The shrinking projection method for a finite family of demimetric mappings with variational inequality problems in a Hilbert space. Fixed Point Theory 2018, 19, 407–419. [Google Scholar] [CrossRef]
- Censor, Y.; Segal, A. The split common fixed point problem for directed operators. J. Convex Anal. 2009, 16, 587–600. [Google Scholar]
- Jailoka, P.; Suantai, S. Split common fixed point and null point problems for demicontractive operators in Hilbert spaces. Optim. Methods Softw. 2019, 34, 248–263. [Google Scholar] [CrossRef]
- Moudafi, A. A note on the split common fixed point problem for quasinonexpansive operators. Nonlinear Anal. 2011, 74, 4083–4087. [Google Scholar] [CrossRef]
- Moudafi, A. The split common fixed point problem for demicontractive mappings. Inverse Probl. 2010, 26, 055007. [Google Scholar] [CrossRef]
- Wang, F. A new method for split common fixed-point problem without priori knowledge of operator norms. J. Fixed Point Theory Appl. 2017, 19, 1–10. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Kim, T.H.; Fang, X.L.; He, H.M. The split common fixed-point problem for demicontractive mappings and quasi-nonexpansive mappings. J. Nonlinear Sci. Appl. 2017, 10, 2976–2985. [Google Scholar] [CrossRef] [Green Version]
- Yao, Y.; Yao, J.-C.; Liou, Y.C.; Postolache, M. Iterative algorithms for split common fixed points of demicontractive operators without priori knowledge of operator norms. Carpathian J. Math. 2018, 34, 459–466. [Google Scholar]
- Yao, Y.; Leng, L.; Postolache, M.; Zheng, X. Mann-type iteration method for solving the split common fixed point problem. J. Nonlinear Convex Anal. 2017, 18, 875–882. [Google Scholar]
- Takahahsi, W.; Yao, J.-C. The split common fixed point problem for two finite families of nonlinear mappings in Hilbert spaces. J. Nonlinear Convex Anal. 2019, 20, 173–195. [Google Scholar]
- Wang, J.; Fang, X. A strong convergence theorem for the split common fixed-point problem of demicontractive mappings. Appl. Set-Valued Anal. Optim. 2019, 1, 105–112. [Google Scholar]
- Yao, Y.; Postolache, M.; Yao, J.-C. An iterative algorithm for solving the generalized variational inequalities and fixed points problems. Mathematics 2019, 7, 61. [Google Scholar] [CrossRef] [Green Version]
- Moudafi, A. Viscosity approximation methods for fixed points problems. J. Math. Anal. Appl. 2000, 241, 46–55. [Google Scholar] [CrossRef] [Green Version]
- Moudafi, A.; Al-Shemas, E. Simultaneous iterative methods for split equality problem. Trans. Math. Program Appl. 2013, 1, 1–11. [Google Scholar]
- Yao, Y.; Liou, Y.C.; Postolache, M. Self-adaptive algorithms for the split problem of the demicontractive operators. Optimization 2018, 67, 1309–1319. [Google Scholar] [CrossRef]
- Yao, Y.; Liou, Y.C.; Yao, J.-C. Split common fixed point problem for two quasi-pseudo-contractive operators and its algorithm construction. Fixed Point Theory Appl. 2015, 2015, 127. [Google Scholar] [CrossRef] [Green Version]
- Yao, Y.; Postolache, M.; Zhu, Z. Gradient methods with selection technique for the multiple-sets split feasibility problem. Optimization 2020, 69, 269–281. [Google Scholar] [CrossRef]
- Wang, F.; Xu, H.K. Weak and strong convergence of two algorithms for the split fixed point problem. Numer. Math. Theor. Meth. Appl. 2018, 11, 770–781. [Google Scholar]
- Cui, H.H.; Ceng, L.C.; Wang, F.H. Weak convergence theorems on the split common fixed point problem for demicontractive continuous mappings. J. Funct. Spaces 2018, 9610257. [Google Scholar] [CrossRef] [Green Version]
- Attouch, H. Viscosity solutions of minimization problems. SIAM J. Optim. 1996, 6, 769–806. [Google Scholar] [CrossRef]
- Yao, Y.; Postolache, M.; Liou, Y.C. Strong convergence of a self-adaptive method for the split feasibility problem. Fixed Point Theory Appl. 2013, 2013, 201. [Google Scholar] [CrossRef] [Green Version]
- Marino, G.; Xu, H.K. General iterative method for nonexpansive mappings in Hilbert spaces. J. Math. Anal. Appl. 2006, 318, 43–52. [Google Scholar] [CrossRef] [Green Version]
- Xu, H.K. Viscosity Approximation Methods for Nonexpansive Mappings. J. Math. Anal. Appl. 2004, 298, 279–291. [Google Scholar] [CrossRef] [Green Version]
- Qin, X.; Yao, J.-C. A viscosity iterative method for a split feasibility problem. J. Nonlinear Convex Anal. 2019, 20, 1497–1506. [Google Scholar]
- Wang, Y.Q.; Kim, T.H. Simultaneous iterative algorithm for the split equality fixed-point problem of demicontractive mappings. J. Nonlinear Sci. Appl. 2017, 10, 154–165. [Google Scholar] [CrossRef] [Green Version]
- Takahashi, W. Nonlinear Functional Analysis; Yokohama Publishers: Yokohama, Japan, 2000. [Google Scholar]
- Goebel, K.; Kirk, W.A. Topics in Metric Fixed Point Theory; Cambridge Studies in Advanced Mathematics 28; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Xu, H.K. Iterative algorithms for nonlinear operators. J. Lond. Math. Soc. 2002, 66, 240–256. [Google Scholar] [CrossRef]
- Marino, G.; Xu, H.K. Weak and strong convergence theorems for strict pseudo-contractions in Hilbert spaces. J. Math. Anal. Appl. 2007, 329, 336–346. [Google Scholar] [CrossRef] [Green Version]
- Opial, Z. Weak convergence of the sequence of successive approximations for nonexpansive mappings. Bull. Am. Math. Soc. 1967, 73, 591–597. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.Q.; Fang, X.L. Viscosity approximation methods for the multiple-set split equality common fixed-point problems of demicontractive mappings. J. Nonlinear Sci. Appl. 2017, 10, 4254–4268. [Google Scholar] [CrossRef] [Green Version]
- Chang, S.S.; Wang, L.; Qin, L.J. Split equality fixed point problem for quasi-pseudo-contrative mappings with applications. Fixed Point Theory Appl. 2015, 2015, 208. [Google Scholar] [CrossRef]
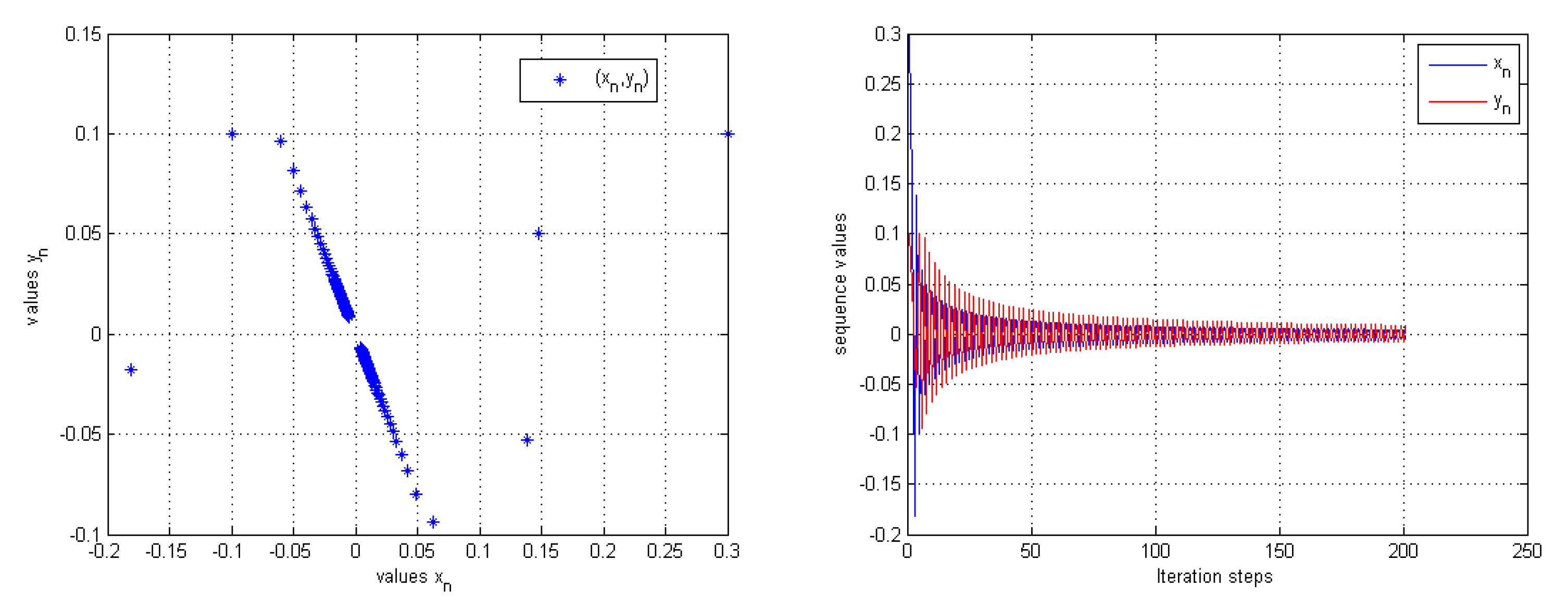
| n | |||
|---|---|---|---|
| 1 | 0.300000000000000 | 0.100000000000000 | |
| 2 | 0.147760103330670 | 0.049916708323414 | |
| 3 | −0.181488306475344 | −0.017546156041863 | |
| 4 | 0.138858140885285 | −0.052994167458393 | |
| 5 | −0.099484842363747 | 0.100270304873921 | |
| ... | ... | ... | |
| 197 | 0.004448866036788 | −0.007198416659655 | |
| 198 | −0.005472189665092 | 0.008854189036970 | |
| 199 | 0.004414260565043 | −0.007142423823788 | |
| 200 | −0.005432678586300 | 0.008790258763243 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Chen, J.; Pitea, A. The Split Equality Fixed Point Problem of Demicontractive Operators with Numerical Example and Application. Symmetry 2020, 12, 902. https://doi.org/10.3390/sym12060902
Wang Y, Chen J, Pitea A. The Split Equality Fixed Point Problem of Demicontractive Operators with Numerical Example and Application. Symmetry. 2020; 12(6):902. https://doi.org/10.3390/sym12060902
Chicago/Turabian StyleWang, Yaqin, Jinzuo Chen, and Ariana Pitea. 2020. "The Split Equality Fixed Point Problem of Demicontractive Operators with Numerical Example and Application" Symmetry 12, no. 6: 902. https://doi.org/10.3390/sym12060902
APA StyleWang, Y., Chen, J., & Pitea, A. (2020). The Split Equality Fixed Point Problem of Demicontractive Operators with Numerical Example and Application. Symmetry, 12(6), 902. https://doi.org/10.3390/sym12060902





