Pseudo Random Binary Sequence Based on Cyclic Difference Set
Abstract
:1. Introduction
2. Preliminaries
2.1. Notation and Convention
- a prime number.
- prime field of p elements.
- finite field of elements where m is a non-negative integer and .
- .
- a primitive polynomial of degree m in characteristic field .
- a primitive element of primitive polynomial, .
- period of sequence.
2.2. Primitive Polynomial
- ①
- ,
- ②
- for .
2.3. Quadratic Residue and Quadratic Nonresidue
2.4. Linear Complexity
3. Proposal of MK Sequence
3.1. Cyclic Difference Set
3.2. Generation Algorithm
| Algorithm 1 Proposed Algorithm for MK Sequence. |
|
4. Experimental Results
4.1. Randomness Analysis
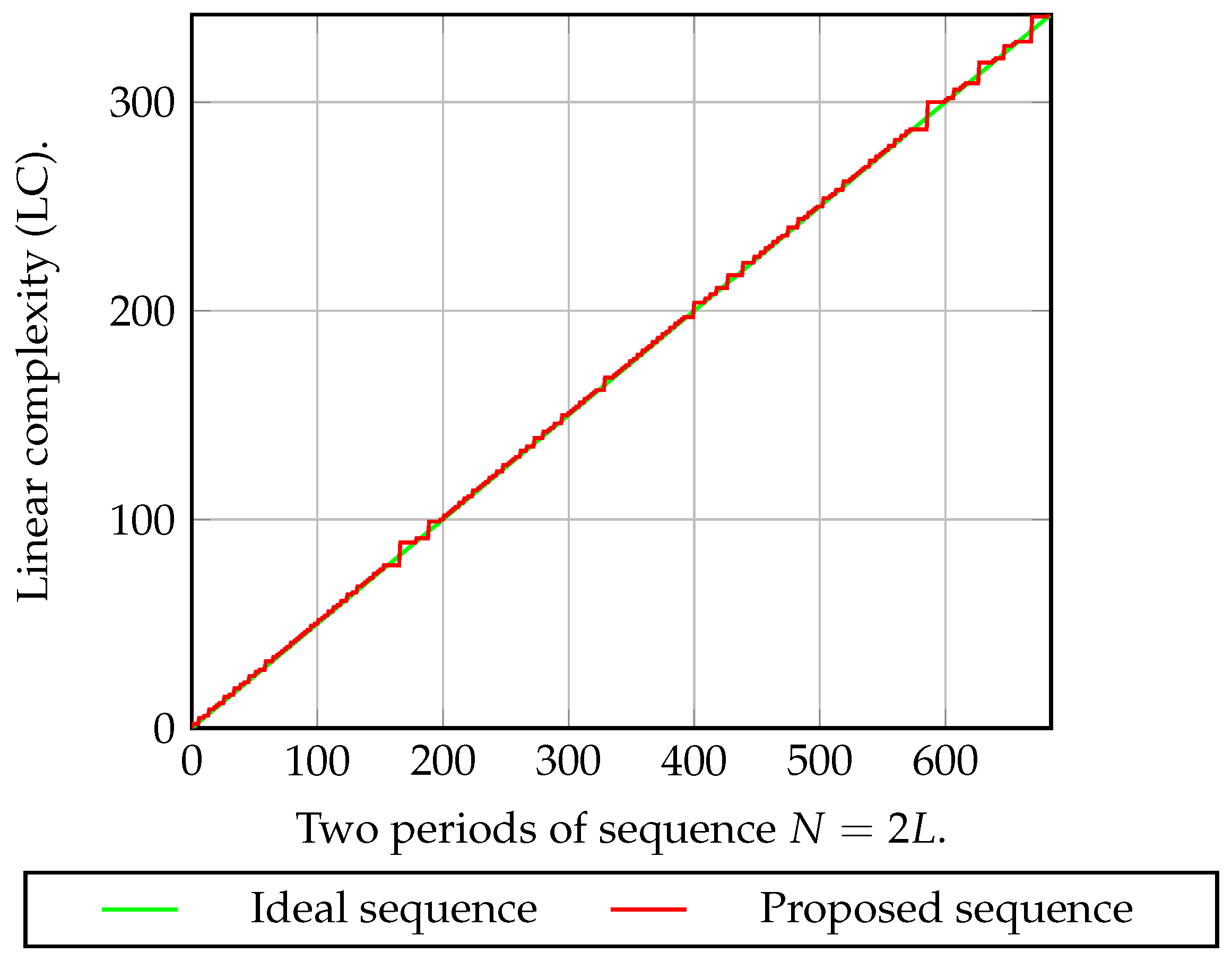
4.2. Linear Complexity Analysis
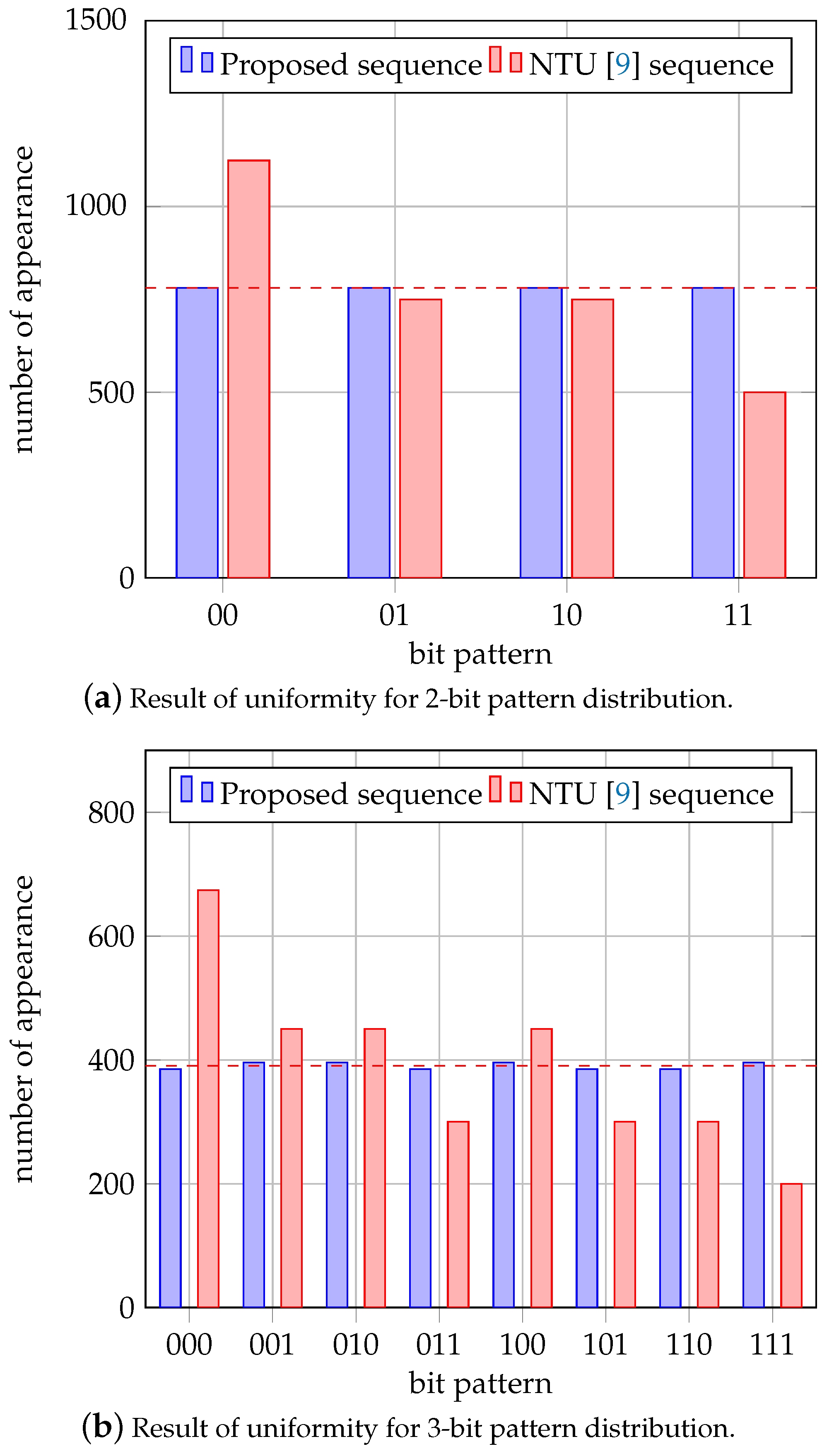
4.3. Result of Uniformity
4.4. Evaluation by Comparison
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lambić, D.; Nikolić, M. Pseudo-random number generator based on discrete-space chaotic map. Nonlinear Dyn. 2017, 90, 223–232. [Google Scholar] [CrossRef]
- Akhter, F.; Nogami, Y.; Kusaka, T.; Taketa, Y.; Tatara, T. Binary sequence generated by alternative trace map function and its properties. In Proceedings of the 2019 Seventh International Symposium on Computing and Networking Workshops (CANDARW), Nagasaki, Japan, 26–29 November 2019; pp. 408–411. [Google Scholar]
- Akhter, F.; Al Mamun, M.S. Pseudo random binary sequence: A new approach over finite field and its properties. In Proceedings of the 2017 International Conference on Electrical, Computer and Communication Engineering (ECCE), Cox’s Bazar, Bangladesh, 16–18 February 2017; pp. 676–680. [Google Scholar]
- Šajić, S.; Maletić, N.; Todorović, B.M.; Šunjevarić, M. Random binary sequences in telecommunications. J. Electr. Eng. 2013, 64, 230–237. [Google Scholar] [CrossRef] [Green Version]
- Pasqualini, L.; Parton, M. Pseudo random number generation: A reinforcement learning approach. Procedia Comput. Sci. 2020, 170, 1122–1127. [Google Scholar] [CrossRef]
- Golomb, S.W. Shift Register Sequences; Aegean Park Press: Walnut Creek, CA, USA, 1967. [Google Scholar]
- Gold, R. Optimal binary sequences for spread spectrum multiplexing (Corresp.). IEEE Trans. Inf. Theory 1967, 13, 619–621. [Google Scholar] [CrossRef] [Green Version]
- Kasami, T. Weight Distribution Formula for Some Class of Cyclic Codes; Report No. R-285; Coordinated Science Laboratory, University of Illinois: Champaign, IL, USA, 1966. [Google Scholar]
- Nogami, Y.; Tada, K.; Uehara, S. A geometric sequence binarized with Legendre symbol over odd characteristic field and its properties. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2014, 97, 2336–2342. [Google Scholar] [CrossRef]
- Yu, N.Y.; Gong, G. New construction of M-ary sequence families with low correlation from the structure of Sidelnikov sequences. IEEE Trans. Inf. Theory 2010, 56, 4061–4070. [Google Scholar] [CrossRef]
- Su, M.; Winterhof, A. Autocorrelation of Legendre–Sidelnikov Sequences. IEEE Trans. Inf. Theory 2010, 56, 1714–1718. [Google Scholar] [CrossRef]
- Kim, Y.T.; San Kim, D.; Song, H.Y. New M-Ary Sequence families with low correlation from the array structure of Sidelnikov sequences. IEEE Trans. Inf. Theory 2014, 61, 655–670. [Google Scholar]
- Zierler, N. Legendre Sequences; Technical Report; Massachusetts Institute of Technology, Lincoln Laboratory: Lincoln, NE, USA, 1958. [Google Scholar]
- No, J.S.; Lee, H.K.; Chung, H.; Song, H.Y.; Yang, K. Trace representation of Legendre sequences of Mersenne prime period. IEEE Trans. Inf. Theory 1996, 42, 2254–2255. [Google Scholar]
- Ding, C.; Hesseseth, T.; Shan, W. On the linear complexity of Legendre sequences. IEEE Trans. Inf. Theory 1998, 44, 1276–1278. [Google Scholar] [CrossRef]
- Rukhin, A.; Soto, J.; Nechvatal, J.; Smid, M.; Barker, E. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications; Technical Report; Booz Allen & Hamilton inc Greensboro Drive: McLean, VA, USA, 2001. [Google Scholar]
- Bassham, L.E., III; Rukhin, A.L.; Soto, J.; Nechvatal, J.R.; Smid, M.E.; Barker, E.B.; Leigh, S.D.; Levenson, M.; Vangel, M.; Banks, D.L.; et al. Sp 800-22 rev. 1a. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications; National Institute of Standards & Technology: Gaithersburg, MD, USA, 2010. [Google Scholar]
- Koblitz, N. A Course in Number Theory and Cryptography; Springer Science & Business Media: Berlin, Germany, 1994; Volume 114. [Google Scholar]
- Lehmer, D. On Euler’s totient function. Bull. Am. Math. Soc. 1932, 38, 745–751. [Google Scholar] [CrossRef] [Green Version]
- Massey, J. Shift-register synthesis and BCH decoding. IEEE Trans. Inf. Theory 1969, 15, 122–127. [Google Scholar] [CrossRef] [Green Version]
- Cohen, S.D. Generators in cyclic difference sets. J. Comb. Theory Ser. A 1989, 51, 227–236. [Google Scholar] [CrossRef] [Green Version]
- Xia, B. Cyclotomic difference sets in finite fields. Math. Comput. 2018, 87, 2461–2482. [Google Scholar] [CrossRef] [Green Version]
- Dillon, J.F.; Dobbertin, H. New cyclic difference sets with Singer parameters. Finite Fields Their Appl. 2004, 10, 342–389. [Google Scholar] [CrossRef]
- Polhill, J. Generalizations of partial difference sets from cyclotomy to nonelementary abelian p-groups. Electron. J. Comb. 2008, 15, R125. [Google Scholar] [CrossRef] [Green Version]
- Murillo-Escobar, M.; Cruz-Hernández, C.; Cardoza-Avendaño, L.; Méndez-Ramírez, R. A novel pseudorandom number generator based on pseudorandomly enhanced logistic map. Nonlinear Dyn. 2017, 87, 407–425. [Google Scholar] [CrossRef]
- Marsaglia, G. DIEHARD Test Suite. 1998, Volume 8. Available online: http://www.Stat.Fsu.Edu/pub/diehard (accessed on 20 March 2014).
- Gustafson, H.; Dawson, E.; Nielsen, L.; Caelli, W. A computer package for measuring the strength of encryption algorithms. Comput. Secur. 1994, 13, 687–697. [Google Scholar] [CrossRef]
- Knuth, G. The Art of Computer Programming, Seminumerical Algorithms—Volume 2: Addition; Wesley: Reading, MA, USA, 1998. [Google Scholar]
- Sulak, F.; Uğuz, M.; Kocak, O.; Doğanaksoy, A. On the independence of statistical randomness tests included in the NIST test suite. Turk. J. Electr. Eng. Comput. Sci. 2017, 25, 3673–3683. [Google Scholar] [CrossRef]
- Patidar, V.; Sud, K.K.; Pareek, N.K. A pseudo random bit generator based on chaotic logistic map and its statistical testing. Informatica 2009, 33, 441–452. [Google Scholar]
- Sỳs, M.; Matyáš, V. Randomness testing: Result interpretation and speed. In The New Codebreakers; Springer: New York, NY, USA, 2016; pp. 389–395. [Google Scholar]
- Hu, H.; Liu, L.; Ding, N. Pseudorandom sequence generator based on the Chen chaotic system. Comput. Phys. Commun. 2013, 184, 765–768. [Google Scholar] [CrossRef]
- Yang, L.; Xiao-Jun, T. A new pseudorandom number generator based on a complex number chaotic equation. Chin. Phys. B 2012, 21, 090506. [Google Scholar]
- Liu, L.; Miao, S.; Hu, H.; Deng, Y. Pseudorandom bit generator based on non-stationary logistic maps. IET Inf. Secur. 2016, 10, 87–94. [Google Scholar] [CrossRef]
- Helleseth, T. Golomb’s randomness postulates. In Encyclopedia of Cryptography and Security; van Tilborg, H.C.A., Jajodia, S., Eds.; Springer: Boston, MA, USA, 2011; pp. 516–517. [Google Scholar] [CrossRef]
- Doğanaksoy, A.; Sulak, F.; Uğuz, M.; Şeker, O.; Akcengiz, Z. New statistical randomness tests based on length of runs. Math. Probl. Eng. 2015, 2015. [Google Scholar] [CrossRef] [Green Version]
- Ers, H.W. On the significance of golomb’s randomness postulates in cryptography. Philips J. Res 1988, 43, 185–222. [Google Scholar]
- Schwabe, P.; Stoffelen, K. All the AES you need on Cortex-M3 and M4. In International Conference on Selected Areas in Cryptography; Springer: Cham, Switzerland, 2016; pp. 180–194. [Google Scholar]
- De Santis, F.; Schauer, A.; Sigl, G. ChaCha20-Poly1305 authenticated encryption for high-speed embedded IoT applications. In Proceedings of the Design, Automation & Test in Europe Conference & Exhibition (DATE), Lausanne, Switzerland, 27–31 March 2017; pp. 692–697. [Google Scholar]
- Gao, X. Comparison analysis of Ding’s RLWE-based key exchange protocol and NewHope variants. Adv. Math. Commun. 2019, 13, 221. [Google Scholar] [CrossRef] [Green Version]

| Statistical Test | Portion of Successful Sequences | Result |
|---|---|---|
| Frequency | 0.997 | ◯ |
| Block frequency | 0.991 | ◯ |
| Cumulative sums (1) | 0.997 | ◯ |
| Cumulative sums (2) | 0.996 | ◯ |
| Runs | 0.995 | ◯ |
| Longest run | 0.992 | ◯ |
| Rank | 0.991 | ◯ |
| Fast fourier transform | 0.989 | ◯ |
| Non-overlapping template | max: 0.997 | ◯ |
| min: 0.983 | ◯ | |
| Overlapping template | 0.986 | ◯ |
| Maurer’s universal statistical | 0.990 | ◯ |
| Approximate entropy | 0.984 | ◯ |
| Random excursions | max: 1.000 | ◯ |
| min: 0.974 | ◯ | |
| Random Excursions Variant | max: 1.000 | ◯ |
| min: 0.983 | ◯ | |
| Serial (1) | 0.987 | ◯ |
| Serial (2) | 0.989 | ◯ |
| Linear complexity | 0.984 | ◯ |
| Length of Sequence | Linear Complexity | |
|---|---|---|
| 124 | 62 | |
| 342 | 171 | |
| 16,806 | 8403 | |
| 161,050 | 80,525 | |
| 1,030,300 | 515,150 | |
| 101,847,562 | 50,923,781 |
| Pattern Length | Bit Pattern | # of Appearance |
|---|---|---|
| 1 | 0 | 1562 |
| 1 | 1562 | |
| 2 | 00 | 781 |
| 01 | 781 | |
| 10 | 781 | |
| 11 | 781 | |
| 3 | 000 | 385 |
| 001 | 396 | |
| 010 | 396 | |
| 011 | 385 | |
| 100 | 396 | |
| 101 | 385 | |
| 110 | 385 | |
| 111 | 396 |
| Pattern Length | Bit Pattern | # of Appearance |
|---|---|---|
| 1 | 0 | 50,923,781 |
| 1 | 50,923,781 | |
| 2 | 00 | 25,461,890 |
| 01 | 25,461,891 | |
| 10 | 25,461,891 | |
| 11 | 25,461,890 | |
| 3 | 000 | 12,731,725 |
| 001 | 12,730,165 | |
| 010 | 12,730,165 | |
| 011 | 12,731,726 | |
| 100 | 12,730,165 | |
| 101 | 12,731,726 | |
| 110 | 12,731,726 | |
| 111 | 12,730,164 |
| Length of Sequence | Linear Complexity | |
|---|---|---|
| Proposed Sequence | NTU Sequence | |
| 62 | 62 | |
| 171 | 114 | |
| 8403 | 5602 | |
| 80,525 | 32,210 | |
| 515,150 | 20,606 | |
| 50,923,781 | 437,114 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mamun, M.S.A.; Akhter, F. Pseudo Random Binary Sequence Based on Cyclic Difference Set. Symmetry 2020, 12, 1202. https://doi.org/10.3390/sym12081202
Mamun MSA, Akhter F. Pseudo Random Binary Sequence Based on Cyclic Difference Set. Symmetry. 2020; 12(8):1202. https://doi.org/10.3390/sym12081202
Chicago/Turabian StyleMamun, Md. Selim Al, and Fatema Akhter. 2020. "Pseudo Random Binary Sequence Based on Cyclic Difference Set" Symmetry 12, no. 8: 1202. https://doi.org/10.3390/sym12081202





