Lorentz Invariance Violation Tests in Astroparticle Physics
Abstract
1. Introduction
2. Modified Dispersion Relation for Astroparticle Tests
3. Energy-Dependent Time Delay
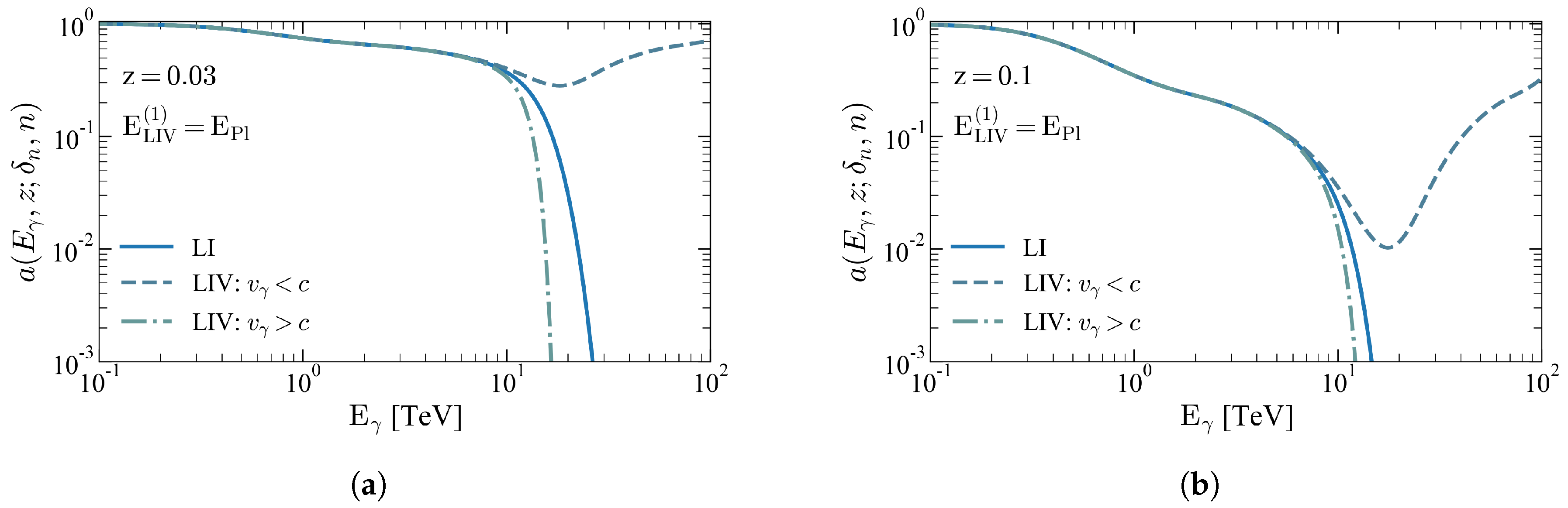
4. Pair-Production Threshold Shift
5. Photon Decay
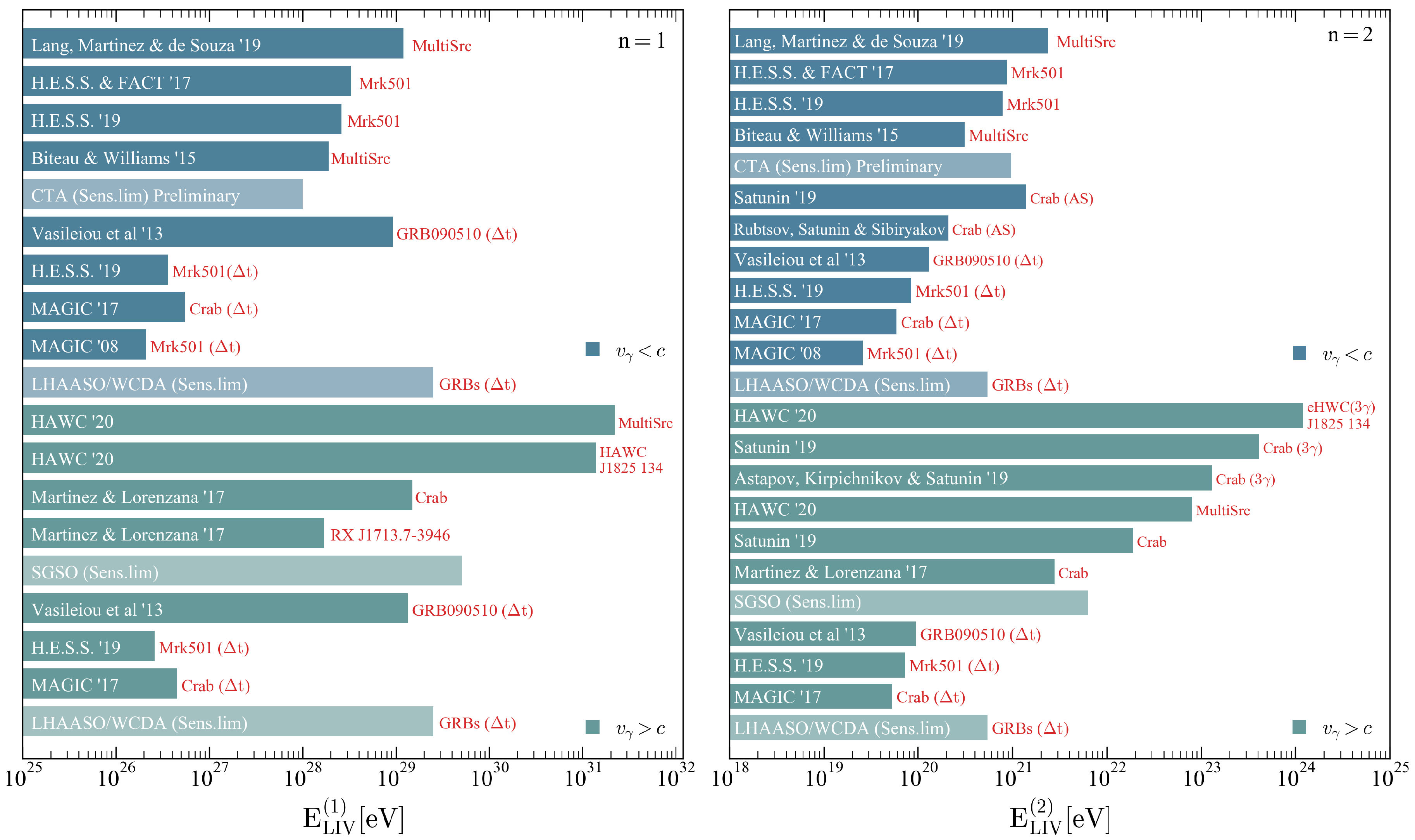
| Type | eV | eV | Bound | Source | Reference | |
|---|---|---|---|---|---|---|
| Limit * | - | 12.08 | 2.38 | PP (−) | MultiSrc | Lang, Martínez, and de Souza (2019) [41] |
| Limit * | - | 3.3 | 0.87 | PP (−) | Mrk501 | H.E.S.S. and FACT (2017) [73] |
| Limit * | - | 2.6 | 0.78 | PP (−) | Mrk 501 | H.E.S.S. (2019) [28] |
| Limit * | - | 1.9 | 0.31 | PP (−) | MultiSrc | Biteau and Williams (2015) [7] |
| Limit | ∼0.001 | ∼ | ∼ | PP (−) | UHECR | Lang, Martínez, and de Souza (2018) [40] |
| Sens.lim. | - | ∼1.22 | ∼0.97 | PP (−) | - | CTA Consortium (2019) [53,54] |
| Limit * | - | 9.3 | 0.13 | (−) | GRB090510 | Vasileiou et al. (2013) [24] |
| Limit * | - | 0.055 | 0.059 | (−) | Crab | MAGIC Collaboration (2017) [26] |
| Limit * | - | 0.036 | 0.085 | (−) | Mrk 501 | H.E.S.S. (2019) [28] |
| Limit * | - | 0.021 | 0.026 | (−) | Mrk 501 | MAGIC Collaboration (2008) [74] |
| Sens.lim. | - | 25 | 0.54 | (−) | GRBs | LHAASO Collaboration (2019) [34] |
| Limit * | - | - | 1.4 | AS (−) | Crab (Tibet) | Satunin (2019) [10] |
| Limit * | - | - | 0.97 | AS (−) | Crab (HAWC) | Satunin (2019) [10] |
| Limit * | - | - | 0.21 | AS (−) | Crab (HEGRA) | Rubtsov, Satunin, and Sibiryakov (2017) [9] |
| Limit * | - | - | 1200 | (+) | eHWC J1825-134 | HAWC Collaboration (2020) [68] |
| Limit * | - | - | 1010 | (+) | eHWC J1907+063 | HAWC Collaboration (2020) [68] |
| Limit * | - | - | 499 | (+) | Crab(HAWC) | HAWC Collaboration (2020) [68] |
| Limit * | - | - | 410 | (+) | Crab (Tibet) | Satunin (2019) [10] |
| Limit * | - | - | 315 | (+) | eHWC J2019+368 | HAWC Collaboration (2020) [68] |
| Limit ** | - | - | 300 | (+) | Crab (HAWC) | Satunin (2019) [10] |
| Limit * | - | - | 130 | (+) | Crab (HEGRA) | Astapov, Kirpichnikov, and Satunin (2019) [75] |
| Limit * | 1.29 | 2220 | 80 | PD (+) | MultiSrc | HAWC Collaboration (2020) [68] |
| Limit * | 1.75 | 1390 | 58 | PD (+) | eHWC J1825-134 | HAWC Collaboration (2020) [68] |
| Limit * | 2.2 | 990 | 47 | PD (+) | eHWC J1907+063 | HAWC Collaboration (2020) [68] |
| Limit * | 4.52 | 340 | 23 | PD (+) | Crab(HAWC) | HAWC Collaboration (2020) [68] |
| Limit ** | - | - | 19 | PD (+) | Crab (Tibet) | Satunin (2019) [10] |
| Limit * | 7.25 | 170 | 14 | PD (+) | eHWC J2019+368 | HAWC Collaboration (2020) [68] |
| Limit ** | - | - | 14 | PD (+) | Crab (HAWC) | Satunin (2019) [10] |
| Limit | - | 15 | 2.8 | PD (+) | Crab (HEGRA) | Martínez and Lorenzana (2017) [8] |
| Limit | - | 1.7 | 0.65 | PD (+) | RX J1713.7-3946 (H.E.S.S.) | Martínez and Lorenzana (2017) [8] |
| Limit | - | - | PD (+) | Tevatron | A. Hohensee et al. (2016) [61] | |
| Limit * | 40 | - | - | PD (+) | Crab (HEGRA) | Schreck (2013) [65] |
| Limit | 50 | - | - | PD (+) | Crab (CANGAROO) | Stecker and Glashow (2001) [49] |
| Limit * | 180 | - | - | PD (+) | RX J1713.7-3946 (H.E.S.S.) | Klinkhamer and Schreck (2008) [6] |
| Limit | 300 | - | - | PD (+) | Crab (Themistocle) | Coleman and Glashow (1997) [13] |
| Sens.lim. | - | ∼ | ∼10 | PD (+) | - | SGSO Alliance [71,72] |
| Limit * | - | 13.4 | 0.09 | (+) | GRB090510 | Vasileiou et al. (2013) [24] |
| Limit * | - | 0.026 | 0.073 | (+) | Mrk 501 | H.E.S.S. (2019) [28] |
| Limit * | - | 0.045 | 0.053 | (+) | Crab | MAGIC Collaboration (2017) [26] |
| Sens.lim. | - | 25 | 0.54 | (+) | GRBs | LHAASO Collaboration (2019) [34] |
6. Photon Splitting
7. Suppression of Air Shower Formation
8. Final Remarks
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| LI | Lorentz invariance |
| LIV | Lorentz invariance violation |
| EBL | Extragalactic background bight |
| CMB | Cosmic microwave background |
| GRB | Gamma-Ray Bursts |
| AGN | Active Galactic Nucleus |
| CTA | Cherenkov Telescope Array |
| H.E.S.S. | High Energy Stereoscopic System |
| MAGIC | Major Atmospheric Gamma ray Imaging Cherenkov |
| HAWC | Hight Altitud Water Cherenkov |
| GZK | Kenneth Greisen, Vadim Kuzmin and Georgiy Zatsepin |
| UHECR | Ultra-high-energy Cosmic Ray |
| UHE | Ultra-high-energy |
| IACT | Imaging Air Cherenkov Telescopes |
| SGSO | Southern Gamma-Ray Survey Observatory |
| SWGO | The Southern Wide-field Gamma ray Observatory |
| LHAASO | Large High Altitude Air Shower Observatory |
| PP | Photon pair production |
| PD | Photon decay |
| Photon splitting into three photons | |
| Energy-dependent time delay | |
| AS | Air shower |
References
- Colladay, D.; Kostelecký, V.A. Lorentz violating extension of the standard model. Phys. Rev. 1998, D58, 116002. [Google Scholar] [CrossRef]
- Kostelecky, V.A.; Russell, N. Data Tables for Lorentz and CPT Violation. Rev. Mod. Phys. 2011, 83, 11–31. [Google Scholar] [CrossRef]
- Alfaro, J. Quantum gravity and Lorentz invariance deformation in the standard model. Phys. Rev. Lett. 2005, 94, 221302. [Google Scholar] [CrossRef] [PubMed]
- Bluhm, R. Observational Constraints on Local Lorentz Invariance. In Springer Handbook of Spacetime; Ashtekar, A., Petkov, V., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 485–507. [Google Scholar] [CrossRef]
- Jacobson, T.; Liberati, S.; Mattingly, D. Threshold effects and Planck scale Lorentz violation: Combined constraints from high energy astrophysics. Phys. Rev. D 2003, 67, 124011. [Google Scholar] [CrossRef]
- Klinkhamer, F.R.; Schreck, M. New two-sided bound on the isotropic Lorentz-violating parameter of modified-Maxwell theory. Phys. Rev. 2008, D78, 085026. [Google Scholar] [CrossRef]
- Biteau, J.; Williams, D.A. The extragalactic background light, the Hubble constant, and anomalies: Conclusions from 20 years of TeV gamma-ray observations. Astrophys. J. 2015, 812, 60. [Google Scholar] [CrossRef]
- Martínez-Huerta, H.; Pérez-Lorenzana, A. Restrictions from Lorentz invariance violation on cosmic ray propagation. Phys. Rev. 2017, D95, 063001. [Google Scholar] [CrossRef]
- Rubtsov, G.; Satunin, P.; Sibiryakov, S. Constraints on violation of Lorentz invariance from atmospheric showers initiated by multi-TeV photons. JCAP 2017, 1705, 049. [Google Scholar] [CrossRef][Green Version]
- Satunin, P. New constraints on Lorentz Invariance violation from Crab Nebula spectrum beyond 100 TeV. Eur. Phys. J. C 2019, 79, 1011. [Google Scholar] [CrossRef]
- Martínez-Huerta, H. Lorentz violation constraints with astroparticle physics. In Proceedings of the 8th Meeting on CPT and Lorentz Symmetry (CPT’19) Bloomington, Bloomington, IN, USA, 12–16 May 2019; Available online: http://xxx.lanl.gov/abs/1906.06293 (accessed on 12 May 2020).
- Nambu, Y. Quantum Electrodynamics in Nonlinear Gauge. Suppl. Prog. Theor. Phys. 1968, 68, 190–195. [Google Scholar] [CrossRef]
- Coleman, S.R.; Glashow, S.L. Cosmic ray and neutrino tests of special relativity. Phys. Lett. 1997, B405, 249–252. [Google Scholar] [CrossRef]
- Sarkar, S. Possible astrophysical probes of quantum gravity. Mod. Phys. Lett. 2002, A17, 1025–1036. [Google Scholar] [CrossRef]
- Amelino-Camelia, G.; Ellis, J.R.; Mavromatos, N.E.; Nanopoulos, D.V.; Sarkar, S. Tests of quantum gravity from observations of gamma-ray bursts. Nature 1998, 393, 763–765. [Google Scholar] [CrossRef]
- Ahluwalia, D.V. Quantum gravity: Testing time for theories. Nature 1999, 398, 199. [Google Scholar] [CrossRef][Green Version]
- Amelino-Camelia, G. A Phenomenological description of quantum gravity induced space-time noise. Nature 2001, 410, 1065–1067. [Google Scholar] [CrossRef]
- Jacob, U.; Piran, T. Lorentz-violation-induced arrival delays of cosmological particles. JCAP 2008, 0801, 031. [Google Scholar] [CrossRef]
- Biller, S.D. Limits to quantum gravity effects from observations of TeV flares in active galaxies. Phys. Rev. Lett. 1999, 83, 2108–2111. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; et al. Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar] [CrossRef]
- Ellis, J.R.; Mavromatos, N.E.; Nanopoulos, D.V.; Sakharov, A.S. Quantum-gravity analysis of gamma-ray bursts using wavelets. Astron. Astrophys. 2003, 402, 409–424. [Google Scholar] [CrossRef]
- Zou, X.B.; Deng, H.K.; Yin, Z.Y.; Wei, H. Model-Independent Constraints on Lorentz Invariance Violation via the Cosmographic Approach. Phys. Lett. 2018, B776, 284–294. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, X.; Qi, J.; Zhang, H. Cosmological Model Independent Time Delay Method. J. Cosmol. Astropart. Phys. 2018, 2018, 027. [Google Scholar] [CrossRef]
- Vasileiou, V.; Jacholkowska, A.; Piron, F.; Bolmont, J.; Couturier, C.; Granot, J.; Stecker, F.W.; Cohen-Tanugi, J.; Longo, F. Constraints on Lorentz Invariance Violation from Fermi-Large Area Telescope Observations of Gamma-Ray Bursts. Phys. Rev. 2013, D87, 122001. [Google Scholar] [CrossRef]
- Zitzer, B. Lorentz Invariance Violation Limits from the Crab Pulsar using VERITAS. In Proceedings of the 33rd International Cosmic Ray Conference (ICRC2013), Rio de Janeiro, Brazil, 2–9 July 2013; p. 1147. Available online: http://xxx.lanl.gov/abs/1307.8382 (accessed on 12 May 2020).
- Ahnen, M.L.; Ansoldi, S.; Antonelli, L.A.; Arcaro, C.; Babić, A.; Banerjee, B.; Bangale, P.; de Almeida, U.B.; Barrio, J.A.; González, J.B.; et al. Constraining Lorentz invariance violation using the Crab Pulsar emission observed up to TeV energies by MAGIC. Astrophys. J. Suppl. 2017, 232, 9. [Google Scholar] [CrossRef]
- Gaug, M.; Garrido, D. Constraining Lorentz invariance violations using the Crab pulsar TeV emission. In Proceedings of the 35th International Cosmic Ray Conference (ICRC2017), Busan, Korea, 10–20 July 2017. [Google Scholar]
- Abdalla, H.; Aharonian, F.; Benkhali, F.A.; Angüner, E.O.; Arakawa, M.; Arcaro, C.; Armand, C.; Arrieta, M.; Backes, M.; Barnard, M.; et al. The 2014 TeV γ-Ray Flare of Mrk 501 Seen with H.E.S.S.: Temporal and Spectral Constraints on Lorentz Invariance Violation. Astrophys. J. 2019, 870, 93. [Google Scholar] [CrossRef]
- Ellis, J.R.; Mavromatos, N.E.; Nanopoulos, D.V.; Sakharov, A.S.; Sarkisyan, E.K.G. Robust limits on Lorentz violation from gamma-ray bursts. Astropart. Phys. 2006, 25, 402–411. [Google Scholar] [CrossRef]
- Ellis, J.R.; Mavromatos, N.E.; Nanopoulos, D.V.; Sakharov, A.S.; Sarkisyan, E.K.G. Robust limits on Lorentz violation from gamma-ray bursts. Astropart. Phys. 2008, 29, 158–159. [Google Scholar] [CrossRef]
- Rodriguez Martinez, M.; Piran, T. Constraining Lorentz violations with gamma-ray bursts. JCAP 2006, 0604, 006. [Google Scholar] [CrossRef]
- Perennes, C.; Sol, H.; Bolmont, J. Modeling spectral lags in active galactic nucleus flares in the context of Lorentz invariance violation searches. Astron. Astrophys. 2020, 633, A143. [Google Scholar] [CrossRef]
- Pan, Y.; Qi, J.; Cao, S.; Liu, T.; Liu, Y.; Geng, S.; Lian, Y.; Zhu, Z.H. Model-independent constraints on Lorentz invariance violation: Implication from updated Gamma-ray burst observations. Astrophys. J. 2020, 890, 169. [Google Scholar] [CrossRef]
- Bai, X. The Large High Altitude Air Shower Observatory (LHAASO) Science White Paper. arXiv 2019, arXiv:1905.02773. [Google Scholar]
- De Angelis, A.; Galanti, G.; Roncadelli, M. Transparency of the Universe to gamma rays. Mon. Not. Roy. Astron. Soc. 2013, 432, 3245–3249. [Google Scholar] [CrossRef]
- Martínez-Huerta, H.; Pérez-Lorenzana, A. Photon emission and decay from generic Lorentz Invariance Violation. J. Phys. Conf. Ser. 2017, 866, 012006. [Google Scholar] [CrossRef]
- Scully, S.T.; Stecker, F.W. Lorentz Invariance Violation and the Observed Spectrum of Ultrahigh Energy Cosmic Rays. Astropart. Phys. 2009, 31, 220–225. [Google Scholar] [CrossRef]
- Stecker, F.W.; Scully, S.T. Searching for New Physics with Ultrahigh Energy Cosmic Rays. New J. Phys. 2009, 11, 085003. [Google Scholar] [CrossRef]
- Galaverni, M.; Sigl, G. Lorentz Violation in the Photon Sector and Ultra-High Energy Cosmic Rays. Phys. Rev. Lett. 2008, 100, 021102. [Google Scholar] [CrossRef] [PubMed]
- Guedes Lang, R.; Martínez-Huerta, H.; de Souza, V. Limits on the Lorentz Invariance Violation from UHECR astrophysics. Astrophys. J. 2018, 853, 23. [Google Scholar] [CrossRef]
- Lang, R.G.; Martínez-Huerta, H.; de Souza, V. Improved limits on Lorentz invariance violation from astrophysical gamma-ray sources. Phys. Rev. 2019, D99, 043015. [Google Scholar] [CrossRef]
- Martínez-Huerta, H.; Lang, R.G.; de Souza, V. The optical depth including Lorentz invariance violation energy threshold shifts. arXiv 2018, arXiv:1901.03205. [Google Scholar]
- Breit, G.; Wheeler, J.A. Collision of Two Light Quanta. Phys. Rev. 1934, 46, 1087–1091. [Google Scholar] [CrossRef]
- Lang, R.G.; Martínez-Huerta, H.; de Souza, V. New stringent LIV limits from astrophysical gamma-ray sources. In Proceedings of the 36th International Cosmic Ray Conference (ICRC2019), Madison, WI, USA, 24 July–1 August 2019; Volume 658. Available online: https://pos.sissa.it/358/658/pdf (accessed on 12 May 2020).
- Lang, R.G.; Martínez-Huerta, H.; de Souza, V. Competitive subluminal LIV limits from ultra-high energy astrophysics. In Proceedings of the 36th International Cosmic Ray Conference (ICRC2019), Madison, WI, USA, 24 July–1 August 2019; Volume 328. Available online: https://pos.sissa.it/358/328/pdf (accessed on 12 May 2020).
- Dominguez, A.; Primack, J.R.; Rosario, D.J.; Prada, F.; Gilmore, R.C.; Faber, S.M.; Koo, D.C.; Somerville, R.S.; Pérez-Torres, M.A.; Pérez-González, P.; et al. Extragalactic Background Light Inferred from AEGIS Galaxy SED-type Fractions. Mon. Not. Roy. Astron. Soc. 2011, 410, 2556. [Google Scholar] [CrossRef]
- Franceschini, A.; Rodighiero, G.; Vaccari, M. The extragalactic optical-infrared background radiations, their time evolution and the cosmic photon-photon opacity. Astron. Astrophys. 2008, 487, 837. [Google Scholar] [CrossRef]
- Gilmore, R.C.; Somerville, R.S.; Primack, J.R.; Dominguez, A. Semi-analytic modeling of the EBL and consequences for extragalactic gamma-ray spectra. Mon. Not. Roy Astron. Soc. 2012, 422, 3189. [Google Scholar] [CrossRef]
- Stecker, F.W.; Glashow, S.L. New tests of Lorentz invariance following from observations of the highest energy cosmic gamma-rays. Astropart. Phys. 2001, 16, 97–99. [Google Scholar] [CrossRef]
- Stecker, F.W. Constraints on Lorentz invariance violating quantum gravity and large extra dimensions models using high energy gamma-ray observations. Astropart. Phys. 2003, 20, 85–90. [Google Scholar] [CrossRef][Green Version]
- Acharya, B.S. Science with the Cherenkov Telescope Array; WSP: Helsinki, Finland, 2018. Available online: http://xxx.lanl.gov/abs/1709.07997 (accessed on 12 May 2020). [CrossRef]
- Daniel, M. Lorentz invariance violation with gamma rays. Nucl. Part. Phys. Proc. 2015, 265–266, 314–316. [Google Scholar] [CrossRef]
- Gaté, F.; Alves Batista, R.; Biteau, J.; Lefaucheur, J.; Mangano, S.; Meyer, M.; Piel, Q.; Pita, S.; Sanchez, D.; Vovk, I. Studying cosmological γ-ray propagation with the Cherenkov Telescope Array. arXiv 2018, arXiv:1709.04185. [Google Scholar] [CrossRef][Green Version]
- Martínez-Huerta, H.; Biteau, J.; Lefaucheur, J.; Meyer, M.; Pita, S.; Vovk, I. Testing cosmology and fundamental physics with the Cherenkov Telescope Array. In Proceedings of the 36th International Cosmic Ray Conference (ICRC 2019), Madison, WI, USA, 24 July–1 August 2019; Available online: http://xxx.lanl.gov/abs/1907.08141 (accessed on 12 May 2020).
- Aab, A.; Abreu, P.; Aglietta, M.; Samarai, I.A.; Albuquerque, I.F.M.; Allekotte, I.; Almela, A.; Castillo, J.A.; Alvarez-Muñiz, J.; Anastasi, G.A.; et al. Search for photons with energies above 1018 eV using the hybrid detector of the Pierre Auger Observatory. JCAP 2017, 1704, 009. [Google Scholar] [CrossRef]
- Galaverni, M.; Sigl, G. Lorentz Violation and Ultrahigh-Energy Photons. Phys. Rev. 2008, D78, 063003. [Google Scholar] [CrossRef]
- Greisen, K. End to the Cosmic-Ray Spectrum? Phys. Rev. Lett. 1966, 16, 748–750. [Google Scholar] [CrossRef]
- Zatsepin, G.T.; Kuzmin, V.A. Upper limit of the spectrum of cosmic rays. JETP Lett. 1966, 4, 78–80. [Google Scholar]
- Unger, M.; Farrar, G.R.; Anchordoqui, L.A. Origin of the ankle in the ultrahigh energy cosmic ray spectrum, and of the extragalactic protons below it. Phys. Rev. 2015, D92, 123001. [Google Scholar] [CrossRef]
- Lang, R.G. Testing Lorentz Invariance Violation at the Pierre Auger Observatory. In Proceedings of the 36th International Cosmic Ray Conference (ICRC2019), Madison, WI, USA, 24 July–1 August 2019; p. 327. Available online: https://pos.sissa.it/358/327/pdf (accessed on 12 May 2020).
- Hohensee, M.A.; Lehnert, R.; Phillips, D.F.; Walsworth, R.L. Limits on isotropic Lorentz violation in QED from collider physics. Phys. Rev. 2009, D80, 036010. [Google Scholar] [CrossRef]
- Tanimori, T.; Sakurazawa, K.; Dazeley, S.A.; Edwards, P.G.; Hara, T.; Hayami, Y.; Kamei, S.; Kifune, T.; Konishi, T.; Matsubara, Y.; et al. Detection of gamma-rays up to 50-TeV from the Crab Nebula. Astrophys. J. 1998, 492, L33–L36. [Google Scholar] [CrossRef]
- Aharonian, F.; Akhperjanian, A.; Beilicke, M.; Bernlöhr, K.; Börst, H.-G.; Bojahr, H.; Bolz, O.; Coarasa, T.; Contreras, J.L.; Cortina, J.; et al. The Crab nebula and pulsar between 500-GeV and 80-TeV. Observations with the HEGRA stereoscopic air Cerenkov telescopes. Astrophys. J. 2004, 614, 897–913. [Google Scholar] [CrossRef]
- Aharonian, F. Primary particle acceleration above 100 TeV in the shell-type Supernova Remnant RX J1713.7-3946 with deep H.E.S.S. observations. Astron. Astrophys. 2007, 464, 235–243. [Google Scholar] [CrossRef]
- Schreck, M. Obtaining bounds from ultra-high energy cosmic rays in isotropic modified Maxwell theory. In Proceedings of the 6th Meeting on CPT and Lorentz Symmetry (CPT 13), Bloomington, IN, USA, 17–21 June 2013; pp. 176–179. Available online: http://xxx.lanl.gov/abs/1310.5159 (accessed on 12 May 2020). [CrossRef]
- Abeysekara, A.U.; Albert, A.; Alfaro, R.; Alvarez, C.; Álvarez, J.D.; Camacho, J.R.A.; Arceo, R.; Arteaga-Velázquez, J.C.; Arunbabu, K.P.; Rojas, D.A.; et al. Measurement of the Crab Nebula Spectrum Past 100 TeV with HAWC. Astrophys. J. 2019, 881, 134. [Google Scholar] [CrossRef]
- Abeysekara, A.U.; Albert, A.; Alfaro, R.; Camacho, J.R.A.; Arteaga-Velázquez, J.C.; Arunbabu, K.P.; Rojas, D.A.; Solares, H.A.A.; Baghmanyan, V.; Belmont-Moreno, E.; et al. A New Population of Ultra-High-Energy Gamma-Ray Sources Detected by HAWC. 2019. Available online: http://xxx.lanl.gov/abs/1909.08609 (accessed on 12 May 2020).
- Albert, A.; Alfaro, R.; Alvarez, C.; Camacho, J.R.A.; Arteaga-Velázquez, J.C.; Arunbabu, K.P.; Rojas, D.A.; Solares, H.A.A.; Baghmanyan, V.; Belmont-Moreno, E.; et al. Constraints on Lorentz invariance violation from HAWC observations of gamma rays above 100 TeV. Phys. Rev. Lett. 2020, 124, 131101. [Google Scholar] [CrossRef]
- Martínez-Huerta, H.; Marinelli, S.; Linnemann, J.T.; Lundeen, J. Constraints on Lorentz invariance violation using HAWC observations above 100 TeV. In Proceedings of the HAWC Contributions to the 36th International Cosmic Ray Conference (ICRC2019), Madison, WI, USA, 24 July–1 August 2019; Available online: http://xxx.lanl.gov/abs/1908.09614 (accessed on 12 May 2020).
- Linnemann, J.T. Lorentz Invariance Violation Limits from HAWC. In Proceedings of the 8th Meeting on CPT and Lorentz Symmetry (CPT’19), Bloomington, IN, USA, 12–16 May 2019. [Google Scholar]
- Abreu, P.; Albert, A.; Alfaro, R.; Alvarez, C.; Arceo, R.; Assis, P.; Barao, F.; Bazo, J.; Beacom, J.F.; Bellido, J.; et al. The Southern Wide-Field Gamma-Ray Observatory (SWGO): A Next-Generation Ground-Based Survey Instrument for VHE Gamma-Ray Astronomy. arXiv 2019, arXiv:1907.07737. [Google Scholar]
- Albert, A.; Alfaro, R.; Ashkar, H.; Alvarez, C.; Álvarez, J.; Arteaga-Velázquez, J.C.; Solares, H.A.A.; Arceo, R.; Bellido, J.A.; BenZvi, S.; et al. Science Case for a Wide Field-of-View Very-High-Energy Gamma-Ray Observatory in the Southern Hemisphere. arXiv 2019, arXiv:1902.08429. [Google Scholar]
- Cologna, G.; Chakraborty, N.; Jacholkowska, A.; Lorentz, M.; Mohamed, M.; Perennes, C.; Romoli, C.; Wagner, S.J.; Wierzcholska, A.; Dorner, D.; et al. The Exceptional Flare of Mrk 501 in 2014: Combined Observations with H.E.S.S. and FACT. AIP Conf. Proc. 2017, 1792, 050019. [Google Scholar] [CrossRef]
- Albert, J.; Aliu, E.; Anderhub, H.; Antonelli, L.A.; Antoranz, P.; Backes, M.; Baixeras, C.; Barrio, J.A.; Bartko, H.; Bastieri, D.; et al. Probing Quantum Gravity using Photons from a flare of the active galactic nucleus Markarian 501 Observed by the MAGIC telescope. Phys. Lett. 2008, B668, 253–257. [Google Scholar] [CrossRef]
- Astapov, K.; Kirpichnikov, D.; Satunin, P. Photon splitting constraint on Lorentz Invariance Violation from Crab Nebula spectrum. JCAP 2019, 1904, 054. [Google Scholar] [CrossRef]
- Gelmini, G.; Nussinov, S.; Yaguna, C.E. On photon splitting in theories with Lorentz invariance violation. JCAP 2005, 0506, 012. [Google Scholar] [CrossRef][Green Version]
- Vankov, H.; Stanev, T. Lorentz invariance violation and the QED formation length. Phys. Lett. B 2002, 538, 251–256. [Google Scholar] [CrossRef]
- Rubtsov, G.; Satunin, P.; Sibiryakov, S. On calculation of cross sections in Lorentz violating theories. Phys. Rev. D 2012, 86, 085012. [Google Scholar] [CrossRef]
- Pimentel, D.d.M.; Moura-Santos, E. Infrared emission from dust and the spectral features of extragalactic gamma-ray sources. JCAP 2019, 04, 043. [Google Scholar] [CrossRef]
- Aab, A.; Abreu, P.; Aglietta, M.; Ahn, E.J.; Samarai, I.A.; Albuquerque, I.F.M.; Allekotte, I.; Allison, P.; Almela, A.; Castillo, J.A.; et al. The Pierre Auger Observatory Upgrade—Preliminary Design Report. arXiv 2019, arXiv:1604.03637. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martínez-Huerta, H.; Lang, R.G.; de Souza, V. Lorentz Invariance Violation Tests in Astroparticle Physics. Symmetry 2020, 12, 1232. https://doi.org/10.3390/sym12081232
Martínez-Huerta H, Lang RG, de Souza V. Lorentz Invariance Violation Tests in Astroparticle Physics. Symmetry. 2020; 12(8):1232. https://doi.org/10.3390/sym12081232
Chicago/Turabian StyleMartínez-Huerta, Humberto, Rodrigo Guedes Lang, and Vitor de Souza. 2020. "Lorentz Invariance Violation Tests in Astroparticle Physics" Symmetry 12, no. 8: 1232. https://doi.org/10.3390/sym12081232
APA StyleMartínez-Huerta, H., Lang, R. G., & de Souza, V. (2020). Lorentz Invariance Violation Tests in Astroparticle Physics. Symmetry, 12(8), 1232. https://doi.org/10.3390/sym12081232






