5.1. Two-Flavor Superconducting Quark Matter and
Phase Diagram under Compact Star Conditions
As mentioned in the Introduction, the analysis of the phase diagram for strong-interaction matter has important applications in astrophysics. In particular, as we discuss in the next subsection, the region of low temperatures and moderate baryon chemical potentials is very interesting for the description of compact star cores [
2,
3]. Thus, in the framework of nonlocal chiral quark models, it is worth analyzing the features of the phase diagram under compact star conditions, i.e., under the requirements of color and electric charge neutrality together with
equilibrium [
177,
178].
An important issue to be addressed in this context is the presence of color superconducting quark matter [
179]. In fact, a great variety of possible diquark pairing patterns has been explored in the literature, and estimations of the order of magnitude of the corresponding pairing gaps have been obtained [
180,
181]. A detailed discussion on this subject within the local NJL model can be found, e.g., in Ref. [
182]. For phenomenological applications in compact stars, one relevant problem is the determination of the number of active flavors. It turns out that at low temperatures one obtains a sequential melting pattern of the light and strange quark chiral condensates, which is rather insensitive to the details of the four-momentum dependence of the interaction, but crucially dependent on a self-consistent determination of the strange quark mass. Results obtained at the mean field level within the three-flavor local NJL model [
183,
184,
185] indicate that under compact star conditions a two-flavor color superconducting (2SC) phase is favored over the three-flavor color-flavor-locking (CFL) one. Even if the third quark flavor occurs at not too high densities to be realized in compact star interiors, star configurations with CFL quark cores are found to be hydrodynamically unstable [
186]. Studies of neutral 2SC quark matter consider also the presence of a so-called gapless phase [
187,
188], which is found to occur at intermediate temperatures and chemical potentials.
Color neutrality arises basically from the interactions between matter and color gauge fields. In NJL-like effective quark models—which do not include explicit gauge field dynamics—the effect of these interactions is taken into account just through current–current quark couplings. Anyway, it is possible to account for gauge interactions leading to color neutrality through the introduction of effective chemical potentials for each quark of flavor f and color c. In addition, the conditions of charge neutrality and equilibrium require the inclusion of electrons, as well as chemical potentials associated with quark electric charges.
If the system is in chemical equilibrium, it can be seen that quark chemical potentials are in general not independent [
189]. Indeed, taking into account the gauge symmetry of the theory, it is shown that only one color chemical potential is needed in order to ensure color charge neutrality. For a two-flavor quark model, all
can be written in terms of only three independent quantities: the baryonic chemical potential
, a quark electric chemical potential
and a color chemical potential
. Defining as usual
, the corresponding relations read [
190]
Notice that red and green quarks remain indistinguishable, owing to the existence of a residual SU(2) color symmetry.
One also has to take into account the presence of electrons and the condition of
equilibrium. The electrons can be easily included as a gas of free Dirac particles, contributing to the full grand canonical thermodynamic potential with a new term
where
is the electron chemical potential. Here, the electron mass is neglected for simplicity. Finally, the condition of
equilibrium arises from the
decay reaction
. Thus, assuming that antineutrinos escape from the stellar core, quark and electron chemical potentials appear to be related by
Under this condition, all effective fermion chemical potentials can be written in terms of , and .
Now, the conditions of electric and color charge neutrality can be imposed by requiring that the electric charge density
and the diagonal color charge densities
and
vanish simultaneously [
178]. The condition
is trivially satisfied, while for the charge densities
and
one has
where the quark and electron densities
and
can be obtained from the derivation of the full grand canonical potential with respect to
and
, respectively.
In the framework of nonlocal NJL-like models, color superconductivity can be accounted for through the inclusion of an interaction that involves nonlocal quark–quark currents. In the context of the two-flavor model analyzed in
Section 2, this interaction reads [
190]
where
Here, one has , while , with , are Gell–Mann matrices acting on color space.
The effective coupling in Equation (
131) might arise via Fierz rearrangement from some underlying more fundamental interactions and is understood to be used—at the mean field level—in the Hartree approximation. In general, taking into account the interactions between quark–antiquark currents in Equation (
1), the ratio of coupling constants
would be determined by these microscopic couplings. For example, one-gluon exchange interactions, as well as instanton model interactions, lead to
. Since the precise derivation of the effective couplings from QCD is not known, there is a significant theoretical uncertainty in this ratio. We consider here values of
within a phenomenologically reasonable range between 0.5 and 1, taking for the quark–quark current in Equation (
132) the same nonlocal form factor as for the quark–antiquark current, i.e.,
.
To carry out the bosonization of the fermionic theory, in addition to the bosonic fields
and
(
) considered in
Section 2.1.1 one has to introduce diquark fields
, with mean field values
. Owing to color SU(3) symmetry, without loss of generality, it is possible to take
,
, which leaves a residual symmetry under a color SU(2) subgroup. The mean field thermodynamic potential per unit volume can be obtained by making use of the Nambu–Gorkov formalism, as detailed, e.g., in Refs. [
190,
191], and a new “gap equation” arises by requiring the minimization of this effective thermodynamic potential with respect to
. In this way, under color neutrality conditions, for each value of
T and
, one should find the values of
,
,
and
that solve the corresponding gap equations, supplemented by Equations (
129) and (
130).
In what follows, we discuss the numerical results obtained in Ref. [
190] for a two-flavor nlNJL model. The parameterization used in that work is similar to PA (see
Section 2.3), i.e., it involves a Gaussian form factor and does not include the derivative currents in Equation (
1). Moreover, for simplicity the analysis in Ref. [
190] does not take into account the coupling between quarks and the Polyakov loop. In principle, these simplifications should not imply qualitative changes in the phase diagram. Even if the inclusion of the couplings involving the Polyakov loop would increase the transition temperatures at low chemical potentials, the phase diagram structure should not be significantly modified in the low temperature region, which is the most interesting one for compact star applications.
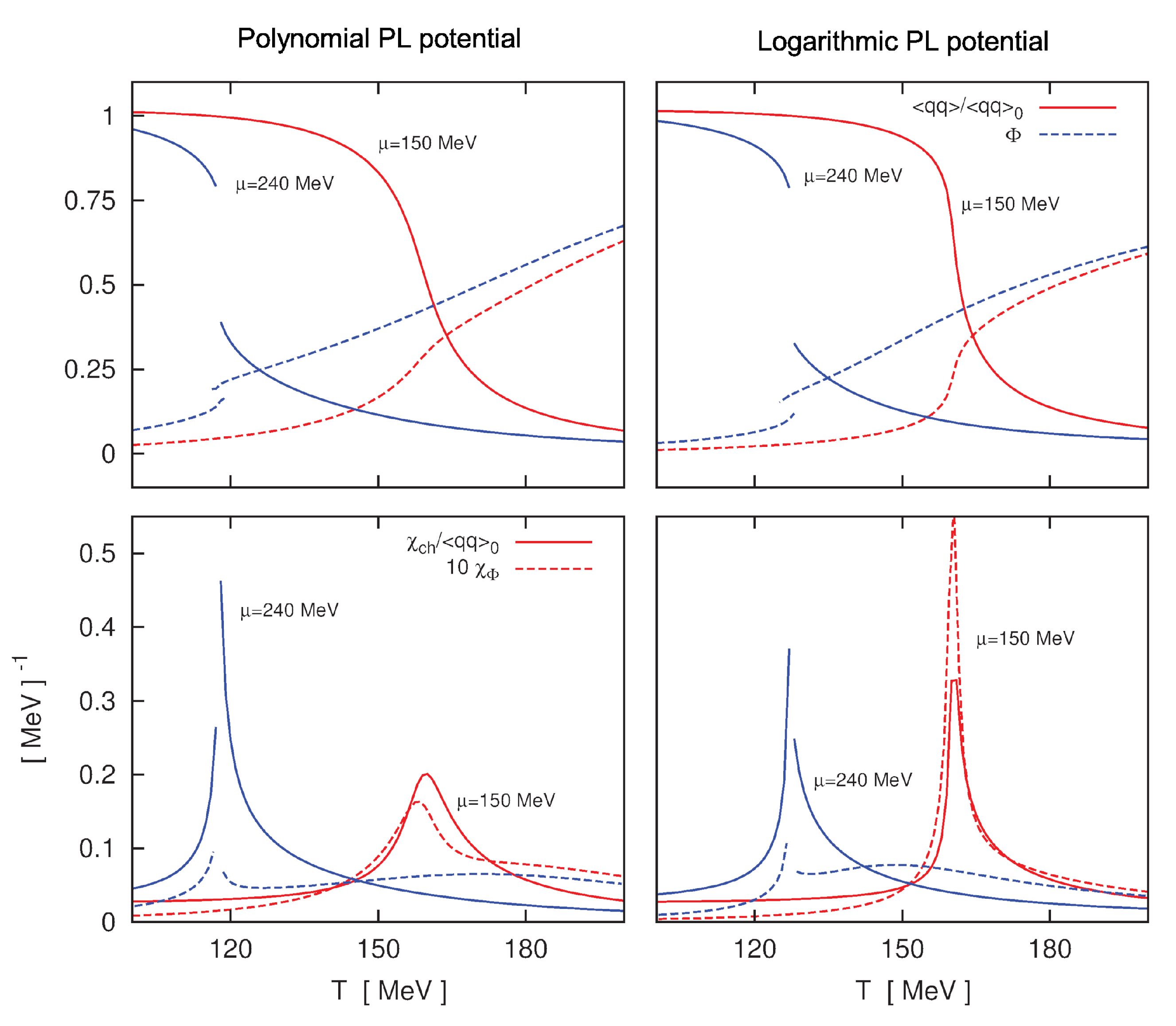
In
Figure 29, we quote the numerical results for the behavior of the mean field values
and
, as well as the effective chemical potentials
and
, as functions of
. The plots correspond to a ratio
. Solid, dashed and dotted lines correspond to
, 40 and 100 MeV respectively. For
, at low chemical potentials the system lies in a chiral symmetry broken phase (CSB), where the quarks acquire large dynamical masses. By increasing the chemical potential one reaches a first order phase transition, in which the chiral symmetry is approximately restored, and a certain fraction of the quark matter undergoes a transition to the 2SC phase, coexisting with the remaining normal quark matter (NQM) phase. The jump of
at the transition is related to that of
, which governs the amount of breakdown of the color symmetry arising from quark pairing. Moreover, it is seen that the chemical potential
(which for
vanishes in the CSB region) also shows a discontinuity across the transition.
The new 2SC-NQM mixed phase is a way in which the constraint of electric neutrality is globally fulfilled: the coexisting phases have opposite electric charges which neutralize each other, at a common equilibrium pressure. In its simplest realization, this mixed phase is treated within an approximation in which Coulomb and surface energies are neglected [
192]. For color superconducting quark matter, this realization of charge neutrality has been considered, e.g., in Refs. [
188,
193] within the NJL model and an instantaneous nonlocal quark model, respectively. On the other hand, notice that color neutrality has been imposed as a local constraint [
194,
195]. This is based on the fact that the color Debye screening length is expected to be short and comparable to the inter-particle distance in the regime of interest. As a consequence, the color chemical potential
turns out to be different in the two components of the mixed phase.
When the temperature is increased up to
MeV, the transition to a mixed phase is no longer favored and the system goes into a pure 2SC phase. As can be seen from the dashed curves in
Figure 29, for
MeV this still shows up as a first order phase transition. For even larger temperatures, it is seen that the 2SC phase is no longer present, and the system undergoes a transition from the CSB phase to a normal quark matter (NQM) phase, in which the chiral symmetry is approximately restored and there is no color superconductivity. For
MeV this transition occurs as a smooth crossover, as shown by the dotted lines in
Figure 29. The full phase diagram for
is displayed in the central panel of
Figure 30. If one moves along the first order transition line from
towards higher temperatures, at
MeV, a triple point (3P) is reached. At this point, the CSB and 2SC phases coexist with a third NQM phase. Finally, if
T is still increased, one reaches a critical end point (CEP) where the first order transition from the CSB to the NQM phase becomes a smooth crossover. For comparison, in
Figure 30, the phase diagrams for
and
are also shown.
Another feature to be discussed is the presence of the so-called gapless 2SC (g2SC) phases. As shown in
Figure 30, g2SC phases are favored in a narrow band close to the 2SC–NQM phase border. In this region, in addition to the two gapless modes corresponding to the unpaired blue quarks, the presence of flavor asymmetric chemical potentials
gives rise to another two gapless fermionic quasiparticles [
187]. Although the corresponding dispersion relations cannot be derived analytically owing to the nonlocality of the interactions, the border of the g2SC region can be found numerically. This is done by determining whether for some value of the quark momentum
the imaginary part of some of the poles of the Euclidean quark propagator vanish in the complex
plane. Although for the cases shown in the figure the g2SC region is given by a narrow band, it appears to be considerable enlarged depending on the model parameterization [
190].
The above phase diagrams can be compared with those obtained for isospin symmetric quark matter. In general, it is seen that the 2SC region becomes reduced when one imposes color and electric charge neutrality conditions. This is what one would expect, since the condition of electric charge neutrality leads in general to unequal
u and
d quark densities, disfavoring the
u–
d pairing. In any case, the effect is found to be relatively small, and the positions of triple points and critical end points, as well as the shapes of critical lines, remain approximately unchanged [
190]. Qualitatively similar results for isospin symmetric quark matter are obtained in the context of a chiral two-flavor quark–meson–diquark model in Ref. [
196].
5.2. Astrophysical Applications
After having analyzed the thermodynamic features of quark matter, it is natural to investigate if such a state can exist in the cores of cold compact stars, where particles appear to be compressed up to densities several times larger than that of nuclear matter ( fm). Unfortunately, a consistent relativistic approach to the quark–hadron phase transition, in which hadrons are treated as bound states of quarks, has not been developed up to now. In this situation, hadronic models, as, e.g., the Walecka model or the relativistic Dirac–Brueckner–Hartree–Fock (DBHF) approach, have been proposed for the description of the hadronic phase, and quark models have been considered in order to account for the quark matter phase. In particular, several works have employed nonlocal NJL-like schemes to provide an effective theoretical description of quark matter states inside compact stellar cores.
From the observational side, early measurements of the pulsar J0751+1807 and other neutron stars (NS) in X-ray binaries have indicated the existence of large mass compact stars. This has been confirmed by the further observation of the binary pulsars PSR J1614-2230, PSR J0348+0423, PSR J2215+5135 and PSR J0740+6620, with masses of the order of
[
197,
198,
199,
200,
201,
202]. The evidence of compact objects of such a large mass can be used as a test for the viability of hadronic and/or quark matter equations of state (EoS) arising from theoretical models [
203]. Given the EoS of a neutron star (i.e., the functional relation between pressure and energy density), the corresponding mass vs. radius relation can be obtained through the Tolman–Oppenheimer–Volkoff (TOV) equations of hydrodynamic stability for self-gravitating matter. In general, it is found that a rather stiff EoS is required in order to satisfy observational constraints for large mass neutron stars.
In the context of covariant nonlocal NJL models (instantaneous nlNJL models have also been analyzed, see [
204]), the study of a possible quark matter phase in the core of compacts stars was first addressed [
205], considering a two-phase description of the NS interior. In this “hybrid star” scheme, the nuclear matter phase is treated within the relativistic DBHF approach [
206] and the transition to quark matter is obtained through a Maxwell construction. The two-flavor nlNJL model considered in Ref. [
205] includes a diquark coupling of the form proposed in Equation (
131), as well as a current–current vector coupling in the
channel, as that in Equation (
66). The presence of a nonvanishing diquark condensate reduces the critical low-temperature transition density (allowing for a quark matter phase in the NS core), whereas the nonzero mean field
arising from the vector coupling has the effect of stiffening the EoS. This leads to an increase of the maximum accessible NS masses up to a magnitude of about
. The model parameters are similar to those considered in
Section 5.1 for the study of phase diagrams under compact star conditions, while the proposed additional interaction in the vector channel is relatively weak, and does not affect the qualitative features of the phase transitions [
205]. The numerical results for this model are found to be in agreement with observational constraints for a given range of the model parameters. Moreover, the corresponding isospin symmetric equations of state are shown to be consistent with flow data analyses from heavy ion collisions.
In Refs. [
207,
208], the existence of quark matter in the core of NSs has been studied using three-flavor nonlocal NJL models, such as those described in
Section 4. Once again, some repulsive current–current interaction in the
channel is included, so as to increase the critical
chemical potential and stiffen the quark matter EoS. In turn, the description of the confined, hadronic phase is carried out by considering the parameterizations GM1 [
209] and NL3 [
210], within the relativistic mean field theory. The phase regions are determined by assuming a smooth Gibbs transition, in which the condition of pressure equilibrium is imposed together with the requirement of global electric charge neutrality and baryon number conservation [
192] in the mixed quark–hadronic phase. The volume fraction of quark matter is given by a parameter
, which ranges continuously from 0 to 1 along the transition. Form the corresponding numerical analysis, it is found that the results are compatible with the existence of extended regions of mixed quark–hadron matter in neutron stars with masses of about
and radii in the canonical range of 12–13 km. This also holds for local versions of NJL-like models. Furthermore, it is seen that pure quark matter can exist in stellar cores for certain parameterizations of the effective quark and hadronic interactions. These works have been complemented by the study of the thermal evolution of NSs, obtained from balance and transport equations under the assumption of spherical symmetry [
211]. It is found that high-mass NSs may contain a fraction of 35–40% of deconfined quark-hybrid matter in their cores, while, for stars with canonical masses of around
(for which cooling curves show a good agreement with experimental data), a pure hadronic composition is predicted. In this same theoretical context, the possible existence of a crystalline quark–hadron mixed phase and its effects on neutrino emissivity are studied in Refs. [
212,
213]. Moreover, in Ref. [
214], the existence of quark matter in the cores of rotating NSs is also considered. On the other hand, in Ref. [
215], it is claimed that if the surface tension at the boundary separating neutral hadronic and neutral quark matter phases is larger than a critical value of about 10 to 40 MeV/fm
[
216,
217,
218], the mixed phase turns out to be disfavored and there should be a sharp interface between both regions (Maxwell construction). If this is the case, the analysis of [
215] concludes that large mass hybrid stars would not be allowed within the three-flavor nlNJL approach for quark matter. Similar results are found for the three-flavor local NJL model.
Turning back to astrophysical observations, in the past few years, important new constraints for the description of compact stars have come out from the direct detection of gravitational waves emitted from the binary NS merger GW170817 [
219]. In particular, the analysis of GW170817 data leads to an upper limit for the tidal deformability—which measures the NS deformation due to the gravitational field of its companion object—and this translates into an upper limit for the NS radius. For a NS mass of 1.4
, it is found that the radius cannot exceed a limit of approximately 13.6 km [
220]. Moreover, it is argued that GW170817 data also imply a general upper limit of about
for the mass of a cold spherical NS [
221]. These constraints have been taken into account for the analysis of EoS arising from hybrid star models that include nlNJL approaches for quark matter [
222,
223,
224,
225,
226,
227,
228].
In Refs. [
223,
225], these new constraints are considered in the context of the above described three-flavor nonlocal NJL models, at both zero and finite temperature. In the finite temperature region, the treatment of quark matter includes the coupling between the quarks and the Polyakov loop, as described in
Section 2.2. In addition, new parameterizations called DD2 and GM1L are used for the description of the purely hadronic phase. They are based on the standard relativistic mean field approach, taking into account medium effects through the inclusion of explicit density dependent meson–baryon couplings [
223,
229]. The hadron–quark transition is treated according to a Maxwell construction in which there is a sharp interface and no mixed phase regions. For the case of cold neutron stars, it is found that the presence of a quark matter core is allowed for a coupling constant ratio
lying in a range from ∼0.33 to 0.38 in order to satisfy observational constraints. This is illustrated in
Figure 31, where we show the curves for NS mass vs. radius obtained in Ref. [
225] after solving the TOV equations, for both GM1L and DD2 hadronic parameterizations. The shaded bands indicate the mass region to be reached in order to fulfill the constraints from the the measurements of PSR J1614-2230 and PSR J0348+0423 masses, while the brown horizontal line indicates the bounds for the radius of a NS star of
arising from the analysis of GW170817 data. The vertical bars on the curves denote the onset of the transition from hadronic to quark matter. On the other hand, from the study of the evolution of proto-neutron stars to neutron stars, it is found that in these models the existence of hybrid stars is allowed only for temperatures not higher than 15–30 MeV. Even in the case in which the model parameters are compatible with a quark matter core at
, this deconfined phase region would disappear for hot neutron or proto-neutron stars. In a more recent work [
228], the analysis is extended (at
) to a three-flavor nlNJL model that includes also a 2SC+s superconducting phase. Depending on the stability criteria for the hadron–quark interface, once again it is found that the existence of neutron stars with a superconducting quark matter core can be compatible with observational data. The study of hybrid star constraints has been also carried out in the context of the quark–meson model for quark matter, considering the DD2 parameterization for the hadronic phase [
230].
Finally, it is worth mentioning that recent works [
226,
227] address, in the context of nonlocal NJL-like models, the so-called “hyperon puzzle”. In principle, the core of a NS should include hyperonic degrees of freedom, which soften the EoS in such a way that NS masses larger than
could become unreachable. A possible solution of this puzzle can arise from hybrid NS models, provided that quark deconfinement occurs at low enough densities so as to prevent the existence of hypernuclear matter in the stellar core. In Refs. [
226,
227], it is seen that such a scenario can be obtained within two-flavor nlNJL models that include color superconductivity and vector current–current couplings, which lead to a stiff EoS [
222]. The hadron–quark phase transition is obtained by a Maxwell construction, considering either fixed or density-dependent couplings. The numerical analysis shows that only in the case of density-dependent couplings an intermediate hypernuclear phase can be found in the cores of hybrid stars. In addition, it is seen that in both situations the onset of deconfinement occurs for compact stars of about 1–
. The observational radius and mass constraints are found to be satisfied, circumventing the hyperon puzzle. There are also alternative ways of dealing with this problem, e.g., by considering the effects of three-body forces that involve hyperons, such as nucleon–nucleon–
interactions. Analyses in this sense are carried out in Refs. [
231,
232].
5.3. Inhomogeneous Phases
In the past few years, it has been claimed that the phase diagram of strong-interaction matter at low temperatures and high densities could include spatially nonuniform phases (for a review, see, e.g., [
233]). Within the framework of the local two-flavor NJL model in the mean field approximation, it has been shown that the critical end point of the first-order chiral restoration transition exactly coincides with the so-called Lifshitz point (LP), where two homogeneous phases and one inhomogeneous phase meet [
234,
235]. This result has been obtained in the chiral limit, where the critical end point becomes a tricritical point (TCP). If vector-like interactions are added, it is seen that the LP remains at the same temperature, while the TCP moves to a lower
T, in such a way that it gets covered by the inhomogeneous phase and disappears from the phase diagram [
236]. In addition, this issue has been studied in the context of a quark–meson model with vacuum fluctuations [
237], where it is found that the LP might coincide or not with the TCP depending on the model parameterization. In fact, in the framework of both the NJL model and quark–meson models, it is found that the TCP tends to becomes covered by the inhomogeneous phase and does not show up in the phase diagram. The analysis of inhomogeneous phase regions in the context of the Polyakov-NJL model [
238] and the three-flavor NJL model [
239], as well as the effects of finite current quark masses [
240], have also been addressed. Moreover, indications of the existence of an inhomogeneous phase have been found in a recent Functional Renormalization Group study of the QCD phase diagram [
241].
In this subsection, we discuss the possible presence of inhomogeneous phases in the context of nlNJL models. We consider in particular the analyses in Refs. [
242,
243], which correspond to a model similar to the one introduced in
Section 2.1. Given the complexity of the problem, the derivative currents
are been included and the chiral limit
is taken.
As discussed in
Section 2.1.1, it is convenient to bosonize the fermionic theory, introducing scalar and pseudoscalar fields that can be expanded around the mean field values
and
. These mean field values are now allowed to be inhomogeneous, hence the explicit dependence on spatial coordinates. The resulting mean field Euclidean action reads
where we define a chiral four-vector
. In this expression, the operator
is given by
where
. The extension to finite temperature
T and quark chemical potential
can be performed by following the usual Matsubara procedure (see, e.g.,
Section 2.2).
The relative locations of the TCP and LP in the
plane can be studied in general through the so-called Ginzburg–Landau (GL) approach, which does not require to specify the explicit form of the inhomogeneity [
234,
244]. Following the analysis proposed in Ref. [
234], the mean field thermodynamic potential can be expanded around the symmetric ground state in powers of the order parameters and their spatial gradients. Up to sixth order in this double expansion, the GL functional has the general form [
245]
where
,
, etc. By looking at this functional, it is seen that for
the system is in the usual homogeneous phase. Now, if in addition one has
, the system undergoes a first-order chiral restoration transition when
(
for
,
for
), which defines a first-order transition line in the
plane. This line ends at the tricritical point, where also
is satisfied. Thus, the position of the TCP can be determined by solving the set of equations
On the other hand, for
, inhomogeneous solutions are favored. Hence, the Lifshitz point (i.e., the point where the onset of the inhomogeneous phase meets the chiral transition line) is obtained from [
233]
This general discussion can also be applied to the NJL model, where it can be shown that the coefficients of the quartic terms are equal to each other, i.e.,
[
234,
242,
245]. Therefore, Equations (
136) and (
137) are simultaneously satisfied, and, as stated above, the TCP and LP are predicted to coincide. This is in general not true in the context of nlNJL models, where the relation becomes modified owing to the presence of the nonlocal form factor [
242]. In fact, a numerical analysis carried out in Ref. [
242] shows that for various phenomenologically acceptable parameterizations the TCP is located at a higher temperature and a lower chemical potential in comparison with the LP. As a consequence, it is seen that nlNJL models favor a scenario in which the TCP
is not covered by the inhomogeneous phase.
Let us investigate, in the framework of nlNJL models, the possible shape of the inhomogeneous phase regions. In principle, a full analysis would require considering general spatial-dependent condensates, looking for the configurations that minimize the mean field thermodynamic potential at each value of the temperature and chemical potential. Since for an arbitrary three-dimensional configuration this turns out to be a very difficult task, even in the case of local models, it is customary to consider one-dimensional modulations, expecting that the qualitative features of the inhomogeneous phases will not be significantly affected by the specific form of the spatial dependence carried by the condensates [
233]. It is worth noticing that, as stated in Ref. [
235], the theoretical problem of finding inhomogeneous phases with a lower dimensional modulation can be reduced to a problem in a lower dimensional theory. Thus, the results from analytically solvable 1 + 1 dimensional chiral models [
246,
247,
248,
249,
250] can be used to study the crystalline phase structure in 3 + 1 dimensions. Here, due to the additional difficulties introduced by the presence of nonlocal quark currents, we consider a simple one-dimensional configuration, namely the so-called dual chiral density wave (DCDW) [
251], in which the chiral condensate rotates along the chiral circle, carrying a constant three-momentum
. The spatial dependence of the quark condensates is given in this case by
for both
and
d quark flavors. This behavior of the chiral condensates can be obtained by considering an adequate ansatz for the mean field configuration of the chiral four-vector in momentum space [
252].
The values of and can be obtained, as usual, by minimization of the mean field thermodynamic potential . A region in which the absolute minimum is reached for a nonzero Q will correspond to an inhomogeneous phase. As expected, if chiral symmetry is not dynamically broken (), the regularized thermodynamic potential reduces to the free quark piece , which does not depend on Q.
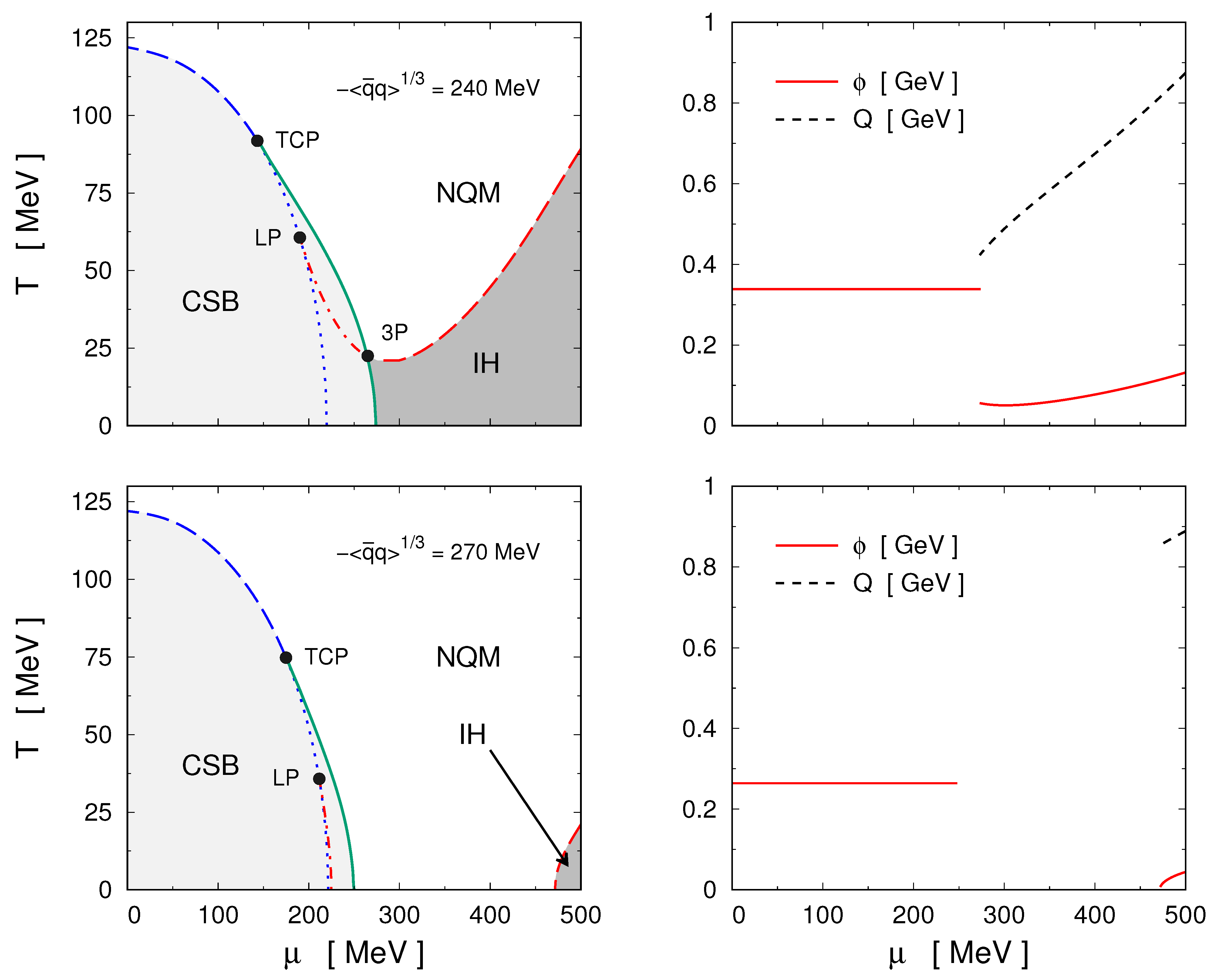
Numerical results for the corresponding phase diagrams within nlNJL models are quoted in Ref. [
243], considering a Gaussian form factor
. Although this analysis does not include the couplings between the quarks and the Polyakov loop, the qualitative features of the phase diagram should not be significantly affected, since one is mostly interested in the low temperature region. In
Figure 32, we quote the results for two parameterizations, which correspond to a pion decay constant
MeV (we recall that the chiral limit is taken) and quark condensate values
and 270 MeV, respectively, at zero
T and
. The various regions of the phase diagram, as well as the corresponding transition curves and critical points, are shown in the left panels of
Figure 32. Solid and dashed lines correspond to first- and second-order transitions, respectively.
Let us analyze in detail the phase diagram in the top left panel, which corresponds to MeV. For low chemical potentials, at temperatures below ∼120 MeV, the system lies in an homogeneous chiral symmetry broken (CSB) phase (notice that the corresponding critical temperature should be higher if couplings with the Polyakov loop are included). Taking a fixed temperature of, e.g., 100 MeV, by increasing the chemical potential one finds at some critical value ( MeV), a second-order phase transition to an homogeneous normal quark matter (NQM) phase in which chiral symmetry is restored. If the temperature is lowered, the second-order transition curve ends at a tricritical point, beyond which it becomes a first-order transition line. Now, by following this line, at a temperature MeV, one arrives at a triple point. For , at a critical chemical potential, the system undergoes a first-order transition from the CSB phase into an inhomogeneous (IH) phase, in which and the chiral symmetry is found to be only approximately restored. On the other hand, if one starts with a system in the IH phase and increases the temperature at constant chemical potential, at some critical value of T one arrives at a second-order phase transition into the NQM phase. As shown in the figure, the corresponding second-order transition line continues beyond the triple point with a dash-dotted line inside the CSB area. The latter is the boundary of a region in which the thermodynamic potential has a local minimum that corresponds to an (unstable) IH phase. Finally, the dotted line in the phase diagram shows the lower spinodal corresponding to the homogeneous chiral restoration transition.
The previously described first-order transition from the CSB to the IH phase is illustrated in
Figure 33 [
243]. The top and bottom panels show contour plots of the mean field thermodynamic potential at zero temperature for
and
MeV, respectively, which correspond to both sides of the transition point
MeV. The plots show the transition from an absolute minimum at
MeV,
, to another one in which
reduces to about 50 MeV, while the chiral condensates get spatial dependences as those given by Equation (
138), with
MeV. These features are also shown in the top right panel of
Figure 32, where the curves for
and
Q at
as functions of the chemical potential are quoted. Notice that on the CSB side (
Figure 33, top) there also exists a local minimum at
MeV,
MeV).
If the dimensionless product
is decreased, the absolute value of the condensate
gets increased, and the onset of the inhomogeneous phase is pushed up to larger values of the chemical potential, leaving a region of homogeneous NQM phase even at
[
243]. This is shown in the bottom left panel of
Figure 32, where we quote the phase diagram for a parameterization leading to
MeV
at zero
T and
. In this case, it is seen that the onset of the IH phase (this region is sometimes called a “continent”) occurs at a chemical potential
of the order of 500 MeV. The discontinuity of
Q at this transition for
becomes increased, as it is shown in the bottom right panel of
Figure 32.
It is worth pointing out that for the considered nlNJL models the would-be Lifshitz point appears to be hidden inside the CSB phase region [
243]. Instead, a triple point can be found if the CSB and inhomogeneous phases meet. It is also worth mentioning that the second-order phase transition curves, as well as both the TCP and would-be LP, can be calculated for these models through a quite precise semianalytical approach [
58,
242]. In addition, it is interesting to notice that, according to the analyses in Refs. [
233,
237,
253], for both the NJL and quark–meson models, some parameterizations lead to phase diagrams that include IH “continents” which extend to arbitrarily high chemical potentials. In fact, it is a matter of discussion whether the emergence of these continents is just a regularization artifact. In nonlocal models, the ultraviolet convergence of loop integrals follows from the behavior of form factors, which effectively embrace the underlying QCD interactions (indeed, as discussed in previous sections, the form factors can be fitted from lattice QCD calculations for the effective quark propagators [
32,
154,
159]). The fact that various quark models including different regularization procedures lead to similar qualitative features of the phase diagram seems to indicate that these features are rather robust. However, it is necessary to mention that in the described works the effects of color superconductivity have not been considered. As discussed in
Section 5.1, the latter are expected to be important at intermediate and large chemical potentials and could have a significant impact on the phase diagram.
5.4. Effects of External Strong Magnetic Fields on
Phase Transitions and Meson Properties
The study of the behavior of strongly-interacting matter under intense external magnetic fields is another subject that has gained significant interest in the past years. Once again, the theoretical analysis requires in general to deal with quantum chromodynamics in nonperturbative regimes, therefore most studies are based either in the predictions of effective models or in the results obtained from lattice QCD calculations. In fact, in view of the theoretical difficulty, most works concentrate on the situations in which one has a uniform and static external magnetic field. Recent reviews on this subject can be found, e.g., in Refs. [
254,
255]. In this subsection, we discuss, in the framework of nonlocal NJL-like models, the features of QCD phase transitions under an intense homogeneous external magnetic field
[
256,
257]. In addition, we show some results on the behavior of
and
meson properties, at both zero and finite temperature [
258,
259].
At zero temperature, the results of low-energy effective models of QCD as well as LQCD calculations indicate that the size of light quark–antiquark condensates should get increased with the magnetic field. Thus, the external field appears to favor the breakdown of chiral symmetry, which is usually known as “magnetic catalysis”. On the contrary, close to the chiral restoration temperature, LQCD calculations carried out with realistic quark masses [
260,
261] show that the condensates behave as nonmonotonic functions of
B, and this leads to a decrease in the transition temperature when the magnetic field is increased. This effect is known as “inverse magnetic catalysis” (IMC). In addition, LQCD calculations predict an entanglement between the chiral restoration and deconfinement critical temperatures [
260]. The observation of IMC has become a challenge for effective models. Indeed, most naive effective approaches to low energy QCD predict that the chiral transition temperature should grow with
B, i.e., they do not find IMC. Interestingly, the corresponding studies carried out in the context of nlNJL models show that the latter are able to describe, at the mean field level, not only the IMC effect but also the entanglement between chiral restoration and deconfinement transition temperatures. Moreover, it is found that the behavior of the mass and decay constant of the
meson as functions of the external magnetic field are also in agreement with LQCD results [
258].
Here, we concentrate on the two-flavor nlPNJL model introduced in
Section 2, considering a parameterization of the type of PA, in which quark–antiquark derivative currents are not included. In fact, the general picture is expected to be similar for parameterizations in which such a coupling is also taken into account. To account for the interaction with the magnetic field, one can proceed as described in previous sections for the case of axial vector gauge fields. As usual, a coupling between the fermions and the external electromagnetic gauge field
is obtained by introducing a covariant derivative in the kinetic term in Equation (
1), i.e., by changing
where
, with
,
, is the electromagnetic quark charge operator. In addition, as discussed in
Section 2.1.3, gauge symmetry requires a further change in the nonlocal currents
and
in Equation (
1), namely
and the corresponding change for
[
32]. The function
is given by
where
s runs over a path connecting
x with
y. As is usually done, we take it to be a straight line. As stated, we consider the case of a constant and homogenous magnetic field, which, without loss of generality, can be taken to be orientated along the 3-axis. For definiteness, the analysis can be carried out using the Landau gauge, in which one has
.
As discussed in previous sections, it is convenient to carry out a bosonization of the fermionic theory, introducing scalar and pseudoscalar meson fields and integrating out the fermions. Next, within the mean field approximation, we assume that the scalar field
has a nontrivial translational invariant mean field value
, while the mean field values of pseudoscalar fields
are zero. It should be stressed at this point that the assumption stating that
is independent of
x does not imply that the resulting quark propagator will be translational invariant. In fact, as discussed below, one can show that this invariance is broken by the appearance of the so-called Schwinger phase. Our assumption just states that the deviations from translational invariance driven by the magnetic field are not affected by the dynamics of the theory. In this way, the mean field bosonized action can be written as
where
with
Here, the function
is the nonlocal form factor in the quark currents defined in Equation (
1). Notice that, contrary to the
case, in the presence of the magnetic field, the charged particles cannot be in states of definite momentum; hence, it is not adequate to transform the action to momentum space. Instead, to deal with the operators
, it is convenient to introduce Ritus transforms
, defined by
where
and
are Ritus functions [
262]. Here,
,
k being an integer quantum number that labels the so-called Landau energy levels. Using the properties of Ritus functions, after some calculation, it can be shown that the operators
are diagonal in this basis. One obtains [
256,
257]
where
with
In these equations, the definitions , , , , , , and are used. The function stands for the Fourier transform of , while are Laguerre polynomials, with the usual convention .
Using the fact that
is diagonal in Ritus space, the corresponding contribution to the mean field action can be readily calculated. One obtains
where
for
, and
is defined by
By regarding at these equations [compare with Equation (
10)], it is seen that the functions
play the role of constituent quark masses in the presence of the external magnetic field.
As done in
Section 2.2, the analysis can be extended to a system at finite temperature using the Matsubara formalism, and a coupling of fermions to the Polyakov loop can be included to account for confinement effects. In what follows, we present the results corresponding to the polynomial PL potential quoted in Equation (
32) [
21]. The full expression of the corresponding mean field thermodynamic potential can be found in Ref. [
257]. As in the
case, this quantity is divergent and can be regularized using the prescription in which one subtracts a free contribution and adds it in a regularized form. In fact, this “free” contribution corresponds to the mean field potential obtained in absence of the effective four-quark coupling (i.e., setting
), but keeping the interaction with the magnetic field and the PL.
By minimizing the regularized mean field thermodynamic potential one can obtain the values of
and the traced Polyakov loop
as functions of the temperature
T and the magnetic field. Then, the magnetic field dependent quark condensates
,
, can be calculated, as usual, by taking the derivatives with respect to the corresponding current quark masses. To make contact with LQCD results given in Ref. [
261], it is convenient to define the quantities
where
MeV. We also introduce the definitions
,
and
, which correspond to a subtracted normalized flavor condensate, a normalized flavor average condensate and a subtracted normalized flavor average condensate, respectively.
In what follows, we quote the numerical results obtained for the case of a Gaussian form factor, i.e., for some parameterizations similar to PA (see
Section 2.3). For comparison, we consider parameter sets leading to quark–antiquark condensates
, 230 and 220 MeV. The corresponding model parameters can be found, e.g., in Ref. [
257].
The behavior of quark condensates at zero temperature within this nlNJL framework is calculated in Ref. [
256]. The results are shown in
Figure 34, where we include the predictions for
and
as functions of
together with the corresponding LQCD data given in Ref. [
261]. Solid, dashed and dotted curves correspond to
, 230 and 220 MeV, respectively. The growth of the condensates clearly show the effect known as “magnetic catalysis”. It can be seen that the predictions for
are very similar for all parameter sets, while for the difference
there is some dependence on the parameterization. In both cases, the predictions show a good agreement with LQCD results.
Let us now look at the results for a system at finite temperature, which are obtained in Ref. [
257]. In
Figure 35 (left), we show the behavior of the averaged chiral condensate
and the traced Polyakov loop
as functions of the temperature, for three representative values of the external magnetic field, namely
, 0.6 and 1 GeV
. The curves correspond to a quark condensate
MeV. Given a value of
B, it is seen from the figure that chiral restoration and deconfinement transitions proceed as smooth crossovers occurring at approximately the same critical temperature
(chiral restoration and deconfinement critical temperatures are defined here from the peaks in the derivatives
and
, respectively). For
,
is found to be approximately equal to 180 MeV, with a variation not larger than a few percent within the above considered parameterization range. This temperature compares well with the value
MeV obtained from
LQCD calculations [
96]. It is worth recalling that in absence of the interaction with the Polyakov loop the value of
is found to drop down to about 130 MeV [
256].
It is interesting to discuss the effect of the magnetic field on the phase transition features. On one hand, in
Figure 35 (left), it is seen that the splitting between the chiral restoration and deconfinement critical temperatures remains very small even for nonzero
B. On the other hand, the curves for the normalized flavor average condensate clearly show the inverse magnetic catalysis effect. Indeed, contrary to what happens, e.g., in the local NJL model [
254,
255] or in the quark–meson model [
263], within the nlNJL approach the chiral restoration critical temperature becomes lower as the external magnetic field is increased. This is related with the fact that the condensates do not show in general a monotonic increase with
B for a fixed value of the temperature. The situation is illustrated in the right panel of
Figure 35, where we show the behavior of the averaged difference
as a function of
, for
and for values of the temperature in the critical region. While the value of
shows a monotonic growth with the external magnetic field, it is seen that when the temperatures get closer to critical values
the curves show a maximum and then start to decrease for increasing
B. This is a typical behavior associated to IMC and nicely agrees with the results obtained from lattice QCD (see, e.g., Figure 2 of [
261]).
In
Figure 36, we show the results given in Ref. [
257] for the normalized chiral restoration critical temperature,
, as a function of
. The curves correspond to the above mentioned nlNJL model parameterizations. For comparison, LQCD results quoted in Ref. [
261] are indicated by the gray band. In the figure, it is clearly seen that the IMC effect is sizeable and fully compatible with LQCD results for phenomenologically adequate values of the chiral condensate. It is also worth mentioning that some effective approaches to low energy QCD are able to obtain IMC by assuming some explicit dependence of the effective coupling parameters on
B and/or
T [
264,
265] or by considering the effect of anomalous magnetic moments in the quark energy dispersion relations [
266]. In turn, it is seen that within nlNJL models one gets IMC in a fully natural way. This can be understood by noticing that for a given Landau level the associated nonlocal form factor carries a dependence on the external magnetic field, which arises from the convolution in Equation (
148).
In what follows, we quote some results concerning the properties of the
meson in the presence of the external magnetic field. At zero temperature, the theoretical expression for the
mass can be obtained by expanding the corresponding bosonic action in powers of the fluctuations
. In momentum space, the corresponding quadratic piece of the bosonized action can be written as
where the polarization function
is given by a quark loop integral that involves the external field
B. Its explicit form can be found in Refs. [
258,
259]. Choosing the frame in which the pion is at rest, its mass can be obtained as a solution of the equation
As shown in Ref. [
267], a relevant feature induced by the presence of the external magnetic field is the fact that the
dispersion relation turns out to be anisotropic, implying that the movement along the direction perpendicular to the magnetic field is characterized by a directional refraction index
which is in general different from one. To normalize the
field, one can expand the action in Equation (
152) around the pion pole (
,
) up to first order in momentum squared. Following [
259], one can define
renormalizing the pion field according to
. Thus, around the pion pole, one has
where
The behavior of the pion mass
predicted by the nlNJL approach is shown in
Figure 37 [
258]. The results, normalized to the empirical
mass value at
, correspond to the parameter set leading to
MeV. It is found that the
mass decreases when the magnetic field gets increased, reaching a value of about 65% of
at
GeV
, which corresponds to a magnetic field of about
G. The figure also includes a gray band that corresponds to lattice QCD results given in Ref. [
268]. The latter have been obtained from a continuum extrapolation of lattice spacing, considering a relatively large current quark mass for which
MeV. For comparison, we also quote in the figure the results obtained within the nlNJL model by shifting
to 56.3 MeV, which leads to this enhanced pion mass. In general, it can be seen that nlNJL model predictions—for which no ad-hoc adjustments or extra parameters have been required—turn out to be in good agreement with LQCD calculations. It is also worth mentioning that the curves in
Figure 37 remain practically unchanged when the value of the
condensate used to fix the parameterization is varied within the range from −(220 MeV)
to −(250 MeV)
.
It is also interesting to study the behavior of the
meson “decay constants”. As shown in Ref. [
269], in the presence of an external magnetic field
, the pion-to-vacuum vector and axial vector amplitudes can be in general parameterized in terms of three form factors. Two of them,
and
, in the
limit reduce to the pion decay constant usually denoted by
. The third one,
, is associated to the vector piece of the quark weak current and vanishes for
. Following the notation in Ref. [
270], these form factors can be defined by the relations
where
are the
-to-vacuum amplitudes for vector and axial vector quark currents,
The matrix elements in Equation (
158) can be obtained by introducing couplings between the quark currents and auxiliary vector and axial vector gauge fields, and then taking the corresponding functional derivatives of the effective action. Once again, gauge invariance requires the couplings to these auxiliary gauge fields to be introduced through the covariant derivative and the parallel transport of the fermion fields. The analytic calculations of the form factors require carrying out combined Laguerre–Fourier transformations of the form factors. Explicit expressions can be found in Ref. [
259].
It is interesting to study the relations involving form factors and renormalization constants in the chiral limit,
. As expected, in this limit, one gets
[
259], which implies
according to Equation (
153). In addition, from the calculations in Refs. [
258,
259], it is seen that the Goldberger–Treiman relation
and the Gell–Mann–Oakes–Renner relation
remain valid in the presence of the external magnetic field (subindices 0 indicate that the involved quantities are evaluated in the chiral limit). The above equations are complemented by the relation [
259]
which implies
This result is also found in the framework of the local NJL model in Ref. [
270] and (using a different notation) in Ref. [
267], where it is obtained from a modified partially-conserved-axial-current (PCAC) relation.
In
Figure 38, we show the numerical results obtained within the nlNJL model for various quantities associated with the neutral pion at zero temperature, as functions of
[
259]. Dashed, solid and dotted red lines correspond to quark condensate values
, 230 and 240 MeV, respectively. For comparison, we also include in the figure the numerical results obtained within the local NJL model, quoted in Ref. [
270]. Solid blue lines correspond to a parameterization leading to a constituent quark mass
MeV (for
), while the limits of the gray bands correspond to
MeV (dashed lines) and
MeV (dotted lines). The values of the
quark–antiquark condensates for these parameterizations of the NJL model are
,
and
, respectively. As shown in the figure, in general nlNJL results do not show a large dependence with the model parameterization. On the other hand, in most cases, the dependence with the external field is significantly stronger for the nlNJL model than for the local NJL approach. In the case of the effective coupling constant
, the behavior is found to be opposite for both models. Concerning the axial form factors, for
, one has spacial rotation symmetry and both
and
reduce to the usual pion decay constant
[see Equation (
158)]. As the magnetic field increases,
is enhanced and
is reduced, in the case of both the nlNJL and the local NJL model. The vector form factor
, shown in the bottom left panel, is zero at vanishing external field and shows a monotonic growth with
, with little dependence on the parameterization within the nlNJL model.
Finally, let us discuss the behavior of
and
meson properties in the context of nlNJL models for a system at finite temperature
T. As in the case of the quark condensates, we quote the results for the model parameterization corresponding to
MeV and a polynomial PL potential. In
Figure 39, we show the behavior of the
and
meson masses (top) and the normalized
axial and vector decay form factors (bottom) as functions of the temperature, for three representative values of the external magnetic field, namely
,
GeV
and
GeV
. These results are obtained in Ref. [
259]. It can be seen that for nonzero
B the masses show a similar qualitative behavior with
T as in the
case. The
mass remains approximately constant up to the critical temperature, and
and
masses match above
, as expected from chiral symmetry. For large temperatures, it is seen that the masses steadily increase, the growth being dominated by pure thermal effects. As stated, the IMC effect is observed, i.e.,
decreases for increasing
B. In the case of the form factors, the curves for
and
show sudden drops at the critical temperatures, exhibiting once again a qualitatively similar behavior for zero and nonzero external magnetic field. The curves for
overlap with those corresponding to
and are not displayed in the figure. We recall that, at any temperature,
is zero for vanishing external field.
For completeness, in
Figure 40, we show the behavior of meson properties as functions of
for three representative values of the temperature, namely
, 165 and 180 MeV [
259]. The results for
, same as those previously shown in
Figure 39, are included just for comparison. The curves for
MeV can be understood by looking at the results in
Figure 35, which show that this is the critical temperature that corresponds to
GeV
. Thus, for this temperature, the pion mass and form factors in
Figure 40 are expected to show approximately the same behavior as for
up to
GeV
. Beyond these values, as expected from the results in
Figure 39, one finds an enhancement of the pion mass and a decrease of the axial and vector form factors. On the other hand, it is seen that for
MeV the values of the pion mass and axial form factors are well separated from the
values already at
. This reflects the fact that at
MeV the system is undergoing the chiral restoration transition for vanishing magnetic field.