An Inexact Optimal Hybrid Conjugate Gradient Method for Solving Symmetric Nonlinear Equations
Abstract
:1. Introduction
2. A Class of Optimal Hybrid CG Method
2.1. The First Choice
2.2. The Second Choice
| Algorithm 1: Optimal hybrid CG method (OHCG). |
step 0: Select , and initialize the constants , . Set and choose the positive sequence . step 1: Whenever , stop, if not go to Step 2. step 3: Determine , satisfying
step 4: Compute using (2). step 5: Set and go to Step 1. |
3. Global Convergence
- 1.
- The level set (31) is bounded.
- 2.
- In a neighborhood W of χ, the Jacobian of is bounded and symmetric positive definite, i.e., there exists some such thatand
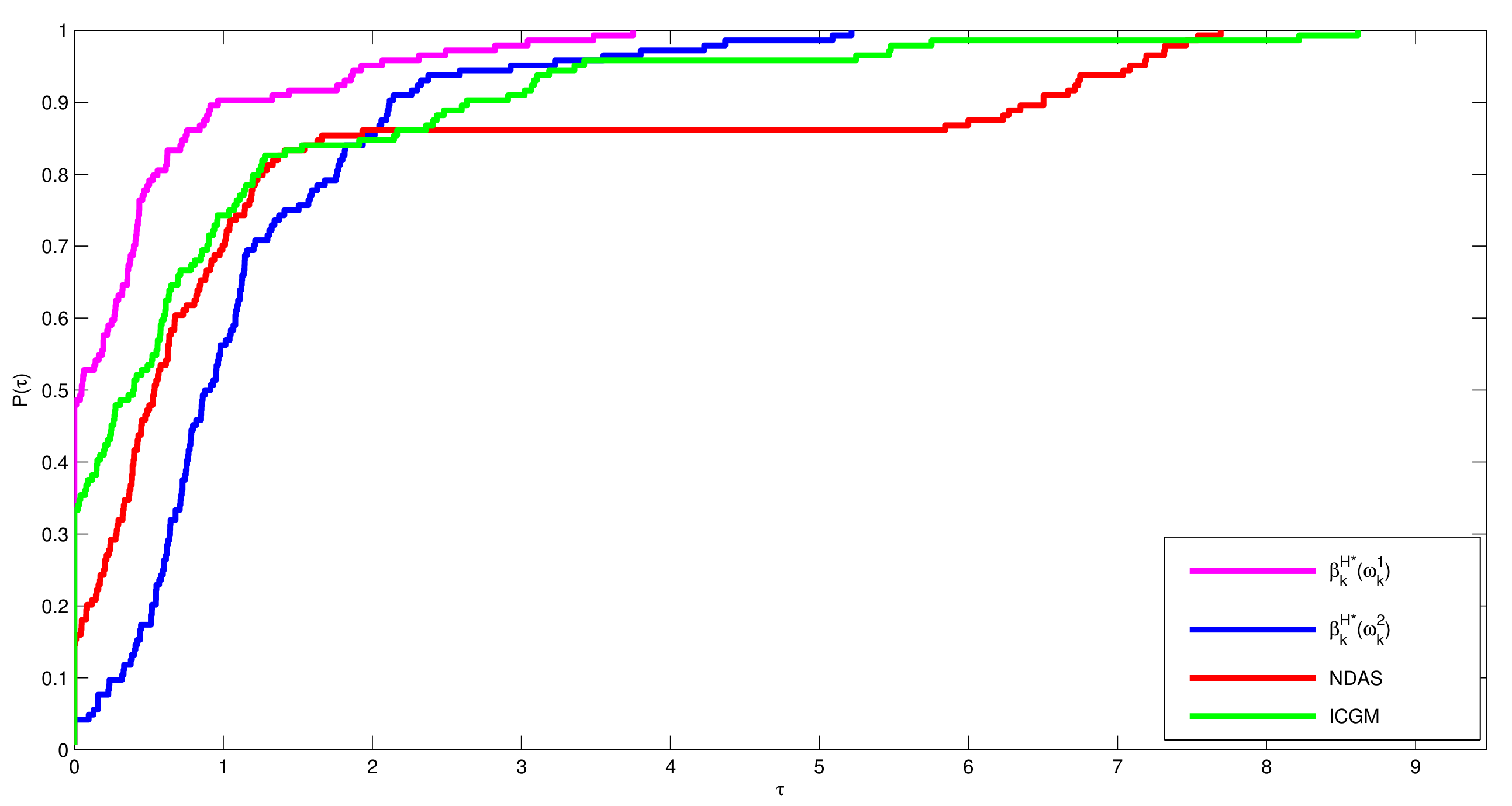
4. Numerical Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Li, D.; Fukushima, M. A Globally and Superlinearly Convergent Gauss-Newton-Based BFGS Method for Symmetric Nonlinear Equations. SIAM J. Numer. Anal. 1999, 37, 152–172. [Google Scholar] [CrossRef]
- Gu, G.Z.; Li, D.H.; Qi, L.; Zhou, S.Z. Descent directions of quasi-Newton methods for symmetric nonlinear equations. SIAM J. Numer. Anal. 2002, 40, 1763–1774. [Google Scholar] [CrossRef] [Green Version]
- Waziri, M.Y.; Sabi’u, J. A derivative-free conjugate gradient method and its global convergence for solving symmetric nonlinear equations. Int. J. Math. Math. Sci. 2015, 2015, 961487. [Google Scholar] [CrossRef] [Green Version]
- Yuan, G.; Lu, X.; Wei, Z. BFGS trust-region method for symmetric nonlinear equations. J. Comput. Appl. Math. 2009, 230, 44–58. [Google Scholar] [CrossRef] [Green Version]
- Zhou, W.; Shen, D. An inexact PRP conjugate gradient method for symmetric nonlinear equations. Num. Funct. Anal. Opt. 2014, 35, 370–388. [Google Scholar] [CrossRef]
- Waziri, M.Y.; Sabi’u, J. An alternative conjugate gradient approach for large-scale symmetric nonlinear equations. J. Math. Comput. Sci. 2016, 6, 855–874. [Google Scholar]
- Li, D.H.; Wang, X.L. A modified Fletcher-Reeves-type derivative-free method for symmetric nonlinear equations. Numer. Algebra Control Optim. 2011, 1, 71–82. [Google Scholar] [CrossRef]
- Polyak, B.T. The conjugate gradientmethod in extreme problems. USSR Comput. Math. Math. Phys. 1969, 9, 94–112. [Google Scholar] [CrossRef]
- Polak, E.; Ribiére, G. Note on the convergence of methods of conjugate directions. RIRO 1969, 3, 35–43. [Google Scholar]
- Babaie-Kafaki, S.; Ghanbari, R. A descent extension of the Polak-Ribiére-Polyak conjugate gradient method. Comput. Math. Appl. 2014, 68, 2005–2011. [Google Scholar] [CrossRef]
- Yu, G.; Guan, L.; Li, G. Global convergence of modified Polak-Ribiére-Polyak conjugate gradient methods with sufficient descent property. J. Ind. Manag. Optim. 2008, 4, 565. [Google Scholar] [CrossRef]
- Sabi’u, J. Enhanced derivative-free conjugate gradient method for solving symmetric nonlinear equations. Int. J. Adv. Appl. Sci. 2016, 5, 50–57. [Google Scholar] [CrossRef]
- Dai, Y.H.; Liao, L.Z. New conjugacy conditions and related nonlinear conjugate gradient methods. Appl. Math. Opt. 2001, 43, 87–101. [Google Scholar] [CrossRef]
- Babaie-Kafaki, S.; Ghanbari, R. The Dai-Liao nonlinear conjugate gradient method with optimal parameter choices. Eur. J. Opt. Res. 2014, 234, 625–630. [Google Scholar] [CrossRef]
- Babaie-Kafaki, S.; Ghanbari, R. An optimal extension of the Polak-Ribiére-Polyak conjugate gradient method. Numer. Func. Anal. Opt. 2017, 38, 1115–1124. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, W.; Li, D.H. Global convergence of a modified Fletcher-Reeves conjugate gradient method with Armijo-type line search. Numer. Math. 2006, 104, 561–572. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, W.; Li, D. Some descent three-term conjugate gradient methods and their global convergence. Optim. Methods Softw. 2007, 22, 697–711. [Google Scholar] [CrossRef]
- Zhou, W.; Chen, X. On the convergence of a derivative-free HS type method for symmetric nonlinear equations. Adv. Model. Opt. 2012, 3, 645–654. [Google Scholar]
- Xiao, Y.; Wu, C.; Wu, S.Y. Norm descent conjugate gradient methods for solving symmetric nonlinear equations. J. Glob. Opt. 2015, 62, 751–762. [Google Scholar] [CrossRef]
- Dauda, M.K.; Mamat, M.; Mohamed, M.A.; Mohamad, F.S.; Waziri, M.Y. Derived Conjugate Gradient Parameter For Solving Symmetric Systems of Nonlinear Equations. Far East J. Math. Sci. FJMS 2017, 102, 2017. [Google Scholar] [CrossRef]
- Liu, J.K.; Feng, Y.M. A norm descent derivative-free algorithm for solving large-scale nonlinear symmetric equations. J. Comput. Appl. Math. 2018, 344, 89–99. [Google Scholar] [CrossRef]
- Abubakar, A.B.; Kumam, P.; Awwal, A.M. An inexact conjugate gradient method for symmetric nonlinear equations. Comput. Math. Methods 2019, 1, e1065. [Google Scholar] [CrossRef] [Green Version]
- Waziri, M.Y.; Yusuf Kufena, M.; Halilu, A.S. Derivative-Free Three-Term Spectral Conjugate Gradient Method for Symmetric Nonlinear Equations. Thai J. Math. 2020, 18, 1417–1431. [Google Scholar]
- Sabi’u, J.; Muangchoo, J.K.; Shah, A.; Abubakar, A.B.; Jolaoso, L.O. A Modified PRP-CG Type Derivative-Free Algorithm with Optimal Choices for Solving Large-Scale Nonlinear Symmetric Equations. Symmetry 2021, 13, 234. [Google Scholar] [CrossRef]
- Dennis, J.E.; More, J.J. A characterization of superlinear convergence and its application to quasi-Newton methods. Math. Comp. 1974, 28, 549–560. [Google Scholar] [CrossRef]
- Yakubu, U.A.; Mamat, M.; Mohamad, M.A.; Rivaie, M.; Sabi’u, J. A recent modification on Dai-Liao conjugate gradient method for solving symmetric nonlinear equations. Far East J. Math. Sci. 2018, 12, 1961–1974. [Google Scholar] [CrossRef]
- Sabi’u, J.; Gadu, A.M. A Projected Hybrid Conjugate Gradient Method for Solving Large-scale System of Nonlinear Equations. Malays. J. Comput. Appl. Math. 2018, 1, 10–20. [Google Scholar]
- Cruz, W.L.; Martínez, J.; Raydan, M. Spectral residual method without gradient information for solving large-scale nonlinear systems of equations. Math. Comput. 2006, 75, 1429–1448. [Google Scholar] [CrossRef] [Green Version]
- Mohammad, H.; Abubakar, A.B. A descent derivative-free algorithm for nonlinear monotone equations with convex constraints. RAIRO Op. Res. 2020, 54, 489–505. [Google Scholar] [CrossRef] [Green Version]
- Dolan, E.D.; Moré, J.J. Benchmarking optimization software with performance profiles. Math. Program. 2002, 91, 201–213. [Google Scholar] [CrossRef]

| Problem 1 | NDAS | ICGM | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DIM | GUESS | ITR | TIME | NORM | ITR | TIME | NORM | ITR | TIME | NORM | ITR | TIME | NORM |
| 50,000 | 4 | 0.051017 | 1.32 | 5 | 0.711194 | 9.38 | 1000 | 5.358113 | 0.000606 | 10 | 0.083581 | 7.98 | |
| 4 | 0.03615 | 1.27 | 6 | 0.127425 | 6.69 | 1000 | 5.769465 | 0.001268 | 12 | 0.08618 | 4.37 | ||
| 5 | 0.064414 | 8.12 | 7 | 0.136223 | 4.81 | 1000 | 6.545712 | 0.001127 | 13 | 0.090501 | 5.89 | ||
| 37 | 0.320713 | 2.01 | 90 | 1.087917 | 2.48 | 51 | 0.313294 | 6.54 | 45 | 0.312344 | 9.66 | ||
| 37 | 0.373899 | 1.33 | 90 | 0.952427 | 2.05 | 51 | 0.385819 | 6.47 | 45 | 0.307783 | 1.04 | ||
| 9 | 0.097553 | 6.76 | 13 | 0.160268 | 7.64 | 1000 | 7.526905 | 0.000645 | 18 | 0.117476 | 3.26 | ||
| 3 | 0.035575 | 4.37 | 4 | 0.1074 | 5.78 | 1000 | 6.622959 | 0.002336 | 8 | 0.069154 | 6.78 | ||
| 7 | 0.073464 | 1.92 | 12 | 0.184662 | 3.25 | 1000 | 6.60593 | 0.000566 | 10 | 0.072791 | 1.17 | ||
| 100,000 | 4 | 0.08817 | 1.86 | 5 | 0.216573 | 1.57 | 1000 | 12.85136 | 0.000858 | 11 | 0.163569 | 3.39 | |
| 4 | 0.112781 | 1.8 | 6 | 0.18873 | 1.31 | 1000 | 12.02928 | 0.001794 | 12 | 0.161687 | 6.18 | ||
| 5 | 0.133655 | 1.15 | 8 | 0.241027 | 1.19 | 1000 | 12.12703 | 0.001593 | 13 | 0.200714 | 8.33 | ||
| 37 | 0.958361 | 2.56 | 90 | 2.439265 | 1.41 | 51 | 0.670645 | 9.21 | 45 | 0.571358 | 1.39 | ||
| 37 | 0.881123 | 2.08 | 90 | 2.389912 | 1.31 | 51 | 0.812228 | 9.16 | 45 | 0.573077 | 1.44 | ||
| 9 | 0.241214 | 9.56 | 13 | 0.329319 | 2.73 | 1000 | 13.23539 | 0.000913 | 18 | 0.230604 | 4.61 | ||
| 3 | 0.080855 | 6.18 | 4 | 0.118452 | 1.32 | 1000 | 12.86233 | 0.003303 | 8 | 0.110558 | 9.59 | ||
| 7 | 0.176245 | 2.71 | 12 | 0.339665 | 1.73 | 1000 | 12.07158 | 0.000801 | 10 | 0.160622 | 1.65 | ||
| Problem 2 | NDAS | ICGM | |||||||||||
| DIM | GUESS | ITR | TIME | NORM | ITR | TIME | NORM | ITR | TIME | NORM | ITR | TIME | NORM |
| 50,000 | 49 | 1.388361 | 9.42 | 73 | 2.309985 | 6.85 | 7 | 0.247055 | NaN | 537 | 10.94105 | 9.91 | |
| 46 | 1.211725 | 9.52 | 63 | 2.034998 | 9.98 | 133 | 3.125014 | 9.48 | 630 | 12.987 | 9.96 | ||
| 68 | 1.560972 | 8.81 | 73 | 2.637633 | 9.47 | 128 | 3.220816 | 9.87 | 543 | 11.74005 | 9.94 | ||
| 129 | 2.932939 | 8.14 | 134 | 3.832334 | 9.47 | 246 | 5.627216 | 9.44 | 373 | 7.827305 | 9.93 | ||
| 117 | 2.406448 | 6.01 | 115 | 3.223662 | 8.55 | 176 | 3.771749 | 3.71 | 681 | 14.5844 | 9.99 | ||
| 72 | 1.532064 | 9.72 | 81 | 2.325501 | 8.45 | 138 | 3.11174 | 9.54 | 620 | 12.9883 | 9.87 | ||
| 137 | 3.046806 | 5.47 | 64 | 2.250733 | 9.24 | 142 | 3.320312 | 9.39 | 175 | 3.640726 | 9.91 | ||
| 153 | 3.155947 | 4.9 | 129 | 4.421972 | 6.39 | 51 | 1.257545 | 9.36 | 490 | 10.21439 | 9.98 | ||
| 100,000 | 56 | 2.134486 | 9.31 | 79 | 6.900653 | 9.86 | 7 | 0.58915 | NaN | 573 | 22.36094 | 9.95 | |
| 75 | 3.026543 | 7.88 | 75 | 6.693699 | 9.03 | 119 | 6.103506 | 9.78 | 653 | 26.02026 | 9.99 | ||
| 68 | 2.695133 | 8.66 | 72 | 6.2076 | 9.2 | 96 | 4.540488 | 9.76 | 376 | 14.5441 | 9.88 | ||
| 134 | 5.237932 | 8.17 | 151 | 8.914932 | 8.62 | 287 | 11.58659 | 9.12 | 622 | 23.51092 | 9.93 | ||
| 127 | 4.708571 | 8.25 | 119 | 6.758494 | 7.34 | 179 | 7.320956 | 5.78 | 645 | 24.98121 | 9.91 | ||
| 85 | 3.38715 | 9.14 | 79 | 3.983438 | 9.18 | 81 | 3.417891 | 9.45 | 501 | 18.89237 | 9.95 | ||
| 170 | 6.837026 | 9.79 | 71 | 3.73959 | 9.81 | 128 | 5.434381 | 9.72 | 505 | 19.19699 | 9.93 | ||
| 138 | 5.192739 | 7.29 | 128 | 6.579588 | 9.15 | 46 | 1.912222 | 6.6 | 487 | 19.58842 | 9.86 |
| Problem 3 | NDAS | ICGM | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DIM | GUESS | ITR | TIME | NORM | ITR | TIME | NORM | ITR | TIME | NORM | ITR | TIME | NORM |
| 50,000 | 7 | 0.130459 | 9.01 | 7 | 0.326768 | 1.05 | 5 | 0.147254 | 9.59 | 6 | 0.161476 | 9.33 | |
| 3 | 0.097567 | 4.49 | 7 | 0.208194 | 5.53 | 3 | 0.100919 | 3.96 | 5 | 0.205028 | 1.46 | ||
| 4 | 0.137949 | 3.04 | 7 | 0.269881 | 1.38 | 8 | 0.304496 | 1.99 | 10 | 0.297645 | 9.95 | ||
| 5 | 0.156842 | 9.3 | 8 | 0.316907 | 2.48 | 9 | 0.36357 | 2.23 | 6 | 0.176784 | 6.58 | ||
| 0 | 0.006896 | 0 | 0 | 0.01035 | 0 | 0 | 0.007833 | 0 | 0 | 0.006028 | 0 | ||
| 7 | 0.271075 | 4.55 | 3 | 0.175715 | 1.79 | 3 | 0.202744 | NaN | 7 | 0.285133 | 4.01 | ||
| 7 | 0.190334 | 9.01 | 7 | 0.296095 | 1.05 | 5 | 0.2407 | 9.59 | 6 | 0.157174 | 9.33 | ||
| 0 | 0.007218 | 0 | 0 | 0.008271 | 0 | 0 | 0.008564 | 0 | 0 | 0.00537 | 0 | ||
| 100,000 | 4 | 0.298726 | 1.8 | 4 | 0.349914 | 3.16 | 7 | 0.595264 | 4.7 | 6 | 0.437588 | 1.72 | |
| 6 | 0.376712 | 4.15 | 7 | 0.739255 | 3.14 | 7 | 0.661026 | 2.1 | 4 | 0.336146 | 2.27 | ||
| 8 | 0.49952 | 2.45 | 7 | 0.64952 | 3.11 | 8 | 0.730984 | 4.59 | 12 | 0.774873 | 8.18 | ||
| 10 | 0.734979 | 2.85 | 13 | 1.327325 | 5.86 | 6 | 0.423914 | 2.68 | 6 | 0.390528 | 4.64 | ||
| 0 | 0.015278 | 0 | 0 | 0.01714 | 0 | 0 | 0.017242 | 0 | 0 | 0.011946 | 0 | ||
| 8 | 0.74008 | 2.32 | 13 | 1.602305 | 1.73 | 2 | 0.396171 | NaN | 7 | 0.606307 | 3.21 | ||
| 4 | 0.267311 | 1.8 | 4 | 0.363102 | 3.16 | 7 | 0.609314 | 4.7 | 6 | 0.393849 | 1.72 | ||
| 0 | 0.015626 | 0 | 0 | 0.017721 | 0 | 0 | 0.017815 | 0 | 0 | 0.015042 | 0 | ||
| Problem 4 | NDAS | ICGM | |||||||||||
| DIM | GUESS | ITR | TIME | NORM | ITR | TIME | NORM | ITR | TIME | NORM | ITR | TIME | NORM |
| 50,000 | 44 | 2.690291 | 8.41 | 43 | 4.617571 | 9.04 | 12 | 1.863923 | NaN | 62 | 4.524161 | 8.63 | |
| 45 | 2.663571 | 9.78 | 44 | 4.521443 | 9.53 | 5 | 3.054371 | NaN | 89 | 7.671063 | 9.14 | ||
| 44 | 2.575053 | 8.38 | 49 | 4.750722 | 7.64 | 3 | 0.230201 | NaN | 6 | 1.01848 | NaN | ||
| 31 | 1.944946 | 6.56 | 36 | 2.844192 | 9.48 | 75 | 5.669829 | 6.84 | 43 | 3.052905 | 8.39 | ||
| 46 | 2.77079 | 7.82 | 40 | 3.092822 | 7.46 | 102 | 6.978015 | 8.05 | 47 | 3.349462 | 8.76 | ||
| 53 | 2.979479 | 5.87 | 56 | 4.566533 | 9.46 | 4 | 0.600135 | NaN | 1000 | 178.8212 | 46.85852 | ||
| 41 | 2.302363 | 8.68 | 46 | 3.301815 | 8.57 | 5 | 0.549722 | NaN | 61 | 4.607346 | 8.1 | ||
| 47 | 2.698441 | 9.37 | 203 | 12.16855 | 7.1 | 4 | 0.327506 | NaN | 1000 | 128.2877 | 3.78474 | ||
| 100,000 | 41 | 4.972517 | 7.93 | 49 | 5.813092 | 7.83 | 8 | 2.774162 | NaN | 63 | 10.42985 | 7.91 | |
| 45 | 5.210847 | 7.98 | 40 | 5.038291 | 4.01 | 5 | 5.590234 | NaN | 70 | 11.08061 | 8.1 | ||
| 45 | 4.763892 | 8.99 | 50 | 6.62348 | 9.66 | 3 | 0.353785 | NaN | 6 | 2.195849 | NaN | ||
| 32 | 3.455663 | 7.19 | 37 | 4.694169 | 9.81 | 50 | 6.988386 | 5.91 | 40 | 6.260133 | 8.2 | ||
| 48 | 5.294363 | 9.67 | 44 | 5.659528 | 7.97 | 123 | 14.07205 | 8.1 | 47 | 6.353586 | 8.95 | ||
| 49 | 5.302793 | 6.83 | 54 | 6.698918 | 8.51 | 4 | 1.395233 | NaN | 234 | 62.21842 | 7.96 | ||
| 43 | 4.615465 | 7.44 | 48 | 5.789132 | 6.57 | 5 | 1.312244 | NaN | 79 | 11.94492 | 9.2 | ||
| 45 | 4.827933 | 7.53 | 202 | 23.19352 | 6.59 | 4 | 0.682058 | NaN | 240 | 36.76278 | 7.83 |
| Problem 5 | NDAS | ICGM | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DIM | GUESS | ITR | TIME | NORM | ITR | TIME | NORM | ITR | TIME | NORM | ITR | TIME | NORM |
| 50,000 | 1 | 0.052829 | 8.57 | 1 | 0.028501 | 8.57 | 1 | 0.039928 | 8.57 | 1 | 0.038071 | 8.57 | |
| 1 | 0.03692 | 9.07 | 1 | 0.029346 | 9.07 | 1 | 0.035869 | 9.07 | 1 | 0.026299 | 9.07 | ||
| 1 | 0.036227 | 9.51 | 1 | 0.038833 | 9.51 | 1 | 0.035661 | 9.51 | 1 | 0.027196 | 9.51 | ||
| 1 | 0.036327 | 9.94 | 1 | 0.039655 | 9.94 | 1 | 0.035812 | 9.94 | 1 | 0.027108 | 9.94 | ||
| 1 | 0.035525 | 9.94 | 1 | 0.043298 | 9.94 | 1 | 0.036387 | 9.94 | 1 | 0.027746 | 9.94 | ||
| 1 | 0.036985 | 1.3 | 1 | 0.042555 | 1.3 | 1 | 0.036066 | 1.3 | 1 | 0.027322 | 1.3 | ||
| 1 | 0.035547 | 8.29 | 1 | 0.042826 | 8.29 | 1 | 0.03719 | 8.29 | 1 | 0.026749 | 8.29 | ||
| 1 | 0.036086 | 4.74 | 1 | 0.057876 | 4.74 | 1 | 0.037694 | 4.74 | 1 | 0.029947 | 4.74 | ||
| 100,000 | 1 | 0.068163 | 3.03 | 1 | 0.128598 | 3.03 | 1 | 0.072784 | 3.03 | 1 | 0.059565 | 3.03 | |
| 1 | 0.063426 | 3.21 | 1 | 0.104958 | 3.21 | 1 | 0.07371 | 3.21 | 1 | 0.067507 | 3.21 | ||
| 1 | 0.070829 | 3.36 | 1 | 0.103859 | 3.36 | 1 | 0.073861 | 3.36 | 1 | 0.056567 | 3.36 | ||
| 1 | 0.072002 | 3.52 | 1 | 0.100046 | 3.52 | 1 | 0.072974 | 3.52 | 1 | 0.055419 | 3.52 | ||
| 1 | 0.071199 | 3.52 | 1 | 0.103975 | 3.52 | 1 | 0.074358 | 3.52 | 1 | 0.050225 | 3.52 | ||
| 1 | 0.070771 | 4.59 | 1 | 0.10815 | 4.59 | 1 | 0.077524 | 4.59 | 1 | 0.05661 | 4.59 | ||
| 1 | 0.07475 | 2.93 | 1 | 0.111332 | 2.93 | 1 | 0.077837 | 2.93 | 1 | 0.054052 | 2.93 | ||
| 1 | 0.074773 | 1.68 | 1 | 0.117776 | 1.68 | 1 | 0.07581 | 1.68 | 1 | 0.050772 | 1.68 | ||
| Problem 6 | NDAS | ICGM | |||||||||||
| DIM | GUESS | ITR | TIME | NORM | ITR | TIME | NORM | ITR | TIME | NORM | ITR | TIME | NORM |
| 50,000 | 3 | 0.062624 | 5.81 | 7 | 0.270178 | 3.31 | 1000 | 8.22562 | 0.056283 | 10 | 0.121959 | 6.44 | |
| 4 | 0.048661 | 9.16 | 7 | 0.200956 | 2.12 | 1000 | 10.06622 | 0.069926 | 11 | 0.111443 | 8.61 | ||
| 5 | 0.067382 | 5.23 | 8 | 0.257818 | 5.23 | 1000 | 9.859871 | 0.071884 | 12 | 0.121548 | 7.02 | ||
| 6 | 0.07856 | 7.36 | 11 | 0.318332 | 1.49 | 6 | 0.061333 | 1.18 | 14 | 0.136175 | 3.66 | ||
| 6 | 0.080187 | 7.36 | 11 | 0.347429 | 1.49 | 6 | 0.070442 | 1.17 | 14 | 0.149883 | 3.66 | ||
| 8 | 0.138834 | 6.23 | 10 | 0.238758 | 2.98 | 1000 | 11.3173 | 0.07266 | 15 | 0.146064 | 4.63 | ||
| 3 | 0.053878 | 5.54 | 5 | 0.137401 | 4.42 | 5 | 0.051718 | 1.07 | 8 | 0.080437 | 3.88 | ||
| 6 | 0.09511 | 7.47 | 10 | 0.24638 | 8.29 | 9 | 0.100924 | 6.67 | 10 | 0.10552 | 1.77 | ||
| 100,000 | 3 | 0.108583 | 7.98 | 7 | 0.470761 | 2.9 | 1000 | 19.14354 | 0.079596 | 10 | 0.22311 | 9.1 | |
| 4 | 0.133273 | 1.06 | 7 | 0.455045 | 3.77 | 1000 | 18.09004 | 0.098893 | 12 | 0.229377 | 3.65 | ||
| 5 | 0.160068 | 3.72 | 8 | 0.513187 | 4.32 | 1000 | 17.21491 | 0.101663 | 12 | 0.242816 | 9.92 | ||
| 7 | 0.22096 | 1.96 | 11 | 0.568055 | 3.09 | 6 | 0.113298 | 1.67 | 14 | 0.271454 | 5.17 | ||
| 7 | 0.250454 | 1.96 | 11 | 0.568372 | 3.09 | 6 | 0.148285 | 1.67 | 14 | 0.284436 | 5.17 | ||
| 8 | 0.329174 | 1.01 | 10 | 0.540962 | 2.59 | 1000 | 19.08673 | 0.102761 | 15 | 0.298349 | 6.56 | ||
| 3 | 0.127818 | 7.87 | 7 | 0.415979 | 2.38 | 5 | 0.096884 | 1.43 | 8 | 0.169584 | 5.47 | ||
| 6 | 0.227238 | 1.08 | 11 | 0.579637 | 1.2 | 9 | 0.215587 | 9.58 | 10 | 0.195059 | 2.5 |
| Problem 7 | NDAS | ICGM | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DIM | GUESS | ITR | TIME | NORM | ITR | TIME | NORM | ITR | TIME | NORM | ITR | TIME | NORM |
| 50,000 | 3 | 0.075366 | 8.32 | 3 | 0.08244 | 8.32 | 10 | 0.142476 | 4.43 | 9 | 0.08795 | 7.07 | |
| 5 | 0.092936 | 7.6 | 6 | 0.142385 | 4.95 | 12 | 0.175039 | 4.6 | 11 | 0.101039 | 5.09 | ||
| 5 | 0.090729 | 4.11 | 6 | 0.155189 | 2.87 | 13 | 0.212816 | 5.58 | 12 | 0.135433 | 5.15 | ||
| 10 | 0.184006 | 7.24 | 10 | 0.231393 | 8.25 | 19 | 0.321698 | 6.65 | 20 | 0.243073 | 8.12 | ||
| 10 | 0.178508 | 7.24 | 10 | 0.236107 | 8.25 | 19 | 0.316433 | 6.65 | 20 | 0.211838 | 8.05 | ||
| 7 | 0.133278 | 8.2 | 9 | 0.208276 | 1.58 | 17 | 0.304249 | 8.33 | 14 | 0.148348 | 4.43 | ||
| 3 | 0.060296 | 7.62 | 4 | 0.108939 | 1.41 | 13 | 0.230127 | 6.01 | 12 | 0.14197 | 6.93 | ||
| 9 | 0.163411 | 4.97 | 19 | 0.4887 | 9.6 | 20 | 0.336258 | 5.31 | 18 | 0.249333 | 6.81 | ||
| 100,000 | 3 | 0.115519 | 1.18 | 3 | 0.15752 | 1.18 | 10 | 0.365394 | 6.26 | 9 | 0.216016 | 9.99 | |
| 5 | 0.186664 | 1.16 | 6 | 0.314727 | 1.03 | 12 | 0.421284 | 6.5 | 11 | 0.245532 | 7.2 | ||
| 5 | 0.183213 | 5.81 | 6 | 0.276542 | 4.06 | 13 | 0.449368 | 7.89 | 12 | 0.241829 | 7.28 | ||
| 10 | 0.363477 | 1.02 | 10 | 0.48296 | 1.17 | 19 | 0.640634 | 9.41 | 21 | 0.535285 | 5.45 | ||
| 10 | 0.360938 | 1.02 | 10 | 0.450866 | 1.17 | 19 | 0.649932 | 9.41 | 21 | 0.519055 | 5.44 | ||
| 7 | 0.264049 | 1.16 | 9 | 0.455213 | 6.79 | 18 | 0.634508 | 4.24 | 14 | 0.31158 | 6.27 | ||
| 4 | 0.147267 | 4.94 | 4 | 0.185584 | 2.66 | 13 | 0.456271 | 8.49 | 12 | 0.275253 | 9.8 | ||
| 9 | 0.319735 | 7.03 | 15 | 0.697124 | 8.88 | 20 | 0.677796 | 7.71 | 18 | 0.477871 | 9.63 | ||
| Problem 8 | NDAS | ICGM | |||||||||||
| DIM | GUESS | ITR | TIME | NORM | ITR | TIME | NORM | ITR | TIME | NORM | ITR | TIME | NORM |
| 50,000 | 1 | 0.033714 | 8.57 | 1 | 0.055597 | 8.57 | 1 | 0.029796 | 8.57 | 1 | 0.028779 | 8.57 | |
| 1 | 0.028881 | 9.07 | 1 | 0.048449 | 9.07 | 1 | 0.028738 | 9.07 | 1 | 0.027902 | 9.07 | ||
| 1 | 0.03261 | 9.51 | 1 | 0.047632 | 9.51 | 1 | 0.02972 | 9.51 | 1 | 0.024409 | 9.51 | ||
| 1 | 0.035589 | 9.94 | 1 | 0.045574 | 9.94 | 1 | 0.032915 | 9.94 | 1 | 0.029429 | 9.94 | ||
| 1 | 0.035606 | 9.94 | 1 | 0.046116 | 9.94 | 1 | 0.035012 | 9.94 | 1 | 0.031084 | 9.94 | ||
| 1 | 0.03751 | 1.3 | 1 | 0.046566 | 1.3 | 1 | 0.034991 | 1.3 | 1 | 0.028503 | 1.3 | ||
| 1 | 0.037605 | 8.29 | 1 | 0.045682 | 8.29 | 1 | 0.035925 | 8.29 | 1 | 0.027888 | 8.29 | ||
| 1 | 0.03789 | 4.74 | 1 | 0.050778 | 4.74 | 1 | 0.036782 | 4.74 | 1 | 0.02298 | 4.74 | ||
| 100,000 | 1 | 0.076523 | 3.03 | 1 | 0.110874 | 3.03 | 1 | 0.076747 | 3.03 | 1 | 0.04965 | 3.03 | |
| 1 | 0.075618 | 3.21 | 1 | 0.098932 | 3.21 | 1 | 0.071353 | 3.21 | 1 | 0.046196 | 3.21 | ||
| 1 | 0.073683 | 3.36 | 1 | 0.089028 | 3.36 | 1 | 0.071895 | 3.36 | 1 | 0.056912 | 3.36 | ||
| 1 | 0.075373 | 3.52 | 1 | 0.097382 | 3.52 | 1 | 0.07301 | 3.52 | 1 | 0.063382 | 3.52 | ||
| 1 | 0.075046 | 3.52 | 1 | 0.107567 | 3.52 | 1 | 0.072606 | 3.52 | 1 | 0.055507 | 3.52 | ||
| 1 | 0.074018 | 4.59 | 1 | 0.092188 | 4.59 | 1 | 0.072067 | 4.59 | 1 | 0.057577 | 4.59 | ||
| 1 | 0.076113 | 2.93 | 1 | 0.097692 | 2.93 | 1 | 0.071651 | 2.93 | 1 | 0.055431 | 2.93 | ||
| 1 | 0.076265 | 1.68 | 1 | 0.108356 | 1.68 | 1 | 0.072278 | 1.68 | 1 | 0.049841 | 1.68 |
| Problem 9 | NDAS | ICGM | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DIM | GUESS | ITR | TIME | NORM | ITR | TIME | NORM | ITR | TIME | NORM | ITR | TIME | NORM |
| 50,000 | 5 | 0.066557 | 7.42 | 7 | 0.189046 | 2.75 | 7 | 0.119231 | 8.69 | 11 | 0.126884 | 2.96 | |
| 5 | 0.06624 | 5.83 | 9 | 0.224013 | 8.41 | 8 | 0.151618 | 1.25 | 11 | 0.151836 | 2.69 | ||
| 5 | 0.083632 | 1.92 | 7 | 0.177367 | 1.33 | 7 | 0.138794 | 8.75 | 10 | 0.128026 | 8.97 | ||
| 9 | 0.145705 | 3.32 | 11 | 0.314592 | 5.97 | 14 | 0.26809 | 1.99 | 18 | 0.21681 | 4.32 | ||
| 9 | 0.166716 | 2.08 | 11 | 0.302915 | 3.68 | 12 | 0.223362 | 4.23 | 18 | 0.198065 | 4.32 | ||
| 6 | 0.119915 | 8.96 | 9 | 0.261753 | 8.82 | 10 | 0.186299 | 7.51 | 12 | 0.137626 | 4.19 | ||
| 9 | 0.168087 | 7.22 | 11 | 0.255316 | 7.07 | 9 | 0.177588 | 7.87 | 18 | 0.193596 | 4.86 | ||
| 42 | 0.873011 | 8.91 | 11 | 0.257521 | 8.54 | 17 | 0.312101 | 4.43 | 24 | 0.262022 | 5.32 | ||
| 100,000 | 6 | 0.240266 | 5.41 | 8 | 0.39591 | 7.43 | 8 | 0.323746 | 1.5 | 11 | 0.247176 | 4.19 | |
| 5 | 0.211107 | 8.24 | 8 | 0.416573 | 2.59 | 8 | 0.326042 | 1.76 | 11 | 0.27141 | 3.81 | ||
| 5 | 0.201544 | 2.72 | 8 | 0.397299 | 4.02 | 8 | 0.321037 | 1.51 | 11 | 0.244046 | 2.88 | ||
| 9 | 0.355143 | 4.39 | 12 | 0.587486 | 4.35 | 13 | 0.48467 | 9.19 | 18 | 0.393596 | 6.11 | ||
| 9 | 0.362649 | 3.53 | 11 | 0.542996 | 5.21 | 13 | 0.486746 | 7.21 | 18 | 0.383299 | 6.11 | ||
| 7 | 0.278369 | 6.54 | 10 | 0.500734 | 6.47 | 11 | 0.419632 | 2.05 | 12 | 0.2268 | 5.93 | ||
| 10 | 0.37336 | 5.27 | 12 | 0.545659 | 9.29 | 10 | 0.394767 | 1.36 | 18 | 0.382106 | 6.87 | ||
| 48 | 1.895847 | 6.76 | 12 | 0.578936 | 5.08 | 17 | 0.612865 | 6.27 | 24 | 0.51844 | 7.52 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sabi’u, J.; Muangchoo, K.; Shah, A.; Abubakar, A.B.; Aremu, K.O. An Inexact Optimal Hybrid Conjugate Gradient Method for Solving Symmetric Nonlinear Equations. Symmetry 2021, 13, 1829. https://doi.org/10.3390/sym13101829
Sabi’u J, Muangchoo K, Shah A, Abubakar AB, Aremu KO. An Inexact Optimal Hybrid Conjugate Gradient Method for Solving Symmetric Nonlinear Equations. Symmetry. 2021; 13(10):1829. https://doi.org/10.3390/sym13101829
Chicago/Turabian StyleSabi’u, Jamilu, Kanikar Muangchoo, Abdullah Shah, Auwal Bala Abubakar, and Kazeem Olalekan Aremu. 2021. "An Inexact Optimal Hybrid Conjugate Gradient Method for Solving Symmetric Nonlinear Equations" Symmetry 13, no. 10: 1829. https://doi.org/10.3390/sym13101829
APA StyleSabi’u, J., Muangchoo, K., Shah, A., Abubakar, A. B., & Aremu, K. O. (2021). An Inexact Optimal Hybrid Conjugate Gradient Method for Solving Symmetric Nonlinear Equations. Symmetry, 13(10), 1829. https://doi.org/10.3390/sym13101829








