Different Mechanisms of Translational Symmetry Breaking in Liquid-Crystal Coil–Rod–Coil Triblock Copolymers
Abstract
:1. Introduction
2. Molecular Theory of Coil–Rod–Coil Triblock Copolymers
3. Direct and Total Correlation Functions of Triblock Copolymers
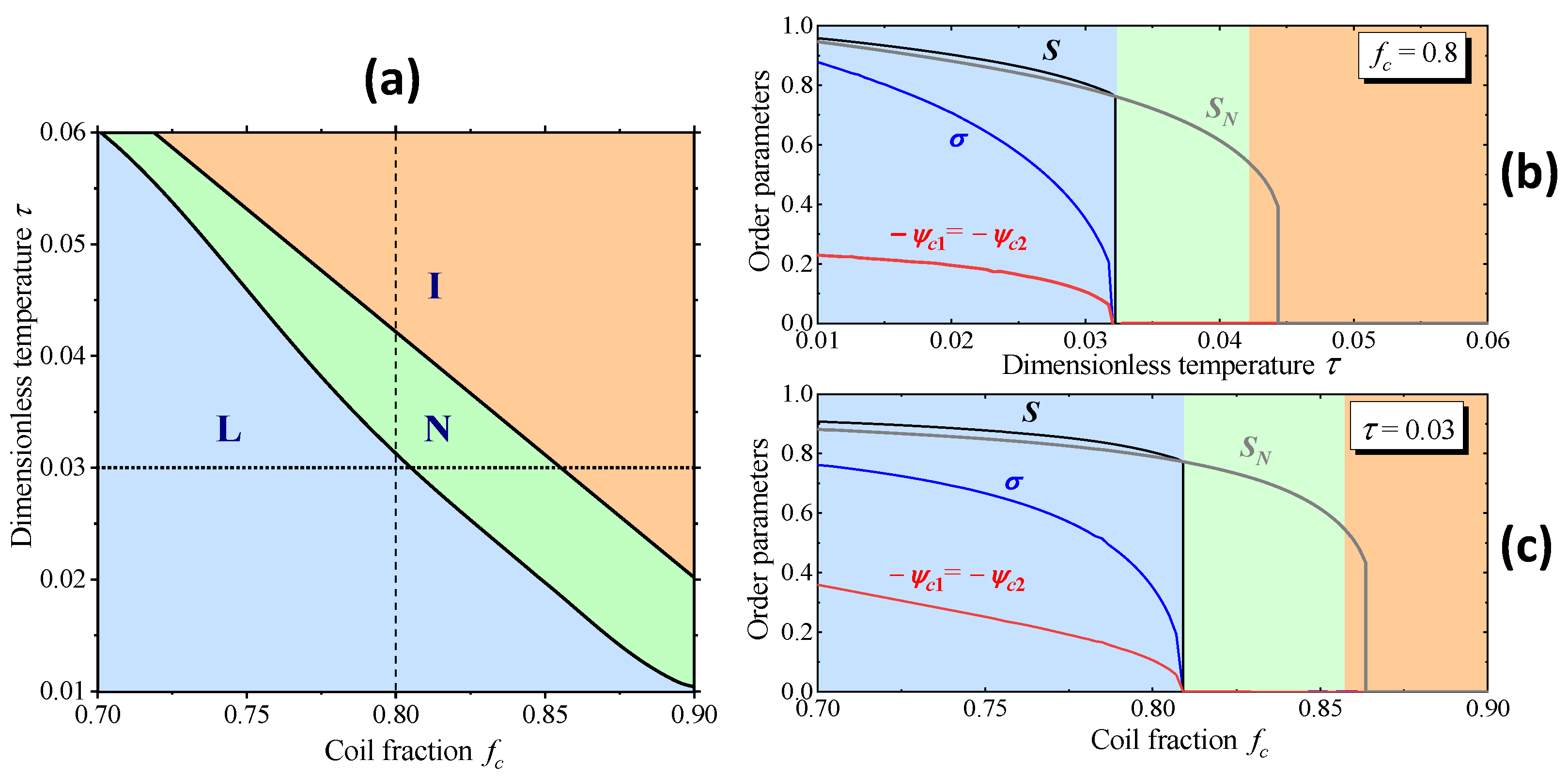
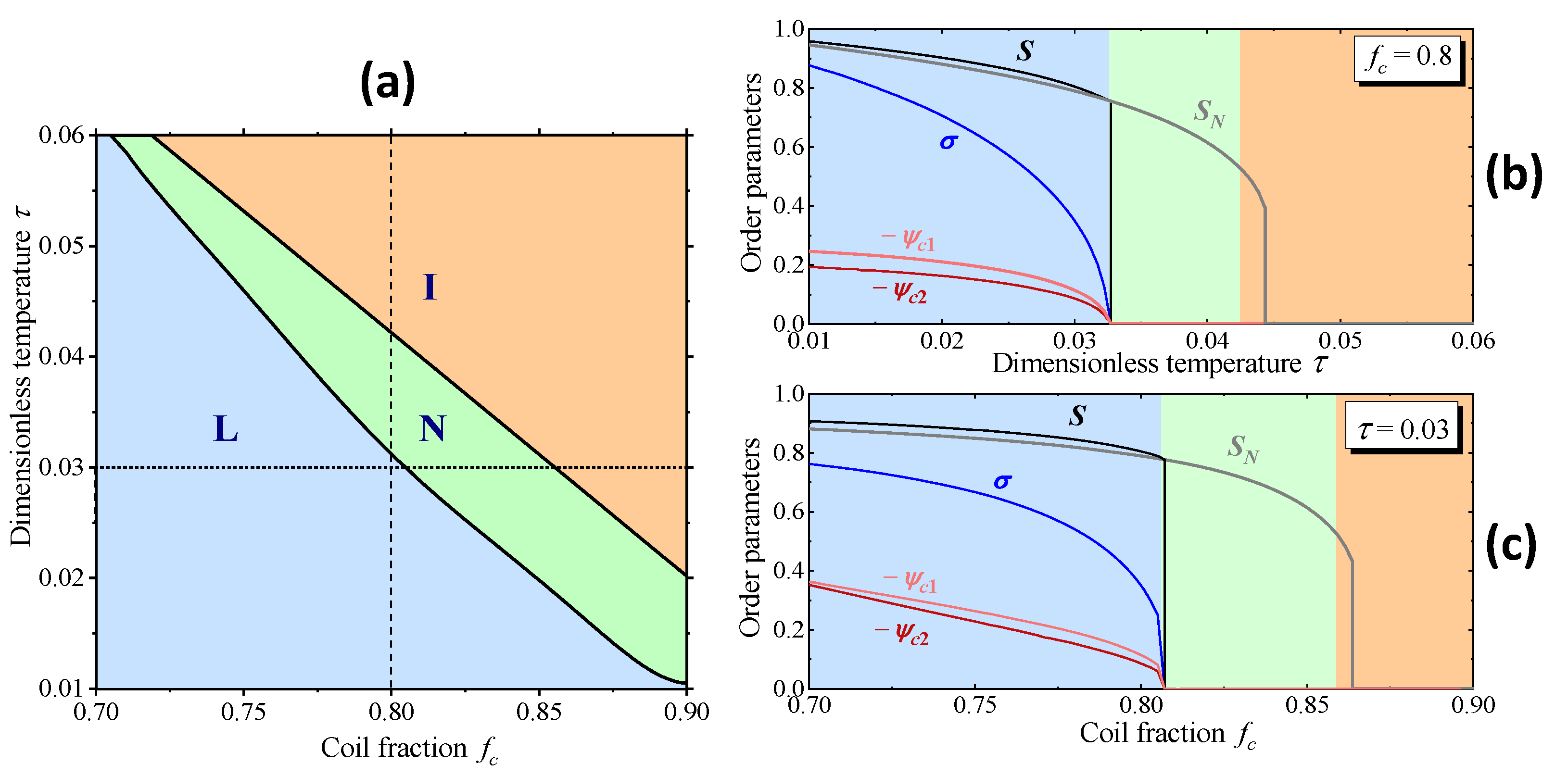
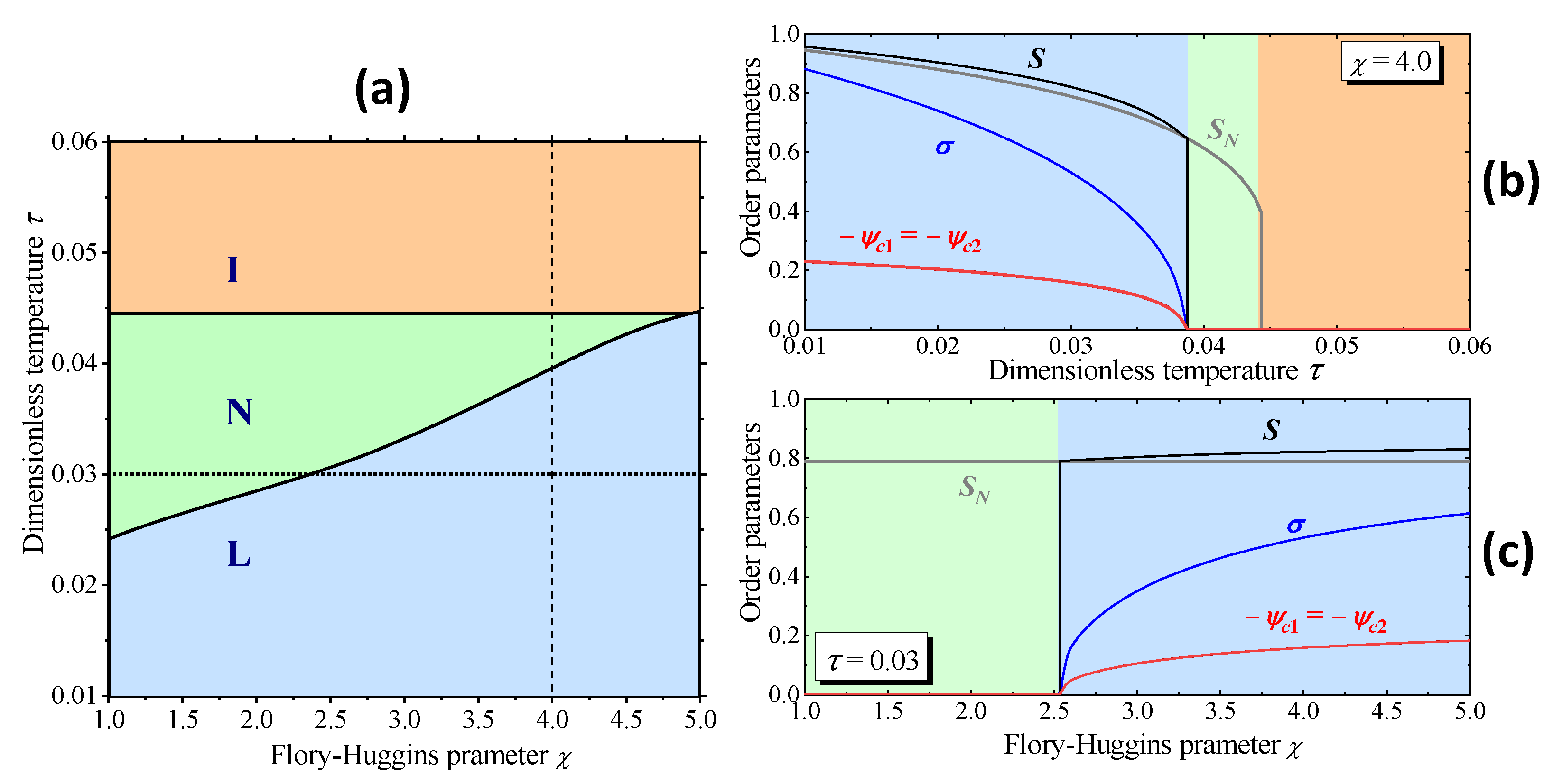
4. Results and Discussion. Phase Diagrams of Symmetric and Asymmetric Triblock Copolymers
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Segalman, R.A.; McCulloch, B.; Kirmayer, S.; Urban, J.J. Block Copolymers for Organic Optoelectronics. Macromolecules 2009, 42, 9205–9216. [Google Scholar] [CrossRef]
- Sivula, K.; Ball, Z.T.; Watanabe, N.; Fréchet, J.M.J. Amphiphilic Diblock Copolymer Compatibilizers and Their Effect on the Morphology and Performance of Polythiophene: Fullerene Solar Cells. Adv. Mater. 2006, 18, 206–210. [Google Scholar] [CrossRef]
- Van Hest, J.C.M. Biosynthetic-Synthetic Polymer Conjugates. Polym. Rev. 2007, 47, 63–92. [Google Scholar] [CrossRef]
- Klok, H.A. Biological-synthetic hybrid block copolymers: Combining the best from two worlds. J. Polym. Sci. Part A Polym. Chem. 2004, 43, 1–17. [Google Scholar] [CrossRef]
- Loos, K.; Müller, A.H.E. New Routes to the Synthesis of Amylose-block-polystyrene Rod-Coil Block Copolymers. Biomacromolecules 2002, 3, 368–373. [Google Scholar] [CrossRef] [PubMed]
- Haddleton, D.M.; Ohno, K. Well-Defined Oligosaccharide-Terminated Polymers from Living Radical Polymerization. Biomacromolecules 2000, 1, 152–156. [Google Scholar] [CrossRef] [PubMed]
- Olsen, B.D.; Segalman, R.A. Self-assembly of rod-coil block copolymers. Mater. Sci. Eng. R Rep. 2008, 62, 37–66. [Google Scholar] [CrossRef]
- Hoeben, F.J.M.; Jonkheijm, P.; Meijer, E.W.; Schenning, A.P.H.J. About Supramolecular Assemblies of π-Conjugated Systems. Chem. Rev. 2005, 105, 1491–1546. [Google Scholar] [CrossRef] [PubMed]
- Ryu, J.H.; Lee, M. Liquid crystalline sssembly of rod–coil molecules. In Liquid Crystalline Functional Assemblies and Their Supramolecular Structures; Springer: Berlin/Heidelberg, Germany, 2007; pp. 63–98. [Google Scholar] [CrossRef]
- Yu, G.; Gao, J.; Hummelen, J.C.; Wudl, F.; Heeger, A.J. Polymer Photovoltaic Cells: Enhanced Efficiencies via a Network of Internal Donor-Acceptor Heterojunctions. Science 1995, 270, 1789–1791. [Google Scholar] [CrossRef] [Green Version]
- Tao, Y.; McCulloch, B.; Kim, S.; Segalman, R.A. The relationship between morphology and performance of donor–acceptor rod–coil block copolymer solar cells. Soft Matter 2009, 5, 4219. [Google Scholar] [CrossRef]
- Chochos, C.L.; Kallitsis, J.K.; Gregoriou, V.G. Rod-Coil Block Copolymers Incorporating Terfluorene Segments for Stable Blue Light Emission. J. Phys. Chem. B 2005, 109, 8755–8760. [Google Scholar] [CrossRef]
- Becker, S.; Ego, C.; Grimsdale, A.C.; List, E.J.; Marsitzky, D.; Pogantsch, A.; Setayesh, S.; Leising, G.; Müllen, K. Optimisation of polyfluorenes for light emitting applications. Synth. Met. 2001, 125, 73–80. [Google Scholar] [CrossRef]
- Tao, Y.; Ma, B.; Segalman, R.A. Self-Assembly of Rod-Coil Block Copolymers and Their Application in Electroluminescent Devices. Macromolecules 2008, 41, 7152–7159. [Google Scholar] [CrossRef]
- McMillan, W.L. Simple Molecular Model for the SmecticAPhase of Liquid Crystals. Phys. Rev. A 1971, 4, 1238–1246. [Google Scholar] [CrossRef]
- Kobayashi, K.K. Theory of Translational and Orientational Melting with Application to Liquid Crystals. Mol. Cryst. Liq. Cryst. 1971, 13, 137–148. [Google Scholar] [CrossRef]
- Mederos, L.; Sullivan, D.E. Molecular theory of smectic—A liquid crystals. Phys. Rev. A 1989, 39, 854–863. [Google Scholar] [CrossRef]
- Gorkunov, M.V.; Osipov, M.A.; Kapernaum, N.; Nonnenmacher, D.; Giesselmann, F. Molecular theory of smectic ordering in liquid crystals with nanoscale segregation of different molecular fragments. Phys. Rev. E 2011, 84, 051704. [Google Scholar] [CrossRef]
- Erukhimovich, I.Y. Weak segregation theory and non-conventional morphologies in the ternary ABC triblock copolymers. Eur. Phys. J. E 2005, 18, 383–406. [Google Scholar] [CrossRef]
- Mayes, A.M.; de la Cruz, M.O. Microphase separation in multiblock copolymer melts. J. Chem. Phys. 1989, 91, 7228–7235. [Google Scholar] [CrossRef]
- Noolandi, J.; Shi, A.C.; Linse, P. Theory of Phase Behavior of Poly(oxyethylene)-Poly(oxypropylene)-Poly(oxyethylene) Triblock Copolymers in Aqueous Solutions. Macromolecules 1996, 29, 5907–5919. [Google Scholar] [CrossRef]
- Matsen, M.W.; Barrett, C. Liquid-crystalline behavior of rod-coil diblock copolymers. J. Chem. Phys. 1998, 109, 4108–4118. [Google Scholar] [CrossRef]
- Müller, M.; Schick, M. Ordered Phases in Rod-Coil Diblock Copolymers. Macromolecules 1996, 29, 8900–8903. [Google Scholar] [CrossRef]
- Pryamitsyn, V.; Ganesan, V. Self-assembly of rod-coil block copolymers. J. Chem. Phys. 2004, 120, 5824–5838. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.Z.; Zhang, C.X.; Sun, Z.Y.; Zheng, Y.S.; An, L.J. A novel self-consistent-field lattice model for block copolymers. J. Chem. Phys. 2006, 124, 104907. [Google Scholar] [CrossRef]
- Shah, M.; Pryamitsyn, V.; Ganesan, V. A Model for Self-Assembly in Side Chain Liquid Crystalline Block Copolymers. Macromolecules 2007, 41, 218–229. [Google Scholar] [CrossRef]
- Kriksin, Y.A.; Khalatur, P.G. Parallel Algorithm for 3D SCF Simulation of Copolymers With Flexible and Rigid Blocks. Macromol. Theory Simulations 2012, 21, 382–399. [Google Scholar] [CrossRef]
- Düchs, D.; Sullivan, D.E. Entropy-induced smectic phases in rod coil copolymers. J. Phys. Condens. Matter 2002, 14, 12189–12202. [Google Scholar] [CrossRef] [Green Version]
- Hidalgo, R.C.; Sullivan, D.E.; Chen, J.Z.Y. Smectic phases in rod-coil diblock copolymers. J. Phys. Condens. Matter 2007, 19, 376107. [Google Scholar] [CrossRef]
- Tang, J.; Jiang, Y.; Zhang, X.; Yan, D.; Chen, J.Z.Y. Phase Diagram of Rod-Coil Diblock Copolymer Melts. Macromolecules 2015, 48, 9060–9070. [Google Scholar] [CrossRef]
- Song, W.; Tang, P.; Qiu, F.; Yang, Y.; Shi, A.C. Phase behavior of semiflexible-coil diblock copolymers: A hybrid numerical SCFT approach. Soft Matter 2011, 7, 929–938. [Google Scholar] [CrossRef]
- Jiang, Y.; Chen, J.Z.Y. Influence of Chain Rigidity on the Phase Behavior of Wormlike Diblock Copolymers. Phys. Rev. Lett. 2013, 110, 138305. [Google Scholar] [CrossRef]
- Li, S.; Jiang, Y.; Chen, J.Z.Y. Phase transitions in semiflexible-rod diblock copolymers: A self-consistent field theory. Soft Matter 2014, 10, 8932–8944. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Jiang, Y.; Chen, J.Z.Y. Complex liquid-crystal nanostructures in semiflexible ABC linear triblock copolymers: A self-consistent field theory. J. Chem. Phys. 2016, 145, 184902. [Google Scholar] [CrossRef]
- Cai, Y.; Zhang, P.; Shi, A.C. Liquid crystalline bilayers self-assembled from rod-coil diblock copolymers. Soft Matter 2017, 13, 4607–4615. [Google Scholar] [CrossRef] [PubMed]
- Gao, J.; Song, W.; Tang, P.; Yang, Y. Self-assembly of semiflexible block copolymers: 2D numerical implementation of self-consistent field theory. Soft Matter 2011, 7, 5208. [Google Scholar] [CrossRef]
- Gao, J.; Tang, P.; Yang, Y. Non-lamellae structures of coil-semiflexible diblock copolymers. Soft Matter 2013, 9, 69–81. [Google Scholar] [CrossRef]
- Song, W.; Tang, P.; Zhang, H.; Yang, Y.; Shi, A.C. New Numerical Implementation of Self-Consistent Field Theory for Semiflexible Polymers. Macromolecules 2009, 42, 6300–6309. [Google Scholar] [CrossRef]
- Xia, Y.; Chen, J.; Sun, Z.; Shi, T.; An, L.; Jia, Y. Self-assembly of linear ABC coil-coil-rod triblock copolymers. Polymer 2010, 51, 3315–3319. [Google Scholar] [CrossRef]
- Han, X.-G.; Liang, N.; Zhang, H. Self-assembly in rod/coil block copolymers: Degenerate behavior under nonconfinement. Condens. Matter Phys. 2020, 23, 33603. [Google Scholar] [CrossRef]
- Osipov, M.A.; Gorkunov, M.V. Molecular theory of liquid-crystal ordering in rod-coil diblock copolymers. Phys. Rev. E 2019, 100, 042701. [Google Scholar] [CrossRef] [Green Version]
- Osipov, M.A.; Gorkunov, M.V.; Antonov, A.A. Density Functional Approach to the Molecular Theory of Rod-Coil Diblock Copolymers. Polym. Sci. Ser. A 2020, 62, 562–577. [Google Scholar] [CrossRef]
- Osipov, M.A.; Gorkunov, M.V.; Berezkin, A.V.; Antonov, A.A.; Kudryavtsev, Y.V. Molecular theory of the tilting transition and computer simulations of the tilted lamellar phase of rod–coil diblock copolymers. J. Chem. Phys. 2020, 152, 184906. [Google Scholar] [CrossRef] [PubMed]
- Singh, Y. Molecular theory of liquid crystals: Application to the nematic phase. Phys. Rev. A 1984, 30, 583–593. [Google Scholar] [CrossRef]
- Sluckin, T.J.; Shukla, P. Molecular field theory of nematics: Density functional approach. I. Bulk effects. J. Phys. A Math. Gen. 1983, 16, 1539–1553. [Google Scholar] [CrossRef]
- Gorkunov, M.V.; Osipov, M.A.; Lagerwall, J.P.F.; Giesselmann, F. Order-disorder molecular model of the smectic-A–smectic-C phase transition in materials with conventional and anomalously weak layer contraction. Phys. Rev. E 2007, 76, 051706. [Google Scholar] [CrossRef] [PubMed]
- Longa, L.; Stelzer, J.; Dunmur, D. Density functional approach to study the elastic constants of biaxial nematic liquid crystals. J. Chem. Phys. 1998, 109, 1555–1566. [Google Scholar] [CrossRef]
- Osipov, M.A. Molecular theories of liquid crystals. In Handbook of Liquid Crystals; Wiley-VCH Verlag GmbH: Weinheim, Germany, 2014; pp. 40–71. [Google Scholar] [CrossRef]
- Perera, A.; Patey, G.N.; Weis, J.J. Density functional theory applied to the isotropic–nematic transition in model liquid crystals. J. Chem. Phys. 1988, 89, 6941–6946. [Google Scholar] [CrossRef]
- Leibler, L. Theory of Microphase Separation in Block Copolymers. Macromolecules 1980, 13, 1602–1617. [Google Scholar] [CrossRef]
- Ohta, T.; Kawasaki, K. Equilibrium morphology of block copolymer melts. Macromolecules 1986, 19, 2621–2632. [Google Scholar] [CrossRef]
- Uneyama, T.; Doi, M. Density Functional Theory for Block Copolymer Melts and Blends. Macromolecules 2005, 38, 196–205. [Google Scholar] [CrossRef] [Green Version]
- Reenders, M.; ten Brinke, G. Compositional and Orientational Ordering in Rod-Coil Diblock Copolymer Melts. Macromolecules 2002, 35, 3266–3280. [Google Scholar] [CrossRef] [Green Version]
- Giesselmann, F.; Zugenmaier, P.; Dierking, I.; Lagerwall, S.T.; Stebler, B.; Kašpar, M.; Hamplová, V.; Glogarová, M. Smectic-A*–smectic-C* transition in a ferroelectric liquid crystal without smectic layer shrinkage. Phys. Rev. E 1999, 60, 598–602. [Google Scholar] [CrossRef] [PubMed]
- Binnemans, K. Ionic Liquid Crystals. Chem. Rev. 2005, 105, 4148–4204. [Google Scholar] [CrossRef] [PubMed]
- Giesselmann, F.; Germer, R.; Saipa, A. Orientational order in smectic liquid-crystalline phases of amphiphilic diols. J. Chem. Phys. 2005, 123, 034906. [Google Scholar] [CrossRef] [PubMed]
- Lagerwall, J.P.F.; Giesselmann, F. Current Topics in Smectic Liquid Crystal Research. ChemPhysChem 2006, 7, 20–45. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Osipov, M.A.; Gorkunov, M.V.; Antonov, A.A. Different Mechanisms of Translational Symmetry Breaking in Liquid-Crystal Coil–Rod–Coil Triblock Copolymers. Symmetry 2021, 13, 1834. https://doi.org/10.3390/sym13101834
Osipov MA, Gorkunov MV, Antonov AA. Different Mechanisms of Translational Symmetry Breaking in Liquid-Crystal Coil–Rod–Coil Triblock Copolymers. Symmetry. 2021; 13(10):1834. https://doi.org/10.3390/sym13101834
Chicago/Turabian StyleOsipov, Mikhail A., Maxim V. Gorkunov, and Alexander A. Antonov. 2021. "Different Mechanisms of Translational Symmetry Breaking in Liquid-Crystal Coil–Rod–Coil Triblock Copolymers" Symmetry 13, no. 10: 1834. https://doi.org/10.3390/sym13101834
APA StyleOsipov, M. A., Gorkunov, M. V., & Antonov, A. A. (2021). Different Mechanisms of Translational Symmetry Breaking in Liquid-Crystal Coil–Rod–Coil Triblock Copolymers. Symmetry, 13(10), 1834. https://doi.org/10.3390/sym13101834





