Sensitivity of Neutron-Rich Nuclear Isomer Behavior to Uncertainties in Direct Transitions †
Abstract
:1. Introduction
2. Methods
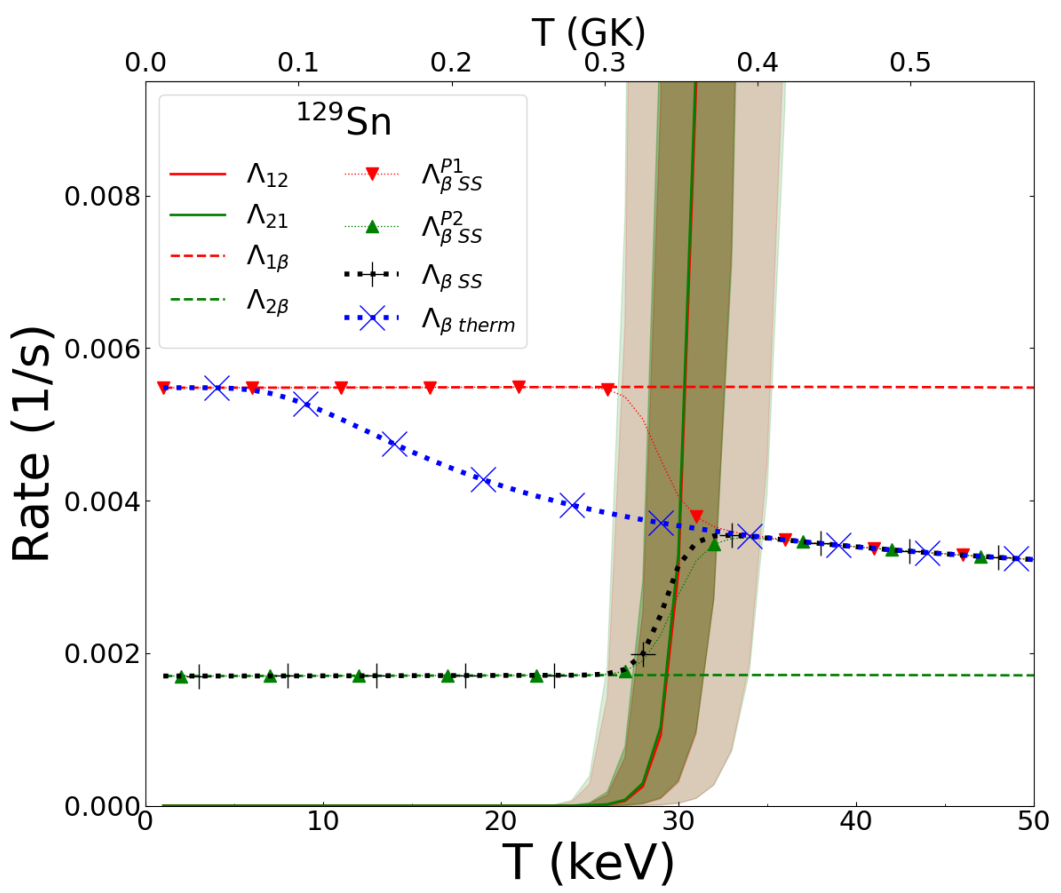
Example: Sn
3. Results
3.1. Zn () Isotopes
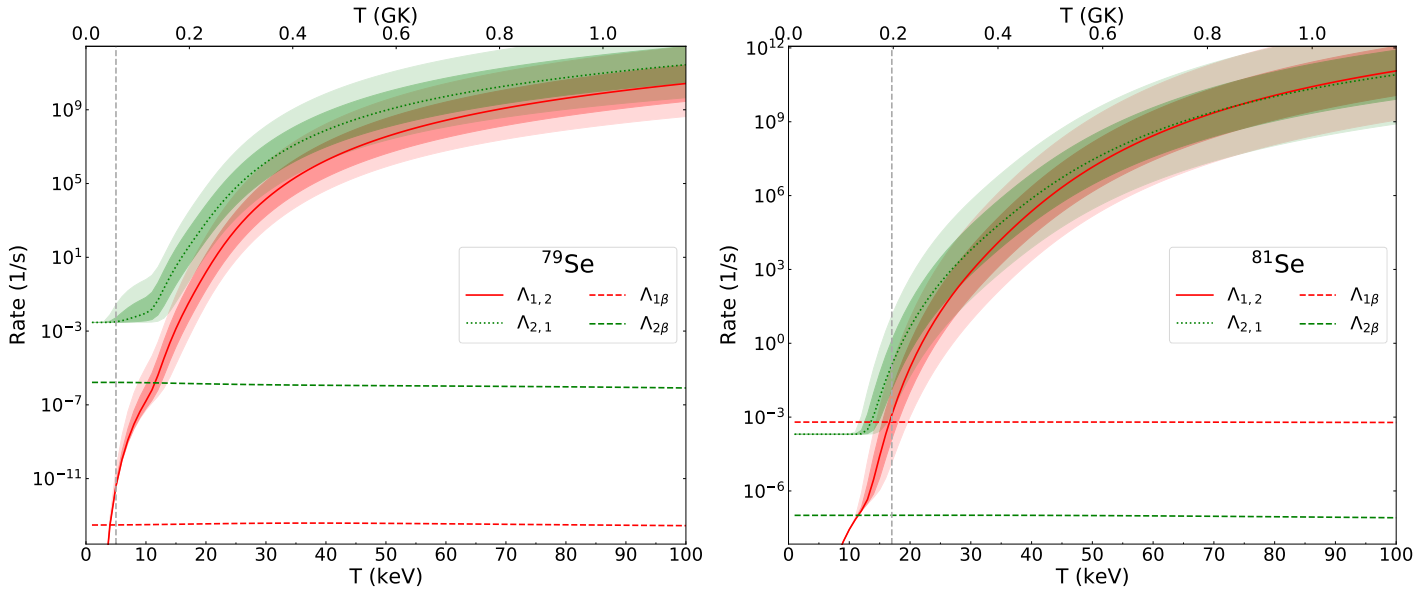
3.2. Se () Isotopes
3.3. Kr () Isotopes
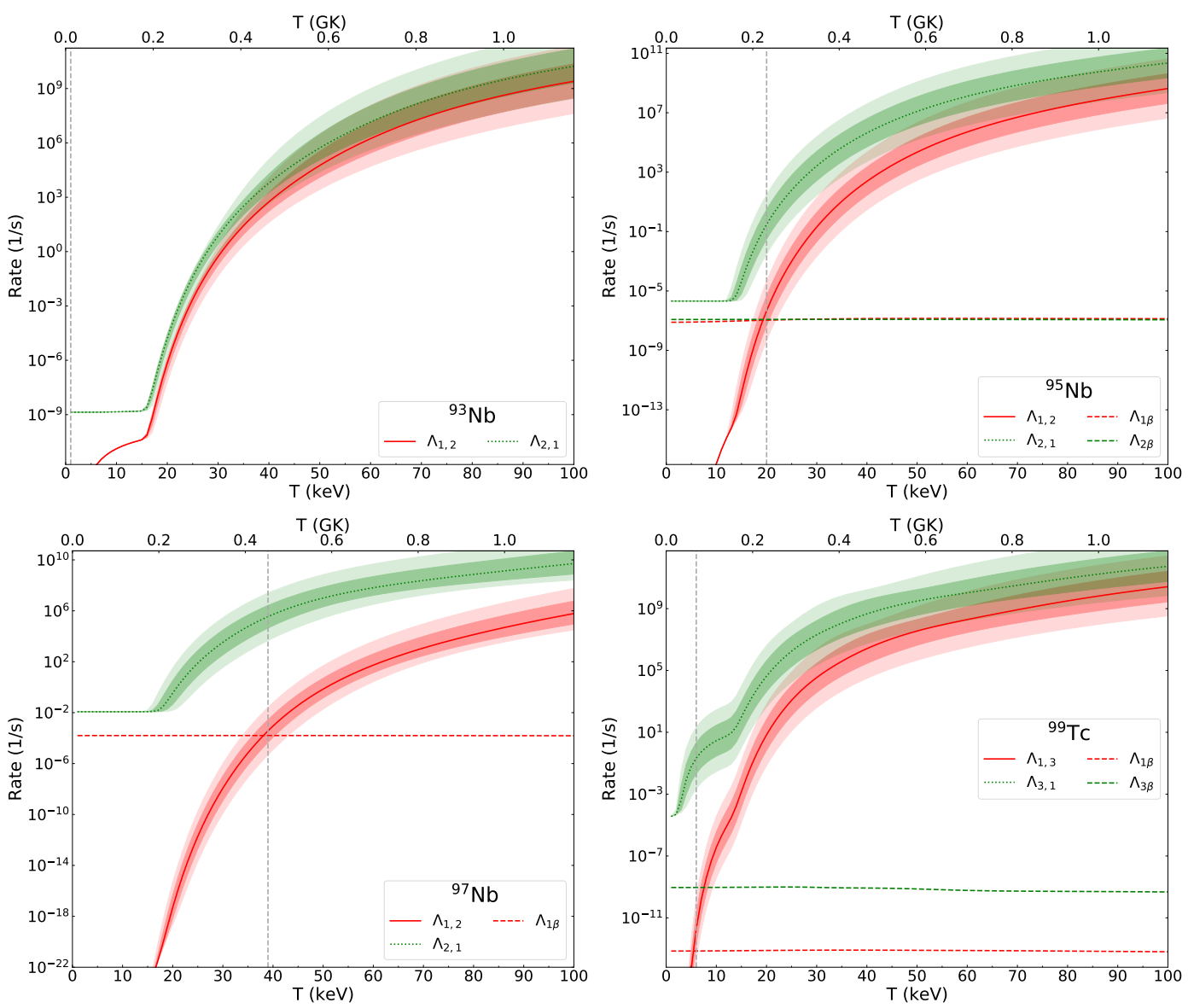
3.4. Nb () and Tc () Isotopes
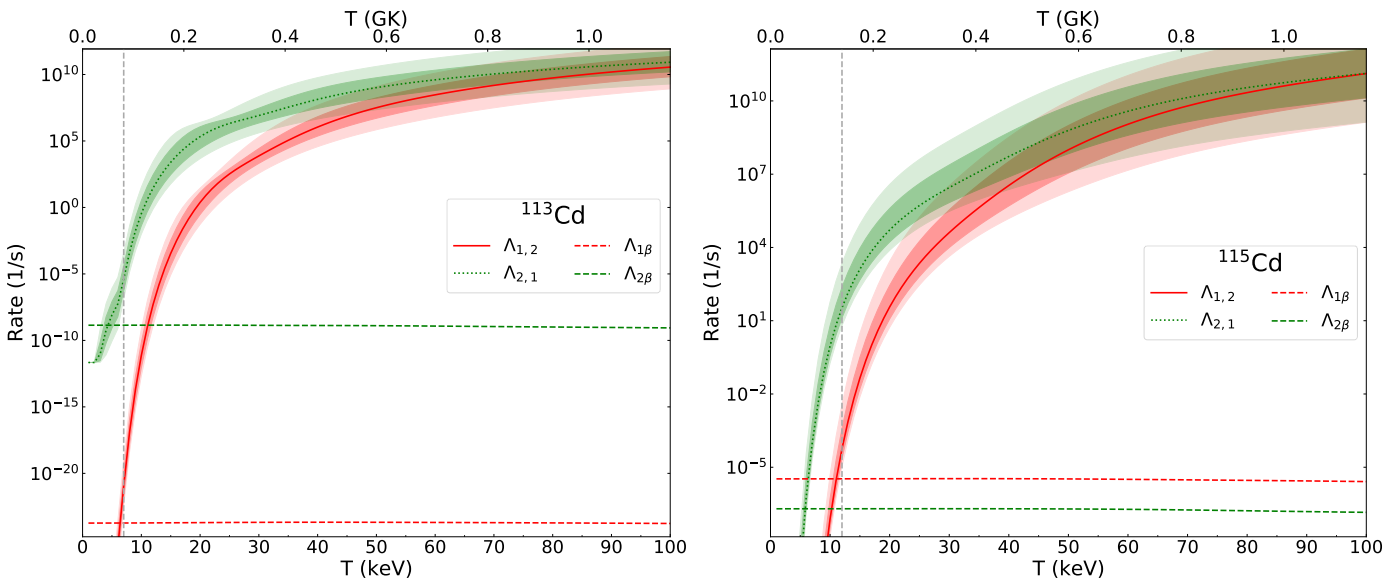
3.5. Cd () Isotopes
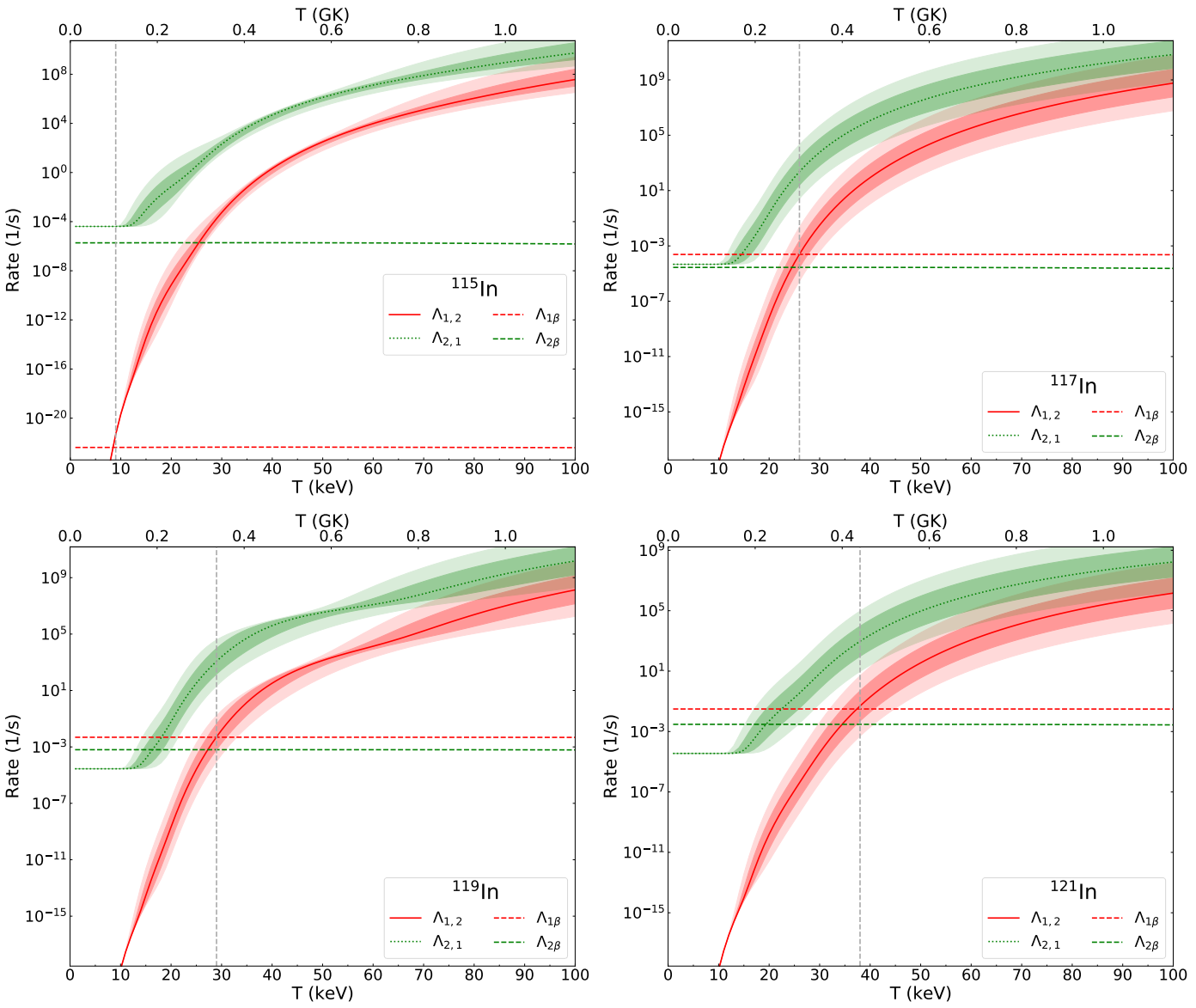
3.6. In () Isotopes
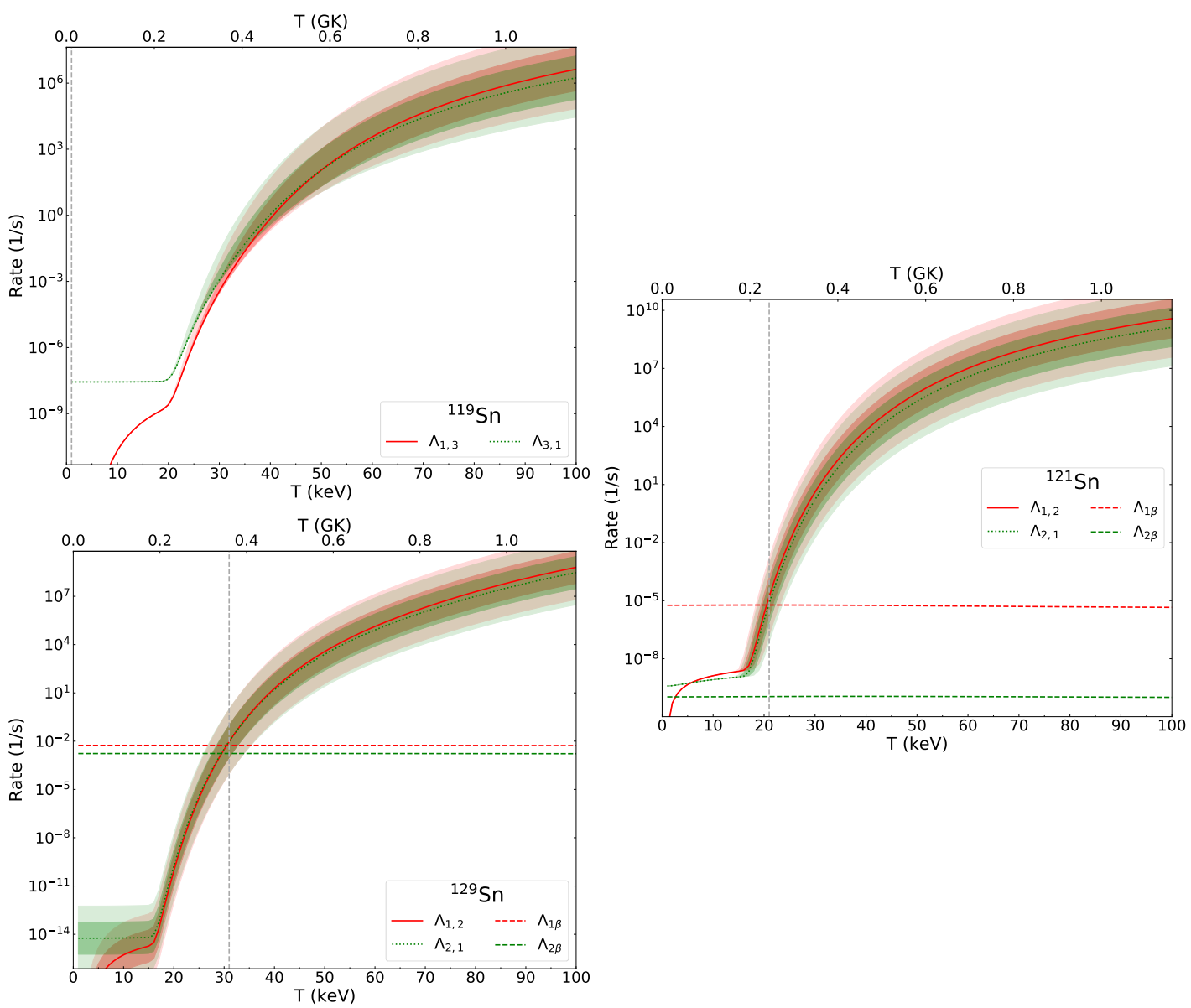
3.7. Sn () Isotopes
3.8. Sb () Isotopes
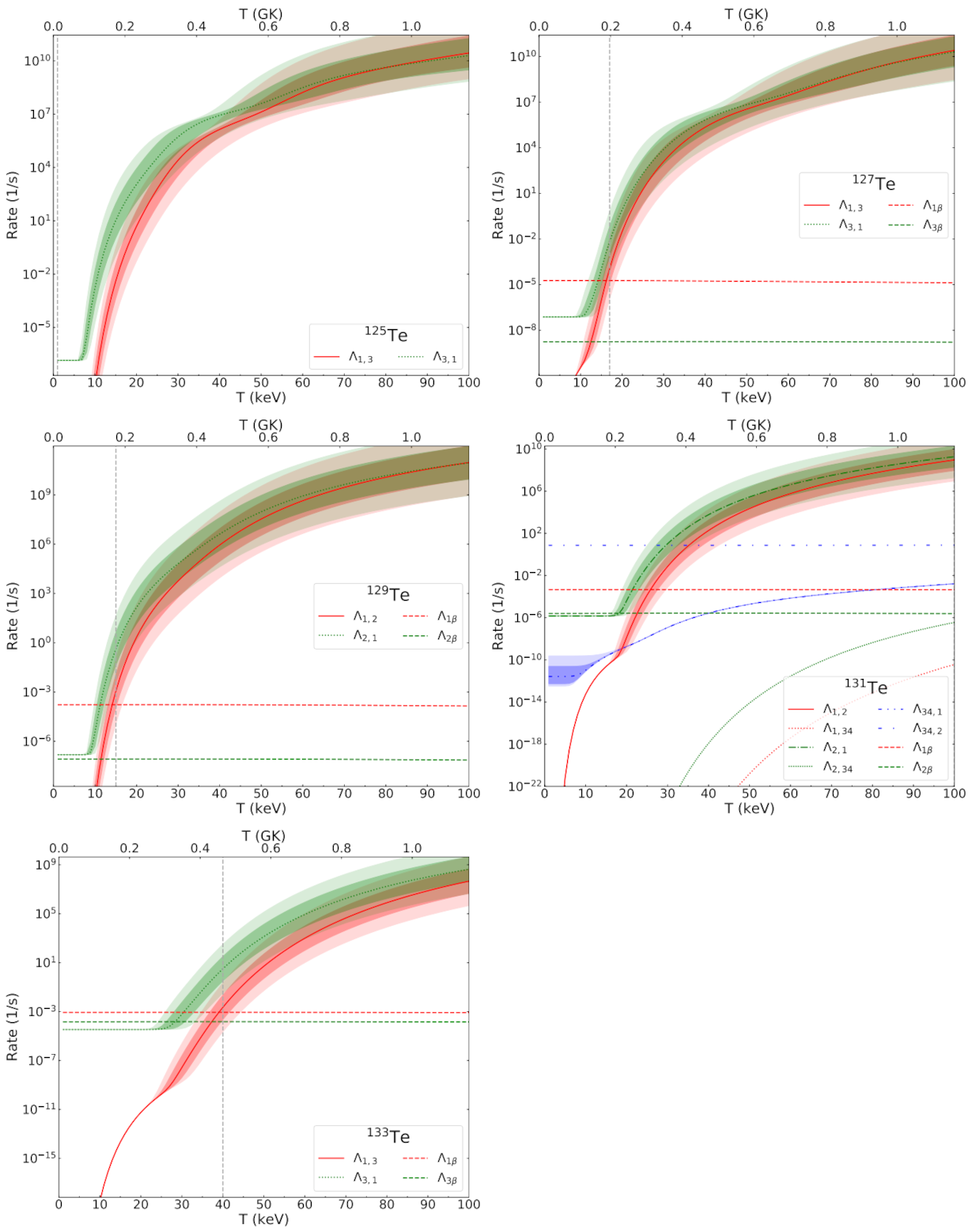
3.9. Te () Isotopes
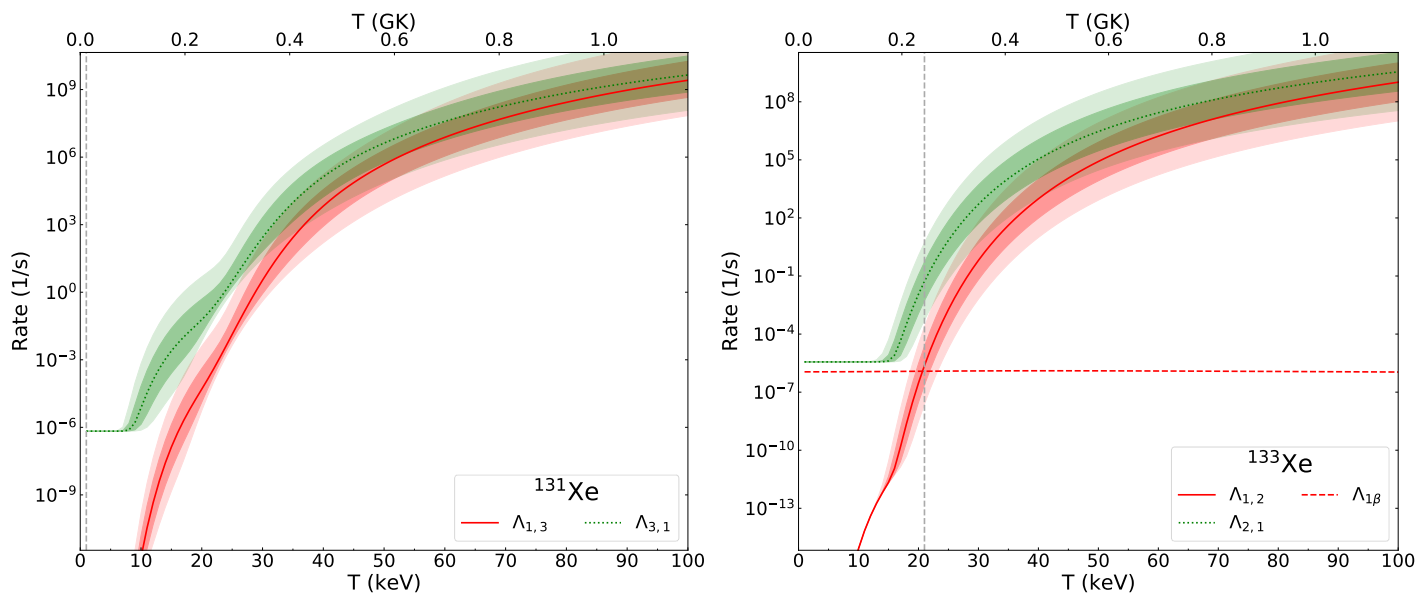
3.10. Xe () Isotopes
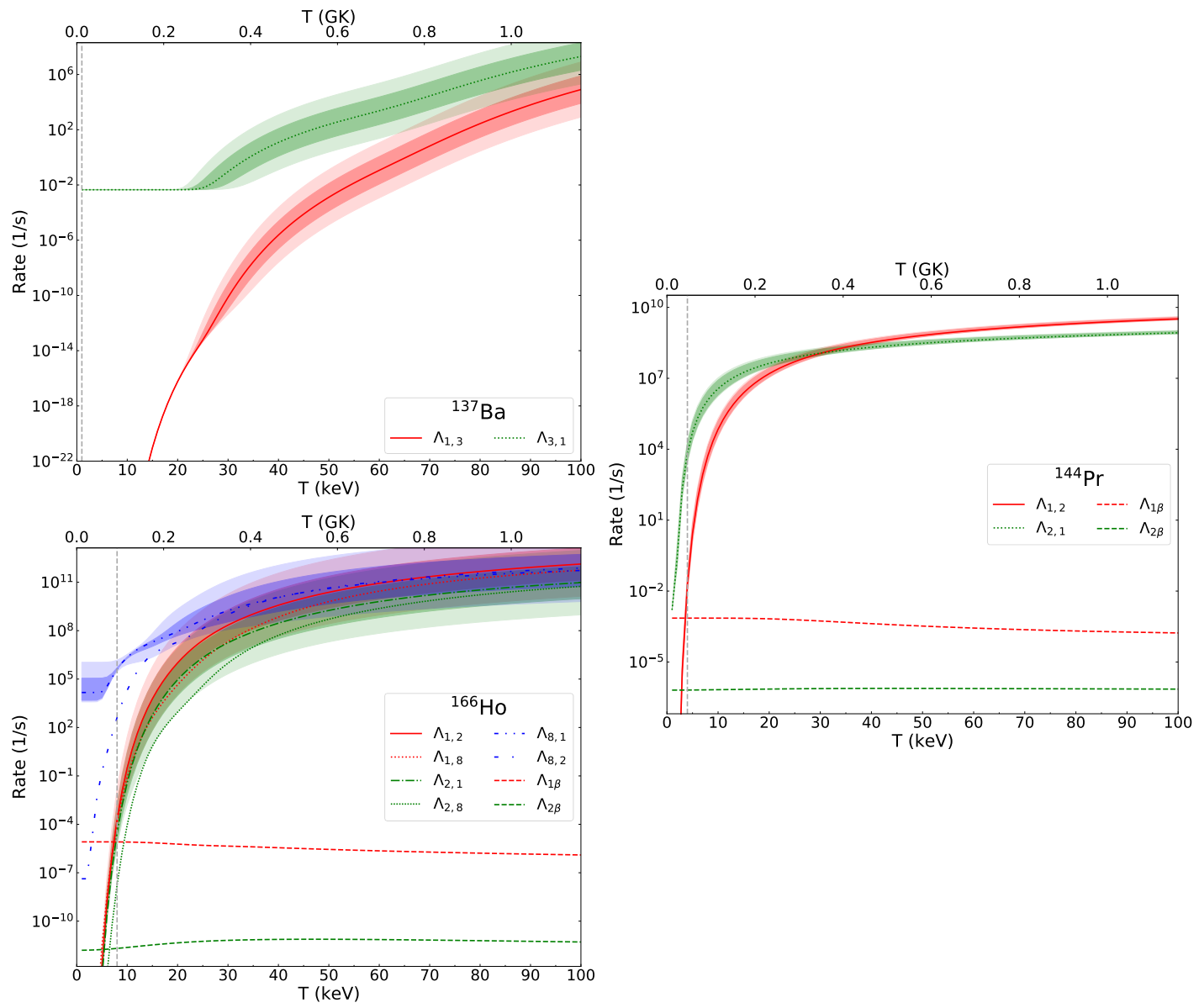
3.11. Ba (), Pr (), and Ho () Isotopes
3.12. Os (), Ir (), and Pt () Isotopes
4. Discussion and Conclusions
4.1. Comments on Selected Isomers and Mass Regions
4.2. Additional Modeling and Data Requirements
4.3. Experimental Prospects
4.4. Observational Prospects
4.5. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Astromer | Astrophysical isomer; isomer which retains its metastable |
| characteristics in a hot environment | |
| GS | Ground state |
| r process | Rapid neutron capture process |
| s process | Slow neutron capture process |
| process | Rapid proton capture process |
| Type A | Astromer which accelerates decay and energy release (“accelerant”) |
| Type B | Astromer which slows decay and stores energy (“battery”) |
| Type N | Astromer which has a negligible effect on energy release (“neutral”) |
Appendix A
| Nucleus | T (keV) | E (keV) | T (s) | B % | Type (keV) | Unmeasured Transitions |
|---|---|---|---|---|---|---|
| Zn | 24–36 | 0.0 438.6 | 0.0 | B (5.0) | (), (), (), () | |
| Zn | 12–17 | 0.0 157.7 | 100.0 | B (6.0) | (), (), (), (), (), (), () | |
| Zn | 9–12 | 0.0 195.5 | 0.0 | N | (), () | |
| Zn | 34–45 | 0.0 772.4 | 65.9 | N | (), (), (), (), (), (), (), (), (), (), () | |
| Zn | 41–57 | 0.0 1100.0 | 0.0 | N | (), (), (), (), (), (), (), (), (), (), (), (), (), () | |
| Ga | 4–5 | 0.0 119.7 | 0.0 | N | (), (), () | |
| Ga | 1 | 0.0 0.3 | 0.0 | N | () | |
| Ga | 4–5 | 0.0 59.6 | 24.2 | A | (), (), (), (), () | |
| Ga | 6–13 | 0.0 22.4 | 100.0 | N | (), (), () | |
| Ge | N/A | 0.0 66.7 | stable | 0.0 | N | (), (), (), (), (), (), () |
| Ge | 8–9 | 0.0 139.7 | 0.0 | N | (), (), (), (), () | |
| Ge | 14–18 | 0.0 159.7 | 81.2 | A | (), (), (), (), (), (), (), (), (), (), () | |
| Ge | 14–19 | 0.0 185.9 | 96.3 | N | (), (), (), () | |
| Ge | 34–44 | 0.0 679.1 | 67.6 | N | (), (), (), (), (), (), (), (), () | |
| As | N/A | 0.0 303.9 | stable | 0.0 | N | (), (), (), (), (), () |
| As | 9–15 | 0.0 131.6 | 94.8 | N | (), (), () | |
| Se | N/A | 0.0 161.9 | stable | 0.0 | N | (), (), (), (), () |
| Se | 4–5 | 0.0 95.8 | 0.1 | A | (), () | |
| Se | 15–20 | 0.0 103.0 | 0.1 | B (13.0) | (), (), (), (), (), (), () | |
| Se | 14–20 | 0.0 228.9 | 100.0 | A | (), (), (), () | |
| Br | N/A | 0.0 207.6 | stable | 0.0 | N | (), (), (), (), (), (), (), () |
| Br | 9 | 0.0 45.9 | 2.5 | A | (), () | |
| Br | 83–100 | 0.0 320.0 | 96.7 | A | () | |
| Kr | N/A | 0.0 41.6 | stable | 0.0 | N | (), (), (), () |
| Kr | 26–29 | 0.0 304.9 | 77.5 | A | (), (), (), (), (), (), () | |
| Rb | 7–9 | 0.0 106.9 | 97.4 | N | (), (), (), () | |
| Rb | 8–11 | 0.0 270.0 | 0.0 | N | (), (), (), () | |
| Y | N/A | 0.0 909.0 | stable | 0.0 | N | (), (), (), (), (), (), (), (), (), (), () |
| Y | 29–38 | 0.0 682.0 | 0.0 | N | (), (), (), (), (), (), (), (), (), () | |
| Y | 25–30 | 0.0 555.6 | 1.5 | A | (), (), (), (), (), (), (), (), (), () | |
| Y | 33–41 | 0.0 758.7 | 0.0 | N | (), (), (), (), (), (), (), (), (), (), (), (), (), (), () | |
| Y | ? | 0.0 1140.0 | 100.0 | N | (), (), (), (), (), (), (), (), (), (), (), () | |
| Y | ? | 0.0 667.5 3522.6 | 99.4 6.1 | A N | (), (), (), (), (), (), (), (), (), (), (), () | |
| Y | 18–25 | 0.0 465.7 | 0.0 | N | (), (), (), (), (), (), (), (), (), (), (), (), (), (), () | |
| Y | 5–7 | 0.0 145.0 | 0.0 | N | (), (), (), (), (), (), () | |
| Zr | N/A | 0.0 2319.0 | stable | 0.0 | N | (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), () |
| Nb | N/A | 0.0 30.8 | stable | 0.0 | N | (), (), (), () |
| Nb | 18–22 | 0.0 235.7 | 5.4 | N | (), (), (), (), (), (), (), () | |
| Nb | 34–44 | 0.0 743.4 | 0.0 | N | (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), () | |
| Nb | 25–37 | 0.0 84.0 | 100.0 | B (26.0) | (), (), (), (), () | |
| Nb | 21–27 | 0.0 365.3 | 96.3 | B (7.0) | (), (), (), (), (), (), (), (), () | |
| Nb | 15–19 | 0.0 314.0 | -0.0 | N | (), (), (), (), (), (), () | |
| Nb | ? | 0.0 215.0 | 100.0 | A | (), (), (), (), (), (), (), (), (), (), (), () | |
| Tc | 5–7 | 0.0 142.7 | 0.0 | A | () | |
| Ru | 10 | 0.0 238.2 | 0.0 | N | (), (), (), (), (), (), (), () | |
| Rh | N/A | 0.0 39.8 | stable | 0.0 | N | (), (), (), (), (), (), (), (), (), (), () |
| Rh | 12–14 | 0.0 129.7 | 0.0 | N | (), (), (), (), (), (), (), (), () | |
| Rh | ? | 0.0 137.0 | 100.0 | B (?) | (), (), () | |
| Rh | ? | 0.0 150.0 | 100.0 | N | () | |
| Pd | 6 | 0.0 214.6 | 0.0 | N | (), () | |
| Pd | 8–10 | 0.0 189.0 | 0.0 | N | (), (), (), (), (), (), (), () | |
| Pd | 7–9 | 0.0 172.2 | 29.0 | B (1.0) | (), () | |
| Pd | 6–8 | 0.0 81.1 | 0.0 | N | (), () | |
| Pd | 8–11 | 0.0 89.2 | 92.0 | N | (), (), (), () | |
| Pd | 22–32 | 0.0 203.3 | 0.0 | N | (), (), (), () | |
| Pd | ? | 0.0 2406.4 | 72.0 | A | (), (), (), (), (), (), () | |
| Ag | N/A | 0.0 93.1 | stable | 0.0 | N | (), (), () |
| Ag | N/A | 0.0 88.0 | stable | 0.0 | N | (), (), (), (), (), (), (), (), (), (), (), () |
| Ag | 7 | 0.0 43.5 | 23.6 | A | (), (), () | |
| Ag | ? | 0.0 199.0 | 0.0 | B (?) | (), (), (), (), (), (), (), () | |
| Ag | 9–12 | 0.0 41.2 | 79.0 | A | (), (), (), (), () | |
| Ag | ? | 0.0 47.9 129.8 | 98.1 86.1 | A A | (), (), (), (), (), (), (), (), (), (), (), () | |
| Ag | 10–15 | 0.0 28.6 | 94.6 | A | (), (), (), (), () | |
| Ag | 10–16 | 0.0 127.6 | 0.0 | N | (), (), (), (), (), (), (), (), (), () | |
| Ag | ? | 0.0 0.0 + X 80.0 | 0.0 0.0 | B (?) B (?) | () | |
| Cd | N/A | 0.0 396.2 | stable | 0.0 | N | (), (), (), (), (), (), (), (), (), (), (), (), (), () |
| Cd | 6–7 | 0.0 263.5 | 99.8 | A | (), (), (), (), (), (), () | |
| Cd | 10–12 | 0.0 181.0 | 100.0 | B (6.0) | (), (), (), (), (), (), (), (), () | |
| Cd | 10–13 | 0.0 136.4 | 100.0 | N | (), (), (), (), (), (), (), (), (), () | |
| Cd | 10–14 | 0.0 146.5 | 100.0 | N | (), (), (), (), (), () | |
| Cd | 14–16 | 0.0 214.9 | 100.0 | N | (), (), (), (), (), (), (), (), () | |
| Cd | 15–20 | 0.0 316.5 | 0.3 | N | (), (), (), (), (), (), () | |
| Cd | ? | 0.0 0+X 1940.0 | 100.0 0.0 | N N | () | |
| In | 9 | 0.0 336.2 | 4.4 | A | () | |
| In | 18–25 | 0.0 127.3 289.7 | 100.0 0.0 | B (9.0) N | (), (), (), (), (), (), (), (), (), (), (), () | |
| In | 24–30 | 0.0 315.3 | 37.4 | B (13.0) | (), (), (), (), (), (), (), (), () | |
| In | ? | 0.0 60.0 200.0 | 100.0 1.4 | B (?) N | () | |
| In | 26–33 | 0.0 311.4 | 95.7 | B (17.0) | (), (), (), (), (), (), (), (), (), () | |
| In | ? | 0.0 0.0 + X 70.0 | 0.1 100.0 | N B (39.0) | (), () | |
| In | 33–45 | 0.0 313.7 | 98.8 | B (21.0) | (), (), (), () | |
| In | ? | 0.0 40.0 290.0 | 100.0 0.2 | B (42.0) N | () | |
| In | 34–48 | 0.0 327.2 | 100.0 | B (24.0) | (), (), (), (), () | |
| In | ? | 0.0 50.0 | 100.0 | N | (), (), (), (), (), (), (), (), () | |
| In | ? | 0.0 360.1 2161.2 | 100.0 0.0 | B (25.0) N | (), (), (), (), (), (), () | |
| In | ? | 0.0 102.0 | 100.0 | N | (), (), (), (), (), () | |
| In | ? | 0.0 408.9 1863.0 | 100.0 100.0 | B (20.0) N | (), (), (), (), (), (), (), () | |
| In | ? | 0.0 340.0 | 100.0 | N | () | |
| In | ? | 0.0 459.0 1630.0 1911.0 | 100.0 100.0 0.0 | B (17.0) N N | (), (), (), (), (), (), (), (), () | |
| In | ? | 0.0 50.0 400.0 | 100.0 10.5 | B (?) N | (), (), (), (), (), () | |
| In | ? | 0.0 302.0 3764.0 | 100.0 89.0 | N B (?) | (), (), (), (), () | |
| In | ? | 0.0 330.0 | 0.0 | B (?) | () | |
| Sn | N/A | 0.0 314.6 | stable | 0.0 | N | (), () |
| Sn | N/A | 0.0 89.5 | stable | 0.0 | N | (), (), (), () |
| Sn | 19–24 | 0.0 6.3 | 21.6 | B (20.0) | (), (), (), (), (), () | |
| Sn | 24–31 | 0.0 24.6 | 100.0 | A | (), (), (), (), (), (), (), (), (), (), (), (), () | |
| Sn | 24–32 | 0.0 27.5 | 100.0 | A | (), (), (), (), () | |
| Sn | 25–33 | 0.0 5.1 | 100.0 | A | (), (), (), (), (), (), (), (), (), (), (), () | |
| Sn | 69–91 | 0.0 2091.5 | 0.0 | N | (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), () | |
| Sn | 27–36 | 0.0 35.1 | 100.0 | B (29.0) | (), (), (), (), (), (), (), (), (), (), (), (), () | |
| Sn | 56–70 | 0.0 1946.9 | 100.0 | A | (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), () | |
| Sb | ? | 0.0 0.0 + X | 99.9 | A | () | |
| Sb | 49–61 | 0.0 1851.3 | 0.0 | A | (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), () | |
| Sb | 3–4 | 0.0 4.8 | 100.0 | A | (), (), () | |
| Sb | 19–26 | 0.0 279.0 | 100.0 | B (10.0) | (), (), (), (), (), (), (), (), (), () | |
| Te | N/A | 0.0 144.8 | stable | 0.0 | N | (), (), (), (), (), (), (), () |
| Te | 15–19 | 0.0 88.2 | 2.3 | B (13.0) | (), (), (), (), (), (), () | |
| Te | 13–17 | 0.0 105.5 | 35.2 | B (10.0) | (), (), (), (), (), () | |
| Te | ? | 0.0 182.3 1940.0 | 62.6 0.0 | B (21.0) N | (), (), (), (), (), (), (), (), (), (), (), () | |
| Te | 35–45 | 0.0 334.3 | 81.0 | B (29.0) | (), (), (), (), (), (), (), (), () | |
| I | 60 | 0.0 120.0 | 12.5 | N | () | |
| I | 40–50 | 0.0 1634.1 | 0.0 | N | (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), () | |
| I | 74 | 0.0 316.5 | 2.0 | N | (), (), (), (), () | |
| I | ? | 0.0 201.0 | 100.0 | N | (), (), (), (), (), (), (), (), (), () | |
| Xe | N/A | 0.0 236.1 | stable | 0.0 | N | (), (), (), (), (), (), (), (), (), (), (), () |
| Xe | N/A | 0.0 163.9 | stable | 0.0 | N | (), (), (), (), (), (), (), (), () |
| Xe | N/A | 0.0 2752.2 | stable | 0.0 | N | (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), () |
| Xe | 19–24 | 0.0 233.2 | 0.0 | N | (), (), (), (), (), (), (), (), () | |
| Xe | N/A | 0.0 1965.5 | 0.0 | N | (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), () | |
| Xe | 34–44 | 0.0 526.6 | 0.7 | N | (), (), (), (), (), (), (), (), () | |
| Cs | 66 | 0.0 1632.9 | 0.0 | N | (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), () | |
| Ba | N/A | 0.0 268.2 | stable | 0.0 | N | (), (), (), (), (), () |
| Ba | N/A | 0.0 661.7 | stable | 0.0 | N | (), (), () |
| Pr | 4 | 0.0 59.0 | 0.0 | N | (), () | |
| Pr | 4–6 | 0.0 76.8 | 15.7 | N | (), () | |
| Sm | 5–6 | 0.0 98.4 | 0.0 | N | (), (), (), (), (), () | |
| Gd | N/A | 0.0 121.1 | stable | 0.0 | N | (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), () |
| Dy | 6–7 | 0.0 108.2 | 2.2 | A | (), (), (), () | |
| Ho | 7–8 | 0.0 6.0 190.9 | 100.0 0.0 | B (7.0) N | (), (), (), (), (), (), (), (), (), (), (), () | |
| Ho | ? | 0.0 120.0 | 100.0 | A | () | |
| Er | N/A | 0.0 207.8 | stable | 0.0 | N | (), (), (), (), (), (), (), (), (), (), () |
| Yb | N/A | 0.0 95.3 | stable | 0.0 | N | (), (), (), (), (), (), (), (), (), (), () |
| Yb | 15–19 | 0.0 514.9 | 0.0 | N | (), (), (), (), (), (), (), () | |
| Yb | N/A | 0.0 1049.8 | stable | 0.0 | N | (), (), (), () |
| Yb | 12–17 | 0.0 331.5 | 0.0 | N | (), (), (), (), (), (), (), () | |
| Lu | 33–45 | 0.0 569.7 970.2 | 0.0 9.6 | N B (3.0) | (), (), (), (), (), (), (), (), (), (), (), (), () | |
| Lu | 12–19 | 0.0 123.8 | 100.0 | N | (), (), (), (), (), (), (), (), () | |
| Lu | 21–26 | 0.0 592.4 | 0.0 | N | (), (), (), (), (), (), (), (), (), (), (), () | |
| Lu | 24–37 | 0.0 624.0 | 0.0 | N | (), (), (), () | |
| Hf | N/A | 0.0 1315.5 2740.0 | stable | 0.0 0.0 | N N | (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), () |
| Hf | N/A | 0.0 1147.4 2446.1 | stable | 0.0 0.0 | N N | (), (), (), (), (), (), (), () |
| Hf | N/A | 0.0 375.0 1105.7 | stable | 0.0 0.0 | N N | (), (), (), (), (), (), (), (), (), (), () |
| Hf | 2 | 0.0 1141.6 | stable | 0.0 | A | (), (), () |
| Hf | 44–74 | 0.0 1043.5 1741.9 | 0.0 0.0 | N N | (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), () | |
| Hf | 21–24 | 0.0 1172.9 | 0.3 | A | (), (), (), (), (), (), (), (), () | |
| Hf | 82–100 | 0.0 1272.2 | 0.0 | N | (), (), (), (), (), (), () | |
| Ta | 47–68 | 0.0 16.3 519.6 | 0.0 0.0 | N N | (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), () | |
| Ta | ? | 0.0 99.0 | 0.0 | B (?) | () | |
| W | N/A | 0.0 309.5 | 0.0 | N | (), (), (), (), (), (), (), (), (), (), () | |
| W | 7–9 | 0.0 197.4 | 0.0 | N | (), (), (), (), (), (), (), (), (), (), (), (), () | |
| W | N/A | 0.0 3542.8 | stable | 0.0 | N | (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), () |
| W | 69–93 | 0.0 2381.0 | 0.0 | N | (), (), (), (), (), (), (), (), (), () | |
| Re | 9–11 | 0.0 172.1 | 0.0 | N | (), (), (), (), (), (), (), (), () | |
| Re | 49–100 | 0.0 210.0 | 5.3 | B (87.0) | (), (), () | |
| Re | ? | 0.0 285.0 833.0 | 100.0 100.0 | B (?) B (?) | (), () | |
| Os | N/A | 0.0 30.8 | stable | 0.0 | N | (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), () |
| Os | N/A | 0.0 1705.4 | stable | 0.0 | N | (), (), (), (), (), (), (), (), () |
| Os | 4–6 | 0.0 74.4 | 0.0 | N | (), () | |
| Os | 3 | 0.0 2015.4 | stable | 7.6 | A | (), (), (), (), (), (), (), () |
| Os | 1 | 0.0 454.0 | 0.0 | N | (), (), () | |
| Ir | N/A | 0.0 171.3 | stable | 0.0 | N | (), (), (), (), () |
| Ir | 32–100 | 0.0 56.7 168.1 | 0.0 0.0 | A B (?) | (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), () | |
| Ir | N/A | 0.0 80.2 2278.9 | stable | 0.0 0.0 | N N | (), (), (), () |
| Ir | ? | 0.0 147.1 190.0 + X | 0.0 100.0 | N B (?) | (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), () | |
| Ir | 14–20 | 0.0 100.0 | 100.0 | N | (), (), (), (), () | |
| Ir | ? | 0.0 410.0 | 100.0 | B (?) | (), (), (), (), (), (), (), (), () | |
| Ir | 26–48 | 0.0 115.0 | 100.0 | N | (), (), (), (), (), (), () | |
| Pt | N/A | 0.0 259.1 | stable | 0.0 | N | (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), () |
| Pt | 16–23 | 0.0 399.6 | 0.0 | N | (), (), (), (), (), (), (), (), (), (), (), (), (), () | |
| Pt | 17–25 | 0.0 424.0 | 0.0 | N | (), (), (), (), (), (), (), (), (), (), (), () | |
| Au | N/A | 0.0 409.1 | stable | 0.0 | N | (), (), (), (), (), (), (), (), () |
| Au | ? | 0.0 962.0 | 100.0 | B (?) | (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), () | |
| Hg | N/A | 0.0 532.5 | stable | 0.0 | N | (), (), (), (), (), (), (), (), (), () |
| Hg | 50–65 | 0.0 1556.4 | 0.0 | N | (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), () | |
| Tl | ? | 0.0 2643.1 | 0.0 | N | (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), (), () | |
| Tl | 62–77 | 0.0 1348.2 | 0.0 | N | (), (), (), (), (), (), (), (), (), (), () | |
| Pb | N/A | 0.0 1633.4 | stable | 0.0 | N | (), (), (), (), () |
| Bi | 17 | 0.0 271.3 | 0.0 | B (8.0) | (), (), (), (), (), (), () | |
| Bi | ? | 0.0 250.0 1910.0 | 100.0 100.0 | N A | (), (), (), (), (), (), (), (), (), () |
References
- Soddy, F. The Complexity of the Chemical Elements. Sci. Mon. 1917, 5, 451–462. [Google Scholar]
- Walker, P.; Dracoulis, G. Energy traps in atomic nuclei. Nature 1999, 399, 35–40. [Google Scholar] [CrossRef]
- Aprahamian, A.; Sun, Y. Long live isomer research. Nat. Phys. 2005, 1, 81–82. [Google Scholar] [CrossRef]
- Dracoulis, G.D.; Walker, P.M.; Kondev, F.G. Review of metastable states in heavy nuclei. Rep. Prog. Phys. 2016, 79, 076301. [Google Scholar] [CrossRef] [PubMed]
- Hahn, O. Über ein neues radioaktives Zerfallsprodukt im Uran. Naturwissenschaften 1921, 9, 84. [Google Scholar] [CrossRef] [Green Version]
- Jain, A.K.; Maheshwari, B.; Garg, S.; Patial, M.; Singh, B. Atlas of nuclear isomers. Nucl. Data Sheets 2015, 128, 1–130. [Google Scholar] [CrossRef]
- Langanke, K.; Martínez-Pinedo, G. Shell-model calculations of stellar weak interaction rates: II. Weak rates for nuclei in the mass range /A = 45–65 in supernovae environments. arXiv 2000, arXiv:nucl-th/nucl-th/0001018. [Google Scholar] [CrossRef] [Green Version]
- Brown, B.; Rae, W. The shell-model code NuShellX@ MSU. Nucl. Data Sheets 2014, 120, 115–118. [Google Scholar] [CrossRef]
- Masuda, T.; Yoshimi, A.; Fujieda, A.; Fujimoto, H.; Haba, H.; Hara, H.; Hiraki, T.; Kaino, H.; Kasamatsu, Y.; Kitao, S.; et al. X-ray pumping of the 229 Th nuclear clock isomer. Nature 2019, 573, 238–242. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G.; Watanabe, H.; Dracoulis, G.; Kondev, F.; Lane, G.; Regan, P.; Söderström, P.A.; Walker, P.; Yoshida, K.; Kanaoka, H.; et al. Interplay of quasiparticle and vibrational excitations: First observation of isomeric states in 168 Dy and 169 Dy. Phys. Lett. B 2019, 799, 135036. [Google Scholar] [CrossRef]
- Liu, J.; Lee, J.; Watanabe, H.; Nishimura, S.; Zhang, G.; Wu, J.; Walker, P.; Regan, P.; Söderström, P.A.; Kanaoka, H.; et al. Isomeric and β-decay spectroscopy of Ho 173, 174. Phys. Rev. C 2020, 102, 024301. [Google Scholar] [CrossRef]
- Nesterenko, D.A.; Kankainen, A.; Kostensalo, J.; Nobs, C.R.; Bruce, A.M.; Beliuskina, O.; Canete, L.; Eronen, T.; Gamba, E.R.; Geldhof, S.; et al. Novel Penning-trap techniques reveal isomeric states in 128In and 130In for the first time. arXiv 2020, arXiv:2005.09398. [Google Scholar]
- Orford, R.; Kondev, F.G.; Savard, G.; Clark, J.A.; Porter, W.S.; Ray, D.; Buchinger, F.; Burkey, M.T.; Gorelov, D.A.; Hartley, D.J.; et al. Spin-trap isomers in deformed, odd-odd nuclei in the light rare-earth region near N = 98. Phys. Rev. C 2020, 102, 011303. [Google Scholar] [CrossRef]
- Sikorsky, T.; Geist, J.; Hengstler, D.; Kempf, S.; Gastaldo, L.; Enss, C.; Mokry, C.; Runke, J.; Düllmann, C.E.; Wobrauschek, P.; et al. Measurement of the Th 229 Isomer Energy with a Magnetic Microcalorimeter. Phys. Rev. Lett. 2020, 125, 142503. [Google Scholar] [CrossRef]
- Walker, P.; Hirayama, Y.; Lane, G.; Watanabe, H.; Dracoulis, G.; Ahmed, M.; Brunet, M.; Hashimoto, T.; Ishizawa, S.; Kondev, F.; et al. Properties of Ta 187 Revealed through Isomeric Decay. Phys. Rev. Lett. 2020, 125, 192505. [Google Scholar] [CrossRef]
- Izzo, C.; Bergmann, J.; Dietrich, K.; Dunling, E.; Fusco, D.; Jacobs, A.; Kootte, B.; Kripkó-Koncz, G.; Lan, Y.; Leistenschneider, E.; et al. Mass measurements of neutron-rich indium isotopes for r-process studies. Phys. Rev. C 2021, 103, 025811. [Google Scholar] [CrossRef]
- Gombas, J.; DeYoung, P.; Spyrou, A.; Dombos, A.; Algora, A.; Baumann, T.; Crider, B.; Engel, J.; Ginter, T.; Kwan, E.; et al. β-decay feeding intensity distributions for Nb 103, 104 m. Phys. Rev. C 2021, 103, 035803. [Google Scholar] [CrossRef]
- Walker, P.; Podolyák, Z. 100 years of nuclear isomers—Then and now. Phys. Scr. 2020, 95, 044004. [Google Scholar] [CrossRef]
- Ward, R.A.; Fowler, W.A. Thermalization of long-lived nuclear isomeric states under stellar conditions. Astrophys. J. 1980, 238, 266–286. [Google Scholar] [CrossRef]
- Misch, G.W.; Ghorui, S.K.; Banerjee, P.; Sun, Y.; Mumpower, M.R. Astromers: Nuclear Isomers in Astrophysics. Astrophys. J. Suppl. Ser. 2020, 252, 2. [Google Scholar] [CrossRef]
- Mahoney, W.A.; Ling, J.C.; Jacobson, A.S.; Lingenfelter, R.E. Diffuse galactic gamma-ray line emission from nucleosynthetic Fe-60, Al-26, and Na-22—Preliminary limits from HEAO 3. Astrophys. J. 1982, 262, 742–748. [Google Scholar] [CrossRef]
- Diehl, R.; Dupraz, C.; Bennett, K.; Bloemen, H.; Hermsen, W.; Knoedlseder, J.; Lichti, G.; Morris, D.; Ryan, J.; Schoenfelder, V.; et al. COMPTEL observations of Galactic 26Al emission. Astron. Astrophys. 1995, 298, 445. [Google Scholar]
- Lugaro, M.; Karakas, A.I. 26Al and 60Fe yields from AGB stars. New Astron. Rev. 2008, 52, 416–418. [Google Scholar] [CrossRef]
- Coc, A.; Porquet, M.G.; Nowacki, F. Lifetimes of 26Al and 34Cl in an astrophysical plasma. Phys. Rev. C 1999, 61, 015801. [Google Scholar] [CrossRef] [Green Version]
- Gupta, S.S.; Meyer, B.S. Internal equilibration of a nucleus with metastable states: 26 Al as an example. Phys. Rev. C 2001, 64, 025805. [Google Scholar] [CrossRef]
- Runkle, R.; Champagne, A.; Engel, J. Thermal Equilibration of 26Al. Astrophys. J. 2001, 556, 970. [Google Scholar] [CrossRef]
- Iliadis, C.; Champagne, A.; Chieffi, A.; Limongi, M. The effects of thermonuclear reaction rate variations on 26 al production in massive stars: A sensitivity study. Astrophys. J. Suppl. Ser. 2011, 193, 16. [Google Scholar] [CrossRef] [Green Version]
- Banerjee, P.; Misch, G.W.; Ghorui, S.K.; Sun, Y. Effective stellar β-decay rates of nuclei with long-lived isomers: Al 26 and Cl 34. Phys. Rev. C 2018, 97, 065807. [Google Scholar] [CrossRef] [Green Version]
- Reifarth, R.; Fiebiger, S.; Göbel, K.; Heftrich, T.; Kausch, T.; Köppchen, C.; Kurtulgil, D.; Langer, C.; Thomas, B.; Weigand, M. Treatment of isomers in nucleosynthesis codes. Int. J. Mod. Phys. A 2018, 33, 1843011. [Google Scholar] [CrossRef] [Green Version]
- Belic, D.; Arlandini, C.; Besserer, J.; De Boer, J.; Carroll, J.; Enders, J.; Hartmann, T.; Käppeler, F.; Kaiser, H.; Kneissl, U.; et al. Photoactivation of 180 Ta m and Its Implications for the Nucleosynthesis of Nature’s Rarest Naturally Occurring Isotope. Phys. Rev. Lett. 1999, 83, 5242. [Google Scholar] [CrossRef]
- Belic, D.; Arlandini, C.; Besserer, J.; De Boer, J.; Carroll, J.; Enders, J.; Hartmann, T.; Käppeler, F.; Kaiser, H.; Kneissl, U.; et al. Photo-induced depopulation of the 180 Ta m isomer via low-lying intermediate states: Structure and astrophysical implications. Phys. Rev. C 2002, 65, 035801. [Google Scholar] [CrossRef]
- Mohr, P.; Käppeler, F.; Gallino, R. Survival of nature’s rarest isotope Ta 180 under stellar conditions. Phys. Rev. C 2007, 75, 012802. [Google Scholar] [CrossRef] [Green Version]
- Hayakawa, T.; Kajino, T.; Chiba, S.; Mathews, G. New estimate for the time-dependent thermal nucleosynthesis of Ta 180 m. Phys. Rev. C 2010, 81, 052801. [Google Scholar] [CrossRef] [Green Version]
- Parikh, A.; Faestermann, T.; Hertenberger, R.; Krücken, R.; Schafstadler, D.; Wirth, H.F.; Behrens, T.; Bildstein, V.; Bishop, S.; Eppinger, K.; et al. New Cl34 proton-threshold states and the thermonuclear S33(p,γ)Cl34 rate in ONe novae. Phys. Rev. C 2009, 80, 015802. [Google Scholar] [CrossRef]
- Abia, C.; Busso, M.; Gallino, R.; Domínguez, I.; Straniero, O.; Isern, J. The 85 Kr s-process branching and the mass of carbon stars. Astrophys. J. 2001, 559, 1117. [Google Scholar] [CrossRef] [Green Version]
- Misch, G.W.; Sprouse, T.; Mumpower, M. Astromers in the radioactive decay of r-process nuclei. Astrophys. J. Lett. 2021, 913, L2. [Google Scholar] [CrossRef]
- Novikov, Y.N.; Schatz, H.; Dendooven, P.; Béraud, R.; Miehé, C.; Popov, A.; Seliverstov, D.; Vorobjev, G.; Baumann, P.; Borge, M.; et al. Isomeric state of 80 Y and its role in the astrophysical rp-process. Eur. Phys. J. A-Hadron. Nucl. 2001, 11, 257–261. [Google Scholar] [CrossRef]
- Grineviciute, J.; Brown, B.; Schatz, H. The role of excited states in rp-process for sd shell nuclei. arXiv 2014, arXiv:1404.7268. [Google Scholar]
- Chipps, K.; Kozub, R.; Sumithrarachchi, C.; Ginter, T.; Baumann, T.; Lund, K.; Lapierre, A.; Villari, A.; Montes, F.; Jin, S.; et al. K 38 isomer production via fast fragmentation. Phys. Rev. Accel. Beams 2018, 21, 121301. [Google Scholar] [CrossRef] [Green Version]
- Pain, S. NSCL Experiment E18037. 2020. Available online: https://publicapps.nscl.msu.edu/completedExperiments/experiments/view/1154 (accessed on 3 March 2021).
- Doll, C.; Börner, H.; Jaag, S.; Käppeler, F.; Andrejtscheff, W. Lifetime measurement in 176 Lu and its astrophysical consequences. Phys. Rev. C 1999, 59, 492. [Google Scholar] [CrossRef]
- Söderlund, U.; Patchett, P.J.; Vervoort, J.D.; Isachsen, C.E. The 176Lu decay constant determined by Lu–Hf and U–Pb isotope systematics of Precambrian mafic intrusions. Earth Planet. Sci. Lett. 2004, 219, 311–324. [Google Scholar] [CrossRef]
- Albarède, F.; Scherer, E.E.; Blichert-Toft, J.; Rosing, M.; Simionovici, A.; Bizzarro, M. γ-ray irradiation in the early Solar System and the conundrum of the 176Lu decay constant. Geochim. Cosmochim. Acta 2006, 70, 1261–1270. [Google Scholar] [CrossRef]
- Shafer, J.; Brandon, A.; Lapen, T.; Righter, M.; Peslier, A.; Beard, B. Trace element systematics and 147 Sm–143 Nd and 176 Lu–176 Hf ages of Larkman Nunatak 06319: Closed-system fractional crystallization of an enriched shergottite magma. Geochim. Cosmochim. Acta 2010, 74, 7307–7328. [Google Scholar] [CrossRef]
- Bloch, E.; Ganguly, J. 176 Lu–176 Hf geochronology of garnet II: Numerical simulations of the development of garnet-whole-rock 176 Lu–176 Hf isochrons and a new method for constraining the thermal history of metamorphic rocks. Contrib. Mineral. Petrol. 2015, 169, 14. [Google Scholar] [CrossRef]
- Thielemann, F.K.; Arcones, A.; Käppeli, R.; Liebendörfer, M.; Rauscher, T.; Winteler, C.; Fröhlich, C.; Dillmann, I.; Fischer, T.; Martinez-Pinedo, G.; et al. What are the astrophysical sites for the r-process and the production of heavy elements? Prog. Part. Nucl. Phys. 2011, 66, 346–353. [Google Scholar] [CrossRef]
- Fujimoto, S.i.; Hashimoto, M.A. The impact of isomers on a kilonova associated with neutron star mergers. Mon. Not. R. Astron. Soc. 2020, 493, L103–L107. [Google Scholar] [CrossRef]
- Nishimura, S.; Kotake, K.; Hashimoto, M.a.; Yamada, S.; Nishimura, N.; Fujimoto, S.; Sato, K. r-Process Nucleosynthesis in Magnetohydrodynamic Jet Explosions of Core-Collapse Supernovae. Astrophys. J. 2006, 642, 410–419. [Google Scholar] [CrossRef] [Green Version]
- Kuroda, T.; Wanajo, S.; Nomoto, K. The r-Process in Supersonic Neutrino-driven Winds: The Role of the Wind Termination Shock. Astrophys. J. 2008, 672, 1068–1078. [Google Scholar] [CrossRef] [Green Version]
- Nakamura, K.; Kajino, T.; Mathews, G.J.; Sato, S.; Harikae, S. r-process nucleosynthesis in the MHD + neutrino-heated collapsar jet. Astron. Astrophys. 2015, 582, A34. [Google Scholar] [CrossRef] [Green Version]
- Miller, J.M.; Ryan, B.R.; Dolence, J.C.; Burrows, A.; Fontes, C.J.; Fryer, C.L.; Korobkin, O.; Lippuner, J.; Mumpower, M.R.; Wollaeger, R.T. Full transport model of GW170817-like disk produces a blue kilonova. Phys. Rev. D 2019, 100, 023008. [Google Scholar] [CrossRef] [Green Version]
- Miller, J.M.; Sprouse, T.M.; Fryer, C.L.; Ryan, B.R.; Dolence, J.C.; Mumpower, M.R.; Surman, R. Full Transport General Relativistic Radiation Magnetohydrodynamics for Nucleosynthesis in Collapsars. Astrophys. J. 2020, 902, 66. [Google Scholar] [CrossRef]
- Wanajo, S.; Hirai, Y.; Prantzos, N. Neutron star mergers as the astrophysical site of the r-process in the Milky Way and its satellite galaxies. Mon. Not. R. Astron. Soc. 2021, 505, 5862–5883. [Google Scholar] [CrossRef]
- Côté, B.; Fryer, C.L.; Belczynski, K.; Korobkin, O.; Chruślińska, M.; Vassh, N.; Mumpower, M.R.; Lippuner, J.; Sprouse, T.M.; Surman, R.; et al. The Origin of r-process Elements in the Milky Way. Astrophys. J. 2018, 855, 99. [Google Scholar] [CrossRef] [Green Version]
- Sprouse, T.M.; Misch, G.W.; Mumpower, M.R. Radioactive decay of r-process nuclei: Isochronic evolution. arXiv 2021, arXiv:2102.03846. [Google Scholar]
- Meyer, B.; Clayton, D.; The, L.S. Molybdenum and zirconium isotopes from a supernova neutron burst. Astrophys. J. Lett. 2000, 540, L49. [Google Scholar] [CrossRef]
- Bhat, M.R. Evaluated Nuclear Structure Data File (ENSDF). In Nuclear Data for Science and Technology; Research Reports in Physics; Springer: Berlin/Heidelberg, Germany, 1992; pp. 817–821. [Google Scholar] [CrossRef] [Green Version]
- Weisskopf, V.; Wigner, E.P. Calculation of the natural brightness of spectral lines on the basis of Dirac’s theory. Z. Phys. 1930, 63, 54–73. [Google Scholar] [CrossRef]
- Misch, G.W.; Ghorui, S.K.; Sun, Y. Using Steady State Behavior to Assess Treatments of Nuclear Isomers in Astrophysical Environments. arXiv 2018, arXiv:1808.02304. [Google Scholar]
- Lippuner, J.; Roberts, L.F. r-process Lanthanide Production and Heating Rates in Kilonovae. Astrophys. J. 2015, 815, 82. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Y.; Wollaeger, R.T.; Vassh, N.; Surman, R.; Sprouse, T.M.; Mumpower, M.R.; Möller, P.; McLaughlin, G.C.; Korobkin, O.; Kawano, T.; et al. Californium-254 and Kilonova Light Curves. Astrophys. J. Lett. 2018, 863, L23. [Google Scholar] [CrossRef]
- Horowitz, C.J.; Arcones, A.; Côté, B.; Dillmann, I.; Nazarewicz, W.; Roederer, I.U.; Schatz, H.; Aprahamian, A.; Atanasov, D.; Bauswein, A.; et al. r-process nucleosynthesis: Connecting rare-isotope beam facilities with the cosmos. J. Phys. Nucl. Phys. 2019, 46, 083001. [Google Scholar] [CrossRef] [Green Version]
- Côté, B.; Eichler, M.; Yagüe López, A.; Vassh, N.; Mumpower, M.R.; Világos, B.; Soós, B.; Arcones, A.; Sprouse, T.M.; Surman, R.; et al. 129I and 247Cm in meteorites constrain the last astrophysical source of solar r-process elements. Science 2021, 371, 945–948. [Google Scholar] [CrossRef] [PubMed]
- Gao, B.; Zegers, R.; Zamora, J.; Bazin, D.; Brown, B.; Bender, P.; Crawford, H.; Engel, J.; Falduto, A.; Gade, A.; et al. Gamow-Teller transitions to Zr 93 via the Nb 93 (t, He 3+ γ) reaction at 115 MeV/u and its application to the stellar electron-capture rates. Phys. Rev. C 2020, 101, 014308. [Google Scholar] [CrossRef]
- Tan, L.; Liu, Y.X.; Wang, L.J.; Li, Z.; Sun, Y. A novel method for stellar electron-capture rates of excited nuclear states. Phys. Lett. B 2020, 805, 135432. [Google Scholar] [CrossRef]
- Richards, P.; Tucker, W.D.; Srivastava, S.C. Technetium-99 m: An historical perspective. Int. J. Appl. Radiat. Isot. 1982, 33, 793–799. [Google Scholar] [CrossRef]
- Górska, M.; Cáceres, L.; Grawe, H.; Pfützner, M.; Jungclaus, A.; Pietri, S.; Werner-Malento, E.; Podolyák, Z.; Regan, P.; Rudolph, D.; et al. Evolution of the N = 82 shell gap below 132 Sn inferred from core excited states in 131 In. Phys. Lett. B 2009, 672, 313–316. [Google Scholar] [CrossRef]
- Jones, K.; Adekola, A.S.; Bardayan, D.W.; Blackmon, J.C.; Chae, K.; Chipps, K.; Cizewski, J.; Erikson, L.; Harlin, C.; Hatarik, R.; et al. The magic nature of 132 Sn explored through the single-particle states of 133 Sn. Nature 2010, 465, 454–457. [Google Scholar] [CrossRef] [Green Version]
- Jin, H.; Hasegawa, M.; Tazaki, S.; Kaneko, K.; Sun, Y. Large-scale shell-model calculation with core excitations for neutron-rich nuclei beyond 132 Sn. Phys. Rev. C 2011, 84, 044324. [Google Scholar] [CrossRef]
- Wang, H.K.; Sun, Y.; Jin, H.; Kaneko, K.; Tazaki, S. Structure analysis for hole-nuclei close to 132 Sn by a large-scale shell-model calculation. Phys. Rev. C 2013, 88, 054310. [Google Scholar] [CrossRef]
- Surman, R.; Engel, J.; Bennett, J.R.; Meyer, B.S. Source of the Rare-Earth Element Peak in r-Process Nucleosynthesis. Phys. Rev. Lett. 1997, 79, 1809–1812. [Google Scholar] [CrossRef] [Green Version]
- Mumpower, M.R.; McLaughlin, G.C.; Surman, R. Influence of neutron capture rates in the rare earth region on the r-process abundance pattern. Phys. Rev. C 2012, 86, 035803. [Google Scholar] [CrossRef] [Green Version]
- Vilen, M.; Kelly, J.M.; Kankainen, A.; Brodeur, M.; Aprahamian, A.; Canete, L.; Eronen, T.; Jokinen, A.; Kuta, T.; Moore, I.D.; et al. Precision Mass Measurements on Neutron-Rich Rare-Earth Isotopes at JYFLTRAP: Reduced Neutron Pairing and Implications for r -Process Calculations. Phys. Rev. Lett. 2018, 120, 262701. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Orford, R.; Vassh, N.; Clark, J.A.; McLaughlin, G.C.; Mumpower, M.R.; Savard, G.; Surman, R.; Aprahamian, A.; Buchinger, F.; Burkey, M.T.; et al. Precision Mass Measurements of Neutron-Rich Neodymium and Samarium Isotopes and Their Role in Understanding Rare-Earth Peak Formation. Phys. Rev. Lett. 2018, 120, 262702. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vilen, M.; Kelly, J.M.; Kankainen, A.; Brodeur, M.; Aprahamian, A.; Canete, L.; de Groote, R.P.; de Roubin, A.; Eronen, T.; Jokinen, A.; et al. Exploring the mass surface near the rare-earth abundance peak via precision mass measurements at JYFLTRAP. Phys. Rev. C 2020, 101, 034312. [Google Scholar] [CrossRef] [Green Version]
- Vassh, N.; McLaughlin, G.C.; Mumpower, M.R.; Surman, R. Markov Chain Monte Carlo Predictions of Neutron-rich Lanthanide Properties as a Probe of r-process Dynamics. Astrophys. J. 2021, 907, 98. [Google Scholar] [CrossRef]
- Mumpower, M.R.; McLaughlin, G.C.; Surman, R.; Steiner, A.W. The Link between Rare-Earth Peak Formation and the Astrophysical Site of the R Process. Astrophys. J. 2016, 833, 282. [Google Scholar] [CrossRef] [Green Version]
- Mumpower, M.R.; McLaughlin, G.C.; Surman, R.; Steiner, A.W. Reverse engineering nuclear properties from rare earth abundances in the r process. J. Phys. G Nucl. Phys. 2017, 44, 034003. [Google Scholar] [CrossRef] [Green Version]
- Hartley, D.; Kondev, F.; Orford, R.; Clark, J.; Savard, G.; Ayangeakaa, A.; Bottoni, S.; Buchinger, F.; Burkey, M.; Carpenter, M.; et al. Masses and β-Decay Spectroscopy of Neutron-Rich Odd-Odd Eu 160, 162 Nuclei: Evidence for a Subshell Gap with Large Deformation at N = 98. Phys. Rev. Lett. 2018, 120, 182502. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.X.; Lv, C.J.; Sun, Y.; Kondev, F.G. Changes of deformed shell gaps at N 100 in light rare-earth, neutron-rich nuclei. J. Phys. G Nucl. Part. Phys. 2020, 47, 055108. [Google Scholar] [CrossRef]
- Manea, V.; Karthein, J.; Atanasov, D.; Bender, M.; Blaum, K.; Cocolios, T.; Eliseev, S.; Herlert, A.; Holt, J.; Huang, W.; et al. First Glimpse of the N = 82 Shell Closure below Z = 50 from Masses of Neutron-Rich Cadmium Isotopes and Isomers. Phys. Rev. Lett. 2020, 124, 092502. [Google Scholar] [CrossRef] [Green Version]
- ISOLDE Yield Database. Available online: https://isoyields2.web.cern.ch/ (accessed on 3 March 2021).
- Abbott, B.P.; Abbott, R.; Abbott, T.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.; Adya, V.; et al. Multi-messenger Observations of a Binary Neutron Star Merger. Astrophys. J. Lett. 2017, 848, L12. [Google Scholar] [CrossRef]




| Isotope | E (keV) | T (s) | T (s) | B (%) | T | Dominant Astromer Effects |
|---|---|---|---|---|---|---|
| Zn | 438.636 | 0.033 | 3 min | Heating slowed from 1 h to 14 h 439 keV ray at ∼14 h | ||
| Zn | 157.7 | 100 | 20 s | Heating slowed from 2 min to 4 h 386 keV ray at ∼4 h | ||
| Se | 103.00 | 0.051 | 30 s | Heating slowed from 20 min to 1 h | ||
| Kr | 41.5575 | stable | 0 | 2.5 h | 9.4 keV ray, 13 keV X-ray at ∼2 h Faint, but may be visible early | |
| Kr | 304.871 | 78.8 | 3 min | Heating accelerated from 11 yr to 5 h 151 keV ray at 5 h | ||
| Cd | 263.54 | 99.86 | 6 h | Weak 264 keV ray at 14 yr Accelerates production of In | ||
| Cd | 181.0 | 100 | 20 min | Heating slowed from 54 h to 45 d Weak 934 ray at 45 d | ||
| Cd | 136.4 | 100 | 70 s | Heating slowed from 2.5 h to 3.4 h 1997 keV ray possibly observable early | ||
| In | 336.244 | 5.0 | 54 h | 336 keV ray at 4.5 h Accelerates production of Sn | ||
| In | 311.37 | 95.6 | 3 min | Heating slowed from 2.5 min to 18 min | ||
| Sn | 89.531 | stable | 0 | 3–18 min | 24 keV ray, 25 keV X-ray at 293 d | |
| Sn | 6.31 | 22.4 | 4 min | Decay/heating slowed from 27 h to 44 yr 26 keV X-ray, faint 3–4.5 keV X-ray | ||
| Sn | 35.15 | 100 | 1 s | Heating slowed from 2.2 to 7 min | ||
| Sb | 0.0 + X | 96.4 | 1 h | Heating accelerated from 9 h to 10 min | ||
| Sb | 4.8 | 100 | 4 min | Heating accelerated from 40 min to 6.3 min | ||
| Te | 88.23 | 2.4 | 4 d | Heating/decay slowed from 9.4 h to 106 d 27 keV X-ray at 106 d | ||
| Te | 105.51 | 36 | 4.5 h | Heating/decay slowed from 70 min to 34 d 27 keV X-ray, faint 696 keV ray at 34 d | ||
| Te | 182.258 | 74.1 | 23 min | Heating slowed from 25 min to 33 h 774 keV ray, 29 keV X-ray at 33 h | ||
| Te | 334.26 | 83.5 | 2.5 min | Heating slowed from 12.5 min to 1 h | ||
| Xe | 163.930 | stable | 0 | 8 d | 30 keV X-ray at 12 d | |
| Xe | 233.221 | 0 | 21 h | 30 keV X-ray at 2 d | ||
| Ho | 5.969 | 100 | 82 h | Decay/heating slowed from 27 h to 1200 y 184, 280, 712, 810 keV rays, 49 keV X-ray | ||
| Ir | 100 | 95 | 7 min | Feeds Pt isomer | ||
| Pt | 259.077 | stable | 0 | 4 h | 99 keV ray, 8–14, ∼65, ∼75 keV X-ray at 4 d |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Misch, G.W.; Sprouse, T.M.; Mumpower, M.R.; Couture, A.J.; Fryer, C.L.; Meyer, B.S.; Sun, Y. Sensitivity of Neutron-Rich Nuclear Isomer Behavior to Uncertainties in Direct Transitions. Symmetry 2021, 13, 1831. https://doi.org/10.3390/sym13101831
Misch GW, Sprouse TM, Mumpower MR, Couture AJ, Fryer CL, Meyer BS, Sun Y. Sensitivity of Neutron-Rich Nuclear Isomer Behavior to Uncertainties in Direct Transitions. Symmetry. 2021; 13(10):1831. https://doi.org/10.3390/sym13101831
Chicago/Turabian StyleMisch, G. Wendell, Trevor M. Sprouse, Matthew R. Mumpower, Aaron J. Couture, Chris L. Fryer, Bradley S. Meyer, and Yang Sun. 2021. "Sensitivity of Neutron-Rich Nuclear Isomer Behavior to Uncertainties in Direct Transitions" Symmetry 13, no. 10: 1831. https://doi.org/10.3390/sym13101831






