Development and Investigation of Fully Ventilated Deep Subwavelength Absorbers
Abstract
:1. Introduction
2. Analysis of the Ventilated AMM Absorber
2.1. Structure of the Ventilated AMM Absorber
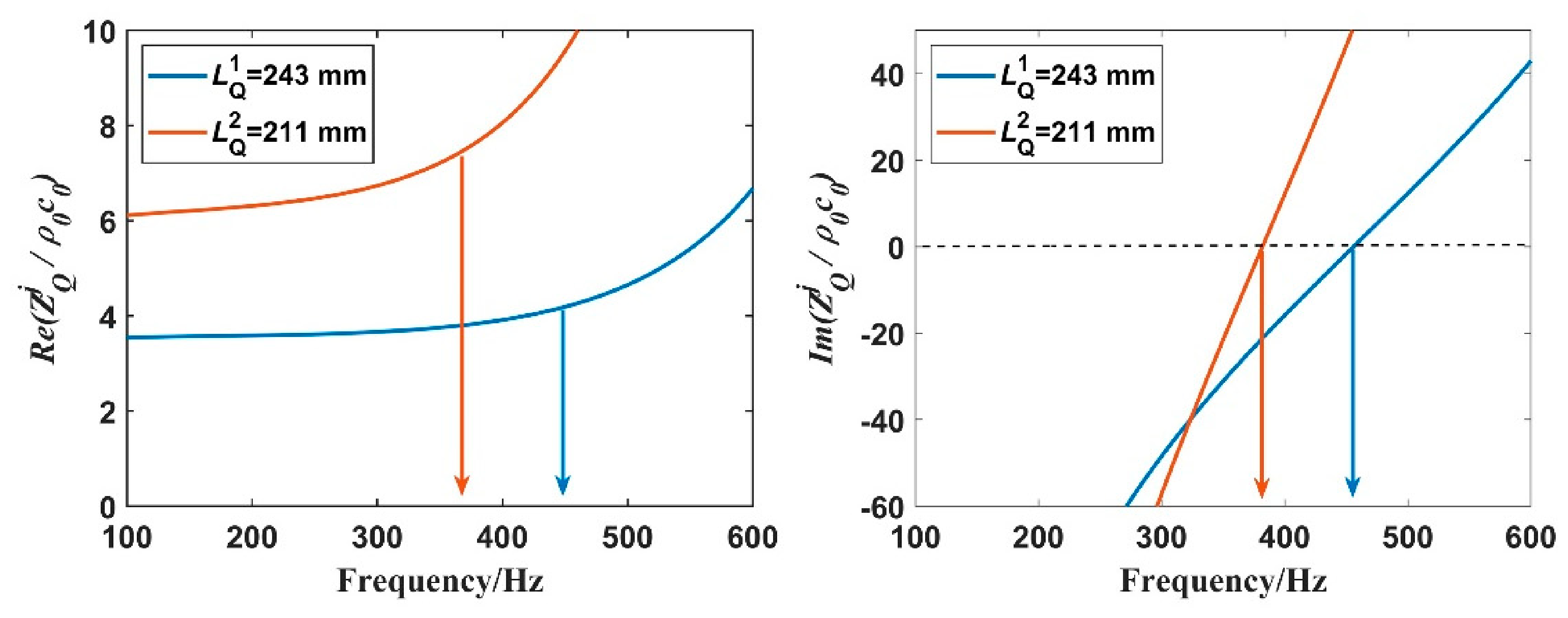
2.2. Sound Absorption Coefficient
2.3. Transmission Loss Based on Transfer Matrix
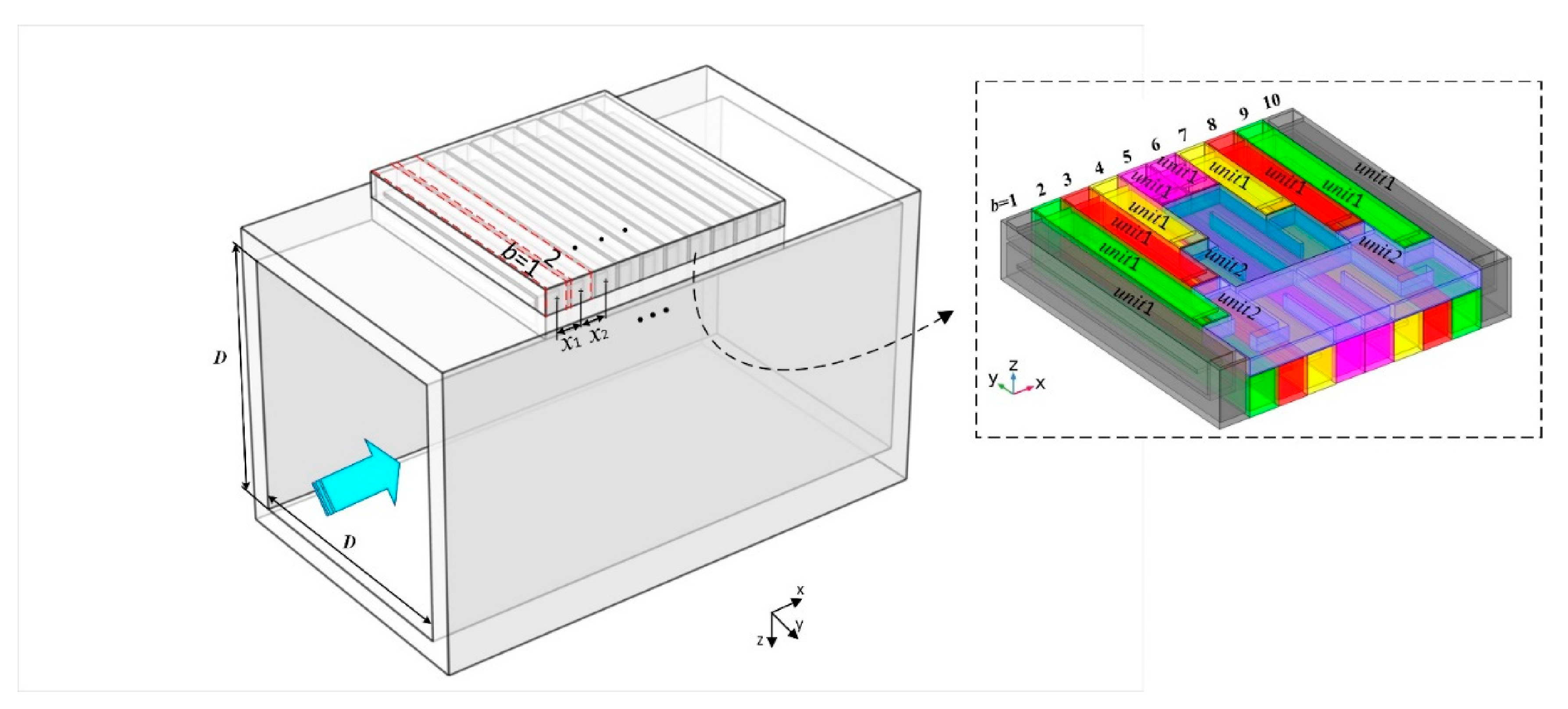
3. Comparison and Analysis of the Results of the Experiment and Calculations
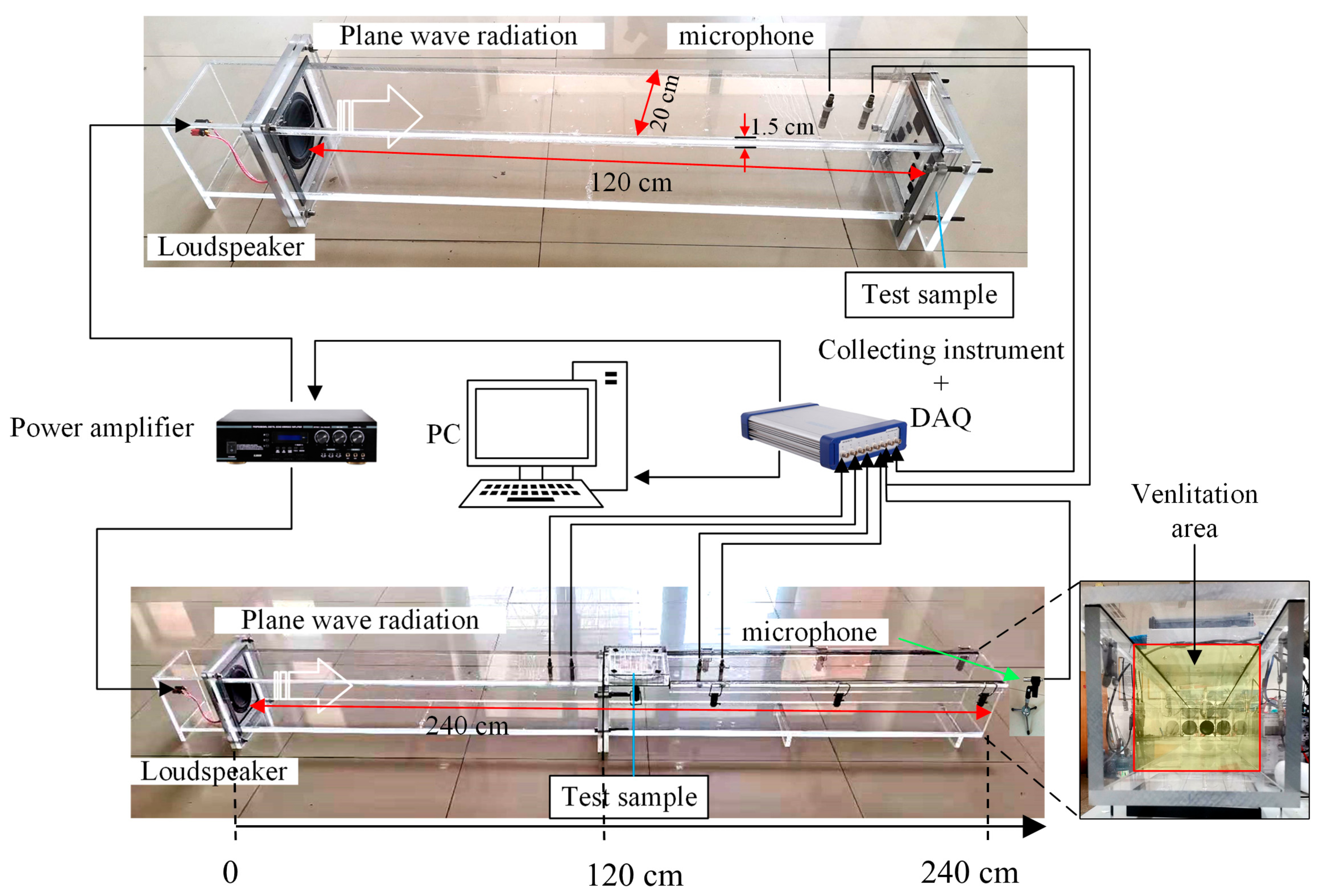
3.1. Experiment Setup
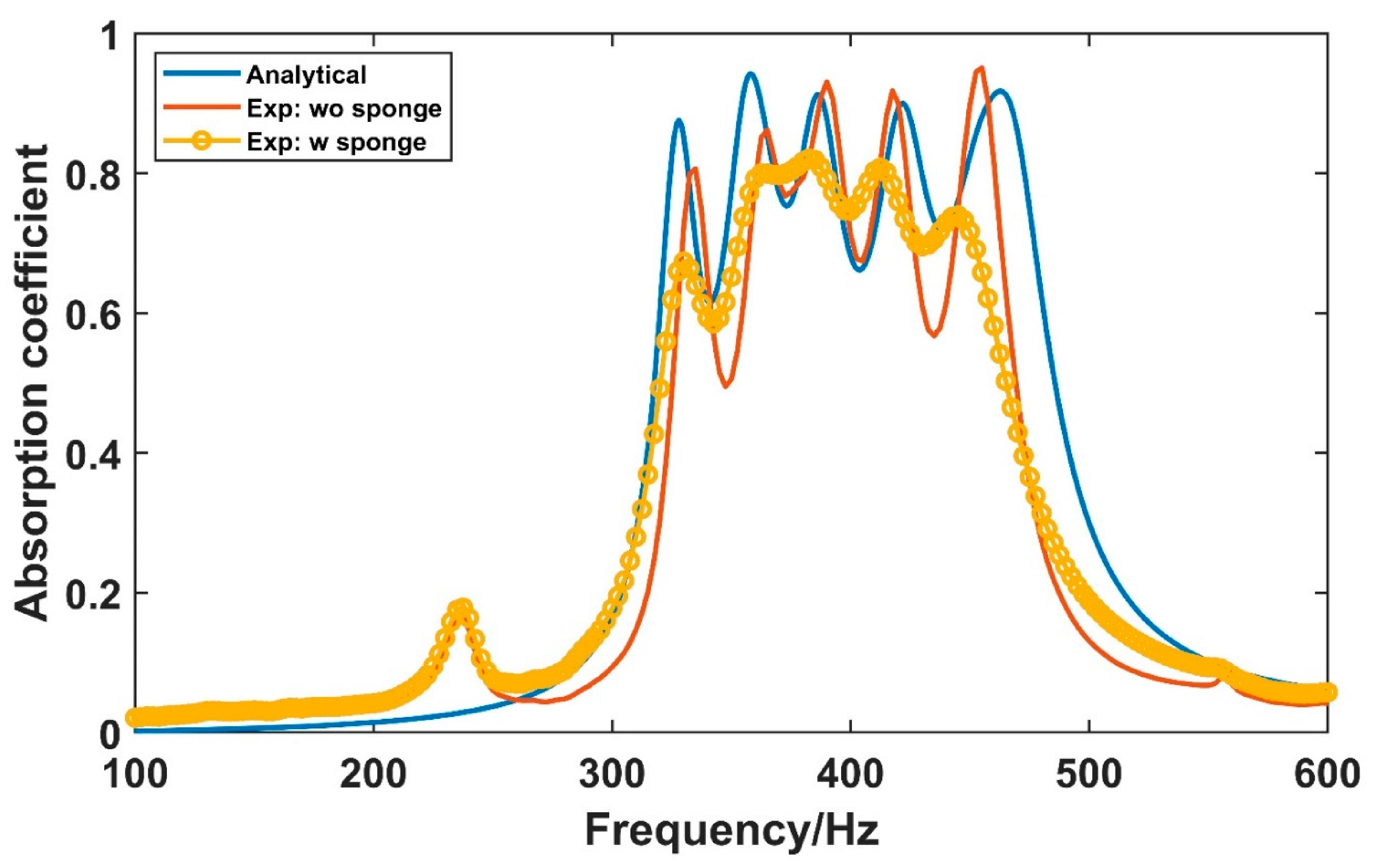
3.2. Sound Absorption
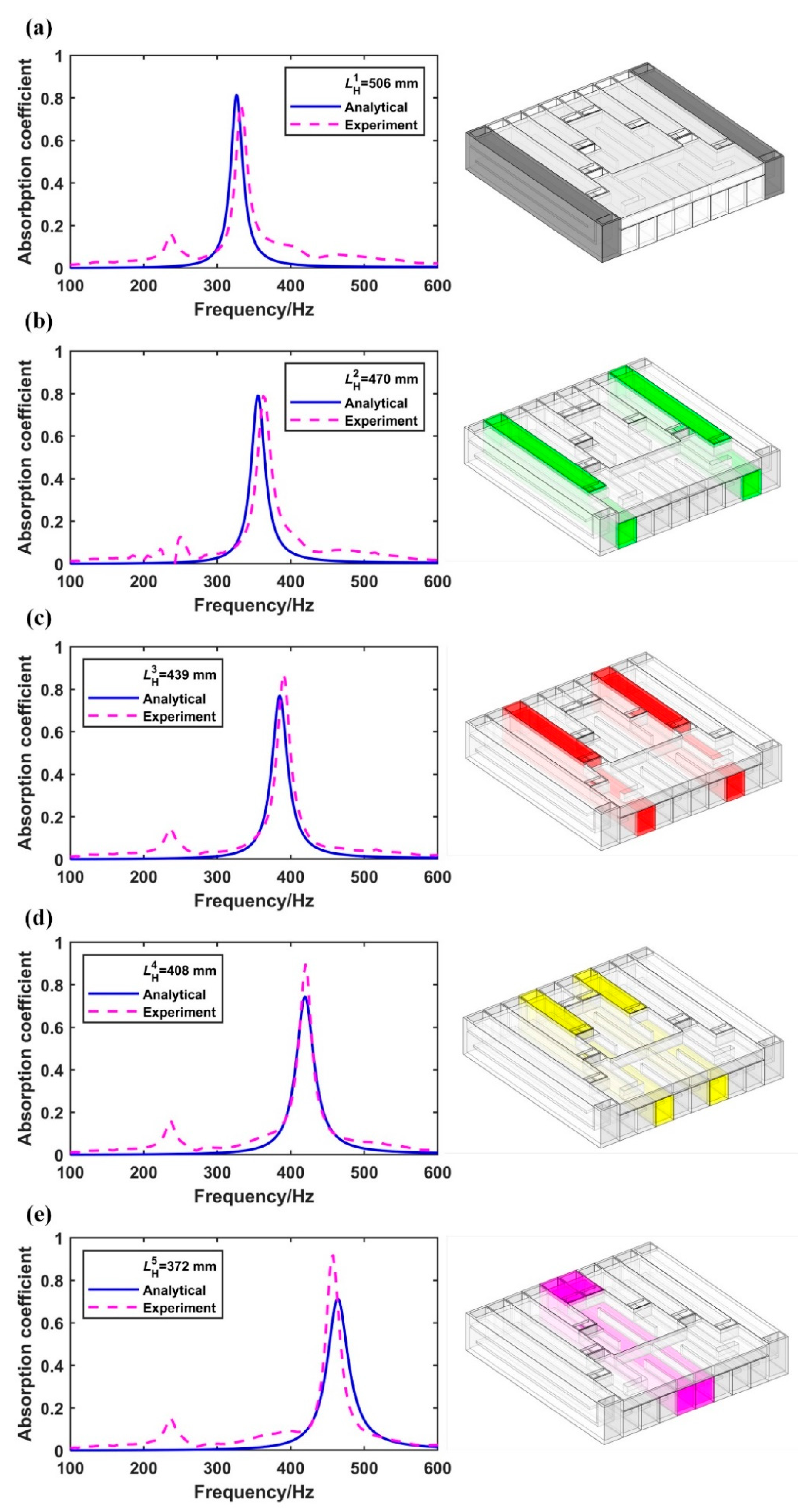
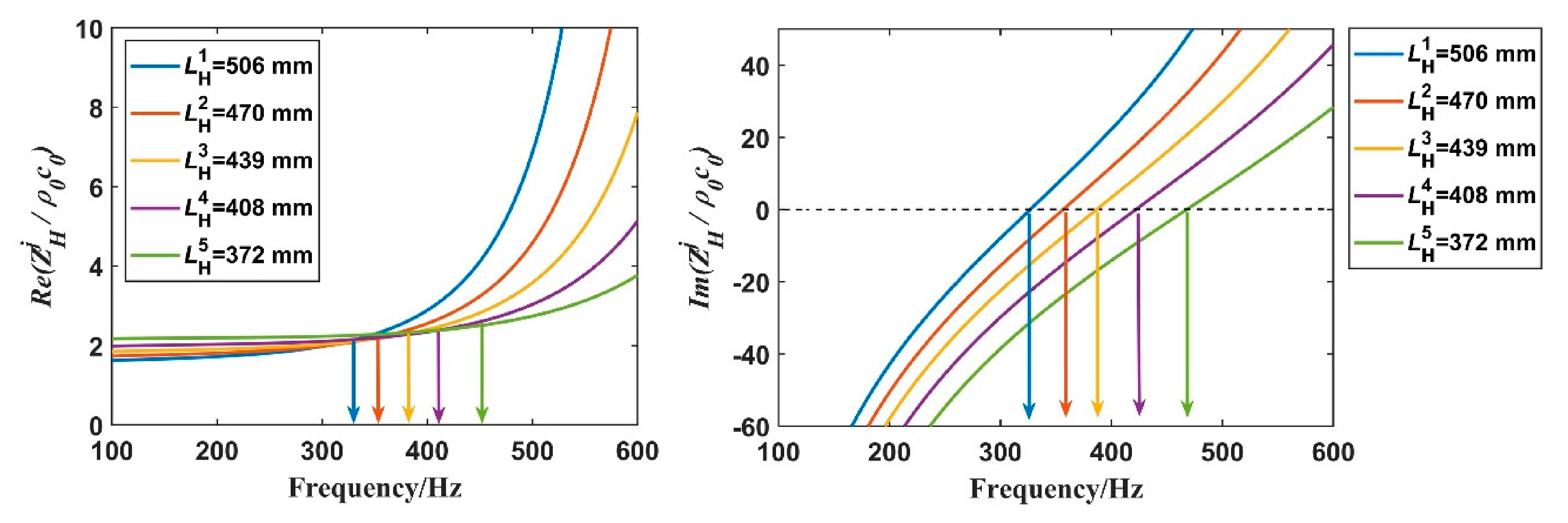
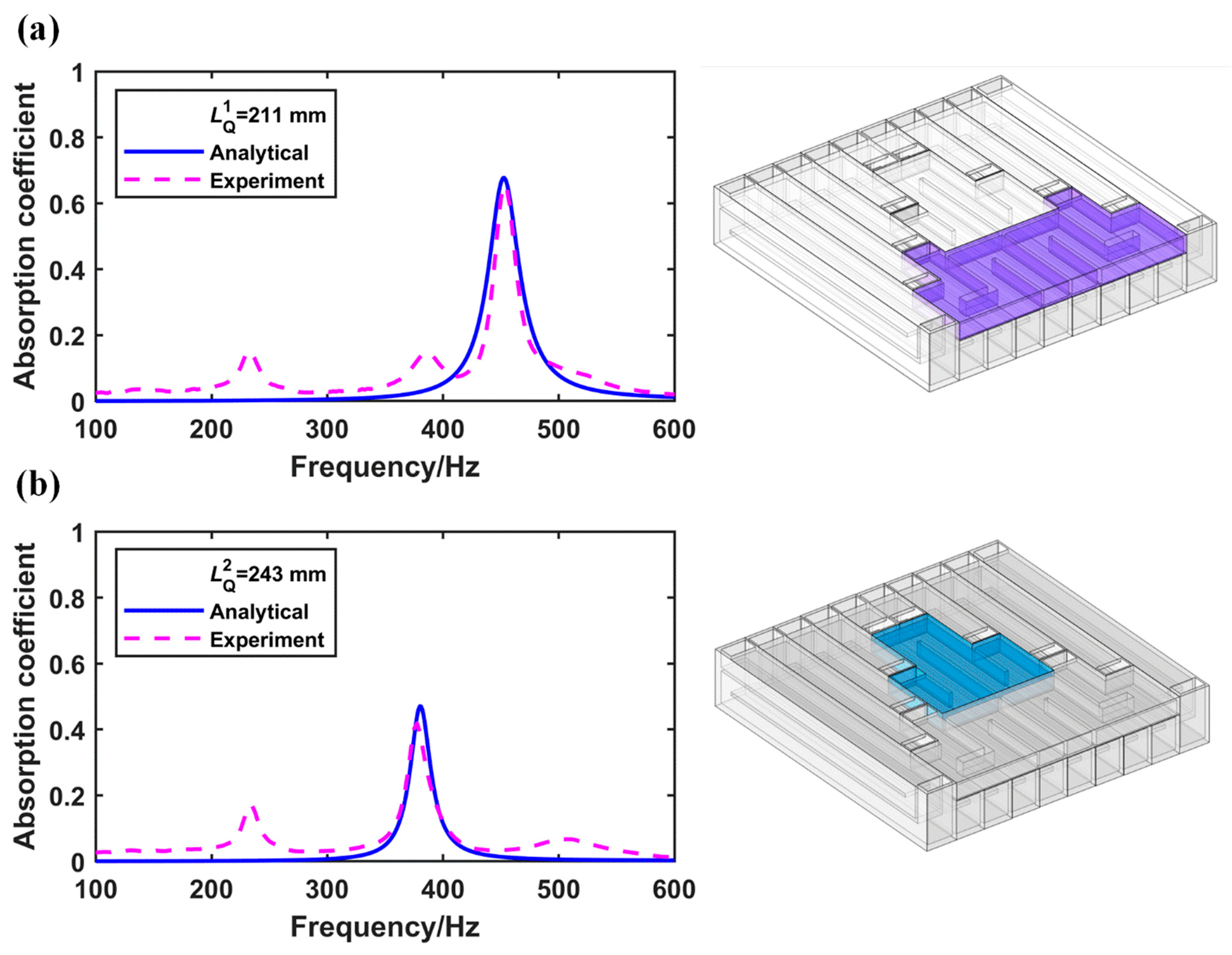
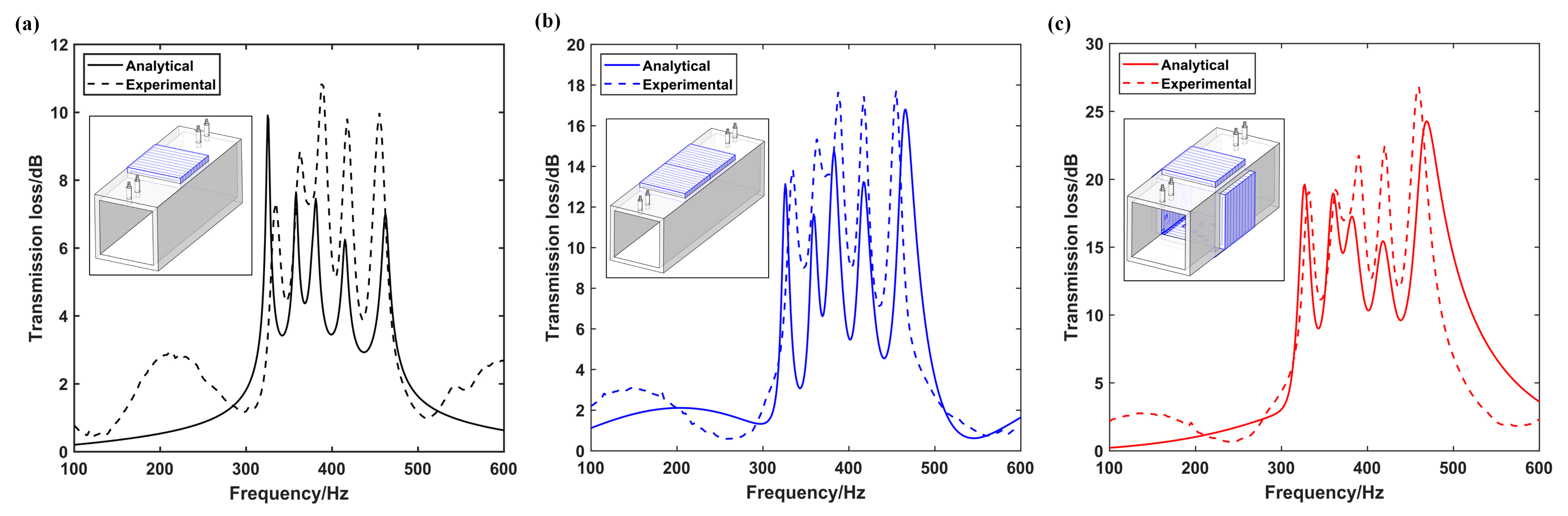
3.3. Sound Transmission Loss (TL) Performance for Complete Cross-Ventilation
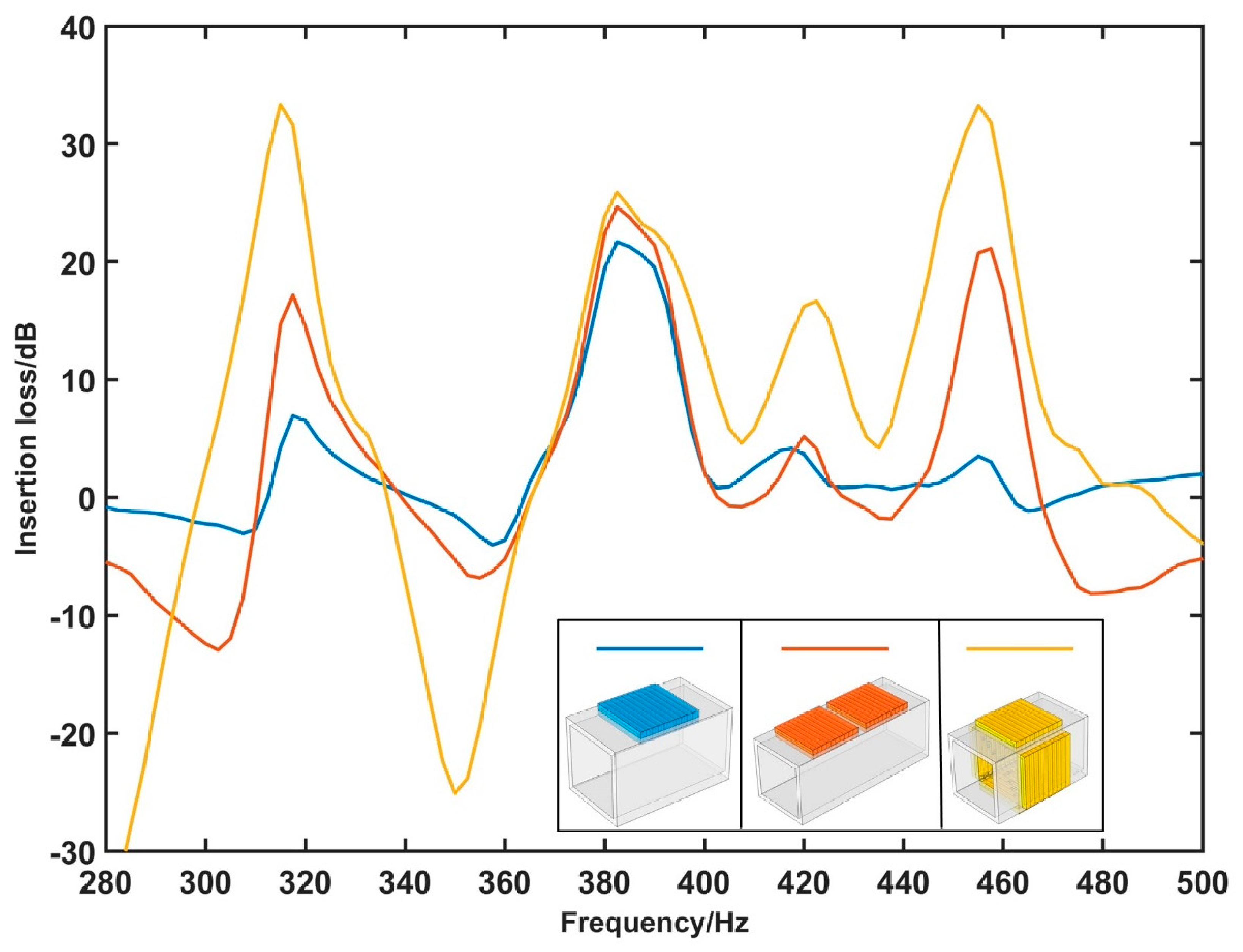
3.4. Sound Insertion Loss (IL) Performance for Complete Cross-Ventilation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Babisch, W.; Beule, B.; Schust, M.; Kersten, N.; Ising, H. Traffic noise and risk of myocardial infarction. Epidemiology 2005, 16, 33–40. [Google Scholar] [CrossRef] [PubMed]
- Dratva, J.; Phuleria, H.C.; Foraster, M.; Gaspoz, J.M.; Keidel, D.; Kunzli, N.; Liu, L.J.; Pons, M.; Zemp, E.; Gerbase, M.W.; et al. Transportation noise and blood pressure in a population-based sample of adults. Environ. Health Perspect. 2012, 120, 50–55. [Google Scholar] [CrossRef] [PubMed]
- Miedema, H.; Groothuis-Oudshoorn, C. Annoyance from Transportation Noise: Relationships with Exposure Metrics DNL and DENL and Their Confidence Intervals. Environ. Health Perspect. 2001, 109, 409–416. [Google Scholar] [CrossRef] [PubMed]
- Minichilli, F.; Gorini, F.; Ascari, E.; Bianchi, F.; Coi, A.; Fredianelli, L.; Licitra, G.; Manzoli, F.; Mezzasalma, L.; Cori, L. Annoyance Judgment and Measurements of Environmental Noise: A Focus on Italian Secondary Schools. Int. J. Environ. Res. Public Health 2018, 15, 208. [Google Scholar] [CrossRef] [Green Version]
- Muzet, A. Environmental noise, sleep and health. Sleep Med. Rev. 2007, 11, 135–142. [Google Scholar] [CrossRef]
- Rossi, L.; Prato, A.; Lesina, L.; Schiavi, A. Effects of low-frequency noise on human cognitive performances in laboratory. Build. Acoust. 2018, 25, 17–33. [Google Scholar] [CrossRef]
- Vukic, L.; Mihanovic, V.; Fredianelli, L.; Plazibat, V. Seafarers’ Perception and Attitudes towards Noise Emission on Board Ships. Int. J. Environ. Res. Public Health 2021, 18, 6671. [Google Scholar] [CrossRef]
- Zacarías, F.F.; Molina, R.H.; Ancela, J.L.C.; López, S.L.; Ojembarrena, A.A. Noise Exposure in Preterm Infants Treated with Respiratory Support Using Neonatal Helmets. Acta Acust. United Acust. 2013, 99, 590–597. [Google Scholar] [CrossRef]
- Fatima, S.; Mohanty, A.R. Acoustical and fire-retardant properties of jute composite materials. Appl. Acoust. 2011, 72, 108–114. [Google Scholar] [CrossRef]
- Guan, D.; Wu, J.H.; Wu, J.; Li, J.; Zhao, W. Acoustic performance of aluminum foams with semiopen cells. Appl. Acoust. 2015, 87, 103–108. [Google Scholar] [CrossRef]
- Han, F.; Seiffert, G.; Zhao, Y.; Gibbs, B.M. Acoustic absorption behaviour of an open-celled aluminium foam. J. Phys. D Appl. Phys. 2003, 36, 294–302. [Google Scholar] [CrossRef] [Green Version]
- Hur, B.Y.; Park, B.K.; Ha, D.-I.; Um, Y.S. Sound Absorption Properties of Fiber and Porous Materials. Mater. Sci. Forum 2005, 475–479, 2687–2690. [Google Scholar] [CrossRef]
- Kim, K.W.; Jeong, Y.-S. Experimental Study on the Comparison of the Material Properties of Glass Wool Used as Building Materials. Mater. Sci. 2014, 20, 103–107. [Google Scholar] [CrossRef] [Green Version]
- Xiang, H.-F.; Tan, S.-X.; Yu, X.-L.; Long, Y.-H.; Zhang, X.-L.; Zhao, N.; Xu, J. Sound absorption behavior of electrospun polyacrylonitrile nanofibrous membranes. Chin. J. Polym. Sci. 2011, 29, 650–657. [Google Scholar] [CrossRef]
- Eerden, F. Noise Reduction with Coupled Prismatic Tubes. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 2000. [Google Scholar]
- Liu, Z.; Zhang, X.; Mao, Y.; Zhu, Y.Y.; Yang, Z.; Chan, C.T.; Sheng, P. Locally resonant sonic materials. Science 2000, 289, 1734–1736. [Google Scholar] [CrossRef]
- Almeida, G.d.N.; Vergara, E.F.; Barbosa, L.R.; Brum, R. Low-frequency sound absorption of a metamaterial with symmetrical-coiled-up spaces. Appl. Acoust. 2021, 172, 107593. [Google Scholar] [CrossRef]
- Chang, H.; Liu, L.; Zhang, C.; Hu, X. Broadband high sound absorption from labyrinthine metasurfaces. AIP Adv. 2018, 8, 045115. [Google Scholar] [CrossRef] [Green Version]
- Jiménez, N.; Huang, W.; Romero-García, V.; Pagneux, V.; Groby, J.P. Ultra-thin metamaterial for perfect and quasi-omnidirectional sound absorption. Appl. Phys. Lett. 2016, 109, 121902. [Google Scholar] [CrossRef]
- Long, H.; Liu, C.; Shao, C.; Cheng, Y.; Chen, K.; Qiu, X.; Liu, X. Subwavelength broadband sound absorber based on a composite metasurface. Sci. Rep. 2020, 10, 13823. [Google Scholar] [CrossRef]
- Wu, F.; Xiao, Y.; Yu, D.; Zhao, H.; Wang, Y.; Wen, J. Low-frequency sound absorption of hybrid absorber based on micro-perforated panel and coiled-up channels. Appl. Phys. Lett. 2019, 114, 151901. [Google Scholar] [CrossRef]
- Jiang, X.; Liang, B.; Li, R.-q.; Zou, X.-y.; Yin, L.-l.; Cheng, J.-c. Ultra-broadband absorption by acoustic metamaterials. Appl. Phys. Lett. 2014, 105, 243505. [Google Scholar] [CrossRef]
- Almeida, G.d.N.; Vergara, E.F.; Barbosa, L.R.; Lenzi, A.; Birch, R.S. A low-frequency sound absorber based on micro-slit and coiled cavity. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 1–9. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.; Xie, S. A lightweight multilayer honeycomb membrane-type acoustic metamaterial. Appl. Acoust. 2020, 168, 107427. [Google Scholar] [CrossRef]
- Lu, Z.; Yu, X.; Lau, S.-K.; Khoo, B.C.; Cui, F. Membrane-type acoustic metamaterial with eccentric masses for broadband sound isolation. Appl. Acoust. 2020, 157, 107003. [Google Scholar] [CrossRef]
- Zhang, H.-L.; Zhu, Y.-F.; Liang, B.; Yang, J.; Yang, J.; Cheng, J.-C. Omnidirectional ventilated acoustic barrier. Appl. Phys. Lett. 2017, 111, 203502. [Google Scholar] [CrossRef] [Green Version]
- Fusaro, G.; Yu, X.; Kang, J.; Cui, F. Development of metacage for noise control and natural ventilation in a window system. Appl. Acoust. 2020, 170, 107510. [Google Scholar] [CrossRef]
- Komkin, A.I.; Mironov, M.A. Radiation impedance of a piston at the wall of a rectangular duct. Acoust. Phys. 2013, 59, 257–260. [Google Scholar] [CrossRef]
- Cummings, A. Sound Propagaton In Narrow Tubes Of Arbitrary Cross-section. J. Sound Vib. 1993, 162, 27–42. [Google Scholar] [CrossRef]
- Stinson, M. The propagation of plane sound waves in narrow and wide circular tubes, and generalization to uniform tubes of arbitrary cross-sectional shape. J. Acoust. Soc. Am. 1991, 89, 550–558. [Google Scholar] [CrossRef]
- Desantes, J.M.; Torregrosa, A.J.; Climent, H.; Moya, D. Acoustic performance of a Herschel–Quincke tube modified with an interconnecting pipe. J. Sound Vib. 2005, 284, 283–298. [Google Scholar] [CrossRef]
- Labašová, E.; Ďuriš, R. Measurement of the Acoustic Absorption Coefficient by Impedance Tube. Res. Pap. Fac. Mater. Sci. Technol. Slovak Univ. Technol. 2019, 27, 94–101. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.S.; He, H.; Geng, A.L. Comparison and application of the experimental methods for multi-layer prediction of acoustical properties of noise control materials in standing wave-duct systems. Appl. Acoust. 2008, 69, 847–857. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Mao, Q. Development and Investigation of Fully Ventilated Deep Subwavelength Absorbers. Symmetry 2021, 13, 1835. https://doi.org/10.3390/sym13101835
Wang H, Mao Q. Development and Investigation of Fully Ventilated Deep Subwavelength Absorbers. Symmetry. 2021; 13(10):1835. https://doi.org/10.3390/sym13101835
Chicago/Turabian StyleWang, Heng, and Qibo Mao. 2021. "Development and Investigation of Fully Ventilated Deep Subwavelength Absorbers" Symmetry 13, no. 10: 1835. https://doi.org/10.3390/sym13101835
APA StyleWang, H., & Mao, Q. (2021). Development and Investigation of Fully Ventilated Deep Subwavelength Absorbers. Symmetry, 13(10), 1835. https://doi.org/10.3390/sym13101835




