Abstract
Based on the current background of airport management and flight-gate scheduling in China, this paper takes Shanghai Pudong International Airport’s flight number of the rising and landing aircraft in a certain day as the research object, and it establishes an uncertain FGAP (Flight-Gate Assignment Problem) multi-objective programming model under the framework of uncertainty theory. Using genetic algorithm to solve the model, the specific flight-gate assignment scheduling plan is given. The research results show that the model in this paper can effectively alleviate the problems, such as unbalanced flight-gate allocation and excessive operating pressure of a single gate, in the conventional model, and make the allocation and scheduling more reasonable and efficient. Finally, we give the future application of uncertainty theory in finance and management, as well as the prospect of combining it with symmetry in physics.
1. Introduction
According to the “National Civil Airport Layout Plan” issued by the State Council of China, by 2020, the total number of civil aviation transportation airports in China have reached 244, with 97 newly added airports [1]. With the increase in the total number of airports, passenger flow has also increased exponentially, and the daily passenger flow of many airports has approached supersaturation. Therefore, how to optimize flight-gate scheduling and reduce the pressure on airport operations is becoming more and more important for airport operators.
Symmetry is the most important physical law in physics theory. It describes the invariance under a certain transformation. Both it and uncertainty are general procedures for re-evolution within consciousness. In addition to having an important connection with symmetry in the field of quantum mechanics, uncertainty has also grown rapidly in the field of mathematics. As a system parallel to probability theory, uncertainty theory has gradually developed since 2000 [2]. In 2004, Liu proposed concepts, such as credibility measurement, in 2007, he established the uncertainty theory system for the first time and in 2010, systematized it, making it a mathematical system that conforms to the normality axiom, duality axiom, subadditivity axiom, and product axiom [3]. In addition, in the time since then, the framework has been continuously completed, and now a conceptual system containing uncertain planning, uncertain risk analysis, uncertainty credibility analysis, uncertain statistics, and uncertain differential equations has been formed. As usually studied, probability theory usually deals with the problem of having sufficient sample data, and the sample frequency is studied under its system. However, in real life, there are often data failure or variable uncertainty. Under the exploration of this phenomenon, the uncertainty theory has emerged. This theoretical system mainly studies sample reliability, can solve indecisive phenomena in the absence of data or invalid historical data, and is excellently applied to real life. As a young system with a relatively short development time, there are few research studies on uncertain theoretical goal programming problem. Wang et al. [4] used the uncertainty theory to study the multi-objective combat planning of UAVs, regarded the variables involved in the combat process as uncertain variables, and carried out model construction and problem analysis; Wei [5] studied the transportation problem of hazardous chemicals under the framework of uncertainty theory.
The problem of flight scheduling has always been a key concern of the airport industry, Avella et al. [6] proposed a MIP method to solve to optimality real-life instances from congested airports. Flight-Gate Assignment Problem (FGAP) is a concrete manifestation of flight scheduling, belongs to a class of optimization problems [7]. The main goal of this problem is to allocate each pair of flights to an available boarding gate, which could limit allocation of existing airport resources, and convenience of passengers and the operational efficiency of the airport can be improved as much as possible, so that the airport can be operated more efficiently [8]. Ornek et al. [9] had proposed FGAP as an integer and constraint programming model formulations. They realize efficient scheduling by considering integer and constraint programming models in mathematics. In 2006, Drexl et al. [10] had formulated fuzzy multicriteria flight gate assignment. This literature deals with a special kind of multi-criteria multi-mode resource constrained project scheduling problem with generalized priority constraints or time windows. Marinelli [11] developed a metaheuristic approach, which could solve high level combinatorial problems with fast convergence performances. Based on above discussion, a survey of the airport Gate Assignment Problem was uncovered in 2014 [12].
Based on the current background of China’s airport management and flight-gate scheduling, this paper makes an empirical analysis with the flight schedule of aircraft on a certain day at Shanghai Pudong International Airport as the research object. Considering the influence of uncertain factors, such as flight delays and temporary transfer of passengers, an FGAP multi-objective programming model based on uncertainty theory is constructed. The conventional FGAP multi-objective programming model and the FGAP multi-objective programming model based on the uncertainty theory are solved by using genetic algorithm, respectively. By comparing the model results, an efficient and reasonable flight-gate scheduling plan is given, which provides reference for the airport flight-gate scheduling. At the end of the article, the conclusion and prospect of this research are given.
The work of this paper lies as follows: the FGAP multi-objective programming under the uncertainty theory system, which is mainly explored in this paper, is still almost in a blank state at present. On the other hand, because probability theory is based on the idea of frequency of a large number of repeated experiments, and, in the actual airport scheduling scenario, the uncertain factors, such as flight delays, cannot be ignored, and temporary scheduling sample data is scarce. Uncertainty theory is used to replace the traditional probability theory method will be more accurate and practical, and it can provide more reasonable and effective reference opinions for airport flight-gate scheduling.
The overall structure of this article is as follows: Section 2 describes and introduces FGAP frame. Section 3 takes Shanghai Pudong International Airport as an example to conduct empirical analysis, establish models, and provide specific applications. Finally, the conclusion and prospect are given in Section 4.
2. FGAP Frame
The assignment docking process is shown in Figure 1. In order to facilitate the understanding of the FGAP process, some proper terms involved in the problem are introduced as follows:
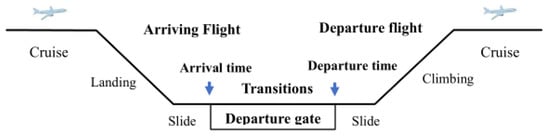
Figure 1.
Aircraft docking diagram.
(1) Neutral interval: The time interval between two adjacent aircraft at the same gate is generally required to be more than 45 min [13].
(2) Transit process time: the time it takes for the transit passenger to complete the process of stopping the flight.
(3) MRT time: MRT (Mass Rapid Transit) refers to the line inside the airport that connects the terminal building and the satellite hall, and the MRT time refers to the travel time of passengers using this line.
(4) Transit time: the difference between the departure time of the next flight and the arrival time of the previous flight [14].
(5) Transit tension: the ratio of the transit time of the transit passenger to the transit time, where the transit time of the transit passenger = transit process time + MRT time + passenger walking time [15].
3. Analysis of Flight-Gate Assignment and Scheduling at Shanghai Pudong International Airport
3.1. Data Sources
This study takes Shanghai Pudong International Airport, which has a relatively large domestic passenger flow and is more representative at present, as an example and selects the flight data of China Eastern Airlines and Shanghai Pudong International Airport on a certain day for empirical analysis. On that day, there were 2755 transit passengers, 1652 groups of fellow transit passengers, 252 transit flights, and 69 available boarding gates. Specifically, it includes the precise time and type of arrival of each transfer flight, the departure time and type of departure from the airport, transfer passenger information, and gate assignment information.
3.2. Research Methods
The typical flight-gate assignment problem is to reduce the number of gates used and the transfer tension of transit passengers as much as possible when the flights and gates are matched, as well as to arrange the number of flights to the maximum, so as to maximize resource utilization. Most scholars currently study airport scheduling in a certain environment. However, in real life, the airport often has uncertain factors, such as flight delays, cancellations, or temporary passenger transfers due to weather, which will have a certain impact on the original scheduling plan [16]. In view of this, we put the problem into the uncertainty theory system for research and establish the FGAP multi-objective programming model based on the uncertainty theory. Taking into account the impact of COVID-19 crisis on the airport industry, it is assumed that the airport strictly complies with Shanghai’s local epidemic prevention and control regulations, and the airport can operate normally without a potential epidemic.
(1). Objective function
Optimization goal 1: Arrange as many flight departures as possible, and reduce passenger flow and pressure at the airport, that is, to maximize the number of flights allocated:
where represents each flight on the day of the airport, and is the number of flights.
Optimization goal 2: Use as few gates as possible, and reduce airport operating costs, that is, to minimize the number of gates used by flights:
where represents usage of the gates, and is the number of gates.
Optimization goal 3: Ensure the smooth transfer of transit passengers, and improve passengers’ satisfaction, that is, to minimize the transit tension of transit passengers:
where represents the transfer tension of transit passengers, is the set of passengers who need to transfer, represents the time transit passengers take to complete the transfer process, represents the time transit passengers spend on MRT process, represents the time spent by transit passengers on foot, and represents transit passengers corresponding transit time.
(2). Constraint conditions
(a) Uniqueness constraint:
where represents allocation of flights and gates, to ensure that each flight can only stop at one gate.
(b) Restrictions on the use of gate:
where , meaning that the gate has been used; when , it means that the gate has not been used.
(c) Flight allocation constraint:
when , it means that the flight is assigned to the gate .
(d) Time constraint of neutral interval
where represents departure time, represents arrival time, and represents the time interval between two successive flights using the same gate. That is, the time interval between arrival and departure between two adjacent flights at the same gate should be greater than or equal to the specified neutral interval.
(e) Flight type matching constraint:
where represents type of gates, = 1 corresponding narrow-body aircraft, and = 2 corresponding wide-body aircraft; represents type of flights, = 1 corresponds to narrow-body aircraft, and = 2 corresponds to wide-body aircraft. That is, if the aircraft type matches the flight type, the flight type of the narrow-body aircraft can be arranged at the gate of the wide-body aircraft, while the flight type of the wide-body aircraft cannot be arranged at the gate of the narrow-body aircraft.
(f) Flight attribute matching constraint:
where represents attributes of gates, = 1 corresponding domestic, = 2 corresponding international; represents attributes of flights, = 1 corresponding domestic, and = 2 corresponding international. That is, according to the attribute matching of the flight and the gate, domestic flights can only stop at the boarding gate of domestic flights, and international flights can only stop at the boarding gate of international flights.
(g) Passenger safety distance restriction:
where represents safe distance between transit passengers, to ensure compliance with the requirement that the safety distance between people in the epidemic should be greater than or equal to 1 m.
Let denote the number of allocated flights, the number of gates used, and the transfer tension of transit passengers, respectively, and the FGAP multi-objective programming model based on uncertainty theory can be constructed as follows:
In view of the uncertain variables cannot be solved directly, first, find their expected value and use the Theorem to transform the above uncertain model into an equivalent deterministic model form:
Theorem [17].
Assume that the objective functionis strictly mono-increased toand strictly mono-decremented to; at the same time, the constraint functionis strictly mono-incremented toand strictly mono-decremented to. In addition, ifare mutually independent uncertain variables and obey the uncertain distribution, respectively, then the uncertain multi-objective programming model is
equivalent to deterministic multi-objective programming model
Due to the conflicts between the three goals involved, the article uses the “linear weighting method” to transform the aforementioned multi-objective determination model into a single-objective mathematical model, and it turns to find its Pareto effective solution under the uncertainty theory system. Substituting the values to get the final FGAP multi-objective programming model based on uncertainty theory:
3.3. Specific Model Establishment
In this case, , , and . It is assumed that the uncertain variables , and are monotonically increasing; the uncertain variables obey the linear uncertainty distribution, the uncertain variables obey the normal uncertainty distribution, and each uncertain variable satisfies , , . Therefore, the inverse uncertainty distributions of each uncertain variable are:
Thus, the deterministic form of FGAP multi-objective programming model based on uncertainty theory can be obtained:
And the constraint conditions are the same as above.
Let , , and , respectively, which means that the first thing we want to achieve in the flight-gate assignment problem is to make full use of the number of flights as much as possible and further reduce the number of gates used [18]. On the basis of achieving the above two goals, the transfer tension of transit passengers is minimized and passenger comfort is improved. Getting the case’s FGAP multi-objective programming model based on uncertainty theory:
3.4. Model Solving and Result Analysis
FGAP is a Non-deterministic Polynomial Hard (NPH) problem. For such problems, heuristic algorithms are often used to solve them [19]. We use genetic algorithm to solve the FGAP model under uncertain conditions, and we calculate the shortest path for airport scheduling. The research results of Yu et al. [19] show that under similar data volume, the parameters can be directly set as follows: Set the population size to 300, the maximum number of iterations to 100, the crossover probability to 0.8, and the mutation probability to 0.2. The average running time is 7.3 s, and the path optimal value is reached after 38 iterations. The result is shown in the Figure 2, and the maximum value of the image is the shortest path length sought. It can be seen that the shortest path obtained by genetic algorithm is about 4100, which is the total length of the route scheduled for Shanghai Pudong International Airport on the day of temporary cancellation of flights and temporary transfers of passengers.
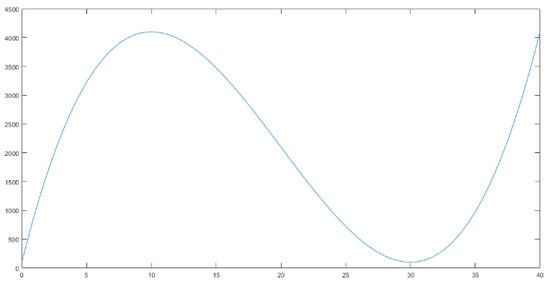
Figure 2.
The shortest path for scheduling using GA.
Regarding the flight number, the usage of the boarding gate, and the transfer tension of the transit passengers in the objective function as ordinary variables, without changing the constraint conditions, we establish the conventional FGAP multi-objective programming model. Furthermore, use the genetic algorithm to solve the conventional FGAP multi-objective programming model and the FGAP multi-objective programming model based on uncertainty theory, compare the flight-gate allocation and scheduling situation of the two models, and draw the Gantt chart of the scheduling results.
It is obvious that, after considering the number of flights, the number of gates, and the tension of the transit passengers as uncertain variables, the airport’s flight-gate assignment and dispatching situation has been greatly improved. Without considering the influence of uncertain factors, the result shown in Figure 3 can be obtained. It can be seen from the figure that, although the resources of each gate are fully utilized, there are problems, such as unbalanced flight-gate allocation, excessive pressure on the operation of a single gate, and insufficient connections between flights. For example, T3, T5, T6, and T10 boarding gates all have “flight relay” phenomenon. One flight has just ended, and the next flight will start immediately, which makes the boarding gate lack of rest adjustment time and excessive pressure on passenger flow operations. While under uncertain conditions, the problem has been significantly improved. Figure 4 shows that the overall allocation of flight-gates is more balanced at this time; moreover, each boarding gate has been given a certain adjustment time under the premise of ensuring the effective use of resources, so that the arrangements between flights are more reasonable. From the comparison of Figure 3 and Figure 4, the overall flight-gate allocation is more balanced when considering uncertainty, which also verifies the effectiveness and feasibility of the model.
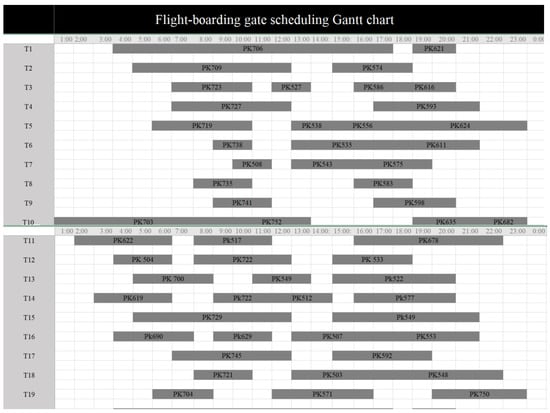


Figure 3.
The conventional FGAP multi-objective programming model flight-gate scheduling Gantt chart (all).


Figure 4.
The FGAP multi-objective programming model based on uncertainty theory flight-gate scheduling Gantt chart (all).
4. Conclusions and Prospects
4.1. Conclusions
This paper aims to study the flight-gate allocation scheduling problem under uncertain conditions. The results show that the model in this paper can effectively alleviate the problems, such as unbalanced flight-gate allocation and excessive operating pressure of a single gate in the conventional model. However, due to the single algorithm, there are still many iterations and long running time. The conclusions of the research are as follows:
(1) At present, the established airports have covered any combination of domestic and international flight types. In comparison, the types of domestic flights are mostly domestic, and the corresponding boarding gate usage is relatively tight.
(2) Based on the results of data processing, after combining the theoretical factors of uncertainty, compared with the traditional method, the flight-gate allocation is more balanced, and the operating pressure of a single gate is reduced, so that a specific gate has sufficient Interval adjustment time. This has a certain enlightening effect on the decision of airport managers on how to allocate flights-gates.
(3) Subsequent research can further consider more detailed constraints and more optimization conditions. For example, in combination with current events, scholars in related fields can treat the COVID-19 situation as an uncertain situation and may lead to a more optimized allocation plan.
4.2. Prospects
As a system parallel to probability theory, uncertainty theory can solve many problems that the framework of probability theory cannot handle. When historical data is invalid or lacks data, or when the research contains uncertain factors, the uncertainty theory can handle such problems well.
(1) As a relatively young system, uncertainty theory is currently growing very fast and has been applied in many fields. For example, uncertain risk analysis [20] and uncertain finance [21] can be applied to financial securities; uncertain planning can be applied to fields, such as transportation [22]. In the future, the applied research of uncertainty theory will also cover other fields.
(2) In view of the fact that uncertainty theory was established and developed only less than 20 years ago, compared with probability theory, the research time is very short. Therefore, there are still many areas can be further studied in the future.
(3) Uncertainty theory also occupies an important position in physics, and its relationship with symmetry is an important law for describing electronic behavior. In-depth exploration of the relationship between uncertainty theory and symmetry is a research hotspot for scholars in the future.
Author Contributions
Conceptualization, X.H. and Y.S.; methodology, J.T.; software, W.W.; validation, J.T., W.W. and Y.L.; formal analysis, Y.L.; investigation, X.H.; resources, Y.S.; data curation, Y.L.; writing—original draft preparation, J.T., W.W. and Y.L.; writing—review and editing, X.H. and Y.S.; visualization, W.W.; supervision, J.T.; project administration, X.H. and Y.S.; funding acquisition, X.H. and Y.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 11961065, U1703237, 12061072, and U1703262.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data in the paper can be requested by email to the corresponding author.
Acknowledgments
Thanks to the reviewers and editors for their guidance and hard work on this paper, which makes the structure of the paper clearer and content smoother. In addition, thanks for the support of the National Natural Science Foundation of China (Nos. 11961065, U1703237, 12061072, and U1703262).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jiang, M.; Fan, S.; Zhao, J. Research on the Optimization of Boarding Gate Assignment Based on Improved Genetic Algorithm. China Logist. Purch. 2021, 12, 28–29. [Google Scholar]
- Liu, B. Some research problems in uncertainty theory. J. Uncertain Syst. 2009, 3, 3–10. [Google Scholar]
- Liu, B. Uncertainty Theory, 5th ed.; Springer: Berlin, Germany, 2021. [Google Scholar]
- Wang, Z.; Guo, J.; Tong, S.; Zhang, P. Multi-target mission planning model for UAVs based on uncertainty theory. In Proceedings of the 2014 (Fifth) China UAV Conference, Beijing, China, 16 September 2014; pp. 795–799. [Google Scholar]
- Wei, M. Research on Optimization Decision-Making of Hazardous Chemicals Transportation Network Based on Uncertainty Theory; Beijing University of Chemical Technology: Beijing, China, 2016. [Google Scholar]
- Avella, P.; Boccia, M.; Mannino, C.; Vasilyev, I. Time-indexed formulations for the runway scheduling problem. Transp. Sci. 2017, 51, 1196–1209. [Google Scholar] [CrossRef] [Green Version]
- Guo, S.; Sun, X. Application of improved particle swarm algorithm in airport boarding gate allocation. Electron. Meas. Technol. 2019, 42, 49–54. [Google Scholar]
- Wang, Q.; Tian, Y.; Lin, L.; Liu, X. A boarding gate assignment model based on passenger transfer at a hub airport. Aviat. Comput. Technol. 2019, 49, 67–71. [Google Scholar]
- Ornek, M.A.; Ozturk, C.; Sugut, I. Integer and constraint programming model formulations for flight-gate assignment problem. Oper. Res. 2020, 3, 1–29. [Google Scholar] [CrossRef]
- Drexl, A.; Nikulin, Y. Fuzzy multicriteria flight gate assignment. Manuskr. Aus. Den. Inst. Für. Betr. Der Univ. Kiel. 2006, 9, 1–15. [Google Scholar]
- Marinelli, M.; Dell’Orco, M.; Sassanelli, D. A Metaheuristic Approach to Solve the Flight Gate Assignment Problem. Transp. Res. Procedia 2015, 5, 211–220. [Google Scholar] [CrossRef] [Green Version]
- Abdelghani, B.; Ghaleb, M.A.; Suryahatmaja, U.S.; Salem, A.M. The Airport Gate Assignment Problem: A Survey. Sci. World J. 2014, 2014, 9165–9172. [Google Scholar]
- Wen, K.; He, Y. An optimization method for airport gate allocation based on improved genetic algorithm. Ind. Control Comput. 2020, 33, 97–99. [Google Scholar]
- Yang, P.; Li, T.; Ru, H.; Chen, H. Evaluation method of the influence of the newly added satellite hall at the airport on the boarding gate. Appl. Math. Mech. 2020, 41, 448–456. [Google Scholar]
- Shen, J. Considering the flight of transit passengers-boarding gate allocation problem. J. Zhoukou Norm. Univ. 2020, 37, 9–13. [Google Scholar]
- Li, N. Uncertain Planning Method for Flight Scheduling Problem; Civil Aviation University of China: Tianjin, China, 2017. [Google Scholar]
- Liu, B. Uncertainty Theory: A Branch of Mathematics for Modeling Human Uncertainty; Springer: Berlin, Germany, 2010. [Google Scholar]
- Dong, B.; Wu, Z.; Lai, G.; Liang, Y.; Pan, W. Research on the boarding gate allocation of airport terminal with satellite hall. Sci. Technol. Eng. 2020, 20, 7545–7551. [Google Scholar]
- Yu, C.; Jiang, J.; Xu, H.; Zhu, P. Multi-objective optimization of flight-gate allocation based on improved genetic algorithm. J. Traffic Transp. Eng. 2020, 20, 121–130. [Google Scholar]
- Kunreuther, H. Risk analysis and risk management in an uncertain world. Risk Anal. 2002, 22, 640–655. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Xu, Y. Comparison of the application of NPV method and real option method in uncertain investment. Mod. Manag. Sci. 2005, 10, 116–117. [Google Scholar]
- Allahyari, S.; Yaghoubi, S.; Woensel, T.V. The secure time-dependent vehicle routing problem with uncertain demands. Comput. Oper. Res. 2021, 131, 105253. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).