On (2-d)-Kernels in Two Generalizations of the Petersen Graph
Abstract
:1. Introduction
2. Main Results
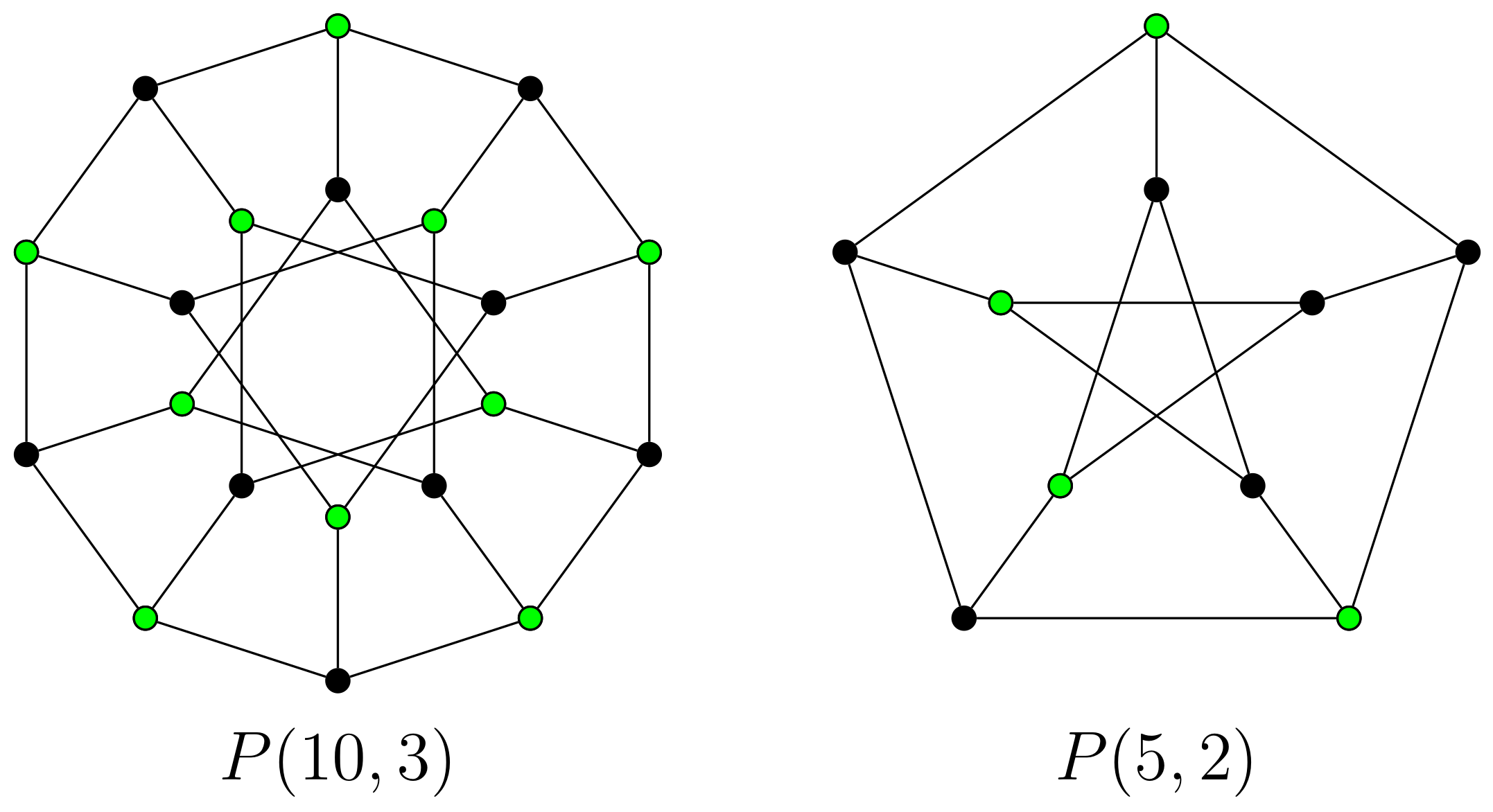
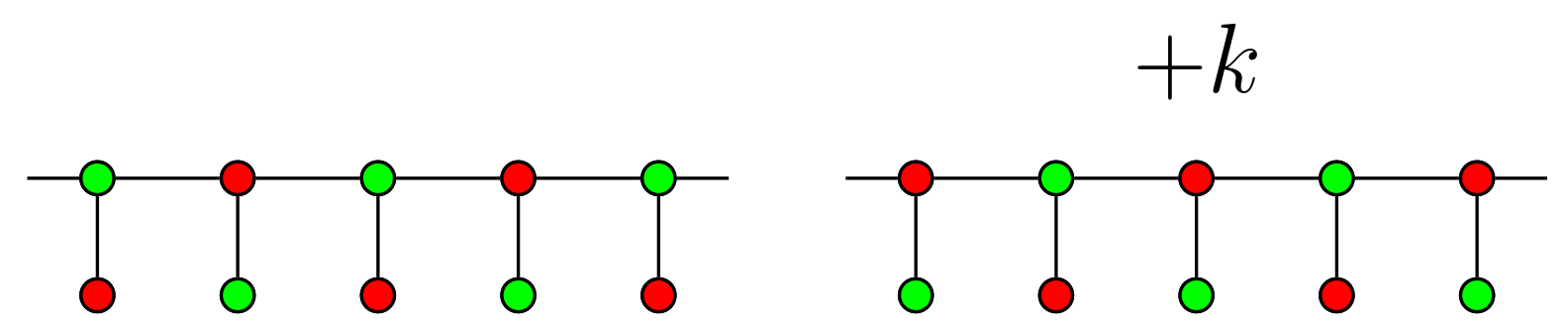
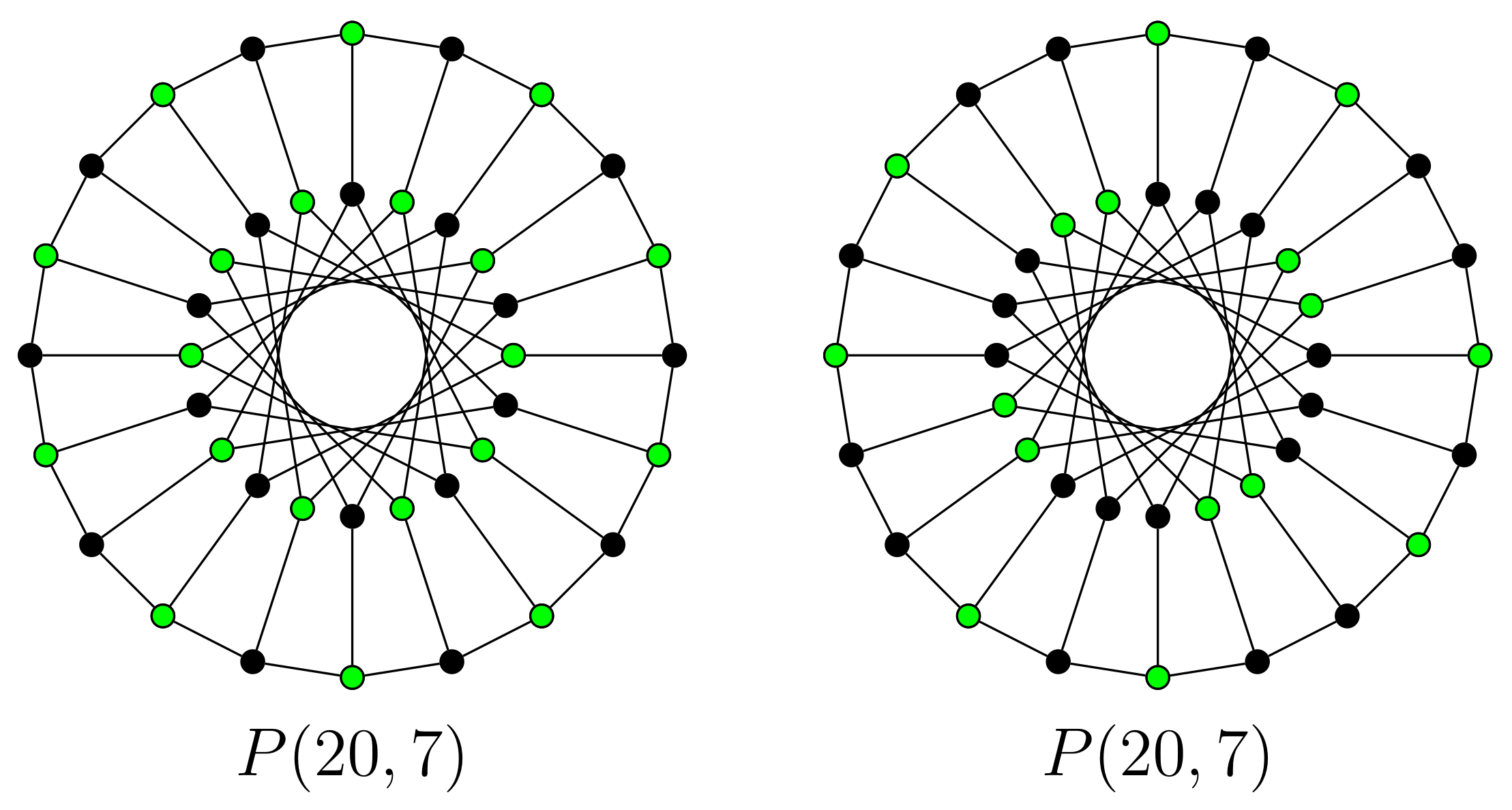
2.1. Generalized Petersen Graph
- (i)
- n is even and k is odd or
- (ii)
- and or
- (iii)
- and .
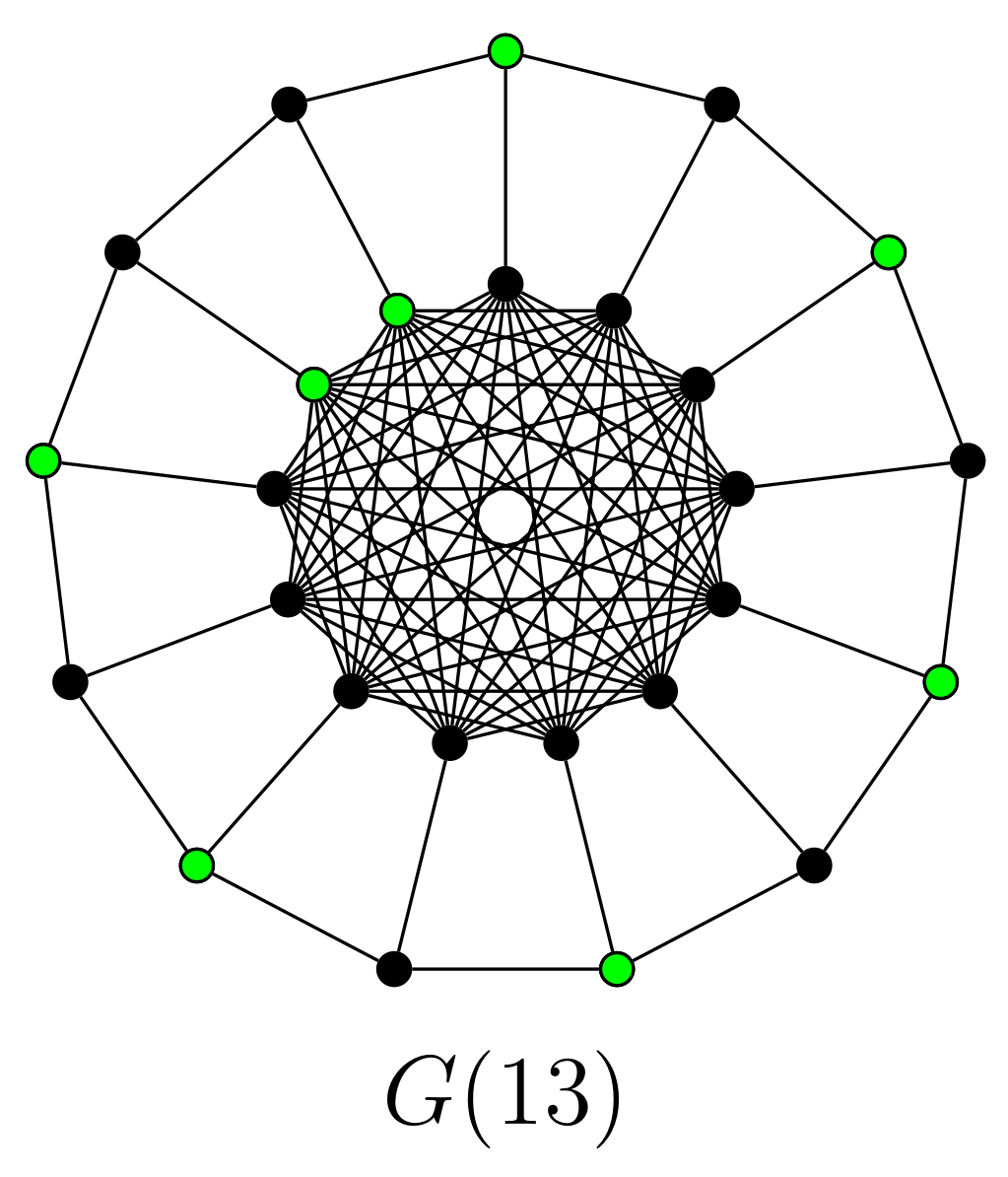
2.2. The Second Generalization of the Petersen Graph
3. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Diestel, R. Graph Theory, 3rd ed.; Springer: New York, NY, USA, 2005. [Google Scholar]
- Morgenstern, O.; Von Neumann, J. Theory of Games and Economic Behavior; Princeton University Press: Princeton, NJ, USA, 1944. [Google Scholar]
- Berge, C. Graphs and Hypergraphs; North-Holland Pub. Co.: Amsterdam, The Netherlands, 1973. [Google Scholar]
- Berge, C.; Duchet, P. Perfect graphs and kernels. Bull. Inst. Math. Acad. Sin. 1988, 16, 263–274. [Google Scholar]
- Berge, C.; Duchet, P. Recent problems and results about kernels in directed graphs. Discrete Math. 1990, 86, 27–31. [Google Scholar] [CrossRef] [Green Version]
- Galeana-Sánchez, H.; Hernández-Cruz, C. On the existence of (k, l)-kernels in infinite digraphs: A survey. Discuss. Math. Graph Theory 2014, 34, 431–466. [Google Scholar] [CrossRef]
- Galeana-Sánchez, H.; Hernández-Cruz, C.; Arumugam, S. On the existence of (k, l)-kernels in digraphs with a given circumference. AKCE Int. J. Graphs Comb. 2013, 10, 15–28. [Google Scholar]
- Kucharska, M. On (k, l)-kernel perfectness of special classes of digraphs. Discuss. Math. Graph Theory 2005, 25, 103–119. [Google Scholar] [CrossRef]
- Włoch, I. On kernels by monochromatic paths in the corona of digraphs. Open Math. 2008, 6, 537–542. [Google Scholar] [CrossRef]
- Bai, Y.; Fujita, S.; Zhang, S. Kernels by properly colored paths in arc-colored digraphs. Discrete Math. 2018, 341, 1523–1533. [Google Scholar] [CrossRef] [Green Version]
- De la Maza, S.G.H.; Hernández-Cruz, C. On the complexity of the k-kernel problem on cyclically k-partite digraphs. Theoret. Comput. Sci. 2019, 795, 9–19. [Google Scholar] [CrossRef]
- Hedetniemi, S.M.; Hedetniemi, S.T.; Knisely, J.; Rall, D.F.; Haynes, T.W. Secondary domination in graphs. AKCE Int. J. Graphs Comb. 2008, 5, 103–115. [Google Scholar]
- Szumny, W.; Włoch, A.; Włoch, I. On the existence and on the number of (k, l)-kernels in the lexicographic product of graphs. Discrete Math. 2008, 308, 4616–4624. [Google Scholar] [CrossRef] [Green Version]
- Włoch, I. On kernels by monochromatic paths in D-join. Ars Combin. 2011, 98, 215–224. [Google Scholar]
- Bednarz, U.; Włoch, I. On strong (1;1;2)-kernels in graphs. Ars Combin. 2020, 152, 32–43. [Google Scholar]
- Bednarz, U. Strong (1;1;2)-kernels in the corona of graphs and some realization problems. Iran. J. Sci. Technol. Trans. A Sci. 2020, 44, 401–406. [Google Scholar] [CrossRef] [Green Version]
- Bednarz, U.; Włoch, I. Fibonacci numbers in graphs with strong (1, 1, 2)-kernels. Bol. Soc. Mat. Mex. 2021, 27, 1–12. [Google Scholar] [CrossRef]
- Michalski, A.; Włoch, I. On the existence and the number of independent (1,2)-dominating sets in the G-join of graphs. Appl. Math. Comput. 2020, 377, 125155. [Google Scholar] [CrossRef]
- Fink, J.F.; Jacobson, M.S. n-domination in graphs. In Graph Theory with Applications to Algorithms and Computer Science; John Wiley & Sons, Inc.: New York, NY, USA, 1985; pp. 283–300. [Google Scholar]
- Włoch, A. On 2-dominating kernels in graphs. Australas. J. Combin. 2012, 53, 273–284. [Google Scholar]
- Bednarz, P.; Włoch, I. An algorithm determining (2-d)-kernels in trees. Util. Math. 2017, 102, 215–222. [Google Scholar]
- Bednarz, P.; Włoch, I. On (2-d)-kernels in the cartesian product of graphs. Ann. Univ. Mariae Curie-Skłodowska Sect. A 2016, 70, 1–8. [Google Scholar] [CrossRef]
- Bednarz, P.; Hernández-Cruz, C.; Włoch, I. On the existence and the number of (2-d)-kernels in graphs. Ars Combin. 2015, 121, 341–351. [Google Scholar]
- Bednarz, P. On (2-d)-Kernels in the Tensor Product of Graphs. Symmetry 2021, 13, 230. [Google Scholar] [CrossRef]
- Nagy, Z.L. On the Number of k-Dominating Independent Sets. J. Graph Theory 2017, 84, 566–580. [Google Scholar] [CrossRef] [Green Version]
- Gerbner, D.; Keszegh, B.; Methuku, A.; Patkós, B.; Vizer, M. An improvement on the maximum number of k-Dominating Independent Sets. J. Graph Theory 2019, 91, 88–97. [Google Scholar] [CrossRef] [Green Version]
- Nagy, Z.L. Generalizing Erdős, Moon and Moser’s result—The number of k-dominating independent sets. Electron. Notes Discrete Math. 2017, 61, 909–915. [Google Scholar] [CrossRef]
- Behzad, A.; Behzad, M.; Praeger, C.E. On the domination number of the generalized Petersen graphs. Discrete Math. 2009, 308, 603–610. [Google Scholar] [CrossRef] [Green Version]
- Ebrahimi, B.J.; Jahanbakht, N.; Mahmoodian, E.S. Vertex domination of generalized Petersen graphs. Discrete Math. 2009, 309, 4355–4361. [Google Scholar] [CrossRef] [Green Version]
- Yan, H.; Kang, L.; Xu, G. The exact domination number of the generalized Petersen graphs. Discrete Math. 2009, 309, 2596–2607. [Google Scholar] [CrossRef] [Green Version]
- Gabrovšek, B.; Peperko, A.; Žerovnik, J. Independent Rainbow Domination Numbers of Generalized Petersen Graphs P(n, 2) and P(n, 3). Mathematics 2020, 8, 996. [Google Scholar] [CrossRef]
- Erveš, R.; Žerovnik, J. On 2-Rainbow Domination Number of Generalized Petersen Graphs P(5k, k). Symmetry 2021, 13, 809. [Google Scholar] [CrossRef]
- Watkins, M.E. A theorem on Tait colorings with an application to the generalized Petersen graphs. J. Combin. Theory 1969, 6, 152–164. [Google Scholar] [CrossRef] [Green Version]
- Alspach, B.; Liu, J. On the Hamilton connectivity of generalized Petersen graphs. Discrete Math. 2009, 309, 5461–5473. [Google Scholar] [CrossRef] [Green Version]
- Boben, M.; Pisanski, T.; Žitnik, A. I-graphs and the corresponding configurations. J. Combin. Des. 2005, 13, 406–424. [Google Scholar] [CrossRef]
- Saražin, M.L.; Pacco, W.; Previtali, A. Generalizing the generalized Petersen graphs. Discrete Math. 2007, 307, 534–543. [Google Scholar] [CrossRef] [Green Version]
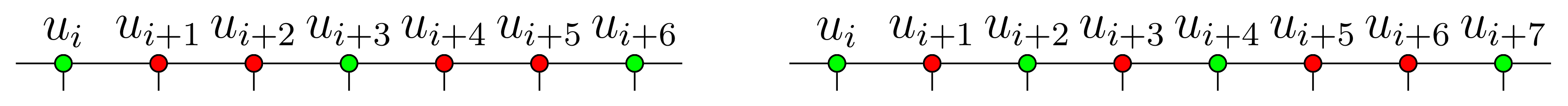







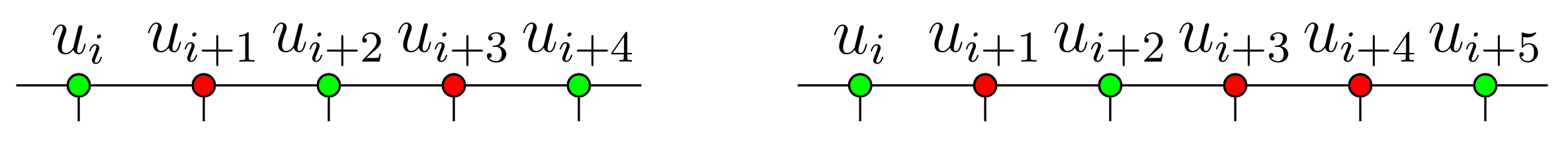








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bednarz, P.; Paja, N. On (2-d)-Kernels in Two Generalizations of the Petersen Graph. Symmetry 2021, 13, 1948. https://doi.org/10.3390/sym13101948
Bednarz P, Paja N. On (2-d)-Kernels in Two Generalizations of the Petersen Graph. Symmetry. 2021; 13(10):1948. https://doi.org/10.3390/sym13101948
Chicago/Turabian StyleBednarz, Paweł, and Natalia Paja. 2021. "On (2-d)-Kernels in Two Generalizations of the Petersen Graph" Symmetry 13, no. 10: 1948. https://doi.org/10.3390/sym13101948





