Multi Stress-Strength Reliability Based on Progressive First Failure for Kumaraswamy Model: Bayesian and Non-Bayesian Estimation
Abstract
:1. Introduction
2. Classical Estimation
2.1. Maximum Likelihood Estimation of R
2.2. Asymptotic Confidence Interval
2.3. Bootstrap Confidence Interval
- From the sample {}, {} and{} compute and .
- A bootstrap progressive first-failure type-II censored sample, denoted by{}, is generated from the KuD( based on the censoring scheme of . A bootstrap progressive first-failure type-II censored sample, denoted by {}, is generated from the KuD( based on the censoring scheme of . A bootstrap progressive first-failure type-II censored sample, denoted by {}, is generated from the KuD( based on the censoring scheme of . Based on {}, {} and {} compute the bootstrap sample estimate of R using (4), say .
- Repeat step 2, number of times.
- Let , denoting the cumulative distribution function of . Define for a given x. The approximate confidence interval of R is given by
- From the sample {}, {} and{} compute and .
- Use to generate a bootstrap sample {}, to generate a bootstrap sample {} and similarly to generate a bootstrap sample{} as before. Based on {}, {} and {} compute the bootstrap sample estimate of R using Equation (4), say . and the following statistic:
- Repeat step 2, number of times.
- Once number of values are obtained, bounds of confidence interval of R are then determined as follows: Suppose follows a cumulative distribution function given as . For a given x, defineThe boot-t confidence interval of R is obtained as
3. Bayes Estimation
3.1. Prior and Posterior Distributions
3.2. Lindley’s Approximation
3.3. Markov Chain Monte Carlo
4. Simulation Study
- The MSE of reliability for multi stress–strength KuD based on progressive first-failure censored samples for both ML and Bayes estimation is decreased as the number of groups n and the effective sample size m increase.
- In most cases, the MSE decreases as k increases for the fixed scheme of reliability for multi stress–strength KuD based on progressive first-failure censored samples.
- The Bayes estimates when compared in terms of MSEs from the ML estimates show better performance with smaller values of MSE in all the considered cases.
- According to MSE and confidence interval, Scheme I is the best Scheme in the majority of situations.
- In MCMC and Lindley’s, BLINEX is better than BSEL estimation.
- In MCMC and in BLINEX, we note MSE decrease as c increases.
- In Lindley’s and in BLINEX, we note MSE decrease as c decreases.
- Boot P is better than boot T.
- Complete sample has the smallest MSE and length of CI.
- It is observed that Bayesian intervals are having smaller interval lengths than the classical interval estimates.
- It is also observed that the CPs of asymptotic confidence intervals is quit low than the nominal level but for boot-p, boot-t and Bayesian interval estimates are showing coverage probabilities higher than nominal level.
5. Data Analysis and Application
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Weerahandi, S.; Johnson, R.A. Testing reliability in a stress-strength model when X and Y are normally distributed. Technometrics 1992, 34, 83–91. [Google Scholar] [CrossRef]
- Surles, J.G.; Padgett, W.J. Inference for reliability and stress-strength for a scaled Burr Type X distribution. Lifetime Data Anal. 2001, 7, 187–200. [Google Scholar] [CrossRef]
- Al-Mutairi, D.K.; Ghitany, M.E.; Kundu, D. Inferences on stress-strength reliability from Lindley distributions. Commun. Stat.-Theory Methods 2013, 42, 1443–1463. [Google Scholar] [CrossRef]
- Rao, G.S.; Aslam, M.; Kundu, D. Burr-XII distribution parametric estimation and estimation of reliability of multicomponent stress-strength. Commun. Stat.-Theory Methods 2015, 44, 4953–4961. [Google Scholar] [CrossRef]
- Singh, S.K.; Singh, U.; Yaday, A.; Viswkarma, P.K. On the estimation of stress strength reliability parameter of inverted exponential distribution. Int. J. Sci. World 2015, 3, 98–112. [Google Scholar] [CrossRef] [Green Version]
- Almetwally, E.M.; Almongy, H.M. Parameter estimation and stress-strength model of Power Lomax distribution: Classical methods and Bayesian estimation. J. Data Sci. 2020, 18, 718–738. [Google Scholar] [CrossRef]
- Alshenawy, R.; Sabry, M.A.; Almetwally, E.M.; Almongy, H.M. Product Spacing of Stress–Strength under Progressive Hybrid Censored for Exponentiated-Gumbel Distribution. Comput. Mater. Contin. 2021, 66, 2973–2995. [Google Scholar] [CrossRef]
- Alamri, O.A.; Abd El-Raouf, M.M.; Ismail, E.A.; Almaspoor, Z.; Alsaedi, B.S.; Khosa, S.K.; Yusuf, M. Estimate stress-strength reliability model using Rayleigh and half-normal distribution. Comput. Intell. Neurosci. 2021, 2021. [Google Scholar] [CrossRef] [PubMed]
- Sabry, M.A.; Almetwally, E.M.; Alamri, O.A.; Yusuf, M.; Almongy, H.M.; Eldeeb, A.S. Inference of fuzzy reliability model for inverse Rayleigh distribution. AIMS Math. 2021, 6, 9770–9785. [Google Scholar] [CrossRef]
- Abu El Azm, W.S.; Almetwally, E.M.; Alghamdi, A.S.; Aljohani, H.M.; Muse, A.H.; Abo-Kasem, O.E. Stress-Strength Reliability for Exponentiated Inverted Weibull Distribution with Application on Breaking of Jute Fiber and Carbon Fibers. Comput. Intell. Neurosci. 2021, 2021. [Google Scholar] [CrossRef]
- Okabe, T.; Otsuka, Y. Proposal of a Validation Method of Failure Mode Analyses based on the Stress-Strength Model with a Support Vector Machine. Reliab. Eng. Syst. Saf. 2021, 205, 107247. [Google Scholar] [CrossRef]
- Bhattacharyya, G.K.; Johnson, R.A. Estimation of reliability in a multicomponent stress-strength model. J. Am. Stat. Assoc. 1974, 69, 966–970. [Google Scholar] [CrossRef]
- Kotb, M.S.; Raqab, M.Z. Estimation of reliability for multi-component stress–strength model based on modified Weibull distribution. Stat. Pap. 2020, 2020, 1–35. [Google Scholar] [CrossRef]
- Maurya, R.K.; Tripathi, Y.M. Reliability estimation in a multicomponent stress-strength model for Burr XII distribution under progressive censoring. Braz. J. Probab. Stat. 2020, 34, 345–369. [Google Scholar] [CrossRef]
- Mahto, A.K.; Tripathi, Y.M.; Kızılaslan, F. Estimation of Reliability in a Multicomponent Stress–Strength Model for a General Class of Inverted Exponentiated Distributions Under Progressive Censoring. J. Stat. Theory Pract. 2020, 14, 1–35. [Google Scholar] [CrossRef]
- Mahto, A.K.; Tripathi, Y.M. Estimation of reliability in a multicomponent stress-strength model for inverted exponentiated Rayleigh distribution under progressive censoring. OPSEARCH 2020, 57, 1043–1069. [Google Scholar] [CrossRef]
- Wang, L.; Dey, S.; Tripathi, Y.M.; Wu, S.J. Reliability inference for a multicomponent stress–strength model based on Kumaraswamy distribution. J. Comput. Appl. Math. 2020, 376, 112823. [Google Scholar] [CrossRef]
- Wang, L.; Wu, K.; Tripathi, Y.M.; Lodhi, C. Reliability analysis of multicomponent stress–strength reliability from a bathtub-shaped distribution. J. Appl. Stat. 2020, 1–21. [Google Scholar] [CrossRef]
- Jha, M.K.; Dey, S.; Alotaibi, R.M.; Tripathi, Y.M. Reliability estimation of a multicomponent stress-strength model for unit Gompertz distribution under progressive Type II censoring. Qual. Reliab. Eng. Int. 2020, 36, 965–987. [Google Scholar] [CrossRef]
- Rasekhi, M.; Saber, M.M.; Yousof, H.M. Bayesian and classical inference of reliability in multicomponent stress-strength under the generalized logistic model. Commun. Stat.-Theory Methods 2020, 1–12. [Google Scholar] [CrossRef]
- Alotaibi, R.M.; Tripathi, Y.M.; Dey, S.; Rezk, H.R. Bayesian and non-Bayesian reliability estimation of multicomponent stress–strength model for unit Weibull distribution. J. Taibah Univ. Sci. 2020, 14, 1164–1181. [Google Scholar] [CrossRef]
- Maurya, R.K.; Tripathi, Y.M.; Kayal, T. Reliability Estimation in a Multicomponent Stress-Strength Model Based on Inverse Weibull Distribution. Sankhya B 2021, 1–38. [Google Scholar] [CrossRef]
- Kohansal, A.; Shoaee, S. Bayesian and classical estimation of reliability in a multicomponent stress-strength model under adaptive hybrid progressive censored data. Stat. Pap. 2021, 62, 309–359. [Google Scholar] [CrossRef]
- Jana, N.; Bera, S. Interval estimation of multicomponent stress–strength reliability based on inverse Weibull distribution. Math. Comput. Simul. 2022, 191, 95–119. [Google Scholar] [CrossRef]
- Chandra, S.; Owen, D.B. On estimating the reliability of a component subject to several different stresses (strengths). Nav. Res. Logist. Quart. 1975, 22, 31–39. [Google Scholar] [CrossRef]
- Hlawka, P. Estimation of the Parameter p = P(X < Y < Z); No.11, Ser. Stud. i Materiaty No. 10 Problemy Rachunku Prawdopodobienstwa; Prace Nauk. Inst. Mat. Politechn.: Wroclaw, Poland, 1975; pp. 55–65. (In Polish) [Google Scholar]
- Singh, N. On the estimation of Pr(X1 < Y < X2). Commun. Statist. Theory Meth. 1980, 9, 1551–1561. [Google Scholar]
- Dutta, K.; Sriwastav, G.L. An n-standby system with P(X < Y < Z). IAPQR Trans. 1986, 12, 95–97. [Google Scholar]
- Ivshin, V.V. On the estimation of the probabilities of a double linear inequality in the case of uniform and two-parameter exponential distributions. J. Math. Sci. 1998, 88, 819–827. [Google Scholar] [CrossRef]
- Hanagal, D.D. Estimation of system reliability in multicomponent series stress—strength model. J. Indian Statist. Assoc. 2003, 41, 1–7. [Google Scholar]
- Waegeman, W.; De Baets, B.; Boullart, L. On the scalability of ordered multi-class ROC analysis. Comput. Statist. Data Anal. 2008, 52, 33–71. [Google Scholar] [CrossRef]
- Chumchum, D.; Munindra, B.; Jonali, G. Cascade System with Pr(X < Y < Z). J. Inform. Math. Sci. 2013, 5, 37–47. [Google Scholar]
- Pan, G.; Wang, X.; Zhou, W. Nonparametric statistical inference for P(X < Y < Z). Indian J. Stat. 2013, 75, 118–138. [Google Scholar]
- Patowary, A.N.; Sriwastav, G.L.; Hazarika, J. Inference of R = P(X < Y < Z) for n-Standby System: A Monte-Carlo Simulation Approach. J. Math. 2016, 12, 18–22. [Google Scholar]
- Saini, S.; Tomer, S.; Garg, R. On the reliability estimation of multicomponent stress–strength model for Burr XII distribution using progressively first-failure censored samples. J. Stat. Comput. Simul. 2021, 1–38. [Google Scholar] [CrossRef]
- Kohansal, A.; Fernández, A.J.; Pérez-González, C.J. Multi-component stress–strength parameter estimation of a non-identical-component strengths system under the adaptive hybrid progressive censoring samples. Statistics 2021, 1–38. [Google Scholar] [CrossRef]
- Hassan, M.K. On Estimating Standby Redundancy System in a MSS Model with GLFRD Based on Progressive Type II Censoring Data. Reliab. Theory Appl. 2021, 16, 206–219. [Google Scholar]
- Wu, S.J.; Kus, C. On estimation based on progressive first-failure-censored sampling. Comput. Stat. Data Anal. 2009, 53, 3659–3670. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Aggarwala, R. Progressive Censoring: Theory, Methods, and Applications; Springer Science & Business Media Birkhauser Boston: Cambridge, MA, USA, 2000. [Google Scholar]
- Kumaraswamy, P. A generalized probability density function for double-bounded random processes. J. Hydrol. 1980, 46, 79–88. [Google Scholar] [CrossRef]
- Jones, M.C. Kumaraswamy’s distribution: A beta-type distribution with some tractability advantages. J. Statist. Methodol. 2009, 6, 70–81. [Google Scholar] [CrossRef]
- Golizadeh, A.; Sherazi, M.A.; Moslamanzadeh, S. Classical and Bayesian estimation on Kumaraswamy distribution using grouped and ungrouped data under difference of loss functions. J. Appl. Sci. 2011, 11, 2154–2162. [Google Scholar] [CrossRef]
- Sindhu, T.N.; Feroze, N.; Aslam, M. Bayesian analysis of the Kumaraswamy distribution under failure censoring sampling scheme. Int. J. Adv. Sci. Technol. 2013, 51, 39–58. [Google Scholar]
- Sharaf EL-Deen, M.M.; AL-Dayian, G.R.; EL-Helbawy, A.A. Statistical inference for Kumaraswamy distribution based on generalized order statistics with applications. J. Adv. Math. Comput. Sci. 2014, 4, 1710–1743. [Google Scholar]
- Wang, L. Inference for the Kumaraswamy distribution under -record values. J. Comput. Appl. Math. 2017, 321, 246–260. [Google Scholar] [CrossRef]
- Kumar, M.; Singh, S.K.; Singh, U.; Pathak, A. Empirical Bayes estimator of parameter, reliability and hazard rate for Kumaraswamy distribution. Life Cycle Reliab. Saf. Eng. 2019, 8, 243–256. [Google Scholar] [CrossRef]
- Fawzy, M.A. Prediction of Kumaraswamy distribution in constant-stress model based on type-I hybrid censored data. Stat. Anal. Data Min. ASA Data Sci. J. 2020, 13, 205–215. [Google Scholar] [CrossRef]
- Ferguson, T. A Course in Large Sample Theory. In Chapman & Hall Texts in Statistical Science Series; Taylor & Francis: Milton Park, VA, USA, 1996. [Google Scholar]
- Efron, B. The Jackknife, the Bootstrap and other Resampling Plans. In CBMS-NSF Regional Conference Series in Applied Mathematics; SIAM: Philadelphia, PA, USA, 1982; Volume 38. [Google Scholar]
- Hall, P. Theoretical comparison of bootstrap confidence intervals. Ann. Stat. 1988, 16, 927–953. [Google Scholar] [CrossRef]
- Zellner, A. Bayesian and non-Bayesian estimation using balanced loss functions. In Statistical Decision Theory and Methods; Berger, J.O., Gupta, S.S., Eds.; Springer: New York, NY, USA, 1994; pp. 337–390. [Google Scholar]
- Ahmadi, J.; Jozani, M.J.; Marchand, E.; Parsian, A. Bayes estimation based on k- record data from a general class of distributions under balanced Type loss functions. J. Stat. Plan. Inference 2009, 139, 1180–1189. [Google Scholar] [CrossRef]
- Lindley, D.V. Approximate Bayesian method. Trab. Estad. 1980, 31, 223–237. [Google Scholar] [CrossRef]
- Chen, M.H.; Shao, Q.M. Monte Carlo estimation of Bayesian credible and HPD intervals. J. Comput. Graph. Stat. 1999, 8, 69–92. [Google Scholar]
- Balakrishnan, N.; Sandhu, R.A. A simple simulational algorithm for generating progressive Type-II censored samples. Am. Stat. 1995, 49, 229–230. [Google Scholar]
- Kundu, D.; Gupta, R.D. Estimation of P[Y < X] for Weibull distributions. IEEE Trans. Reliab. 2016, 55, 270–280. [Google Scholar]
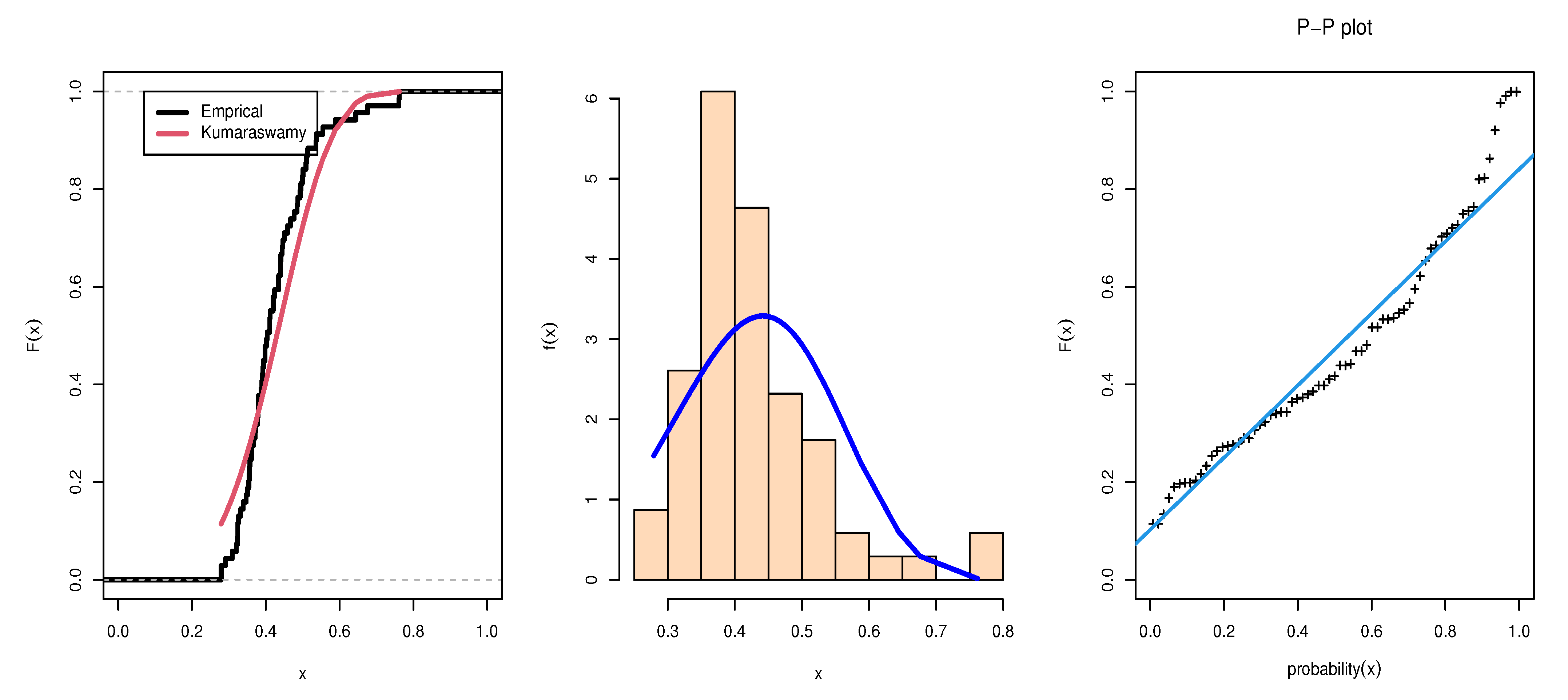
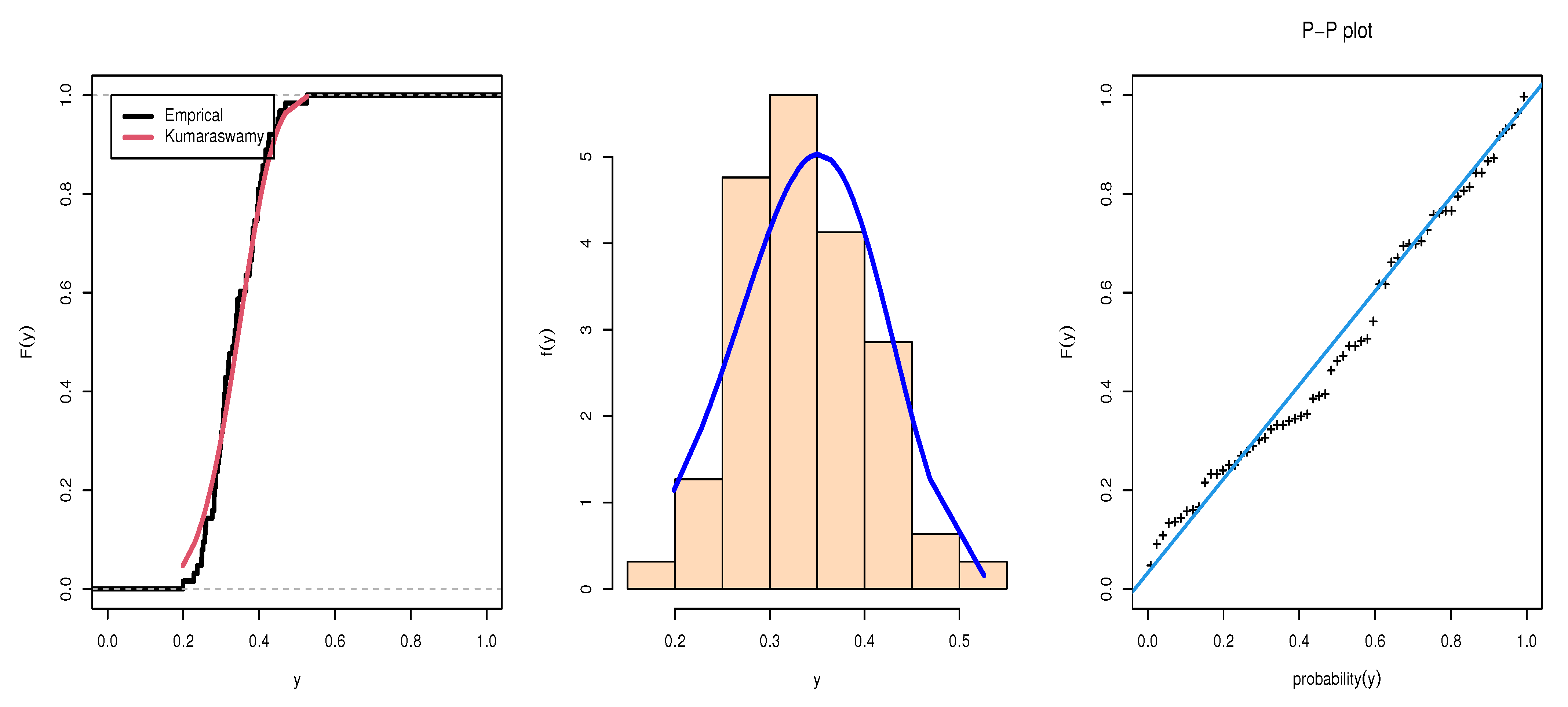


| ML | Bayes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lindley’s | MCMC | |||||||||||
| BSEL | BLINEX | BSEL | BLINEX | |||||||||
| n | m | k | Sch | −2 | 0.5 | 2 | −2 | 0.5 | 2 | |||
| 20 | 12 | 1 | I | 0.00323 | 0.00163 | 0.00157 | 0.00165 | 0.00169 | 0.00207 | 0.00309 | 0.00194 | 0.00167 |
| II | 0.00328 | 0.00167 | 0.00161 | 0.00168 | 0.00173 | 0.00208 | 0.00303 | 0.00195 | 0.00169 | |||
| III | 0.00333 | 0.00170 | 0.00164 | 0.00171 | 0.00176 | 0.00213 | 0.00314 | 0.00199 | 0.00171 | |||
| 16 | I | 0.00235 | 0.00143 | 0.00140 | 0.00144 | 0.00147 | 0.00166 | 0.00222 | 0.00158 | 0.0014 | ||
| II | 0.00238 | 0.00136 | 0.00132 | 0.00137 | 0.00139 | 0.00161 | 0.00222 | 0.00152 | 0.00133 | |||
| III | 0.00252 | 0.00152 | 0.00148 | 0.00153 | 0.00156 | 0.00177 | 0.00239 | 0.00168 | 0.00148 | |||
| 20 | 0.00202 | 0.00129 | 0.00126 | 0.00129 | 0.00131 | 0.00145 | 0.00189 | 0.00138 | 0.00122 | |||
| 40 | 24 | I | 0.00158 | 0.00114 | 0.00113 | 0.00114 | 0.00115 | 0.00124 | 0.00156 | 0.00119 | 0.00107 | |
| II | 0.00150 | 0.00103 | 0.00102 | 0.00103 | 0.00105 | 0.00114 | 0.00145 | 0.00108 | 0.00097 | |||
| III | 0.00161 | 0.00114 | 0.00112 | 0.00114 | 0.00115 | 0.00124 | 0.00155 | 0.00119 | 0.00107 | |||
| 32 | I | 0.00117 | 0.00090 | 0.00090 | 0.00090 | 0.00091 | 0.00095 | 0.00112 | 0.00092 | 0.00085 | ||
| II | 0.00126 | 0.00096 | 0.00096 | 0.00097 | 0.00097 | 0.00102 | 0.00120 | 0.00099 | 0.0009 | |||
| III | 0.00113 | 0.00089 | 0.00088 | 0.00089 | 0.00090 | 0.00094 | 0.00112 | 0.00091 | 0.00083 | |||
| 40 | 0.00099 | 0.00080 | 0.00079 | 0.00080 | 0.00080 | 0.00083 | 0.00095 | 0.00081 | 0.00075 | |||
| 20 | 12 | 3 | I | 0.00313 | 0.00165 | 0.00159 | 0.00166 | 0.00171 | 0.00206 | 0.00308 | 0.00193 | 0.00166 |
| II | 0.00316 | 0.00155 | 0.00149 | 0.00157 | 0.00161 | 0.00197 | 0.00292 | 0.00184 | 0.00159 | |||
| III | 0.00344 | 0.00169 | 0.00163 | 0.00170 | 0.00175 | 0.00212 | 0.00311 | 0.00199 | 0.00172 | |||
| 16 | I | 0.00230 | 0.00140 | 0.00137 | 0.00141 | 0.00144 | 0.00164 | 0.00226 | 0.00155 | 0.00135 | ||
| II | 0.00254 | 0.00147 | 0.00143 | 0.00148 | 0.00151 | 0.00173 | 0.00234 | 0.00164 | 0.00144 | |||
| III | 0.00232 | 0.00149 | 0.00146 | 0.00150 | 0.00153 | 0.00173 | 0.00238 | 0.00164 | 0.00144 | |||
| 20 | 20 | 0.00189 | 0.00133 | 0.00131 | 0.00133 | 0.00135 | 0.00148 | 0.00191 | 0.00141 | 0.00126 | ||
| 40 | 24 | I | 0.00190 | 0.00128 | 0.00127 | 0.00129 | 0.00130 | 0.00140 | 0.00173 | 0.00135 | 0.00122 | |
| II | 0.00162 | 0.00115 | 0.00114 | 0.00116 | 0.00117 | 0.00126 | 0.00157 | 0.00120 | 0.00108 | |||
| III | 0.00158 | 0.00116 | 0.00115 | 0.00116 | 0.00117 | 0.00126 | 0.00159 | 0.00121 | 0.00109 | |||
| 32 | I | 0.00138 | 0.00103 | 0.00102 | 0.00103 | 0.00104 | 0.00109 | 0.00129 | 0.00105 | 0.00096 | ||
| II | 0.00119 | 0.00092 | 0.00091 | 0.00092 | 0.00093 | 0.00097 | 0.00116 | 0.00094 | 0.00086 | |||
| III | 0.00114 | 0.00087 | 0.00086 | 0.00087 | 0.00087 | 0.00092 | 0.00108 | 0.00089 | 0.00082 | |||
| 40 | 40 | 0.00103 | 0.00083 | 0.00082 | 0.00083 | 0.00083 | 0.00086 | 0.00098 | 0.00084 | 0.00078 | ||
| ML | Bayes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lindley’s | MCMC | |||||||||||
| BSEL | BLINEX | BSEL | BLINEX | |||||||||
| n | m | k | Sch | −2 | 0.5 | 2 | −2 | 0.5 | 2 | |||
| 20 | 12 | 1 | I | 0.00324 | 0.00211 | 0.00209 | 0.00212 | 0.00214 | 0.00251 | 0.00301 | 0.00228 | 0.00172 |
| II | 0.00338 | 0.00225 | 0.00223 | 0.00226 | 0.00228 | 0.00265 | 0.00313 | 0.00242 | 0.00186 | |||
| III | 0.00342 | 0.00221 | 0.00218 | 0.00222 | 0.00224 | 0.00262 | 0.00313 | 0.00239 | 0.00182 | |||
| 16 | I | 0.00255 | 0.00188 | 0.00187 | 0.00188 | 0.00189 | 0.00207 | 0.00236 | 0.00195 | 0.00160 | ||
| II | 0.00229 | 0.00170 | 0.00169 | 0.00170 | 0.00171 | 0.00187 | 0.00215 | 0.00176 | 0.00144 | |||
| III | 0.00221 | 0.00163 | 0.00162 | 0.00163 | 0.00164 | 0.00180 | 0.00208 | 0.00169 | 0.00137 | |||
| 20 | 0.00180 | 0.00141 | 0.00140 | 0.00141 | 0.00141 | 0.00151 | 0.00170 | 0.00144 | 0.00120 | |||
| 40 | 24 | I | 0.00148 | 0.00121 | 0.00121 | 0.00121 | 0.00121 | 0.00127 | 0.00140 | 0.00122 | 0.00106 | |
| II | 0.00164 | 0.00136 | 0.00136 | 0.00136 | 0.00136 | 0.00143 | 0.00156 | 0.00138 | 0.00121 | |||
| III | 0.00162 | 0.00133 | 0.00132 | 0.00133 | 0.00133 | 0.00139 | 0.00153 | 0.00134 | 0.00118 | |||
| 32 | I | 0.00110 | 0.00095 | 0.00095 | 0.00095 | 0.00095 | 0.00098 | 0.00105 | 0.00095 | 0.00087 | ||
| II | 0.00114 | 0.00100 | 0.00100 | 0.00100 | 0.00100 | 0.00103 | 0.00111 | 0.00100 | 0.00091 | |||
| III | 0.00110 | 0.00096 | 0.00096 | 0.00096 | 0.00096 | 0.00098 | 0.00106 | 0.00096 | 0.00088 | |||
| 40 | 0.00097 | 0.00086 | 0.00086 | 0.00086 | 0.00086 | 0.00088 | 0.00093 | 0.00086 | 0.00080 | |||
| 20 | 12 | 3 | I | 0.00306 | 0.00204 | 0.00202 | 0.00205 | 0.00207 | 0.00241 | 0.00291 | 0.00219 | 0.00165 |
| II | 0.00308 | 0.00204 | 0.00201 | 0.00204 | 0.00206 | 0.00241 | 0.00289 | 0.00219 | 0.00166 | |||
| III | 0.00310 | 0.00208 | 0.00205 | 0.00209 | 0.00210 | 0.00244 | 0.00294 | 0.00223 | 0.00169 | |||
| 16 | I | 0.00234 | 0.00176 | 0.00175 | 0.00176 | 0.00177 | 0.00194 | 0.00224 | 0.00182 | 0.00147 | ||
| II | 0.00236 | 0.00180 | 0.00179 | 0.00180 | 0.00181 | 0.00198 | 0.00227 | 0.00186 | 0.00152 | |||
| III | 0.00259 | 0.00191 | 0.00190 | 0.00191 | 0.00192 | 0.00211 | 0.00244 | 0.00198 | 0.00158 | |||
| 20 | 20 | 0.00188 | 0.00147 | 0.00146 | 0.00147 | 0.00147 | 0.00157 | 0.00176 | 0.00150 | 0.00127 | ||
| 40 | 24 | I | 0.00164 | 0.00137 | 0.00136 | 0.00137 | 0.00137 | 0.00143 | 0.00157 | 0.00138 | 0.00121 | |
| II | 0.00160 | 0.00131 | 0.00131 | 0.00131 | 0.00131 | 0.00137 | 0.00151 | 0.00132 | 0.00116 | |||
| III | 0.00167 | 0.00137 | 0.00137 | 0.00137 | 0.00137 | 0.00144 | 0.00158 | 0.00139 | 0.00121 | |||
| 32 | I | 0.00111 | 0.00095 | 0.00095 | 0.00095 | 0.00095 | 0.00098 | 0.00105 | 0.00096 | 0.00087 | ||
| II | 0.00120 | 0.00103 | 0.00103 | 0.00103 | 0.00103 | 0.00106 | 0.00114 | 0.00103 | 0.00093 | |||
| III | 0.00125 | 0.00107 | 0.00107 | 0.00107 | 0.00107 | 0.00110 | 0.00118 | 0.00107 | 0.00098 | |||
| 40 | 40 | 0.00094 | 0.00084 | 0.00084 | 0.00084 | 0.00084 | 0.00086 | 0.00091 | 0.00084 | 0.00078 | ||
| ML | Boot P | Boot T | Bayes | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| n | m | k | Sch | Length | CP | Length | CP | Length | CP | Length | CP |
| 20 | 12 | 1 | I | 0.20341 | 0.906 | 0.22648 | 1 | 0.25300 | 0.998 | 0.19428 | 0.949 |
| II | 0.20268 | 0.909 | 0.22508 | 1 | 0.25318 | 0.996 | 0.19407 | 0.959 | |||
| III | 0.20105 | 0.885 | 0.22593 | 1 | 0.25052 | 0.995 | 0.19308 | 0.947 | |||
| 16 | I | 0.17669 | 0.922 | 0.19270 | 1 | 0.21195 | 0.998 | 0.17292 | 0.958 | ||
| II | 0.17692 | 0.924 | 0.19294 | 1 | 0.21243 | 0.998 | 0.17330 | 0.960 | |||
| III | 0.17595 | 0.898 | 0.19304 | 1 | 0.21051 | 0.997 | 0.17225 | 0.942 | |||
| 20 | 0.15833 | 0.899 | 0.17175 | 1 | 0.18595 | 0.999 | 0.15758 | 0.940 | |||
| 40 | 24 | I | 0.14372 | 0.918 | 0.15677 | 1 | 0.16488 | 0.999 | 0.14466 | 0.951 | |
| II | 0.14519 | 0.933 | 0.15603 | 1 | 0.16717 | 1 | 0.14563 | 0.969 | |||
| III | 0.14464 | 0.912 | 0.15626 | 1 | 0.16658 | 1 | 0.14520 | 0.952 | |||
| 32 | I | 0.12591 | 0.930 | 0.13508 | 1 | 0.14227 | 1 | 0.12811 | 0.963 | ||
| II | 0.12523 | 0.924 | 0.13516 | 1 | 0.14161 | 1 | 0.12775 | 0.961 | |||
| III | 0.12493 | 0.927 | 0.13518 | 1 | 0.14059 | 1 | 0.12738 | 0.958 | |||
| 40 | 0.11271 | 0.925 | 0.12085 | 1 | 0.12586 | 1 | 0.11566 | 0.949 | |||
| 20 | 12 | 3 | I | 0.20207 | 0.909 | 0.22640 | 1 | 0.24959 | 0.997 | 0.19323 | 0.953 |
| II | 0.20321 | 0.921 | 0.22460 | 1 | 0.25364 | 1 | 0.19447 | 0.974 | |||
| III | 0.20270 | 0.912 | 0.22519 | 1 | 0.25415 | 0.993 | 0.19440 | 0.954 | |||
| 16 | I | 0.17549 | 0.917 | 0.19284 | 1 | 0.20942 | 1 | 0.17205 | 0.964 | ||
| II | 0.17580 | 0.909 | 0.19263 | 1 | 0.21183 | 0.998 | 0.17250 | 0.956 | |||
| III | 0.17455 | 0.911 | 0.19350 | 1 | 0.20750 | 0.997 | 0.17121 | 0.956 | |||
| 20 | 0.15670 | 0.908 | 0.17140 | 1 | 0.18217 | 0.997 | 0.15597 | 0.944 | |||
| 40 | 24 | I | 0.14448 | 0.898 | 0.15626 | 1 | 0.16697 | 1 | 0.14539 | 0.942 | |
| II | 0.14415 | 0.923 | 0.15649 | 1 | 0.16536 | 1 | 0.14495 | 0.948 | |||
| III | 0.14375 | 0.917 | 0.15635 | 1 | 0.16446 | 0.999 | 0.14461 | 0.951 | |||
| 32 | I | 0.12554 | 0.909 | 0.13496 | 1 | 0.14192 | 1 | 0.12796 | 0.951 | ||
| II | 0.12537 | 0.924 | 0.13508 | 1 | 0.14149 | 1 | 0.12775 | 0.962 | |||
| III | 0.12576 | 0.927 | 0.13505 | 1 | 0.14212 | 1 | 0.12820 | 0.958 | |||
| 40 | 0.11233 | 0.915 | 0.12093 | 1 | 0.12523 | 1 | 0.11546 | 0.944 | |||
| ML | Boot P | Boot T | Bayes | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| n | m | k | Sch | Length | CP | Length | CP | Length | CP | Length | CP |
| 20 | 12 | 1 | I | 0.20257 | 0.905 | 0.22534 | 1 | 0.25213 | 0.997 | 0.19396 | 0.958 |
| II | 0.20158 | 0.907 | 0.22521 | 1 | 0.25124 | 0.996 | 0.19336 | 0.961 | |||
| III | 0.20355 | 0.906 | 0.22705 | 1 | 0.25511 | 0.997 | 0.19464 | 0.951 | |||
| 16 | I | 0.17676 | 0.914 | 0.19386 | 1 | 0.21239 | 0.996 | 0.17308 | 0.955 | ||
| II | 0.17652 | 0.919 | 0.19316 | 1 | 0.21097 | 0.998 | 0.17278 | 0.962 | |||
| III | 0.17616 | 0.916 | 0.19275 | 1 | 0.21065 | 0.997 | 0.17278 | 0.962 | |||
| 20 | 0.15859 | 0.929 | 0.17151 | 1 | 0.18521 | 0.998 | 0.15754 | 0.968 | |||
| 40 | 24 | I | 0.14496 | 0.932 | 0.15637 | 1 | 0.16693 | 1 | 0.14552 | 0.964 | |
| II | 0.14388 | 0.917 | 0.15614 | 1 | 0.16565 | 0.999 | 0.14479 | 0.957 | |||
| III | 0.14443 | 0.914 | 0.15624 | 1 | 0.16630 | 0.999 | 0.14510 | 0.957 | |||
| 32 | I | 0.12534 | 0.942 | 0.13518 | 1 | 0.14174 | 1 | 0.12783 | 0.971 | ||
| II | 0.12478 | 0.934 | 0.13492 | 1 | 0.14009 | 1 | 0.12713 | 0.956 | |||
| III | 0.12520 | 0.938 | 0.13517 | 1 | 0.14116 | 1 | 0.12760 | 0.963 | |||
| 40 | 0.11240 | 0.928 | 0.12080 | 1 | 0.12521 | 1 | 0.11546 | 0.956 | |||
| 20 | 12 | 3 | I | 0.20140 | 0.916 | 0.22511 | 1 | 0.24916 | 0.995 | 0.19297 | 0.956 |
| II | 0.20296 | 0.902 | 0.22555 | 1 | 0.25274 | 0.995 | 0.19410 | 0.962 | |||
| III | 0.20158 | 0.917 | 0.22617 | 1 | 0.24971 | 0.999 | 0.19299 | 0.954 | |||
| 16 | I | 0.17544 | 0.907 | 0.19221 | 1 | 0.20873 | 0.994 | 0.17179 | 0.948 | ||
| II | 0.17411 | 0.912 | 0.19301 | 1 | 0.20722 | 0.998 | 0.17111 | 0.948 | |||
| III | 0.17549 | 0.901 | 0.19324 | 1 | 0.21033 | 0.995 | 0.17201 | 0.952 | |||
| 20 | 0.15812 | 0.914 | 0.17131 | 1 | 0.18533 | 1 | 0.15741 | 0.961 | |||
| 40 | 24 | I | 0.14416 | 0.909 | 0.15645 | 1 | 0.16555 | 0.999 | 0.14473 | 0.943 | |
| II | 0.14491 | 0.914 | 0.15643 | 1 | 0.16712 | 0.998 | 0.14544 | 0.957 | |||
| III | 0.14449 | 0.913 | 0.15619 | 1 | 0.16627 | 1 | 0.14516 | 0.952 | |||
| 32 | I | 0.12598 | 0.932 | 0.13498 | 1 | 0.14217 | 1 | 0.12826 | 0.962 | ||
| II | 0.12539 | 0.918 | 0.13539 | 1 | 0.14172 | 0.999 | 0.12778 | 0.955 | |||
| III | 0.12593 | 0.911 | 0.13509 | 1 | 0.14266 | 1 | 0.12812 | 0.945 | |||
| 40 | 40 | 0.11221 | 0.929 | 0.12077 | 1 | 0.12491 | 0.999 | 0.11516 | 0.958 | ||
| Estimates | SE | KS | p-Value | CvM | AD | AIC | BIC | ||
|---|---|---|---|---|---|---|---|---|---|
| 3.9923 | 0.3559 | 0.1439 | 0.1150 | 0.4242 | 2.7357 | −106.9507 | −102.4825 | ||
| 19.8261 | 5.2178 | ||||||||
| 4.9097 | 0.3914 | 0.0861 | 0.7387 | 0.1062 | 0.5857 | −153.7927 | −149.5065 | ||
| 134.8420 | 50.0833 |
| MLE | Bayesian | ||||||
|---|---|---|---|---|---|---|---|
| Scheme | Estimates | SE | R | Estimates | SE | R | |
| Complelet | 3.9891 | 0.3556 | 0.7344 | 4.0046 | 0.3115 | 0.7418 | |
| 19.7760 | 5.2003 | 20.3114 | 4.6123 | ||||
| 5.1278 | 0.4444 | 5.3213 | 0.4118 | ||||
| 169.5333 | 71.7588 | 218.8506 | 68.1867 | ||||
| 1 | 6.3335 | 1.2231 | 0.7487 | 5.9833 | 0.7817 | 0.7723 | |
| 59.9327 | 61.2251 | 49.1219 | 29.0219 | ||||
| 5.6170 | 0.9304 | 5.7488 | 0.7462 | ||||
| 100.6982 | 94.3161 | 137.1196 | 87.5453 | ||||
| 2 | 4.5667 | 0.7452 | 0.7802 | 4.7140 | 0.5886 | 0.8055 | |
| 10.8924 | 6.1630 | 12.8144 | 5.4122 | ||||
| 5.1437 | 0.6808 | 5.4287 | 0.6144 | ||||
| 60.6901 | 39.9974 | 95.0598 | 31.6362 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yousef, M.M.; Almetwally, E.M. Multi Stress-Strength Reliability Based on Progressive First Failure for Kumaraswamy Model: Bayesian and Non-Bayesian Estimation. Symmetry 2021, 13, 2120. https://doi.org/10.3390/sym13112120
Yousef MM, Almetwally EM. Multi Stress-Strength Reliability Based on Progressive First Failure for Kumaraswamy Model: Bayesian and Non-Bayesian Estimation. Symmetry. 2021; 13(11):2120. https://doi.org/10.3390/sym13112120
Chicago/Turabian StyleYousef, Manal M., and Ehab M. Almetwally. 2021. "Multi Stress-Strength Reliability Based on Progressive First Failure for Kumaraswamy Model: Bayesian and Non-Bayesian Estimation" Symmetry 13, no. 11: 2120. https://doi.org/10.3390/sym13112120
APA StyleYousef, M. M., & Almetwally, E. M. (2021). Multi Stress-Strength Reliability Based on Progressive First Failure for Kumaraswamy Model: Bayesian and Non-Bayesian Estimation. Symmetry, 13(11), 2120. https://doi.org/10.3390/sym13112120







