Traveling Wave Solutions to the Nonlinear Evolution Equation Using Expansion Method and Addendum to Kudryashov’s Method
Abstract
:1. Introduction
2. Methodology of the Expansion Method
- First, when and we have the hyperbolic function solutions:orwhere E is the integration constant.
- Second, when and we have solutions as:
- Third, when we obtain the periodic solutions as:or
- Fourth, when we obtain the solution as:
- Fifth, when we obtain the solution as:
3. Application
- Case 1: when and the complex and the real scalar fields can be expressed respectively as:and
- Case 2: when and the complex and the real scalar fields can be expressed, respectively, as:
- Case 3: when and the complex and the real scalar fields can be expressed respectively as:
- Case 4: when and the complex and the real scalar fields can be expressed, respectively, as:
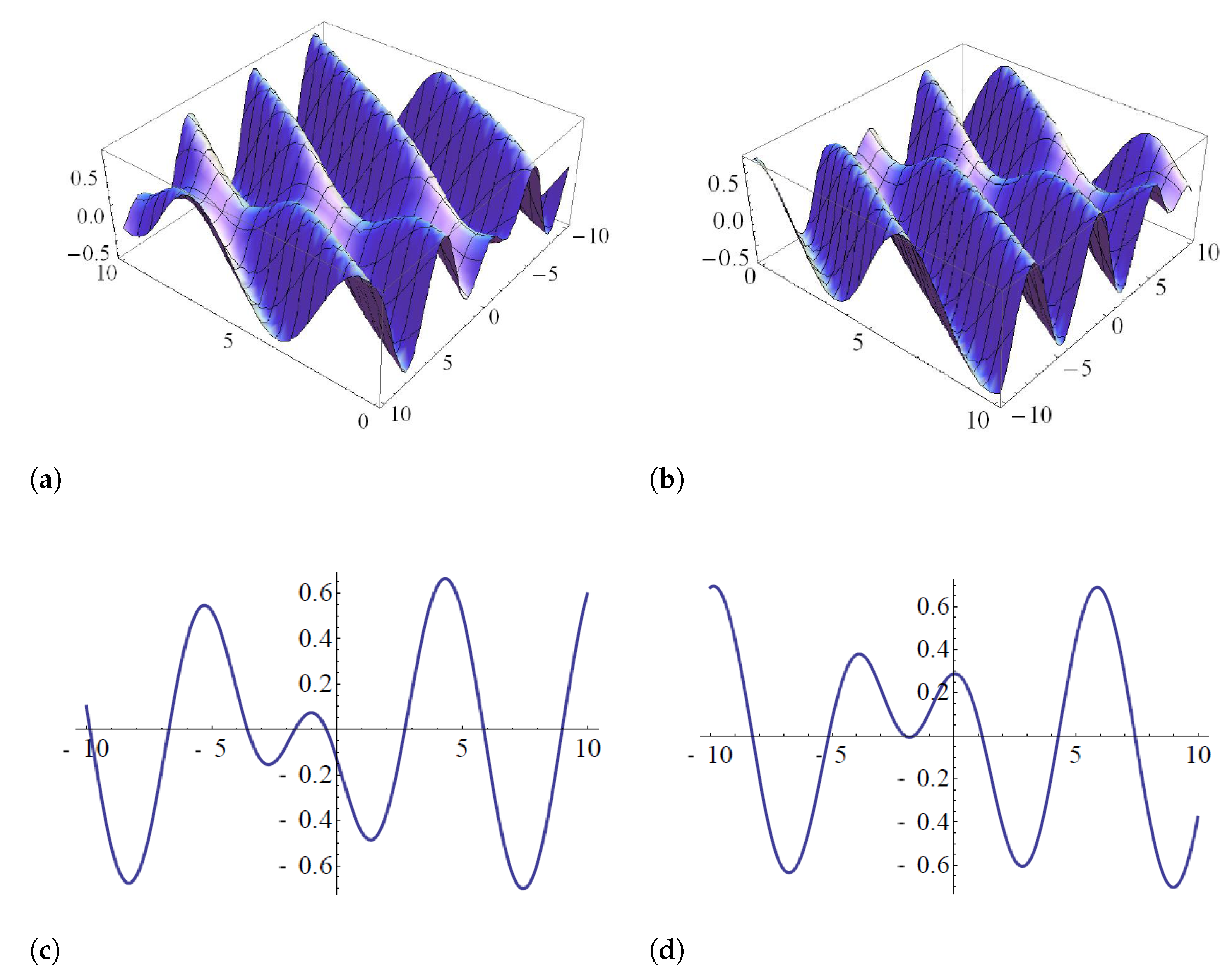
- Case 5: when and the complex and the real scalar fields can be expressed, respectively, as:Figure 7 represents the singular Kink wave solution of the real part (Figure 7a) and imaginary part (Figure 7b) of (29a) and its projections (Figure 7c) and (Figure 7d), respectively, while the singular Kink wave solution (29b) and its projections are shown in Figure 8, for special values of parameters.
4. Addendum to Kudryashov’s Method (AKM) for -Dimensional Hirota–Maccari Equation
- Step 1: Assuming that (17) has a solution in the following formwhere for are constants can be determined, and satisfies the node so thatwhere is an arbitrary constant. We can verify that Equation (31) can be written in the form:where A represents a non- zero real number, T is a natural number, and .
- Step 2: The relation between N and T can be calculated as follows: Setting then , , hence and
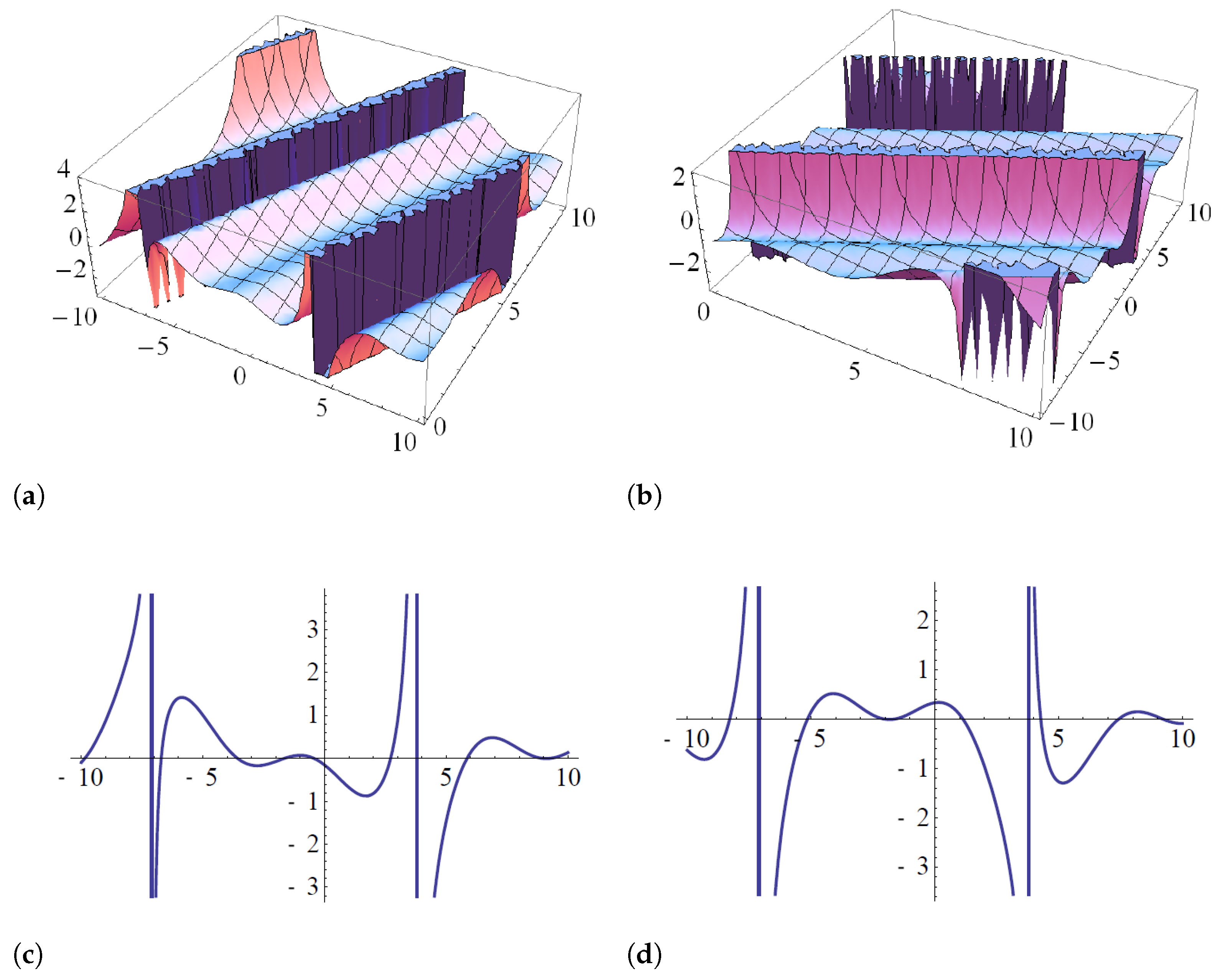
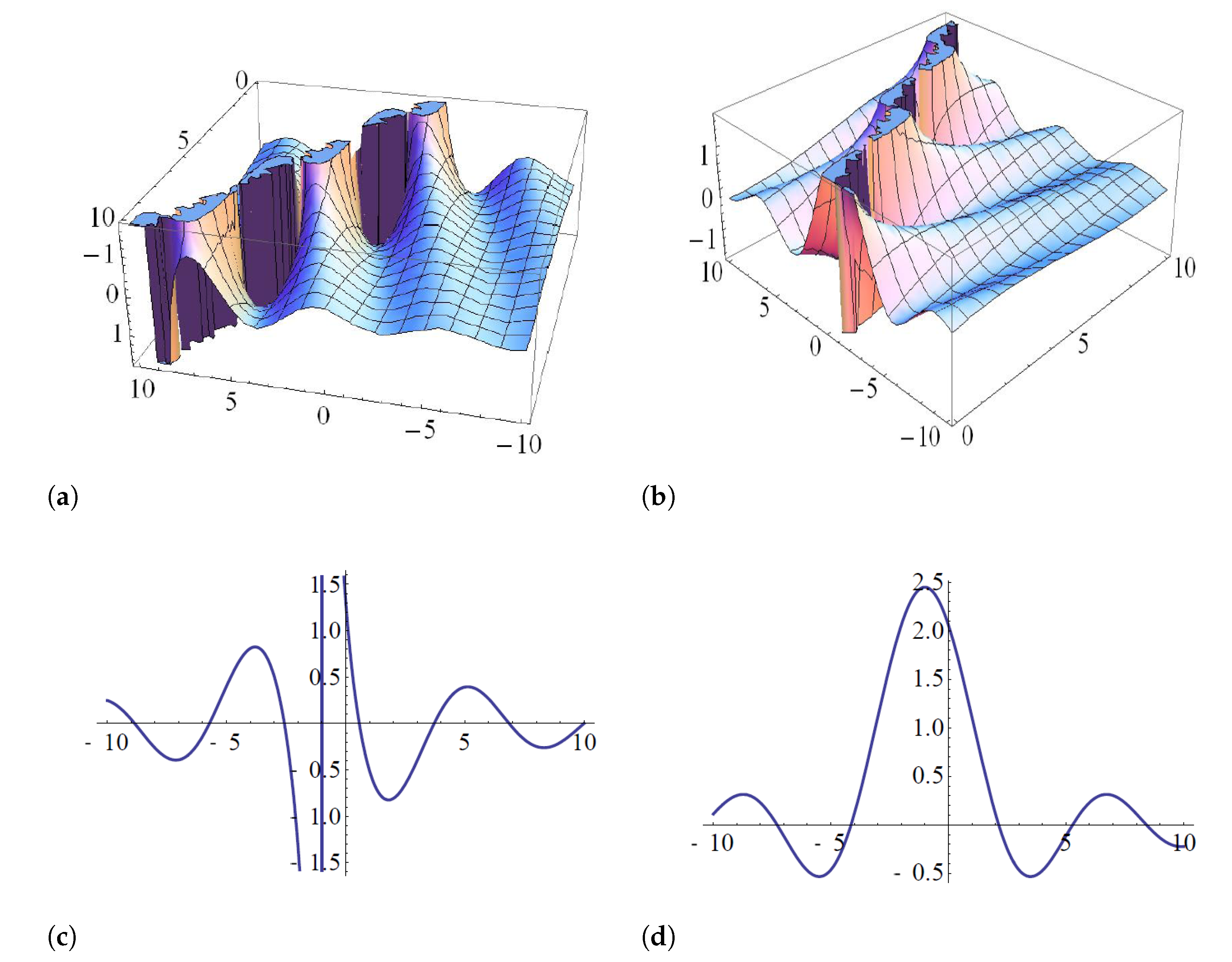
- Case 1. Setting hence Then, we deduce from Equation (33) thatwhere and are constants and Substituting Equations (34) and (31) into Equation (17) and collecting all the transactions of this term for ( and ), and setting them to zero, leads to a system of equations that can be solved to obtain:andprovided Substituting Equations (35) and (32) into Equation (34), and calculating the straddled solitary solution of Equation (17) gives:andprovide In particular, setting in Equation (38), we obtain the singular soliton solution to Equation (17) asand
- Case 2. Setting hence Then, we deduce from Equation (30) that Equation (17) has solutions in following form:where , and are constants, and Substituting Equations (41) and (12) into Equation (17) and collecting all the transactions of this term for ( and ), and setting them to zero, we obtain a system of equations that can be solved to obtain the following results:andprovided Substituting Equations (42) and (43) into Equation (41), and calculating the straddled solitary solution of Equation (17) leads toandproviding In particular, setting in Equation (38), we obtain the singular soliton solution to Equation (17) asandNote that by choosing different values for the parameters T and N, we can obtain several solitary wave solutions of Equation (17).
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dolbow, J.; Khaleel, M.A.; Mitchell, J. Multiscale Mathematics Initiative: A Roadmap; Report from the 3rd DoE Workshop on Multiscale Mathematics, Technical Report; Department of Energy: Washington, DC, USA, 2004. Available online: http://www.sc.doe.gov/ascr/mics/amr (accessed on 8 November 2021).
- Baleanu, D.; Machado, A.T.; Luo, A.C.J. Fractional Dynamics Control; Springer Science & Business Media: New York, NY, USA, 2011; pp. 49–57. [Google Scholar]
- Boudjehem, B.; Boudjehem, D. Parameter tuning of a fractional-order PI Controller using the ITAE Criteria. Fractional Dyn. Control 2011, 49–57. [Google Scholar] [CrossRef]
- Alotaibi, H. Developing Multiscale Methodologies for Computational Fluid Mechanics. Ph.D. Thesis, The University of Adelaide, Adelaide, Australia, 2017. [Google Scholar]
- Choucha, A.; Ouchenane, D.; Boulaaras, S. A Backlund transformation and the inverse scattering transform method for the generalised Vakhnenko equation. Nonlinear Funct. Anal. 2020, 1–10. [Google Scholar] [CrossRef]
- Zhong, B.; Jiang, J.; Feng, Y. New exact solutions of fractional Boussinesq-like equations. Commun. Optim. Theory 2020, 1–17. [Google Scholar] [CrossRef]
- Simbanefayi, I.; Khalique, C.M. Travelling wave solutions and conservation laws for the Korteweg-de Vries-Bejamin-Bona-Mahony equation. Results Phys. 2018, 8, 57–63. [Google Scholar] [CrossRef]
- Vakhnenko, V.O.; Parkes, E.J.; Morrison, A.J. A Backlund transformation and the inverse scat-tering transform method for the generalised Vakhnenko equation. Chaos Solitons Fractals 2003, 17, 683–692. [Google Scholar] [CrossRef]
- Wazwaz, A.M. A sine-cosine method for handlingnonlinear wave equations. Math. Comput. Model. 2004, 40, 499–508. [Google Scholar] [CrossRef]
- Duffy, B.R.; Parkes, E.J. Traveling solitary wave solutions to a seventh-order generalized KdV equation. Phys. Lett. A 1996, 214, 271–272. [Google Scholar] [CrossRef]
- Fan, E.G. Extended tanh-function method and its applications to nonlinear equations. Phys. Lett. A 2000, 277, 212–218. [Google Scholar] [CrossRef]
- Zayed, E.M.; Gepreel, K.A. The modified (G/G) -expansion method and its applications to construct exact solutions for nonlinear PDEs. WSEAS Trans. Math. 2011, 10, 270–278. [Google Scholar]
- Ebadi, G.; Biswas, A. The G′/G method and topological Solitons solution of the K(m, n) equation. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 2377–2382. [Google Scholar] [CrossRef]
- He, J.H.; Wu, X.H. Exp-function method for nonlinear wave equations. Chaos Solitons Fractals 2006, 30, 700–708. [Google Scholar] [CrossRef]
- Cariello, F.; Tabor, M. Similarity reductions from extended Painleve’ expansions for nonin-tegrable evolution equations. Phys. D 1991, 53, 59–70. [Google Scholar] [CrossRef]
- Abdou, M.A. The extended F-expansion method and its application for a class of nonlinear evolution equations. Chaos Solitons Fractals 2007, 31, 95–104. [Google Scholar] [CrossRef]
- Jawad, A.J.; Petkovic, M.D.; Biswas, A. Modified simple equation method for nonlinear evo-lution equations. Appl. Math. Comp. 2010, 217, 869–877. [Google Scholar] [CrossRef]
- Zayed, E.M.; Arnous, A.H. Exact solutions of the nonlinear ZK-MEW and the Potential YTSF equations using the modified simple equation method. AIP Conf. Proc. ICNAAM 2012, 1479, 2044–2048. [Google Scholar]
- Taghizadeh, N.; Mirzazadeh, M. The Modified Extended Tanh Method with the Riccati Equa-tion for Solving Nonlinear Partial Differential Equations. Math. Aeterna 2012, 2, 145–153. [Google Scholar]
- Hafez, M.G.; Alam, M.N.; Akber, M.A. Application of the exp(−ϕ(ξ)))-expansion method to find exact solutions for the solitary wave equation in an unmagnetized dusty plasma. World Appl. Sci. J. 2014, 32, 2150–2155. [Google Scholar]
- Ege, S.M.; Misirli, E. Extended Kudryashov Method for Fractional Nonlinear Differential Equations. Math. Sci. Appl. 2018, 6, 19–28. [Google Scholar] [CrossRef]
- Kaplan, M.; Bekir, A.; Akbulut, A. A generalized Kudryashov method to some nonlinear evolution equations in mathematical physics. Nonlinear Dyn. 2016, 85, 2843–2850. [Google Scholar] [CrossRef]
- Zayed, E.M.; Shohib, R.M.; Alngar, M.E. New extended generalized Kudryashov method for solving three nonlinear partial differential equations. Nonlinear Anal. Model. Control 2020, 25, 598–617. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Alngar, M.E.M.; Biswas, A.; Kara, A.H.; Ekici, M.; Alzahrani, A.K.; Belic, M.R. Cubicquartic optical solitons and conservation laws with Kudryashov’s sextic power-law of refractive index. Optik 2021, 227, 166059. [Google Scholar] [CrossRef]
- Hafez, M.G.; Alam, M.N.; Akber, M.A.; Roshid, H.O. Exact traveling wave solutions of the (3 + 1)-Dimensional mkdv-zk and the (2 + 1)-Dimensional Burgers equations via exp(−ϕ(ξ)))-expansion method. Alex Eng. 2015, 54, 635–644. [Google Scholar]
- Hafez, M.G.; Ali, M.Y.; Chowdary, M.K.; Kauser, M.A. Application of the exp(−ϕ(ξ)))-expansion method for solving nonlinear TRLW and Gardner equations. Int. J. Math. Comput. 2016, 27, 44–56. [Google Scholar]
- Liang, Z.F.; Tang, X.Y. Modulational instability and variable separation solution for a general-ized (2+1)-dimensional Hirota equation. Chin. Phys. Lett. 2010, 27, 1–4. [Google Scholar]
- Hirota, R. Exact evelope-soliton solutions of a nonlinear wave equation. J. Math. Phys. 1973, 14, 805–809. [Google Scholar] [CrossRef]
- Fan, E. Uniformly constructing a series of explicit exact solutions to non-linear equations in mathematical physics. Chaos Solitons Fractals 2003, 16, 819–839. [Google Scholar] [CrossRef]
- Chen, Y.; Yan, Z. The Weierstrass elliptic function expansion method and its applications in nonlinear wave equations. Chaos Solitons Fractals 2006, 29, 948–964. [Google Scholar] [CrossRef] [Green Version]
- Jia, T.T.; Chai, Y.Z.; Hao, H.Q. Multi-soliton solutions and Breathers for the generalized coupled nonlinear Hirota equations via the Hirota method. Superlattices Microstruct. 2006, 127, 1848–1859. [Google Scholar] [CrossRef]
- Gepreel, K.A. Exact Soliton Solutions for Nonlinear Perturbed Schrödinger Equations with Nonlinear Optical Media. Appl. Sci. 2020, 10, 8929. [Google Scholar] [CrossRef]
- Wang, M.; Li, X.Z. Extended F-expansion method and periodic wave solutions for the gen-eralized Zakharov equations. Phys. Lett. A 2005, 343, 48–54. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Method for finding highly dispersive optical solitons of nonlinear differential equations. Optik 2020, 206, 163550. [Google Scholar] [CrossRef]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alotaibi, H. Traveling Wave Solutions to the Nonlinear Evolution Equation Using Expansion Method and Addendum to Kudryashov’s Method. Symmetry 2021, 13, 2126. https://doi.org/10.3390/sym13112126
Alotaibi H. Traveling Wave Solutions to the Nonlinear Evolution Equation Using Expansion Method and Addendum to Kudryashov’s Method. Symmetry. 2021; 13(11):2126. https://doi.org/10.3390/sym13112126
Chicago/Turabian StyleAlotaibi, Hammad. 2021. "Traveling Wave Solutions to the Nonlinear Evolution Equation Using Expansion Method and Addendum to Kudryashov’s Method" Symmetry 13, no. 11: 2126. https://doi.org/10.3390/sym13112126
APA StyleAlotaibi, H. (2021). Traveling Wave Solutions to the Nonlinear Evolution Equation Using Expansion Method and Addendum to Kudryashov’s Method. Symmetry, 13(11), 2126. https://doi.org/10.3390/sym13112126





