Symbol Error-Rate Analytical Expressions for a Two-User PD-NOMA System with Square QAM
Abstract
:1. Introduction
2. System Model
3. BER and SER for Conventional Square QAM Signal
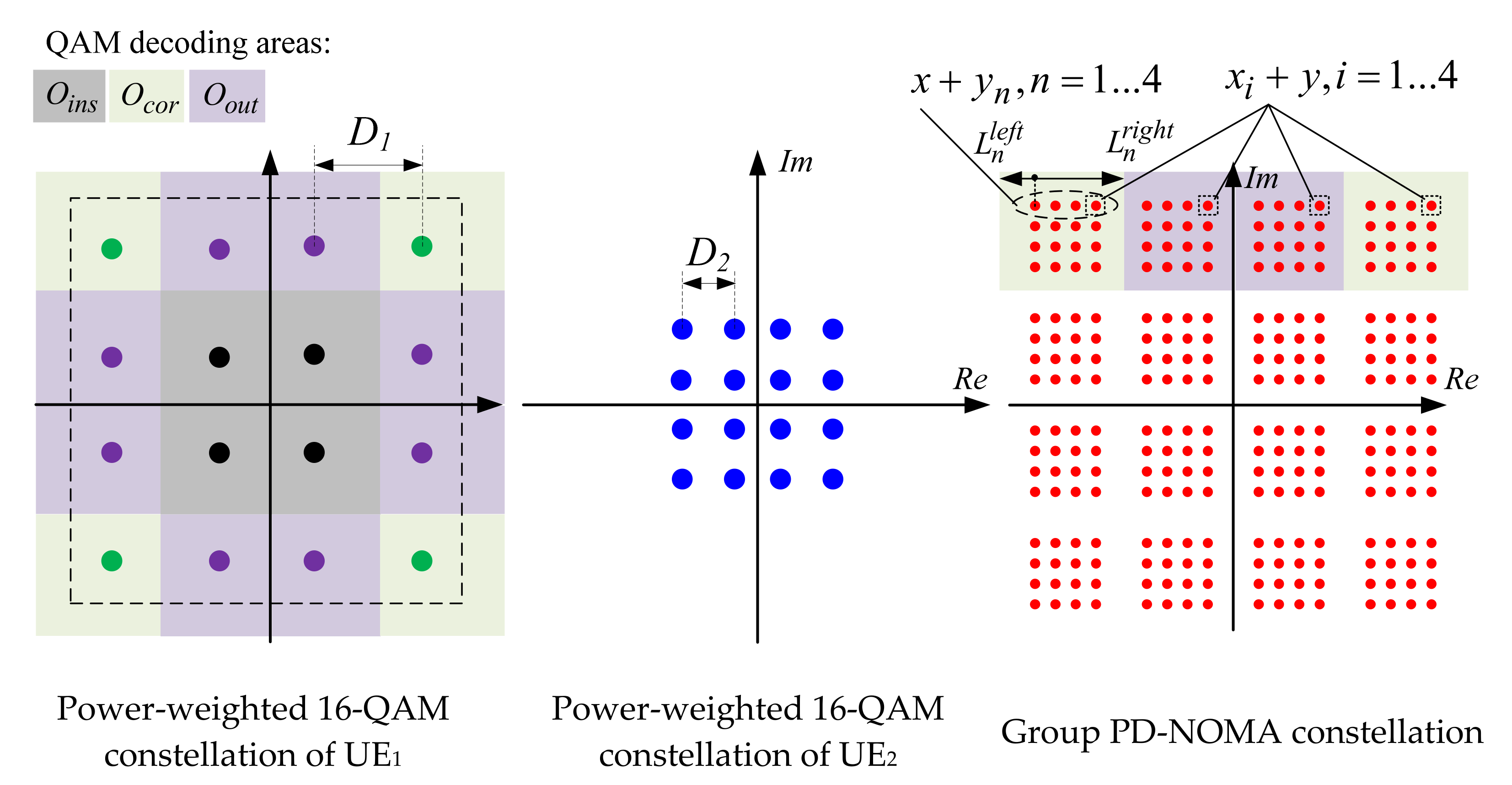
4. BER and SER for PD-NOMA Square QAM Signal
4.1. First Layer Decoding
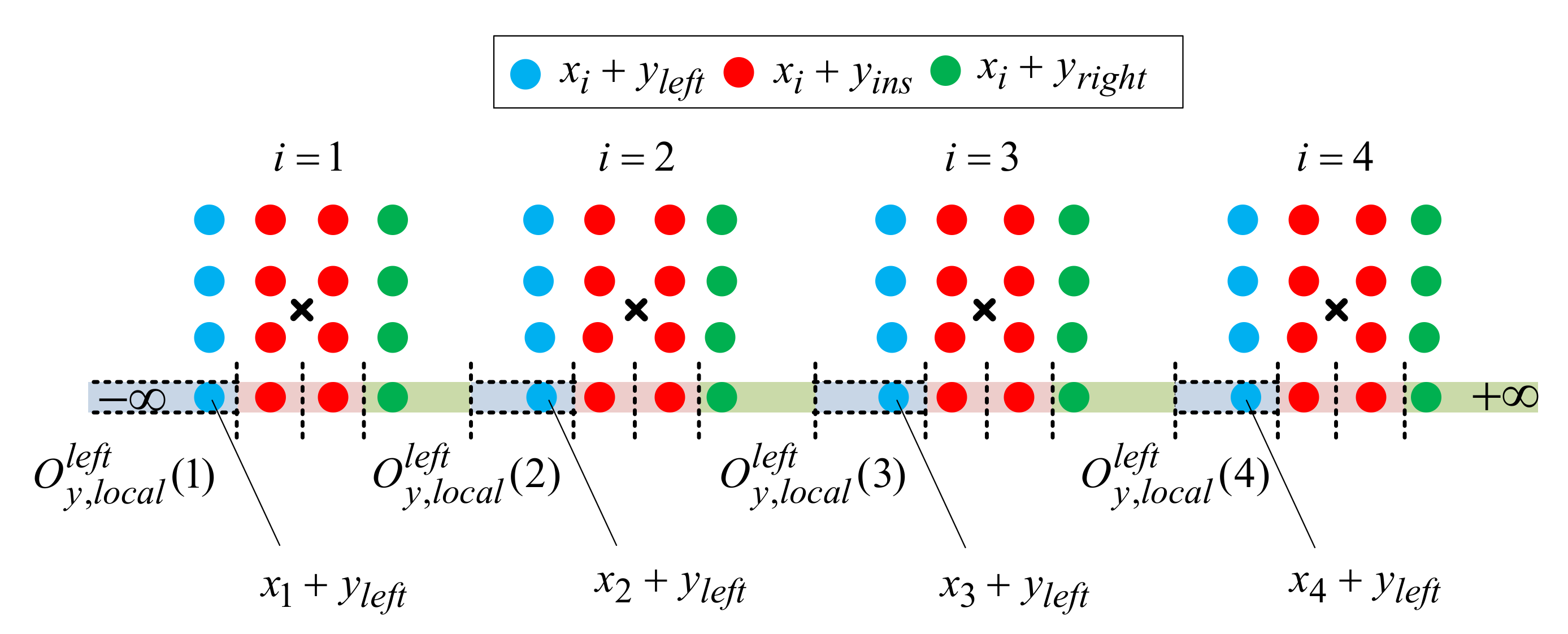
4.2. Second Layer Decoding
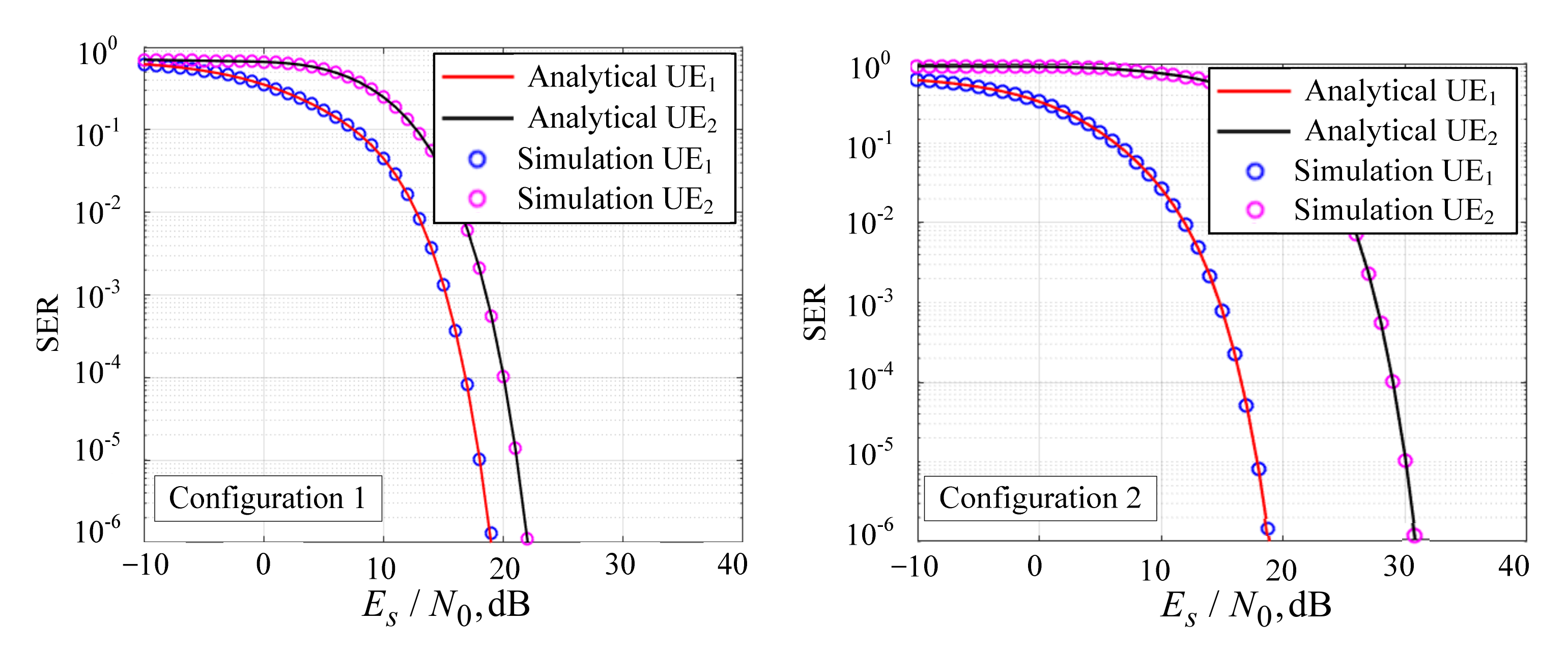
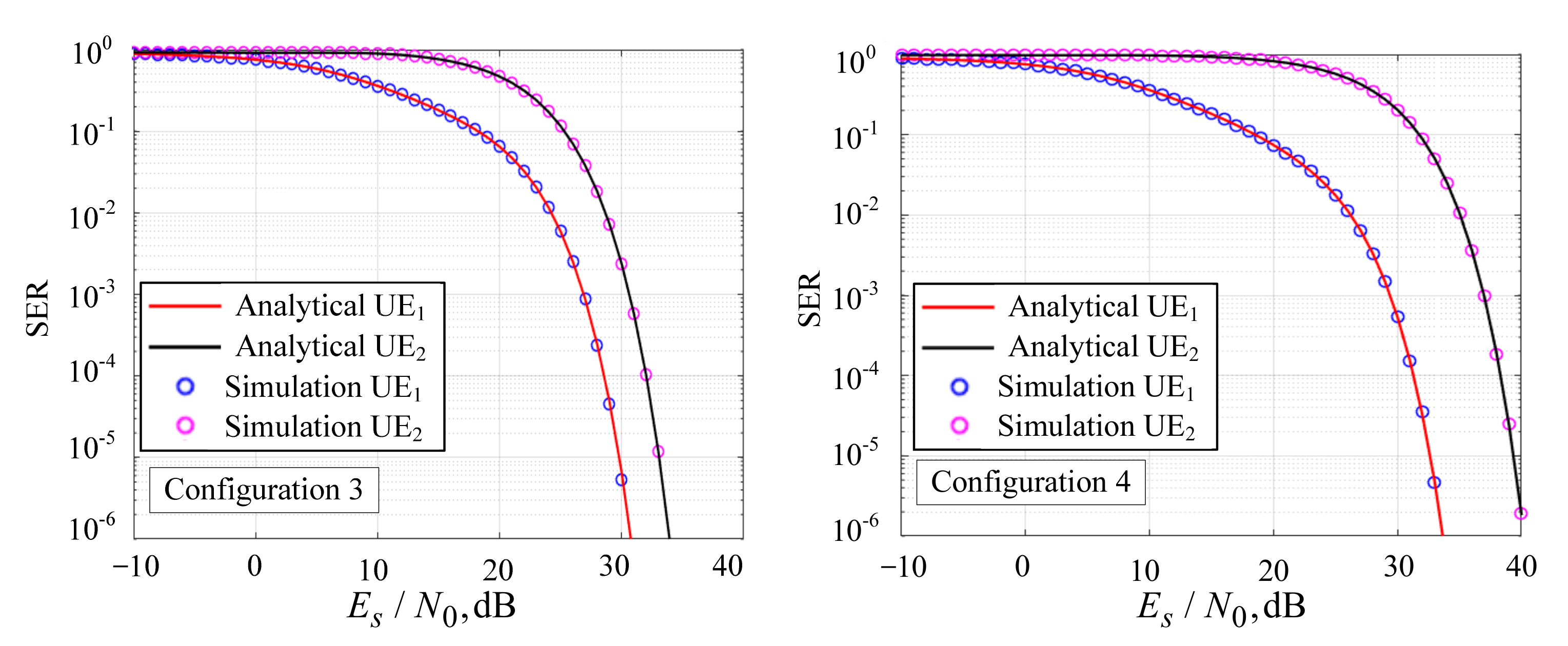
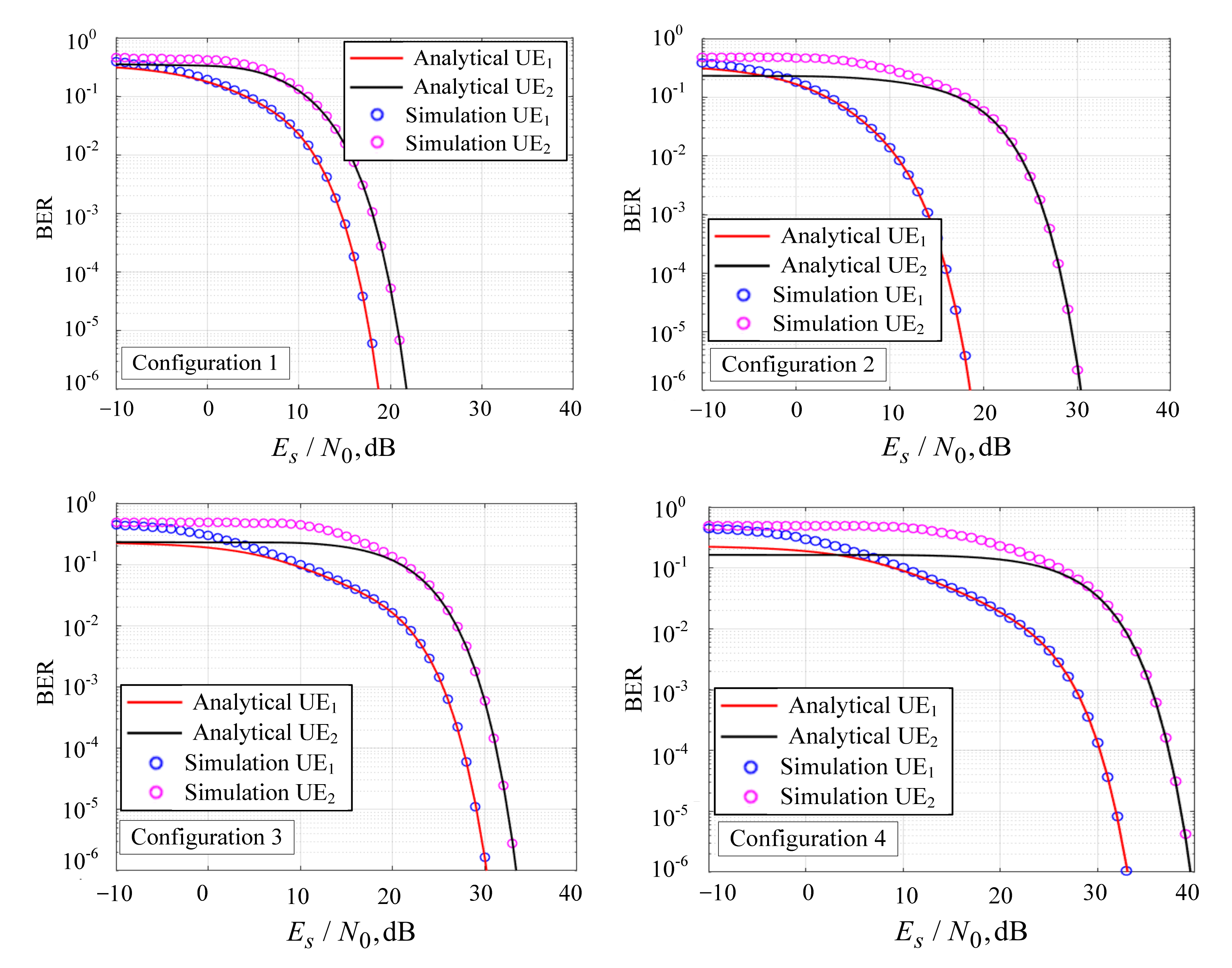
5. BER and SER Simulation
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Saito, Y.; Benjebbour, A.; Kishiyama, Y.; Nakamura, T. System-level performance evaluation of downlink non-orthogonal multiple access (NOMA). In Proceedings of the 2013 IEEE 24th International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), London, UK, 8–11 September 2013; pp. 611–615. [Google Scholar]
- Saito, Y. Non-orthogonal multiple access (NOMA) for cellular future radio access. In Proceedings of the 2013 IEEE 77th Vehicular Technology Conference (VTC Spring), Dresden, Germany, 2–5 June 2013. [Google Scholar]
- Ding, Z.; Lei, X.; Karagiannidis, G.K.; Schober, R.; Yuan, J.; Bhargava, V.K. A survey on non-orthogonal multiple access for 5G networks: Research challenges and future trends. IEEE J. Sel. Areas Commun. 2017, 35, 2181–2195. [Google Scholar] [CrossRef] [Green Version]
- Benjebbour, A.; Saito, K.; Li, A.; Kishiyama, Y.; Nakamura, T. Non-orthogonal multiple access (NOMA): Concept, performance evaluation and experimental trials. In Proceedings of the 2015 International Conference on Wireless Networks and Mobile Communications (WINCOM), Marrakech, Morocco, 20–23 October 2015. [Google Scholar]
- Shin, W.; Vaezi, M.; Lee, B.; Love, D.J.; Lee, J.; Poor, H.V. Non-orthogonal multiple access in multi-cell networks: Theory, performance, and practical challenges. IEEE Commun. Mag. 2017, 55, 176–183. [Google Scholar] [CrossRef] [Green Version]
- Islam, S.R.; Avazov, N.; Dobre, O.A.; Kwak, K.S. Power-domain non-orthogonal multiple access (NOMA) in 5G systems: Potentials and challenges. IEEE Commun. Surv. Tutor. 2016, 19, 721–742. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.H.; Liang, D.C. Heterogeneous networks with power-domain NOMA: Coverage, throughput, and power allocation analysis. IEEE Trans. Wirel. Commun. 2018, 17, 3524–3539. [Google Scholar] [CrossRef] [Green Version]
- Higuchi, K.; Benjebbour, A. Non-orthogonal multiple access (NOMA) with successive interference cancellation for future radio access. IEICE Trans. Commun. 2015, 98, 403–414. [Google Scholar] [CrossRef] [Green Version]
- Cui, J.; Liu, Y.; Ding, Z.; Fan, P.; Nallanathan, A. Optimal user scheduling and power allocation for millimeter wave NOMA systems. IEEE Trans. Wirel. Commun. 2017, 17, 1502–1517. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Benjebbour, A.; Li, A.; Harada, A. Multi-user proportional fair scheduling for uplink non-orthogonal multiple access (NOMA). In Proceedings of the 2014 IEEE 79th Vehicular Technology Conference (VTC Spring), Seoul, Korea, 18–21 May 2014. [Google Scholar]
- Rai, R.; Zhu, H.; Wang, J. Resource scheduling in non-orthogonal multiple access (NOMA) based cloud-RAN systems. In Proceedings of the 2017 IEEE 8th Annual Ubiquitous Computing, Electronics and Mobile Communication Conference (UEMCON), New York, NY, USA, 19–21 October 2017; pp. 418–422. [Google Scholar]
- Uddin, M.F. Energy efficiency maximization by joint transmission scheduling and resource allocation in downlink NOMA cellular networks. Comput. Netw. 2019, 159, 37–50. [Google Scholar] [CrossRef]
- Fang, F.; Zhang, H.; Cheng, J.; Roy, S.; Leung, V.C. Joint user scheduling and power allocation optimization for energy-efficient NOMA systems with imperfect CSI. IEEE J. Sel. Areas Commun. 2017, 35, 2874–2885. [Google Scholar] [CrossRef]
- Kryukov, Y.V.; Brovkin, A.A.; Pokamestov, D.A.; Kvashnina, A.S. A simple proportional fair scheduling for downlink power domain non-orthogonal multiple access systems. Journal of Physics: Conference Series. IOP Publ. 2020, 1679, 032055. [Google Scholar]
- Kryukov, Y.V.; Pokamestov, D.A.; Brovkin, A.A.; Rogozhnikov, E.V. Power and Frequency Scheduling Using Equal Throughput Strategy in PD-NOMA Systems. In Computer Science Online Conference; Springer: Cham, Switzerland, 2020; pp. 584–595. [Google Scholar]
- Zeng, M.; Yadav, A.; Dobre, O.A.; Tsiropoulos, G.I.; Poor, H.V. Capacity comparison between MIMO-NOMA and MIMO-OMA with multiple users in a cluster. IEEE J. Sel. Areas Commun. 2017, 35, 2413–2424. [Google Scholar] [CrossRef]
- Wei, Z.; Yang, L.; Ng, D.W.K.; Yuan, J.; Hanzo, L. On the performance gain of NOMA over OMA in uplink communication systems. IEEE Trans. Commun. 2019, 68, 536–568. [Google Scholar] [CrossRef] [Green Version]
- Wyner, A. Recent results in the Shannon theory. IEEE Trans. Inf. Theory 1974, 20, 2–10. [Google Scholar] [CrossRef]
- Meghdadi, V. BER calculation. In Wireless Communications; 2008; Available online: https://www.unilim.fr/pages_perso/vahid.meghdadi-neyshabouri/notes/ber_awgn.pdf (accessed on 1 October 2021).
- Kara, F.; Kaya, H. BER performances of downlink and uplink NOMA in the presence of SIC errors over fading channels. IET Commun. 2018, 12, 1834–1844. [Google Scholar] [CrossRef]
- Assaf, T.; Al-Dweik, A.; Moursi, M.E.; Zeineldin, H. Exact BER performance analysis for downlink NOMA systems over Nakagami-m fading channels. IEEE Access 2019, 7, 134539–134555. [Google Scholar] [CrossRef]
- Wang, X.; Labeau, F.; Mei, L. Closed-form BER expressions of QPSK constellation for uplink non-orthogonal multiple access (NOMA). IEEE Commun. Lett. 2017, 21, 2242–2245. [Google Scholar] [CrossRef]
- Han, W.; Wang, Y.; Tang, D.; Hou, R.; Ma, X. Study of the Symbol Error Rate/Bit Error Rate in Non-orthogonal Multiple Access (NOMA) Systems. In Proceedings of the 2018 IEEE/CIC International Conference on Communications in China (ICCC Workshops), Beijing, China, 16–18 August 2018; pp. 101–106. [Google Scholar]
- Huang, H.; Wang, J.; Wang, J.; Yang, J.; Xiong, J.; Gui, G. Symbol error rate performance analysis of non-orthogonal multiple access for visible light communications. China Commun. 2017, 14, 153–161. [Google Scholar] [CrossRef]
- Almohimmah, E.M.; Alresheedi, M.T. Error analysis of NOMAbased VLC systems with higher order modulation schemes. IEEE Access 2020, 8, 2792–2803. [Google Scholar] [CrossRef]
- Lee, E.A.; Messerschmitt, D.G. Digital Communication; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Available online: https://www.amazon.com/Digital-Communication-John-R-Barry-dp-1461349753/dp/1461349753/ref=mt_other?_encoding=UTF8&me=&qid= (accessed on 1 October 2021).

| No. | First Layer (UE1) | Second Layer (UE2) | ||
|---|---|---|---|---|
| p1 | Q1 | p2 | Q2 | |
| 1 | 0.85 | 4 | 0.15 | 4 |
| 2 | 0.9 | 4 | 0.1 | 16 |
| 3 | 0.95 | 16 | 0.05 | 16 |
| 4 | 0.95 | 16 | 0.05 | 64 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kryukov, Y.V.; Pokamestov, D.A.; Novichkov, S.A. Symbol Error-Rate Analytical Expressions for a Two-User PD-NOMA System with Square QAM. Symmetry 2021, 13, 2153. https://doi.org/10.3390/sym13112153
Kryukov YV, Pokamestov DA, Novichkov SA. Symbol Error-Rate Analytical Expressions for a Two-User PD-NOMA System with Square QAM. Symmetry. 2021; 13(11):2153. https://doi.org/10.3390/sym13112153
Chicago/Turabian StyleKryukov, Yakov V., Dmitriy A. Pokamestov, and Serafim A. Novichkov. 2021. "Symbol Error-Rate Analytical Expressions for a Two-User PD-NOMA System with Square QAM" Symmetry 13, no. 11: 2153. https://doi.org/10.3390/sym13112153
APA StyleKryukov, Y. V., Pokamestov, D. A., & Novichkov, S. A. (2021). Symbol Error-Rate Analytical Expressions for a Two-User PD-NOMA System with Square QAM. Symmetry, 13(11), 2153. https://doi.org/10.3390/sym13112153







