On Dynamic Investigations of Cournot Duopoly Game: When Firms Want to Maximize Their Relative Profits
Abstract
:1. Introduction
2. The Model
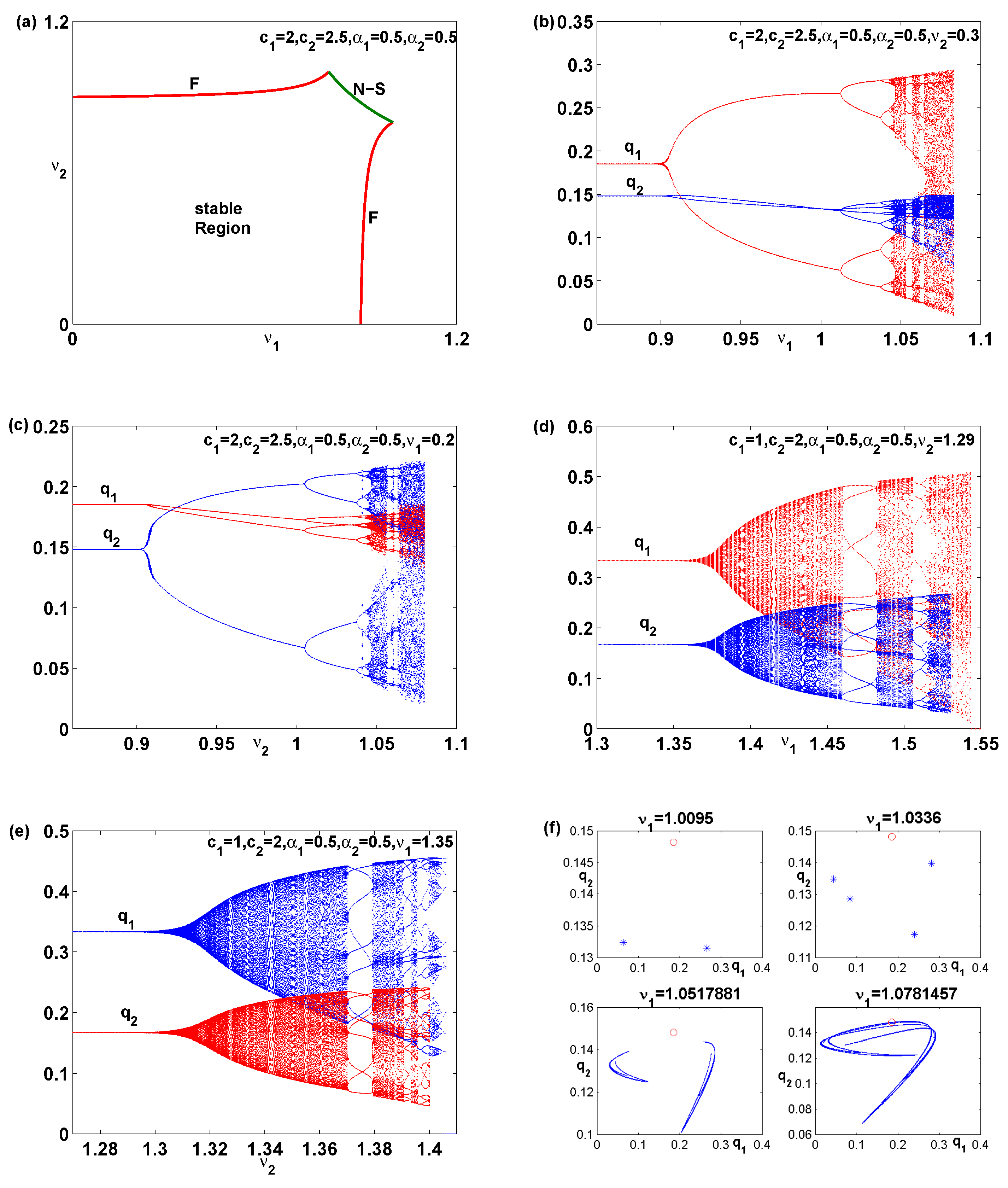
3. Local Stability
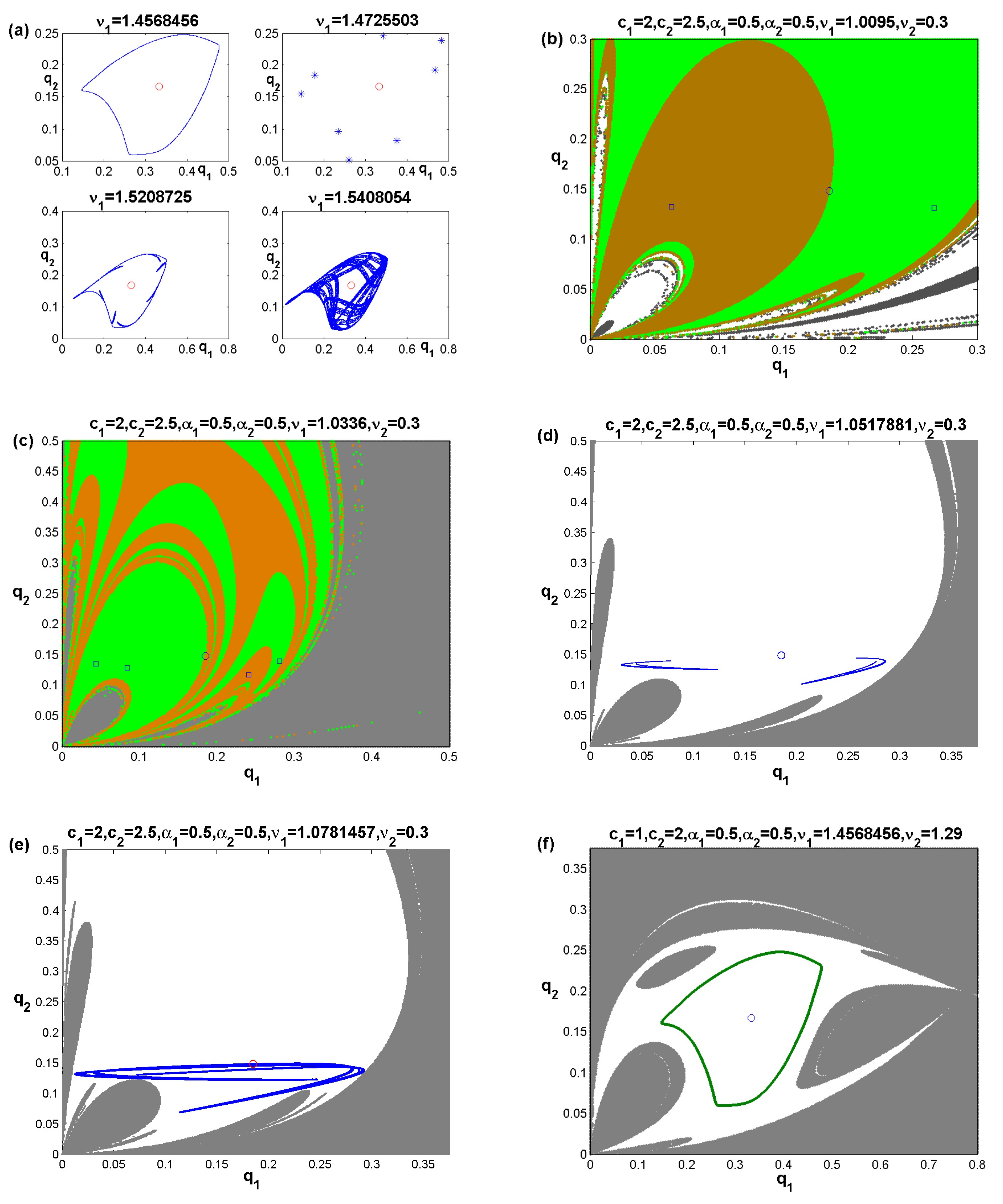
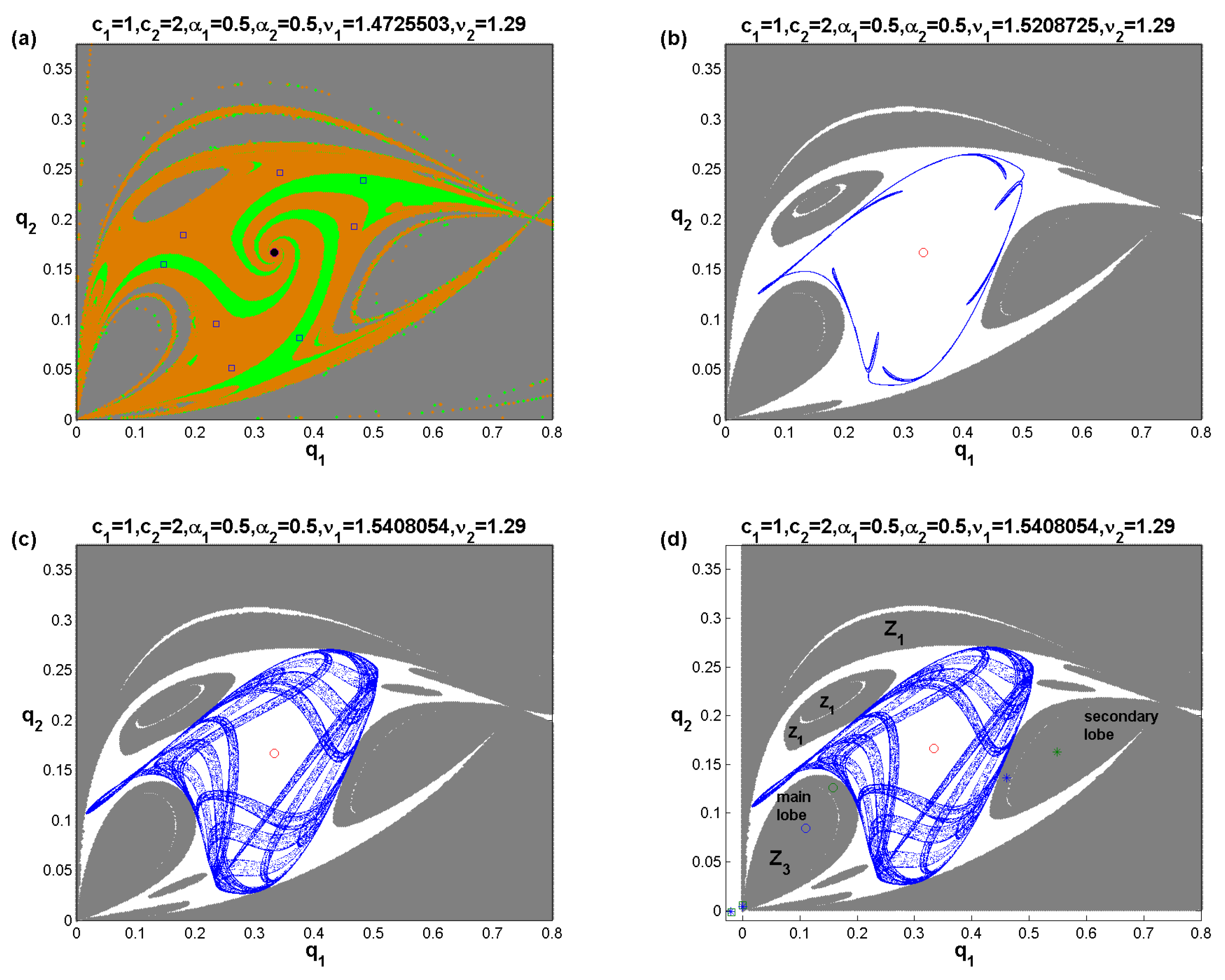
4. Global Analysis
4.1. Noninvertible Map
4.2. Focal Point and Lobes
4.3. Lobes Construction
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Singh, N.; Vives, X. Price and quantity competition in a differentiated duopoly. Rand J. Econ. 1984, 15, 546–554. [Google Scholar] [CrossRef]
- Elsadany, A.A. Dynamics of a Cournot duopoly game with bounded rationality based on relative profit maximization. Appl. Math. Comput. 2017, 294, 253–263. [Google Scholar] [CrossRef]
- Tuinstra, J. A price adjustment process in a model of monopolistic competition. Int. Game Theory Rev. 2004, 6, 417–442. [Google Scholar] [CrossRef]
- Naimzada, A.K.; Raimondo, R. Chaotic congestion games. Appl. Math. Comput. 2018, 321, 333–348. [Google Scholar] [CrossRef]
- Ueda, M. Effect of information asymmetry in Cournot duopoly game with bounded rationality. Appl. Math. Comput. 2019, 362, 124535. [Google Scholar] [CrossRef] [Green Version]
- Puu, T. Chaos in duopoly pricing. Chaos Solitons Fractals 1991, 1, 573–581. [Google Scholar] [CrossRef]
- Askar, S.S.; Al-khedhairi, A. Dynamic investigations in a duopoly game with price competition based on relative profit and profit maximization. J. Comput. Appl. Math. 2020, 367, 112464. [Google Scholar] [CrossRef]
- Askar, S.S. On Cournot–Bertrand competition with differentiated products. Ann. Oper. Res. 2014, 223, 81–93. [Google Scholar] [CrossRef]
- Askar, S.S. Tripoly Stackelberg game model: One leader versus two followers. Appl. Math. Comput. 2018, 328, 301–311. [Google Scholar] [CrossRef]
- Askar, S.S.; Al-Khedhairi, A. Analysis of nonlinear duopoly games with product differentiation: Stability, global dynamics, and control. Discret. Dyn. Nat. Soc. 2017, 2017, 2585708. [Google Scholar] [CrossRef] [Green Version]
- Bylka, S.; Komar, J. Cournot-Bertrand mixed oligopolies. In Warsaw Fall Seminars in Mathematical Economics 1975. Lecture Notes in Economics and Mathematical Systems; Łoś, M., Łoś, J., Wieczorek, A., Eds.; Springer: Berlin/Heidelberg, Germany, 1976; Volume 133. [Google Scholar]
- Häckner, J. A note on price and quantity competition in differentiated oligopolies. J. Econ. Theory 2000, 93, 233–239. [Google Scholar] [CrossRef] [Green Version]
- Zanchettin, P. Differentiated duopoly with asymmetric costs. J. Econ. Manag. Strategy 2006, 15, 999–1015. [Google Scholar] [CrossRef]
- Arya, A.; Mittendorf, B.; Sappington, D.E.M. Outsourcing, vertical integration, and price vesus quantity competition. Int. J. Ind. Organ. 2008, 26, 1–16. [Google Scholar] [CrossRef]
- Tremblay, C.H.; Tremblay, V.J. The Cournot-Bertrand model and the degree of product differentiation. Econ. Lett. 2011, 111, 233–235. [Google Scholar] [CrossRef]
- Askar, S.S. On complex dynamics of cournot-bertrand game with asymmetric market information. Appl. Math. Comput. 2021, 393, 125823. [Google Scholar] [CrossRef]
- Naimzada, A.K.; Tramontana, F. Dynamic properties of a Cournot-Bertrand duopoly game with differentiated products. Econ. Model. 2012, 290, 1436–1439. [Google Scholar] [CrossRef]
- Ma, J.; Sun, L.; Hou, S.; Zhan, X. Complexity study on the Cournot-Bertrand mixed duopoly game model with market share preference. Chaos 2018, 28, 023101–023110. [Google Scholar] [CrossRef]
- Ahmed, E.; Hegazi, A.S.; Elettreby, M.F.; Askar, S.S. On multi-team games. Phys. A Stat. Mech. Appl. 2006, 369, 809–816. [Google Scholar] [CrossRef]
- Ahmed, E.; Elettreby, M.F. Controls of the complex dynamics of a multi-market Cournot model. Econ. Model. 2014, 37, 251–254. [Google Scholar] [CrossRef]
- Peng, Y.; Lu, Q. Complex dynamics analysis for a duopoly Stackelberg game model with bounded rationality. Appl. Math. Comput. 2015, 271, 259–268. [Google Scholar] [CrossRef]
- Tramontana, F. Heterogeneous duopoly with isoelastic demand function. Econ. Model. 2010, 27, 350–357. [Google Scholar] [CrossRef]
- Tanimoto, J. Evolutionary Games with Sociophysics; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Tanimoto, J. Fundamentals of Evolutionary Game Theory and Its Applications; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Tanimoto, J. Mathematical Analysis of Environmental System; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Zhong, W.; Kokubo, S.; Tanimoto, J. How is the equilibrium of continuous strategy game different from that of discrete strategy game? Biosystems 2012, 107, 88–94. [Google Scholar] [CrossRef] [PubMed]
- Kokubo, S.; Wang, Z.; Tanimoto, J. Spatial reciprocity for discrete, continuous and mixed strategy setups. Appl. Math. Comput. 2015, 259, 552–568. [Google Scholar] [CrossRef]
- Wang, H.; Ma, J. Complexity analysis of a Cournot-Bertrand duopoly game model with limited information. Discret. Nat. Soc. 2013, 2013, 287371. [Google Scholar] [CrossRef]
- Fanti, L.; Gori, L.; Sodini, M. Nonlinear dynamics in a Cournot duopoly with relative profit delegation. Chaos Solitons Fractals 2012, 45, 1469–1478. [Google Scholar] [CrossRef] [Green Version]
- Cavalli, F.; Naimzada, A.; Tramontana, F. Nonlinear dynamics and global analysis of a heterogeneous Cournot duopoly with a local monopolistic approach versus a gradient rule with endogenous reactivity. Commun. Nonlinear Sci. Numer. Simul. 2015, 23, 245–262. [Google Scholar] [CrossRef] [Green Version]
- Caravaggio, A.; Sodini, M. Nonlinear Dynamics in Coevolution of Economic and Environmental Systems. Front. Appl. Math. Stat. 2018, 4, 26. [Google Scholar] [CrossRef]
- Bischi, G.I.; Naimzada, A.K. Global Analysis of a Dynamic Duopoly Game with Bounded Rationality. In Advances in Dynamic Games and Applications; Birkhäuser: Boston, MA, USA, 2000; pp. 361–385. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Askar, S. On Dynamic Investigations of Cournot Duopoly Game: When Firms Want to Maximize Their Relative Profits. Symmetry 2021, 13, 2235. https://doi.org/10.3390/sym13122235
Askar S. On Dynamic Investigations of Cournot Duopoly Game: When Firms Want to Maximize Their Relative Profits. Symmetry. 2021; 13(12):2235. https://doi.org/10.3390/sym13122235
Chicago/Turabian StyleAskar, Sameh. 2021. "On Dynamic Investigations of Cournot Duopoly Game: When Firms Want to Maximize Their Relative Profits" Symmetry 13, no. 12: 2235. https://doi.org/10.3390/sym13122235
APA StyleAskar, S. (2021). On Dynamic Investigations of Cournot Duopoly Game: When Firms Want to Maximize Their Relative Profits. Symmetry, 13(12), 2235. https://doi.org/10.3390/sym13122235





