On Convex Functions Associated with Symmetric Cardioid Domain

Abstract

The geometry of the image domain plays an important role in the characterization of analytic functions. Therefore, for a comprehensive and detailed study of these functions, a thorough analysis of the geometrical properties of their domains is of prime interest. In this regard, new geometrical structures are introduced and studied as an image domain and then their subsequent analytic functions are defined. Inspired and motivated by ongoing research, Malik et al. introduced a very innovative domain named the cardioid domain, which is symmetric about a real axis. Extending the same work on this symmetric cardioid domain, in this article, we provide a deeper analysis and define and study the convex functions associated with the symmetric cardioid domain, named cardio-convex functions.

1. Introduction

In classical mathematics, the theory of analytic functions is one of the outstanding and elegant parts. In this theory, we study the analytic structure as well as the geometric properties of univalent and multivalent functions. In recent decades, there has been remarkable growth in the research on structural and geometrical properties of analytic functions. We can see the applications of analytic functions in mathematics such as in complex analysis, algebraic geometry, and number theory. Other than mathematical analysis, these functions are extensively used in various fields including fractional calculus, ODEs and PDEs, and operators’ theory, to name a few. There are many other problems in physics and other sciences that use differential equations and benefit from analytic functions. An interesting fact is that the relationship between the theory of analytic function and the logarithmic potential is the same as that between the theory of three-dimensional functions and the Newtonian potential. Moreover, some results of potential theory can be studied in the framework of this theory.

Analytic functions have also been used in image processing to define the mathematical background of analytic signals. In the late 40s, in the framework of communication theory, analytical signals were introduced. From then onward, these signals were used to represent real valued signals. To give an idea of the approach taken to relate the analytic functions and analytic signals, one can notice that the analytic signals represent the boundary values of an analytic function in the upper half plane or that the periodic signals represent the boundary values of a periodic function in the unit disc. An interested reader can find further details in [1] and the references therein.

Let $\mathcal{A}$ denote the class of functions f of the following form:

$$f\left(\varsigma \right)=\varsigma +\sum _{n=2}^{\infty }{a}_n{\varsigma }^n,$$

(1)

which are analytical in the open unit disk $\mathcal{U}=\left\{\varsigma :\left|\varsigma \right|<1,\varsigma \in \mathbb{C}\right\}$. Let $\mathcal{S}$ represent the class of analytic and univalent functions such that it satisfies (1). A function f is said to be subordinate to a function g if there exists a function $\varpi$ with $\varpi \left(0\right)=0,\left|\varpi \left(\varsigma \right)\right|<1$ such that $f\left(\varsigma \right)=g\left(\varpi \left(\varsigma \right)\right)$ for $\varsigma \in \mathcal{U}$, written as $f\prec g$. The class of convex univalent functions, denoted by $\mathcal{C}$, contains all those functions $f\in \mathcal{S}$ such that

$$1+\frac{\varsigma f^{″}\left(\varsigma \right)}{f^{\prime }\left(\varsigma \right)}\prec p\left(\varsigma \right),$$

where $p\left(\varsigma \right)\in \mathcal{P}=\left\{p:p\left(0\right)=1,\Re p\left(\varsigma \right)>0,\varsigma \in \mathcal{U}\right\}$. Additionally, ${\mathcal{S}}^{*}\left(\alpha \right)$ denotes the class of functions that are star-like of order $\alpha$ such that

$${\mathcal{S}}^{*}\left(\alpha \right)=\left\{f\in \mathcal{S}:\Re \frac{\varsigma f^{\prime }\left(\varsigma \right)}{f\left(\varsigma \right)}>\alpha ,0\le \alpha <1,\varsigma \in \mathcal{U}\right\}.$$

The class $\mathcal{P}$ is further subdivided into classes depending upon the geometrical interpretation of $p\left(\mathcal{U}\right)$. The geometrical structures of these image domains appear to be very interesting. Using the concept of differential subordinations, the class $\mathcal{P}$ can be rephrased as follows:

$$\mathcal{P}=\left\{p:p\left(0\right)=1,p\left(\varsigma \right)\prec \frac{1+\varsigma }{1-\varsigma },\varsigma \in \mathcal{U}\right\},$$

where the geometry of the image domain of the function $h\left(\varsigma \right)=\frac{1+\varsigma }{1-\varsigma }$ is the right half plane. By replacing this function $\frac{1+\varsigma }{1-\varsigma }$ with the following suitable functions, one can obtain several subclasses of the class $\mathcal{P}$, which are associated with the indicated symmetric domains.

• $h_1\left(\varsigma \right)=\frac{1+\left(1-2\alpha \right)\varsigma }{1-\varsigma },0\le \alpha <1.$ (The plane to the right of the vertical line $u=\alpha$; see [2])
• $h_2\left(\varsigma \right)=\frac{1+A\varsigma }{1+B\varsigma },-1\le B<A\le 1.$ (The circular domain centered at $\frac{1-AB}{1-B^2}$ and radius $\frac{A-B}{1-B^2}$; see [3,4])
• $h_3\left(\varsigma \right)=\sqrt{1+\varsigma }.$ (The right half of the lemniscate of Bernoulli $\left|w^2-1\right|=1$; see [5])
• $h_4\left(\varsigma \right)=1+\frac{2}{{\pi }^2}{\left(log\frac{1+\sqrt{\varsigma }}{1-\sqrt{\varsigma }}\right)}^2.$ (The parabolic domain; see [6,7,8])
• $h_5\left(\varsigma \right)=1+\frac{2}{1-k^2}{sinh}^2\left[\left(\frac{2}{\pi }arccosk\right)arctanh\sqrt{\varsigma }\right]$, $0<k<1.$ (The hyperbolic domain; see [6,7])
• $h_6\left(\varsigma \right)=1+\frac{1}{k^2-1}sin\left(\frac{\pi }{2R\left(t\right)}\underset{0}{\overset{\frac{u\left(\varsigma \right)}{\sqrt{t}}}{\int }}\frac{1}{\sqrt{1-x^2}\sqrt{1-{\left(tx\right)}^2}}dx\right)+\frac{1}{k^2-1}$, $k>1,$ where $u\left(\varsigma \right)=\frac{\varsigma -\sqrt{t}}{1-\sqrt{t\varsigma }}$, $t\in (0,1)$ and $\varsigma$ is chosen such that $k=cosh\left(\frac{\pi R^{\prime }\left(t\right)}{4R\left(t\right)}\right)$, $R\left(t\right)$ is Legendre’s complete elliptic integral of the first kind and $R^{\prime }\left(t\right)$ is the complementary integral of $R\left(t\right)$. (The elliptic domain; see [6,7])
• $h_7\left(\varsigma \right)=\frac{\left(A+1\right)h_i\left(\varsigma \right)-\left(A-1\right)}{\left(B+1\right)h_i\left(\varsigma \right)-\left(B-1\right)},$$-1\le B<A\le 1,$$i=3,4,5.$ (The oval and petal type domain; see [9,10,11])
• $h_8\left(\varsigma \right)={\left(\frac{1+\varsigma }{1+\frac{1-\beta }{\beta }\varsigma }\right)}^{1/\alpha },\alpha \ge 1,\beta \ge \frac{1}{2}.$(The leaf-like domain; see [12])
• $h_9\left(\varsigma \right)=\sqrt{2}-\left(\sqrt{2}-1\right)\sqrt{\frac{1-\varsigma }{1+2\left(\sqrt{2}-1\right)\varsigma }}.$ (The left half of lemniscate of Bernoulli $\left|{\left(w-\sqrt{2}\right)}^2-1\right|=1$; see [13])
• $h_{10}\left(\varsigma \right)=\varsigma +\sqrt{1+{\varsigma }^2}.$ (The crescent-shaped region; see [14])
• $h_{11}\left(\varsigma \right)={\left(1+s\varsigma \right)}^2,0<s\le \frac{1}{\sqrt{2}}.$ (The limaçon-shaped region; see [15])
• $h_{12}\left(\varsigma \right)=1+\frac{\varsigma }{1-\alpha {\varsigma }^2},0\le \alpha <1.$ (The booth lemniscate; see [16])
• $h_{13}\left(\varsigma \right)=1+sin\varsigma .$ (The eight-shaped region; see [17])
• $h_{14}\left(\varsigma \right)=1+\varsigma -\frac{{\varsigma }^3}{3}.$ (The nephroid domain; see [18])
• $h_{15}\left(\varsigma \right)=\frac{2\left(1-\gamma \right)\varsigma }{{\left(1-\alpha \varsigma \right)}^2},\alpha \in \left(-1,1\right)\setminus \left\{0\right\},0\le \gamma <1.$ (The Pascal snail regions; see [19])

The abovementioned functions and their associated domains have been studied thoroughly and can be found in the literature; see [20,21,22,23,24,25,26,27]. However, the one most related to our work is a shell-like curve [28,29]. The function $p\left(\varsigma \right)=\frac{1+{\tau }^2{\varsigma }^2}{1-\tau \varsigma -{\tau }^2{\varsigma }^2},$ generates the shell-like curve, where $\tau =\frac{1-\sqrt{5}}{2}.$ In a more elaborated manner, the mapping of unit circle through the function $p\left(\varsigma \right)=\frac{1+{\tau }^2{\varsigma }^2}{1-\tau \varsigma -{\tau }^2{\varsigma }^2}$ gives the conchoid of Maclaurin, which is also called a shell-like curve:

$$p\left(e^{i\phi }\right)=\frac{\sqrt{5}}{2\left(3-2cos\phi \right)}+i\frac{sin\phi \left(4cos\phi -1\right)}{2\left(3-2cos\phi \right)\left(1+cos\phi \right)},0\le \phi <2\pi .$$

This important function has the following series representation:

$$p\left(\varsigma \right)=\frac{1+{\tau }^2{\varsigma }^2}{1-\tau \varsigma -{\tau }^2{\varsigma }^2}=1+\stackrel{\infty }{\sum _{n=1}}\left(u_{n-1}+u_{n+1}\right){\tau }^n{\varsigma }^n,$$

where $u_n=\frac{{\left(1-\tau \right)}^n-{\tau }^n}{\sqrt{5}},$$\tau =\frac{1-\sqrt{5}}{2}$, which generates a Fibonacci series of coefficient constants that makes it closer to Fibonacci numbers. Inspired and motivated by the ongoing research in the area of image domains, especially shell-like and circular domains, Malik et al. [30] defined and discussed a new geometrical structure as the image domain.

Let $\mathcal{CP}\left[A,B\right]$ be the class of functions p that are analytic and $p\left(\varsigma \right)\prec \tilde{p}\left(A,B;\varsigma \right)$, where $\tilde{p}\left(A,B;\varsigma \right)$ is given as

$$\tilde{p}\left(A,B;\varsigma \right)=\frac{2A{\tau }^2{\varsigma }^2+\left(A-1\right)\tau \varsigma +2}{2B{\tau }^2{\varsigma }^2+\left(B-1\right)\tau \varsigma +2},$$

(2)

with $-1\le B<A\le 1$ and $\tau =\frac{1-\sqrt{5}}{2},\varsigma \in \mathcal{U}.$ If we denote $\Re \tilde{p}\left(A,B;e^{i\theta }\right)=u$ and $\Im \tilde{p}\left(A,B;e^{i\theta }\right)=v,$ then the image $\tilde{p}\left(A,B;e^{i\theta }\right)$ of the unit circle is a cardioid-like curve defined by the parametric form as

$$\begin{array}{ccc}\hfill u& =& \frac{4+\left(A-1\right)\left(B-1\right){\tau }^2+4AB{\tau }^4+2\lambda cos\theta +4\left(A+B\right){\tau }^{2}cos2\theta }{4+{\left(B-1\right)}^2{\tau }^2+4B^2{\tau }^4+4\left(B-1\right)\left(\tau +B{\tau }^3\right)cos\theta +8B{\tau }^{2}cos2\theta },\hfill \\ \hfill v& =& \frac{2\left(A-B\right)\left(\tau -{\tau }^3\right)sin\theta +2{\tau }^{2}sin2\theta }{4+{\left(B-1\right)}^2{\tau }^2+4B^2{\tau }^4+4\left(B-1\right)\left(\tau +B{\tau }^3\right)cos\theta +8B{\tau }^{2}cos2\theta },\hfill \end{array}$$

(3)

where $\lambda =\left(A+B-2\right)\tau +\left(2AB-A-B\right){\tau }^3,$$-1\le B<A\le 1$ and $0\le \theta <2\pi$. In addition, we note that

$$\tilde{p}\left(A,B;0\right)=1\mathrm{and}\tilde{p}\left(A,B;1\right)=\frac{AB+9\left(A+B\right)+1+4\left(B-A\right)\sqrt{5}}{B^2+18B+1}.$$

The cusp defined by (3) of the cardioid-like curve is given by

$$\gamma \left(A,B\right)=\tilde{p}\left(A,B;e^{\pm iarccos\left(1/4\right)}\right)=\frac{2AB-3\left(A+B\right)+2+\left(A-B\right)\sqrt{5}}{2\left(B^2-3B+1\right)}.$$

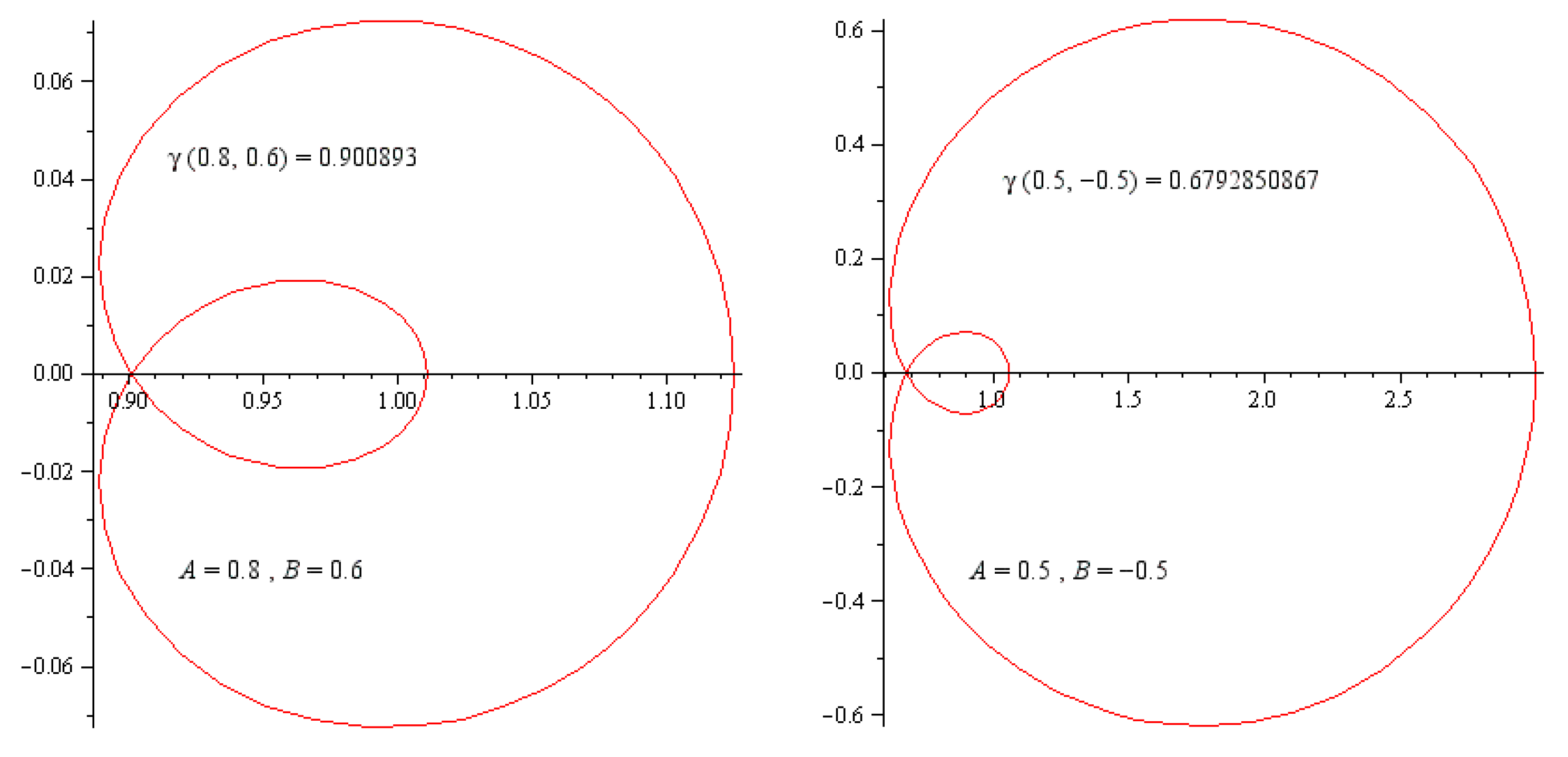
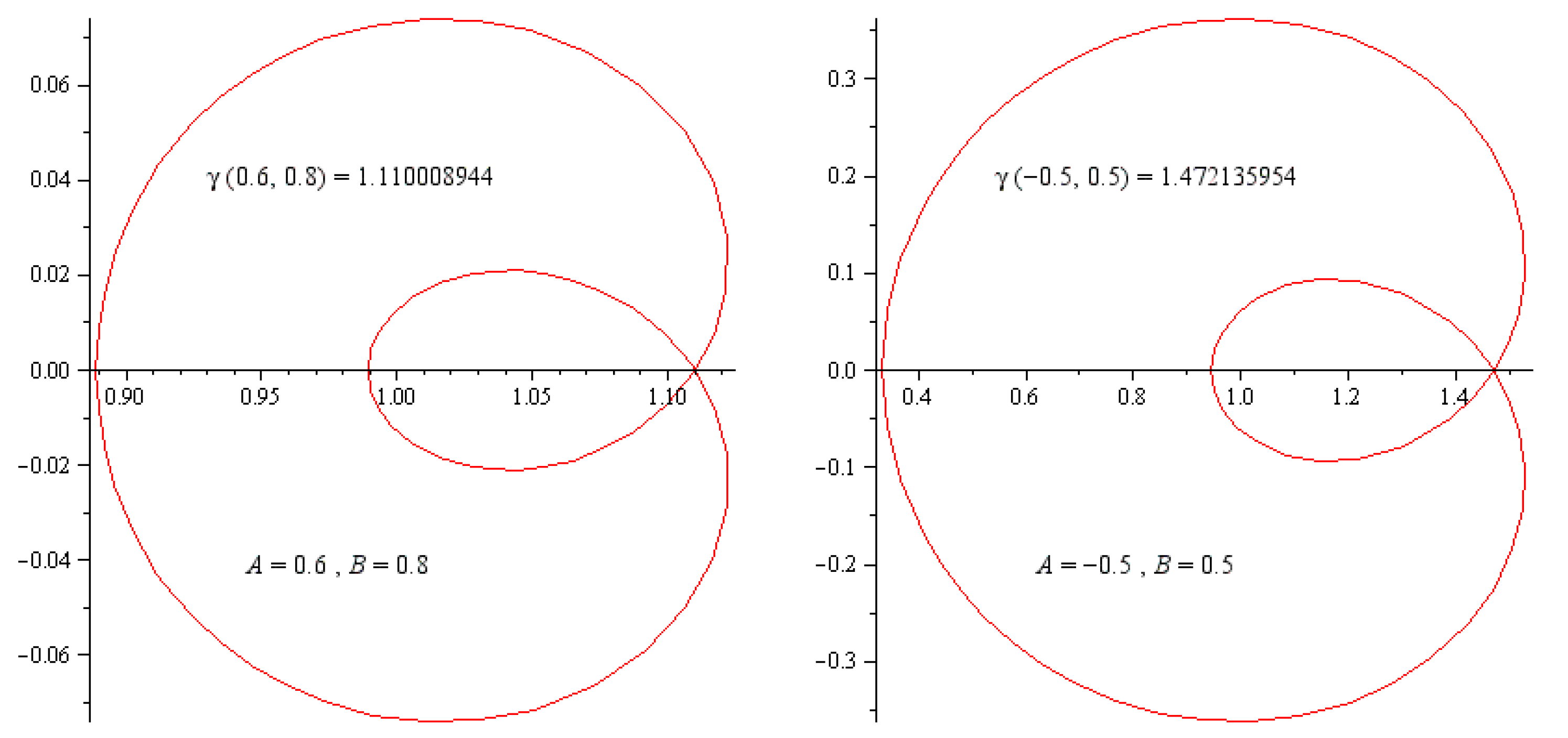
The above discussed symmetric cardioid curve with different values of parameters can be seen in Figure 1. The violation of condition $B<A$ flips over the cardioid curve as shown in Figure 2.

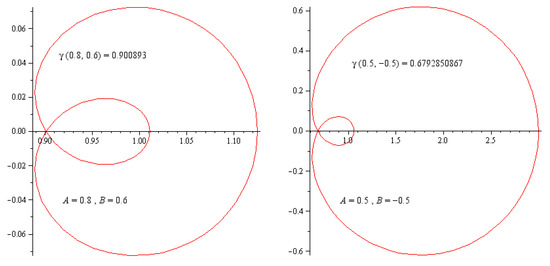
Figure 1. The curves presented by (3) with certain values of A and B with $B<A$.

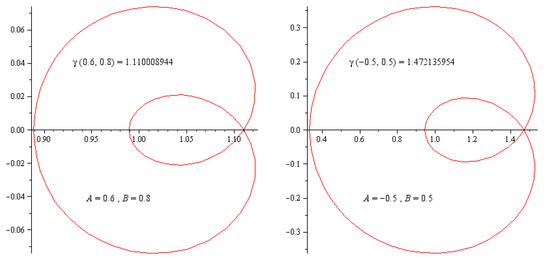
Figure 2. The curves presented by (3) with certain values of A and B with $B>A$.

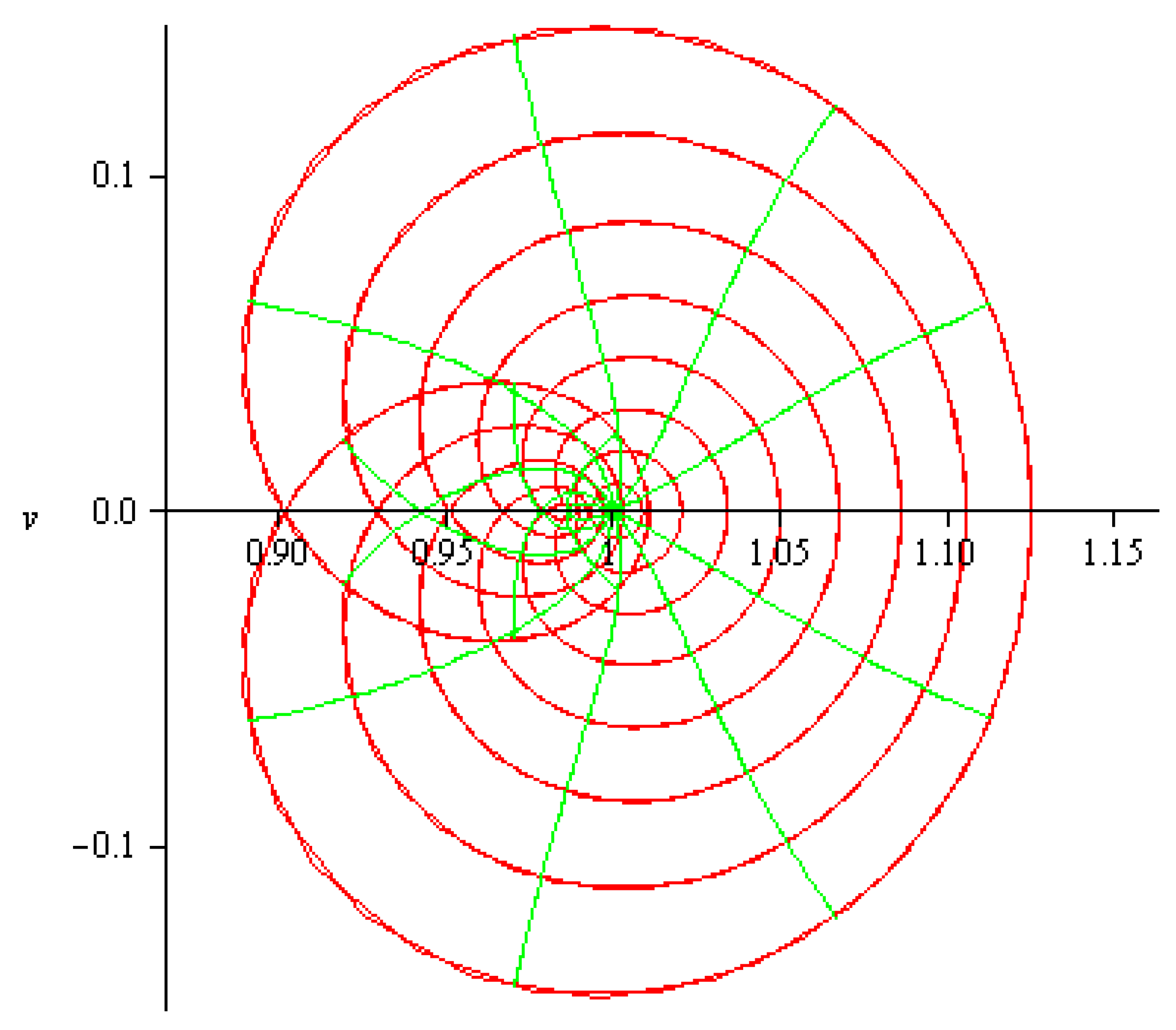
In this regard, it is interesting to observe that, if we consider the open unit disk $\mathcal{U}$ as the collection of concentric circles in which the center is at the origin, then we notice that the image of each inner circle is a nested symmetric cardioid-like curve. Consequently, the function $\tilde{p}\left(A,B;\varsigma \right)$ gives the cardioid region as an image of the open unit disk $\mathcal{U}$. That is, $\tilde{p}\left(A,B;\mathcal{U}\right)$ is a cardioid domain that is symmetric about the real axis, as shown in the Figure 3.

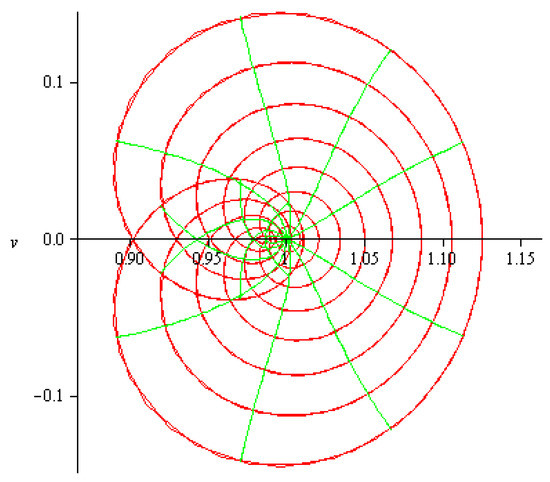
Figure 3. The image of $\mathcal{U}$ under $\tilde{p}\left(A,B;\varsigma \right)$.

Here, $\tilde{p}\left(A,B;\varsigma \right)$ is univalent in $\left|\varsigma \right|<{\tau }^2$ only. Inspired by the idea of a symmetric cardioid domain, we contribute to the literature by introducing convex functions that are associated with symmetric cardioid domain, named cardio-convex functions. The class $\mathcal{CC}\left[A,B\right]$ of such functions is defined below.

Before studying the class, first, we state the following lemma, which is useful in our main results.

Lemma 1.

[31] If $p\left(\varsigma \right)=1+{\sum }_{n=1}^{\infty }{p}_n{\varsigma }^n$ is a function with a positive real part in $\mathcal{U},$ then for v, a complex number

$$\left|p_2-v{p}_1^2\right|\le 2max\left\{1,\left|2v-1\right|\right\}.$$

2. Main Results

First, we include the definition of the class of convex functions that are associated with the cardioid domain.

Definition 1.

The class $\mathcal{CC}\left[A,B\right]$ of convex functions associated with the cardioid domain is defined as the set of functions f of the form (1) satisfying the condition

$$\frac{{\left(\varsigma f^{\prime }\left(\varsigma \right)\right)}^{\prime }}{f^{\prime }\left(\varsigma \right)}\prec \tilde{p}\left(A,B;\varsigma \right),$$

(4)

where $\tilde{p}\left(A,B;\varsigma \right)$ is given by (2).

Therefore, it is easy to say that $\frac{{\left(\varsigma f^{\prime }\left(\varsigma \right)\right)}^{\prime }}{f^{\prime }\left(\varsigma \right)}$ takes all of the values in the cardioid $\tilde{p}\left(A,B;\mathcal{U}\right)$. In addition, it is worth mentioning that

• The class of convex functions associated with the cardioid domain with $A=1$ and $B=-1$ reduces to the class $\mathcal{KSL}$ of those convex functions that are connected with Fibonacci numbers. This class was introduced and studied by Sokół [29]; see also [28].
• $\mathcal{CC}\left[A,B\right]\subset \mathcal{C}\left(\rho \right)=\left\{f\in \mathcal{S}:\Re \frac{{\left(\varsigma f^{\prime }\left(\varsigma \right)\right)}^{\prime }}{f^{\prime }\left(\varsigma \right)}>\rho ,\varsigma \in \mathcal{U}\right\}$, where $\rho$ is given by

  $$\rho =\frac{2\left(A+B-2\right)\tau +2\left(2AB-A-B\right){\tau }^3+16\left(A+B\right){\tau }^2\eta }{4\left(B-1\right)\left(\tau +B{\tau }^3\right)+32B{\tau }^2\eta }.$$

Theorem 1.

If $f\left(\varsigma \right)\in \mathcal{CC}\left[A,B\right],-1\le B<A\le 1$ and is of the form (1), then for $n=2,3,4,...$, we have

$$\begin{array}{ccc}\hfill {\left|a_n\right|}^2& \le & \frac{1}{4n^2{\left(n-1\right)}^2}\left\{\left(\begin{array}{c}{\left|\tau \left(\left(n-1\right)\left(A-1\right)-{\left(n-1\right)}^2\left(B-1\right)\right)\right|}^2\\ -4{\left(n-1\right)}^2{\left(n-2\right)}^2\end{array}\right){\left|a_{n-1}\right|}^2\right.\hfill \\ & & +\left.\sum _{k=1}^{n-2}\left({\left(\left|\tau \right|\left|k\left(A-1\right)-k^2\left(B-1\right)\right|+2{\tau }^2\left|Ak-B{k}^2\right|\right)}^2-4k^2{\left(k-1\right)}^2\right){\left|a_k\right|}^2\right\}.\hfill \end{array}$$

Proof. 

Since $f\left(\varsigma \right)\in \mathcal{CC}\left[A,B\right],-1\le B<A\le 1,$ therefore from (4), we obtain

$$\frac{{\left(\varsigma f^{\prime }\left(\varsigma \right)\right)}^{\prime }}{f^{\prime }\left(\varsigma \right)}=\tilde{p}\left(A,B;\varpi \left(\varsigma \right)\right),$$

where $\varpi \left(0\right)=0,\left|\varpi \left(\varsigma \right)\right|<1$ for $\varsigma \in \mathcal{U}$. It is easy to see that

$$\frac{{\left(\varsigma f^{\prime }\left(\varsigma \right)\right)}^{\prime }}{f^{\prime }\left(\varsigma \right)}=\frac{2A{\tau }^2{\varpi }^2\left(\varsigma \right)+\left(A-1\right)\tau \varpi \left(\varsigma \right)+2}{2B{\tau }^2{\varpi }^2\left(\varsigma \right)+\left(B-1\right)\tau \varpi \left(\varsigma \right)+2},$$

which, upon simplification, gives

$$\begin{array}{c}2\left({\left(\varsigma f^{\prime }\left(\varsigma \right)\right)}^{\prime }-f^{\prime }\left(\varsigma \right)\right)=\tau \varpi \left(\varsigma \right)\left(\left(A-1\right)f^{\prime }\left(\varsigma \right)-\left(B-1\right){\left(\varsigma f^{\prime }\right)}^{\prime }\right)\\ +2{\tau }^2{\varpi }^2\left(\varsigma \right)\left(A{f}^{\prime }\left(\varsigma \right)-B{\left(\varsigma f^{\prime }\right)}^{\prime }\right).\end{array}$$

Combining it with (1) takes the form

$$\begin{array}{c}{\displaystyle \sum _{k=1}^{\infty }}2k\left(k-1\right)a_k{\varsigma }^{k-1}=\tau \varpi \left(\varsigma \right)\sum _{k=1}^{\infty }\left(\left(A-1\right)k-\left(B-1\right)k^2\right)a_k{\varsigma }^{k-1}\\ +2{\tau }^2{\varpi }^2\left(\varsigma \right)\sum _{k=1}^{\infty }\left(Ak-B{k}^2\right)a_k{\varsigma }^{k-1}.\end{array}$$

Upon multiplication by $\varsigma$, we obtain

$$\begin{array}{c}{\displaystyle \sum _{k=1}^{\infty }}2k\left(k-1\right)a_k{\varsigma }^k=\tau \varpi \left(\varsigma \right)\sum _{k=1}^{\infty }\left(\left(A-1\right)k-\left(B-1\right)k^2\right)a_k{\varsigma }^k\\ +2{\tau }^2{\varpi }^2\left(\varsigma \right)\sum _{k=1}^{\infty }\left(Ak-B{k}^2\right)a_k{\varsigma }^k.\end{array}$$

Therefore,

$$\begin{array}{c}\hfill \sum _{k=1}^{n}2k\left(k-1\right)a_k{\varsigma }^k+\sum _{k=n+1}^{\infty }{b}_k{\varsigma }^k=\tau \varpi \left(\varsigma \right)\sum _{k=1}^{n-1}\left(\left(A-1\right)k-\left(B-1\right)k^2\right)a_k{\varsigma }^k\\ \hfill +2{\tau }^2{\varpi }^2\left(\varsigma \right)\sum _{k=1}^{n-2}\left(Ak-B{k}^2\right)a_k{\varsigma }^k,\end{array}$$

(5)

where

$$\begin{array}{c}\sum _{k=n+1}^{\infty }{b}_k{\varsigma }^k={\displaystyle \sum _{k=n+1}^{\infty }}2k\left(k-1\right)a_k{\varsigma }^k-\tau \varpi \left(\varsigma \right)\sum _{k=n}^{\infty }\left(\left(A-1\right)k-\left(B-1\right)k^2\right)a_k{\varsigma }^k\\ -2{\tau }^2{\varpi }^2\left(\varsigma \right)\sum _{k=n-1}^{\infty }\left(Ak-B{k}^2\right)a_k{\varsigma }^k.\end{array}$$

Now, from (5), we have

$${\left|\sum _{k=1}^{n}2k\left(k-1\right)a_k{\varsigma }^k+\sum _{k=n+1}^{\infty }{b}_k{\varsigma }^k\right|}^2={\left|\begin{array}{c}\tau \varpi \left(\varsigma \right)\sum _{k=1}^{n-1}\left(\left(A-1\right)k-\left(B-1\right)k^2\right)a_k{\varsigma }^k+\\ 2{\tau }^2{\varpi }^2\left(\varsigma \right)\sum _{k=1}^{n-2}\left(Ak-B{k}^2\right)a_k{\varsigma }^k\end{array}\right|}^2.$$

Since $\left|\varpi \left(\varsigma \right)\right|<1$, we have

$${\left|\sum _{k=1}^{\infty }{d}_k{\varsigma }^k\right|}^2<{\left|\begin{array}{c}\tau \left(\left(A-1\right)\left(n-1\right)-\left(B-1\right){\left(n-1\right)}^2\right)a_{n-1}{\varsigma }^{n-1}+\\ \sum _{k=1}^{n-2}\left(\left(\tau \left(A-1\right)k-\left(B-1\right)k^2\right)+2{\tau }^2\left(Ak-B{k}^2\right)\varpi \left(\varsigma \right)\right)a_k{\varsigma }^k\end{array}\right|}^2,$$

where

$$d_k=\left\{\begin{array}{c}2k\left(k-1\right)a_k,1\le k\le n,\\ b_k,k>n.\end{array}\right.$$

Using the formula $\frac{1}{2\pi }\underset{0}{\overset{2\pi }{\int }}{\left|{\displaystyle \sum _{k=1}^{\infty }}{d}_k{\left(r{e}^{i\theta }\right)}^k\right|}^{2}d\theta ={\displaystyle \sum _{k=1}^{\infty }}{\left|d_k\right|}^2{r}^{2k},$ (see [2]) and then integrating on $\varsigma =r{e}^{i\theta },0<r<1,0\le \theta <2\pi$, we obtain

$$\begin{array}{c}{\displaystyle \sum _{k=1}^{\infty }}{\left|d_k\right|}^2{r}^{2k}<\frac{1}{2\pi }{\int }_0^{2\pi }{\left|\begin{array}{c}\tau \left(\left(A-1\right)\left(n-1\right)-\left(B-1\right){\left(n-1\right)}^2\right)a_{n-1}{\left(r{e}^{i\theta }\right)}^{n-1}+\\ \sum _{k=1}^{n-2}\left(\begin{array}{c}\tau \left(\left(A-1\right)k-\left(B-1\right)k^2\right)+\\ 2{\tau }^2\left(Ak-B{k}^2\right)\varpi \left(r{e}^{i\theta }\right)\end{array}\right)a_k{r}^k{e}^{ik\theta }\end{array}\right|}^{2}d\theta \\ =\frac{1}{2\pi }{\int }_0^{2\pi }\left(\begin{array}{c}\tau \left(\left(A-1\right)\left(n-1\right)-\left(B-1\right){\left(n-1\right)}^2\right)a_{n-1}{r}^{n-1}{e}^{i\left(n-1\right)\theta }+\\ \sum _{k=1}^{n-2}\left(\begin{array}{c}\tau \left(\left(A-1\right)k-\left(B-1\right)k^2\right)+\\ 2{\tau }^2\left(Ak-B{k}^2\right)\varpi \left(r{e}^{i\theta }\right)\end{array}\right)a_k{r}^k{e}^{ik\theta }\end{array}\right)\times \\ \left(\begin{array}{c}\tau \left(\left(A-1\right)\left(n-1\right)-\left(B-1\right){\left(n-1\right)}^2\right)\overline{a_{n-1}}{r}^{n-1}{e}^{-i\left(n-1\right)\theta }+\\ \sum _{l=1}^{n-2}\left(\begin{array}{c}\tau \left(\left(A-1\right)l-\left(B-1\right)l^2\right)+\\ 2{\tau }^2\left(Al-B{l}^2\right)\overline{\varpi \left(r{e}^{i\theta }\right)}\end{array}\right)\overline{a_l}{r}^l{e}^{-il\theta }\end{array}\right)d\theta .\end{array}$$

Since the integral of product with $k\ne l$ gives 0, as a result, we obtain

$$\begin{array}{c}\sum _{k=1}^n{\left|2k\left(k-1\right)a_k\right|}^2{r}^{2k}+\sum _{k=n+1}^{\infty }{\left|b_k\right|}^2{r}^{2k}\\ <{\left|\tau \left(\left(A-1\right)\left(n-1\right)-\left(B-1\right){\left(n-1\right)}^2\right)\right|}^2{\left|a_{n-1}\right|}^2{r}^{2n-2}\\ +\sum _{k=1}^{n-2}{\left|\left(\tau \left(\left(A-1\right)k-\left(B-1\right)k^2\right)+2{\tau }^2\left(Ak-B{k}^2\right)\varpi \left(\varsigma \right)\right)\right|}^2{\left|a_k\right|}^2{r}^{2k}.\end{array}$$

Furthermore, we have

$$\begin{array}{c}\left|\tau \left(\left(A-1\right)k-\left(B-1\right)k^2\right)+2{\tau }^2\left(Ak-B{k}^2\right)\varpi \left(\varsigma \right)\right|\\ \le \left|\tau \left(A-1\right)k-\left(B-1\right)k^2\right|+\left|2{\tau }^2\left(Ak-B{k}^2\right)\right|\left|\varpi \left(\varsigma \right)\right|\\ <\left|\tau \right|\left|\left(A-1\right)k-\left(B-1\right)k^2\right|+2{\tau }^2\left|Ak-B{k}^2\right|.\end{array}$$

Thus, we have

$$\begin{array}{c}\sum _{k=1}^n{\left|2k\left(k-1\right)a_k\right|}^2{r}^{2k}+\sum _{k=n+1}^{\infty }{\left|b_k\right|}^2{r}^{2k}\\ \le {\left|\tau \left(\left(A-1\right)\left(n-1\right)-\left(B-1\right){\left(n-1\right)}^2\right)\right|}^2{\left|a_{n-1}\right|}^2{r}^{2n-2}\\ +\sum _{k=1}^{n-2}{\left(\left|\tau \right|\left|\left(A-1\right)k-\left(B-1\right)k^2\right|+2{\tau }^2\left|Ak-B{k}^2\right|\right)}^2{\left|a_k\right|}^2{r}^{2k},\end{array}$$

which reduces to

$$\begin{array}{c}4\sum _{k=1}^n{k}^2{\left(k-1\right)}^2{\left|a_k\right|}^2{r}^{2k}\le {\left|\tau \left(\left(A-1\right)\left(n-1\right)-\left(B-1\right){\left(n-1\right)}^2\right)\right|}^2{\left|a_{n-1}\right|}^2{r}^{2n-2}\\ +\sum _{k=1}^{n-2}{\left(\left|\tau \right|\left|\left(A-1\right)k-\left(B-1\right)k^2\right|+2{\tau }^2\left|Ak-B{k}^2\right|\right)}^2{\left|a_k\right|}^2{r}^{2k}.\end{array}$$

Letting $r\to 1$, one may have

$$\begin{array}{c}\sum _{k=1}^{n-2}4k^2{\left(k-1\right)}^2{\left|a_k\right|}^2+4{\left(n-1\right)}^2{\left(n-2\right)}^2{\left|a_{n-1}\right|}^2+4n^2{\left(n-1\right)}^2{\left|a_n\right|}^2\\ \le {\left|\tau \left(\left(A-1\right)\left(n-1\right)-\left(B-1\right){\left(n-1\right)}^2\right)\right|}^2{\left|a_{n-1}\right|}^2\\ +\sum _{k=1}^{n-2}{\left(\left|\tau \right|\left|\left(A-1\right)k-\left(B-1\right)k^2\right|+2{\tau }^2\left|Ak-B{k}^2\right|\right)}^2{\left|a_k\right|}^2.\end{array}$$

and consequently, we obtain the required form. □

Theorem 2.

Let $f\in \mathcal{CC}\left[A,B\right],-1\le B<A\le 1$ and of the form (1). Then

$$\left|a_2\right|\le \frac{1}{4}\left(A-B\right)\left|\tau \right|,\left|a_3\right|\le \frac{\left|\tau \right|}{12}\left(A-B\right)max\left\{1,\left|\frac{\tau }{2}\left(A-2B+5\right)\right|\right\}.$$

Proof. 

Since $f\left(\varsigma \right)\in \mathcal{CC}\left[A,B\right],-1\le B<A\le 1,$ we have

$$\frac{{\left(\varsigma f^{\prime }\left(\varsigma \right)\right)}^{\prime }}{f^{\prime }\left(\varsigma \right)}\prec \tilde{p}\left(A,B;\varsigma \right),$$

(6)

where $\tilde{p}\left(A,B;\varsigma \right)$ is given by (2). Consider the function

$$p\left(\varsigma \right)=\frac{1+\varpi \left(\varsigma \right)}{1-\varpi \left(\varsigma \right)}=1+p_1\varsigma +p_2{\varsigma }^2+\cdots$$

such that $\varpi \left(0\right)=0,\left|\varpi \left(\varsigma \right)\right|<1$ for $\varsigma \in \mathcal{U}.$ It is clear that $p\in \mathcal{P}$. Thus, we have $\varpi \left(\varsigma \right)=\frac{p\left(\varsigma \right)-1}{p\left(\varsigma \right)+1}$. Using (6), we have $\frac{{\left(\varsigma f^{\prime }\left(\varsigma \right)\right)}^{\prime }}{f^{\prime }\left(\varsigma \right)}=\tilde{p}\left(A,B;\varpi \left(\varsigma \right)\right)$, where

$$\varpi \left(\varsigma \right)=\frac{p\left(\varsigma \right)-1}{p\left(\varsigma \right)+1}=\frac{1}{2}{p}_1\varsigma +\frac{1}{4}\left(2p_2-p_1^2\right){\varsigma }^2+\cdots .$$

Simple calculations lead us to

$$\tilde{p}\left(A,B;\varpi \left(\varsigma \right)\right)=1+\frac{\tau p_1}{4}\left(A-B\right)\varsigma +\frac{\tau }{16}(A-B)\left\{\left(5\tau -2-\tau B\right)p_1^2+4p_2\right\}{\varsigma }^2+\cdots .$$

(7)

Additionally, it is easy to see that

$$\frac{{\left(\varsigma f^{\prime }\left(\varsigma \right)\right)}^{\prime }}{f^{\prime }\left(\varsigma \right)}=1+2a_2\varsigma +\left(6a_3-4a_2^2\right){\varsigma }^2+\cdots .$$

(8)

Comparing the coefficients from (7) and (8), we obtain

$$a_2=\frac{1}{8}\left(A-B\right)\tau p_1,a_3=\frac{\tau }{96}\left(A-B\right)\left\{\left(-2+\tau \left(A-2B+5\right)\right)p_1^2+4p_2\right\}.$$

(9)

Therefore, by using the well-known result $\left|p_n\right|\le 2$ for coefficients of class $\mathcal{P}$, we obtain a bound for second coefficients. Now,

$$\left|a_3\right|=\frac{\tau }{24}\left(A-B\right)\left|p_2-v{p}_1^2\right|,$$

where $v=\frac{1}{4}\left(2-\tau \left(A-2B+5\right)\right).$ Now, using Lemma 1, we obtain the required result. This result is sharp for the functions $f_0\left(\varsigma \right)=\underset{0}{\overset{\varsigma }{\int }}\left[exp{\int }_0^{\varpi }\frac{\tilde{p}\left(A,B;t\right)-1}{t}dt\right]d\varpi$ and $f_1\left(\varsigma \right)$

$=\underset{0}{\overset{\varsigma }{\int }}\left[exp{\int }_0^{\varpi }\frac{\tilde{p}\left(A,B;t^2\right)-1}{t}dt\right]d\varpi$, where $\tilde{p}\left(A,B;.\right)$ is defined in (2). □

Based upon the Theorem 2, we have the following.

Conjecture If $f\left(\varsigma \right)\in \mathcal{CC}\left[A,B\right],-1\le B<0,B<A\le 1$ and is of the form (1), then

$$\left|a_n\right|\le \frac{{\left|\tau \right|}^{n-1}}{n}\sum _{m=0}^{n-1}\left[\begin{array}{c}\left[{\displaystyle \sum _{k=0}^{⌊\frac{m}{2}⌋}}\left(\frac{{\left|\frac{B-1}{2}\right|}^{m-2k}{\left|B\right|}^k}{\left(m-2k\right)!k!}{\displaystyle \prod _{j=0}^{m-1-k}}\left|\frac{A-B}{2B}-\left(m-1-k\right)+j\right|\right)\right]\times \\ \left[{\displaystyle \sum _{l=0}^{n-1-m}}\left(\left(\genfrac{}{}{0pt}{}{\delta }{l}\right)\left(\genfrac{}{}{0pt}{}{\delta +n-m-l-2}{n-1-m-l}\right){\left|c\right|}^l{\left|d\right|}^{n-1-m-l}\right)\right]\end{array}\right],$$

(10)

where $\delta =\frac{(A-B)\left(1+B\right)}{2B\sqrt{B^2-18B+1}},c=\frac{1-B-\sqrt{B^2-18B+1}}{4}$ and $d=\frac{1-B+\sqrt{B^2-18B+1}}{4}.$ This bound is sharp and sharpness is due to the function

$$\tilde{F}\left(\varsigma \right)={\int }_0^{\varsigma }\frac{\tilde{f}\left(\xi \right)}{\xi }d\xi ,$$

where

$$\tilde{f}\left(\varsigma \right)=\varsigma {\left[1+\frac{B-1}{2}\tau \varsigma +B{t}^2{\varsigma }^2\right]}^{\frac{A-B}{2B}}{\left[\frac{1-\left(\frac{1-B-\sqrt{B^2-18B+1}}{4}\right)\tau \varsigma }{1-\left(\frac{1-B+\sqrt{B^2-18B+1}}{4}\right)\tau \varsigma }\right]}^{\frac{(A-B)\left(1+B\right)}{2B\sqrt{B^2-18B+1}}}.$$

Theorem 3.

The function $h\left(\varsigma \right)=\varsigma +c{\varsigma }^n$ does not belong to the class $\mathcal{CC}\left[A,B\right]$ with $-1\le B\le \left(3-\sqrt{5}\right)/2,$$B<A\le 1$ if

$$\left|c\right|>\frac{\left(A-B\right)\left(3-\sqrt{5}-2B\right)}{n\left(2n\left(B^2-3B+1\right)-2AB+3\left(A+B\right)-2-\left(A-B\right)\sqrt{5}\right)}.$$

(11)

Proof. 

Let

$$H\left(\varsigma \right)=1+\frac{\varsigma h^{″}\left(\varsigma \right)}{h^{\prime }\left(\varsigma \right)}=\frac{1+n^{2}c{\varsigma }^{n-1}}{1+nc{\varsigma }^{n-1}}.$$

The image domain $H\left(\mathcal{U}\right)$ is a disk with diameter end points ${\mathcal{D}}_1=\frac{1-n^2\left|c\right|}{1-n\left|c\right|}$ and ${\mathcal{D}}_2=\frac{1+n^2\left|c\right|}{1+n\left|c\right|}.$ If (11) is satisfied, then one of ${\mathcal{D}}_i$ would satisfy ${\mathcal{D}}_i<\gamma \left(A,B\right)$, but this as a consequence gives the negation of inclusion relation $H\left(\mathcal{U}\right)\subset \tilde{p}\left(A,B;\mathcal{U}\right).$ Thus, $H\left(\varsigma \right)\nprec \tilde{p}\left(A,B;\varsigma \right)$ and, hence, it leads to the required result. □

For $A=1,$$B=-1,$ the above result reduces to the one given below, and it is proved in [28].

Corollary 1.

The function $h\left(\varsigma \right)=\varsigma +c{\varsigma }^n$ does not belong to the class $\mathcal{KSL}$ if

$$\left|c\right|>\frac{\sqrt{5}-1}{n\left(n\sqrt{5}-1\right)}.$$

Let $\varsigma =r{e}^{i\theta },0\le \theta <2\pi$. Then, we have

$$\begin{array}{ccc}\hfill \tilde{p}\left(A,B;r{e}^{i\theta }\right)& =& \frac{2A{\tau }^2{r}^2{e}^{2i\theta }+\left(A-1\right)\tau r{e}^{i\theta }+2}{2B{\tau }^2{r}^2{e}^{2i\theta }+\left(B-1\right)\tau r{e}^{i\theta }+2}\hfill \\ & =& \frac{4+\left(A-1\right)\left(B-1\right){\tau }^2{r}^2+4AB{\tau }^4{r}^4+2{\lambda }_{r}cos\theta +4\left(A+B\right){\tau }^2{r}^{2}cos2\theta }{{\left|2B{\tau }^2{r}^2{e}^{2i\theta }+\left(B-1\right)\tau r{e}^{i\theta }+2\right|}^2}\hfill \\ & & +i2\left(A-B\right)\frac{\left(\tau r-{\tau }^3{r}^3\right)sin\theta +2{\tau }^2{r}^{2}sin2\theta }{{\left|2B{\tau }^2{r}^2{e}^{2i\theta }+\left(B-1\right)\tau r{e}^{i\theta }+2\right|}^2},\hfill \end{array}$$

where ${\lambda }_r=\left(A+B-2\right)\tau r+\left(2AB-A-B\right){\tau }^3{r}^3.$ Using the above given representation, we have

$$\begin{array}{ccc}\hfill \left|\frac{\Im \tilde{p}\left(A,B;r{e}^{i\theta }\right)}{\Re \tilde{p}\left(A,B;r{e}^{i\theta }\right)}\right|& =& \left|\frac{2\left(A-B\right)\tau r\left(1-{\tau }^2{r}^2+4\tau rcos\theta \right)sin\theta }{\begin{array}{c}4+\left(A-1\right)\left(B-1\right){\tau }^2{r}^2+4AB{\tau }^4{r}^4+2{\lambda }_{r}cos\theta \\ +4\left(A+B\right){\tau }^2{r}^2\left(2{cos}^2\theta -1\right)\end{array}}\right|\hfill \\ & \le & \frac{-2\left(A-B\right)\tau r\left(1-{\tau }^2{r}^2-4\tau r\right)}{4+\left(A-1\right)\left(B-1\right){\tau }^2{r}^2+4AB{\tau }^4{r}^4-2{\lambda }_r+4\left(A+B\right){\tau }^2{r}^2}\hfill \\ & =& \frac{-2\left(A-B\right)\tau r\left(1-{\tau }^2{r}^2-4\tau r\right)}{\left(2+\left(1-B\right)\tau r+2B{\tau }^2{r}^2\right)\left(2+\left(1-A\right)\tau r+2A{\tau }^2{r}^2\right)}:=\psi \left(A,B;r\right).\hfill \end{array}$$

The radius of univalency for the function $\tilde{p}\left(A,B;\varsigma \right)$ is $r_u=\frac{3-\sqrt{5}}{2}$. That is, for an r, the curve $\tilde{p}\left(A,B;r{e}^{i\theta }\right),\theta \in \left[0,2\pi \right)\setminus \left\{\pi \right\}$ has no loops; see [30].

Lemma 2.

A function f belongs to the class $\mathcal{CC}\left[A,B\right]$ if and only if there exists an analytic function $q\prec \tilde{p}\left(A,B;\varsigma \right),$ such that

$$f\left(\varsigma \right)=\underset{0}{\overset{\varsigma }{\int }}\left[exp{\int }_0^{\varpi }\frac{q\left(t\right)-1}{t}dt\right]d\varpi .$$

(12)

Proof. 

The proof follows the same lines as given in [28]. □

Theorem 4.

Let f belong to the class $\mathcal{CC}\left[A,B\right]$. Then,

$$f^{\prime }\left(\varsigma \right)={\left\{\frac{g\left(\varsigma \right)}{\varsigma }\right\}}^{\alpha }{\left\{\frac{h\left(\varsigma \right)}{\varsigma }\right\}}^{\beta }$$

for some $g\in S^{*}\left(\frac{1}{1+c\tau }\right)$ and $h\in S^{*}\left(\frac{1}{1+d\tau }\right)$, where

$$c=\frac{1-B-\sqrt{B^2-18B+1}}{4}$$

(13)

and

$$d=\frac{1-B+\sqrt{B^2-18B+1}}{4}.$$

(14)

Proof. 

Let $f\in \mathcal{CC}\left[A,B\right]$, then using (12) shows that there exists an analytic function $\varpi \left(\varsigma \right)$ with $\varpi \left(0\right)=0$ and $\left|\varpi \left(\varsigma \right)\right|<1$ such that

$$f^{\prime }\left(\varsigma \right)=exp\underset{0}{\overset{\varsigma }{\int }}\frac{\tilde{p}\left(A,B;\varpi \left(t\right)\right)-1}{t}dt,\varsigma \in \mathcal{U}.$$

Now,

$$\tilde{p}\left(A,B;\varsigma \right)=\frac{2A{\tau }^2{\varsigma }^2+(A-1)\tau \varsigma +2}{2B{\tau }^2{\varsigma }^2+(B-1)\tau \varsigma +2}=\frac{A}{B}+\frac{\alpha }{1-c\tau \varsigma }+\frac{\beta }{1-d\tau \varsigma },$$

where

$$\alpha =\frac{B-A}{2B}\left(1+\frac{1+B}{\sqrt{B^2-18B+1}}\right),\beta =\frac{B-A}{2B}\left(1-\frac{1+B}{\sqrt{B^2-18B+1}}\right)$$

with $-1\le B<0$, with $B<A\le 1$, and where c and d are defined by (13) and (14) respectively. Therefore,

$$\begin{array}{ccc}\hfill f^{\prime }\left(\varsigma \right)& =& exp\underset{0}{\overset{\varsigma }{\int }}\frac{\left(\frac{A}{B}+\frac{\alpha }{1-c\tau \varpi \left(t\right)}+\frac{\beta }{1-d\tau \varpi \left(t\right)}\right)-1}{t}dt\hfill \\ & =& exp\underset{0}{\overset{\varsigma }{\int }}\frac{\left(\frac{\alpha }{1-c\tau \varpi \left(t\right)}-\alpha \right)+\left(\frac{\beta }{1-d\tau \varpi \left(t\right)}-\beta \right)}{t}dt\hfill \\ & =& exp\left[\alpha \underset{0}{\overset{\varsigma }{\int }}\frac{\frac{1}{1-c\tau \varpi \left(t\right)}-1}{t}dt+\beta \underset{0}{\overset{\varsigma }{\int }}\frac{\frac{1}{1-d\tau \varpi \left(t\right)}-1}{t}dt\right]\hfill \\ & =& {\left\{\frac{g\left(\varsigma \right)}{\varsigma }\right\}}^{\alpha }{\left\{\frac{h\left(\varsigma \right)}{\varsigma }\right\}}^{\beta },\hfill \end{array}$$

where $g\left(\varsigma \right)=\varsigma exp\underset{0}{\overset{\varsigma }{\int }}\frac{\frac{1}{1-c\tau \varpi \left(t\right)}-1}{t}$ and $h\left(\varsigma \right)=\varsigma exp\underset{0}{\overset{\varsigma }{\int }}\frac{\frac{1}{1-d\tau \varpi \left(t\right)}-1}{t}$. Thus, we have

$$\mathfrak{R}\frac{\varsigma g^{\prime }\left(\varsigma \right)}{g\left(\varsigma \right)}=\mathfrak{R}\frac{1}{1-c\tau \varpi \left(\varsigma \right)}>1/(1+c\tau ),and\mathfrak{R}\frac{\varsigma h^{\prime }\left(\varsigma \right)}{h\left(\varsigma \right)}=\mathfrak{R}\frac{1}{1-d\tau \varpi \left(\varsigma \right)}>1/(1+d\tau )$$

with $\varpi \left(0\right)=0$ and $\left|\varpi \left(\varsigma \right)\right|<1$, $\varsigma \in \mathcal{U}$. Consequently, this depicts that $g\left(\varsigma \right)=\varsigma exp\underset{0}{\overset{\varsigma }{\int }}\frac{\frac{1}{1-c\tau \varpi \left(t\right)}-1}{t}\in S^{*}(1/(1+c\tau ))$ and $h\left(\varsigma \right)=\varsigma exp\underset{0}{\overset{\varsigma }{\int }}\frac{\frac{1}{1-d\tau \varpi \left(t\right)}-1}{t}\in S^{*}(1/(1+d\tau ))$. □

3. Conclusions

We introduced and studied the convex functions associated with the symmetric cardioid domain, named cardio-convex functions. These functions have the convex image domain bounded by the cardioid curve on the right half of the complex plane. The extremal function for said convex region was introduced, which gives the convex curve, lying entirely inside the cardioid domain. Moreover, certain geometrical properties related to cardio-convex functions have been discussed. Since this cardioid domain has just been introduced, there is a lot of roam to explore and investigate, and this work can be useful for future work in this direction.