Harris Hawks Optimization with Multi-Strategy Search and Application
Abstract
:1. Introduction
2. Harris Hawks Optimization Algorithm
3. HHO Algorithm Based on Multi-Search Strategy
3.1. Reasons for Improving the Basic HHO Algorithm
3.2. Chaotic Mapping
- Step 1: Randomly generate M Harris hawks in D-dimensional space, i.e., .
- Step 2: Iterate each dimension of each Harris hawk M times, resulting in M Harris hawks.
- Step 3: After all Harris hawk iterations were completed, chaotic mapping (21) was applied to the solution space.
3.3. Adaptive Weight
3.4. Variable Spiral Position Update
3.5. Optimal Neighborhood Disturbance
3.6. Computational Complexity
3.7. Algorithm Procedure
| Algorithm 1: CSHHO algorithm |
| Input: The population size N, maximum number of iterations T. |
| Output: The location of rabbit and its fitness value. |
| Using Seven chaotic maps to initialize the population: |
| Through chaotic variables [0, 1], k = 1, 2, …, M. M indicates the initial population dimension and Equations (14)–(21)generate initial chaotic vector; |
| Inverse mapping to get the initial population of the corresponding solution space through Equation (22); |
| While stopping condition is not meet do |
| Calculate the fitness values of hawks; |
| Set as best location of rabbit; |
| For do |
| Update the E using Equation (3); if then |
| ; |
| ; |
| If then |
| ; |
| end |
| if q < 0.5 then |
| ; |
| end |
| end |
| if |E| < 1 then |
| if ≥ 0.5 and |E| ≥ 0.5 then |
| using Equations (4)–(6); |
| end |
| else if r ≥ 0.5 and |E| < 0.5 then |
| using Equation (7); |
| end |
| else if r < 0.5 and E |≥ 0.5 |
| using Equations (8)–(11); |
| end |
| else if r < 0.5and |E| < 0.5 |
| using Equations (12) and (13); |
| end |
| end |
| end |
| Optimal neighborhood disturbance using Equations (27) and (28); |
| ; |
| ; |
| end |
| Return; |
4. Experiments and Discussion
4.1. Benchmark Functions Verification
4.2. Efficiency Analysis of the Improvement Strategy
- HHO without any modification, i.e., basic HHO;
- WOA without any modification, i.e., basic WOA;
- SCA without any modification, i.e., basic SCA;
- CSO without any modification, i.e., basic CSO;
- HHO with dimension decision logic and Gaussian mutation (GCHHO);
- Hybrid PSO Algorithm with Adaptive Step Search (DEPSOASS);
- Gravitational search algorithm with linearly decreasing gravitational constant (Improved GSA);
- Dynamic Generalized Opposition-based Learning Fruit Fly Algorithm (DGOBLFOA).
4.2.1. Influence of Seven Common Chaotic Mappings on HHO Algorithm
4.2.2. Comparison with Conventional Techniques
4.2.3. Comparison with HHO Variants
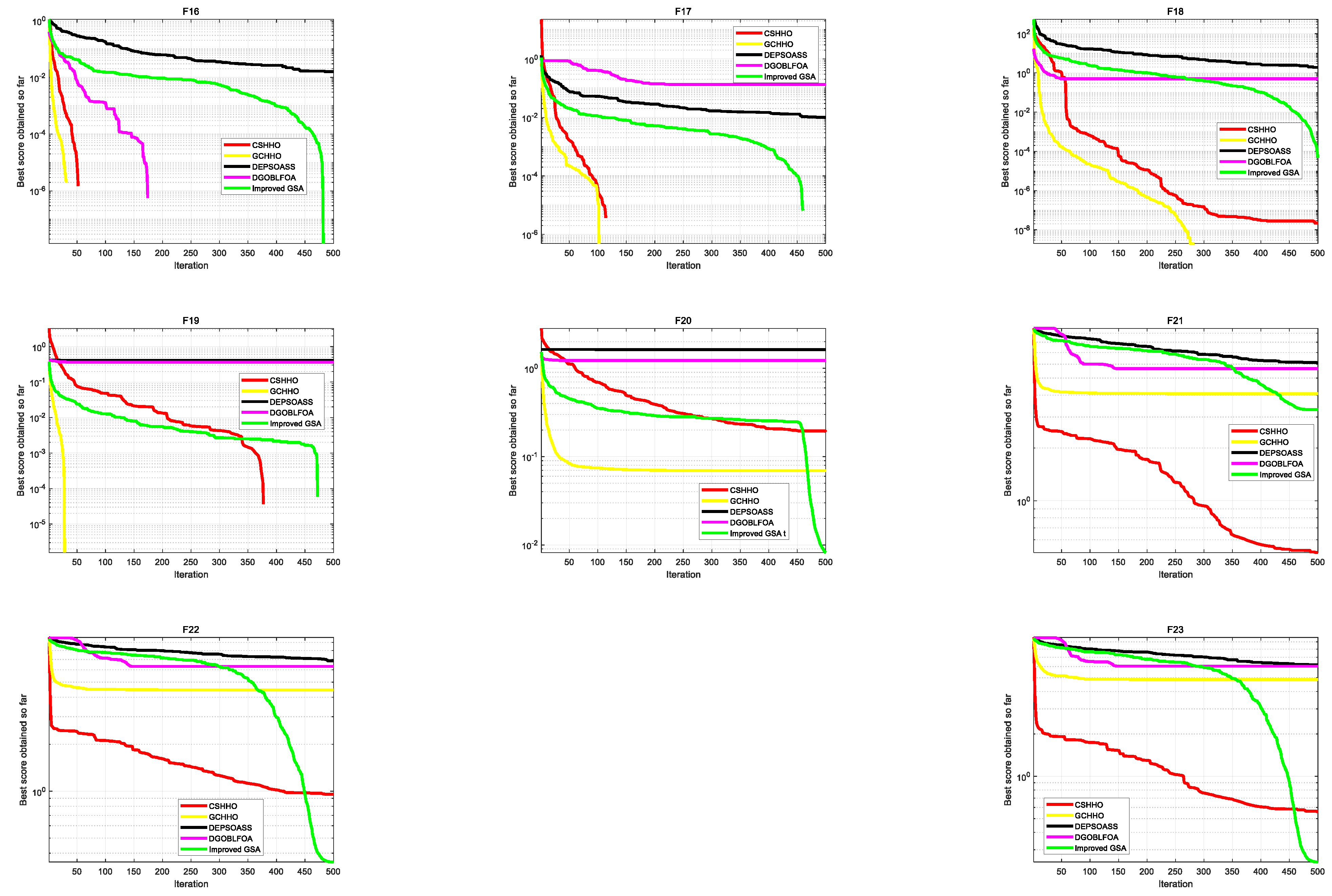
4.2.4. Scalability Test on CSHHO
5. Engineering Application
5.1. Principle of LSSVM
5.2. Simulation and Verification
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Function | Dimensions | Range | |
|---|---|---|---|
| unimodal benchmark functions | |||
| 30,100, 500, 1000 | [100, 100] | 0 | |
| 30,100, 500, 1000 | [10, 10] | 0 | |
| 30,100, 500, 1000 | [100, 100] | 0 | |
| 30,100, 500, 1000 | [100, 100] | 0 | |
| 30,100, 500, 1000 | [30, 30] | 0 | |
| 30,100, 500, 1000 | [100, 100] | 0 | |
| 30,100, 500, 1000 | [128, 128] | 0 | |
| multimodal benchmark functions | |||
| 30,100, 500, 1000 | [500, 500] | −418.9829 × n | |
| 30,100, 500, 1000 | [5.12, 5.12] | 0 | |
| 30,100, 500, 1000 | [32, 32] | 0 | |
| 30,100, 500, 1000 | [600, 600] | 0 | |
| 30,100, 500, 1000 | [50, 50] | 0 | |
| 30,100, 500, 1000 | [50, 50] | 0 | |
| fixed-dimension multimodal benchmark functions | |||
| 2 | [−65, 65] | 1 | |
| 4 | [−5, 5] | 0.00030 | |
| 2 | [−5, 5] | −1.0316 | |
| 2 | [−5, 5] | 0.398 | |
| 2 | [−2, 2] | 3 | |
| 3 | [1, 3] | −3.86 | |
| 6 | [0, 1] | −3.32 | |
| 4 | [0, 10] | −10.1532 | |
| 4 | [0, 10] | −10.4028 | |
| 4 | [0, 10] | −10.5363 | |
References
- Kundu, T.; Garg, H. A Hybrid ITLHHO Algorithm for Numerical and Engineering Optimization Problems. Int. J. Intell. Syst. 2021, 36, 1–81. [Google Scholar] [CrossRef]
- Garg, H. A Hybrid GSA-GA Algorithm for Constrained Optimization Problems. Inf. Sci. 2019, 478, 499–523. [Google Scholar] [CrossRef]
- Garg, H. A hybrid PSO-GA algorithm for constrained optimization problems. Appl. Math. Comput. 2016, 274, 292–305. [Google Scholar] [CrossRef]
- Wu, Y. A Survey on Population-Based Meta-Heuristic Algorithms for Motion Planning of Aircraft. Swarm Evol. Comput. 2021, 62, 100844. [Google Scholar] [CrossRef]
- Alabool, H.M.; Alarabiat, D.; Abualigah, L.; Heidari, A.A. Harris hawks optimization: A comprehensive review of recent variants and applications. Neural Comput. Appl. 2021, 33, 8939–8980. [Google Scholar] [CrossRef]
- Vasant, P. Handbook of Research on Artificial Intelligence Techniques and Algorithms; IGI Global: Hershey, PA, USA, 2015. [Google Scholar] [CrossRef]
- Simon, D. Evolutionary Optimization Algorithms: Biologically-Inspired and Population-Based Approaches to Computer Intelligence; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2013; ISBN 978-0-470-93741-9. [Google Scholar]
- Dréo, J. (Ed.) Metaheuristics for Hard Optimization: Methods and Case Studies; Springer: Berlin, Germany, 2006; ISBN 978-3-540-23022-9. [Google Scholar]
- Salcedo-Sanz, S. Modern Meta-Heuristics Based on Nonlinear Physics Processes: A Review of Models and Design Procedures. Phys. Rep. 2016, 655, 1–70. [Google Scholar] [CrossRef]
- Adeyanju, O.M.; Canha, L.N. Decentralized Multi-Area Multi-Agent Economic Dispatch Model Using Select Meta-Heuristic Optimization Algorithms. Electr. Power Syst. Res. 2021, 195, 107128. [Google Scholar] [CrossRef]
- Zhu, M.; Chu, S.-C.; Yang, Q.; Li, W.; Pan, J.-S. Compact Sine Cosine Algorithm with Multigroup and Multistrategy for Dispatching System of Public Transit Vehicles. J. Adv. Transp. 2021, 2021, 1–16. [Google Scholar] [CrossRef]
- Fu, X.; Fortino, G.; Li, W.; Pace, P.; Yang, Y. WSNs-Assisted Opportunistic Network for Low-Latency Message Forwarding in Sparse Settings. Future Gener. Comput. Syst. 2019, 91, 223–237. [Google Scholar] [CrossRef]
- Dhiman, G. SSC: A Hybrid Nature-Inspired Meta-Heuristic Optimization Algorithm for Engineering Applications. Knowl.-Based Syst. 2021, 222, 106926. [Google Scholar] [CrossRef]
- Han, Y.; Gu, X. Improved Multipopulation Discrete Differential Evolution Algorithm for the Scheduling of Multipurpose Batch Plants. Ind. Eng. Chem. Res. 2021, 60, 5530–5547. [Google Scholar] [CrossRef]
- Loukil, T.; Teghem, J.; Tuyttens, D. Solving multi-objective production scheduling problems using meta-heuristics. Eur. J.Oper. Res. 2005, 161, 42–61. [Google Scholar] [CrossRef]
- Li, Q.; Chen, H.; Huang, H.; Zhao, X.; Cai, Z.; Tong, C.; Liu, W.; Tian, X. An Enhanced Grey Wolf Optimization Based Feature Selection Wrapped Kernel Extreme Learning Machine for Medical Diagnosis. Comput. Math. Methods Med. 2017, 1–15. [Google Scholar] [CrossRef]
- Li, Y.; Liu, J.; Tang, Z.; Lei, B. Deep Spatial-Temporal Feature Fusion From Adaptive Dynamic Functional Connectivity for MCI Identification. IEEE Trans. Med. Imaging. 2020, 39, 2818–2830. [Google Scholar] [CrossRef] [PubMed]
- Corazza, M.; di Tollo, G.; Fasano, G.; Pesenti, R. A Novel Hybrid PSO-Based Metaheuristic for Costly Portfolio Selection Problems. Ann. Oper. Res. 2021, 304, 109–137. [Google Scholar] [CrossRef]
- Gaspero, L.D.; Tollo, G.D.; Roli, A.; Schaerf, A. Hybrid Metaheuristics for Constrained Portfolio Selection Problems. Quant. Financ. 2011, 11, 1473–1487. [Google Scholar] [CrossRef]
- Shen, L.; Chen, H.; Yu, Z.; Kang, W.; Zhang, B.; Li, H.; Yang, B.; Liu, D. Evolving Support Vector Machines Using Fruit Fly Optimization for Medical Data Classification. Knowl.-Based Syst. 2016, 96, 61–75. [Google Scholar] [CrossRef]
- Wang, M.; Chen, H.; Yang, B.; Zhao, X.; Hu, L.; Cai, Z.; Huang, H.; Tong, C. Toward an Optimal Kernel Extreme Learning Machine Using a Chaotic Moth-Flame Optimization Strategy with Applications in Medical Diagnoses. Neurocomputing 2017, 267, 69–84. [Google Scholar] [CrossRef]
- Song, J.; Zheng, W.X.; Niu, Y. Self-Triggered Sliding Mode Control for Networked PMSM Speed Regulation System: A PSO-Optimized Super-Twisting Algorithm. IEEE Trans. Ind. Electron. 2021, 69, 763–773. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gen. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Dong, W.; Zhou, M. A Supervised Learning and Control Method to Improve Particle Swarm Optimization Algorithms. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 1135–1148. [Google Scholar] [CrossRef]
- Mareda, T.; Gaudard, L.; Romerio, F. A Parametric Genetic Algorithm Approach to Assess Complementary Options of Large Scale Windsolar Coupling. IEEE/CAA J. Autom. Sin. 2017, 4, 260–272. [Google Scholar] [CrossRef] [Green Version]
- Jian, Z.; Liu, S.; Zhou, M. Modified cuckoo search algorithm to solve economic power dispatch optimization problems. IEEE/CAA J. Autom. Sin. 2018, 5, 794–806. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science. 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Xing, B.; Gao, W.-J. Gravitational Search Algorithm. In Innovative Computational Intelligence: A Rough Guide to 134 Clever Algorithms; Intelligent Systems Reference Library; Springer International Publishing: Cham, Germany, 2014; Volume 62, pp. 355–364. ISBN 978-3-319-03403-4. [Google Scholar]
- Alatas, B. ACROA: Artificial chemical reaction optimization algorithm for global optimization. Expert Syst. Appl. 2011, 38, 13170–13180. [Google Scholar] [CrossRef]
- Patel, V.K.; Savsani, V.J. Heat transfer search (HTS): A novel optimization algorithm. Inf. Sci. 2015, 324, 217–246. [Google Scholar] [CrossRef]
- Abdechiri, M.; Meybodi, M.R.; Bahrami, H. Gases brownian motion optimization: An algorithm for optimization (GBMO). Appl. Soft Comput. 2013, 13, 2932–2946. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Mabrouk, M.S.; Al-Atabany, W.; Mirjalili, S. Henry gas solubility optimization: A novel physics-based algorithm. Future Gener. Comput. Syst. 2019, 101, 646–667. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic Algorithms. Sci. Am. 1992, 267, 66–72. [Google Scholar] [CrossRef]
- Schneider, B.; Ranft, U. Simulationsmethoden in der Medizin und Biologie; Springer: Berlin/Heidelberg, Germany, 1978. [Google Scholar]
- Yang, X.-S. Differential evolution. In Nature-Inspired Optimization Algorithms. Algorithms; Elsevier: London UK, 2021; Volume 6, pp. 101–109. [Google Scholar]
- Storn, R.; Price, K. Differential evolution–A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Simon, D. Biogeography-Based Optimization. IEEE Trans. Evol. Comput. 2008, 12, 702–713. [Google Scholar] [CrossRef] [Green Version]
- Karaboga, D.; Akay, B. A comparative study of Artificial Bee Colony algorithm. Appl. Math. Comput. 2009, 214, 108–132. [Google Scholar] [CrossRef]
- Yang, X.S. Firefly algorithm, stochastic test functions and design optimization. Int. J. Bio-Inspired Comput. 2010, 2, 78. [Google Scholar] [CrossRef]
- Jiang, X.; Li, S. BAS: Beetle antennae search algorithm for optimization problems. Int. J. Robot. Control 2018, 1, 1. [Google Scholar] [CrossRef]
- Okwu, M.O. (Ed.) Grey Wolf Optimizer, Metaheuristic Optimization, Nature-Inspired Algorithms Swarm and Computational Intelligence, Theory and Applications; Springer International Publishing: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Li, M.D.; Zhao, H.; Weng, X.W.; Han, T. A novel nature-inspired algorithm for optimization: Virus colony search. Adv. Eng. Softw. 2016, 92, 65–88. [Google Scholar] [CrossRef]
- Glover, F. Tabu search—Part I. ORSA J. Comput. 1989, 1, 190–206. [Google Scholar] [CrossRef] [Green Version]
- Kumar, M.; Kulkarni, A.J.; Satapathy, S.C. Socio evolution & learning optimization algorithm: A socio-inspired optimization methodology. Future Gener. Comput. Syst. 2018, 81, 252–272. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching–learning-based optimization: An optimization method for continuous non-linear large scale problems. Inf. Sci. 2012, 183, 1–15. [Google Scholar] [CrossRef]
- Hosseini, S.; Al Khaled, A. A Survey on the Imperialist Competitive Algorithm Metaheuristic: Implementation in Engineering Domain and Directions for Future Research. Appl. Soft. Comput. 2014, 24, 1078–1094. [Google Scholar] [CrossRef]
- Jia, H.; Peng, X.; Kang, L.; Li, Y.; Jiang, Z.; Sun, K. Pulse coupled neural network based on Harris hawks optimization algorithm for image segmentation. Multimed Tools Appl. 2020, 79, 28369–28392. [Google Scholar] [CrossRef]
- Fan, C.; Zhou, Y.; Tang, Z. Neighborhood centroid opposite-based learning harris hawks optimization for training neural networks. Evol. Intell. 2020, 14, 1847–1867. [Google Scholar] [CrossRef]
- Saravanan, G.; Ibrahim, A.M.; Kumar, D.S.; Vanitha, U.; Chandrika, V.S. Iot Based Speed Control of BLDC Motor with Harris Hawks Optimization Controller. Int. J. Grid Distrib. Comput. 2020, 13, 1902–1919. [Google Scholar]
- Qu, C.; He, W.; Peng, X.; Peng, X. Harris hawks optimization with information exchange. Appl. Math. Model. 2020, 84, 52–75. [Google Scholar] [CrossRef]
- Devarapalli, R.; Bhattacharyya, B. Application of modified harris hawks Optimization in power system oscillations damping controller design. In Proceedings of the 2019 8th International Conference on Power Systems (ICPS), Jaipur, India, 20–22 December 2019. [Google Scholar]
- Elgamal, Z.M.; Yasin, N.B.M.; Tubishat, M.; Alswaitti, M.; Mirjalili, S. An improved harris hawks optimization algorithm with simulated annealing for feature selection in the Medical Field. IEEE Access. 2020, 8, 186638–186652. [Google Scholar] [CrossRef]
- Song, S.; Wang, P.; Heidari, A.A.; Wang, M.; Zhao, X.; Chen, H.; He, W.; Xu, S. Dimension decided harris hawks optimization with gaussian mutation: Balance analysis and diversity patterns. Knowl.-Based Syst. 2021, 215, 106425. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No Free Lunch Theorems for Optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–83. [Google Scholar] [CrossRef] [Green Version]
- Bednarz, J.C. Cooperative Hunting Harris’ Hawks (Parabuteo unicinctus). Science 1988, 239, 1525–1527. [Google Scholar] [CrossRef] [PubMed]
- Lefebvre, L.; Whittle, P.; Lascaris, E.; Finkelstein, A. Feeding innovations and forebrain size in birds. Anim. Behav. 1997, 53, 549–560. [Google Scholar] [CrossRef] [Green Version]
- Sol, D.; Duncan, R.P.; Blackburn, T.M.; Cassey, P.; Lefebvre, L. Big brains, Enhanced Cognition, and Response of birds to Novel environments. Proc. Natl. Acad. Sci. USA 2005, 102, 5460–5465. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kazimipour, B.; Li, X.; Qin, A.K. A review of population initialization techniques for evolutionary algorithms. In Proceedings of the 2014 IEEE Congress on Evolutionary Computation (CEC), Beijing, China, 6–11 July 2014; pp. 2585–2592. [Google Scholar] [CrossRef]
- Migallón, H.; Jimeno-Morenilla, A.; Rico, H.; Sánchez-Romero, J.L.; Belazi, A. Multi-Level Parallel Chaotic Jaya Optimization Algorithms for Solving Constrained Engineering Design Problems. J. Supercomput. 2021, 77, 12280–12319. [Google Scholar] [CrossRef]
- Alatas, B.; Akin, E. Multi-Objective Rule Mining Using a Chaotic Particle Swarm Optimization Algorithm. Knowl.-Based Syst. 2009, 22, 455–460. [Google Scholar] [CrossRef]
- Arora, S.; Anand, P. Chaotic Grasshopper Optimization Algorithm for Global Optimization. Neural Comput. Appl. 2019, 31, 4385–4405. [Google Scholar] [CrossRef]
- Wang, G.-G.; Guo, L.; Gandomi, A.H.; Hao, G.-S.; Wang, H. Chaotic Krill Herd Algorithm. Inf. Sci. 2014, 274, 17–34. [Google Scholar] [CrossRef]
- Mitić, M.; Vuković, N.; Petrović, M.; Miljković, Z. Chaotic Fruit Fly Optimization Algorithm. Knowl.-Based Syst. 2015, 89, 446–458. [Google Scholar] [CrossRef]
- Kumar, Y.; Singh, P.K. A Chaotic Teaching Learning Based Optimization Algorithm for Clustering Problems. Appl. Intell. 2019, 49, 1036–1062. [Google Scholar] [CrossRef]
- Pierezan, J.; dos Santos Coelho, L.; Mariani, V.C.; de Vasconcelos Segundo, E.H.; Prayogo, D. Chaotic Coyote Algorithm Applied to Truss Optimization Problems. Comput. Struct. 2021, 242, 106353. [Google Scholar] [CrossRef]
- Sayed, G.I.; Tharwat, A.; Hassanien, A.E. Chaotic Dragonfly Algorithm: An Improved Metaheuristic Algorithm for Feature Selection. Appl. Intell. 2019, 49, 188–205. [Google Scholar] [CrossRef]
- Chen, K.; Zhou, F.; Liu, A. Chaotic Dynamic Weight Particle Swarm Optimization for Numerical Function Optimization. Knowl.-Based Syst. 2018, 139, 23–40. [Google Scholar] [CrossRef]
- Anand, P.; Arora, S. A Novel Chaotic Selfish Herd Optimizer for Global Optimization and Feature Selection. Artif. Intell. Rev. 2020, 53, 1441–1486. [Google Scholar] [CrossRef]
- Yao, X.; Liu, Y.; Lin, G. Evolutionary Programming Made Faster. IEEE Trans. Evol. Comput. 1999, 3, 82–102. [Google Scholar] [CrossRef] [Green Version]
- Digalakis, J.G.; Margaritis, K.G. On benchmarking functions for genetic algorithms. Int. J. Comput. Math. 2001, 77, 481–506. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, Q.; Luo, J. An enhanced Bacterial Foraging Optimization and its application for training kernel extreme learning machine. Appl. Soft. Comput. 2020, 86, 105–884. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A Sine Cosine Algorithm for Solving Optimization Problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Meng, X.; Liu, Y.; Gao, X.; Zhang, H. A new bio-inspired algorithm: Chicken swarm optimization. In Advances in Swarm Intelligence; Tan, Y., Shi, Y., Coello, C.A.C., Eds.; Springer International Publishing: Cham, Germany, 2014; pp. 86–94. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, J.; Che, L. Hybrid PSO Algorithm with Adaptive Step Search in Noisy and Noise-Free Environments. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation (CEC), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar]
- Jordehi, A.R. Gravitational Search Algorithm with Linearly Decreasing Gravitational Constant for Parameter Estimation of Photovoltaic Cells. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation (CEC), Donostia, Spain, 5–8 June 2017; pp. 37–42. [Google Scholar]
- Feng, X.; Liu, A.; Sun, W.; Yue, X.; Liu, B. A Dynamic Generalized Opposition-Based Learning Fruit Fly Algorithm for Function Optimization. In Proceedings of the 2018 IEEE Congress on Evolutionary Computation (CEC), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–7. [Google Scholar]
- Demsar, J. Statistical comparisons of classifiers over multiple data sets. J. Mach. Learn. Res. 2006, 7, 1–30. [Google Scholar]
- García, S.; Fernández, A.; Luengo, J.; Herrera, F. Advanced nonparametric tests for multiple comparisons in the design of experiments in computational intelligence and data mining: Experimental analysis of power. Inf. Sci. 2010, 180, 2044–2064. [Google Scholar] [CrossRef]
- Groppe, D.M.; Urbach, T.P.; Kutas, M. Mass univariate analysis of event-related brain potentials/fields I: A critical tutorial review. Psychophysiology 2011, 48, 1711–1725. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Deliparaschos, K.M.; Nenedakis, F.I.; Tzafestas, S.G. Design and implementation of a fast digital fuzzy logic controller using FPGA Technology. J. Intell. Robot. Syst. 2006, 45, 77–96. [Google Scholar] [CrossRef]
- Sapkota, B.; Vittal, V. Dynamic VAr planning in a large power system using trajectory sensitivities. IEEE Trans. Power Syst. 2010, 25, 461–469. [Google Scholar] [CrossRef]
- Huang, H.; Xu, Z.; Lin, X. Improving performance of Multi-infeed HVDC systems using grid dynamic segmentation technique based on fault current limiters. IEEE Trans. Power Syst. 2012, 27, 1664–1672. [Google Scholar] [CrossRef]
- Yong, T. A discussion about standard parameter models of synchronous machine. Power Syst. Technol. 2007, 12, 47. [Google Scholar]
- Grigsby, L.L. (Ed.) Power system Stability and Control, 3rd ed.; Taylor & Francis: Boca Raton, FL, USA, 2012. [Google Scholar]
- Tian, Z. Backtracking search optimization algorithm-based least square support vector machine and its applications. Eng. Appl. Artif. Intell. 2020, 94, 103801. [Google Scholar] [CrossRef]
- Suykens, J.A.K.; Vandewalle, J. Least squares support vector machine classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Zendehboudi, A. Implementation of GA-LSSVM modelling approach for estimating the performance of solid desiccant wheels. Energy Convers. Manag. 2016, 127, 245–255. [Google Scholar] [CrossRef]
- Chamkalani, A.; Zendehboudi, S.; Bahadori, A.; Kharrat, R.; Chamkalani, R.; James, L.; Chatzis, I. Integration of LSSVM technique with PSO to determine asphaltene deposition. J. Pet. Sci. Eng. 2014, 124, 243–253. [Google Scholar] [CrossRef]
- Zhongda, T.; Shujiang, L.; Yanhong, W.; Yi, S. A prediction method based on wavelet transform and multiple models fusion for chaotic time series. Chaos Solitons Fractals 2017, 98, 158–172. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, X. Research on the supply chain risk assessment based on the improved LSSVM algorithm. Int. J. U-Serv. Sci. Technol. 2016, 9, 297–306. [Google Scholar] [CrossRef]
- Jain, S.; Bajaj, V.; Kumar, A. Efficient algorithm for classification of electrocardiogram beats based on artificial bee colony-based least-squares support vector machines classifier. Electron. Lett. 2016, 52, 1198–1200. [Google Scholar] [CrossRef]
- Yang, A.; Li, W.; Yang, X. Short-term electricity load forecasting based on feature selection and Least Squares Support Vector Machines. Knowl.-Based Syst. 2019, 163, 159–173. [Google Scholar] [CrossRef]
- Adankon, M.M.; Cheriet, M. Support vector machine. In Encyclopedia of Biometrics; Springer: Boston, MA, USA, 2014; Volume 3, pp. 1–9. [Google Scholar] [CrossRef]
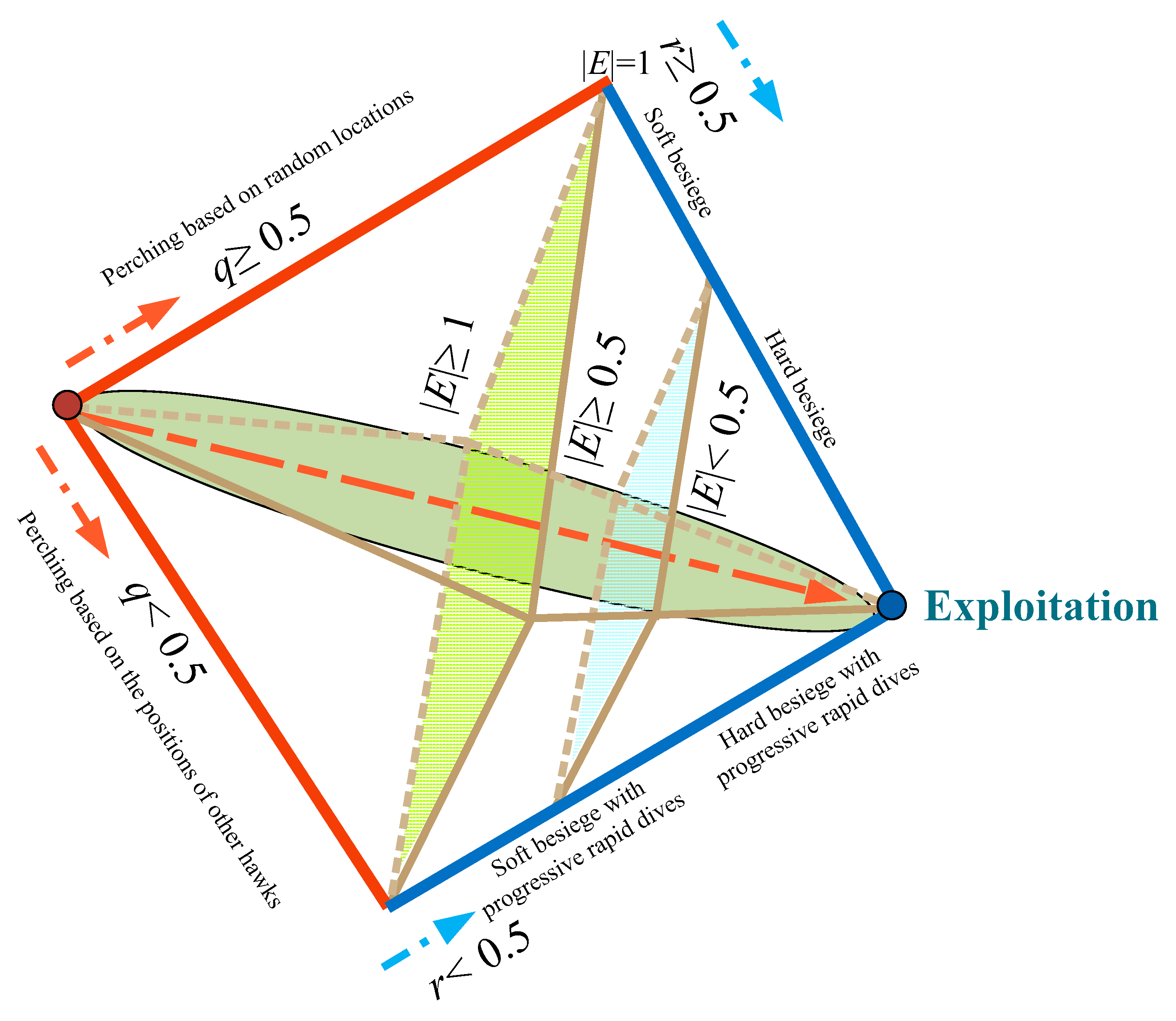








| Strategy | The value of r and |E| | |
| Soft besiege | r ≥ 0.5 and |E| ≥ 0.5 | |
| (4) | ||
| (5) | ||
| (6) | ||
| Hard besiege | r ≥ 0.5 and |E| < 0.5 | |
| (7) | ||
| Soft besiege with progressive rapid dives | r < 0.5 and |E| ≥ 0.5 | |
| (8) | ||
| (9) | ||
| (10) | ||
| (11) | ||
| Hard besiege with progressive rapid dives | r < 0.5 and |E| < 0.5 | |
| (12) | ||
| (13) | ||
| ID | Description | Type | Dimension | Range | Optimum |
|---|---|---|---|---|---|
| F1 | Shifted and Rotated Bent Cigar Function | Unimodal | 30, 50, 100 | [−100, 100] | 100 |
| F2 | Shifted and Rotated Zakharov function | Unimodal | 30, 50, 100 | [−100, 100] | 300 |
| F3 | Shifted and Rotated Rosenbrock’s function | Multimodal | 30, 50, 100 | [−100, 100] | 400 |
| F4 | Shifted and Rotated Rastrigin’s function | Multimodal | 30, 50, 100 | [−100, 100] | 500 |
| F5 | Shifted and Rotated Expanded Scaffer’s F6 function | Multimodal | 30, 50, 100 | [−100, 100] | 600 |
| F6 | Shifted and Rotated Lunacek Bi-Rastrigin function | Multimodal | 30, 50, 100 | [−100, 100] | 700 |
| F7 | Shifted and Rotated Non-Continuous Rastrigin’s function | Multimodal | 30, 50, 100 | [−100, 100] | 800 |
| F8 | Shifted and Rotated Lévy function | Multimodal | 30, 50, 100 | [−100, 100] | 900 |
| F9 | Shifted and Rotated Schwefel’s function | Multimodal | 30, 50, 100 | [−100, 100] | 1000 |
| F10 | Hybrid Function 1 (N = 3) | Hybrid | 30, 50, 100 | [−100, 100] | 1100 |
| F11 | Hybrid Function 2 (N = 3) | Hybrid | 30, 50, 100 | [−100, 100] | 1200 |
| F12 | Hybrid Function 3 (N = 3) | Hybrid | 30, 50, 100 | [−100, 100] | 1300 |
| F13 | Hybrid Function 4 (N = 4) | Hybrid | 30, 50, 100 | [−100, 100] | 1400 |
| F14 | Hybrid Function 5 (N = 4) | Hybrid | 30, 50, 100 | [−100, 100] | 1500 |
| F15 | Hybrid Function 6 (N = 4) | Hybrid | 30, 50, 100 | [−100, 100] | 1600 |
| F16 | Hybrid Function 6 (N = 5) | Hybrid | 30, 50, 100 | [−100, 100] | 1700 |
| F17 | Hybrid Function 6 (N = 5) | Hybrid | 30, 50, 100 | [−100, 100] | 1800 |
| F18 | Hybrid Function 6 (N = 5) | Hybrid | 30, 50, 100 | [−100, 100] | 1900 |
| F19 | Hybrid Function 6 (N = 6) | Hybrid | 30, 50, 100 | [−100, 100] | 2000 |
| F20 | Composition Function 1 (N = 3) | Composition | 30, 50, 100 | [−100, 100] | 2100 |
| F21 | Composition Function 2 (N = 3) | Composition | 30, 50, 100 | [−100, 100] | 2200 |
| F22 | Composition Function 3 (N = 4) | Composition | 30, 50, 100 | [−100, 100] | 2300 |
| F23 | Composition Function 4 (N = 4) | Composition | 30, 50, 100 | [−100, 100] | 2400 |
| F24 | Composition Function 5 (N = 5) | Composition | 30, 50, 100 | [−100, 100] | 2500 |
| F25 | Composition Function 6 (N = 5) | Composition | 30, 50, 100 | [−100, 100] | 2600 |
| F26 | Composition Function 7 (N = 6) | Composition | 30, 50, 100 | [−100, 100] | 2700 |
| F27 | Composition Function 7 (N = 6) | Composition | 30, 50, 100 | [−100, 100] | 2800 |
| F28 | Composition Function 9 (N = 3) | Composition | 30, 50, 100 | [−100, 100] | 2900 |
| F29 | Composition Function 10 (N = 3) | Composition | 30, 50, 100 | [−100, 100] | 3000 |
| Benchmark | Circle | Sinusoidal | Tent | Kent | Cubic | Logistic | Gauss | |
|---|---|---|---|---|---|---|---|---|
| F1 | Mean | 4.37 × 10−110 | 2.73 × 10−96 | 7.91 × 10−101 | 3.68 × 10−99 | 8.75 × 10−100 | 7.28 × 10−99 | 1.4 × 10−109 |
| Std | 3.05 × 10−109 | 1.09 × 10−95 | 3.91 × 10−100 | 1.82 × 10−98 | 4.06 × 10−99 | 5.13 × 10−98 | 9.69 × 10−109 | |
| Rank | 1 | 7 | 3 | 5 | 4 | 6 | 2 | |
| Best\Worst | 2.15 × 10−108\6.44 × 10−135 | 4.36 × 10−95\3.01 × 10−115 | 2.21 × 10−99\1.1 × 10−119 | 9.39 × 10−98\3.69 × 10−116 | 2.11 × 10−98\1.4 × 10−116 | 3.63 × 10−97\1.96 × 10−116 | 6.85 × 10−108\1.18 × 10−137 | |
| F2 | Mean | 6.4 × 10−59 | 3.88 × 10−53 | 3.45 × 10−53 | 7.39 × 10−53 | 8.12 × 10−53 | 8.59 × 10−53 | 8.05× 10−61 |
| Std | 3.12 × 10−58 | 1.74 × 10−52 | 1.5 × 10−52 | 4.9 × 10−52 | 5.03 × 10−52 | 4.9 × 10−52 | 2.37× 10−60 | |
| Rank | 2 | 4 | 3 | 5 | 6 | 7 | 1 | |
| Best\Worst | 1.97 × 10−57\5.03 × 10−77 | 1.20 × 10−51\6.33 × 10−60 | 8.88 × 10−52\1.72 × 10−61 | 3.47 × 10−51\1.86 × 10−64 | 3.56 × 10−51\2.76 × 10−68 | 3.4391 × 10−51\3.91 × 10−62 | 1.0834× 10−59\3.80 × 10−68 | |
| F3 | Mean | 2.90 × 10−86 | 2.51 × 10−86 | 5.22 × 10−82 | 5.28 × 10−78 | 3.08 × 10−83 | 9.34 × 10−86 | 7.29 × 10−78 |
| Std | 2.01 × 10−85 | 9.38 × 10−86 | 3.13 × 10−81 | 3.73 × 10−77 | 2.15 × 10−82 | 3.43 × 10−85 | 5.15 × 10−77 | |
| Rank | 2 | 1 | 5 | 6 | 4 | 3 | 7 | |
| Best\Worst | 1.42 × 10−84\8.08 × 10−104 | 3.51 × 10−85\9.55 × 10−104 | 2.18 × 10−80\1.01 × 10−108 | 2.63 × 10−76\5.02 × 10−101 | 1.52 × 10−81\2.2 × 10−107 | 1.90 × 10−84\5.74 × 10−105 | 3.64 × 10−76\1.58 × 10−107 | |
| F4 | Mean | 8.48 × 10−56 | 1.23 × 10−50 | 7.91 × 10−51 | 8.72 × 10−51 | 3.65 × 10−50 | 9.39 × 10−50 | 9.3 × 10−53 |
| Std | 4.24 × 10−55 | 4.28 × 10−50 | 5.22 × 10−50 | 3.6 × 10−50 | 2.4 × 10−49 | 6.51 × 10−49 | 6.49 × 10−52 | |
| Rank | 1 | 5 | 3 | 4 | 6 | 7 | 2 | |
| Best\Worst | 2.64 × 10−54\9.93 × 10−69 | 1.91 × 10−49\1.3 × 10−55 | 3.69 × 10−49\2.77 × 10−59 | 1.97 × 10−49\4.06 × 10−58 | 1.70 × 10−48\2.16 × 10−60 | 4.60 × 10−48\4.39 × 10−58 | 4.59 × 10−51\1.13 × 10−65 | |
| F5 | Mean | 8.55 × 10−2 | 4.17 × 10−2 | 5.42 × 10−2 | 4.65 × 10−2 | 7.29 × 10−2 | 4.85 × 10−2 | 8.33 × 10−2 |
| Std | 5.63 × 10−1 | 4.90 × 10−3 | 9.52 × 10−3 | 7.56 × 10−3 | 9.62 × 10−3 | 8.98 × 10−3 | 5.64 × 10−1 | |
| Rank | 7 | 1 | 4 | 2 | 5 | 3 | 6 | |
| Best\Worst | 3.9896\4.3262 × 10−5 | 0.021867\3.3302 × 10−6 | 0.048302\8.4348 × 10−7 | 0.0425\8.3416 × 10−7 | 0.043385\3.4475 × 10−5 | 0.051141\6.6967 × 10−6 | 3.9896\6.6344 × 10−6 | |
| F6 | Mean | 3.34 × 10−5 | 7.87 × 10−5 | 5.47 × 10−5 | 4.72 × 10−5 | 6.85 × 10−5 | 4.45 × 10−5 | 2.48× 10−5 |
| Std | 6.12 × 10−5 | 1.10 × 10−4 | 9.45 × 10−5 | 5.54 × 10−5 | 8.89 × 10−56 | 6.00 × 10−5 | 3.13× 10−5 | |
| Rank | 2 | 7 | 5 | 4 | 6 | 3 | 1 | |
| Best\Worst | 3.42 × 10−4\1.6931 × 10−8 | 4.27 × 10−4\7.8651 × 10−8 | 3.71 × 10−4\2.4303 × 10−9 | 3.16 × 10−4\3.9886 × 10−8 | 4.33 × 10−4\1.2627 × 10−8 | 2.77 × 10−4\2.6747 × 10−8 | 1.48× 10−4\1.1473× 10−10 | |
| F7 | Mean | 1.02 × 10−4 | 7.60 × 10−5 | 8.41 × 10−5 | 9.33 × 10−5 | 7.99 × 10−5 | 7.62 × 10−5 | 9.17 × 10−5 |
| Std | 9.77 × 10−5 | 4.66 × 10−5 | 1.02 × 10−4 | 9.06 × 10−5 | 8.17 × 10−5 | 7.35 × 10−5 | 8.83 × 10−5 | |
| Rank | 7 | 1 | 4 | 6 | 3 | 2 | 5 | |
| Best\Worst | 4.09 × 10−4\1.85 × 10−6 | 1.92 × 10−4\1.62 × 10−6 | 5.44 × 10−4\1.26 × 10−6 | 3.88 × 10−4\4.19 × 10−6 | 5.07 × 10−4\1.77 × 10−6 | 4.39 × 10−4\8.40 × 10−7 | 4.36 × 10−4\1.72 × 10−6 | |
| F8 | Mean | −1.26 × 104 | −1.26 × 104 | −1.26 × 104 | −1.26 × 104 | −1.25 × 104 | −1.26 × 104 | −1.26 × 104 |
| Std | 52.1 | 0.232 | 0.453 | 0.508 | 0.378 | 0.226 | 30.7 | |
| Rank | 1 | 1 | 1 | 1 | 7 | 1 | 1 | |
| Best\Worst | −1.23 × 104\−1.25 × 104 | −1.25 × 104\−1.25 × 104 | −1.25 × 104\−1.25 × 104 | −1.25 × 104\−1.25 × 104 | −9.90 × 103\−1.25 × 104 | −1.25 × 104\−1.25 × 104 | −1.23× 104\−1.25 × 104 | |
| F9 | Mean | 0 | 0 | 0 | 0 | 0\0 | 0 | 0 |
| Std | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Rank | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| Best\Worst | 0\0 | 0\0 | 0\0 | 0\0 | 0\0 | 0\0 | 0\0 | |
| F10 | Mean | 8.88 × 10−16 | 8.88 × 10−16 | 8.88 × 10−16 | 8.88 × 10−16 | 8.88 × 10−16 | 8.88 × 10−16 | 8.88× 10−16 |
| Std | 1.99 × 10−31 | 1.99 × 10−31 | 1.99 × 10−31 | 1.99 × 10−31 | 1.99 × 10−31 | 1.99 × 10−31 | 1.99× 10−31 | |
| Rank | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| Best\Worst | 8.88 × 10−16\8.88 × 10−16 | 8.88 × 10−16\8.88 × 10−16 | 8.88 × 10−16\8.88 × 10−16 | 8.88 × 10−16\8.88 × 10−16 | 8.88 × 10−16\8.88 × 10−16 | 8.88 × 10−16\8.88 × 10−16 | 8.88× 10−16\8.88 × 10−16 | |
| F11 | Mean | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Std | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Rank | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| Best\Worst | 0\0 | 0\0 | 0\0 | 0\0 | 0\0 | 0\0 | 0\0 | |
| F12 | Mean | 1.31 × 10−6 | 2.79 × 10−6 | 4.21 × 10−6 | 2.75 × 10−6 | 4.02 × 10−6 | 4.18 × 10−6 | 1.18× 10−6 |
| Std | 1.49 × 10−6 | 3.23 × 10−6 | 8.73 × 10−6 | 3.36 × 10−6 | 5.88 × 10−6 | 5.65 × 10−6 | 1.52× 10−6 | |
| Rank | 2 | 4 | 7 | 3 | 5 | 6 | 1 | |
| Best\Worst | 7.06 × 10−6\5.43 × 10−9 | 1.46 × 10−5\2.19 × 10−8 | 5.17 × 10−5\1.09 × 10−8 | 1.75 × 10−5\2.96 × 10−9 | 3.25 × 10−5\2.30 × 10−9 | 2.80 × 10−5\5.59 × 10−9 | 6.68× 10−6\5.16 × 10−10 | |
| F13 | Mean | 2.66 × 10−4 | 3.31 × 10−4 | 3.91 × 10−5 | 2.56 × 10−5 | 4.15 × 10−5 | 2.68 × 10−5 | 4.62 × 10−4 |
| Std | 1.55 × 10−3 | 2.07 × 10−3 | 5.02 × 10−5 | 4.26 × 10−5 | 5.82 × 10−54 | 3.68 × 10−5 | 2.17 × 10−3 | |
| Rank | 5 | 6 | 3 | 1 | 4 | 2 | 7 | |
| Best\Worst | 0.010987\1.4769 × 10−7 | 0.014637\1.0906 × 10−7 | 0.00023743\4.4639 × 10−8 | 0.00026746\5.4412 × 10−7 | 0.00024897\2.9199 × 10−11 | 0.00016986\8.1121 × 10−8 | 0.010987\5.0129 × 10−8 | |
| F14 | Mean | 1.20 | 9.97 × 10−1 | 9.98 × 10−1 | 1.22 | 1.02 | 1.12 | 1.57 |
| Std | 9.76 × 10−1 | 5.61 × 10−16 | 5.61 × 10−16 | 9.82 × 10−1 | 1.41 × 10−1 | 7.10 × 10−1 | 1.49 | |
| Rank | 5 | 1 | 2 | 6 | 3 | 4 | 7 | |
| Best\Worst | 5.93\9.98 × 10−1 | 9.98 × 10−1\9.98 × 10−1 | 9.98 × 10−1\9.98 × 10−1 | 5.93\9.98 × 10−1 | 1.99\9.98 × 10−1 | 5.93\9.98 × 10−1 | 5.93\9.98 × 10−1 | |
| F15 | Mean | 3.24 × 10−4 | 3.19 × 10−4 | 3.22 × 10−4 | 3.27 × 10−4 | 3.72 × 10−4 | 3.28 × 10−4 | 3.25 × 10−4 |
| Std | 1.45 × 10−5 | 1.03 × 10−5 | 1.70 × 10−5 | 1.93 × 10−5 | 2.24 × 10−4 | 1.79 × 10−5 | 1.23 × 10−5 | |
| Rank | 3 | 1 | 2 | 5 | 7 | 6 | 4 | |
| Best\Worst | 3.82 × 10−4\3.08 × 10−4 | 3.48 × 10−4\3.08 × 10−4 | 3.72 × 10−4\3.08 × 10−4 | 3.92 × 10−4\3.08 × 10−4 | 1.63 × 10−3\3.08 × 10−4 | 3.86 × 10−4\3.08 × 10−4 | 3.95 × 10−4\3.08 × 10−4 | |
| F16 | Mean | −1.03 | −1.03 | −1.03 | −1.03 | −1.03 | −1.03 | −1.03 |
| Std | 1.35 × 10−15 | 1.35 × 10−15 | 1.35 × 10−15 | 1.35 × 10−15 | 1.35 × 10−15 | 1.35 × 10−15 | 1.35× 10−15 | |
| Rank | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| Best\Worst | −1.03\−1.03 | −1.03\−1.031 | −1.03\−1.03 | −1.03\−1.03 | −1.03\−1.03 | −1.03\−1.03 | −1.03\−1.03 | |
| F17 | Mean | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 3.9× 10−9 |
| Std | 7.97 × 10−8 | 4.58 × 10−8 | 2.57 × 10−7 | 1.65 × 10−7 | 3.38 × 10−7 | 7.58 × 10−8 | 4.17× 10−8 | |
| Rank | 2 | 2 | 2 | 2 | 2 | 2 | 1 | |
| Best\Worst | 3.97 × 10−1\3.97 × 10−1 | 3.97 × 10−1\3.97 × 10−1 | 3.97 × 10−1\3.97 × 10−1 | 3.97 × 10−1\3.97 × 10−1 | 3.97 × 10−1\0.3.97 × 10−1 | 3.97 × 10−1\0.3.97 × 10−1 | 3.97× 10−1\0.3.97 × 10−1 | |
| F18 | Mean | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| Std | 1.41 × 10−8 | 1.31 × 10−7 | 1.98 × 10−8 | 5.48 × 10−8 | 1.41 × 10−8 | 7.00 × 10−8 | 4.63× 10−8 | |
| Rank | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| Best\Worst | 3\3 | 3\3 | 3\3 | 3\3 | 3\3 | 3\3 | 3\3 | |
| F19 | Mean | −3.86 | −3.86 | −3.86 | −3.86 | −3.86 | −3.86 | −3.86 |
| Std | 2.09 × 10−3 | 2.52 × 10−3 | 2.35 × 10−3 | 2.43 × 10−3 | 1.61 × 10−3 | 3.02 × 10−3 | 1.32× 10−3 | |
| Rank | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| Best\Worst | −3.85\−3.86 | −3.85\−3.86 | −3.85\−3.86 | −3.85\−3.86 | −3.86\−3.86 | −3.85\−3.86 | −3.86\−3.86 | |
| F20 | Mean | −3.12 | −3.12 | −3.14 | −3.12 | −3.13 | −3.11 | −3.12 |
| Std | 1.10 × 10−1 | 1.12 × 10−1 | 1.10 × 10−1 | 1.10 × 10−1 | 1.10 × 10−1 | 1.12 × 10−1 | 9.95 × 10−2 | |
| Rank | 3 | 3 | 1 | 3 | 2 | 7 | 3 | |
| Best\Worst | −2.88\−3.31 | −2.80\−3.30 | −2.89\−3.30 | −2.86\−3.30 | −2.90\−3.30 | −2.82\−3.30 | −2.81\−3.27 | |
| F21 | Mean | −8.77 | −7.05 | −7.04 | −8.75 | −5.36 | −7.03 | −8.45 |
| Std | 2.23 | 2.47 | 2.46 | 2.21 | 1.21 | 2.45 | 2.36 | |
| Rank | 1 | 4 | 5 | 2 | 7 | 6 | 3 | |
| Best\Worst | −5.05\−1.01 × 101 | −5.05\−1.01 × 101 | −5.05\−1.01 × 101 | −5.05\−1.01 × 101 | −5.04\−1.01 × 101 | −5.05\−1.01 × 101 | −5.05\−1.01 × 101 | |
| F22 | Mean | −8.44 | −8.62 | −7.06 | −8.95 | −5.49 | −7.04 | −9.06 |
| Std | 2.54 | 2.45 | 2.55 | 2.32 | 1.38 | 2.53 | 1.26 | |
| Rank | 4 | 3 | 5 | 2 | 7 | 6 | 1 | |
| Best\Worst | −5.08\−1.04 × 101 | −5.07\−1.04 × 101 | −5.08\−1.04 × 101 | −5.09\−1.04 × 101 | −5.08\−1.04 × 101 | −5.08\−1.04 × 101 | −5.09\−1.04× 101 | |
| F23 | Mean | −9.27 | −8.61 | −6.84 | −9.54 | −5.38 | −7.34 | −8.92 |
| Std | 2.23 | 2.53 | 2.52 | 1.95 | 1.33 | 2.63 | 2.4 | |
| Rank | 2 | 4 | 6 | 1 | 7 | 5 | 3 | |
| Best\Worst | −5.12\−1.05 × 101 | −5.123\−1.05 × 101 | −5.12\−1.05 × 101 | −5.12\−1.05 × 101 | −2.41\−1.05 × 101 | −5.13\−1.05 × 101 | −5.12\−1.05 × 101 |
| Benchmark | Gauss | Circle | Sinusoidal | Tent | Kent | Cubic | Logistic | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Corrected p-Value | +\=\− | Corrected p-Value | +\=\− | Corrected p-Value | +\=\− | Corrected p-Value | +\=\− | Corrected p-Value | +\=\− | Corrected p-Value | +\=\− | ||
| F1 | N/A | 2.12 × 101 | 28\0\22 | 1.043 × 10−7 | 50\0\0 | 5.40 × 10−7 | 48\0\2 | 1.04 × 10−7 | 50\0\0 | 1.08 × 10−7 | 49\0\1 | 6.77 × 10−7 | 48\0\2 |
| F2 | N/A | 3.05 × 101 | 26\0\24 | 1.043 × 10−7 | 50\0\0 | 1.20 × 10−7 | 49\0\1 | 1.08 × 10−7 | 49\0\1 | 1.20 × 10−7 | 48\0\2 | 1.03 × 10−7 | 50\0\0 |
| F3 | N/A | 3.23 × 101 | 25\0\25 | 3.20 × 101 | 24\0\26 | 2.27 × 101 | 29\0\21 | 2.01 × 100 | 32\0\18 | 6.39 × 100 | 31\0\19 | 8.66 × 100 | 28\0\22 |
| F4 | N/A | 1.64 × 101 | 23\0\27 | 1.02 × 10−5 | 47\0\3 | 2.74 × 10−5 | 46\0\4 | 3.24 × 10−7 | 48\0\2 | 3.71 × 10−5 | 46\0\4 | 3.61 × 10−7 | 48\0\2 |
| F5 | N/A | 2.02 × 101 | 30\0\20 | 2.79 × 101 | 27\0\23 | 2.79 × 101 | 27\0\23 | 2.85 × 101 | 26\0\24 | 6.12 × 100 | 31\0\19 | 2.59 × 101 | 28\0\22 |
| F6 | N/A | 2.66 × 101 | 23\0\27 | 4.67 × 10−2 | 36\0\14 | 8.66 × 100 | 33\0\17 | 1.74 × 100 | 32\0\18 | 2.25 × 10−2 | 37\0\13 | 6.18 × 100 | 32\0\18 |
| F7 | N/A | 3.34 × 101 | 26\0\24 | 3.13 × 101 | 28\0\22 | 3.22 × 101 | 23\0\27 | 2.72 × 101 | 23\0\27 | 3.26 × 101 | 23\0\27 | 3.12 × 101 | 24\0\26 |
| F8 | N/A | 1.64 × 101 | 20\0\30 | 3.26 × 101 | 24\1\25 | 2.03 × 101 | 21\0\29 | 3.27 × 101 | 24\0\26 | 3.25 × 101 | 28\1\21 | 2.71 × 101 | 20\1\29 |
| F9 | N/A | 2.49 × 101 | 0\50\0 | 2.10 × 101 | 0\50\0 | 1.70 × 101 | 0\50\0 | 1.30 × 101 | 0\50\0 | 9.00 × 100 | 0\50\0 | 5.00 × 100 | 0\50\0 |
| F10 | N/A | 2.40 × 101 | 0\50\0 | 2.00 × 101 | 0\50\0 | 1.60 × 101 | 0\50\0 | 1.20 × 101 | 0\50\0 | 8.00 × 100 | 0\50\0 | 4.00 × 100 | 0\50\0 |
| F11 | N/A | 2.30 × 101 | 0\50\0 | 1.90 × 101 | 0\50\0 | 1.50 × 101 | 0\50\0 | 1.10 × 101 | 0\50\0 | 7.00 × 100 | 0\50\0 | 3.00 × 100 | 0\50\0 |
| F12 | N/A | 3.02 × 101 | 31\0\19 | 3.32 × 10−1 | 33\0\17 | 5.13 × 10−1 | 36\0\14 | 9.84 × 10−1 | 31\0\19 | 1.26 × 10−2 | 37\0\13 | 6.20 × 10−2 | 36\0\14 |
| F13 | N/A | 2.84 × 101 | 22\0\28 | 2.91 × 101 | 26\0\24 | 8.84 × 100 | 29\0\21 | 3.15 × 101 | 23\0\27 | 2.71 × 101 | 27\0\23 | 3.29 × 101 | 22\0\28 |
| F14 | N/A | 1.26 × 101 | 2\39\9 | 4.30 × 10−1 | 0\41\9 | 4.30 × 10−1 | 0\41\9 | 1.32 × 101 | 3\39\8 | 1.23 × 100 | 1\40\9 | 4.88 × 100 | 1\40\9 |
| F15 | N/A | 2.49 × 101 | 20\0\30 | 5.13 × 10−1 | 14\0\36 | 1.31 × 101 | 18\0\32 | 2.79 × 101 | 21\0\29 | 1.99 × 101 | 29\0\21 | 2.27 × 101 | 27\0\23 |
| F16 | N/A | 2.20 × 101 | 0\50\0 | 1.80 × 101 | 0\50\0 | 1.40 × 101 | 0\50\0 | 1.00 × 101 | 0\50\0 | 6.00 × 100 | 0\50\0 | 2.00 × 100 | 0\50\0 |
| F17 | N/A | 3.23 × 101 | 10\28\12 | 2.68 × 101 | 11\28\11 | 2.20 × 101 | 12\27\11 | 9.10 × 100 | 20\21\9 | 9.18 × 100 | 22\17\11 | 3.25 × 101 | 8\31\11 |
| F18 | N/A | 3.22 × 101 | 0\48\2 | 3.28 × 101 | 5\42\3 | 3.06 × 101 | 2\45\3 | 3.32 × 101 | 5\42\3 | 3.20 × 101 | 0\48\2 | 2.76 × 101 | 2\45\3 |
| F19 | N/A | 3.28 × 101 | 25\0\25 | 1.32 × 101 | 30\0\20 | 3.23 × 101 | 27\0\23 | 3.26 × 101 | 25\0\25 | 2.92 × 101 | 25\0\25 | 3.24 × 101 | 22\0\28 |
| F20 | N/A | 3.34 × 101 | 25\0\25 | 3.00 × 101 | 23\0\27 | 2.12 × 101 | 20\0\30 | 3.00 × 101 | 23\0\27 | 3.24 × 101 | 24\0\26 | 3.27 × 101 | 24\0\26 |
| F21 | N/A | 2.03 × 101 | 21\0\29 | 2.15 × 100 | 32\0\18 | 2.87 × 10−1 | 37\0\13 | 2.85 × 101 | 28\0\22 | 6.425 × 10−5 | 40\0\10 | 8.45 × 10−2 | 38\0\12 |
| F22 | N/A | 2.20 × 101 | 29\0\21 | 1.89 × 101 | 30\0\20 | 4.39 × 10−2 | 37\0\13 | 2.79 × 101 | 28\0\22 | 3.068 × 10−7 | 47\0\3 | 1.22 × 10−2 | 39\0\11 |
| F23 | N/A | 2.75 × 101 | 23\0\27 | 3.05 × 101 | 28\0\22 | 2.31 × 10−1 | 31\0\19 | 3.26 × 101 | 24\0\26 | 9.225 × 10−6 | 40\0\10 | 1.24 × 100 | 30\0\20 |
| Chaotic Mapping | Average Rankings |
|---|---|
| Gauss | 3.50 |
| Circle | 3.74 |
| Sinusoidal | 3.89 |
| Tent | 3.85 |
| Kent | 4.85 |
| Cubic | 4.57 |
| Logistic | 3.61 |
| Benchmark | CSHHO | HHO | WOA | SCA | CSO | |
|---|---|---|---|---|---|---|
| F1 | Mean | 1.96 × 10−113 | 1.24 × 10−88 | 6.15 × 10−74 | 2.92 × 10−13 | 2.82 × 10−19 |
| Std | 1.38 × 10−112 | 8.75 × 10−88 | 2.79 × 10−73 | 1.33 × 10−12 | 7.98 × 10−19 | |
| Rank | 1 | 2 | 3 | 5 | 4 | |
| Best\Worst | 1.44 × 10−138\9.78 × 10−112 | 5.93 × 10−111\6.19 × 10−87 | 1.16 × 10−87\1.85 × 10−72 | 2.12 × 10−20\8.05 × 10−12 | 4.81 × 10−26\4.63 × 10−18 | |
| F2 | Mean | 1.66 × 10−59 | 1 × 10−49 | 8.97 × 10−51 | 1.04 × 10−10 | 1.05 × 10−18 |
| Std | 1.06 × 10−58 | 4.8 × 10−49 | 4.65 × 10−50 | 2.43 × 10−10 | 2.76 × 10−18 | |
| Rank | 1 | 3 | 2 | 5 | 4 | |
| Best\Worst | 7.47 × 10−58\8.54 × 10−70 | 1.86 × 10−74\1.28 × 10−73 | 4.54 × 104\1.25 × 104 | 2.19 × 10−4\1.31 × 10−3 | 6.13 × 103\3.20 × 103 | |
| F3 | Mean | 4.96 × 10−88 | 1.86 × 10−74 | 4.54 × 104 | 0.000219 | 6.13 × 103 |
| Std | 2.81 × 10−87 | 1.28 × 10−73 | 1.25 × 104 | 1.31 × 10−3 | 3.2 × 103 | |
| Rank | 1 | 2 | 5 | 3 | 4 | |
| Best\Worst | 5.85 × 10−108\1.96 × 10−86 | 4.26 × 10−99\9.05 × 10−73 | 1.81 × 104\7.29 × 104 | 1.75 × 10−12\9.26 × 10−3 | 3.04 × 102\1.65 × 104 | |
| F4 | Mean | 1.05 × 10−55 | 7.88 × 10−49 | 53.4 | 7.27 × 10−5 | 21.6 |
| Std | 6.13 × 10−55 | 4.62 × 10−48 | 2.82 × 101 | 1.38 × 10−4 | 1.28 × 101 | |
| Rank | 1 | 2 | 5 | 3 | 4 | |
| Best\Worst | 1.83 × 10−68\4.25 × 10−54 | 2.8 × 10−58\3.25 × 10−47 | 9.79 × 10−1\8.84 × 101 | 2.56 × 10−7\6.9 × 10−4 | 0.0748\4.11 × 101 | |
| F5 | Mean | 8.57 × 10−3 | 1.02 × 10−2 | 2.79 × 101 | 1.11 × 101 | 4.77 × 101 |
| Std | 2.23 × 10−2 | 1.43 × 10−2 | 4.98 × 10−1 | 2.78 × 101 | 9.63 × 101 | |
| Rank | 1 | 2 | 4 | 3 | 5 | |
| Best\Worst | 1.29 × 10−8\0.132 | 1.25 × 10−5\0.0723 | 26.9\28.8 | 6.48\204 | 27.1\583 | |
| F6 | Mean | 6.73 × 10−7 | 1.59 × 10−4 | 0.374 | 0.377 | 3.73 |
| Std | 1.85 × 10−6 | 2.76 × 10−4 | 2.44 × 10−1 | 1.42 × 10−1 | 4.16 × 10−1 | |
| Rank | 1 | 2 | 3 | 4 | 5 | |
| Best\Worst | 4.40 × 10−14\8.8 × 10−6 | 4.85 × 10−9\0.00181 | 0.0422\1.25 | 0.117\0.627 | 3.05\4.99 | |
| F7 | Mean | 5.98 × 10−5 | 2.02 × 10−4 | 3.67 × 10−3 | 1.84 × 10−3 | 9.11 × 10−2 |
| Std | 7.15 × 10−5 | 3.26 × 10−4 | 3.79 × 10−3 | 2.02 × 10−3 | 1.82 × 10−1 | |
| Rank | 1 | 2 | 4 | 3 | 5 | |
| Best\Worst | 2.03 × 10−7\4.65 × 10−4 | 3.13 × 10−7\2.10 × 10−3 | 9.46 × 10−6\1.75 × 10−2 | 6.53 × 10−5\1.02 × 10−2 | 2.66 × 10−3\1.07 | |
| F8 | Mean | −1.24 × 104 | −1.26 × 104 | −1.04 × 104 | −2.24 × 103 | −7.12 × 103 |
| Std | 2.71 × 102 | 9.50 × 101 | 1.67 × 103 | 1.52 × 102 | 6.62 × 102 | |
| Rank | 2 | 1 | 3 | 5 | 4 | |
| Best\Worst | −1.26 × 104\−1.15 × 104 | −1.26 × 104\−1.19 × 104 | −1.26 × 104\−7.76 × 103 | −2.61 × 103\−1.81 × 103 | −8.89 × 103\−5.91 × 103 | |
| F9 | Mean | 0 | 0 | 3.41 × 10−15 | 0.572 | 0.725 |
| Std | 0 | 0 | 1.78 × 10−14 | 2.03 | 3.34 | |
| Rank | 1 | 1 | 3 | 4 | 5 | |
| Best\Worst | 0\0 | 0\0 | 0\1.14 × 10−13 | 0\1.12 × 101 | 0\2.11 × 101 | |
| F10 | Mean | 8.88 × 10−16 | 8.88 × 10−16 | 4.3 × 10−15 | 5.46 × 10−8 | 9.39 × 10−11 |
| Std | 1.99 × 10−31 | 1.99 × 10−31 | 2.68 × 10−15 | 1.41 × 10−7 | 2.5 × 10−10 | |
| Rank | 1 | 1 | 3 | 5 | 4 | |
| Best\Worst | 8.88 × 10−16\8.88 × 10−16 | 8.88 × 10−16\8.88 × 10−16 | 8.88 × 10−16\7.99 × 10−15 | 6.45 × 10−11\7.1 × 10−7 | 2.82 × 10−13\1.66 × 10−9 | |
| F11 | Mean | 0 | 0 | 1.97 × 10−2 | 9.43 × 10−2 | 1.22 × 10−2 |
| Std | 0 | 0 | 7.55 × 10−2 | 1.56 × 10−1 | 4.49 × 10−2 | |
| Rank | 1 | 1 | 4 | 5 | 3 | |
| Best\Worst | 0\0 | 0\0 | 0\4.34 × 10−1 | 0\7.65 × 10−1 | 0\2.47 × 10−1 | |
| F12 | Mean | 5.26 × 10−7 | 9.97 × 10−6 | 2.69 × 10−2 | 7.80 × 10−2 | 229 |
| Std | 1.2 × 10−6 | 1.36 × 10−5 | 0.04 | 2.80 × 10−2 | 1.1 × 103 | |
| Rank | 1 | 2 | 3 | 4 | 5 | |
| Best\Worst | 1.68 × 10−11\5 × 10−6 | 3.07 × 10−8\7.06 × 10−5 | 4.58 × 10−3\2.64 × 10−1 | 3.41 × 10−2\1.63 × 10−1 | 1.57 × 10−1\7.34 × 103 | |
| F13 | Mean | 1.64 × 10−5 | 1.26 × 10−4 | 5.05 × 10−1 | 2.64 × 10−1 | 5.48 |
| Std | 2.86 × 10−5 | 2.49 × 10−4 | 2.57 × 10−1 | 8.66 × 10−2 | 2.07 × 101 | |
| Rank | 1 | 2 | 4 | 3 | 5 | |
| Best\Worst | 6.14 × 10−10\1.23 × 10−4 | 3.21 × 10−7\1.31 × 10−3 | 9.14 × 10−2\1.19 | 8.80 × 10−2\5.17 × 10−1 | 1.38\1.47 × 102 | |
| F14 | Mean | 1.39 | 1.37 | 3.06 | 1.63 | 1.34 |
| Std | 1.23 | 0.796 | 3.15 | 0.935 | 1.45 | |
| Rank | 3 | 2 | 5 | 4 | 1 | |
| Best\Worst | 9.98 × 10−1\5.93 | 9.98 × 10−1\5.93 | 0.9.98 × 10−1\10.8 | 0.9.98 × 10−1\2.98 | 0.9.98 × 10−1\10.8 | |
| F15 | Mean | 3.40 × 10−4 | 3.60 × 10−4 | 7.04 × 10−4 | 9.44 × 10−4 | 7.90 × 10−4 |
| Std | 3.39 × 10−5 | 1.45 × 10−4 | 4.57 × 10−4 | 3.72 × 10−4 | 2.78 × 10−4 | |
| Rank | 1 | 2 | 3 | 5 | 4 | |
| Best\Worst | 3.14 × 10−4\5.55 × 10−4 | 3.08 × 10−4\1.34 × 10−3 | 3.10 × 10−4\2.25 × 10−3 | 3.63 × 10−4\1.59 × 10−3 | 3.19 × 10−4\1.62 × 10−3 | |
| F16 | Mean | −1.03 | −1.03 | −1.03 | −1.03 | −1.03 |
| Std | 1.35 × 10−15 | 1.98 × 10−8 | 2.4 × 10−8 | 2.16 × 10−5 | 2.6 × 10−6 | |
| Rank | 1 | 2 | 3 | 5 | 4 | |
| Best\Worst | −1.03\−1.03 | −1.03\−1.03 | −1.03\−1.03 | −1.03\−1.03 | −1.03\−1.03 | |
| F17 | Mean | 3.98 × 10−1 | 0.3.98 × 10−1 | 0.398 × 10−1 | 0.399 × 10−1 | 0.398 × 10−1 |
| Std | 1.88 × 10−8 | 2.62 × 10−5 | 2.15 × 10−5 | 7.21 × 10−4 | 1.86 × 10−5 | |
| Rank | 1 | 1 | 1 | 1 | 1 | |
| Best\Worst | 3.98 × 10−1\3.98 × 10−1 | 3.98 × 10−1\3.98 × 10−1 | 3.98 × 10−1\3.98 × 10−1 | 3.98 × 10−1\0.401 | 3.98 × 10−1\3.98 × 10−1 | |
| F18 | Mean | 3.00 | 3.00 | 3.00 | 3.00 | 3.00 |
| Std | 1.15 × 10−7 | 1.01 × 10−6 | 1.62 × 10−4 | 5.88 × 10−5 | 2.09 × 10−4 | |
| Rank | 1 | 1 | 1 | 1 | 1 | |
| Best\Worst | 3.00\3.00 | 3.00\3.00 | 3.00\3.00 | 3.00\3.00 | 3.00\3.00 | |
| F19 | Mean | −3.86 | −3.86 | −3.85 | −3.85 | −3.86 |
| Std | 1.83 × 10−3 | 3.29 × 10−3 | 1.71 × 10−2 | 2.18 × 10−3 | 1.01 × 10−2 | |
| Rank | 1 | 1 | 1 | 1 | 1 | |
| Best\Worst | −3.86\−3.86 | −3.86\−3.85 | −3.86\−3.75 | −3.86\−3.85 | −3.86\−3.8 | |
| F20 | Mean | −3.13 | −3.07 | −3.26 | −3.01 | −3.24 |
| Std | 1.05 × 10−1 | 1.41 × 10−1 | 8.66 × 10−2 | 1.27 × 10−1 | 7.31 × 10−2 | |
| Rank | 3 | 4 | 1 | 5 | 2 | |
| Best\Worst | −3.31\−2.74 | −3.30\−2.73 | −3.32\−3.04 | −3.19\−2.59 | −3.32\−3.02 | |
| F21 | Mean | −9.65 | −5.35 | −8.24 | −3.02 | −7.64 |
| Std | 1.38 | 1.18 | 2.54 | 1.83 | 3.02 | |
| Rank | 1 | 4 | 2 | 5 | 3 | |
| Best\Worst | −10.2\−5.02 | −10.1\−5.04 | −10.2\−2.63 | −5.82\−0.497 | −10.2\−2.55 | |
| F22 | Mean | −9.45 | −5.46 | −7.83 | −3.59 | −8.19 |
| Std | 1.94 | 1.29 | \.97 | 1.79 | 2.98 | |
| Rank | 1 | 4 | 3 | 5 | 2 | |
| Best\Worst | −10.4\−5.03 | −10.1\−5.03 | −10.4\−2.76 | −8.23\−0.906 | −10.4\−2.74 | |
| F23 | Mean | −9.97 | −5.04 | −7.59 | −4.1 | −8.05 |
| Std | 1.46 | 1.02 | 3.29 | 1.59 | 3.28 | |
| Rank | 1 | 4 | 3 | 5 | 2 | |
| Best\Worst | −10.5\−5.09 | −9.96\−1.65 | −10.5\−1.67 | −9.42\−0.945 | −10.5\−2.37 |
| Benchmark | CSHHO | HHO | WOA | SCA | CSO | ||||
|---|---|---|---|---|---|---|---|---|---|
| Corrected p-Value | +\=\− | Corrected p-Value | +\=\− | Corrected p-Value | +\=\− | Corrected p-Value | +\=\− | ||
| F1 | N/A | 6.80 × 10−8 | 0\0\50 | 6.50 × 10−8 | 0\0\50 | 5.89 × 10−8 | 0\0\50 | 4.84 × 10−8 | 0\0\50 |
| F2 | N/A | 6.73 × 10−8 | 0\0\50 | 6.42 × 10−8 | 0\0\50 | 5.82 × 10−8 | 0\0\50 | 4.76 × 10−8 | 0\0\50 |
| F3 | N/A | 1.38 × 10−6 | 5\0\45 | 6.35 × 10−8 | 0\0\50 | 5.74 × 10−8 | 0\0\50 | 4.69 × 10−8 | 0\0\50 |
| F4 | N/A | 6.65 × 10−8 | 0\0\50 | 6.27 × 10−8 | 0\0\50 | 5.67 × 10−8 | 0\0\50 | 4.61 × 10−8 | 0\0\50 |
| F5 | N/A | 5.24 × 10−1 | 18\0\32 | 6.20 × 10−8 | 0\0\50 | 5.59 × 10−8 | 0\0\50 | 4.53 × 10−8 | 0\0\50 |
| F6 | N/A | 6.57 × 10−8 | 0\0\50 | 6.12 × 10−8 | 0\0\50 | 5.52 × 10−8 | 0\0\50 | 4.46 × 10−8 | 0\0\50 |
| F7 | N/A | 4.11 × 10−4 | 11\0\39 | 4.27 × 10−8 | 1\0\49 | 4.18 × 10−8 | 1\0\49 | 4.38 × 10−8 | 0\0\50 |
| F8 | N/A | 1.22 × 10−3 | 35\0\15 | 1.77 × 10−6 | 8\0\42 | 5.44 × 10−8 | 0\0\50 | 4.31 × 10−8 | 0\0\50 |
| F9 | N/A | 3.00 × 100 | 0\50\0 | 4.00 × 100 | 0\48\2 | 6.92 × 10−7 | 0\8\42 | 8.13 × 10−1 | 0\45\5 |
| F10 | N/A | 3.00 × 100 | 0\50\0 | 3.17 × 10−6 | 0\15\35 | 5.37 × 10−8 | 0\0\50 | 4.23 × 10−8 | 0\0\50 |
| F11 | N/A | 2.00 × 100 | 0\50\0 | 8.13 × 10−1 | 0\45\5 | 1.10 × 10−7 | 0\3\47 | 3.17 × 10−3 | 0\36\14 |
| F12 | N/A | 6.92 × 10−7 | 5\0\45 | 6.05 × 10−8 | 0\0\50 | 5.29 × 10−8 | 0\0\50 | 4.16 × 10−8 | 0\0\50 |
| F13 | N/A | 1.44 × 10−3 | 11\0\39 | 5.97 × 10−8 | 0\0\50 | 5.21 × 10−8 | 0\0\50 | 4.08 × 10−8 | 0\0\50 |
| F14 | N/A | 3.93 × 100 | 6\30\14 | 1.15 × 10−2 | 6\16\28 | 4.60 × 10−3 | 6\2\42 | 3.93 × 100 | 5\38\7 |
| F15 | N/A | 3.57 × 100 | 26\0\24 | 1.81 × 10−7 | 5\0\45 | 5.14 × 10−8 | 0\0\50 | 4.18 × 10−8 | 1\0\49 |
| F16 | N/A | 4.00 × 100 | 0\48\2 | 2.25 × 100 | 0\47\3 | 6.94 × 10−8 | 0\0\50 | 1.15 × 10−2 | 0\38\12 |
| F17 | N/A | 3.58 × 10−5 | 1\17\32 | 2.72 × 10−6 | 1\11\38 | 5.06 × 10−8 | 0\0\50 | 3.09 × 10−2 | 3\32\15 |
| F18 | N/A | 2.96 × 10−1 | 2\36\12 | 6.87 × 10−8 | 0\0\50 | 6.94 × 10−8 | 0\0\50 | 5.00 × 10−1 | 2\41\7 |
| F19 | N/A | 3.02 × 10−2 | 13\0\37 | 1.16 × 10−4 | 10\0\40 | 5.33 × 10−8 | 1\0\49 | 6.77 × 10−1 | 21\0\29 |
| F20 | N/A | 2.96 × 10−1 | 19\0\31 | 1.04 × 10−5 | 41\0\9 | 2.34 × 10−4 | 13\0\37 | 5.59 × 10−5 | 38\0\12 |
| F21 | N/A | 2.23 × 10−7 | 3\0\47 | 1.10 × 100 | 22\0\28 | 4.99 × 10−8 | 0\0\50 | 2.49 × 10−4 | 10\0\40 |
| F22 | N/A | 2.59 × 10−7 | 7\0\43 | 1.54 × 100 | 25\0\25 | 5.33 × 10−8 | 1\0\49 | 9.79 × 10−2 | 16\0\34 |
| F23 | N/A | 5.43 × 10−8 | 2\0\48 | 1.02 × 10−1 | 18\0\32 | 4.91 × 10−8 | 0\0\50 | 4.73 × 10−4 | 14\0\36 |
| Chaotic Mapping | Average Rankings |
|---|---|
| CSHHO | 2.57 |
| HHO | 3.67 |
| WOA | 4.74 |
| SCA | 5.96 |
| CSO | 5.00 |
| Benchmark | CSHHO | GCHHO | DEPSOASS | Improved GSA | DGOBLFOA | |
|---|---|---|---|---|---|---|
| F1 | Mean | 1.96 × 10−113 | 3.91 × 10−97 | 1.45 × 10−3 | 2.84 × 101 | 2.88 × 10−8 |
| Std | 1.38 × 10−112 | 2.55 × 10−96 | 1.45 × 10−3 | 2.84 × 101 | 2.88 × 10−8 | |
| Rank | 1 | 2 | 4 | 5 | 3 | |
| Best\Worst | 9.78 × 10−112\1.44 × 10−138 | 1.80 × 10−95\1.25 × 10−119 | 3.22 × 10−3\3.86 × 10−4 | 4.68 × 101\1.51 × 101 | 1.42 × 10−6\0.00 × 100 | |
| F2 | Mean | 1.66 × 10−59 | 1.62 × 10−50 | 1.88 × 10−1 | 2.81 × 101 | 2.54 × 10−1 |
| Std | 1.06 × 10−58 | 9.45 × 10−50 | 1.88 × 10−1 | 2.81 × 101 | 2.54 × 10−1 | |
| Rank | 1 | 2 | 3 | 5 | 4 | |
| Best\Worst | 7.47 × 10−58\8.54 × 10−70 | 6.63 × 10−49\3.57 × 10−60 | 2.84 × 10−1\1.19 × 10−1 | 3.46 × 101\1.44 × 101 | 1.03 × 100\8.72 × 10−4 | |
| F3 | Mean | 4.96 × 10−88 | 1.46 × 10−65 | 5.37 × 10−1 | 3.32 × 102 | 1.18 × 10−2 |
| Std | 2.81 × 10−87 | 1.01 × 10−64 | 5.37 × 10−1 | 3.32 × 102 | 1.18 × 10−2 | |
| Rank | 1 | 2 | 4 | 5 | 3 | |
| Best\Worst | 1.96 × 10−86\5.85 × 10−108 | 7.16 × 10−64\1.16 × 10−91 | 1.44 × 100\9.11 × 10−2 | 5.38 × 102\1.39 × 102 | 4.66 × 10−1\1.45 × 10−24 | |
| F4 | Mean | 1.05 × 10−55 | 1.82 × 10−48 | 3.49 × 10−2 | 2.31 × 100 | 1.74 × 10−4 |
| Std | 6.13 × 10−55 | 9.06 × 10−48 | 3.49 × 10−2 | 2.31 × 100 | 1.74 × 10−4 | |
| Rank | 1 | 2 | 4 | 5 | 3 | |
| Best\Worst | 4.25 × 10−54\1.83 × 10−68 | 5.94 × 10−47\2.66 × 10−58 | 5.40 × 10−2\1.75 × 10−2 | 2.83 × 100\1.44 × 100 | 8.57 × 10−3\1.29 × 10−20 | |
| F5 | Mean | 8.57 × 10−3 | 7.14 × 10−4 | 2.76 × 101 | 1.19 × 104 | 2.87 × 101 |
| Std | 2.23 × 10−2 | 7.02 × 10−4 | 2.76 × 101 | 1.19 × 104 | 2.87 × 101 | |
| Rank | 2 | 1 | 3 | 5 | 4 | |
| Best\Worst | 1.32 × 10−1\1.29 × 10−8 | 3.28 × 10−3\2.96 × 10−5 | 2.95 × 101\2.59 × 101 | 2.60 × 104\1.29 × 103 | 3.20 × 101\2.79 × 101 | |
| F6 | Mean | 6.73 × 10−7 | 1.20 × 10−6 | 1.30 × 10−3 | 2.83 × 101 | 5.35 × 100 |
| Std | 1.85 × 10−6 | 1.61 × 10−6 | 1.30 × 10−3 | 2.83 × 101 | 5.35 × 100 | |
| Rank | 1 | 2 | 3 | 5 | 4 | |
| Best\Worst | 8.80 × 10−6\4.40 × 10−14 | 1.02 × 10−5\1.47 × 10−7 | 3.27 × 10−3\3.91 × 10−4 | 4.15 × 101\1.43 × 101 | 6.03 × 100\4.32 × 100 | |
| F7 | Mean | 5.98 × 10−5 | 1.94 × 10−4 | 1.26 × 10−1 | 1.04 × 102 | 6.10 × 10−1 |
| Std | 7.15 × 10−5 | 1.92 × 10−4 | 1.26 × 10−1 | 1.04 × 102 | 6.10 × 10−1 | |
| Rank | 1 | 2 | 3 | 5 | 4 | |
| Best\Worst | 4.65 × 10−4\2.03 × 10−7 | 7.84 × 10−4\5.01 × 10−6 | 2.21 × 10−1\7.33 × 10−2 | 1.52 × 102\3.44 × 100 | 1.44 × 100\1.01 × 10−1 | |
| F8 | Mean | −1.24 × 104 | −1.25 × 104 | −2.78 × 103 | −2.70 × 103 | −3.70 × 102 |
| Std | 2.71 × 102 | 1.67 × 102 | −2.78 × 103 | −2.70 × 103 | 1.69 × 102 | |
| Rank | 2 | 1 | 3 | 4 | 5 | |
| Best\Worst | −1.15 × 104\−1.26 × 104 | −1.18 × 104\−1.26 × 104 | −1.79 × 103\−3.79 × 103 | −1.74 × 103\−3.42 × 103 | −1.79 × 103\−3.46 × 103 | |
| F9 | Mean | 0.00 | 0.00 | 3.72 × 101 | 2.54 × 102 | 8.95 × 100 |
| Std | 0.00 | 0.00 | 3.72 × 101 | 2.54 × 102 | 8.95 × 100 | |
| Rank | 1 | 1 | 4 | 5 | 3 | |
| Best\Worst | 0.00\0.00 | 0.00\0.00 | 6.02 × 101\2.00 × 101 | 2.91 × 102\1.96 × 102 | 2.81 × 101\2.18 × 10−3 | |
| F10 | Mean | 8.88 × 10−16 | 8.88 × 10−16 | 3.06 × 10−2 | 5.11 × 100 | 4.23 × 10−2 |
| Std | 1.99 × 10−31 | 1.99 × 10−31 | 3.06 × 10−2 | 5.11 × 100 | 4.23 × 10−2 | |
| Rank | 1 | 1 | 3 | 5 | 4 | |
| Best\Worst | 8.88 × 10−16\8.88 × 10−16 | 8.88 × 10−16\8.88 × 10−16 | 4.31 × 10−2\1.67 × 10−2 | 6.09 × 100\3.64 × 100 | 6.08 × 10−1\8.88 × 10−16 | |
| F11 | Mean | 0.00 × 100 | 0.00 × 100 | 5.90 × 10−4 | 7.85 × 10−1 | 1.09 × 10−9 |
| Std | 0.00 × 100 | 0.00 × 100 | 5.90 × 10−4 | 7.85 × 10−1 | 1.09 × 10−9 | |
| Rank | 1 | 1 | 4 | 5 | 3 | |
| Best\Worst | 0.00\0.00 | 0.00\0.00 | 1.97 × 10−2\2.27 × 10−5 | 9.59 × 10−1\4.58 × 10−1 | 5.46 × 10−8\0.00 × 100 | |
| F12 | Mean | 5.26 × 10−7 | 8.05 × 10−8 | 9.89 × 10−6 | 1.29 × 100 | 6.98 × 10−1 |
| Std | 1.20 × 10−6 | 9.54 × 10−8 | 9.89 × 10−6 | 1.29 × 100 | 6.98 × 10−1 | |
| Rank | 2 | 1 | 3 | 5 | 4 | |
| Best\Worst | 5.00 × 10−6\1.68 × 10−11 | 5.02 × 10−7\5.77 × 10−9 | 2.58 × 10−5\4.76 × 10−6 | 2.32 × 100\6.10 × 10−1 | 1.01 × 100\3.67 × 10−1 | |
| F13 | Mean | 1.64 × 10−5 | 1.26 × 10−6 | 1.69 × 10−3 | 6.34 × 100 | 2.44 × 100 |
| Std | 2.86 × 10−5 | 1.48 × 10−6 | 1.69 × 10−3 | 6.34 × 100 | 2.44 × 100 | |
| Rank | 2 | 1 | 3 | 5 | 4 | |
| Best\Worst | 1.23 × 10−4\6.14 × 10−10 | 6.48 × 10−6\4.00 × 10−8 | 1.12 × 10−2\6.80 × 10−5 | 9.67 × 100\2.90 × 100 | 2.88 × 100\1.60 × 100 | |
| F14 | Mean | 1.39 × 100 | 9.98 × 10−1 | 1.52 × 100 | 7.07 × 100 | 4.34 × 100 |
| Std | 1.23 × 100 | 5.61 × 10−16 | 1.52 × 100 | 7.07 × 100 | 4.34 × 100 | |
| Rank | 2 | 1 | 3 | 5 | 4 | |
| Best\Worst | 5.93 × 100\9.98 × 10−1 | 9.98 × 10−1\9.98 × 10−1 | 3.02 × 100\9.98 × 10−1 | 1.55 × 101\1.01 × 100 | 1.18 × 101\9.98 × 10−1 | |
| F15 | Mean | 3.40 × 10−4 | 3.17 × 10−4 | 9.62 × 10−4 | 1.39 × 10−3 | 2.61 × 10−2 |
| Std | 3.39 × 10−5 | 4.50 × 10−5 | 9.62 × 10−4 | 1.39 × 10−3 | 2.61 × 10−2 | |
| Rank | 2 | 1 | 3 | 4 | 5 | |
| Best\Worst | 5.55 × 10−4\3.14 × 10−4 | 5.41 × 10−4\3.07 × 10−4 | 4.55 × 10−3\5.50 × 10−4 | 3.18 × 10−3\1.03 × 10−3 | 6.88 × 10−2\1.81 × 10−3 | |
| F16 | Mean | −1.03 × 100 | −1.03 × 100 | −1.03 × 100 | −1.02 × 100 | −1.03 × 100 |
| Std | 1.35 × 10−15 | 1.35 × 10−15 | −1.03 × 100 | −1.02 × 100 | −1.03 × 100 | |
| Rank | 1 | 1 | 1 | 5 | 1 | |
| Best\Worst | −1.03 × 100\−1.03 × 100 | −1.03 × 100\−1.03 × 100 | −1.03 × 100\−1.03 × 100 | −9.22 × 10−1\−1.03 × 100 | −1.03 × 100\−1.03 × 100 | |
| F17 | Mean | 3.98 × 10−1 | 3.98 × 10−1 | 3.98 × 10−1 | 4.08 × 10−1 | 5.30 × 10−1 |
| Std | 1.88 × 10−8 | 1.12 × 10−16 | 3.98 × 10−1 | 4.08 × 10−1 | 5.30 × 10−1 | |
| Rank | 1 | 1 | 1 | 4 | 5 | |
| Best\Worst | 3.98 × 10−13\98 × 10−1 | 3.98 × 10−1\3.98 × 10−1 | 3.98 × 10−1\3.98 × 10−1 | 4.35 × 10−1\3.98 × 10−1 | 1.70 × 100\4.00 × 10−1 | |
| F18 | Mean | 3.00 × 100 | 3.00 × 100 | 3.00 × 100 | 4.91 × 100 | 3.50 × 100 |
| Std | 1.15 × 10−7 | 0.00 × 100 | 3.00 × 100 | 4.91 × 100 | 3.50 × 100 | |
| Rank | 1 | 1 | 1 | 5 | 4 | |
| Best\Worst | 3.00 × 100\3.00 × 100 | 3.00 × 100\3.00 × 100 | 3.00 × 100\3.00 × 100 | 1.25 × 101\3.01 × 100 | 6.51 × 100\3.01 × 100 | |
| F19 | Mean | −3.86 × 100 | −3.86 × 100 | −3.86 × 100 | −3.45 × 100 | −3.50 × 100 |
| Std | 1.83 × 10−3 | 2.24 × 10−15 | −3.86 × 100 | −3.45 × 100 | −3.50 × 100 | |
| Rank | 1 | 1 | 1 | 5 | 4 | |
| Best\Worst | −3.86 × 100\−3.86 × 100 | −3.86 × 100\−3.86 × 100 | −3.86 × 100\−3.86 × 100 | −2.90 × 100\−3.86 × 100 | −2.69 × 100\−3.85 × 100 | |
| F20 | Mean | −3.13 × 100 | −3.25 × 100 | −3.31 × 100 | −1.69 × 100 | −2.09 × 100 |
| Std | 1.05 × 10−1 | 5.88 × 10−2 | −3.31 × 100 | −1.69 × 100 | −2.09 × 100 | |
| Rank | 3 | 2 | 1 | 5 | 4 | |
| Best\Worst | −2.74 × 100\−3.31 × 100 | −3.20 × 100\−3.32 × 100 | −3.18 × 100\−3.32 × 100 | −6.72 × 10−1\−2.55 × 100 | −1.11 × 100\−3.10 × 100 | |
| F21 | Mean | −9.65 × 100 | −6.07 × 100 | −6.85 × 100 | −4.05 × 100 | −4.49 × 100 |
| Std | 1.38 × 100 | 2.06 × 100 | −6.85 × 100 | −4.05 × 100 | −4.49 × 100 | |
| Rank | 1 | 3 | 2 | 5 | 4 | |
| Best\Worst | −5.02 × 100\−1.02 × 101 | −5.06 × 100\−1.02 × 101 | −2.68 × 100\−1.02 × 101 | −1.99 × 100\−7.93 × 100 | −2.67 × 100\−7.66 × 100 | |
| F22 | Mean | −9.45 × 100 | −5.94 × 100 | −1.01 × 101 | −3.55 × 100 | −4.08 × 100 |
| Std | 1.94 × 100 | 1.97 × 100 | −1.01 × 101 | −3.55 × 100 | −4.08 × 100 | |
| Rank | 2 | 3 | 1 | 5 | 4 | |
| Best\Worst | −5.03 × 100\−1.04 × 101 | −5.09 × 100\−1.04 × 101 | −6.48 × 100\−1.04 × 101 | −1.93 × 100\−7.27 × 100 | −1.67 × 100\−8.98 × 100 | |
| F23 | Mean | −9.97 × 100 | −5.67 × 100 | −1.03 × 101 | −4.34 × 100 | −4.48 × 100 |
| Std | 1.46 × 100 | 1.64 × 100 | −1.03 × 101 | −4.34 × 100 | −4.48 × 100 | |
| Rank | 2 | 3 | 1 | 5 | 4 | |
| Best\Worst | −5.09 × 100\−1.05 × 101 | −5.13 × 100\−1.05 × 101 | −5.42 × 100\−1.05 × 101 | −2.61 × 100\−7.03 × 100 | −2.43 × 100\−9.12 × 100 |
| Benchmark | GCHHO | DEPSOASS | GSA | FOA | |||||
|---|---|---|---|---|---|---|---|---|---|
| Corrected p-Value | +\=\− | Corrected p-Value | +\=\− | Corrected p-Value | +\=\− | Corrected p-Value | +\=\− | ||
| F1 | N/A | 3.07 × 10−8 | 1\0\49 | 6.57 × 10−8 | 0\0\50 | 5.06 × 10−8 | 0\0\50 | 2.99 × 10−8 | 2\0\48 |
| F2 | N/A | 6.80 × 10−8 | 0\0\50 | 6.50 × 10−8 | 0\0\50 | 4.99 × 10−8 | 0\0\50 | 4.01 × 10−8 | 0\0\50 |
| F3 | N/A | 6.73 × 10−8 | 0\0\50 | 6.42 × 10−8 | 0\0\50 | 4.91 × 10−8 | 0\0\50 | 3.93 × 10−8 | 0\0\50 |
| F4 | N/A | 6.65 × 10−8 | 0\0\50 | 6.35 × 10−8 | 0\0\50 | 4.84 × 10−8 | 0\0\50 | 3.85 × 10−8 | 0\0\50 |
| F5 | N/A | 3.46 × 10−1 | 25\0\25 | 6.27 × 10−8 | 0\0\50 | 4.76 × 10−8 | 0\0\50 | 3.78 × 10−8 | 0\0\50 |
| F6 | N/A | 4.84 × 10−3 | 9\0\41 | 6.20 × 10−8 | 0\0\50 | 4.69 × 10−8 | 0\0\50 | 3.70 × 10−8 | 0\0\50 |
| F7 | N/A | 4.72 × 10−4 | 12\0\38 | 6.12 × 10−8 | 0\0\50 | 4.61 × 10−8 | 0\0\50 | 3.63 × 10−8 | 0\0\50 |
| F8 | N/A | 3.70 × 10−1 | 35\0\15 | 6.05 × 10−8 | 0\0\50 | 4.53 × 10−8 | 0\0\50 | 3.55 × 10−8 | 50\0\0 |
| F9 | N/A | 4.00 × 100 | 0\50\0 | 5.97 × 10−8 | 0\0\50 | 4.46 × 10−8 | 0\0\50 | 3.48 × 10−8 | 0\0\50 |
| F10 | N/A | 4.00 × 100 | 0\50\0 | 5.89 × 10−8 | 0\0\50 | 4.38 × 10−8 | 0\0\50 | 4.71 × 10−8 | 0\2\48 |
| F11 | N/A | 3.00 × 100 | 0\50\0 | 5.82 × 10−8 | 0\0\50 | 4.31 × 10−8 | 0\0\50 | 8.59 × 10−2 | 0\42\8 |
| F12 | N/A | 8.60 × 10−1 | 26\0\24 | 5.74 × 10−8 | 0\0\50 | 4.23 × 10−8 | 0\0\50 | 3.40 × 10−8 | 0\0\50 |
| F13 | N/A | 7.25 × 10−4 | 36\0\14 | 5.67 × 10−8 | 0\0\50 | 4.16 × 10−8 | 0\0\50 | 3.33 × 10−8 | 0\0\50 |
| F14 | N/A | 3.13 × 10−1 | 6\44\0 | 1.02 × 10−7 | 2\0\48 | 1.20 × 10−3 | 5\1\44 | 1.39 × 10−7 | 1\0\49 |
| F15 | N/A | 3.99 × 10−6 | 48\0\2 | 5.59 × 10−8 | 0\0\50 | 4.08 × 10−8 | 0\0\50 | 3.25 × 10−8 | 0\0\50 |
| F16 | N/A | 2.00 × 100 | 0\50\0 | 5.52 × 10−8 | 0\0\50 | 6.75 × 10−8 | 0\0\50 | 3.17 × 10−4 | 0\26\24 |
| F17 | N/A | 8.75 × 10−1 | 4\46\0 | 5.44 × 10−8 | 0\0\50 | 4.71 × 10−8 | 0\2\48 | 3.17 × 10−8 | 0\0\50 |
| F18 | N/A | 8.75 × 10−1 | 4\46\0 | 5.37 × 10−8 | 0\0\50 | 6.88 × 10−8 | 0\0\50 | 3.10 × 10−8 | 0\0\50 |
| F19 | N/A | 6.88 × 10−8 | 50\0\0 | 5.29 × 10−8 | 0\0\50 | 3.04 × 10−7 | 43\0\7 | 3.02 × 10−8 | 0\0\50 |
| F20 | N/A | 1.10 × 10−6 | 45\0\5 | 5.21 × 10−8 | 0\0\50 | 2.99 × 10−8 | 49\0\1 | 3.08 × 10−8 | 1\0\49 |
| F21 | N/A | 1.83 × 10−5 | 13\0\37 | 3.08 × 10−8 | 2\0\48 | 1.89 × 10−3 | 19\0\31 | 3.26 × 10−8 | 2\0\48 |
| F22 | N/A | 4.72 × 10−4 | 13\0\37 | 5.14 × 10−8 | 0\0\50 | 1.55 × 10−3 | 44\0\6 | 2.95 × 10−8 | 0\0\50 |
| F23 | N/A | 2.67 × 10−7 | 9\0\41 | 3.07 × 10−8 | 1\0\49 | 2.46 × 10−5 | 47\0\3 | 2.97 × 10−8 | 1\0\49 |
| Chaotic Mapping | Average Rankings |
|---|---|
| CSHHO | 1.70 |
| GCHHO | 1.83 |
| DEPSOASS | 2.76 |
| GSA | 4.87 |
| FOA | 3.85 |
| Benchmark | Metric | 50 | 100 | ||
|---|---|---|---|---|---|
| CSHHO | HHO | CSHHO | HHO | ||
| F1 | Mean\Std | 3.49 × 107\1.19 × 108 | 3.30 × 108\9.91 × 107 | 1.08 × 1010\2.06 × 109 | 1.10 × 1010\2.09 × 109 |
| F2 | Mean\Std | 9.88 × 104\1.66 × 104 | 1.03 × 105\1.38 × 104 | 2.78 × 105\1.73 × 104 | 2.90 × 105\1.42 × 104 |
| F3 | Mean\Std | 8.65 × 102\1.16 × 102 | 9.00 × 102\1.52 × 102 | 2.89 × 102\4.96 × 102 | 3.01 × 103\5.84 × 102 |
| F4 | Mean\Std | 8.95 × 102\2.82 × 101 | 8.96 × 102\3.47 × 101 | 1.56 × 103\4.55 × 101 | 1.56 × 103\5.35 × 101 |
| F5 | Mean\Std | 6.71 × 102\4.36 × 100 | 6.74 × 102\4.16 × 100 | 6.85 × 102\2.82 × 100 | 6.85 × 102\3.25 × 100 |
| F6 | Mean\Std | 1.84 × 103\9.07 × 101 | 1.84 × 103\7.88 × 101 | 3.71 × 103\1.41 × 102 | 3.69 × 103\1.46 × 102 |
| F7 | Mean\Std | 1.20 × 103\3.34 × 101 | 1.20 × 103\3.11 × 101 | 2.01 × 103\7.14 × 101 | 2.01 × 103\6.02 × 101 |
| F8 | Mean\Std | 2.52 × 104\2.86 × 103 | 2.54 × 104\3.63 × 103 | 5.24 × 104\5.53 × 103 | 5.72 × 104\5.52 × 103 |
| F9 | Mean\Std | 9.41 × 103\9.83 × 102 | 9.49 × 103\8.76 × 102 | 2.21 × 104\1.46 × 103 | 2.28 × 104\2.12 × 103 |
| F10 | Mean\Std | 1.65 × 103\1.47 × 102 | 1.66 × 103\1.21 × 102 | 5.03 × 104\1.59 × 104 | 5.06 × 104\1.06 × 104 |
| F11 | Mean\Std | 2.17 × 108\1.28 × 108 | 1.88 × 108\1.05 × 108 | 1.58 × 109\5.29 × 108 | 1.68 × 109\5.46 × 108 |
| F12 | Mean\Std | 3.82 × 106\1.44 × 106 | 5.20 × 106\4.28 × 106 | 1.75 × 107\7.23 × 106 | 1.62 × 107\6.97 × 106 |
| F13 | Mean\Std | 1.54 × 106\1.01 × 106 | 2.07 × 106\2.53 × 106 | 4.81 × 106\1.82 × 106 | 5.41 × 106\1.64 × 106 |
| F14 | Mean\Std | 6.00 × 105\2.65 × 105 | 6.35 × 105\2.81 × 105 | 3.36 × 106\9.38 × 105 | 4.35 × 106\4.49 × 106 |
| F15 | Mean\Std | 4.38 × 103\6.23 × 102 | 4.52 × 103\6.15 × 102 | 8.55 × 103\1.00 × 103 | 8.56 × 103\8.52 × 102 |
| F16 | Mean\Std | 3.78 × 103\3.76 × 102 | 3.90 × 103\4.41 × 102 | 6.73 × 103\7.03 × 102 | 6.84 × 103\7.62 × 102 |
| F17 | Mean\Std | 5.39 × 105\4.79 × 106 | 4.63 × 106\4.40 × 106 | 5.75 × 106\2.56 × 106 | 6.62 × 106\3.52 × 106 |
| F18 | Mean\Std | 5.82 × 105\6.11 × 105 | 1.12 × 106\7.19 × 105 | 1.20 × 107\4.90 × 106 | 1.55 × 107\6.97 × 106 |
| F19 | Mean\Std | 3.63 × 102\3.07 × 102 | 3.39 × 103\3.20 × 102 | 6.05 × 103\5.46 × 102 | 6.06 × 103\4.89 × 102 |
| F20 | Mean\Std | 2.46 × 103\8.32 × 101 | 2.85 × 103\6.82 × 101 | 4.17 × 103\1.82 × 102 | 4.13 × 103\1.86 × 102 |
| F21 | Mean\Std | 1.03 × 104\1.09 × 103 | 1.14 × 104\1.04 × 103 | 2.56 × 104\1.24 × 103 | 2.56 × 104\1.48 × 103 |
| F22 | Mean\Std | 3.74 × 103\2.31 × 102 | 3.74 × 103\1.77 × 102 | 5.35 × 103\3.78 × 102 | 5.35 × 103\2.91 × 102 |
| F23 | Mean\Std | 4.20 × 103\2.15 × 102 | 4.18 × 103\1.76 × 102 | 7.25 × 103\5.84 × 102 | 7.25 × 103\4.62 × 102 |
| F24 | Mean\Std | 3.28 × 103\6.13 × 101 | 3.30 × 103\7.30 × 101 | 4.73 × 103\2.76 × 102 | 4.73 × 103\2.60 × 102 |
| F25 | Mean\Std | 1.08 × 104\1.79 × 103 | 1.10 × 104\1.63 × 103 | 2.85 × 104\2.46 × 103 | 2.86 × 104\4.26 × 103 |
| F26 | Mean\Std | 4.44 × 103\5.43 × 102 | 4.44 × 103\3.71 × 102 | 5.70 × 103\1.25 × 103 | 5.43 × 103\6.12 × 102 |
| F27 | Mean\Std | 3.82 × 103\1.43 × 102 | 3.89 × 103\1.77 × 102 | 5.79 × 103\4.35 × 102 | 5.86 × 103\4.88 × 102 |
| F28 | Mean\Std | 6.09 × 103\7.55 × 102 | 6.38 × 103\7.33 × 102 | 1.10 × 104\1.01 × 103 | 1.11 × 104\9.60 × 102 |
| F29 | Mean\Std | 5.23 × 107\1.82 × 107 | 5.25 × 107\1.55 × 107 | 1.52 × 108\6.75 × 107 | 1.54 × 108\7.05 × 107 |
| Input Sample | Output Sample | ||
|---|---|---|---|
| Excitation Current/A | Exciting Voltage/V | Reactive Power/Mvar | System Voltage/kV |
| 25.488 | 29.267 | 305.0 | 228.4 |
| 23.364 | 26.103 | 261.5 | 228.2 |
| 21.594 | 24.521 | 232.5 | 228.5 |
| 20.154 | 22.939 | 212.5 | 228.5 |
| 19.6824 | 22.148 | 197.5 | 228.6 |
| 18.8328 | 21.159 | 186.4 | 228.6 |
| 18.408 | 20.408 | 177.4 | 228.7 |
| 17.9124 | 19.9728 | 170.2 | 228.75 |
| 17.7 | 19.775 | 163.8 | 228.8 |
| 17.346 | 19.3795 | 158.5 | 228.8 |
| 16.992 | 18.984 | 154.2 | 228.8 |
| 16.7088 | 18.7863 | 150.5 | 228.8 |
| 16.638 | 18.5727 | 147.0 | 228.78 |
| 16.461 | 18.3987 | 144.2 | 228.85 |
| 16.1424 | 17.9715 | 137.4 | 228.84 |
| 15.6822 | 17.402 | 131.1 | 228.9 |
| 15.222 | 17.0065 | 125.0 | 228.9 |
| 14.868 | 16.611 | 118.35 | 229 |
| 14.2308 | 15.9782 | 108.75 | 229 |
| 12.9564 | 14.5346 | 88.5 | 229.1 |
| 12.39 | 13.8425 | 78.3 | 229.1 |
| 11.682 | 12.953 | 67.8 | 229.2 |
| 10.974 | 12.458 | 57.5 | 229.3 |
| 10.3368 | 11.4695 | 47.5 | 229.3 |
| 9.912 | 11.074 | 37.0 | 229.4 |
| 8.9916 | 10.283 | 27.5 | 229.4 |
| 8.4252 | 9.1756 | 17.2 | 229.48 |
| 7.8588 | 8.8592 | 7.5 | 229.5 |
| 7.2924 | 8.3055 | 1.75 | 229.57 |
| 6.9738 | 7.91 | −2.5 | 229.6 |
| 6.372 | 6.9213 | −11.7 | 229.6 |
| 5.8056 | 6.7235 | −21.0 | 229.62 |
| 5.664 | 6.4467 | −30.5 | 229.7 |
| 4.956 | 5.1415 | −39.6 | 229.71 |
| 4.248 | 4.5483 | −48.5 | 229.8 |
| 3.54 | 4.351 | −57.5 | 229.875 |
| 2.832 | 3.164 | −57.5 | 229.875 |
| 2.124 | 2.4521 | −66.5 | 229.9 |
| Prediction Value | Sample Value | Absolute Error | Relative Error | ||
|---|---|---|---|---|---|
| 9 | Reactive Power/MVar | 163.0515 | 163.8 | −0.7485 | −0.4570 |
| System Voltage/kV | 228.7877 | 228.8 | −0.0123 | −0.0054 | |
| 14 | Reactive Power/MVar | 144.5989 | 144.2 | 0.3989 | 0.2766 |
| System Voltage/kV | 228.8882 | 228.85 | 0.0382 | 0.0167 | |
| 26 | Reactive Power/MVar | 28.1322 | 27.6 | 0.5322 | 1.9282 |
| System Voltage/kV | 229.4014 | 229.45 | −0.0486 | −0.0212 | |
| 35 | Reactive Power/MVar | −40.5890 | −39.6 | −0.989 | 2.4975 |
| System Voltage/kV | 229.7915 | 229.75 | 0.0415 | 0.0181 |
| Prediction Value | Sample Value | Absolute Error | Relative Error | ||
|---|---|---|---|---|---|
| LSSVM | 9 | 162.9631 | 163.8 | −0.8369 | −0.5128 |
| 35 | −40.8531 | −39.6 | −1.2531 | 3.1649 | |
| CSHHO−LSSVM | 9 | 163.0515 | 163.8 | −0.7485 | −0.4570 |
| 35 | −40.5890 | −39.6 | −0.989 | 2.4975 |
| Prediction Value | Sample Value | Absolute Error | Relative Error | ||
|---|---|---|---|---|---|
| LSSVM | 9 | 228.6717 | 228.8 | −0.1283 | −0.0561 |
| 35 | 229.8859 | 229.75 | 0.1359 | 0.0591 | |
| CSHHO−LSSVM | 9 | 228.7877 | 228.8 | −0.0123 | −0.0054 |
| 35 | 229.7915 | 229.75 | 0.0415 | 0.0181 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiao, S.; Wang, C.; Gao, R.; Li, Y.; Zhang, Q. Harris Hawks Optimization with Multi-Strategy Search and Application. Symmetry 2021, 13, 2364. https://doi.org/10.3390/sym13122364
Jiao S, Wang C, Gao R, Li Y, Zhang Q. Harris Hawks Optimization with Multi-Strategy Search and Application. Symmetry. 2021; 13(12):2364. https://doi.org/10.3390/sym13122364
Chicago/Turabian StyleJiao, Shangbin, Chen Wang, Rui Gao, Yuxing Li, and Qing Zhang. 2021. "Harris Hawks Optimization with Multi-Strategy Search and Application" Symmetry 13, no. 12: 2364. https://doi.org/10.3390/sym13122364
APA StyleJiao, S., Wang, C., Gao, R., Li, Y., & Zhang, Q. (2021). Harris Hawks Optimization with Multi-Strategy Search and Application. Symmetry, 13(12), 2364. https://doi.org/10.3390/sym13122364







