High Harmonic Generation in Monolayer and Bilayer of Transition Metal Dichalcogenide
Abstract
:1. Introduction
2. Current and Time-Dependent Density Matrix
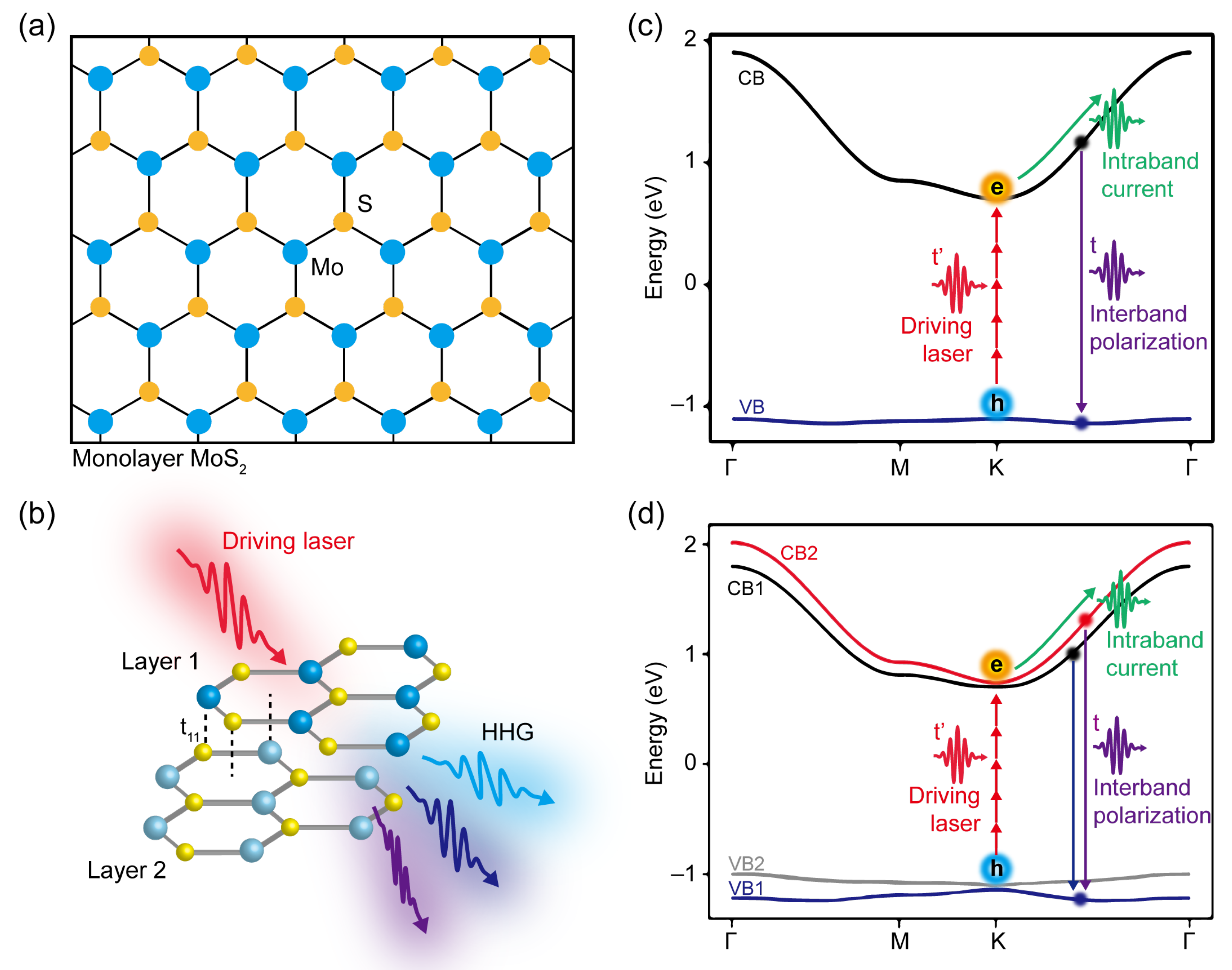
3. Hamiltonian Model for Monolayer and Bilayer MoS
4. Harmonics from Monolayers and Bilayers
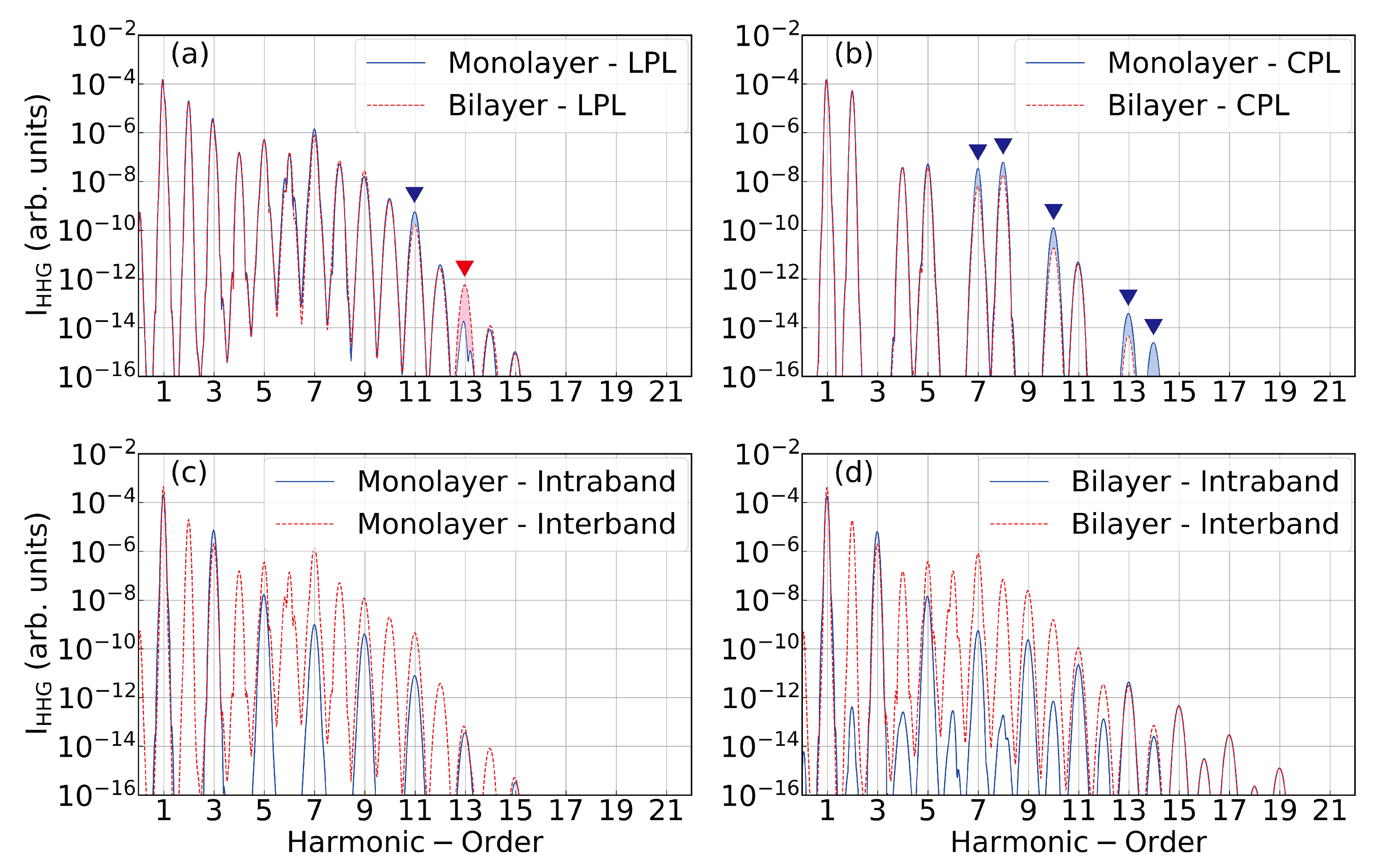
4.1. Response to Linear Polarized Lasers
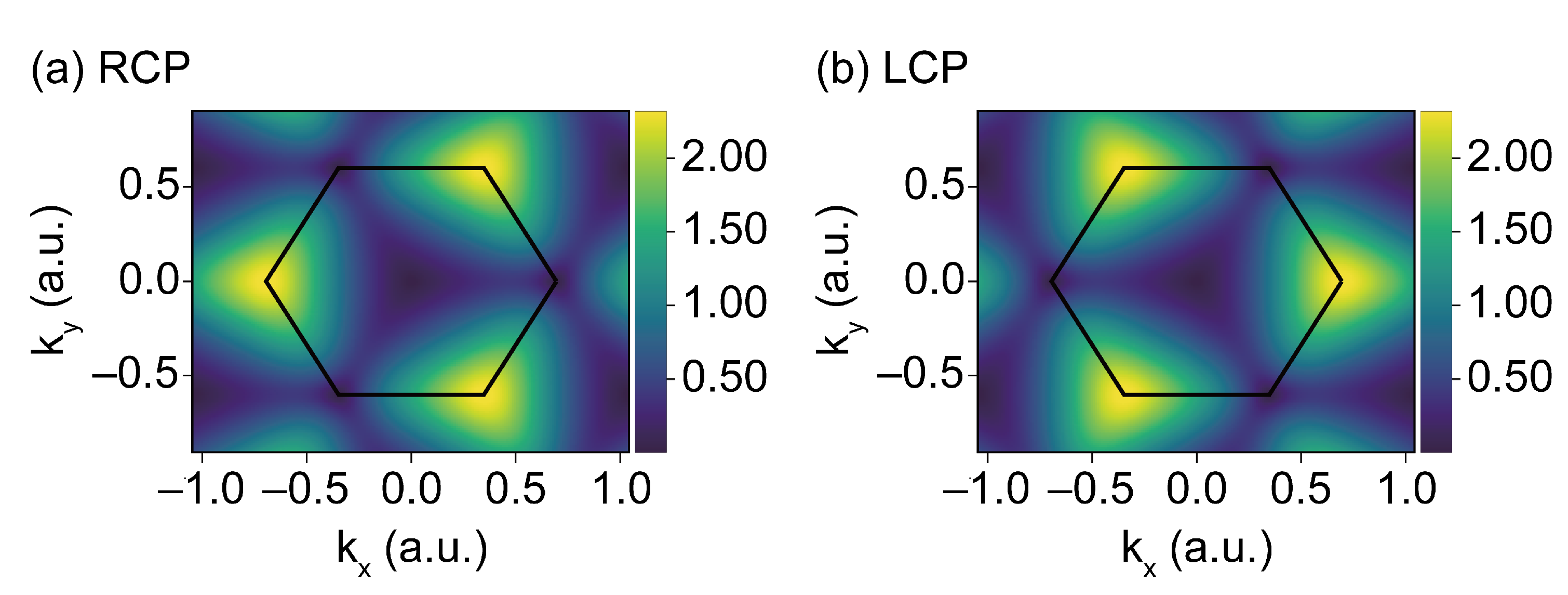
4.2. Response to Circularly Polarized Lasers
- A surprising enhancement by almost one order of magnitude in the harmonics emitted around the plateau region is observed between the monolayer and bilayer (see blue triangles),
- All the harmonics follow the three-fold symmetry of the system with the co-rotating () and contra-rotating () harmonic orders in the plateau region, as has already been experimentally observed in Reference [37] in solids with a three-fold rotational symmetry. Our results fully capture these selection rules. As such, it is clear that circularly-polarized drivers have significant potential in bringing out the signatures between the monolayers and bilayers configurations, their differences and, in particular, the valley index and pseudospin information as a function of the layers [10].
4.3. Interlayer Strength in High-Order Harmonics
4.4. Structural Angular Rotation of the High-Order Harmonics
4.5. Ellipticity Dependence of Low- and High-Order Harmonics
5. Conclusions and Outlook
- Capable of observing differences of the nonlinear optical emission related to the band gap between monolayers and bilayers of TMDCs.
- Capable of describing a unique difference between the angular rotations and ellipticity dependence of the emitted harmonics as a function of the number of layers concerning the ellipticity of the laser, via the selection rule of the dipole matrix element and Berry Curvature to a linear and circularly polarized laser beam.
- Susceptible to breaking the inversion symmetries (IS, respectively) and thus sensitives to the Berry Curvature and its pseudospin character.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
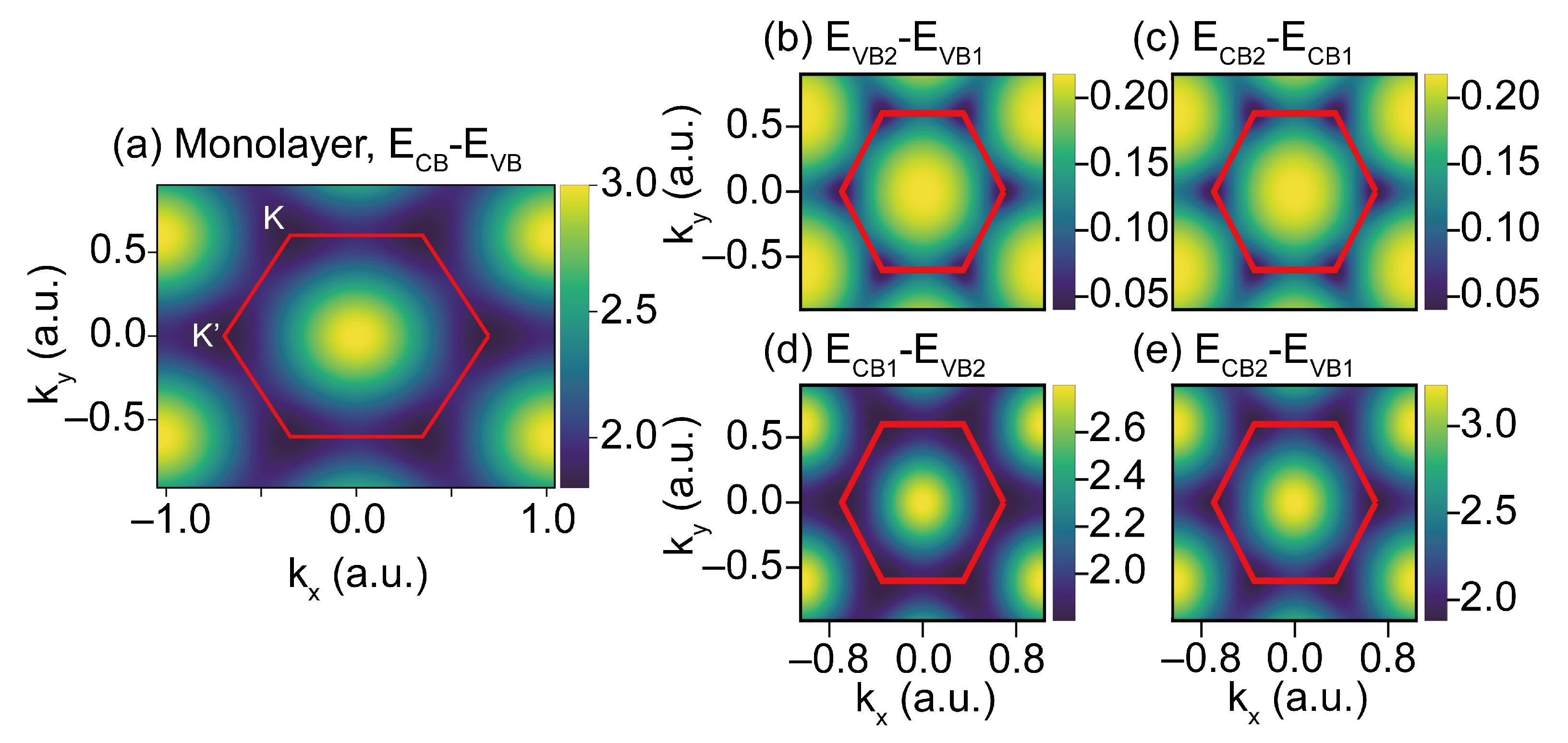
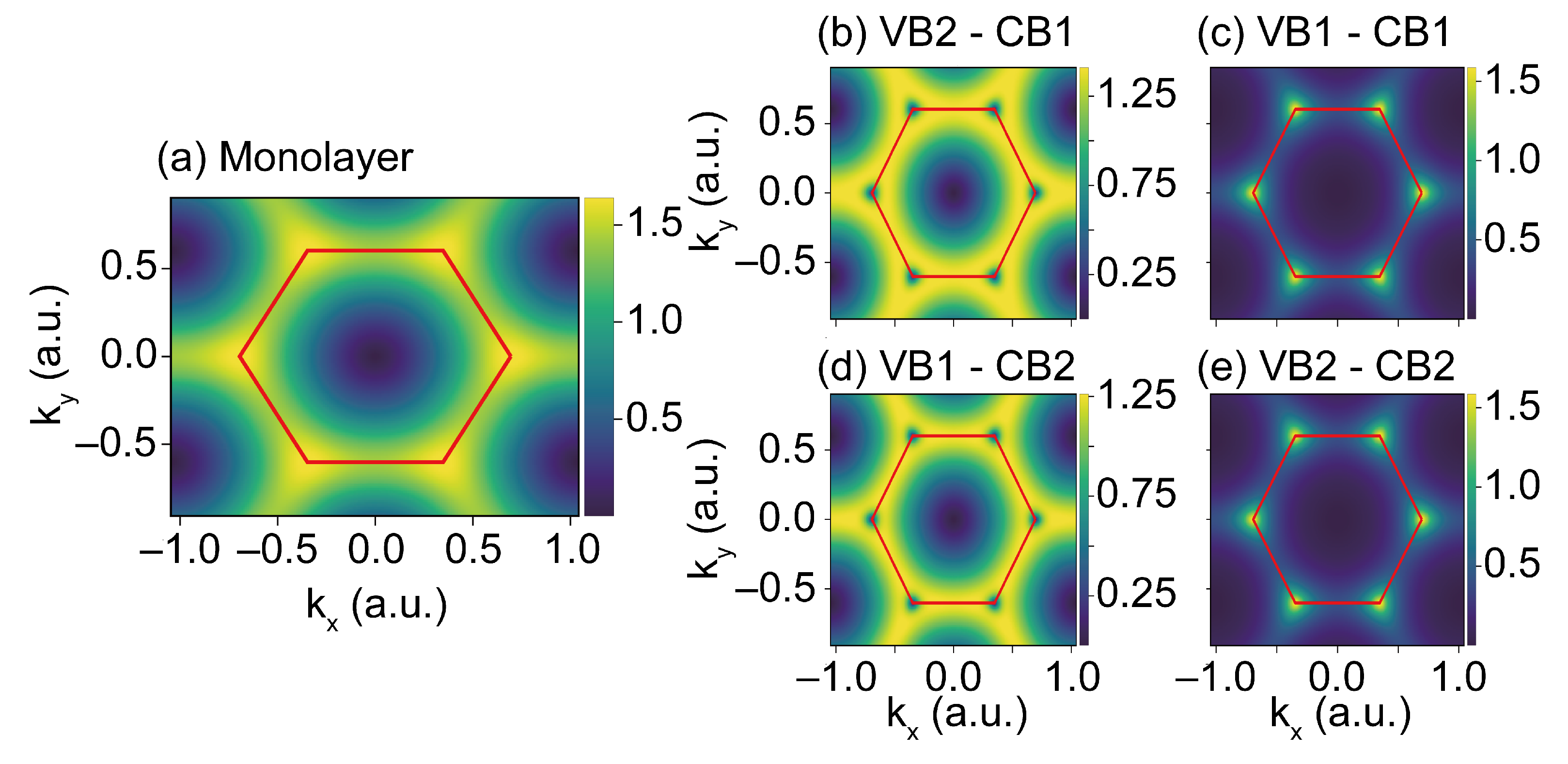
Appendix A. Band Gap Structure in the BZ
Appendix B. Keldysh Approximation and Quasi-Classical Analysis
Appendix B.1. Inter-Band Current
Appendix B.2. Quasi-Classical Electron-Hole Pair Quantum Paths
Appendix B.3. Berry Connection, Berry Curvature, and Chern Number


Appendix B.4. Dipole Moment and Berry Curvature in the Haldane Model (HM)
References
- Ghimire, S.; Di Chiara, A.D.; Sistrunk, E.; Agostini, P.; DiMauro, L.F.; Reis, D.A. Observation of high-order harmonic generation in a bulk crystal. Nat. Phys. 2011, 7, 138–141. [Google Scholar] [CrossRef]
- Liu, H.; Li, Y.; You, Y.S.; Ghimire, S.; Heinz, T.F.; Reis, D.A. High-harmonic generation from an atomically thin semiconductor. Nat. Phys. 2017, 13, 262. [Google Scholar] [CrossRef]
- Vampa, G.; Hammond, T.; Thiré, N.; Schmidt, B.; Légaré, F.; McDonald, C.; Brabec, T.; Corkum, P. Linking high harmonics from gases and solids. Nature 2015, 522, 462. [Google Scholar] [CrossRef] [PubMed]
- Itatani, J.; Levesque, J.; Zeidler, D.; Niikura, H.; Pépin, H.; Kieffer, J.C.; Corkum, P.B.; Villeneuve, D.M. Tomographic imaging of molecular orbitals. Nature 2004, 432, 867–871. [Google Scholar] [CrossRef] [PubMed]
- Ghimire, S.; Reis, D.A. High-harmonic generation from solids. Nat. Phys. 2019, 15, 10–16. [Google Scholar] [CrossRef]
- Amini, K.; Biegert, J.; Calegari, F.; Chacón, A.; Ciappina, M.F.; Dauphin, A.; Efimov, D.K.; de Morisson Faria, C.F.; Giergiel, K.; Gniewek, P.; et al. Symphony on strong field approximation. Rep. Prog. Phys. 2019, 82, 116001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vampa, G.; McDonald, C.R.; Orlando, G.; Klug, D.D.; Corkum, P.B.; Brabec, T. Theoretical Analysis of High-Harmonic Generation in Solids. Phys. Rev. Lett. 2014, 113, 073901. [Google Scholar] [CrossRef] [PubMed]
- Osika, E.N.; Chacón, A.; Ortmann, L.; Suárez, N.; Pérez-Hernández, J.A.; Szafran, B.; Ciappina, M.F.; Sols, F.; Landsman, A.S.; Lewenstein, M. Wannier-Bloch Approach to Localization in High-Harmonics Generation in Solids. Phys. Rev. X 2017, 7, 021017. [Google Scholar] [CrossRef] [Green Version]
- Kruchinin, S.Y.; Krausz, F.; Yakovlev, V.S. Colloquium: Strong-field phenomena in periodic systems. Rev. Mod. Phys. 2018, 90, 021002. [Google Scholar] [CrossRef] [Green Version]
- Kormányos, A.; Zólyomi, V.; Fal’ko, V.I.; Burkard, G. Tunable Berry curvature and valley and spin Hall effect in bilayer MoS2. Phys. Rev. B 2018, 98, 035408. [Google Scholar] [CrossRef] [Green Version]
- Gong, Z.; Liu, G.B.; Yu, H.; Xiao, D.; Cui, X.; Xu, X.; Yao, W. Magnetoelectric effects and valley-controlled spin quantum gates in transition metal dichalcogenide bilayers. Nat. Commun. 2013, 4, 2053. [Google Scholar] [CrossRef] [Green Version]
- Zhai, X.; Blanter, Y.M. Spin-valley polarized quantum anomalous Hall effect and a valley-controlled half-metal in bilayer graphene. Phys. Rev. B 2020, 101, 155425. [Google Scholar] [CrossRef]
- Damascelli, A.; Hussain, Z.; Shen, Z.X. Angle-resolved photoemission studies of the cuprate superconductors. Rev. Mod. Phys. 2003, 75, 473–541. [Google Scholar] [CrossRef] [Green Version]
- Chiu, C.K.; Teo, J.C.Y.; Schnyder, A.P.; Ryu, S. Classification of topological quantum matter with symmetries. Rev. Mod. Phys. 2016, 88, 035005. [Google Scholar] [CrossRef]
- Vampa, G.; Brabec, T. Merge of high harmonic generation from gases and solids and its implications for attosecond science. J. Phys. B At. Mol. Opt. Phys. 2017, 50, 083001. [Google Scholar] [CrossRef]
- Luu, T.T.; Wörner, H.J. Measurement of the Berry curvature of solids using high-harmonic spectroscopy. Nat. Commun. 2018, 9, 916. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vampa, G.; Hammond, T.J.; Thiré, N.; Schmidt, B.E.; Légaré, F.; McDonald, C.R.; Brabec, T.; Klug, D.D.; Corkum, P.B. All-Optical Reconstruction of Crystal Band Structure. Phys. Rev. Lett. 2015, 115, 193603. [Google Scholar] [CrossRef] [Green Version]
- Chacón, A.; Kim, D.; Zhu, W.; Kelly, S.P.; Dauphin, A.; Pisanty, E.; Maxwell, A.S.; Picón, A.; Ciappina, M.F.; Kim, D.E.; et al. Circular dichroism in higher-order harmonic generation: Heralding topological phases and transitions in Chern insulators. Phys. Rev. B 2020, 102, 134115. [Google Scholar] [CrossRef]
- Baykusheva, D.; Chacón, A.; Kim, D.; Kim, D.E.; Reis, D.A.; Ghimire, S. Strong-field physics in three-dimensional topological insulators. Phys. Rev. A 2021, 103, 023101. [Google Scholar] [CrossRef]
- Tancogne-Dejean, N.; Mücke, O.D.; Kärtner, F.X.; Rubio, A. Ellipticity dependence of high-harmonic generation in solids originating from coupled intraband and interband dynamics. Nat. Commun. 2017, 8, 2041. [Google Scholar]
- Baykusheva, D.; Chacón, A.; Lu, J.; Bailey, T.P.; Sobota, J.A.; Soifer, H.; Kirchmann, P.S.; Rotundu, C.; Uher, C.; Heinz, T.F.; et al. All-Optical Probe of Three-Dimensional Topological Insulators Based on High-Harmonic Generation by Circularly Polarized Laser Fields. Nano Lett. 2021, 21, 8970. [Google Scholar] [CrossRef] [PubMed]
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045–3067. [Google Scholar] [CrossRef] [Green Version]
- Haldane, F.D.M. Nobel Lecture: Topological quantum matter. Rev. Mod. Phys. 2017, 89, 040502. [Google Scholar] [CrossRef]
- Langer, F.; Schmid, C.P.; Schlauderer, S.; Gmitra, M.; Fabian, J.; Nagler, P.; Schüller, C.; Korn, T.; Hawkins, P.G.; Steiner, J.T.; et al. Lightwave valleytronics in a monolayer of tungsten diselenide. Nature 2018, 557, 1476–4687. [Google Scholar] [CrossRef]
- Xiao, D.; Liu, G.B.; Feng, W.; Xu, X.; Yao, W. Coupled Spin and Valley Physics in Monolayers of MoS2 and Other Group-VI Dichalcogenides. Phys. Rev. Lett. 2012, 108, 196802. [Google Scholar] [CrossRef] [Green Version]
- Shin, D.; Sato, S.A.; Hübener, H.; De Giovannini, U.; Kim, J.; Park, N.; Rubio, A. Unraveling Materials Berry Curvature and Chern Numbers from Real-Time Evolution of Bloch States. Proc. Natl. Acad. Sci. USA 2019, 116, 4135–4140. [Google Scholar] [CrossRef] [Green Version]
- Yoshikawa, N.; Tamaya, T.; Tanaka, K. High-harmonic generation in graphene enhanced by elliptically polarized light excitation. Science 2017, 356, 736–738. [Google Scholar] [CrossRef]
- Mrudul, M.S.; Dixit, G. High-harmonic generation from monolayer and bilayer graphene. Phys. Rev. B 2021, 103, 094308. [Google Scholar] [CrossRef]
- Tancogne-Dejean, N.; Oliveira, M.J.T.; Andrade, X.; Appel, H.; Borca, C.H.; Le Breton, G.; Buchholz, F.; Castro, A.; Corni, S.; Correa, A.A.; et al. Octopus, a computational framework for exploring light-driven phenomena and quantum dynamics in extended and finite systems. J. Chem. Phys. 2020, 152, 124119. [Google Scholar] [CrossRef] [PubMed]
- Yue, L.; Gaarde, M.B. Structure gauges and laser gauges for the semiconductor Bloch equations in high-order harmonic generation in solids. Phys. Rev. A 2020, 101, 053411. [Google Scholar] [CrossRef]
- Kruchinin, S.Y.; Korbman, M.; Yakovlev, V.S. Theory of strong-field injection and control of photocurrent in dielectrics and wide band gap semiconductors. Phys. Rev. B 2013, 87, 115201. [Google Scholar] [CrossRef] [Green Version]
- Wismer, M.S.; Yakovlev, V.S. Gauge-independent decoherence models for solids in external fields. Phys. Rev. B 2018, 97, 144302. [Google Scholar] [CrossRef]
- Silva, R.E.F.; Martín, F.; Ivanov, M. High harmonic generation in crystals using maximally localized Wannier functions. Phys. Rev. B 2019, 100, 195201. [Google Scholar] [CrossRef] [Green Version]
- Kim, D.; Shin, D.; Landsman, A.S.; Kim, D.E.; Chacón, A. Theory for all-optical responses in topological materials: The velocity gauge picture. arXiv 2021, arXiv:2105.12294. [Google Scholar]
- Li, S.; Liu, C.C.; Yao, Y. Floquet high Chern insulators in periodically driven chirally stacked multilayer graphene. New J. Phys. 2018, 20, 033025. [Google Scholar] [CrossRef]
- Toh, R.J.; Sofer, Z.; Luxa, J.; Sedmidubský, D.; Pumera, M. 3R phase of MoS2 and WS2 outperforms the corresponding 2H phase for hydrogen evolution. Chem. Commun. 2017, 53, 3054–3057. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Saito, N.; Xia, P.; Lu, F.; Kanai, T.; Itatani, J.; Ishii, N. Observation of selection rules for circularly polarized fields in high-harmonic generation from a crystalline solid. Optica 2017, 4, 1333–1336. [Google Scholar] [CrossRef]
- Drake, G.W.F.; Cassar, M.M. Springer Handbooks of Atomic, Molecular and Optical Physics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Karsten, L.H.; Smith, J. Lattice fermions: Species doubling, chiral invariance and the triangle anomaly. Nucl. Phys. B 1981, 183, 103–140. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Q.; Zhu, X.; Huang, T.; Lan, P.; Lu, P. Orientation dependence of high-order harmonic generation in nanowire. Phys. Rev. A 2019, 99, 033421. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, L.; Li, J.; Huang, T.; Lan, P.; Lu, P. Orientation dependence of high-order harmonic generation in graphene. Phys. Rev. A 2021, 104, 033110. [Google Scholar] [CrossRef]
- Acín, A.; Bloch, I.; Buhrman, H.; Calarco, T.; Eichler, C.; Eisert, J.; Esteve, D.; Gisin, N.; Glaser, S.J.; Jelezko, F.; et al. The quantum technologies roadmap: A European community view. New J. Phys. 2018, 20, 080201. [Google Scholar] [CrossRef]
- Lewenstein, M.; Sanpera, A.; Ahufinger, V. Ultracold Atoms in Optical Lattices: Simulating Quantum Many-Body Systems; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Bloch, I.; Dalibard, J.; Zwerger, W. Many-body physics with ultracold gases. Rev. Mod. Phys. 2008, 80, 885–964. [Google Scholar] [CrossRef] [Green Version]
- Cirac, J.I.; Zoller, P. Goals and opportunities in quantum simulation. Nat. Phys. 2012, 8, 264–266. [Google Scholar] [CrossRef]
- Bloch, I.; Dalibard, J.; Nascimbène, S. Quantum simulations with ultracold quantum gases. Nat. Phys. 2012, 8, 267–276. [Google Scholar] [CrossRef]
- Blatt, R.; Roos, C.F. Quantum simulations with trapped ions. Nat. Phys. 2012, 8, 277–284. [Google Scholar] [CrossRef]
- Aspuru-Guzik, A.; Walther, P. Photonic quantum simulators. Nat. Phys. 2012, 8, 285–291. [Google Scholar] [CrossRef] [Green Version]
- Houck, A.A.; Türeci, H.E.; Koch, J. On-chip quantum simulation with superconducting circuits. Nat. Phys. 2012, 8, 292–299. [Google Scholar] [CrossRef]
- Sala, S.; Förster, J.; Saenz, A. Ultracold-atom quantum simulator for attosecond science. Phys. Rev. A 2017, 95, 011403. [Google Scholar] [CrossRef] [Green Version]
- Senaratne, R.; Rajagopal, S.V.; Shimasaki, T.; Dotti, P.E.; Fujiwara, K.M.; Singh, K.; Geiger, Z.A.; Weld, D.M. Quantum simulation of ultrafast dynamics using trapped ultracold atoms. Nat. Commun. 2018, 9, 2065. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ramos, R.; Spiering, D.; Racicot, I.; Steinberg, A.M. Measuring the time a tunnelling atom spends in the barrier. arXiv 2019, arXiv:1907.13523. [Google Scholar]
- Corkum, P.B. Plasma perspective on strong field multiphoton ionization. Phys. Rev. Lett. 1993, 71, 1994. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lewenstein, M.; Balcou, P.; Ivanov, M.Y.; L’Huillier, A.; Corkum, P.B. Theory of high-harmonic generation by low-frequency laser fields. Phys. Rev. A 1994, 49, 2117. [Google Scholar] [CrossRef] [PubMed]
- Pechukas, P.; George, T.F.; Morokuma, K.; McLafferty, F.J.; Laing, J.R. Analytic structure of the eigenvalue problem as used in semiclassical theory of electronically inelastic collisions. J. Chem. Phys. 1976, 64, 1099–1105. [Google Scholar] [CrossRef]
- Hwang, J.T.; Pechukas, P. The adiabatic theorem in the complex plane and the semiclassical calculation of nonadiabatic transition amplitudes. J. Chem. Phys. 1977, 67, 4640–4653. [Google Scholar] [CrossRef]
- Reuter, M.G. A unified perspective of complex band structure: Interpretations, formulations, and applications. J. Phys. Condens. Matter 2016, 29, 053001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Blount, E. Formalisms of Band Theory. In Solid State Physics; Seitz, F., Turnbull, D., Eds.; Academic Press: Cambridge, MA, USA, 1962; Volume 13, pp. 305–373. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, Y.; Kim, D.; Kim, D.-E.; Chacón, A. High Harmonic Generation in Monolayer and Bilayer of Transition Metal Dichalcogenide. Symmetry 2021, 13, 2403. https://doi.org/10.3390/sym13122403
Lee Y, Kim D, Kim D-E, Chacón A. High Harmonic Generation in Monolayer and Bilayer of Transition Metal Dichalcogenide. Symmetry. 2021; 13(12):2403. https://doi.org/10.3390/sym13122403
Chicago/Turabian StyleLee, Yeon, Dasol Kim, Dong-Eon Kim, and Alexis Chacón. 2021. "High Harmonic Generation in Monolayer and Bilayer of Transition Metal Dichalcogenide" Symmetry 13, no. 12: 2403. https://doi.org/10.3390/sym13122403
APA StyleLee, Y., Kim, D., Kim, D.-E., & Chacón, A. (2021). High Harmonic Generation in Monolayer and Bilayer of Transition Metal Dichalcogenide. Symmetry, 13(12), 2403. https://doi.org/10.3390/sym13122403






