H-Irregularity Strengths of Plane Graphs

Abstract

Graph labeling is the mapping of elements of a graph (which can be vertices, edges, faces or a combination) to a set of numbers. The mapping usually produces partial sums (weights) of the labeled elements of the graph, and they often have an asymmetrical distribution. In this paper, we study vertex–face and edge–face labelings of two-connected plane graphs. We introduce two new graph characteristics, namely the vertex–face H-irregularity strength and edge–face H-irregularity strength of plane graphs. Estimations of these characteristics are obtained, and exact values for two families of graphs are determined.

1. Introduction

All graphs $G=\left(V\right(G),E(G\left)\right)$ considered in this paper are simple graphs with a vertex set $V\left(G\right)$ and an edge set $E\left(G\right)$. If we consider a plane graph $G=\left(V\right(G),E(G),F(G\left)\right)$, then $F\left(G\right)$ is its face set. For the notation and terminology not defined here, see the work presented in [1].

Graph labeling is the mapping of elements of a graph (which can be vertices, edges, faces or a combination) to a set of numbers. The mapping usually produces partial sums (weights) of the labeled elements of the graph, and they often have an asymmetrical distribution.

For a given edge k-labeling $\alpha :E\left(G\right)\to \{1,2,\dots ,k\}$, where k is a positive integer, the associated weight of a vertex $x\in V\left(G\right)$ is $w_{\alpha }\left(x\right)={\sum }_{xy\in E\left(G\right)}\alpha \left(xy\right)$. Such a labeling $\alpha$ is called irregular if $w_{\alpha }\left(x\right)\ne w_{\alpha }\left(y\right)$ for every pair $x,y$ of vertices of G. The smallest integer k for which an irregular labeling of G exists is known as the irregularity strength of G and is denoted by $\mathrm{s}\left(G\right)$. The notion of irregularity strength was introduced by Chartrand et al. in [2]. It is known that $s\left(G\right)\le \left|V\right(G\left)\right|-1$ for graphs with no component with an order of at most two (see [3,4]). This upper bound was gradually improved by Cuckler and Lazebnik in [5], Przybyło in [6], Kalkowski, Karonski and Pfender in [7] and recently by Majerski and Przybylo in [8]. Other interesting results regarding the irregularity strength can be found in [9,10,11,12].

Let $H_1,H_2,\dots ,H_t$ be all subgraphs in G isomorphic to a given graph H. If every edge of $E\left(G\right)$ belongs to at least one of the subgraphs $H_i$, $i=1,2,\dots ,t$, we say that graph G admits an H-covering.

Motivated by the irregularity strength of a graph G, Ashraf et al. in [13] introduced two parameters: edge H-irregularity strength $\mathrm{ehs}(G,H)$ and vertex H-irregularity strength $\mathrm{vhs}(G,H)$, as a natural extension of the parameter $\mathrm{s}\left(G\right)$. The bounds of the parameters $\mathrm{ehs}(G,H)$ and $\mathrm{vhs}(G,H)$ are estimated in [13], and the exact values of the edge (vertex) H-irregularity strength are determined for several families of graphs, namely paths, ladders and fan graphs.

If we consider a plane graph, it is natural to label not only the vertices and edges of the plane graph but also its faces. Motivated by the edge (vertex) H-irregularity strength and the entire face irregularity strength of plane graphs introduced in [14], we study a vertex–face (edge–face) H-irregularity strength of two-connected plane graphs, which is a natural extension of the edge (vertex) H-irregularity strength of graphs.

A plane graph is a particular drawing of a planar graph on the Euclidean plane. Suppose that $G=\left(V\right(G),E(G),F(G\left)\right)$ is a two-connected plane graph with a vertex set $V\left(G\right)$, an edge set $E\left(G\right)$ and a face set $F\left(G\right)$, where $F_{int}\left(G\right)$ denotes the set of internal faces of G. In this paper, we consider only such subgraphs H of a plane graph G that every inner face of H is also an inner face of G.

For a subgraph $H\subseteq G$ under vertex–face k-labeling $\phi :V\left(G\right)\cup F_{int}\left(G\right)\to \{1,2,\dots ,k\}$, the associated H-weight is

$$w_{\phi }\left(H\right)=\sum _{v\in V\left(H\right)}\phi \left(v\right)+\sum _{f\in F_{int}\left(H\right)}\phi \left(f\right),$$

and under edge–face k-labeling $\psi :E\left(G\right)\cup F_{int}\left(G\right)\to \{1,2,\dots ,k\}$, the associated H-weight is

$$w_{\psi }\left(H\right)=\sum _{e\in E\left(H\right)}\psi \left(e\right)+\sum _{f\in F_{int}\left(H\right)}\psi \left(f\right).$$

Vertex–face k-labeling $\phi$ is said to represent the H-irregular vertex–face k-labeling of the plane graph G admitting an H-covering if for every two different subgraphs $H^{\prime }$ and $H^{″}$ isomorphic to H there is $w_{\phi }\left(H^{\prime }\right)\ne w_{\phi }\left(H^{″}\right)$. The vertex–face H-irregularity strength of a plane graph G, denoted by $\mathrm{vfhs}(G,H)$, is the smallest integer k such that G has H-irregular vertex–face k-labeling.

Similarly, edge–face k-labeling $\psi$ is said to be an H-irregular edge-face k-labeling of the plane graph G admitting an H-covering if for every two different subgraphs $H^{\prime }$ and $H^{″}$ isomorphic to H there is $w_{\psi }\left(H^{\prime }\right)\ne w_{\psi }\left(H^{″}\right)$. The edge–face H-irregularity strength of a plane graph G, denoted by $\mathrm{efhs}(G,H)$, is the smallest integer k such that G has H-irregular edge-face k-labeling.

The main aim of this paper is to estimate the lower bound and an upper bound for the parameters $\mathrm{vfhs}(G,H)$ and $\mathrm{efhs}(G,H)$. We determine the exact values of the vertex–face (edge–face) H-irregularity strengths for some graphs in order to prove the sharpness of the lower bounds of these graph invariants.

2. Results

2.1. Lower Bounds

The next theorem gives a lower bound for the vertex–face H-irregularity strength for plane graphs.

Theorem 1.

Given a two-connected plane graph $G=\left(V\right(G),E(G),F(G\left)\right)$ admitting an H-covering with t subgraphs isomorphic to H, it holds that

$$\mathrm{vfhs}(G,H)\ge ⌈1+\frac{t-1}{\left|V\left(H\right)\right|+|F_{int}\left(H\right)|}⌉.$$

Proof. 

Assume that $G=(V,E,F)$ is a two-connected plane graph admitting an H-covering with t subgraphs isomorphic to H and $\phi$ is an H-irregular vertex–face k-labeling of G. Let $\mathrm{vfhs}(G,H)=k$. The smallest H-weight for every subgraph $H\subseteq G$ under vertex–face k-labeling $\phi$ is at least $\left|V\left(H\right)\right|+|F_{int}\left(H\right)|$. Since the H-covering of G is given by t subgraphs, then the largest H-weight admits the value at least $\left|V\left(H\right)\right|+|F_{int}\left(H\right)|+t-1$ and at most $\left(\right|V\left(H\right)|+|F_{int}\left(H\right)\left|\right)k$. Thus,

$$\left|V\left(H\right)\right|+|F_{int}\left(H\right)|+t-1\le (\left|V\left(H\right)\right|+|F_{int}\left(H\right)\left|\right)k.$$

This implies that

$$k=\mathrm{vfhs}(G,H)\ge ⌈1+\frac{t-1}{\left|V\left(H\right)\right|+|F_{int}\left(H\right)|}⌉.$$

□

By applying a similar reasoning, we get a lower bound for the edge–face H-irregularity strength of plane graphs as follows.

Theorem 2.

Given a two-connected plane graph $G=\left(V\right(G),E(G),F(G\left)\right)$ admitting an H-covering with t subgraphs isomorphic to H, it holds that

$$\mathrm{efhs}(G,H)\ge ⌈1+\frac{t-1}{\left|E\left(H\right)\right|+|F_{int}\left(H\right)|}⌉.$$

The lower bounds in Theorems 1 and 2 are tight. This can be seen from the following two theorems, which determine the exact values of the vertex–face and edge–face ladder-irregularity strengths for ladders. First, we recall the definition and properties of a ladder.

Let $L_n\cong P_n\square P_2$, $n\ge 2$ be a ladder with the vertex set $V\left(L_n\right)=\{u_i,v_i:i=1,2,\dots ,n\}$, edge set $E\left(L_n\right)=\{u_i{u}_{i+1},v_i{v}_{i+1}:i=1,2,\dots ,n-1\}\cup \{u_i{v}_i:i=1,2,\dots ,n\}$ and set of internal faces $F_{int}\left(L_n\right)=\{f_i:i=1,2,\dots ,n-1\}$, where $f_i$ is a four-sided face surrounded by vertices $u_i,u_{i+1},v_i,v_{i+1}$ and edges $u_i{u}_{i+1}$, $v_i{v}_{i+1}$, $u_i{v}_i$, $u_{i+1}{v}_{i+1}$. Thus, the ladder $L_n$ contains $2n$ vertices, $3n-2$ edges, and a number of four-sided face of $n-1$, and the ladder has one $2n$-sided face.

Theorem 3.

Let $n,m$ be positive integers, $n\ge 2$, $2\le m\le n$. Then

$$\mathrm{vfhs}(L_n,L_m)=⌈\frac{2m+n-1}{3m-1}⌉.$$

Proof. 

For every m, $2\le m\le n$, the ladder $L_n$ admits an $L_m$-covering with exactly $n-m+1$ subgraphs $L_m^j$, $j=1,2,\dots ,n-m+1$, where $V\left(L_m^j\right)=\{u_{j+i},v_{j+i}:i=0,1,\dots ,m-1\}$ is the vertex set, $E\left(L_m^j\right)=\{u_{j+i}{v}_{j+i}:i=0,1,\dots ,m-1\}\cup \{u_{j+i}{u}_{j+i+1},v_{j+i}{v}_{j+i+1}:i=0,1,\dots ,m-2\}$ is the edge set and the set of internal faces is $F_{int}\left(L_m^j\right)=\{f_{j+i}:i=0,1,\dots ,m-2\}.$ It is clearly visible that every edge of $L_n$ belongs to at least one ladder $L_m^j$ if $m=2,3,\dots ,n$.

Using Theorem 1, we find that $\mathrm{vfhs}(L_n,L_m)\ge ⌈(2m+n-1)/(3m-1)⌉=k$. To prove the equality, it suffices to show the existence of an optimal $L_m$-irregular vertex–face k-labeling of ladder $L_n$.

For every $m=2,3,\dots ,n$ we define a vertex–face k-labeling ${\phi }_m:V\left(L_n\right)\cup F_{int}\left(L_n\right)\to \{1,2,\dots ,k\}$ in the following way:

$$\begin{array}{cccc}\hfill {\phi }_m\left(u_i\right)=& ⌈\frac{i+m-1}{3m-1}⌉\hfill & \hfill & \mathrm{for}i=1,2,\dots ,n,\hfill \\ \hfill {\phi }_m\left(v_i\right)=& ⌈\frac{i+2m-1}{3m-1}⌉\hfill & \hfill & \mathrm{for}i=1,2,\dots ,n,\hfill \\ \hfill {\phi }_m\left(f_i\right)=& ⌈\frac{i}{3m-1}⌉\hfill & \hfill & \mathrm{for}i=1,2,\dots ,n-1.\hfill \end{array}$$

We can see that under the vertex–face labeling ${\phi }_m$, all vertex and face labels are at most k. For the $L_m$-weight of the ladder $L_m^j$, $j=1,2,\dots ,n-m+1$, under the vertex–face labeling ${\phi }_m$, $m=2,3,\dots ,n$, we get

$$\begin{array}{c}\hfill w_{{\phi }_m}\left(L_m^j\right)=\sum _{v\in V\left(L_m^j\right)}{\phi }_m\left(v\right)+\sum _{f\in F_{int}\left(L_m^j\right)}{\phi }_m\left(f\right).\end{array}$$

Consider the difference of weights of subgraphs $L_m^{j+1}$ and $L_m^j$, for $j=1,2,\dots ,n-m$, as follows:

$$\begin{array}{cc}\hfill w_{{\phi }_m}\left(L_m^{j+1}\right)-w_{{\phi }_m}\left(L_m^j\right)=& {\phi }_m\left(u_{j+m}\right)+{\phi }_m\left(v_{j+m}\right)+{\phi }_m\left(f_{j+m-1}\right)-{\phi }_m\left(u_j\right)-{\phi }_m\left(v_j\right)-{\phi }_m\left(f_j\right)\hfill \\ \hfill =& ⌈\frac{j+2m-1}{3m-1}⌉+⌈\frac{j+3m-1}{3m-1}⌉+⌈\frac{j+m-1}{3m-1}⌉-⌈\frac{j+m-1}{3m-1}⌉-⌈\frac{j+2m-1}{3m-1}⌉-⌈\frac{j}{3m-1}⌉\hfill \\ \hfill =& ⌈\frac{j+3m-1}{3m-1}⌉-⌈\frac{j}{3m-1}⌉=1.\hfill \end{array}$$

Since all vertex labels and face labels under the vertex–face labeling ${\phi }_m$ form non-decreasing sequences and $w_{{\phi }_m}\left(L_m^{j+1}\right)=w_{{\phi }_m}\left(L_m^j\right)+1$ for every $m=2,3,\dots ,n$, $j=1,2,\dots ,n-m$, it follows that the labeling ${\phi }_m$ is an optimal $L_m$-irregular vertex–face k-labeling of $L_n$. Thus, we arrive at the desired result. □

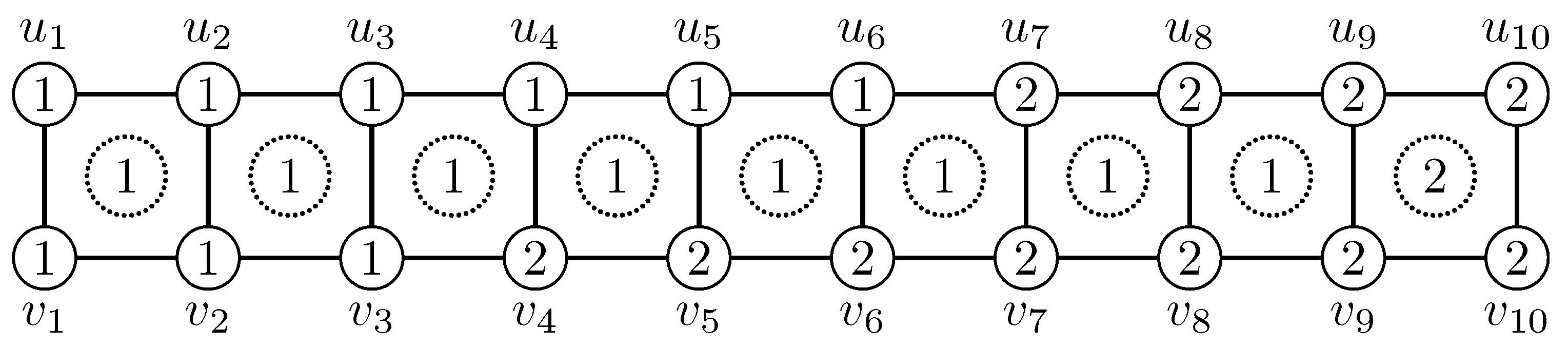
Figure 1 illustrates an $L_3$-irregular vertex–face 2-labeling of the ladder $L_{10}$, where every number in a circle is the face label. The $L_3$-weights of the ladders $L_3^j$ are $7+j$ for $j=1,2,\dots ,8$.

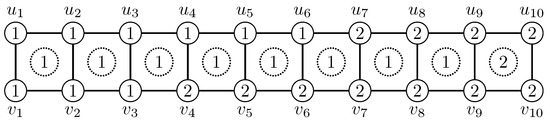
Figure 1. $L_3$-irregular vertex–face two-labeling of $L_{10}$.

Theorem 4.

Let $n,m$ be positive integers, $n\ge 2$, $2\le m\le n$. Then

$$\mathrm{efhs}(L_n,L_m)=⌈\frac{3m+n-3}{4m-3}⌉.$$

Proof. 

Let the $L_m$-covering of the ladder $L_n$ be defined by subgraphs $L_m^j$, $j=1,2,\dots ,n-m+1$ and $m=2,3,\dots ,n$. From Theorem 2, we find that $\mathrm{efhs}(L_n,L_m)\ge$$⌈(3m+n-3)/(4m-3)⌉=k$. To show that k is an upper bound for the edge–face $L_m$-irregularity strength of $L_n$ we define an edge–face k-labeling ${\psi }_m:E\left(L_n\right)\cup F_{int}\left(L_n\right)\to \{1,2,\dots ,k\}$, $m=2,3,\dots ,n$, as follows:

$$\begin{array}{cccc}\hfill {\psi }_m\left(u_i{u}_{i+1}\right)=& ⌈\frac{i+m-1}{4m-3}⌉\hfill & \hfill & \mathrm{for}i=1,2,\dots ,n-1,\hfill \\ \hfill {\psi }_m\left(v_i{v}_{i+1}\right)=& ⌈\frac{i+3m-2}{4m-3}⌉\hfill & \hfill & \mathrm{for}i=1,2,\dots ,n-1,\hfill \\ \hfill {\psi }_m\left(u_i{v}_i\right)=& ⌈\frac{i+2m-2}{4m-3}⌉\hfill & \hfill & \mathrm{for}i=1,2,\dots ,n,\hfill \\ \hfill {\psi }_m\left(f_i\right)=& ⌈\frac{i}{4m-3}⌉\hfill & \hfill & \mathrm{for}i=1,2,\dots ,n-1.\hfill \end{array}$$

Evidently, the labeling ${\psi }_m$ is assigned to the edges and faces of $L_n$ the labels less than or equal to k. If the $L_m$-weight of the ladder $L_m^j$ under the edge–face labeling ${\psi }_m$ is given by the form

$$\begin{array}{c}\hfill w_{{\psi }_m}\left(L_m^j\right)=\sum _{e\in E\left(L_m^j\right)}{\psi }_m\left(e\right)+\sum _{f\in F_{int}\left(L_m^j\right)}{\phi }_m\left(f\right),\end{array}$$

then, for the difference of weights of subgraphs $L_m^{j+1}$ and $L_m^j$, for $j=1,2,\dots ,n-m$, $m=2,3,\dots ,n$, we get

$$\begin{array}{cc}\hfill w_{{\psi }_m}\left(L_m^{j+1}\right)-w_{{\psi }_m}\left(L_m^j\right)=& {\psi }_m\left(u_{j+m-1}{u}_{j+m}\right)+{\psi }_m\left(v_{j+m-1}{v}_{j+m}\right)+{\psi }_m\left(u_{j+m}{v}_{j+m}\right)+{\psi }_m\left(f_{j+m-1}\right)\hfill \\ & -{\psi }_m\left(u_j{u}_{j+1}\right)-{\psi }_m\left(v_j{v}_{j+1}\right)-{\psi }_m\left(u_j{v}_j\right)-{\psi }_m\left(f_j\right)\hfill \\ \hfill =& ⌈\frac{j+2m-2}{4m-3}⌉+⌈\frac{j+4m-3}{4m-3}⌉+⌈\frac{j+3m-2}{4m-3}⌉+⌈\frac{j+m-1}{4m-3}⌉-⌈\frac{j+m-1}{4m-3}⌉-⌈\frac{j+3m-2}{4m-3}⌉\hfill \\ & -⌈\frac{j+2m-2}{4m-3}⌉-⌈\frac{j}{4m-3}⌉=⌈\frac{j+4m-3}{4m-3}⌉-⌈\frac{j}{4m-3}⌉=1.\hfill \end{array}$$

This proves that $w_{{\psi }_m}\left(L_m^j\right)<w_{{\psi }_m}\left(L_m^{j+1}\right)$ for every $j=1,2,\dots ,n-m$ and $m=2,3,\dots ,n$. Therefore the labeling ${\psi }_m$ is an $L_m$-irregular edge–face k-labeling of $L_n$, and thus $\mathrm{efhs}(L_n,L_m)\le k$. This concludes the proof. □

Figure 2 depicts an $L_3$-irregular edge–face 2-labeling of the ladder $L_{10}$, where every number in a circle is the face label. The $L_3$-weights of the ladders $L_3^j$, $j=1,2,\dots ,8$, successively assume the values $9,10,\dots ,15,16$.

Figure 2. $L_3$-irregular edge–face 2-labeling of $L_{10}$.

The lower bounds from Theorems 1 and 2 can be improved in the case when the subgraphs of a plane graph G contain a common subgraph.

Consider a plane graph G with an H-covering. The symbol ${\mathbb{H}}_r^S=(H_1^S,H_2^S,$$\dots ,H_r^S)$ denotes the set of all subgraphs of G isomorphic to H such that the graph S, $S\ncong H$ is their maximum common subgraph. Thus, $V\left(S\right)\subset V\left(H_i^S\right)$, $E\left(S\right)\subset E\left(H_i^S\right)$ and $F_{int}\left(S\right)\subset F_{int}\left(H_i^S\right)$ for every $i=1,2,\dots ,r$. The following theorem provides another lower bound for the vertex–face H-irregularity strength, where if H and S are graphs, then $V(H\backslash S)$ ($E(H\backslash S)$ or $F(H\backslash S)$, respectively) denotes the set of vertices (edges or faces, respectively) of H which do not belong to S.

Theorem 5.

Given a two-connected plane graph $G=\left(V\right(G),E(G),F(G\left)\right)$ admitting an H-covering, let $S_i$, $i=1,2,\dots ,s$ be all subgraphs of G such that $S_i$ is a maximum common subgraph of $r_i$, $r_i\ge 2$, subgraphs of G isomorphic to H. Then

$$\mathrm{vfhs}(G,H)\ge max\left\{⌈1+\frac{r_1-1}{|V(H\backslash S_1)|+|F_{int}(H\backslash S_1)|}⌉,\dots ,⌈1+\frac{r_s-1}{|V(H\backslash S_s)|+|F_{int}(H\backslash S_s)|}⌉\right\}.$$

Proof. 

Consider a two-connected plane graph G admitting an H-covering. Let ${\mathbb{H}}_{r_i}^{S_i}$, $i=1,2,\dots ,$s, be the set of all subgraphs $H_1^{S_i},H_2^{S_i},\dots ,H_{r_i}^{S_i}$, where each of them is isomorphic to H, and $S_i$ is their maximum common subgraph. Let $\phi$ be an optimal H-irregular vertex–face labeling of G. Then for $j=1,2,\dots ,r_i$ the $H_j^{S_i}$-weights given in the form

$$w_{\phi }\left(H_j^{S_i}\right)=\sum _{v\in V\left(S_i\right)}\phi \left(v\right)+\sum _{f\in F_{int}\left(S_i\right)}\phi \left(f\right)+\sum _{v\in V(H_j^{S_i}\backslash S_i)}\phi \left(v\right)+\sum _{f\in F_{int}(H_j^{S_i}\backslash S_i)}\phi \left(f\right)$$

are all distinct, and each of them contains the value

$$\sum _{v\in V\left(S_i\right)}\phi \left(v\right)+\sum _{f\in F_{int}\left(S_i\right)}\phi \left(f\right).$$

The largest among these $H_j^{S_i}$-weights must be at least

$$\sum _{v\in V\left(S_i\right)}\phi \left(v\right)+\sum _{f\in F_{int}\left(S_i\right)}\phi \left(f\right)+|V(H\backslash S_i)|+|F_{int}(H\backslash S_i)|+r_i-1.$$

The value ${\sum }_{v\in V\left(S_i\right)}\phi \left(v\right)+{\sum }_{f\in F_{int}\left(S_i\right)}\phi \left(f\right)$ does not have any impact on the estimation of the vertex–face irregularity strength. The term $|V(H\backslash S_i)|+|F_{int}(H\backslash S_i)|+r_i-1$, for $i=1,2,\dots ,$s is the sum of $|V(H\backslash S_i)|+|F_{int}(H\backslash S_i)|$ labels, and therefore, by Theorem 1, at least one label is lower-bounded by $⌈1+(r_i-1)/\left(\right|V(H\backslash S_i)|+|F_{int}(H\backslash S_i)\left|\right)⌉$. Consequently, we deduce the desired inequality. □

Similarly, we get a lower bound for the edge–face H-irregularity strength for plane graphs as follows.

Theorem 6.

Given a two-connected plane graph $G=\left(V\right(G),E(G),F(G\left)\right)$ admitting an H-covering, let $S_i$, $i=1,2,\dots ,s$, be all subgraphs of G such that $S_i$ is a maximum common subgraph of $r_i$, $r_i\ge 2$, subgraphs of G isomorphic to H. Then,

$$\mathrm{efhs}(G,H)\ge max\left\{⌈1+\frac{r_1-1}{|E(H\backslash S_1)|+|F_{int}(H\backslash S_1)|}⌉,\dots ,⌈1+\frac{r_s-1}{|E(H\backslash S_s)|+|F_{int}(H\backslash S_s)|}⌉\right\}.$$

The sharpness of lower bounds from Theorems 5 and 6 results from the following two theorems, which determine the exact values of the vertex–face and edge–face H-irregularity strengths for some graphs.

Let $G_i$, $i=1,2$ be a connected graph. Fix a vertex in $G_i$, say $v_i$. If we identify the vertices $v_1$ and $v_2$, the resulting graph can be denoted by the symbol $A(G_1\left(v_1\right),G_2\left(v_2\right))$. Let $F_n$ be a fan graph with the center w and let G be an arbitrary two-connected plane graph with a fixed vertex v belonging to the boundary of its external face. Now, we insert the fan graph $F_n$ into the external face of G and identify the vertices w and v. The resulting graph $A(F_n\left(w\right),G\left(v\right))=A(F_n,G)$ is a two-connected plane graph with $n+\left|V\right(G\left)\right|$ vertices, $2n+\left|E\right(G\left)\right|-1$ edges, $n+|F_{int}\left(G\right)|-1$ internal faces and one external face. Observe that the graph operation has no impact on the number and also size of internal faces in graph G as the subgraph of $A(F_n,G)$.

Denote $V\left(A(F_n,G)\right)=\{u_i:i=1,2,\dots ,n\}\cup V\left(G\right)$ as the vertex set, $E\left(A(F_n,G)\right)=\{u_i{u}_{i+1}:i=1,2,\dots ,n-1\}\cup \{u_{i}w:i=1,2,\dots ,n\}\cup E\left(G\right)$ as the edge set and $F_{int}\left(A(F_n,G)\right)$$=\{f_i:i=1,2,\dots ,n-1\}\cup F_{int}\left(G\right)\}$ as the set of internal faces, where $f_i$ is the three-sided face surrounded by vertices $u_i,u_{i+1},w$ and edges $u_i{u}_{i+1},u_{i}w,u_{i+1}w$.

Theorem 7.

Let $n,m$ be positive integers, $2\le m\le n$, and let G be a two-connected plane graph, $G\ncong F_k$ for every $k>m$. Then,

$$\mathrm{vfhs}(A(F_n,G),A(F_m,G))=⌈\frac{m+n-1}{2m-1}⌉.$$

Proof. 

If the graph G is not isomorphic to $F_k$ for every $k>m$, then the graph $A(F_n,G)$, $n\ge 2$ admits an $A(F_m,G)$-covering with exactly $n-m+1$ graphs $A(F_m,G)$, $2\le m\le n$. Thus, every graph $A{(F_m,G)}^j$, $j=1,2,\dots ,n-m+1$ has the vertex set $V\left(A{(F_m,G)}^j\right)=\{u_{j+i}:i=0,1,\dots ,m-1\}\cup V\left(G\right)$, edge set $E\left(A{(F_m,G)}^j\right)=\{u_{j+i}w:i=0,1,\dots ,m-1\}\cup \{u_{j+i}{u}_{j+i+1},:i=0,1,\dots ,m-2\}\cup E\left(G\right)$ and set of internal faces $F_{int}\left(A{(F_m,G)}^j\right)=\{f_{j+i}:i=0,1,\dots ,m-2\}\cup F_{int}\left(G\right)$. Clearly, every edge of $A(F_n,G)$ belongs to at least one graph $A{(F_m,G)}^j$ if $m=2,3,\dots ,n$.

Since every graph $A{(F_m,G)}^j$ contains the graph $G\cong S_1$ with the vertex set $V\left(S_1\right)=V\left(G\right)$, edge set $E\left(S_1\right)=E\left(G\right)$ and face set $F_{int}\left(S_1\right)=F_{int}\left(G\right)$ as the maximum common subgraph, it follows that $\left|V\right(A(F_m,G)\backslash S_1\left)\right|=m$, $|F_{int}(A(F_m,G)\backslash S_1)|=m-1$, $r_1=n-m+1$, and from Theorem 5, we have

$$\mathrm{vfhs}(A(F_n,G),A(F_m,G))\ge ⌈1+\frac{r_1-1}{|V(A(F_m,G)\backslash S_1)|+|F_{int}(A(F_m,G)\backslash S_1)|}⌉=⌈\frac{m+n-1}{2m-1}⌉.$$

To show that $k=⌈(m+n-1)/(2m-1)⌉$ is an upper bound for the vertex–face $A(F_m,G)$-irregularity strength of $A(F_n,G)$, it suffices to prove the existence of an optimal vertex–face k-labeling ${\phi }_m:V\left(A(F_n,G)\right)\cup F_{int}\left(A(F_n,G)\right)$$\to \{1,2,\dots ,k\}$. For $m=2,3,\dots ,n$, we define the function ${\phi }_m$ in the following way:

$$\begin{array}{cccc}\hfill {\phi }_m\left(u_i\right)=& ⌈\frac{i+m-1}{2m-1}⌉\hfill & \hfill & \mathrm{for}i=1,2,\dots ,n,\hfill \\ \hfill {\phi }_m\left(f_i\right)=& ⌈\frac{i}{2m-1}⌉\hfill & \hfill & \mathrm{for}i=1,2,\dots ,n-1,\hfill \\ \hfill {\phi }_m\left(v\right)=& 1\hfill & \hfill & \mathrm{for}v\in V\left(G\right),\hfill \\ \hfill {\phi }_m\left(f\right)=& 1\hfill & \hfill & \mathrm{for}f\in F_{int}\left(G\right).\hfill \end{array}$$

Indeed, it is readily seen that all vertex and face labels are at most k. Since the $A(F_m,G)$-weight of the graph $A{(F_m,G)}^j$, under the vertex–face labeling ${\phi }_m$, is given by the form

$$\begin{array}{cc}\hfill w_{{\phi }_m}\left(A{(F_m,G)}^j\right)=& \sum _{v\in V\left(A{(F_m,G)}^j\right)}{\phi }_m\left(v\right)+\sum _{f\in F_{int}\left(A{(F_m,G)}^j\right)}{\phi }_m\left(f\right)=\sum _{i=0}^{m-1}{\phi }_m\left(u_{j+i}\right)+\sum _{v\in V\left(G\right)}{\phi }_m\left(v\right)\hfill \\ & +\sum _{i=0}^{m-2}{\phi }_m\left(f_{j+i}\right)+\sum _{f\in F_{int}\left(G\right)}{\phi }_m\left(f\right)\hfill \end{array}$$

then, for the difference of weights of subgraphs $A{(F_m,G)}^{j+1}$ and $A{(F_m,G)}^j$, for $j=1,2,\dots ,$$n-m$, $m=2,3,\dots ,n$, we have

$$\begin{array}{cc}\hfill w_{{\phi }_m}\left(A{(F_m,G)}^{j+1}\right)-w_{{\phi }_m}\left(A{(F_m,G)}^j\right)=& {\phi }_m\left(u_{j+m}\right)+{\phi }_m\left(f_{j+m-1}\right)-{\phi }_m\left(u_j\right)-{\phi }_m\left(f_j\right)=⌈\frac{j+2m-1}{2m-1}⌉\hfill \\ & +⌈\frac{j+m-1}{2m-1}⌉-⌈\frac{j+m-1}{2m-1}⌉-⌈\frac{j}{2m-1}⌉=⌈\frac{j+2m-1}{2m-1}⌉-⌈\frac{j}{2m-1}⌉=1.\hfill \end{array}$$

In fact, $w_{{\phi }_m}\left(A{(F_m,G)}^j\right)<w_{{\phi }_m}\left(A{(F_m,G)}^{j+1}\right)$ for every $j=1,2,\dots ,n-m$ and $m=2,3,\dots ,n$. Thus, the labeling ${\phi }_m$ has the required properties of $A(F_m,G)$-irregular vertex–face k-labeling of $A(F_n,G)$. □

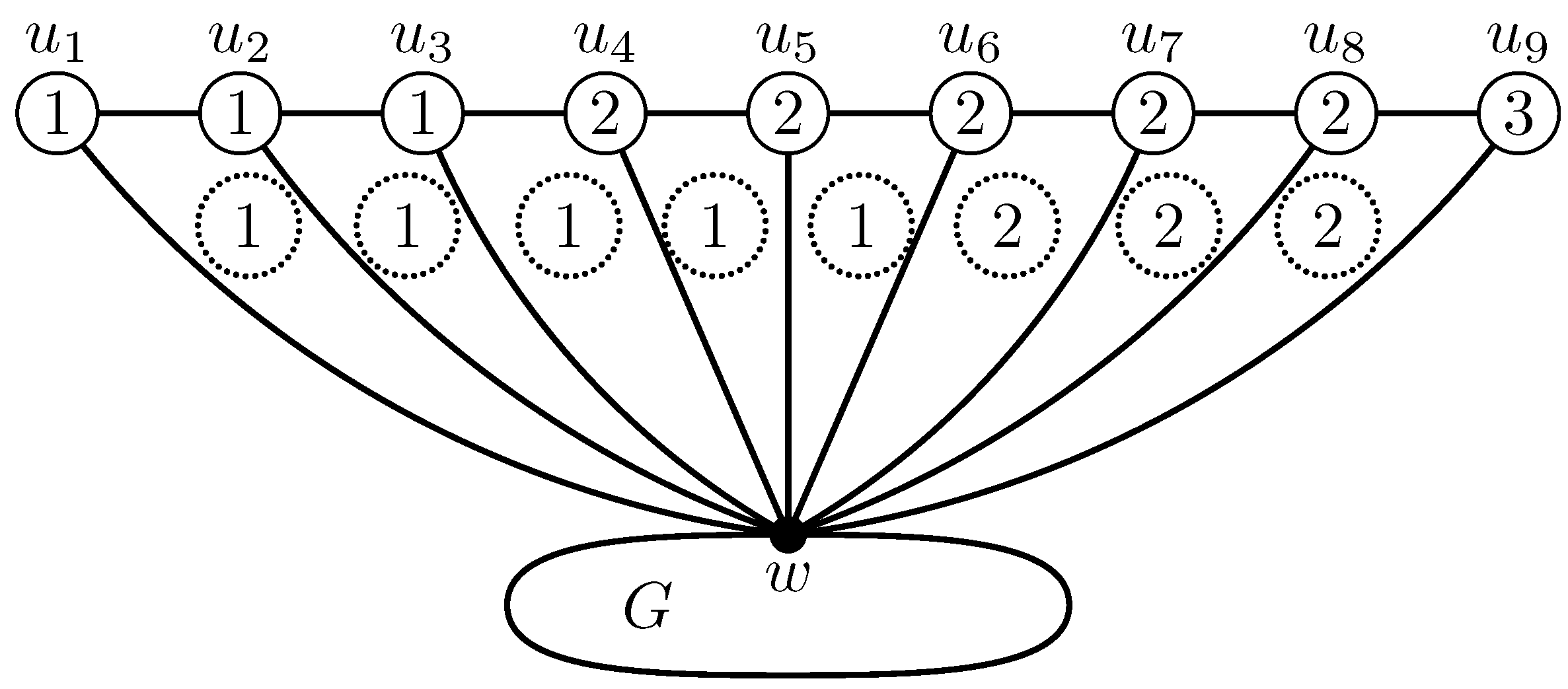
Figure 3 gives an illustration of an $A(F_3,G)$-irregular vertex–face 3-labeling of $A(F_9,G)$, where G is a two-connected plane graph, $G\ncong F_k$ for every $k>3$, and w is the common vertex of the fan $F_9$ and G. The $A(F_3,G)$-weights of the subgraphs $A{(F_3,G)}^j$, $j=1,2,\dots ,7$, successively obtaining the values $5+\left|V\left(G\right)\right|+|F_{int}\left(G\right)|,6+|V\left(G\right)|+|F_{int}\left(G\right)|,\dots ,10+|V\left(G\right)|+|F_{int}\left(G\right)|,11+|V\left(G\right)|+|F_{int}\left(G\right)|$.

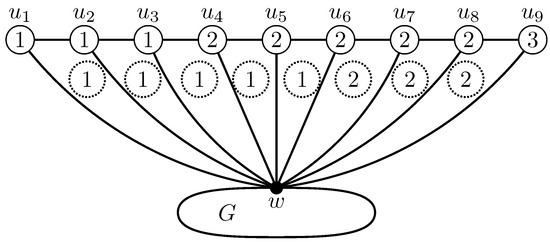
Figure 3. An $A(F_3,G)$-irregular vertex–face 3-labeling of $A(F_9,G)$.

Theorem 8.

Let $n,m$ be positive integers, $2\le m\le n$, and let G be a two-connected plane graph, $G\ncong F_k$ for every $k>m$. Then,

$$\mathrm{efhs}(A(F_n,G),A(F_m,G))=⌈\frac{2m+n-2}{3m-2}⌉.$$

Proof. 

Let G be not isomorphic to $F_k$ for every $k>m$. Let the $A(F_m,G)$-covering of the graph $A(F_n,G)$ be given by subgraphs $A{(F_m,G)}^j$, $j=1,2,\dots ,n-m+1$ and $m=2,3,\dots ,n$. Using the fact that every graph $A{(F_m,G)}^j$ contains the graph $G\cong S_1$ as the maximum common subgraph, it follows that $\left|E\right(A(F_m,G)\backslash S_1\left)\right|=2m-1$, $|F_{int}(A(F_m,G)\backslash S_1)|=m-1$ and $r_1=n-m+1$. Thus, according to Theorem 6, we have

$$\mathrm{efhs}(A(F_n,G),A(F_m,G))\ge ⌈1+\frac{r_1-1}{|E(A(F_m,G)\backslash S_1)|+|F_{int}(A(F_m,G)\backslash S_1)|}⌉=⌈\frac{2m+n-2}{3m-2}⌉.$$

To show that $k=⌈(2m+n-2)/(3m-2)⌉$ is an upper bound for the edge–face $A(F_m,G)$-irregularity strength of $A(F_n,G)$ we describe an edge–face k-labeling ${\psi }_m:E\left(A\right(F_m,$$G\left)\right)\cup F_{int}\left(A(F_m,G)\right)\to \{1,2,\dots ,k\}$. For $m=2,3,\dots ,n$, we construct the function ${\psi }_m$ as follows:

$$\begin{array}{cccc}\hfill {\psi }_m\left(u_i{u}_{i+1}\right)=& ⌈\frac{i+2m-1}{3m-2}⌉\hfill & \hfill & \mathrm{for}i=1,2,\dots ,n-1,\hfill \\ \hfill {\psi }_m\left(u_{i}w\right)=& ⌈\frac{i+m-1}{3m-2}⌉\hfill & \hfill & \mathrm{for}i=1,2,\dots ,n,\hfill \\ \hfill {\psi }_m\left(f_i\right)=& ⌈\frac{i}{3m-2}⌉\hfill & \hfill & \mathrm{for}i=1,2,\dots ,n-1,\hfill \\ \hfill {\psi }_m\left(e\right)=& 1\hfill & \hfill & \mathrm{for}e\in E\left(G\right),\hfill \\ \hfill {\psi }_m\left(f\right)=& 1\hfill & \hfill & \mathrm{for}f\in F_{int}\left(G\right).\hfill \end{array}$$

Observe that all vertex and face labels under the labeling ${\psi }_m$ are at most k. Denote the $A(F_m,G)$-weight of the graph $A{(F_m,G)}^j$, under the edge–face labeling ${\psi }_m$, by

$$\begin{array}{cc}\hfill w_{{\psi }_m}\left(A{(F_m,G)}^j\right)=& \sum _{e\in E\left(A{(F_m,G)}^j\right)}{\psi }_m\left(e\right)+\sum _{f\in F_{int}\left(A{(F_m,G)}^j\right)}{\psi }_m\left(f\right)=\sum _{i=0}^{m-1}{\psi }_m\left(u_{j+i}w\right)+\sum _{i=0}^{m-2}{\psi }_m\left(u_{j+i}{u}_{j+i+1}\right)\hfill \\ & +\sum _{e\in E\left(G\right)}{\psi }_m\left(e\right)+\sum _{i=0}^{m-2}{\psi }_m\left(f_{j+i}\right)+\sum _{f\in F_{int}\left(G\right)}{\psi }_m\left(f\right).\hfill \end{array}$$

For the difference of weights of subgraphs $A{(F_m,G)}^{j+1}$ and $A{(F_m,G)}^j$, for $j=1,2,\dots ,$$n-m$, $m=2,3,\dots ,n$, we get

$$\begin{array}{cc}\hfill w_{{\psi }_m}\left(A{(F_m,G)}^{j+1}\right)-w_{{\psi }_m}\left(A{(F_m,G)}^j\right)=& {\psi }_m\left(u_{j+m-1}{u}_{j+m}\right)+{\psi }_m\left(u_{j+m}w\right)+{\psi }_m\left(f_{j+m-1}\right)-{\psi }_m\left(u_j{u}_{j+1}\right)\hfill \\ & -{\psi }_m\left(u_{j}w\right)-{\psi }_m\left(f_j\right)=⌈\frac{j+3m-2}{3m-2}⌉+⌈\frac{j+2m-1}{3m-2}⌉+⌈\frac{j+m-1}{3m-2}⌉\hfill \\ & -⌈\frac{j+2m-1}{3m-2}⌉-⌈\frac{j+m-1}{3m-2}⌉-⌈\frac{j}{3m-2}⌉=⌈\frac{j+3m-2}{3m-2}⌉-⌈\frac{j}{3m-2}⌉=1.\hfill \end{array}$$

We can see that $w_{{\psi }_m}\left(A{(F_m,G)}^j\right)<w_{{\psi }_m}\left(A{(F_m,G)}^{j+1}\right)$ for every $j=1,2,\dots ,n-m$ and $m=2,3,\dots ,n$. Thus, the labeling ${\psi }_m$ is a desired $A(F_m,G)$-irregular edge–face k-labeling of $A(F_n,G)$. □

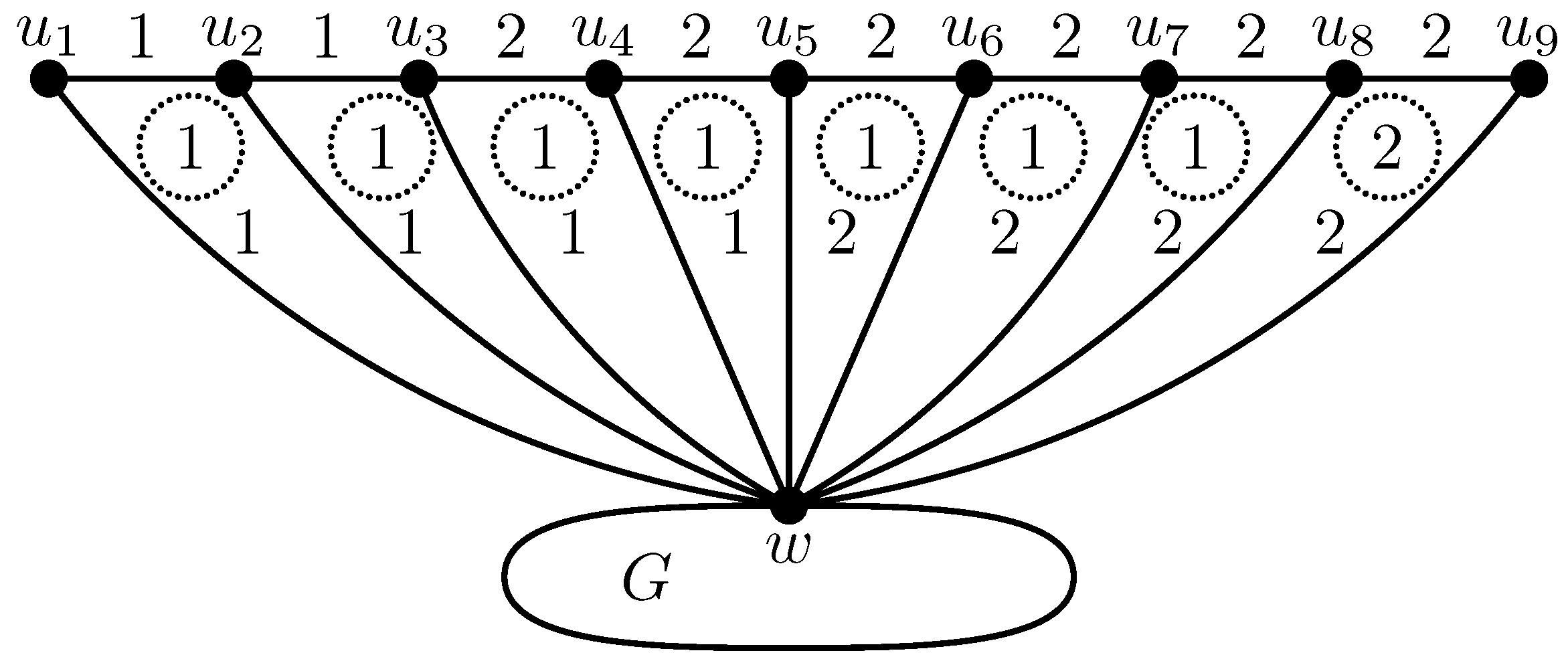
Figure 4 depicts an $A(F_3,G)$-irregular edge–face two-labeling of $A(F_9,G)$, where G is a two-connected plane graph, $G\ncong F_k$ for every $k>3$, and w is the common vertex of the fan $F_9$ and G. The weights of the subgraphs $A{(F_3,G)}^j$, $j=1,2,\dots ,7$ constitute the set of consecutive integers $\{7+|E\left(G\right)|+|F_{int}\left(G\right)|,8+|E\left(G\right)|+|F_{int}\left(G\right)|,\dots ,12+|E\left(G\right)|+|F_{int}\left(G\right)|,13+|E\left(G\right)|+|F_{int}\left(G\right)\left|\right\}$.

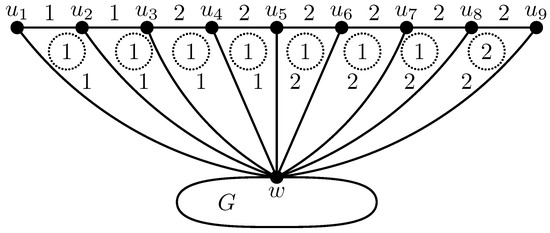
Figure 4. An $A(F_3,G)$-irregular edge-face two-labeling of $A(F_9,G)$.

2.2. Upper Bounds

The next theorem gives upper bounds of the parameters $\mathrm{vfhs}(G,H)$ and $\mathrm{efhs}(G,H)$ and shows that these graph invariants are always finite.

Theorem 9.

Given a two-connected plane graph $G=\left(V\right(G),E(G),F(G\left)\right)$ admitting an H-covering with t subgraphs isomorphic to H, it holds that

$$\begin{array}{cc}\hfill \mathrm{vfhs}(G,H)& \le 2^{|F_{int}\left(G\right)|-1},\hfill \\ \hfill \mathrm{efhs}(G,H)& \le 2^{|F_{int}\left(G\right)|-1}.\hfill \end{array}$$

Proof. 

Consider a plane graph G admitting the H-covering given by subgraphs $H_1,H_2,\dots ,$$H_t$. Denote the internal faces of G arbitrarily by the symbols $f_1,f_2,\dots ,f_{|F_{int}\left(G\right)|}$.

First, we define a vertex-face $2^{|F_{int}\left(G\right)|-1}$-labeling $\phi$ of G in the following way.

$$\begin{array}{cccc}\hfill \phi \left(v\right)& =1\hfill & \hfill & \mathrm{for}v\in V\left(G\right),\hfill \\ \hfill \phi \left(f_i\right)& =2^{i-1}\hfill & \hfill & \mathrm{for}i=1,2,\dots ,|F_{int}\left(G\right)|.\hfill \end{array}$$

Let us define the labeling $\theta$ such that

$$\begin{array}{c}\hfill {\theta }_{i,j}=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}{f}_i\in F_{int}\left(H_j\right),\hfill \\ 0,\hfill & \mathrm{if}{f}_i\notin F_{int}\left(H_j\right),\hfill \end{array}\right.\end{array}$$

where $i=1,2,\dots ,|F_{int}\left(G\right)|$, $j=1,2,\dots ,t$.

The associated H-weights are the sums of all vertex labels and face labels of vertices and faces in the given subgraph. Thus, for $j=1,2,\dots ,t$ we have

$$\begin{array}{cc}\hfill w_{\phi }\left(H_j\right)=& \sum _{v\in V\left(H_j\right)}\phi \left(v\right)+\sum _{f\in F_{int}\left(H_j\right)}\phi \left(f\right)=\sum _{v\in V\left(H_j\right)}1+\sum _{f_i\in F_{int}\left(H_j\right)}{2}^{i-1}=\left|V\left(H_j\right)\right|+\sum _{i=1}^{|F_{int}\left(G\right)|}{\theta }_{i,j}{2}^{i-1}.\hfill \end{array}$$

(1)

As we have $|V\left(H_j\right)|=|V\left(H\right)|$ for every $j=1,2,\dots ,t$, to prove that the H-weights are all distinct, it is enough to show that the sums ${\sum }_{i=1}^{|F_{int}\left(G\right)|}{\theta }_{i,j}{2}^{i-1}$ are distinct for every $j=1,2,\dots ,t$. However, this is evident if we consider that the ordered $\left(\right|F_{int}\left(G\right)\left|\right)$-tuple $({\theta }_{|F_{int}\left(G\right)|,j}{\theta }_{|F_{int}\left(G\right)|-1,j}$$\dots {\theta }_{2,j}{\theta }_{1,j})$ corresponds to binary code representation of the sum (1). As different subgraphs isomorphic to H cannot have the same face sets, we immediately find that the $\left(\right|F_{int}\left(G\right)\left|\right)$-tuples are different for different subgraphs. Thus, we have

$$\begin{array}{c}\hfill \mathrm{vfhs}(G,H)\le 2^{|F_{int}\left(G\right)|-1}.\end{array}$$

To prove that $\mathrm{efhs}(G,H)\le 2^{|F_{int}\left(G\right)|-1}$, it suffices to consider the edge–face $2^{|F_{int}\left(G\right)|-1}$-labeling $\psi$ of G defined by

$$\begin{array}{cccc}\hfill \psi \left(e\right)& =1\hfill & \hfill & \mathrm{for}e\in E\left(G\right),\hfill \\ \hfill \psi \left(f_i\right)& =2^{i-1}\hfill & \hfill & \mathrm{for}i=1,2,\dots ,|F_{int}\left(G\right)|.\hfill \end{array}$$

Using similar arguments as in the previous case, we prove that this labeling has desired properties. □

3. Conclusions

In this paper, we have introduced two new graph parameters—the vertex–face H-irregularity strength $\mathrm{vfhs}(G,H)$ and the edge–face H-irregularity strength $\mathrm{efhs}(G,H)$—as a natural extension of the edge (vertex) H-irregularity strength and the entire face irregularity strength of plane graphs.

We have estimated lower and upper bounds for these parameters and determined the exact values of $\mathrm{vfhs}(L_n,L_m)$, $\mathrm{efhs}(L_n,L_m)$, $\mathrm{vfhs}(A(F_n,G),A(F_m,G))$ and $\mathrm{efhs}(A(F_n,G),$$A(F_m,G))$ for every $m,n$, where $2\le m\le n$ and $G\ncong F_k$ for every $k>m$. These obtained exact values prove the sharpness of the lower bounds of the vertex–face H-irregularity strength and the edge–face H-irregularity strength.

This leads us to suggest the following conjecture.

Conjecture 1.

Let $G=\left(V\right(G),E(G),F(G\left)\right)$ be a two-connected plane graph admitting an H-covering given by t subgraphs isomorphic to H. Let $S_i$, $i=1,2,\dots ,s$ be all subgraphs of G such that $S_i$ is a maximum common subgraph of $r_i$, $r_i\ge 2$, subgraphs of G isomorphic to H. Then,

$$\begin{array}{cc}\hfill \mathrm{vfhs}(G,H)=& max\left\{⌈1+\frac{t-1}{\left|V\left(H\right)\right|+|F_{int}\left(H\right)|}⌉,⌈1+\frac{r_1-1}{|V(H\backslash S_1)|+|F_{int}(H\backslash S_1)|}⌉,\dots ,⌈1+\frac{r_s-1}{|V(H\backslash S_s)|+|F_{int}(H\backslash S_s)|}⌉\right\},\hfill \\ \hfill \mathrm{efhs}(G,H)=& max\left\{⌈1+\frac{t-1}{\left|E\left(H\right)\right|+|F_{int}\left(H\right)|}⌉,⌈1+\frac{r_1-1}{|E(H\backslash S_1)|+|F_{int}(H\backslash S_1)|}⌉,\dots ,⌈1+\frac{r_s-1}{|E(H\backslash S_s)|+|F_{int}(H\backslash S_s)|}⌉\right\}.\hfill \end{array}$$