Siberian Snakes, Figure-8 and Spin Transparency Techniques for High Precision Experiments with Polarized Hadron Beams in Colliders
Abstract
:1. Introduction
2. General Requirements to Polarized Colliders
3. Polarized Sources, Polarimetry and Spin Flipping
3.1. Polarized Sources
3.2. Polarimetry
3.3. Spin Flipping
4. Spin Resonances
5. Spin Dynamics in Stationary Conditions: General Theory
5.1. Spin Dynamics on a Closed Orbit in a Ring
5.2. Spin Field and Adiabatic Invariant
6. Spin Echo Techniques for Spin Stabilization in Synchrotrons
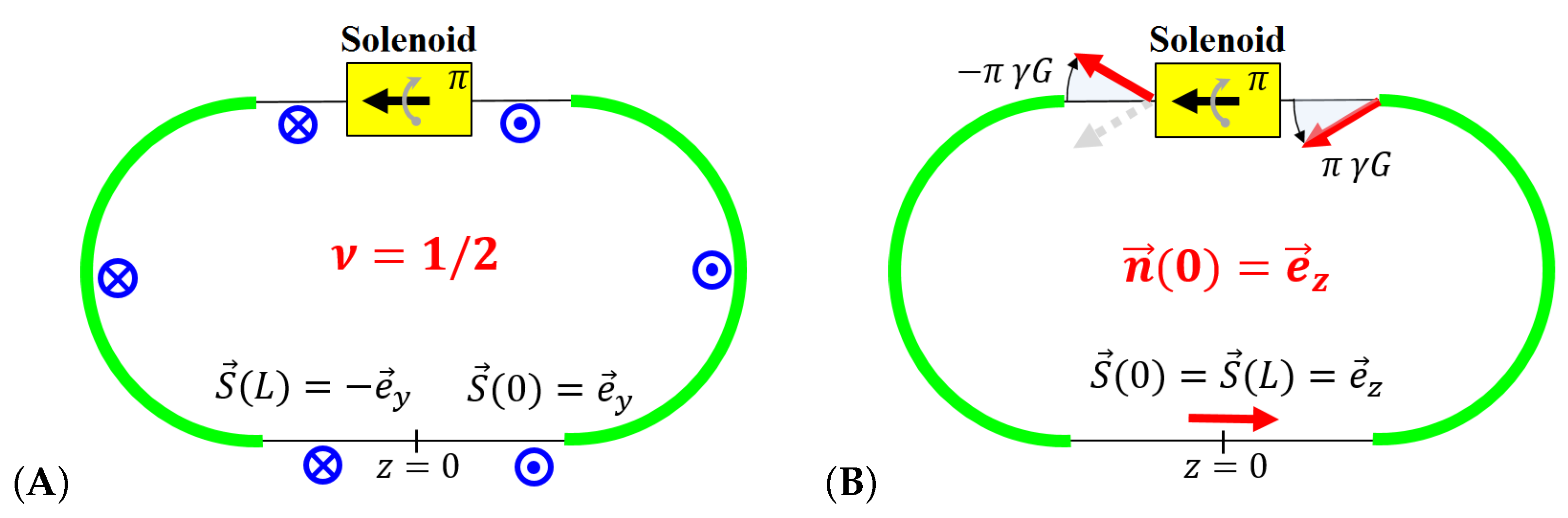
6.1. Siberian Snakes
6.2. Figure-8 Ring
7. Spin Transparency
7.1. General Idea
7.2. Spin Transparency of Figure-8
7.3. Spin Transparency in a Racetrack with Two Identical Siberian Snakes
7.4. Spin Navigators
7.5. Spin Response Function in the ST Mode
7.6. Long-Term Spin Stability in ST Collider Mode
7.7. Deuteron Tensor Polarization
7.8. Spin Transparency Benefits
- Energy-independent spin tune
- Preservation of polarization of any ion species including deuterons during acceleration by maintaining a small constant spin tune using weak magnetic fields
- Extendibility to arbitrary energy through compensation of the zero-integer spin resonance strength and/or use of pairs of compact Siberian snakes
- Ease of polarization control by weak magnetic fields
- Adiabatic spin manipulation including spin flip without polarization loss
- Manipulation of the polarization with no impact on the orbital dynamics
- Possibility of ultra-high precision polarized beam experiments
- Equalization of the up and down polarization life times for electron beams
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Accardi, A.; Albacete, J.L.; Anselmino, M.; Armesto, N.; Aschenauer, E.C.; Bacchetta, A.; Boer, D.; Brooks, W.K.; Burton, T.; Chang, N.-B.; et al. Electron Ion Collider: The Next QCD Frontier. Eur. Phys. J. A 2016, 52, 268. [Google Scholar] [CrossRef] [Green Version]
- Okun, L.B. Note concerning CP parity. Yad. Fiz. 1965, 1, 938. [Google Scholar]
- Prentki, J.; Veltman, M.J.G. Possibility of CP violation in semistrong interactions. Phys. Lett. 1965, 15, 88. [Google Scholar] [CrossRef]
- Lee, T.D.; Wolfenstein, L. Analysis of CP Noninvariant Interactions and the K0(1), K0(2) System. Phys. Rev. 1965, 138, B1490. [Google Scholar] [CrossRef] [Green Version]
- Bernreuther, W. CP violation and baryogenesis. In CP Violation in Particle, Nuclear and Astrophysics; Springer: Berlin/Heidelberg, Germany, 2002; pp. 237–293. [Google Scholar]
- Aschenauer, E.C.; Baker, M.D.; Bazilevsky, A.; Boyle, K.; Belomestnykh, S.; Ben-Zvi, I.; Brooks, S.; Brutus, C.; Burton, T.; Fazio, S.; et al. eRHIC design study: An electron-ion collider at BNL. arXiv 2014, arXiv:1409.1633. [Google Scholar]
- Kekelidze, V.D.; Lednicky, R.; Matveev, V.A.; Meshkov, I.N.; Sorin, A.S.; Trubnikov, G.V. Three stages of the NICA accelerator complex. Eur. Phys. J. A 2016, 52, 211. [Google Scholar] [CrossRef]
- Semertzidis, Y. Axion dark matter searches. PoS ICHEP 2019, 2018, 729. [Google Scholar]
- Chen, X. A Plan for EIC in China. arXiv 2018, arXiv:1809.00448. [Google Scholar]
- Derbenev, Y.S.; Kondratenko, A.M. Polarized particle acceleration. Dokl. Acad. Nauk SSSR 1975, 223, 830. [Google Scholar]
- Derbenev, Y.S. University of Michigan Report; UM HE 96-05; University of Michigan: Ann Arbor, Michigan, 1996. [Google Scholar]
- Abeyratne, S.; Accardi, A.; Ahmed, S.; Barber, D.; Bisognano, J.; Bogacz, A.; Castilla, A.; Chevtsov, P.; Corneliussen, S.; Deconinck, W.; et al. Science Requirements and Conceptual Design for a Polarized Medium Energy Electron-Ion Collider at Jefferson Lab. arXiv 2012, arXiv:1209.0757. [Google Scholar]
- Filatov, Y.N.; Kondratenko, A.M.; Kondratenko, M.A.; Derbenev, Y.S.; Morozov, V.S. Transparent spin method for spin control of hadron beams in colliders. Phys. Rev. Lett. 2020, 124, 194801. [Google Scholar] [CrossRef]
- Milner, R.G. PoS PSTP2013. arXiv 2013, arXiv:1311.5016. [Google Scholar]
- Sy, A. ICFA-BD Newsletter; International Committee for Future Accelerators: Batavia, IL, USA, 2018; Volume 74, p. 99. [Google Scholar]
- Fischer, W.; Bazilevsky, A. Impact of three-dimensional polarization profiles on spin-dependent measurements in colliding beam experiments. Phys. Rev. ST Accel. Beams 2012, 15, 041001. [Google Scholar] [CrossRef] [Green Version]
- Froisart, M.; Stora, R. Depolarisation d’un faisceau de protons polarises dans un synchrotron. Nucl. Instrum. Methods 1960, 7, 297. [Google Scholar] [CrossRef]
- Cohen, D. Feasibility of Accelerating Polarized Protons with the Argonne ZGS. Rev. Sci. Instrum. 1962, 33, 161. [Google Scholar] [CrossRef]
- Simonyan, K.A.; Orlov, Y.F. Anomalous Resonance Spin Flip of a Particle in a Magnetic Field. Zh. Eksp. Teor. Fiz. 1963, 45, 173. [Google Scholar]
- Plis, Y.A.; Soroko, L.M. The current state of the physics and technology of obtaining polarized particle beams. Uspekhi Fiz. Nauk 1972, 107, 281. [Google Scholar] [CrossRef]
- Khoe, T.; Ratner, L.G.; Martin, R.L.; Parker, E.F.; Potts, C.W.; Ratner, L.G.; Timm, R.E. Acceleration of polarized protons to 8.5 GeV/c. Part. Accel. 1975, 6, 213. [Google Scholar]
- Montague, B.W. Polarized beams in high energy storage rings. Phys. Rep. 1984, 113, 1. [Google Scholar] [CrossRef]
- Khiari, F.Z.; Cameron, P.R.; Crabb, D.G.; Fujisaki, M.; Gialas, I. Acceleration of polarized protons to 22 GeV/c and the measurement of spin-spin effects in p↑+p↑→p+p. Phys. Rev. D 1989, 39, 45. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.Y. Spin-depolarization mechanisms due to overlapping spin resonances in synchrotrons. Phys. Rev. E 1993, 47, 3631. [Google Scholar] [CrossRef]
- Lee, S.Y. Spin Dynamics and Snakes in Synchrotrons; World Scientific: Singapore, 1997. [Google Scholar]
- Ranjbar, V.H.; Lee, S.Y.; Huang, H.; Luccio, A.U.; MacKay, W.W.; Ptitsyn, V.; Roser, T.; Tepikian, S. Observation of higher-order snake resonances in polarized proton acceleration in RHIC. Phys. Rev. Lett. 2003, 91, 034801. [Google Scholar] [CrossRef]
- Hoffstaetter, G.H.; Vogt, M. Strength of higher-order spin-orbit resonances. Phys. Rev. E 2004, 70, 056501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, C.; Kewisch, J.; Huang, H.; Minty, M. Minimization of spin tune spread for preservation of spin polarization at RHIC. Phys. Rev. Accel. Beams 2019, 22, 061002. [Google Scholar] [CrossRef] [Green Version]
- Ptitsin, V.I.; Shatunov, Y.M. Helical spin rotators and snakes. Nucl. Instrum. Methods Phys. Res. Sect. A 1997, 398, 126. [Google Scholar] [CrossRef]
- Caussyn, D.D.; Derbenev, Y.S.; Ellison, T.J.P.; Lee, S.Y.; Rinckel, T.; Schwandt, P.; Sperisen, F.; Stephenson, E.J.; von Przewoski, B.; Blinov, B.B.; et al. Spin Flipping a Stored Polarized Proton Beam. Phys. Rev. Lett. 1994, 73, 2857. [Google Scholar] [CrossRef] [PubMed]
- Koop, I.; Shatunov, Y. Spin flip by RF-field at storage rings with Siberian snakes. AIP Conf. Proc. 1995, 343, 317. [Google Scholar]
- Blinov, B.B.; Etienne, Z.B.; Krisch, A.D.; Leonova, M.A.; Lorenzon, W.; Morozov, V.S.; Peters, C.C.; Wong, K.V.; Yonehara, K.; Anferov, V.A.; et al. 99.6% Spin-Flip Efficiency in the Presence of a Strong Siberian Snake. Phys. Rev. Lett. 2001, 88, 014801. [Google Scholar] [CrossRef] [Green Version]
- Morozov, V.S.; Etienne, Z.B.; Kandes, M.C.; Krisch, A.D.; Leonova, M.A.; Sivers, D.W.; Wong, V.K.; Yonehara, K.; Anferov, V.A.; Meyer, H.O.; et al. First Spin Flipping of a Stored Spin-1 Polarized Beam. Phys. Rev. Lett. 2003, 91, 214801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mane, S.R. Spin flipping in rings with Siberian snakes. Nucl. Instrum. Methods Phys. Res. Sect. A 2009, 605, 266. [Google Scholar] [CrossRef]
- Shatunov, Y.M. Spin control by rf fields at accelerators and storage rings. In XIII Advanced Research Workshop on High Energy Spin Physics (DSPIN-09); 2011; Available online: https://inspirehep.net/files/fc8db800ac20136cdbd0f7269faea0db (accessed on 18 December 2020).
- Huang, H.; Kewisch, J.; Liu, C.; Marusic, A.; Meng, W.; Méot, F.; Oddo, P.; Ptitsyn, V.; Ranjbar, V. and Roser, T. High Spin-Flip Efficiency at 255 GeV for Polarized Protons in a Ring With Two Full Siberian Snakes. Phys. Rev. Lett. 2018, 120, 264804. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Derbenev, Y.S.; Anferov, V.A. RF driven stable spin-flipping motion of a stored polarized beam. Phys. Rev. ST Accel. Beams 2000, 3, 094001. [Google Scholar] [CrossRef] [Green Version]
- Derbenev, Y.; Kondratenko, A.; Kondratenko, M.; Morozov, V.; Filatov, Y. Spin-flipping systems for storage rings. In Proceedings of the XIV Advanced Research Workshop on High Energy Spin Physics (DSPIN-11), JINR, Dubna, Russia, 20–24 September 2011; p. 377. [Google Scholar]
- Kondratenko, A.M.; Kondratenko, M.A.; Filatov, Y.N.; Morozov, V.S.; Derbenev, Y.S.; Lin, F.; Zhang, Y. Spin Flipping System in the JLEIC Collider Ring. In Proceedings of the NAPAC’16, Chicago, IL, USA, 9–14 October 2016. [Google Scholar]
- Belov, A.S.; Esin, S.K.; Netchaeva, L.P.; Plokhinski, Y.V.; Vasil’ev, G.A.; Klenov, V.S.; Turbabin, A.V.; Yakushev, V.P. High-intensity source of polarized negative hydrogen ions with a resonant charge-exchange plasma ionizer. Rev. Sci. Instrum. 1996, 67, 1293. [Google Scholar] [CrossRef]
- Belov, A.S.; Netchaeva, L.P.; Turbabin, A.V. Intensity improvements of pulsed source of polarized negative hydrogen ions. Rev. Sci. Instrum. 2006, 77, 03A522. [Google Scholar] [CrossRef]
- Belov, A.S. Production of Polarized Ions with Nearly Resonant Charge-Exchange Collisions in Plasma. AIP Conf. Proc. 2008, 980, 209. [Google Scholar]
- Belov, A.S.; Donets, D.E.; Fimushkin, V.V.; Kovalenko, A.D.; Kutuzova, L.V.; Prokofichev, Y.V.; Shutov, V.B.; Turbabin, A.V.; Zubets, V.N. Source of polarized ions for the JINR accelerator complex. J. Phys. Conf. Ser. 2017, 938, 012017. [Google Scholar] [CrossRef]
- Belov, A.S. A scheme for a polarized 3He ion source with a resonant charge-exchange plasma ionizer. Nucl. Instrum. Methods Phys. Res. Sect. A 1998, 402, 205. [Google Scholar] [CrossRef]
- Zelenski, A.; Kponou, A.; Ritter, J.; Belov, A.; Zubets, V. The RHIC polarized H− source. Rev. Sci. Instrum. 2016, 87, 02B705. [Google Scholar] [CrossRef]
- Zelenski, A. Optically-Pumped Polarized H− and 3He++ Ion Sources Development at RHIC. In Proceedings of the IPAC’18, TUYGBE4, Vancouver, BC, Canada, 29 April 29–4 May 2018. [Google Scholar]
- Maxwell, J.; Epstein, C.; Milner, R.; Alessi, J.; Beebe, E.; Pikin, A.; Ritter, J.; Zelenski, A. Development of a Polarized Helium-3 Source for RHIC and eRHIC. Int. J. Mod. Phys. Conf. Ser. 2016, 40, 1660102. [Google Scholar] [CrossRef] [Green Version]
- Colegrove, F.D.; Schearer, L.D.; K, G. Walters, Polarization of 3He Gas by Optical Pumping. Phys. Rev. 1963, 132, 2561. [Google Scholar] [CrossRef]
- Barschall, H.H.; Haeberli, W. (Eds.) Madison Convention. In Proceedings of the 3rd International Symposium on Polarization Phenomena in Nuclear Physics, Madison, WI, USA, 31 August–4 September 1970; University of Wisconsin Press: Madison, WI, USA, 1971; p. xxv. [Google Scholar]
- Thomas, L.H.I. The kinematics of an electron with an axis. Philos. Mag. 1927, 3, 1. [Google Scholar] [CrossRef]
- Bargmann, V.; Michel, L.; Telegdi, V.L. Precession of the polarization of particles moving in a homogeneous electromagnetic field. Phys. Rev. Lett. 1959, 2, 435. [Google Scholar] [CrossRef]
- Courant, E.D. The ultrastructure of pulmonary lymphatic capillaries of newborn rabbits and of human infants. Bull. Am. Phys. Soc. 1962, 7, 33. [Google Scholar]
- Courant, E.D.; Ruth, R.D. BNL Report; BNL-51270. 1980. Available online: https://www.osti.gov/servlets/purl/7034691 (accessed on 25 December 2020).
- Derbenev, Y.S.; Kondratenko, A.M.; Skrinskii, A.N. Dynamics of the Polarization of Particles Near Spin Resonances. Zh. Eksp. Teor. Fiz. 1971, 60, 1216. [Google Scholar]
- Derbenev, Y.S.; Kondratenko, A.M.; Skrinsky, A.N. Particle spin motion in storage ring with arbitrary field. Dokl. Akad. Nauk SSSR 1970, 192, 1255. [Google Scholar]
- Derbenev, Y.S.; Serednyakov, S.I.; Shatunov, Y.M.; Kondratenko, A.M.; Skrinsky, A.N.; Tumaikin, G.M.; Shatunov, Y.M. Accurate calibration of the beam energy in a storage ring based on measurement of spin precession frequency of polarized particles. Part. Accel. 1980, 10, 177. [Google Scholar]
- Kondratenko, A.M.; Kondratenko, M.A.; Filatov, Y.N. Compensation for Particle Beam Depolarization of Spin Resonance Intersection at Accelerators. Part. Nucl. Lett. 2004, 1, 266. [Google Scholar]
- Kondratenko, A.M.; Kondratenko, M.A.; Filatov, Y.N. On Compensation of Beam Depolarization at Crossing of a Spin Resonance, in Proc. SPIN’17, Kyoto, Japan. AIP Conf. Proc. 2007, 915, 874. [Google Scholar]
- Kondratenko, A.M.; Kondratenko, M.A.; Filatov, Y.N. Multiple Spin Resonance Crossing in Accelerators. AIP Conf. Proc. 2009, 1149, 789. [Google Scholar]
- Morozov, V.S.; Chao, A.W.; Krisch, A.D.; Leonova, M.A.; Raymond, R.S.; Sivers, D.W.; Wong, V.K.; Garishvili, A.; Gebel, R.; Lehrach, A.; et al. Experimental Test of a New Technique to Overcome Spin-Depolarizing Resonances. Phys. Rev. Lett. 2009, 102, 244801. [Google Scholar] [CrossRef] [Green Version]
- Derbenev, Y.S.; Kondratenko, A.M. Particle spin diffusion in storage rings. Zh. Eksp. Teor. Fiz. 1972, 62, 430. [Google Scholar]
- Barber, D.P.; Ellison, J.A.; Heinemann, K. Quasiperiodic spin-orbit motion and spin tunes in storage rings. Phys. Rev. ST Accel. Beams 2004, 7, 124002. [Google Scholar] [CrossRef] [Green Version]
- Chao, A.W.; Courant, E.D. Spin echo in synchrotrons. Phys. Rev. Accel. Beams 2007, 10, 014001. [Google Scholar] [CrossRef] [Green Version]
- Derbenev, Y.S.; Kondratenko, A.M. Acceleration of polarized particles in synchrotrons to high energies. In Proceedings of the 10th International Conference on High Energy Accelerators, Protvino, Russia, 11–17 July 1977; pp. 70–75. [Google Scholar]
- Derbenev, Y.S.; Kondratenko, A.M. On the Possibilities to Obtain High-Energy Polarized Particles in Accelerators and Storage Rings. AIP Conf. Proc. 1979, 51, 292. [Google Scholar]
- Kondratenko, A.M. Polarized Beams in Storage Rings and Cyclic Accelerators. Ph.D. Thesis, INP, Siberian Branch of the Academy of Sciences of USSR, Novosibirsk, Russia, 1982. [Google Scholar]
- Courant, E.D. Helical Siberian snakes. AIP Conf. Proc. 1989, 187, 1085. [Google Scholar]
- Derbenev, Y.S.; Kondratenko, A.M. On polarization preservation criteria in accelerator with Siberian snakes. J. Tech. Phys. 1989, 59, 104. [Google Scholar]
- Derbenev, Y.S.; Kondratenko, A.M. Possibilities of polarized protons acceleration up to energy 1 TeV and above. In Proceedings of the XII Int. Conference on High Energy Accelerators, Fermilab, Batavia, 11–16 August 1983; pp. 413–415. [Google Scholar]
- Lee, S.Y.; Courant, E.D. Tolerance of imperfections in high-energy circular accelerators for polarized protons. Phys. Rev. D 1990, 41, 292. [Google Scholar] [CrossRef] [PubMed]
- Chao, A.W.; Derbenev, Y.S. Cancellation of the Quadrupole Effect on Spin in High-Energy Accelerators. Part. Accel. 1991, 36, 25. [Google Scholar]
- Mane, S.R.; Shatunov, Y.M.; Yokoya, K. Siberian Snakes in high-energy accelerators. J. Phys. G Nucl. Part. Phys. 2005, 31, R151. [Google Scholar] [CrossRef]
- Harrison, M.; Peggs, S.; Roser, T. The RHIC accelerator. Annu. Rev. Nucl. Part. Sci. 2002, 52, 425–469. [Google Scholar] [CrossRef] [Green Version]
- Krisch, A.D.; Mane, S.R.; Raymond, R.S.; Roser, T.; Stewart, J.A.; Terwilliger, K.M.; Vuaridel, B.; Goodwin, J.E.; Meyer, H.-O.; Minty, M.G.; et al. First test of the Siberian snake magnet arrangement to overcome depolarizing resonances in a circular accelerator. Phys. Rev. Lett. 1989, 63, 1137. [Google Scholar] [CrossRef]
- Kovalenko, A.; Agapov, N.; Kekelidze, V.; Kekelidze, V.; Lednicky, R.; Meshkov, I.; Mikhaylov, V.; Sidorin, A.; Sorin, A.; Trubnikov, G. The NICA Facility in polarized proton operation mode. In Proceedings of the IPAC’11, San Sebastian, Spain, 4–9 September 2011. [Google Scholar]
- Kovalenko, A.D.; Butenko, A.V.; Kekelidze, V.D.; Mikhaylov, V.A.; Kondratenko, M.A.; Kondratenko, A.M.; Filatov, Y.N. Orbital Parameters of Proton and Deuteron Beams in NICA Collider with Solenoid Siberian Snakes. J. Phys. Conf. Ser. 2016, 678, 012022. [Google Scholar] [CrossRef] [Green Version]
- Ptitsin, V.I.; Shatunov, Y.M.; Peggs, G. 1996, pp. 3331–3333. Available online: https://accelconf.web.cern.ch/p95/ARTICLES/RAQ/RAQ21.PDF (accessed on 25 December 2020).
- Courant, E.D.; Fischer, W.; Luccio, A.; Mariam, F.; Okamura, M.; Peggs, S.; Pilat, F.; Ptitsin, V.; Roser, T.; Shatunov, Y.; et al. The use of helical dipole magnets in the RHIC spin project. In Proceedings of the 12th International Symposium on High Energy Spin Physics, Amsterdam, The Netherlands, 10–14 September 1996; pp. 579–581. [Google Scholar]
- Ptitsyn, V.I. Polarized Beams in Accelerators and Storage Rings with Siberian Snakes. Ph.D. Dissertation, INP, Siberian Branch of the Russian Academy of Sciences, Novosibirsk, Russia, 2005. [Google Scholar]
- Courant, E.D.; Ratner, L.G. Depolarization during acceleration and storage of polarized protons and deuterons. AIP Conf. Proc. 1978, 42, 101. [Google Scholar]
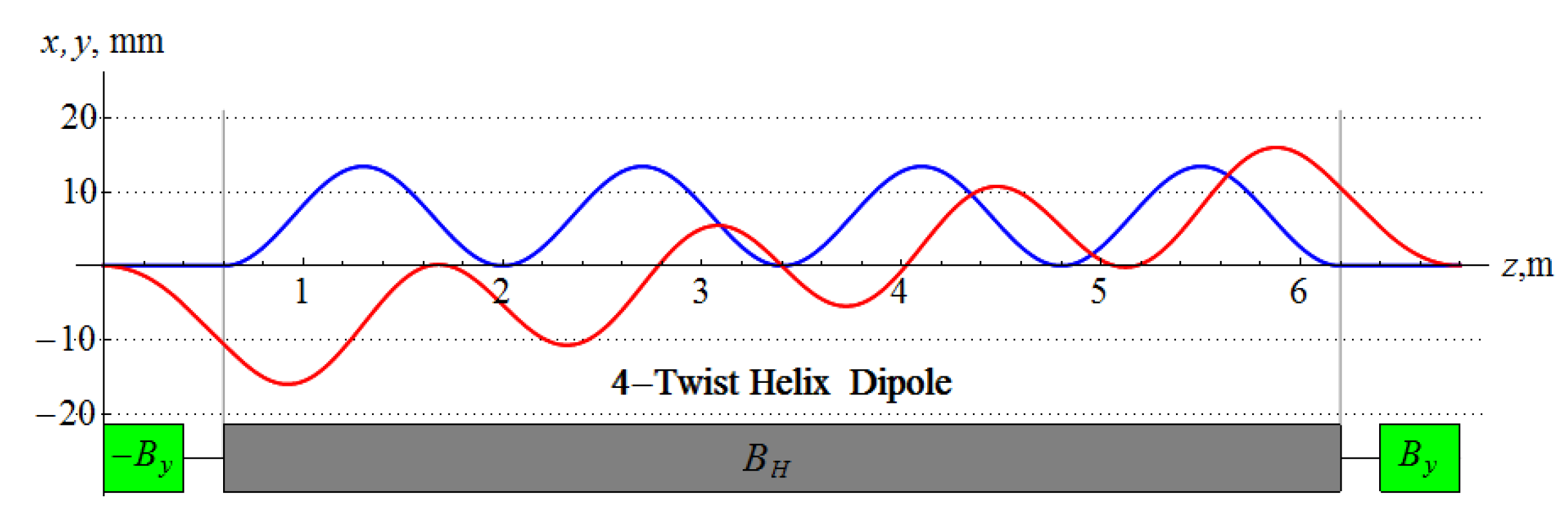
- Antoulinakis, F.; Chen, Y.; Dutton, A.; De La Fuente, E.R.; Haupert, S.; Ljungman, E.A.; Myers, P.D.; Thompson, J.K.; Tai, A.; Aidala, C.A.; et al. 4-twist helix snake to maintain polarization in multi-GeV proton rings. Phys. Rev. Accel. Beams 2017, 20, 091003. [Google Scholar] [CrossRef] [Green Version]
- Filatov, Y.N.; Kondratenko, A.M.; Kondratenko, M.A. Spin response function technique in spin-transparent synchrotrons. Eur. Phys. J. C 2020, 80, 778. [Google Scholar] [CrossRef]
- Morozov, V.S.; Derbenev, Y.S.; Lin, F.; Zhang, Y.; Kondratenko, A.; Kondratenko, M.; Filatov, Y. Ion polarization control in MEIC rings using small magnetic fields integrals. PoS (PSTP 2013) 2014, 182, 026. [Google Scholar]
- Kovalenko, A.D.; Butenko, A.V.; Kekelidze, V.D.; Mikhaylov, V.A.; Filatov, Y.; Kondratenko, A.M.; Kondratenko, M.A. Ion polarization control in the MPD and SPD detectors of the NICA collider. In Proceedings of the IPAC’15, Richmond, VA, USA, 3–8 May 2015; pp. 2031–2033. [Google Scholar]
- Kondratenko, A.M.; Derbenev, Y.S.; Filatov, Y.N.; Lin, F.; Morozov, V.S.; Kondratenko, M.A.; Zhang, Y. Preservation And Control Of The Proton And Deuteron Polarizations In The Proposed Electron-Ion Collider At Jefferson Lab. Phys. Part. Nucl. 2014, 45, 319. [Google Scholar] [CrossRef]
- Morozov, V.S.; Derbenev, Y.S.; Lin, F.; Zhang, Y.; Filatov, Y.; Kondratenko, A.M.; Kondratenko, M.A. Baseline Scheme for Polarization Preservation and Control in the MEIC Ion Complex. In Proceedings of the IPAC’15, Richmond, VA, USA, 3–8 May 2015; pp. 2301–2303. [Google Scholar]
- Filatov, Y.N.; Kovalenko, A.D.; Butenko, A.V.; Syresin, E.M.; Mikhailov, V.A.; Shimanskiy, S.S.; Kondratenko, A.M.; Kondratenko, M.A. Spin transparency mode in the NICA collider. EPJ Web Conf. 2019, 204, 10014. [Google Scholar] [CrossRef]
- Morozov, V.S.; Adams, P.; Derbenev, Y.S.; Filatov, Y.; Huang, H.; Kondratenko, A.M.; Kondratenko, M.A.; Lin, F.; Méot, F.; Ptitsyn, V.; et al. Experimental verification of transparent spin mode in RHIC. In Proceedings of the IPAC’19, Melbourne, Australia, 19–24 May 2019; pp. 2783–2786. [Google Scholar]
- Basdevant, J.-L. Lectures on Quantum Mechanics; Springer: New York, NY, USA, 2007; p. 232. [Google Scholar]

















Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Derbenev, Y.S.; Filatov, Y.N.; Kondratenko, A.M.; Kondratenko, M.A.; Morozov, V.S. Siberian Snakes, Figure-8 and Spin Transparency Techniques for High Precision Experiments with Polarized Hadron Beams in Colliders. Symmetry 2021, 13, 398. https://doi.org/10.3390/sym13030398
Derbenev YS, Filatov YN, Kondratenko AM, Kondratenko MA, Morozov VS. Siberian Snakes, Figure-8 and Spin Transparency Techniques for High Precision Experiments with Polarized Hadron Beams in Colliders. Symmetry. 2021; 13(3):398. https://doi.org/10.3390/sym13030398
Chicago/Turabian StyleDerbenev, Yaroslav S., Yury N. Filatov, Anatoliy M. Kondratenko, Mikhail A. Kondratenko, and Vasiliy S. Morozov. 2021. "Siberian Snakes, Figure-8 and Spin Transparency Techniques for High Precision Experiments with Polarized Hadron Beams in Colliders" Symmetry 13, no. 3: 398. https://doi.org/10.3390/sym13030398
APA StyleDerbenev, Y. S., Filatov, Y. N., Kondratenko, A. M., Kondratenko, M. A., & Morozov, V. S. (2021). Siberian Snakes, Figure-8 and Spin Transparency Techniques for High Precision Experiments with Polarized Hadron Beams in Colliders. Symmetry, 13(3), 398. https://doi.org/10.3390/sym13030398





