Tricomi’s Method for the Laplace Transform and Orthogonal Polynomials

Abstract

Tricomi’s method for computing a set of inverse Laplace transforms in terms of Laguerre polynomials is revisited. By using the more recent results about the inversion and the connection coefficients for the series of orthogonal polynomials, we find the possibility to extend the Tricomi method to more general series expansions. Some examples showing the effectiveness of the considered procedure are shown.

1. Introduction

In three notes presented to the Accademia dei Lincei in 1935 [1,2], Francesco G. Tricomi introduced a method for the computation of the Laplace transform of functions that can be developed in a series of Laguerre polynomials. Precisely, he proved the following proposition:

Proposition 1.

If the analytic function $F\left(s\right)$ is regular at infinity and we can find a real number h such that it can be represented with a series of the form

$$\begin{array}{c}\hfill {\displaystyle F\left(s\right)=\frac{1}{s+h}\sum _{n=0}^{\infty }{a}_n{\left({\displaystyle \frac{s+h-1}{s+h}}\right)}^n,}\end{array}$$

(1)

then it is the Laplace transform of the sum of the series of Laguerre polynomials

$$\begin{array}{c}\hfill f\left(t\right)=e^{-ht}\sum _{n=0}^{\infty }{a}_n{L}_n\left(t\right),\end{array}$$

(2)

which is absolutely and uniformly convergent for $t>0$.

In particular, for $h=0$, that is, avoiding the shift that follows from a basic rule of the Laplace transform, Tricomi found the functions pair $\left(F\right(s),f(t\left)\right)$:

$$\begin{array}{c}\hfill {\displaystyle F\left(s\right)=\frac{1}{s}\sum _{n=0}^{\infty }{a}_n{\left({\displaystyle \frac{s-1}{s}}\right)}^n\leftrightarrow f\left(t\right)=\sum _{n=0}^{\infty }{a}_n{L}_n\left(t\right).}\end{array}$$

(3)

We recall that the Laguerre polynomials are obtained by letting $\alpha =0$ in the general formula

$$\begin{array}{c}\hfill {\displaystyle L_n^{\left(\alpha \right)}\left(x\right)=\frac{{(\alpha +1)}_n}{n!}{}_1{F}_1\left(\begin{array}{c}-n\\ \alpha +1\end{array};x\right),}\end{array}$$

where ${\left(a\right)}_n=a(a+1)\cdots (a+n-1)$ denotes the rising factorial and, in particular, it results ${\left(1\right)}_n=n!$.

Tricomi says that the correspondence of the above functions was suggested to him by the series expansion of the Bessel function, in terms of Laguerre polynomials:

$$\begin{array}{c}\hfill {\displaystyle J_0\left(2\sqrt{x}\right)=\frac{1}{e}\sum _{k=0}^{\infty }\frac{L_k\left(x\right)}{k!},}\end{array}$$

(4)

where

$$\begin{array}{c}\hfill {\displaystyle L_k\left(x\right)=\sum _{n=0}^k\left(\genfrac{}{}{0pt}{}{k}{n}\right)\frac{{(-1)}^n{x}^n}{n!}.}\end{array}$$

(5)

More recently it was observed [3] that the same Bessel function admits another expansion, making use of a power series, the so-called Laguerre type exponential, namely:

$$\begin{array}{c}\hfill {\displaystyle J_0\left(2\sqrt{x}\right)=\sum _{k=0}^{\infty }\frac{{(-1)}^k{x}^k}{{(k!)}^2}.}\end{array}$$

(6)

In fact, it turns out that the expansions (4) and (6) are equivalent, since:

$$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle J_0\left(2\sqrt{x}\right)=\frac{1}{e}\sum _{k=0}^{\infty }\frac{1}{k!}\sum _{\ell =0}^k\left(\genfrac{}{}{0pt}{}{k}{\ell }\right)\frac{{(-1)}^{\ell }{x}^{\ell }}{\ell !}=\frac{1}{e}\sum _{\ell =0}^{\infty }\sum _{k=\ell }^{\infty }\left(\genfrac{}{}{0pt}{}{k}{\ell }\right)\frac{{(-1)}^{\ell }{x}^{\ell }}{k!\ell !}=}\\ {\displaystyle \phantom{1pt30pt}=\frac{1}{e}\sum _{\ell =0}^{\infty }\sum _{k=\ell }^{\infty }\frac{{(-1)}^{\ell }{x}^{\ell }}{(k-\ell )!{(\ell !)}^2}=\frac{1}{e}\sum _{\ell =0}^{\infty }\frac{{(-1)}^{\ell }{x}^{\ell }}{{(\ell !)}^2}\sum _{k=\ell }^{\infty }\frac{1}{(k-\ell )!}=\sum _{\ell =0}^{\infty }\frac{{(-1)}^{\ell }{x}^{\ell }}{{(\ell !)}^2}.}\end{array}\end{array}$$

It is worth noting that the Laguerre-type exponentials were previously considered by Le Roi [4] and used in [5,6] in the framework of generalised Wright functions. Actually they are a particular case of more general special functions previously considered by V. Kiryakova [7].

As it is possible to transform the expansions in Laguerre polynomials, by using the inversion or the connection coefficients, into different expansions in terms of other polynomial sets, as it is shown in many articles [8,9,10,11], the above considerations suggest that we extend the Tricomi method in order to find different Laplace function pairs. This is done even on the basis of preceding results in [12] and the connection of the Laplace transform with orthogonal polynomials, reported in [13].

In what follows, we first apply the inversion coefficients in order to find the Laplace transform corresponding to a given power series, then we apply the same methodology to the series of orthogonal polynomials.

2. Tricomi LT of Laguerre Series

We use the classical notations. We denote the Laplace transform by $LT$ by using for it the symbol $\mathcal{L}$.

$$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle \mathcal{L}\left(f\left(t\right)\right):={\int }_0^{\infty }{exp}^{-1}\left(st\right)f\left(t\right)dt=F\left(s\right),}\end{array}\end{array}$$

(7)

and for the Laguerre polynomials of degree n the symbol $L_n$,

$$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle \mathcal{L}\left(L_n\left(t\right)\right):={\int }_0^{\infty }{exp}^{-1}\left(st\right)L_n\left(t\right)dt=F\left(s\right)=\frac{1}{s}{\left(\frac{s-1}{s}\right)}^n.}\end{array}\end{array}$$

(8)

Then the Proposition 1, asserts that under the conditions recalled in [1], assuming:

$$\begin{array}{c}\hfill {\displaystyle \begin{array}{c}\end{array}f\left(t\right)=e^{-ht}\sum _{n=0}^{\infty }{a}_n{L}_n\left(t\right),}\end{array}$$

(9)

it results:

$$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle \mathcal{L}\left(f\left(t\right)\right):=\frac{1}{s+h}\sum _{n=0}^{\infty }{a}_n{\left({\displaystyle \frac{s+h-1}{s+h}}\right)}^n.}\end{array}\end{array}$$

(10)

3. LT of Power Series

The inversion coefficients of Laguerre polynomials are reported in [8,9], in the form:

$$\begin{array}{c}\hfill {\displaystyle t^n=\sum _{m=0}^n{I}_m\left(n\right)L_m\left(t\right),}\end{array}$$

(11)

where

$$\begin{array}{c}\hfill {\displaystyle I_m\left(n\right)={(-n)}_m\frac{1_n}{1_m}={(-1)}^m\left(\genfrac{}{}{0pt}{}{n}{m}\right)n!.}\end{array}$$

(12)

Then it results:

$$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle \sum _{n=0}^{\infty }{a}_n{t}^n=\sum _{n=0}^{\infty }\sum _{m=0}^n{a}_n{I}_m\left(n\right)L_m\left(t\right)=}\\ {\displaystyle =\sum _{m=0}^{\infty }\left(\sum _{n=m}^{\infty }{a}_n{I}_m\left(n\right)\right)L_m\left(t\right)=\sum _{m=0}^{\infty }{b}_m{L}_m\left(t\right),}\end{array}\end{array}$$

(13)

where

$$\begin{array}{c}\hfill {\displaystyle b_m=\sum _{n=m}^{\infty }{a}_n{I}_m\left(n\right)}\end{array}$$

(14)

Then we can proclaim the result

Theorem 1.

If the analytic function $F\left(s\right)$ is regular at infinity, decreasing at least as 1/s and such that it can be represented with the power series:

$$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle F\left(s\right)=\frac{1}{s+h}\sum _{m=0}^{\infty }{b}_m{\left(\frac{s+h-1}{s+h}\right)}^m,}\end{array}\end{array}$$

(15)

then it is the Laplace transform of the power series

$$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle f\left(t\right)=e^{-ht}\sum _{n=0}^{\infty }{a}_n{t}^n,}\end{array}\end{array}$$

(16)

where the coefficients $a_n$ and $b_m$ are linked by Equation (14), with the $I_m\left(n\right)$ in Equation (12).

Therefore, under the condition (14), we have found the pair:

$$\begin{array}{c}\hfill {\displaystyle F\left(s\right)=\frac{1}{s+h}\sum _{m=0}^{\infty }{b}_m{\left(\frac{s+h-1}{s+h}\right)}^m\leftrightarrow f\left(t\right)=e^{-ht}\sum _{n=0}^{\infty }{a}_n{t}^n.}\end{array}$$

(17)

4. LT of Orthogonal Polynomial Expansions

Suppose now that a function $f\left(t\right)$ satisfies the conditions:

• it admits the Laplace transform,
• by choosing a suitable h, it admits a series expansion with respect to a given orthogonal polynomial system $\left\{Q_n\left(t\right)\right\}$, of the type:

  $$\begin{array}{c}\hfill {\displaystyle f\left(t\right)=e^{-ht}\sum _{n=0}^{\infty }{c}_n{Q}_n\left(t\right),}\end{array}$$

  (18)

  where the coefficients $c_n$ are known.

The polynomials $Q_n\left(t\right)$ can be represented in terms of a different orthogonal polynomials system $P_m\left(t\right)$ by means of the equation

$$\begin{array}{c}\hfill {\displaystyle Q_n\left(t\right)=\sum _{m=0}^n{C}_m\left(n\right)P_m\left(t\right),}\end{array}$$

(19)

where the connection coefficients $C_m\left(n\right)$ are reported in [8].

In particular we can choose the basis of Laguerre polynomials $P_m\left(t\right)\equiv L_m\left(t\right)$, so that

$$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle f\left(t\right)=e^{-ht}\sum _{n=0}^{\infty }{c}_n\sum _{m=0}^n{C}_m\left(n\right)L_m\left(t\right)=e^{-ht}\sum _{m=0}^{\infty }\left(\sum _{n=m}^{\infty }{c}_n{C}_m\left(n\right)\right)L_m\left(t\right)=}\\ {\displaystyle =e^{-ht}\sum _{m=0}^{\infty }{d}_m{L}_m\left(t\right),}\end{array}\end{array}$$

(20)

where

$$\begin{array}{c}\hfill d_m=\sum _{n=m}^{\infty }{c}_n{C}_m\left(n\right).\end{array}$$

(21)

After this transformation, the function $f\left(t\right)$ is expressed in terms of Laguerre polynomials and the Tricomi method gives the result:

Theorem 2.

If the analytic function $F\left(s\right)$ is regular at infinity, decreasing at least as $1/s$ and such that, for a suitable choice of the parameter h, it can be represented with the power series:

$$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle F\left(s\right)=\frac{1}{s+h}\sum _{m=0}^{\infty }{d}_m{\left(\frac{s+h-1}{s+h}\right)}^m,}\end{array}\end{array}$$

(22)

then it is the Laplace transform of the power series

$$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle f\left(t\right)=e^{-ht}\sum _{n=0}^{\infty }{c}_n{Q}_n\left(t\right),}\end{array}\end{array}$$

(23)

where the coefficients $c_n$ and $d_m$ are linked by Equation (21), with the $C_m\left(n\right)$, reported in [8], depending on the considered polynomial set $Q_n\left(t\right)$.

Therefore, under the condition (21), we have found the pair:

$$\begin{array}{c}\hfill {\displaystyle F\left(s\right)=\frac{1}{s+h}\sum _{m=0}^{\infty }{d}_m{\left(\frac{s+h-1}{s+h}\right)}^m\leftrightarrow f\left(t\right)=e^{-ht}\sum _{n=0}^{\infty }{c}_n{Q}_n\left(t\right).}\end{array}$$

(24)

Remark 1.

In [8] the inversion and connection coefficients are reported for many other polynomial sets, including the generalized Laguerre polynomials $L_n^{\left(\alpha \right)}\left(t\right)$; however, we could avoid the use of these polynomials since the result stated in this section can be applied even to them.

Example 1.

As an example, assuming $Q_n\left(t\right)=H_n\left(t\right)$, that is the Hermite polynomials, according to [9], p. 687, it results:

$$\begin{array}{c}\hfill {\displaystyle C_m\left(n\right)=\frac{1_n{(-n)}_m{2}^n}{1_m}{}_2{F}_2\left(\begin{array}{c}\frac{m-n}{2},\frac{m-n+1}{2}\\ \frac{-n}{2},\frac{-n+1}{2}\end{array};-\frac{1}{4}\right)}\end{array}$$

(25)

that is:

$$\begin{array}{c}\hfill {\displaystyle C_m\left(n\right)={(-1)}^m{2}^{n}n!\left(\genfrac{}{}{0pt}{}{n}{m}\right)\sum _{k=0}^{\infty }\frac{{(m-n)}_k{(m-n+1)}_k}{{(-n)}_k{(-n+1)}_k}\frac{{(-1)}^k}{4^{k}k!},}\end{array}$$

(26)

and consequently, by Theorem 2, it results:

$$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle \mathcal{L}\left({\displaystyle e^{-ht}\sum _{n=0}^{\infty }{c}_n{H}_n\left(t\right)}\right):=\frac{1}{s+h}\sum _{m=0}^{\infty }\sum _{n=m}^{\infty }{c}_n{C}_m\left(n\right){\left(\frac{s+h-1}{s+h}\right)}^m,}\end{array}\end{array}$$

(27)

where the connection coefficients $C_m\left(n\right)$ are explicitly given above.

5. Numerical Results

In what follows we show some numerical examples of the considered procedure, assuming $h=0$, since a different choice does not affect the results.

The experiments have highlighted the benefit, in terms of numerical accuracy, arising from a direct numerical implementation rather than the use of automatic routines embedded in the Mathematica© computing system.

5.1. Example: LT of $e^{\mathrm{i}\pi t}$

Let us consider the function:

$$\begin{array}{c}\hfill f\left(t\right)=e^{\mathrm{i}\pi t},\end{array}$$

(28)

whose Laplace transform can be trivially evaluated as:

$$\begin{array}{c}\hfill {\displaystyle F\left(s\right)=\mathcal{L}\left(f\left(t\right)\right)\left(s\right)={\int }_0^{\infty }{exp}^{-1}\left(st\right)f\left(t\right)dt=\frac{1}{s-\mathrm{i}\pi }.}\end{array}$$

(29)

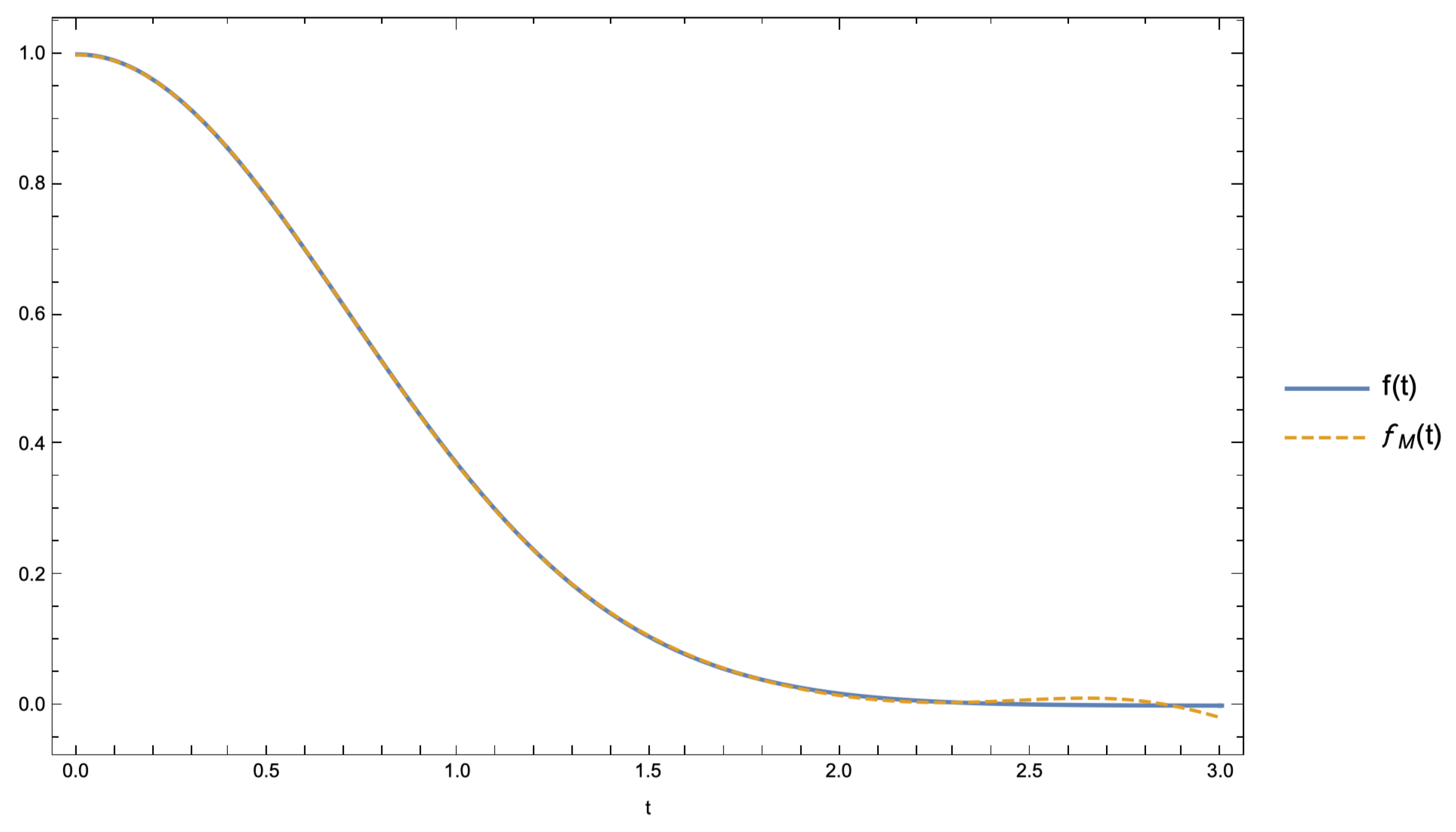
The Laguerre polynomial series approximant of $f\left(t\right)$ is given by:

$$\begin{array}{c}\hfill f_M\left(t\right)=\sum _{m=0}^M{a}_m{L}_m\left(t\right),\end{array}$$

(30)

with:

$$\begin{array}{c}\hfill a_m={\int }_0^{\infty }{e}^{-t}f\left(t\right)L_m\left(t\right)dt=\frac{\mathrm{i}}{\pi }{\left(1+\frac{\mathrm{i}}{\pi }\right)}^{-m-1}.\end{array}$$

(31)

Hence, using Tricomi’s method, the Laplace transform $F\left(s\right)$ can be approximated as:

$$\begin{array}{c}\hfill {\displaystyle F_M\left(s\right)=\frac{1}{s}\sum _{m=0}^M{a}_m{\left(\frac{s-1}{s}\right)}^m.}\end{array}$$

(32)

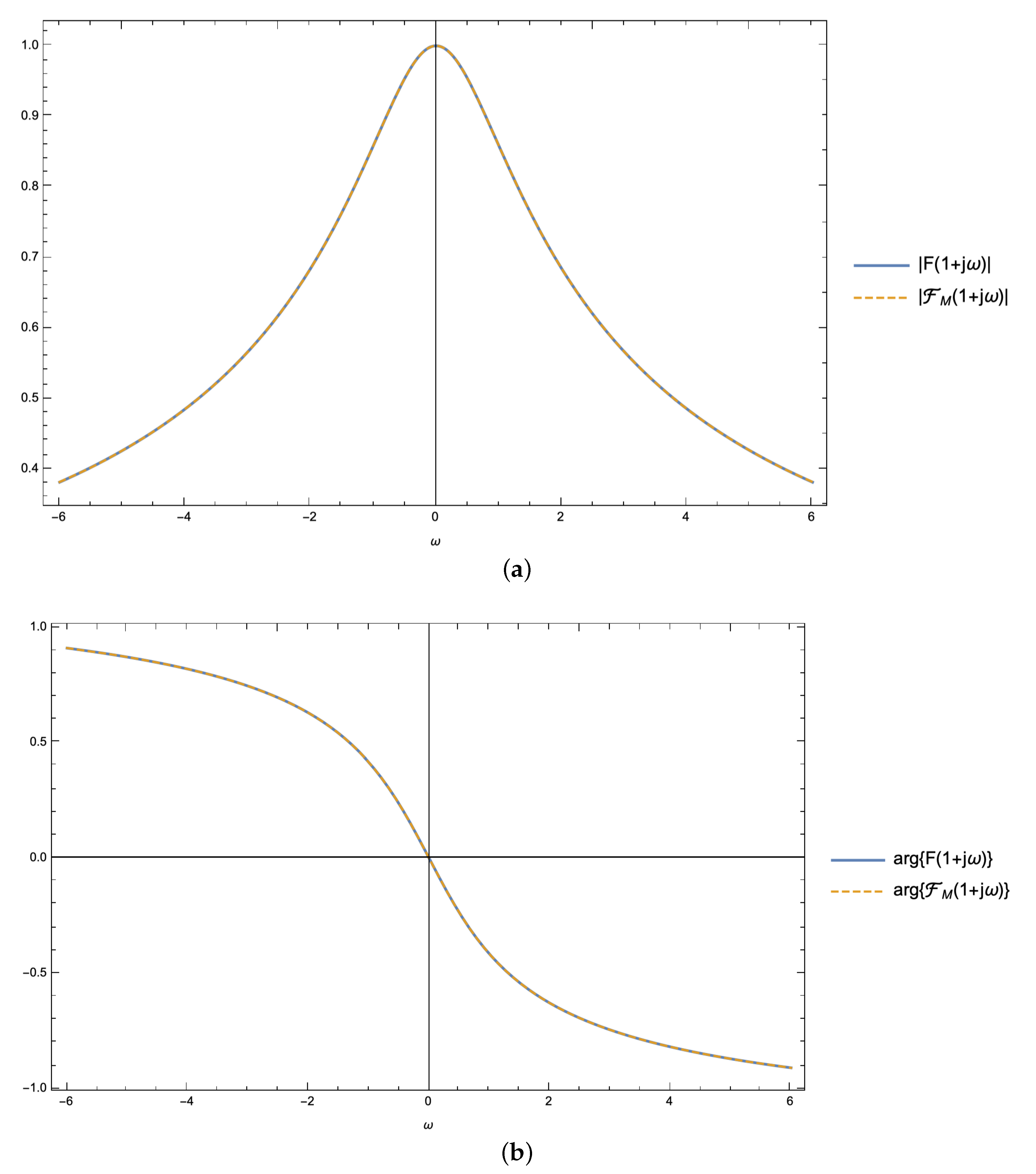
Upon selecting the expansion order $M=100$, one can readily verify that the approximant $f_M\left(t\right)$ in (30) and (31) is characterized by the distribution shown in Figure 1, whereas the relevant LT in (32) shows, along the cut plane $\sigma =\mathrm{Re}\left\{s\right\}=1$, the behavior plotted in Figure 2. It can be noticed that the agreement between the exact expression of $F\left(s\right)$ in (29) and its Tricomi’s approximation $F_M\left(s\right)$ is excellent.

5.2. Example: LT of $J_0\left(2\sqrt{t}\right)$

Let us consider the function:

$$\begin{array}{c}\hfill f\left(t\right)=J_0\left(2\sqrt{t}\right),\end{array}$$

(33)

whose Laplace transform can be evaluated as:

$$\begin{array}{c}\hfill {\displaystyle F\left(s\right)=\mathcal{L}\left(f\left(t\right)\right)\left(s\right)={\int }_0^{\infty }{exp}^{-1}\left(st\right)f\left(t\right)dt=\frac{e^{-1/s}}{s}.}\end{array}$$

(34)

The Laguerre polynomial series approximant of $f\left(t\right)$ is given by:

$$\begin{array}{c}\hfill f_M\left(t\right)=\sum _{m=0}^M{a}_m{L}_m\left(t\right),\end{array}$$

(35)

with:

$$\begin{array}{c}\hfill a_m={\int }_0^{\infty }{e}^{-t}f\left(t\right)L_m\left(t\right)dt=\frac{1}{em!}.\end{array}$$

(36)

Hence, using Tricomi’s method, the Laplace transform $F\left(s\right)$ can be approximated as:

$$\begin{array}{c}\hfill {\displaystyle F_M\left(s\right)=\frac{1}{s}\sum _{m=0}^M{a}_m{\left(\frac{s-1}{s}\right)}^m.}\end{array}$$

(37)

Upon selecting the expansion order $M=100$, one can readily verify that the approximant $f_M\left(t\right)$ in (35) and (36) is characterized by the distribution shown in Figure 3, whereas the relevant LT in (37) shows, along the cut plane $\omega =\mathrm{Im}\left\{s\right\}=1$, the behavior plotted in Figure 4. It can be noticed that the agreement between the exact expression of $F\left(s\right)$ in (34) and its Tricomi’s approximation $F_M\left(s\right)$ is excellent.

5.3. Example: LT of $e^t\mathsf{\Gamma }\left(t\right)$

Let us consider the function:

$$\begin{array}{c}\hfill f\left(t\right)=e^t\mathsf{\Gamma }\left(t\right),\end{array}$$

(38)

whose Laplace transform can be evaluated as:

$$\begin{array}{c}\hfill {\displaystyle F\left(s\right)=\mathcal{L}\left(f\left(t\right)\right)\left(s\right)={\int }_0^{\infty }{exp}^{-1}\left(st\right)f\left(t\right)dt=\frac{log\left(s\right)}{s-1}.}\end{array}$$

(39)

The Laguerre polynomial series approximant of $f\left(t\right)$ is given by:

$$\begin{array}{c}\hfill f_M\left(t\right)=\sum _{m=0}^M{a}_m{L}_m\left(t\right),\end{array}$$

(40)

with:

$$\begin{array}{c}\hfill a_m={\int }_0^{\infty }{e}^{-t}f\left(t\right)L_m\left(t\right)dt=\frac{1}{m+1}.\end{array}$$

(41)

Hence, using Tricomi’s method, the Laplace transform $F\left(s\right)$ can be approximated as:

$$\begin{array}{c}\hfill {\displaystyle F_M\left(s\right)=\frac{1}{s}\sum _{m=0}^M{a}_m{\left(\frac{s-1}{s}\right)}^m.}\end{array}$$

(42)

Upon selecting the expansion order $M=200$, one can readily verify that the approximant $f_M\left(t\right)$ in (40) and (41) is characterized by the distribution shown in Figure 5, whereas the relevant LT in (42) shows, along the cut plane $\sigma =\mathrm{Re}\left\{s\right\}=1$, the behavior plotted in Figure 6. It can be noticed that the agreement between the exact expression of $F\left(s\right)$ in (39) and its Tricomi’s approximation $F_M\left(s\right)$ is excellent.

5.4. Example: LT of $sin\left(t\right)$

Let us consider the function:

$$\begin{array}{c}\hfill f\left(t\right)=sin\left(t\right),\end{array}$$

(43)

whose Laplace transform can be trivially evaluated as:

$$\begin{array}{c}\hfill {\displaystyle F\left(s\right)=\mathcal{L}\left(f\left(t\right)\right)\left(s\right)={\int }_0^{\infty }{exp}^{-1}\left(st\right)f\left(t\right)dt=\frac{1}{s^2+1}.}\end{array}$$

(44)

The Maclaurin series approximant of $f\left(t\right)$ is given by:

$$\begin{array}{c}\hfill f_M\left(t\right)=\sum _{m=0}^M{b}_m{t}^m,\end{array}$$

(45)

where:

$$\begin{array}{c}\hfill b_m=\frac{f^{\left(m\right)}\left(0\right)}{m!}=\frac{1}{m!}sin\left(\frac{m\pi }{2}\right),\end{array}$$

(46)

with $f^{\left(m\right)}\left(0\right)$ denoting the m-th derivative of $f\left(t\right)$ in the origin. In the light of (11) and (12), the expansion (45) can be recast in terms of Laguerre polynomials as follows:

$$\begin{array}{c}\hfill f_M\left(t\right)=\sum _{m=0}^M{a}_m{L}_m\left(t\right),\end{array}$$

(47)

where:

$$\begin{array}{c}\hfill {\displaystyle a_m=\sum _{n=m}^M{b}_n{I}_m\left(n\right).}\end{array}$$

(48)

Hence, using Tricomi’s method, the Laplace transform $F\left(s\right)$ can be approximated as:

$$\begin{array}{c}\hfill {\displaystyle F_M\left(s\right)=\frac{1}{s}\sum _{m=0}^M{a}_m{\left(\frac{s-1}{s}\right)}^m.}\end{array}$$

(49)

Upon selecting the expansion order $M=100$, one can readily verify that the approximant $f_M\left(t\right)$ in (47) and (48) is characterized by the distribution shown in Figure 7, whereas the relevant LT in (49) shows, along the cut plane $\omega =\mathrm{Im}\left\{s\right\}=1$, the behavior plotted in Figure 8. It can be noticed that the agreement between the exact expression of $F\left(s\right)$ in (44) and its Tricomi’s approximation $F_M\left(s\right)$ is excellent.

5.5. Example: LT of $e^{-t^2}$

Let us consider the function:

$$\begin{array}{c}\hfill f\left(t\right)=e^{-t^2},\end{array}$$

(50)

whose Laplace transform can be easily evaluated as:

$$\begin{array}{c}\hfill {\displaystyle F\left(s\right)=\mathcal{L}\left(f\left(t\right)\right)\left(s\right)={\int }_0^{\infty }{exp}^{-1}\left(st\right)f\left(t\right)dt=\frac{1}{2}\sqrt{\pi }{e}^{\frac{s^2}{4}}\mathrm{erfc}\left(\frac{s}{2}\right).}\end{array}$$

(51)

The Hermite series approximant of $f\left(t\right)$ is given by:

$$\begin{array}{c}\hfill f_M\left(t\right)=\sum _{m=0}^M{b}_m{H}_m\left(t\right),\end{array}$$

(52)

where:

$$\begin{array}{c}\hfill {\displaystyle b_m=\frac{1}{2^{m}m!\sqrt{\pi }}{\int }_{-\infty }^{\infty }f\left(t\right)e^{-t^2}{H}_m\left(t\right)dt.}\end{array}$$

(53)

The general polynomial $H_n\left(t\right)$ can be represented in terms of $L_m\left(t\right)$ ($m=0,1,\dots ,n$) by means of the equation:

$$\begin{array}{c}\hfill {\displaystyle H_n\left(t\right)=\sum _{m=0}^n{C}_m\left(n\right)L_m\left(t\right),}\end{array}$$

(54)

where the connection coefficients $C_m\left(n\right)$ are computed using (25) or (26). In this way, the expansion (52) can be recast as follows:

$$\begin{array}{c}\hfill f_M\left(t\right)=\sum _{m=0}^M{a}_m{L}_m\left(t\right),\end{array}$$

(55)

where:

$$\begin{array}{c}\hfill {\displaystyle a_m=\sum _{n=m}^M{b}_n{C}_m\left(n\right).}\end{array}$$

(56)

Hence, using Tricomi’s method, the Laplace transform $F\left(s\right)$ can be approximated as:

$$\begin{array}{c}\hfill {\displaystyle F_M\left(s\right)=\frac{1}{s}\sum _{m=0}^M{a}_m{\left(\frac{s-1}{s}\right)}^m.}\end{array}$$

(57)

Upon selecting the expansion order $M=16$, one can readily verify that the approximant $f_M\left(t\right)$ in (55) and (56) is characterized by the distribution shown in Figure 9, whereas the relevant LT in (57) shows, along the cut plane $\sigma =\mathrm{Re}\left\{s\right\}=5$, the behavior plotted in Figure 10. It can be noticed that the agreement between the exact expression of $F\left(s\right)$ in (51) and its Tricomi’s approximation $F_M\left(s\right)$ is rather good.

5.6. Example: LT of $\frac{t+1}{t^2+1}$

Let us consider the function:

$$\begin{array}{c}\hfill f\left(t\right)=\frac{t+1}{t^2+1},\end{array}$$

(58)

whose Laplace transform can be easily evaluated as:

$$\begin{array}{c}\hfill {\displaystyle F\left(s\right)=\mathcal{L}\left(f\left(t\right)\right)\left(s\right)={\int }_0^{\infty }{exp}^{-1}\left(st\right)f\left(t\right)dt=}\\ \hfill =\mathrm{Ci}\left(s\right)(sin\left(s\right)-cos\left(s\right))+\frac{1}{2}(\pi -2\mathrm{Si}\left(s\right))(sin\left(s\right)+cos\left(s\right)).\end{array}$$

(59)

The Hermite series approximant of $f\left(t\right)$ is given by:

$$\begin{array}{c}\hfill f_M\left(t\right)=\sum _{m=0}^M{b}_m{H}_m\left(t\right),\end{array}$$

(60)

where:

$$\begin{array}{c}\hfill {\displaystyle b_m=\frac{1}{2^{m}m!\sqrt{\pi }}{\int }_{-\infty }^{\infty }f\left(t\right)e^{-t^2}{H}_m\left(t\right)dt.}\end{array}$$

(61)

The expansion (60) can be recast in terms of Laguerre polynomials as follows:

$$\begin{array}{c}\hfill f_M\left(t\right)=\sum _{m=0}^M{a}_m{L}_m\left(t\right),\end{array}$$

(62)

with:

$$\begin{array}{c}\hfill {\displaystyle a_m=\sum _{n=m}^M{b}_n{C}_m\left(n\right).}\end{array}$$

(63)

where the connection coefficients $C_m\left(n\right)$ are computed using (25) or (26). Hence, using Tricomi’s method, the Laplace transform $F\left(s\right)$ can be approximated as:

$$\begin{array}{c}\hfill {\displaystyle F_M\left(s\right)=\frac{1}{s}\sum _{m=0}^M{a}_m{\left(\frac{s-1}{s}\right)}^m.}\end{array}$$

(64)

Upon selecting the expansion order $M=16$, one can readily verify that the approximant $f_M\left(t\right)$ in (62)–(63) is characterized by the distribution shown in Figure 11, whereas the relevant LT in (64) shows, along the cut plane $\omega =\mathrm{Im}\left\{s\right\}=1$, the behavior plotted in Figure 12. It can be noticed that the agreement between the exact expression of $F\left(s\right)$ in (59) and its Tricomi’s approximation $F_M\left(s\right)$ is rather good.

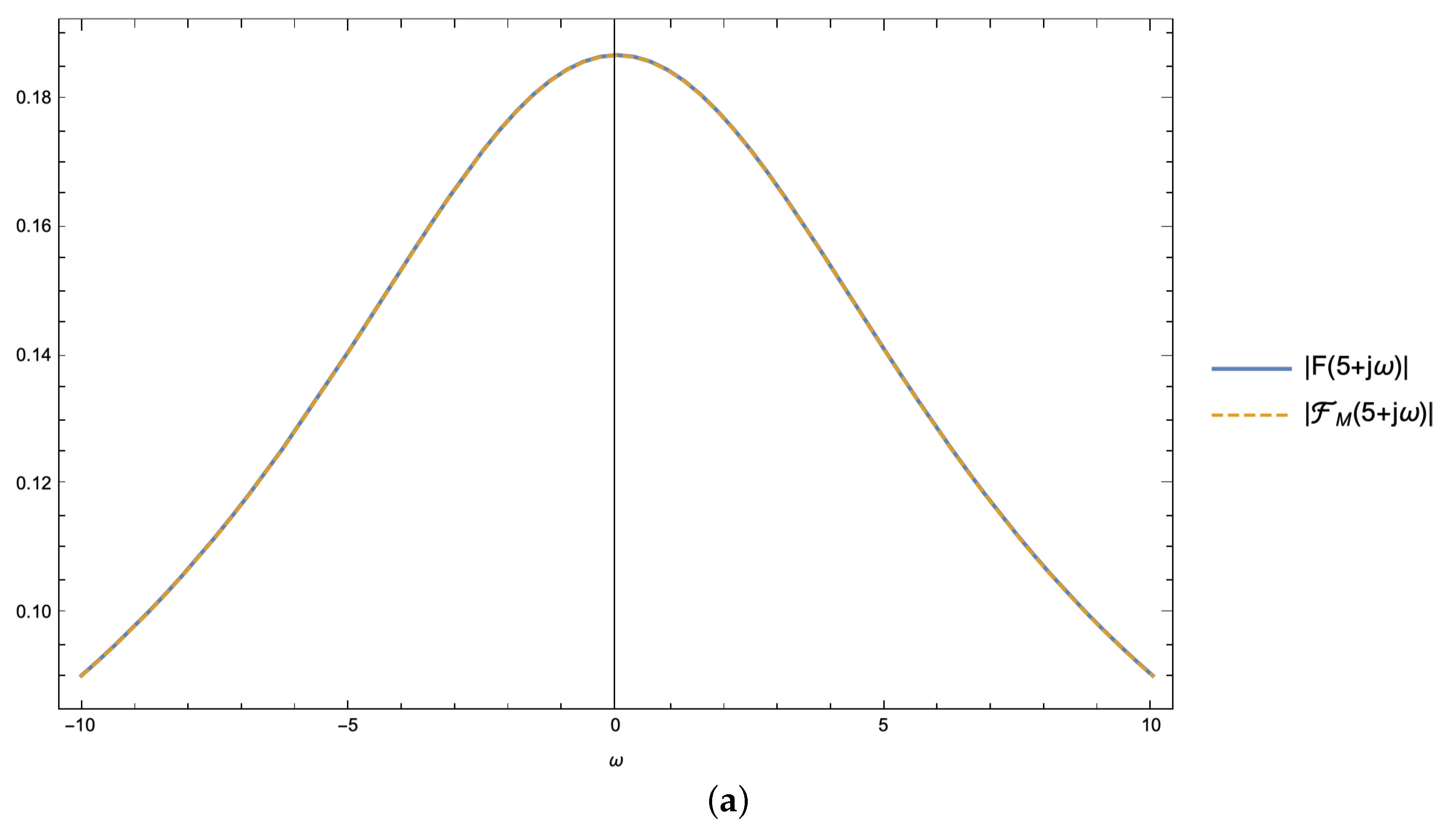
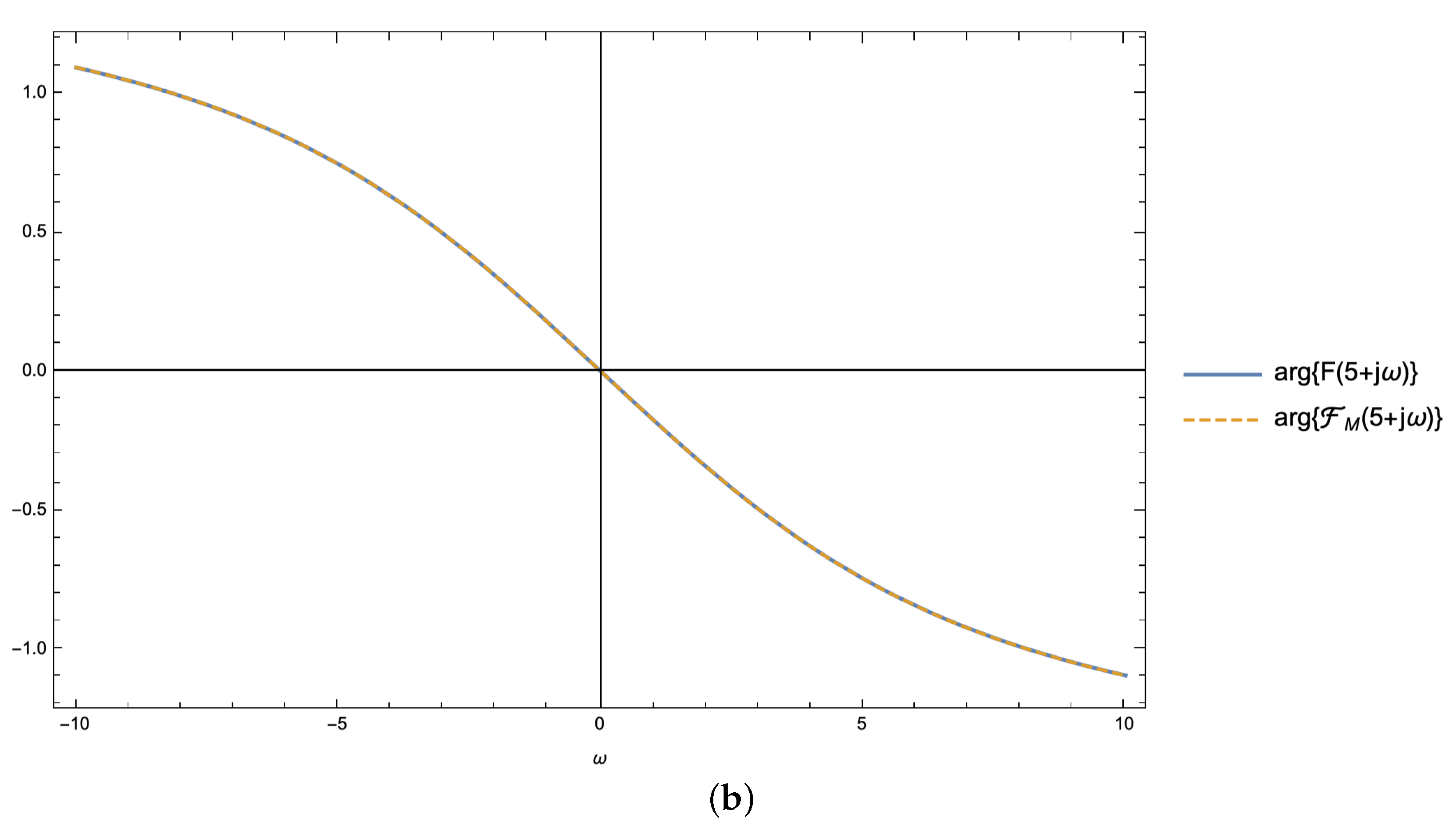
From the visual inspection of Figure 12 and Figure 13, one can readily notice that the derivation of Tricomi’s series approximant directly from the truncated Laguerre expansion of $f\left(t\right)$ with a fixed order M, as per the expression (3), enables a more accurate representation of the Laplace transform $F\left(s\right)=\mathcal{L}\left(f\right(t\left)\right)$ when compared to the relevant Tricomi’s approximant derived from a truncated Hermite expansion of $f\left(t\right)$ with the same order M.

6. Conclusions

Starting from a classical result by F.G. Tricomi, showing the possibility to use expansions in terms of Laguerre polynomials for obtaining the corresponding Laplace transforms, we have exploited the link between different polynomial sets, via inversion or connection coefficients, in order to apply the Tricomi method to more general expansions.

It has been shown that the described procedure works and that from the numerical point of view, the direct expansion in Laguerre polynomials guarantees a tremendously greater numerical stability of the Tricomi method. This confirms the special role played by Laguerre polynomials in the framework of the Laplace transform, as had been highlighted by the pioneering work of Tricomi.