Sovereign Debt and Currency Crises Prediction Models Using Machine Learning Techniques

Abstract

Sovereign debt and currencies play an increasingly influential role in the development of any country, given the need to obtain financing and establish international relations. A recurring theme in the literature on financial crises has been the prediction of sovereign debt and currency crises due to their extreme importance in international economic activity. Nevertheless, the limitations of the existing models are related to accuracy and the literature calls for more investigation on the subject and lacks geographic diversity in the samples used. This article presents new models for the prediction of sovereign debt and currency crises, using various computational techniques, which increase their precision. Also, these models present experiences with a wide global sample of the main geographical world zones, such as Africa and the Middle East, Latin America, Asia, Europe, and globally. Our models demonstrate the superiority of computational techniques concerning statistics in terms of the level of precision, which are the best methods for the sovereign debt crisis: fuzzy decision trees, AdaBoost, extreme gradient boosting, and deep learning neural decision trees, and for forecasting the currency crisis: deep learning neural decision trees, extreme gradient boosting, random forests, and deep belief network. Our research has a large and potentially significant impact on the macroeconomic policy adequacy of the countries against the risks arising from financial crises and provides instruments that make it possible to improve the balance in the finance of the countries.

1. Introduction

The study of crisis events in international finance has received considerable attention in the field of economics over the last two decades, especially the prediction of sovereign debt and currency crises, due to their enormous importance in economic activity. This great research effort has produced a huge range of prediction models, supported in turn by varied methodologies [1,2,3,4].

The current importance of models for predicting crisis events is increased by the last global financial crisis, which showed that even developed countries, that is, those that in theory, are in a better situation and economic stability. The globalization process and economic development have led to the emergence of greater complexity in the macroeconomic and financial environment [1]. This has created a new space for research, and the demand to build new models to forecast this event, not just at the level of a country but to explain the common characteristics of these crises for a wide geographic spectrum [4,5].

One of the paths initially taken by the literature on the prediction of international financial crisis events was the development of models built with samples made up of emerging economies since they tend to be more vulnerable countries and have statistically suffered a higher frequency of crises. However, at this initial stage, specific samples composed of only one country, or a reduced set of countries, were considered, and therefore could well be considered as regional models. Subsequently, the development of the literature in the construction of regional models was due to mere necessity [6]. Recently, various so-called global models have also appeared that have used samples of economies from different regions of the world for their construction. Almost all of these global models have been built to predict situations in emerging economies, including some advanced economies [7].

The results obtained by studies, such as that of [8], confirm the convenience, both explanatory and potential classification capacity, of global models for predicting these crisis events in comparison with regional models or with information from a single country. Besides, there is a demand for more research on global models connected with the increase of accuracy and the scope of the information used, since the studies that have obtained high levels of precision used very small samples, mainly from a single country, and, therefore, with short-term conclusions [6,9,10]. Many of these works have lacked methodological comparisons to find which empirical technique or which type of method could be the most appropriate for prediction [11,12,13]. Therefore, the literature shows how necessary it is to deepen the use of computational techniques, also called ‘machine learning techniques’, to find alternatives with greater precision to anticipate and prevent future financial crises [3,4].

These sovereign debt and currency crises prediction models can be useful to more accurately assess the reputation of a country in the world [14,15,16,17,18,19]. Country reputation explains how the most important characteristics of a country, for example, social and economic factors, influence the image or brand in which the country is projected to the world. In particular, it can influence the market expectations of energy companies, where bilateral relations between countries are key, and the role of reputation shows the international trust that exists in the country. Various authors [16,17,18,19,20,21,22] have expressed the need to incorporate data and variables on the economic and financial stability of the countries as one more important factor concerning the reputation of the country.

The present study tries to answer the research question of whether it is possible to make global crisis prediction models more accurate relative to those in previous literature, taking into account not only statistical techniques such as logistic regression or function Probit but also computational techniques that have yielded excellent classification results in recent decades in matters of economic prediction [23]. To offer greater explanatory and comparative diversity, both global and regional models have been used for Africa and the Middle East, Asia, Latin America, and Europe. The results reached have made it possible to verify a greater precision of computational methods compared to traditional statistical techniques. Even very novel computational techniques have shown interesting potential in the precision of these events of the crisis.

The structure of this research work is as described below. In Section 2, a review of the previous literature on the prediction of the mentioned crisis events is carried out: sovereign debt crisis and currency crisis. Section 3 presents the methodology used. Section 4 details the variables and data used in the research, and the results achieved are examined in Section 5. Lastly, the conclusions of the investigation and its implications are presented.

2. Literature Review

The review carried out on the sovereign debt and currency crisis prediction literature has allowed us to obtain precise conclusions on the studies carried out to date and on where future research should be oriented. In this sense, it has been found that, on the one hand, there are studies that aim to develop a prediction model to forecast some of the two mentioned crisis events, and that facilitate classifying countries as in a state of crisis or without crisis episodes. These are by far the majority of studies. This group could also include those whose model proposes to be an “early warning” in anticipation of the event of the crisis. On the other hand, it has also been found that in the last decade, global models have emerged to predict these crises, or with samples from various regions. These models have generally looked for the determinants of crises in countries of a relatively broad geographic region.

2.1. Sovereign Debt Crises Prediction

The existing literature on sovereign debt crisis prediction has focused mainly on emerging countries [7,10,11,24,25,26,27,28]. For their part, some studies have addressed predictions of the sovereign debt crisis in emerging and developing countries [3,29,30]. Finally, refs. [5,31] modeled public debt default to predict it both for different regions (Africa, Latin America, Asia, and Europe) and globally. Among them, Reference [26] proved that not every crisis is the same: they vary according to if the government is faced with insolvency, lack of liquidity, or diverse macroeconomic risks. Besides, they characterized the group of fundamental elements that can be linked to a so-called “risk-free” zone. This is an important classification for discussing appropriate policy options to avoid crises and respond to them promptly.

Regarding the methods used, a considerable number of researchers have applied statistical methods to predict the sovereign debt crisis, highlighting the logit model [5,10,24,25,26,29,32]. On the other hand, the authors [3,7] develop regression models to forecast the sovereign debt crisis. For their part, [11] applies a non-parametric method based on artificial neural networks (ANN). Finally, Reference [27] develops the application of the self-organization map (SOM), a display instrument based on ANN. Among them, Reference [11] concludes that thanks to the excellent versatility of ANNs and their nonlinear relationship approximation capability, an early warning system founded on ANN can, in certain conditions, improve on more conventional techniques. Reference [27] shows that the SOM is a viable tool to monitor sovereign default indicators, facilitating the monitoring of multidimensional financial data.

On the other hand, it is also found that previous studies have determined a series of significant variables in the previous literature in the prediction of the sovereign debt crisis. For example, Reference [11] exposes as explanatory variables the growth of Gross Domestic Product (GDP), the profitability of the US Treasury bill, and the level of external debt over total reserves. Other authors have shown that the interest rate of the US Federal Reserve has an essential role to play in increasing the probability of default [3,30]. Finally, Reference [5] shows that the country’s total debt, the global interest rate, and the current account in the payment balance are the main determinants of the defaults of countries at the global level.

Finally, regarding the level of precision achieved in said sovereign debt crisis prediction literature, the studies by [10,24,25,29,30] stand out with a precision range between 70% and 80%. With a higher rank level (80–90%), we find the investigations of [3,5,11,26]. These last authors proposed a new crisis variable specification that allows for the prediction of new-onset of crises, and their results were more precise in comparison with those in the existing literature. They yielded a forecast capacity of 87% for the global model.

2.2. Currency Crises Prediction

The literature that has previously covered the prediction of currency crises has been mostly for emerging economies; therefore, the evidence is poor for advanced economies. Among the research from emerging countries, we highlight those of [2,12,33,34,35,36,37,38]. Other authors have focused on Asian countries for currency crisis prediction [39,40,41,42]. For their part, Reference [43] investigates the differences in a common set of indicators used in early alert systems for currency crises in the situation of Jordan and Egypt. Reference [44] empirically analyzes the causes of currency crises for a set of Organisation for Economic Co-operation and Development (OECD) countries.

Regarding the methods used, a considerable number of researchers have applied statistical methods to predict the currency crisis, highlighting Logit [2,12,37,38,43,45], and Probit [44,46,47]. Also, previous studies have developed computational techniques such as RNA [6,33,40,41], auto-organization map [34], support vector machine (SVM) [35], and deep neural decision trees [48]. For their part, Reference [39] used a switching model of nonlinear Markov to carry out a systemic analogy and assessment of three different causes of currency crises: contagion, fundamentals, and soft economics. Reference [34] concluded that their model based on the self-organization map (SOM) is a viable tool to predict currency crises, obtaining an accuracy of 91.6%. For their part, Reference [35] showed that the support vector machine computing technique provides reasonably accurate results and helps policymakers to identify situations in which a currency crisis may occur.

From another point of view, taking into account the explanatory variables of the models, the most prominent among the authors have been exports [2,6,33,34,36,43,44,49], the real exchange rate of the currency [33,36,43,44,49,50], relationship between the reserve and the money supply [2,33,34,43,49], current account balance [12,34,51], and GDP growth [12,49,51]. For their part, Reference [42] found that global financial shocks and the growth rate of domestic credit are the main currency crisis indicators.

Following the level of precision of the models, most of the previous studies reach a precision range of 67–85% [2,38,39,46,50,51]. With a higher precision range level (90–97%) we find the investigations of [6,12,33,34,35,36,37,40,41,48]. Among them, Reference [35] achieved 96% accuracy and his results showed that the currency crisis could be adequately predicted using only a small fraction of sample data.

Therefore, the previous literature shows a greater predictive capacity of machine learning methodologies over statistical methodologies. But this same literature shows that the results obtained so far are not enough and that this type of methodologies can achieve a higher level of precision [8,11]. Also, it is detailed in previous works that the use of data has been very limited in time horizon and geographic space, making it a challenge to increase it for future works [4,9,13]. Finally, there is a need to test different computational methodologies in the prediction of financial crises [3,5,10,12]. This is due to the weaknesses shown by some methodologies such as SVM and ANN on the difficulty of managing large databases and the difficulty of interpretation.

3. Methodologies

As previously stated, to resolve the research question, we used a variety of methods in the design of the crisis prediction models. Applying different methods aims to achieve a robust model, which is tested not only through one classification technique but also by implementing all previous classification techniques that have been successful in previous literature. Specifically, multilayer perceptron, support vector machines, fuzzy decision trees, AdaBoost, extreme gradient boosting, random forests, deep belief network, and deep learning neural decision trees have been applied. The following is a summary of the methodological aspects of each of these classification techniques.

3.1. Multilayer Perceptron

The multilayer perceptron (MLP) is an RNA methodology composed of a layer of input units, an output layer and other intermediate layers also called hidden layers. These last layers have no connections with the outside. The system is designed for supervised feedback. All the layers would be connected so that the input nodes are connected with the nodes of the second layer, these in turn with those of the third layer, and so on. The methodology aims to form a correspondence between a set of initial observations at the input with the set of outputs desired for the output layer.

The work [52] develops the MLP learning scheme as its case, in which initially there is no knowledge about the underlying model of the applied data. This scheme needs to find a function that captures the learning patterns, as well as a generalization process to be able to analyze individuals not included in the learning stage [53]. It is necessary to adjust the weights considering the sample data, assuming that the information on the architecture of the network is available, where the objective is to achieve weights that minimize the learning error. Therefore, given a set of pairs of learning patterns {(x1, y1), (x2, y2)… (xp, yp)} and an error function ε (W, X, Y), the training stage is It composes in identifying the set of weights that minimizes the learning error E (W) [54], as it appears in (1).

$$\underset{W}{\mathit{min}} E\left(W\right)= \underset{W}{\mathit{min}}\sum _{i=1}^p\epsilon (W, x_i, y_i)$$

(1)

3.2. Support Vector Machines

Support vector machines (SVM) have registered good results when applied to problems of a very diverse nature, where the generalization error needs to be minimized. SVM is defined as the attempt to classify a surface (σ_i) that divides positive and negative data by as large a margin as possible [55].

All possible surfaces (σ₁, σ₂, …) in the A-dimensional space that differentiates the positive data from the negative ones in the training observations are used to find the smallest possible distance. The positive and negative data are linearly separable and therefore the decision surfaces are |A|-1-hyperplanes. Attention must be paid to the best decision surface and is identified through a small set of training data called support vectors. SVM allows the construction of non-linear classifiers, that is, the algorithm represents non-linear training data in a high-dimensional space.

In our analysis, the minimum sequential optimization (SMO) method is applied to train the SVM algorithm. The SMO technique separates quadratic programming (QP) problems to be solved in SVM by smaller QP problems.

3.3. Fuzzy Decision Trees (FDT)

This is an algorithm based on the famous C4.5 technique where a decision tree is built based on characteristics that are composed of smaller subsets, basing the decision of the formation of the decision tree on the possibility of deriving a value from the information [56]. This algorithm can collect hidden information from large data sets and produce its own rules for optimal classification [57]. Therefore, C4.5 is made up of features such as the selection of attributes as root, the possibility of producing a branch for each value, and being able to repeat the process for each branch until all branch cases have the same class. The highest gain is used for the selection of attributes as the root, as expressed in Equation (2):

$$Gain \left(S,A\right)=Entropy\left(S\right)-\sum _{i=1}^n\frac{\left|S_i\right|}{\left|S\right|}=Entropy\left(S\right)$$

(2)

where S is the set of cases, A is the attributes, n represents the partition number of the attribute A, and S_i represents the number of cases in the partition i-th.

The result of Entropy is computed as appears in Equation (3):

$$Entropy\left(S\right)=\sum _{i=1}^n-p_i\times lo{g}_2\times p_i$$

(3)

where S establishes the set of cases, n identifies the number of partitions of S, and p_i represents the proportion of S.

The fuzzy decision trees show an initial architecture identical to the decision trees developed at the beginning. Fuzzy decision trees allow observations to be developed in different branches of a node at the same time and with different levels of satisfaction in the interval (0–1) [58,59]. Fuzzy decision trees differ from standard decision trees because they apply division criteria related to fuzzy constraints, their inference techniques are different, and the fuzzy sets representing the observations should not change. On the other hand, the stimulus of the fuzzy decision tree is composed of two factors, such as a procedure to build a fuzzy decision tree and an inference development for decision making. The fuzzy modification has achieved better results in previous studies in comparison with the C4.5 algorithm [59].

3.4. AdaBoost

AdaBoost is a meta-algorithm-based learning technique that can be applied to other types of learning algorithms to increase your ability to hit. This procedure performs a weighted sum to obtain the result from the other algorithms, called weak classifiers, with the driven classifier such as AdaBoost. This classifier adapts to the rest of the weak algorithms to hit in favor of the cases badly classified by the previous classifiers. AdaBoost has the characteristic of being sensitive to samples with noise and outliers, but, in some classification problems, it may be less sensitive than other classifiers [60].

AdaBoost develops a particular technique of training a powered classifier [61]. A Boost classifier is a classifier composed as it shows in Equation (4):

$$F_T\left(x\right)=\sum _{t=1}^T{f}_t\left(x\right)$$

(4)

where a f_t represents a weak learner which takes an object x as input and returns a real value result pointing out the class of the object. The predicted object class and absolute value show a level of confidence in the classification problem through the signal from the weak classifier output. For its part, the sign T of the classifier will be positive in the case that the sample is within a positive class, and negative otherwise.

Every classifier indicates an output, the hypothesis h(x_i), for each sample in the training set. In iteration t, a weak classifier has chosen f_t and provides a coefficient α_t, so the training error adds E_t, this classifier having the mission of minimizing the level of error, as shown in Equation (5).

$$E_t=\sum _{i}E\left[F_{t-1}\left(x_i\right)+{\alpha }_{t}h\left(x_i\right)\right]$$

(5)

where F_t−1 represents the driven classifier generated in the prior step of training, E(F) defines the error function, and ft(x) = α_th(x) is the weak beginner that sums to the final classifier.

3.5. Extreme Gradient Boosting (XGBoost)

XGBoost is an algorithm based on increasing the gradient and has shown superior predictive power to many computational methodologies widely used in the previous literature [58,62,63]. It is an algorithm that can be applied to supervised learning situations and is made up of sets of regression and classification trees (CART). Initially, the variable to be predicted can be defined as yi, XGBoost is defined as it appears in Equation (6).

$${\widehat{y}}_i=\sum _{k=1}^K{f}_k\left(x_i\right)f_k\in F$$

(6)

where K represents the total number of trees, $f_k$ for the tree, $kih$ defines a function in the functional space F, and F shows the possible set of all CARTs.

For the trained and trained CART, they will try to mimic the level of residues thrown by the model in the training step. The objective function is optimized in step (t + 1) as defined in Equation (7).

$$obj=\sum _{i=1}^{n}l(y_{i, }{\widehat{y}}_i^{\left(t\right)})+\sum _{i=1}^t\mathsf{\Omega }\left(f_i\right)$$

(7)

where l (.) represents the loss function in the training step, $y_{i, }$ shows the validation value in this training step, ${\widehat{y}}_i^{\left(t\right)}$ describes the prediction value in step t, and $\mathsf{\Omega }\left(f_i\right)$ is fixed starting the regularization defines in Equation (8).

$$\mathsf{\Omega }\left(f\right)=\gamma T+\frac{1}{2}\lambda \sum _{j=1}^T{w}_j^2$$

(8)

In this Equation (8), T represents the number of leaves and w_j defines the score obtained for the sheet jth. Once optimized (8), the expansive Taylor rule is applied to carry out the descent of the gradient and collect different loss functions. Significant variables are chosen during the training step as a node in the trees, eliminating non-significant variables.

3.6. Random Forests

Random forests (RF) are an ensemble method that averages the forecasts of a high number of uncorrelated decision trees [64,65]. They usually display good performance with better generalization properties than individual trees, are generally relatively robust to outliers, and need virtually no parameter turning [66]. Random forests are supported by two domain ideas: packaging to build each tree on a different starter sample of the training data and random selection of features to decorate the trees. The training algorithm is quite simple and can be described as follows: For each of the trees in the set, a sample of the training data is drawn. By growing the tree T_b over Z, characteristics that are available as candidates for the division at the respective node are randomly chosen [67]. Lastly, the grown tree is added T_b to the whole. During the inference, each of the trees provides a prediction ${\widehat{c}}_b\left(x\right)$ for the class label of the new observation x. The final random forest prediction ${\widehat{c}}_{RF}\left(x\right)$ is then the majority vote of the trees, that is, ${\widehat{c}}_{RF}\left(x\right)=majority vote \left\{{\widehat{c}}_b\left(x\right)\right\}$.

Inspired by [64], RF holds 100 trees, each with a maximum depth of 10 for the simulation study. The trees all use cross-entropy as the error minimization measure and m = √p characteristics are set as the default option for the classification configuration of this algorithm.

3.7. Deep Belief Network

The Deep Belief Network (DBN) is a variant of a deep neural network made up of two upper layers joined together as an undirected bipartite associative memory, called restricted Boltzmann machines (RBM).

The lower layers form a directed graphical pattern, called the sigmoid belief network. The difference between sigmoid belief networks and DBN is found in the way the hidden layers are parameterized [68], as indicated in Equation (9).

$$P(v,h^1,\dots ,h^l)=P(h^{l-1},h^l)({\displaystyle \prod _{k=0}^{l-2}P(h^{k|}|h^{k+1})}$$

(9)

where v represents the vector of visible units, $P(h^{k-1}|h^k)$ defines the conditional probability of visible units at the level k. The joint distribution at the top level, $P(h^{l-1},h)$, is an RBM, being $x(n)={[1,x_1(n),x_2(n),\dots ,x_m(n)]}^T$. Another way to show DBN as a generative model can be pointed out in the expression (10):

$$w(n)={[b,w_1(n),w_2(n),\dots ,w_m(n)]}^T$$

(10)

DBN is made up of the accumulation of RBMs. The visible layer of each RBM in this composition constitutes the hidden layer of the previous RBM. In the way that a model fits a data set, the mission is to establish a model $Q(h^{l-1},h)$ for the true posterior $P(h^{l-1},h)$. The approximations for the higher-level posterior are determined by the posterior $Q(h^{l-1},h)$, $P(h^{l-1},h)$, where the upper-level RBM gives the possibility to calculate the inference procedure [68].

3.8. Deep Neural Decision Trees

Deep Neural Decision Trees (DNDT) are composed of decision tree models computed using deep learning neural networks. In these trees, a combination of weights is assigned to DNDT, which belongs to a specific decision tree, its result being interpretable [69]. DNDT starts with a “soft clustering” function [70] to evaluate the level of residues contained in each node, which allows obtaining split decisions in DNDT. The “grouping” function is defined as using a real scalar as input x and getting an index of the “containers” that x belongs to.

In the case of having a variable x, it can be joined in n + 1 intervals. The need to generate n cut points is created, which are trainable variables within the algorithm. These cutoff points are called [β1, β2, …, βn] and move in an increasing monotonic fashion, hence, β1 < β2 < … < βn.

The function of the activation of the DNDT method starts from a neural network to make the computation, as is defined in Equation (11).

π = f_w,b,τ (x) = softmax((wx + b)/τ)

(11)

where w is a constant and its value is set as w = [1, 2, …, n + 1], τ > 0 is a factor temperature, and b is constructed as defined by Equation (12).

b = [0, −β₁, −β₁ − β₂, …, −β₁ − β₂ − … − β_n]

(12)

The neural network, which is defined in Equation (12), produces an encoding of the ‘binning’ function x. In case τ approaches 0 (which is the case most often), the vector is sampled via the straight-through (ST) method Gumbel-Softmax [71]. Considering our ‘binning’ function defined above, the main idea is to create the decision tree through the Kronecker product. Suppose we get an input instance x ∈ R^D with D features. Interleaving each feature x_d with its neural network f_d(x_d), we can find all the final nodes of the decision trees, as expressed in Equation (13).

z = f₁(x₁) ⊗ f₂(x₂) ⊗ ⋯ ⊗ f_D(x_D)

(13)

where z is now also a vector indicating the index of the leaf node where the instance arrives x. Finally, we suppose that a linear classifier at every sheet z sorts the instances that arrive there. DNDT scales well with the number of inputs because of the mini-batch training of the neural network. However, a key design drawback is that, due to the use of the Kronecker product, it is not scalable concerning the number of features. In our implementation today, we avoid this problem with large data sets by having a forest with random subspace training [65].

3.9. Sensitivity Analysis

In Machine Learning techniques, it is also necessary to analyze the impact of variables as occurs in traditional statistical techniques, after using data samples that contain a wide variety of variables. To carry out this evaluation, a sensitivity analysis must be applied. The objective of this procedure is to determine the level of significance of the independent variables over the dependent variable [72,73]. Therefore, it tries to determine those models that are made up of the most important ones, and therefore, eliminate the variables that are not significant. For a variable to be considered significant, it must have a variance greater than the mean of the rest of the variables that make up the model. The Sobol method [74] is the technique chosen to decompose the variance of the total V (Y) given by the following equations expressed in (14).

$$V\left(Y\right)=\sum _i{V}_i+\sum _i\sum _{j>1}{V}_{ij}+V_{1,2,\dots ,k}$$

(14)

where V_i = V(E(Y|X_i)y, V_ij = V(E|X_i, X_j)) − V_i − V_j.

The sensitivity indices are obtained by S_ij = V_ij/V, where S_ij denotes the effect of interaction between two factors. The Sobol decomposition makes it possible to estimate a total sensitivity index S_Ti, measuring the total sensitivity effects implied by the independent variables.

4. Sample, Data, and Variables

4.1. Sample and Data

From the 1970–2017 period, two samples have been obtained, each used for its purpose, which has been for analyzing the forecast of a sovereign debt crisis and the prediction of a currency crisis. For this, the samples have been classified by world regions, specifically Africa and the Middle East, Latin America, Asia, Europe, and the total (global) set. The database has been obtained from macroeconomic and financial data from the main international economic institutions like the International Monetary Fund (the database called ‘The World Economic Outlook’) and the World Bank (the database called ‘Open World Bank Data’).

The dataset of the sample has been classified into three groups that are mutually exclusive, reserving 70% for training samples, 10% for validation samples, and for the test samples, the remaining 20%. Next, we selected the variables set that provided the most number of classification hits in the verification set, and we have presented results based on the average number of hits in the test set. The classification and prediction finally involve using the developed model to produce predictions for the analyzed crises.

4.2. Variables

4.2.1. Sovereign Debt Crises

The database used for the construction of the sovereign debt crisis prediction models consisting of a comprehensive set of information (30 crude or converted significant variables, with annual periodicity) concerning a panel (unbalanced) of 115 developed and emerging markets in the period 1970–2017. An attempt is made to replicate the sample used by Dawood, Horsewood, and Strobel (2017) as a reference work, expanding the time range and the number of countries, as well as including the attributes of the indicators on policy conditions and credit scoring. The macroeconomic variables have been obtained from the World Bank, while the credit rating indicators are derived from Fitch Ratings statistics and the political variables from the POLITY IV project, carried out by the Center for Systemic Peace (http://www.systemicpeace.org/inscrdata.html (accessed on 5 March 2020)). The sample includes the four main regions worldwide, such as Africa and the Middle East, Asia, Latin America and Europe.

The dependent variable is formed like most of the previous literature, like the work of Dawood, Horsewood, and Strobel (2017). For emerging emerging countries, the dependent variable indicates the value 1 in the event of any of the following events and zero otherwise: interest and/or capital arrears increase above 5% of the pending debt; loans obtained from the International Monetary Fund (IMF) that exceed 100% of the country’s quota; the accumulated credit lent by the IMF exceeds 200% of the quota; participation in a debt restructuring or rescheduling plan involving a volume greater than 20% of the outstanding debt. For developed countries, in addition to the two related events around IMF loans, the dependent variable is identified as 1 if public debt exceeds 150% of GDP.

Table 1. Definition of the independent variables for the sovereign debt crises.

Attribute	Abbreviation	Description	Exp. Sign.
Exposure to debt	TDEB	Gross external debt as% of GDP	+
	IMFC	Loans from the IMF as% of GDP	+
	GINT	Global LIR	+
Foreign Sector	FXR	Total reserves (excluding gold) as% of GDP	−
	TRO	Ratio of exports plus imports to GDP	+/−
	EXPG	Annual export growth ratio	−
	CACC	Balance of payments account as% of GDP	−
	FDI	Foreign direct investment flows as% of GDP	−
Domestic Macroeconomic Factors	RGDP	Annual growth of real GDP	−
	INF	Rate of change in the consumer price index	+
	M2R	Money supply ratio (M2) divided by reserves	+
	REER	Deviation of the ratio of the real effective exchange rate of the currency (moving average of the last 5 years)	−
	GOVS	Final central government spending as% of GDP	+/−
	NSAV	Total savings as% of GDP	−
	CON	Sovereign debt crisis event in a country in the same region (t − 1)	+
Banking Sector	DCRE	Domestic credit ratio as% of GDP	+/−
	BASS	Ratio of bank assets as% of GDP	−
	GBL	Net bank claims on the central government	+
Credit Rating Indicators	SCLR	Local currency long-term government bond credit quality scale	+/−
	SCFR	Scale of the credit quality of the long-term government bond in foreign currency	+/−
	SBS	Ratio of interest paid on 10-year public debt bond	+
	CDS	Price of public debt bond default insurance	+
Political Factors	FRAG	Political fragmentation score (regional/ethnic tensions)	+
	POLI	Combined politics score (autocracy score minus democracy score)	+/−
	DUR	Durability of the political regime (‘POLI’ control variable)	+
	PERS	Number of years since the last radical and abrupt political change. (‘POLI’ control variable)	+
	RIR	Score of the magnitude of civil war episodes involving the country (by year)	+
	SFI	State fragility index	+
	EFEE	Effectiveness of economic policy measured by GDP per capita	−

describes the variables used, and

Table A1. Sovereign debt crisis by country and by year.

Country	Years	Country	Years	Country	Years
Albania	1990	Finland		Nicaragua	1980
Germany		Francia		Niger	1983
Algeria		Gabon	1986, 2002	Nigeria	1983
Angola	1988	Gambia	1986	Norway
Argentina	1982, 2001, 2014	Georgia		New Zealand
Armenia		Ghana		Netherlands
Australia		Grenada	2004	Panama	1983
Austria		Greece	2012	Paraguay	1982
Bangladesh		Guinea	1985	Perú	1978
Belgium		Equatorial Guinea		Poland	1981
Belize	2007, 2012, 2017	Guyana	1982	Portugal
Bolivia	1980	Haiti		United Kingdom
Brazil	1983	Honduras	1981	Central African Republic
Brunei		Hong Kong		Czech Republic
Bulgaria	1990	Hungary		Dominican Rep.	1982, 2003
Camerún	1989	India		Romania	1982
Canada		Indonesia	1999	Russia	1998
Chad		Iran, R.I.	1992	Senegal	1981
Chile	1983	Ireland		Seychelles	2008
China, R.P.		Israel		Sierra Leone	1977
Cyprus	2013	Italy		Singapore
Colombia		Jamaica	1978, 2010	Syria
Congo, Rep.	1986	Japan		South Africa	1985
Congo, D.R.	1976	Jordan	1989	Sudan	1979
South Korea		Kazajistan		Sweden
Ivory Coast	1984, 2001, 2010	Kenya		Switzerland
Costa Rica	1981	Kuwait		Thailand
Croatia		Lebanon		Tanzania	1984
Denmark		Liberia	1980	Togo	1979
Dominica	2002	Libya		Trinidad y Tobago	1989
Ecuador	1982, 1999, 2008	Madagascar	1981	Tunisia
Egypt	1984	Malasia		Turkey	1978
Slovakia		Malawi	1982	Ukraine	1998, 2015
Spain		Morocco	1983	Uganda	1981
United States		Mexico	1982	Uruguay	1983, 2002
Estonia		Moldavia	2002	Venezuela	1982, 2017
Ethiopia		Mozambique	1984	Vietnam	1985
Philippines	1983	Namibia		Zambia	1983

in Appendix A shows the selected crisis years for each country from the database used.

4.2.2. Currency Crises

The database used for the construction of the currency crisis prediction models includes 32 explanatory variables from 163 developed, emerging, and developing countries in the period 1970–2017. The dependent variable is constructed from the definition of [75]: a currency crisis is a depreciation of the nominal value of the currency against the US dollar of at least 30 percent, which is at least 10 points percentage higher than the depreciation index in the previous year. The macroeconomic variables have been extracted from the World Bank Open Data (see: https://data.worldbank.org/ (accessed on 11 March 2020)) and chosen from the experiences of [6,36,76]. For their part, the political variables come from the POLITY IV project, following the factors used by [77].

Table 2. Definition of the independent variables for the currency crises.

Attribute	Abbreviation	Description	Exp. Sign.
Exposure to debt	TDEB	Gross external debt as % of GDP Short-term gross external debt as% of GDP Credit interest rate adjusted for inflation	+
	STD	Gross external debt as % of GDP Short-term gross external debt as% of GDP Credit interest rate adjusted for inflation	+
	RIR	Gross external debt as % of GDP Short-term gross external debt as% of GDP Credit interest rate adjusted for inflation	+
Foreign Sector	FXR	Total reserves (excluding gold) as % of GDP	−
	TRO	Ratio of exports plus imports to GDP	+/−
	IMP	Imports of goods and services in current dollars (USD)	+/−
	EXP	Exports of goods and services in current dollars (USD)	−
	CACC	Balance of payments account as % of GDP	−
	PINV	Net portfolio investment in current dollars (USD)	−
	FDI	Foreign direct investment flows as % of GDP	−
Domestic Macroeconomic Factors	RGDP	Annual real GDP in current dollars (USD)	−
	GDPG	Annual growth of real GDP	−
	INF	Rate of change in the consumer price index	+
	M2M	Annual growth of money supply (M2)	+
	M2R	Money supply ratio (M2) divided by reserves	+
	REER	Deviation of the ratio of the real effective exchange rate of the currency (moving average of the last five years)	−
	GOVS	Final central government spending as % of GDP	+/−
	FCF	Gross fixed capital formation in current dollars (USD)	−
	UNE	Total unemployment as % of the total labor force	+
	CON	Sovereign debt crisis event in a country in the same region (with a delay of one year)	+
	SPEG	Exchange rate regime applied to a currency to keep its value stable against a reserve currency.	+
	PEG	Exchange rate regime in which the value of a currency is set against the value of another country’s currency.	+
Banking Sector	DCRE	Domestic credit ratio as % of GDP	+/−
	LIR	Bank rate that meets the financing needs in the short and medium term	−
	DIR	Rate paid by banks for demand, time, or savings deposits	−
Political Factors	POLI	Combined politics score (autocracy score minus democracy score)	−
	DUR	Durability of the political regime expressed in years (‘POLI’ control variable)	+
	PERS	Number of years elapsed since the last radical and abrupt political change (control variable for ‘POLI’)	+
	SFI	State frailty index (The higher the score, the greater the risk of frailty)	+
	LGOV	Binary variable denoted by 1 if the government has a left ideology, and 0 otherwise	+
	ELEC	Binary variable denoted by 1 if it is the year of general elections, and 0 otherwise	+
	TURN	Annual rotation of political agents with veto (1—year in which there has been a change of government; 0—otherwise)	+
	YEAR	Years in office as president of the national government	+
	EFEE	Effectiveness of economic policy measured by GDP per capita	−

shows the set of variables used, with their definition and expected sign, and

Table A2. Currency crisis by country and by year.

Country	Years	Country	Years	Country	Years
Albania	1997	Denmark		Jordan	1989
Germany		Dominica		Kazajistan	1999, 2015
Algeria	1988, 1994	Ecuador	1982, 1999	Kenya	1993
Angola	1991, 1996, 2015	Egypt	1979, 1990, 2016	Kirguistan	1997
Argentina	1975, 1981, 1987, 2002, 2013	El Salvador	1986	Kuwait
Armenia		Eritrea		Laos, R.D.P.	1972, 1978, 1986, 1997
Australia		Slovakia		Lesoto	1985, 2015
Austria		Slovenia		Latvia	1992
Azerbaiyán	2015	Spain	1983	Lebanon	1984, 1990
Bangladesh	1976	United States		Liberia
Barbados		Estonia	1992	Libya	2002
Belgium		Ethiopia	1993	Lithuania	1992
Belice		Fiji	1998	Luxemburgo
Benín	1994	Filipinas	1983, 1998	Macedonia
Belarus	1997, 2009, 2015	Finland	1993	Madagascar	1984, 1994, 2004
Bolivia	1973, 1981	Francia		Malasia	1998
Bosnia y Herzegovina		Gabon	1994	Malawi	1994, 2012
Botsuana	1984	Gambia	1985, 2003	Maldives	1975
Brazil	1976, 1982, 1987, 1992, 1999, 2015	Georgia	1992, 1999	Mali	1994
Brunei		Ghana	1978, 1983, 1993, 2000, 2009, 2014	Morocco	1981
Bulgaria	1996	Grenada		Mauricio
Burkina Faso	1994	Greece	1983	Mauritania	1993
Burundi		Guatemala	1986	Mexico	1977, 1982, 1995
Bhutan		Guinea	1982, 2005	Moldavia	1999
Cape Verde		Equatorial Guinea	1980, 1994	Mongolia	1990, 1997
Camboya	1971, 1992	Guinea-Bissau	1980, 1994	Mozambique	1987, 2015
Cameroon	1994	Guyana	1987	Myanmar	1975, 1990, 1996, 2001,2007, 2012
Canada		Haiti	1992, 2003	Namibia	1984, 2015
Chad	1994	Honduras	1990	Nepal	1984, 1992
Chile	1972, 1982	Hong Kong		Nicaragua	1979, 1985, 1990
China, R.P.		Hungary		Niger	1994
Cyprus		India		Nigeria	1983, 1989, 1997, 2016
Perú	1976, 1981, 1988	Sierra Leona	1983, 1989, 1998	Trinidad and Tobago	1986
Poland		Singapore		Tunisia
Portugal	1983	Syria	1988	Turkmenistan	2008
United Kingdom		Sri Lanka	1978	Turkey	1978, 1984, 1991, 1996, 2001
Central African Republic	1994	Swaziland	1985, 2015	Ukraine	1998, 2009, 2014
Czech Republic		South Africa	1984, 2015	Uganda	1980, 1988
Dominican Rep.	1985, 1990, 2003	Sudan	1981, 1988, 1993, 2012	Uruguay	1972, 1983, 1990, 2002
Ruanda	1991	South Sudan	2015	Uzbekistan	2000
Romania	1996	Sweden	1993	Venezuela	1984, 1989, 1994, 2002, 2010
Russia	1998, 2014	Switzerland		Vietnam	1972, 1981, 1987
San Cristóbal y Nieves		Surinam	1990, 1995, 2001, 2016	Yemen	1985, 1995
São Tomé and Príncipe	1987, 1992, 1997	Thailand	1998	Zambia	1983, 1989, 1996, 2009, 2015
Senegal	1994	Tayikistan	1999, 2015	Zimbabue	1983, 1991, 1998, 2003
Serbia	2000	Tanzania	1985, 1990
Seychelles	2008	Togo	1994

of Appendix A details the years of crisis for the country by country in the sample. The

Table A3. Frequency of crisis event (number per year).

Year	Currency Crises	Sovereign Debt Crises
1970
1971	1
1972	5
1973	1
1974
1975	5
1976	4	1
1977	1	1
1978	5	3
1979	3	2
1980	4	3
1981	10	6
1982	5	9
1983	12	9
1984	10	4
1985	10	3
1986	4	3
1987	6
1988	5	1
1989	8	3
1990	10	2
1991	6
1992	6	1
1993	8
1994	20
1995	4
1996	6
1997	7
1998	10	2
1999	7	2
2000	4
2001	3	2
2002	5	4
2003	4	1
2004	1	1
2005	1
2006
2007	1	1
2008	3	2
2009	5
2010	1	2
2011
2012	3	2
2013	2	1
2014	3	1
2015	13	1
2016	4
2017		2
Total	236	75

of Appendix A summaries the number of crises occurred in the period previously mentioned.

5. Results

This chapter completes the development of the empirical aspects of this research work, offering detail of the results obtained. These results are presented for the global and regional models, and for each of the crisis events considered. The results of the sensitivity analysis have been performed using the Sobol method described in Section 3.9, and those variables that have yielded a sensitivity level equal to or greater than 0.4 have been chosen as the most significant of each model.

To be more effective in demonstrating the superiority of machine learning techniques for the prediction of the crises treated in this study, a Logit analysis has been carried out (see results in

Table A4. Results of Logit analysis for sovereign debt crises.

	Variables	Coefficients	Sig. (Wald)	ROC Curve	R2 Nagelkerke	Classification (%)
						Training	Testing
Global	SBS	0.731	0.000	0.675	0.582	79.17	77.38
	TRO	−0.826	0.006
	FXR	−0.294	−0.005
	INF	0.502	0.000
Africa and Middle East	IMFC	1.038	0.001	0.718	0.638	85.36	81.24
	GOVS	0.592	0.007
	TDEB	0.291	−0.004
	SCFR	−0.374	0.000
	POLI	−0.105	0.000
Asia	REER	−1.274	0.000	0.659	0.572	81.93	78.51
	CACC	−0.682	0.000
	NSAV	−0.719	0.007
	POLI	−0.073	0.000
	TDEB	0.388	−0.009
Latin America	TRO	−0.737	0.000	0.725	0.653	80.28	78.14
	GOVS	1.193	−0.008
	SFI	0.159	0.000
	IMFC	0.461	0.003
	SCLR	−0.153	0.005
	INF	0.274	0.000
Europe	TDEB	0.955	−0.012	0.750	0.674	82.46	79.62
	M2R	0.684	0.000
	GOVS	1.003	0.000
	GINT	0.241	−0.003
	EFEE	−0.639	0.000
	CDS	0.146	0.000

The sample has been divided into 70% for training and 30% for testing.

and

Table A5. Results of Logit analysis for currency crises.

	Variables	Coefficients	Sig. (Wald)	ROC Curve	R2 Nagelkerke	Classification (%)
						Training	Testing
Global	M2M	1.048	−0.003	0.625	0.545	83.48	80.57
	M2R	0.734	0.000
	POLI	−0.382	−0.004
	REER	−0.285	0.013
	CACC	−0.419	0.000
	TRO	−0.118	0.000
Africa and Middle East	FDI	−0.892	0.000	0.727	0.621	85.94	82.26
	FCF	−0.537	−0.008
	DCRE	0.583	0.000
	CACC	−0.242	0.006
Asia	CACC	−1.235	0.000	0.650	0.529	86.11	83.03
	TRO	−0.728	0.000
	EXP	−0.326	0.000
	PINV	−0.440	−0.017
	REER	−0.962	0.005
	DCRE	0.287
Latin America	TRO	−0.937	0.006	0.715	0.692	84.20	81.83
	FCF	−0.629	−0.004
	RGDP	−0.249	0.000
	TDEB	0.385	0.000
	DCRE	0.273	−0.001
Europe	DCRE	0.849	−0.011	0.725	0.644	85.19	82.62
	M2M	0.393	−0.003
	RGDP	−0.741	0.000
	TDEB	0.361	0.004
	FCF	−0.104	0.000
	STD	0.215	0.003

The sample has been divided 70% for training and 30% for testing.

of Appendix A). The results of the Logit models performed show an accuracy of 86.11–79.17% for training data and an accuracy range of 83.03–78.14% for testing data. As explained in the Introduction, we applied machine learning techniques to increase the precision capacity.

5.1. Results for Sovereign Debt Crises

The results of the sensitivity and precision analysis obtained in each stage according to the data subsample (training, validation, and testing) of the global model, Africa, and the Middle East, Asia, Latin America, and Europe, are shown in

Table 3. Sensitivity analysis of sovereign debt crises.

	MLP		SVM		FDT		AdaBoost		XGBoost		RF		DBN		DNDT
	Variables	Sensitivity	Variables	Sensitivity	Variables	Sensitivity	Variables	Sensitivity	Variables	Sensitivity	Variables	Sensitivity	Variables	Sensitivity	Variables	Sensitivity
Global	SBS	0.624	SBS	0.482	TRO	0.875	TRO	0.915	TRO	0.767	TRO	0.927	TRO	0.712	TRO	0.755
	TRO	0.619	FXR	0.428	FXR	0.752	SCFR	0.651	FXR	0.724	INF	0.452	FXR	0.561	FXR	0.727
	FXR	0.482	INF	0.415	SCFR	0.452	SBS	0.562	SFI	0.406	SFI	0.451	SFI	0.325	SFI	0.652
	SFI	0.375	TRO	0.345	INF	0.375	FXR	0.519	SCFR	0.319	SCFR	0.282			SCFR	0.321
	GINT	0.304			SFI	0.375
Africa & Middle East	IMFC	1.294	IMFC	1.601	IMFC	1.370	IMFC	0.916	IMFC	1.039	IMFC	1.023	IMFC	1.261	IMFC	1.069
	POLI	0.621	TDEB	0.612	TDEB	0.493	SCFR	0.634	GOVS	0.526	TDEB	0.521	POLI	0.542	TDEB	0.653
	SCFR	0.458	POLI	0.452	GOVS	0.452	TDEB	0.451	TDEB	0.427	M2R	0.378	GOVS	0.346	M2R	0.631
			M2R	0.325	POLI	0.452	GOVS	0.175	SCFR	0.237	SBS	0.325	M2R	0.315	POLI	0.329
			GDPG	0.321	SCFR	0.355			POLI	0.194	GOVS	0.315	SCFR	0.301
			GOVS	0.305							GDPG	0.312
Asia	CACC	1.350	CACC	1.342	CACC	1.157	CACC	0.897	CACC	1.309	CACC	1.215	CACC	0.945	CACC	1.051
	POLI	0.615	GDPG	0.621	REER	0.626	TDEB	0.436	REER	0.571	SCLR	0.623	TDEB	0.621	REER	0.548
	SCLR	0.521	M2R	0.385	NSAV	0.502	NSAV	0.421	TDEB	0.425	POLI	0.525	IMFC	0.324	NSAV	0.451
	NSAV	0.502	POLI	0.317	TDEB	0.428	GINT	0.325	FXR	0.381	REER	0.519	POLI	0.317	SCLR	0.329
	REER	0.493			POLI	0.317			NSAV	0.359	FXR	0.417			POLI	0.308
									GDPG	0.345	TDEB	0.314
											GDPG	0.312
Latin America	TRO	1.682	GOVS	0.910	TRO	1.145	TRO	1.206	TRO	1.243	TRO	1.324	TRO	0.910	TRO	1.231
	SFI	0.956	TDEB	0.653	SFI	0.625	SFI	0.625	SCLR	0.652	GOVS	0.563	IMFC	0.675	SCLR	0.634
	SCLR	0.679	IMFC	0.611	SCLR	0.452	IMFC	0.362	GOVS	0.423	SCLR	0.458	SCLR	0.452	IMFC	0.564
	IMFC	0.454	TRO	0.563	IMFC	0.427	GOVS	0.324	INF	0.321	GINT	0.328	SFI	0.346	SFI	0.415
	REER	0.428	INF	0.510	REER	0.329					SFI	0.315	SBS	0.324	GINT	0.357
	SBS	0.421	SFI	0.462	GINT	0.317							GINT	0.314
			SCLR	0.452
			REER	0.323
			FXR	0.322
Europe	TDEB	1.428	TDEB	1.351	TDEB	1.351	TDEB	1.452	TDEB	1.046	M2R	1.014	M2R	0.988	TDEB	1.152
	M2R	1.145	M2R	1.05	M2R	1.145	M2R	1.231	M2R	1.023	TDEB	0.965	TDEB	0.872	M2R	1.061
	GOVS	0.851	GINT	0.452	GOVS	0.325	GINT	0.514	GOVS	0.627	GDPG	0.621	GINT	0.329	GOVS	0.324
	EFEE	0.462	EFEE	0.344			CACC	0.347	CDS	0.325	GOVS	0.384	GOVS	0.314	CACC	0.314
			CACC	0.321			CDS	0.322	GINT	0.316	CDS	0.312
			GOVS	0.307			EFEE	0.261

Note: Variables with a significance coefficient greater than 0.4 have been chosen.

and

Table 4. Accuracy analysis for sovereign debt crises.

Method	Classification	Global	Africa and Middle East	Asia	Latin America	Europe
MLP	Training	88.88	90.28	88.70	87.35	88.82
	Validation	87.96	89.04	86.04	86.39	86.76
	Testing	87.67	88.67	85.44	87.65	86.36
SVM	Training	91.09	92.80	91.30	90.06	91.12
	Validation	89.41	90.98	88.41	89.72	90.67
	Testing	88.62	90.02	88.01	88.42	89.45
FDT	Training	98.95	100.00	100.00	99.22	100.00
	Validation	98.13	100.00	98.52	99.03	99.91
	Testing	97.80	100.00	96.82	98.95	99.76
AdaBoost	Training	98.48	97.30	99.49	98.74	99.49
	Validation	97.63	99.34	96.54	98.33	99.75
	Testing	96.08	98.40	95.97	97.13	99.45
XGBoost	Training	97.38	96.71	97.84	97.33	99.29
	Validation	96.65	96.12	96.02	97.81	99.65
	Testing	94.42	95.26	95.43	95.44	98.19
RF	Training	95.46	97.95	97.25	94.88	98.92
	Validation	94.68	96.25	95.89	96.28	97.80
	Testing	92.49	95.40	94.98	93.83	95.50
DBN	Training	95.30	95.27	96.83	94.10	98.46
	Validation	93.17	94.69	94.20	95.06	96.46
	Testing	91.71	93.70	93.95	93.76	94.02
DNDT	Training	96.29	97.13	97.81	94.12	99.36
	Validation	94.79	96.22	96.44	95.70	98.94
	Testing	93.43	95.30	95.20	94.23	97.58

Note: Values expressed in percentage.

, respectively. After observing the results of the sensitivity analysis, the global model shows that variables such as ORR are significant in all the applied methodologies. Another variable that shows the same dynamics is FXR, showing high levels of sensitivity. For their part, the variables that represent credit quality, such as SCFR and SBS, also have high importance according to the results obtained. If we generalize the model in the test sample, the classification level moves in the range 87.67–97.80%, showing the FDT technique with a precision of 97.80% with test data. Finally, the Root Mean Squared Error (RMSE) values (Figure 1) resulting from the methodologies used move in an interval of 0.33–0.22, showing that FDT provides the lowest error (0.22).

The results of the analysis of the sensitivity of the model built with the sample from Africa and the Middle East indicate that the most significant variables are IMFC, M2R, SCFR, and SBS. Regarding the precision results obtained, if we generalize the model in the test sample, the classification level moves in a range of 88.67–100%, with the FDT technique being the one with the highest precision, 100% (testing). Other techniques like AdaBoost and XGBoost show a high level of precision (exceeding 95%). The RMSE values (Figure 1) produced by the methodologies used move in an interval of 0.24–0.07, showing again the FDT technique as the algorithm with the lowest error (0.07).

The variables TRO, FXR, SCFR, and SBS have the greatest impact on the sensitivity analysis of the Asian model. Regarding the precision results, the classification level moves in a range of 8.44–96.82%, showing that FDT presents a precision of 96.82% with test data. In this Asian model, the RMSE values (Figure 1) move in an interval of 0.38–0.26, being again the FDT technique as the algorithm that yields the lowest error (0.26). Regarding the Latin American model, it is observed that the most significant variables are TRO, FXR, SCFR, and SBS. The classification level moves in a range of 87.65–98.85%, showing that FDT obtains the best precision results. In this model, FDT also achieves a lower RMSE. Finally, after examining the results of the sensitivity analysis, the European model shows that the variables with the greatest impact are TDEB, M2R, FXR, SCFR, and SBS. The classification level moves in a range of 86.36–99.76%, with the FDT technique being the one with the highest precision (99.76%). Other techniques such as AdaBoost and XGBoost have also obtained high levels of precision, exceeding 98% in the sample of testing. In this European model, the FDT technique shows the lowest error (0.14).

5.2. Results for Currency Crises

Table 5. Sensitivity analysis of currency crises.

	MLP		SVM		FDT		AdaBoost		XGBoost		RF		DBN		DNDT
	Variables	Sensitivity	Variables	Sensitivity	Variables	Sensitivity	Variables	Sensitivity	Variables	Sensitivity	Variables	Sensitivity	Variables	Sensitivity	Variables	Sensitivity
Global	M2M	1.315	TRO	1.314	TDEB	0.872	M2M	1.248	M2R	1.627	M2M	1.248	M2M	1.307	M2M	1.248
	POLI	0.632	M2R	0.981	M2M	0.865	M2R	1.172	M2M	0.827	RGDP	0.624	M2R	1.152	M2R	1.172
	FCF	0.553	FCF	0.814	M2R	0.691	TRO	0.834	TRO	0.725	REER	0.524	TRO	0.928	TRO	0.834
	M2R	0.523	TDEB	0.720	REER	0.482	CACC	0.624	FDI	0.608	TDEB	0.501	TDEB	0.563	CACC	0.624
	TDEB	0.497	FDI	0.689	FDI	0.387	REER	0.597	TDEB	0.472	TRO	0.442	CACC	0.528	REER	0.597
	CACC	0.437	POLI	0.445	POLI	0.382	POLI	0.382	REER	0.425	POLI	0.331	GOVS	0.520	TDEB	0.439
	TRO	0.435	GOVS	0.421	PINV	0.335	FDI	0.375	POLI	0.422	FDI	0.324	REER	0.517	POLI	0.382
	REER	0.321	CACC	0.418	DCRE	0.317	TDEB	0.318					FCF	0.341	FDI	0.375
Africa and Middle East	FDI	1.237	PINV	1.428	FDI	1.342	FDI	1.304	FDI	1.12	M2R	1.542	FDI	1.248	M2M	1.732
	M2M	1.226	FDI	1.121	FCF	0.837	FCF	1.283	TRI	0.953	M2M	1.173	M2M	1.228	FDI	1.178
	REER	0.985	TRO	0.925	PINV	0.628	M2M	0.728	DCRE	0.871	FDI	0.924	M2R	0.824	FCF	0.785
	FCF	0.742	M2M	0.825	M2R	0.62	TRO	0.685	FCF	0.843	FCF	0.824	DCRE	0.708	TRO	0.748
	M2R	0.653	GOVS	0.756	TRO	0.582	CACC	0.572	PINV	0.781	CACC	0.651	TRO	0.694	DCRE	0.627
	POLI	0.653	FCF	0.647	POLI	0.573	GOVS	0.561	M2M	0.527	TRO	0.546	PINV	0.675	M2R	0.62
	CACC	0.652	DCRE	0.357	GOVS	0.561	POLI	0.452	REER	0.473	GDPG	0.379	CACC	0.639	PINV	0.531
	SFI	0.582	POLI	0.349	SFI	0.525	M2R	0.34	POLI	0.375			FCF	0.624	POLI	0.493
	DCRE	0.538			CACC	0.391			SFI	0.304			POLI	0.315	CACC	0.483
	PINV	0.368
Asia	CACC	1.652	PINV	1.562	M2R	1.582	TRO	1.351	TRO	1.067	TRO	0.952	CACC	1.275	TRO	1.351
	TRO	1.223	TRO	1.132	TRO	1.214	CACC	1.181	DCRE	0.705	REER	0.951	TRO	1.274	CACC	1.181
	M2R	0.562	FXR	0.924	EXP	1.159	EXP	0.657	EXP	0.621	FCF	0.572	REER	0.854	EXP	0.657
	RIR	0.523	FDI	0.896	CACC	0.859	FXR	0.634	FDI	0.571	PINV	0.412	FXR	0.634	FXR	0.634
	TDEB	0.452	POLI	0.651	FCF	0.625	REER	0.349	M2R	0.481	RGDP	0.354	EXP	0.512	REER	0.349
	EXP	0.377	CACC	0.563	DCRE	0.527			CACC	0.437	TDEB	0.198
	FCF	0.327	EXP	0.547	REER	0.349			RIR	0.309	POLI	0.185
	POLI	0.324	GDPG	0.524	RGDP	0.345
Latin America	TRO	1.314	GDPG	1.505	TRO	1.528	TRO	1.253	TRO	1.342	TRO	1.321	TRO	1.164	TRO	1.253
	RGDP	1.256	TRO	1.285	TDEB	0.899	RGDP	1.173	RGDP	1.206	GOVS	0.851	RGDP	1.132	RGDP	1.173
	FCF	0.788	M2M	0.895	GDPG	0.649	FCF	0.593	FCF	0.972	TDEB	0.715	TDEB	0.627	TDEB	0.726
	TDEB	0.687	DCRE	0.852	M2M	0.618	TDEB	0.435	DCRE	0.628	FCF	0.627	FCF	0.505	FCF	0.593
	FDI	0.649	FCF	0.683	POLI	0.524	IMP	0.415	TDEB	0.582	FDI	0.582	DCRE	0.425	IMP	0.415
	DCRE	0.427	TDEB	0.652	DCRE	0.521	RIR	0.317	FDI	0.418	POLI	0.537			DCRE	0.301
	POLI	0.354	FDI	0.649	FDI	0.415	DCRE	0.301	REER	0.391	EXP	0.324
Europe	DCRE	1.528	FCF	1.528	RGDP	1.162	DCRE	1.518	M2M	1.62	M2M	1.494	M2M	1.529	DCRE	1.518
	M2M	1.234	M2M	1.293	M2M	0.925	M2M	1.494	DCRE	1.372	RGDP	0.952	DCRE	1.152	M2M	1.494
	FCF	1.176	DCRE	1.184	DCRE	0.693	FCF	0.843	TDEB	0.983	TDEB	0.925	FCF	0.581	FCF	0.843
	PINV	0.965	STD	0.765	STD	0.641	TDEB	0.648	FCF	0.843	DCRE	0.527	TDEB	0.421	TDEB	0.586
	TDEB	0.326	TDEB	0.652	PINV	0.581	STD	0.415	PINV	0.721	EXP	0.517
	EXP	0.315	PINV	0.541	GOVS	0.521			STD	0.473	FCF	0.355
			SFI	0.437	TDEB	0.458			GDPG	0.318

Note: Variables with a significance coefficient greater than 0.4 have been chosen.

and

Table 6. Accuracy analysis for currency crises.

Method	Classification	Global	Africa & Middle East	Asia	Latin America	Europe
MLP	Training	94.84	94.44	95.06	94.12	95.43
	Validation	94.27	93.91	94.52	93.37	95.10
	Testing	93.76	93.62	94.13	92.85	94.46
SVM	Training	93.33	93.38	93.47	93.04	93.81
	Validation	92.65	92.57	93.02	92.68	93.22
	Testing	91.83	92.18	92.61	91.95	92.93
FDT	Training	96.52	95.90	95.18	94.62	95.56
	Validation	96.14	95.08	93.73	93.20	93.87
	Testing	95.79	94.59	93.03	92.72	93.06
AdaBoost	Training	95.95	95.25	96.17	95.08	96.86
	Validation	95.34	94.57	95.64	94.21	96.42
	Testing	94.28	94.11	95.19	93.36	95.73
XGBoost	Training	98.36	96.81	96.45	98.26	97.78
	Validation	97.87	98.87	95.52	96.19	96.23
	Testing	97.25	95.41	95.34	95.71	96.33
RF	Training	96.48	98.83	98.38	98.01	98.88
	Validation	94.79	97.79	97.07	97.12	97.58
	Testing	94.01	96.52	96.17	95.93	97.01
DBN	Training	96.63	98.97	99.42	98.27	99.70
	Validation	95.80	97.52	97.42	97.61	98.90
	Testing	94.57	96.79	96.45	96.17	98.13
DNDT	Training	99.16	99.17	99.68	98.42	100.00
	Validation	98.87	98.85	99.03	97.79	99.61
	Testing	98.43	98.24	98.54	96.90	99.07

Note: Values expressed in percentage.

detail the results of the sensitivity and precision analysis obtained in each stage according to the data subsample (training, validation, and testing) with the data related to currency crises. In the global model, the most significant variables are M2M, M2R, TRO, FDI, and REER. This shows that a considerable rise in the money supply and foreign investment flows can decide the existence of a global currency crisis. If we generalize the model in the test sample, the classification level moves in a range of 91.83–98.43%, showing that the DNDT technique reaches the highest precision (98.43% with test data). In this global model, the RMSE values (Figure 2) are within the interval 0.35–0.23, showing that the lowest error (0.23) is obtained with FDT.

The Africa and Middle East model shows that M2M, M2R, and FDI are significant with most of the techniques used. Therefore, increases in the money supply and with it, a growth in the proportion of this supply over the country’s foreign exchange reserves, and a low rate of foreign direct investment flows are the best predictors of currency crises in Europe. Regarding the precision of this model, the classification level moves in a range of 92.18–98.24%, showing that the DNDT technique obtains the best fit (precision of 98.24% with test data). Figure 2 details the RMSE values, being the DNDT technique the one with the lowest error (0.19).

The Asian model shows that the variables FXR, TRO, M2R, and CACC show high levels of sensitivity. Therefore, a large increase in the money supply and poor balance of payments and foreign exchange reserve levels appear to be the best currency crisis predictors in Asia. The DNDT technique is the one that offers the highest precision (98.54% with test data). The error range is 0.34–0.18, again being the DNDT technique the one that obtains the lowest (Figure 2). The variables TRO, RGDP, TDEB, and M2R are significant in most of the models built in Latin America. These results indicate that a significant rise in the proportion of the money supply to reserves and a low level of economic growth and trade openness, as well as a high level of public debt, are the main factors in predicting a currency crisis. For its part, the DNDT method is the best prediction technique, with a precision of 96.90% in test data. In this Latin American model, the RMSE values presented by the methods used are located in the interval of 0.34–0.26, with the RF technique being the algorithm with the lowest error (0.26). The results of the sensitivity analysis in the European model show that the variables of M2M, DCRE, FCF, and TDEB are the ones with the greatest impact in most of the applied techniques. These results suggest that an important expansion in the growth of the money supply and high levels of the balance of payments credit and public debt are especially significant in detecting currency crises in Europe. The level of precision is in the range of 92.93–99.07%, with the DNDT technique being the one that reaches a greater success of 99.07% in the testing stage. Figure 2 also details the RMSE values, being the DNDT technique the one with the lowest error (0.14).

5.3. Discussion of Results

The results obtained for the sovereign debt crises forecast reveal a set of robust variables that are reproduced in almost all of the estimated models. Variables of the debt exposure attribute such as TDEB and IMFC mean that the increase in debt levels also causes an increased likelihood of a public debt crisis. These significant variables coincide with the results of the previous works by [3,5], which indicate the great relevance of the debt level on the probability of default. For their part, banking sector variables are significant in previous studies [5], but they have not been validated in our estimates. On the contrary, it has been more common in our models to observe greater significance in variables of the foreign sector attribute such as FXR and M2R, which imply a high accumulation of foreign currency for the payment of the debt of the public institutions of a country. This fact has not been refuted, or at least not with such significance by previous works [7,10]. There are other significant variables such as SCFR and SBS that have not been contrasted either by the prior literature. These variables reflect the fact that a downgrading of the country’s credit rating and an increase in interest payments make it more difficult to access financing and pay the debt, which increases the risk of default due to difficulties in refinancing said debt [3,78]. Lastly, the most sensitive political variables, but with a weaker intensity than those mentioned above, have been: SFI (in the Latin American and Global models) which shows the state’s capacity to carry out public policies, and POLI that shows the country’s level of democracy. In previous literature, only POLI has been identified as significant [3].

The results on sovereign debt default show that models developing with fuzzy C4.5 (FDT) raise the ability to forecast sovereign debt crises, obtaining better ratios of both precision and other selection criteria. Most notably, the global model achieves an accuracy of 97.8%, higher than the 87.1% obtained by [5] employing logistic regression. The same work also reveals the improvement of the precision of their regional models. Along the same lines, it improves the results reported by [3], which had 87% accuracy with regression trees for emerging countries. Likewise, our methodology also improves the prediction capacity of other computational techniques such as neural networks used by [11], with which it obtained 85% accuracy for a sample of emerging countries. Reference [29] achieved 88.6% accuracy with their K-means method for a sample of emerging and developing countries. Even so, other methodologies have shown a consistent predictive capacity throughout the models built, both globally and regionally. These are the case of the AdaBoost, XGBoost, and DNDT techniques, which have shown an average prediction in testing close to 95% correct, making them interesting options to treat the prediction of a sovereign debt crisis. Regarding the level of residuals measured by RMSE, the levels obtained show that the models carried out have a high degree of fit, since the specific statistical literature indicates that those levels below unity present good goodness of fit and that those results less than 0.5 indicate particularly good goodness of fit [79,80]. Therefore, our results show a unique set of variables, in addition to achieving better precision results than the rest of the previous literature.

For their part, the results obtained in the study of currency crises also show a group of explanatory variables that is common in a large part of the estimated models. The FCF variable has been important in most of the models, showing the importance of the evolution of a country’s net investment in increasing the threat of a currency crisis. This result is in contradiction to the findings of [7], in which this variable was not statistically relevant. Continuing with the domestic macroeconomic variables, the variables concerning the money supply (M2M and M2R) have shown high significance, showing that a drastic increase in the money supply hurts the price of the currency. On the other side, the INF variable is not significant, in contrast to works like those of [6,35]. Another variable such as REER has not been refuted as a significant factor either, unlike that shown in the works of [38,45]. Likewise, variables of the foreign sector attribute such as TRO and CACC are shown as more significant variables due to the importance of a country’s international trade performance on price, something that refutes the results of the previous works of [2,36]. In turn, the variables of the banking sector have been relevant in previous investigations [2,6], but they have not obtained a huge significance in our estimates. Regarding the debt variables, the TDEB variable (in connection with the debt accumulation) has been largely significant, indicating that high public debt ratios decrease the currency’s value. Finally, the most important political variables in our models have been: DUR and YEAR (Africa and Asia) that show the state’s capacity to implement public policies, and POLI that shows the level of democracy in the country. These variables have not been pointed as significant in the prior literature [77].

The results on the case of currency crises conclude that the models built with DNDT obtain a forecasting ability close to 100% for currency crises in the regional and global models, with higher levels of accuracy than in other studies. The precision of the global model is 96.38%, but a comparison of this model is complex as it is the first model developed to predict currency crises worldwide. Other studies have obtained lower levels of precision, such as [2], with an accuracy of 84.62% based on the dynamic panel model. In the same way, we have also improved the results obtained by [6], who reached 93.8% accuracy employing neural networks for Turkey. Our methodology is also more powerful in prediction than other computational methods such as the k-nearest neighbor hybrid algorithm and vector support machines (kNN-SVM), which had an accuracy of 97% for a sample of emerging markets [36].

6. Conclusions

The present study developed robust global and regional models to predict international financial crises, specifically those related to sovereign debt and the price of the currency. Similarly, an attempt is made to show the superiority of computational techniques over statistics in terms of the level of precision. An attempt has been made to clarify these issues by overcoming the previous absence of definitive conclusions due to the lack of homogeneity caused by the disparity of methodologies, approaches, available databases, periods, and countries, among other issues.

The results of the study carried out have allowed us to obtain the conclusions that appear below. First, to confirm the existence of differences between the global and regional models, and that the global models can even show a precision capacity similar to the mean of the regional models. To this end, the global sovereign debt prediction models for the studied regions (Africa and the Middle East, Asia, Latin America, and Europe) have obtained an accuracy capacity of 97.80%, 100%, 96.82%, 98%, 85%, and 99.76%, respectively. For its part, this precision relationship for the models built in the study of the currency crisis shows a precision of 98.43%, 98.24%, 98.54%, 96.90%, and 99.07% for the Global sample, Africa and the Middle East, Asia, Latin America, and Europe, respectively. This shows the high level of robustness of the models built concerning previous works.

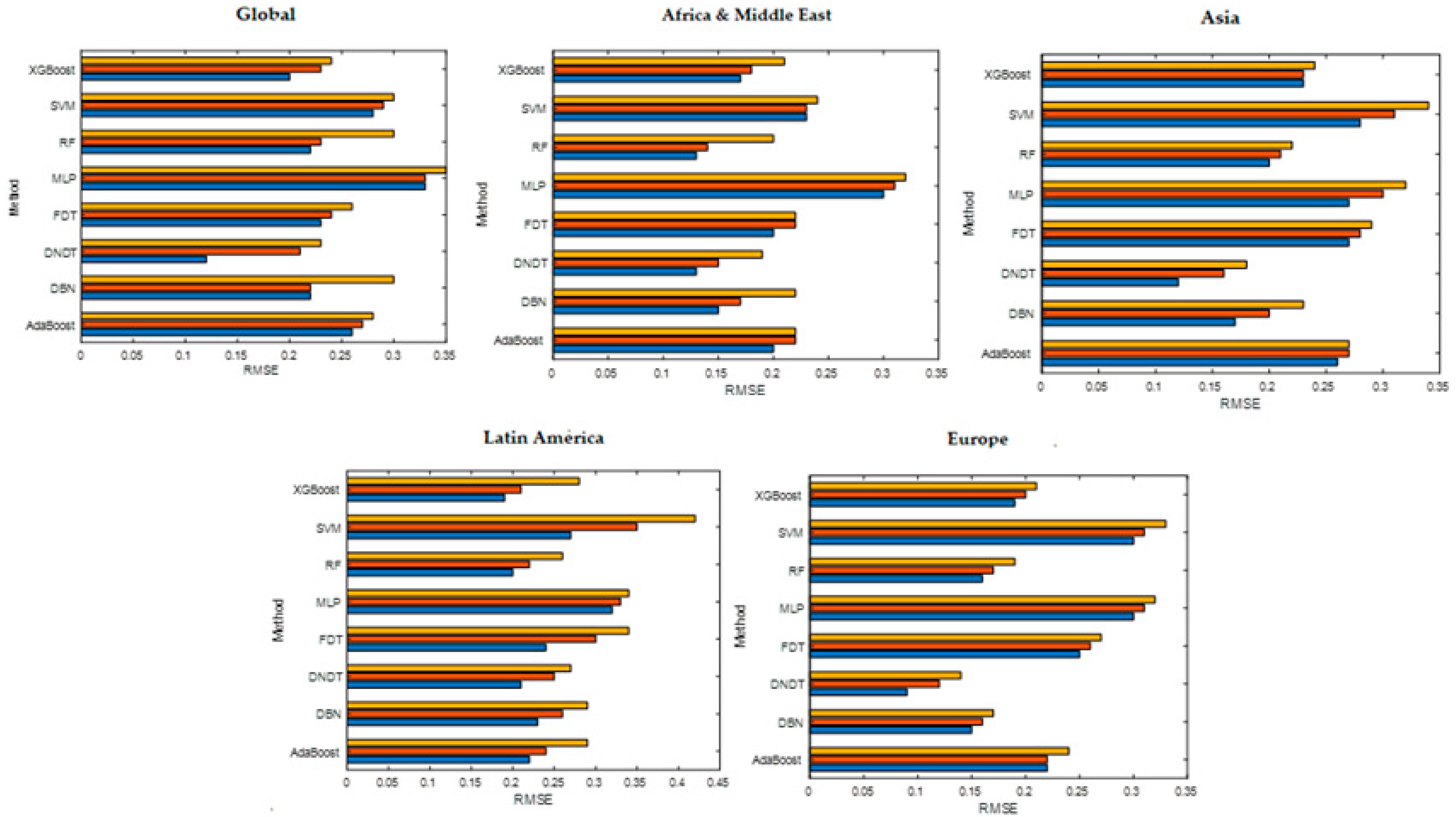
Second, about the objective that postulated that the application of computational methods could improve the level of precision shown by statistical techniques, our empirical evidence has allowed us to accept it for the analyzed crises, all based on the comparison made between levels of success for test sample data and obtained RMSE values. The best methods for the sovereign debt crisis have been FDT, AdaBoost, XGBoost, and DNDT. While for the prediction of the currency crisis, the best techniques have been DNDT, XGBoost, RF, and DBN.

Regarding the explanatory variables of sovereign debt crises, in the set of estimated models, some variables have appeared as significant continuously. They are the variables related to the exposure to the country’s debt, more specifically TDEB, which shows the importance of a high level of public debt in sovereign default, and IMFC, which indicates the influence of high dependence on credit provided by the IMF as a possible cause of the increased probability of default. On the other hand, the foreign sector variables related to the amount of foreign exchange reserves accumulated by a country, such as FXR and M2R, show the importance of a high level of foreign exchange reserves with which to be able to face international debt payments. Lastly, the SCFR and SBS variables also show continued significance, showing that interest paid and credit rating are important factors when evaluating the possibility of a sovereign default.

The results of the currency crisis prediction models also show that a small group of variables are consistently significant. This is the case of the FCF variable, indicating how a low level of dynamism in net investment in the country can cause a strong drop in the currency’s value. Similarly, the variables that the money supply represents, such as M2M and M2R, indicate that a rise in the money supply in the market makes the currency lose its price. Variables of the foreign sector attribute such as TRO and CACC are also presented as significant variables due to the importance of the commercial opening of a country in the price of its currency. Finally, in the case of naming the most significant political variables in a general way, the variables DUR and YEAR indicate a higher incidence of currency crises in those countries where political regimes are perpetuated, i.e., close to totalitarianism.

6.1. Implications

The above conclusions have important theoretical and practical implications. From a theoretical approach, the models developed can help provide tools for the prevision of sovereign debt and currency crises that are able to avoid international financial crises both at the regional level and as a whole (global), since a high level of robustness in these models concerning previous works. This study is a great contribution to the field of international finance, as the results presented in this work have considerable implications for further decisions, providing tools that help governments and financial markets achieve financial stability. Given the need of countries to obtain financing and establish international relations, our models can help to foresee sovereign debt and currency crises in them, avoiding financial disturbances and imbalances and reducing the possibility of damages in the financial intermediation process. All this implies an improvement in the functioning of financial markets, debt sustainability, the profitability of credit institutions, and the non-banking financial sector, such as investment funds. From a practical point of view, our sovereign debt and currency crisis prediction models can be useful to assess the reputation of a country more accurately. In a globalized world, companies always try to expand into markets outside their own, which makes it vital to enjoying a good image of the country of origin to improve the perception of the goods and services offered. A poor reputation of a country in terms of paying its debt obligations, as well as an unstable currency, can have a negative impact on companies from that country in other markets about seeking financing, suppliers, and partnerships with other companies. Therefore, a better perception of the country’s financial management can improve on the one hand, its position in the financial markets, and, on the other side, the country’s reputation for the benefit of its companies.

6.2. Limitations and Further Research

This investigation has certain limitations, principally the historical data available for emerging economies. As this research was conducted from a globally oriented perspective, it requires a much larger range of information compared to other studies in this field. Furthermore, future studies may delve into other types of political information to deepen their influence both on the financial crises studied and on the impact of the country’s reputation. It would be convenient to relate the influence of the financial crises suffered by a country on exports or tourism, important dimensions in the country’s reputation through modifications of the country strength models, as the main tools for measuring reputation. Likewise, and to increase the generalization of the results in the study of the country’s reputation, further analysis could be included on the impact that the financial strength of a country has on corporate reputation, both in large companies and in those that wish to expand internationally, for instance energy companies.

Machine learning techniques show a great capacity to absorb observations, the use of large data samples being vital to obtain a high level of accuracy. Therefore, it shows a greater margin to achieve better precision ratios and a low level of error. But some of the weaknesses of these computational techniques compared to statistics is their higher computational cost to perform the analyzes, as well as greater difficulty in interpreting some methodologies. Therefore, leaving aside the superiority of machine learning methodologies demonstrated in this study and a multitude of previous works, it is necessary to find new techniques that can mitigate the weaknesses described. An interesting technique to test powerful alternatives for predicting international financial crises, such as their effect on the management of the country’s reputation, would be dynamic systems. This technique has been used in different areas of management, obtaining very satisfactory results in simulations of medium and long-term scenarios [81,82,83,84].