Feedback Control for a Diffusive and Delayed Brusselator Model: Semi-Analytical Solutions
Abstract
:1. Introduction
2. Mathematical Formulations Model
3. The Galerkin Technique Methodology
4. Theoretical Framework for the Existence of Hopf Bifurcation
5. Stability and Hopf Bifurcation Analysis
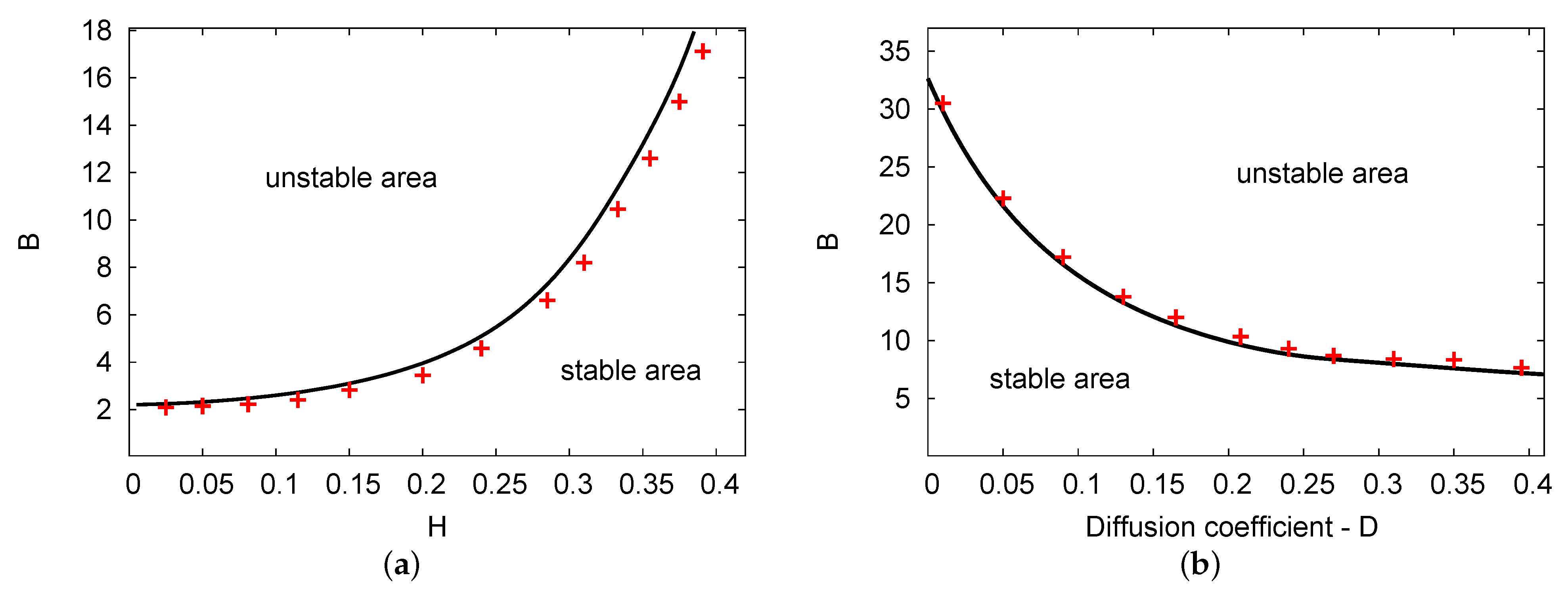
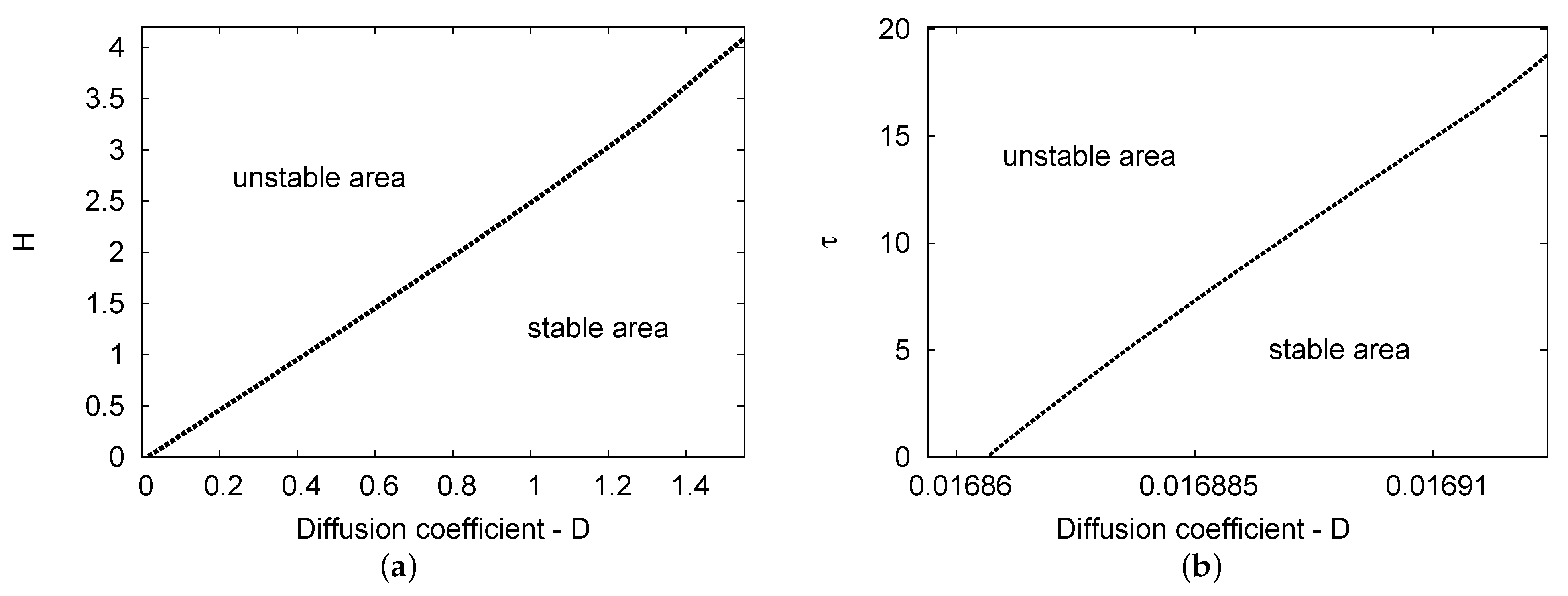
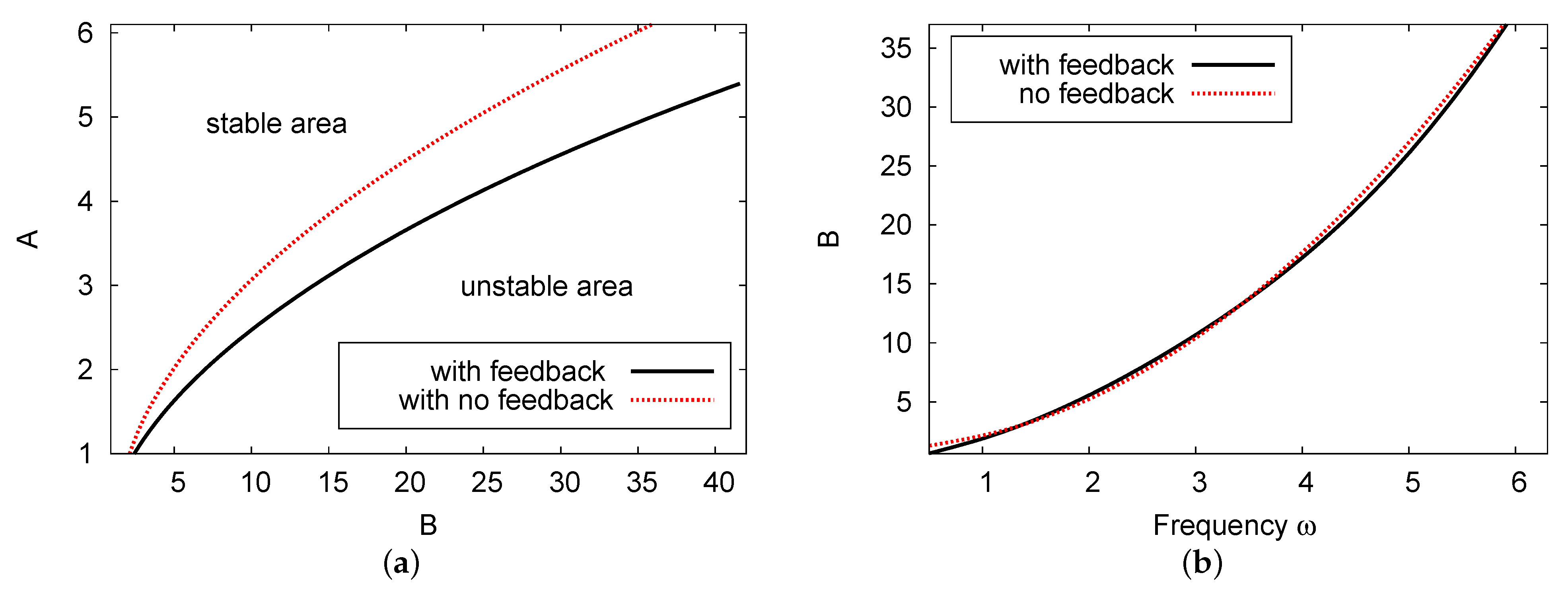
5.1. Hopf Bifurcation Areas
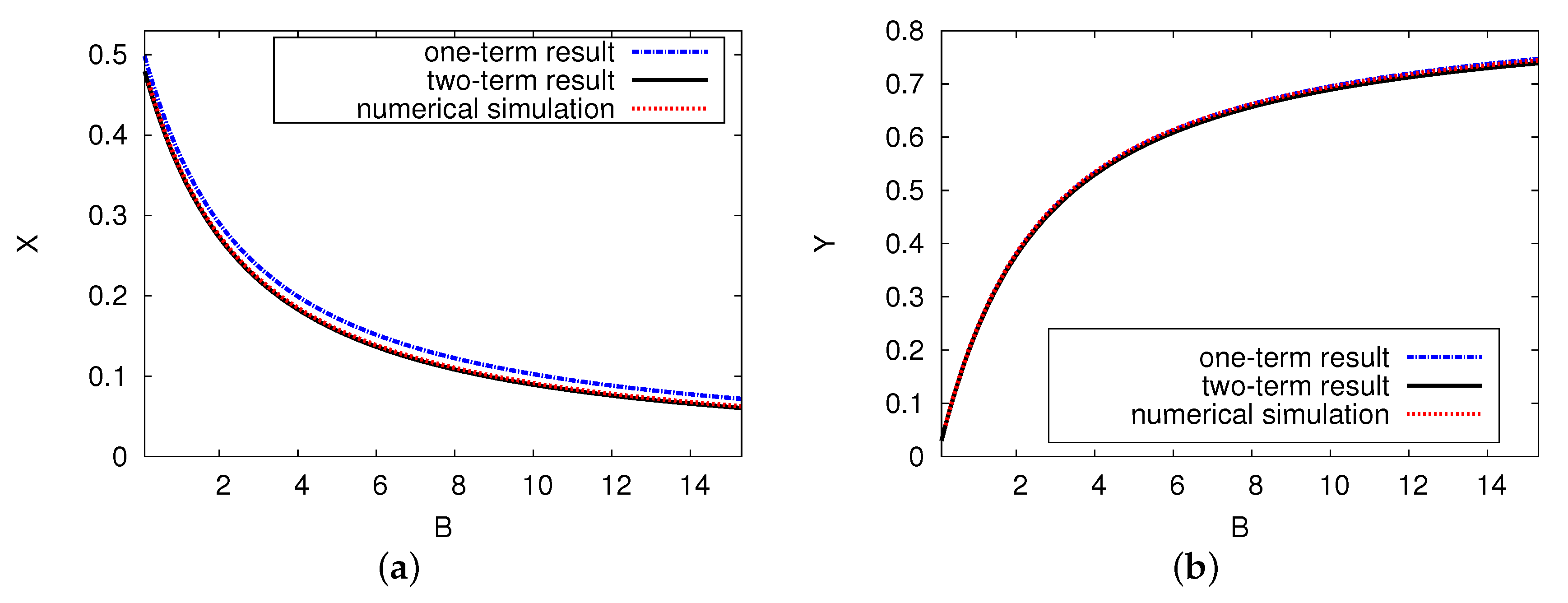
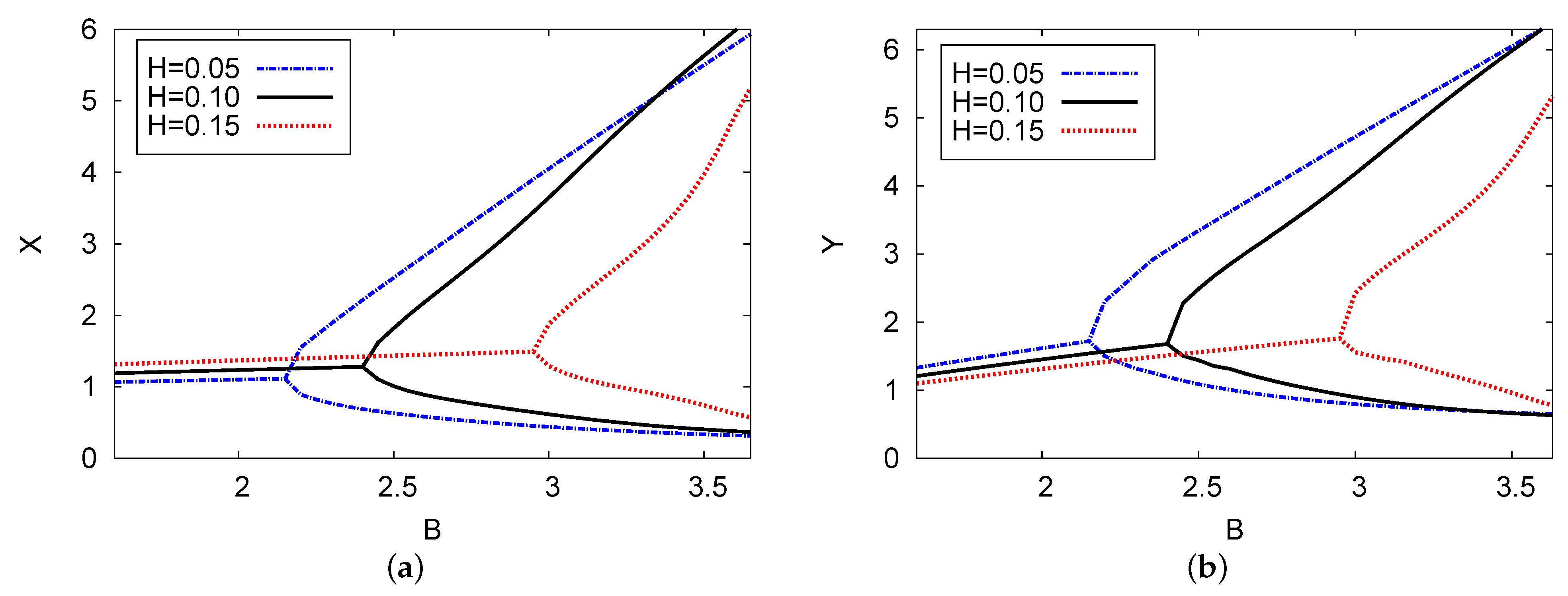
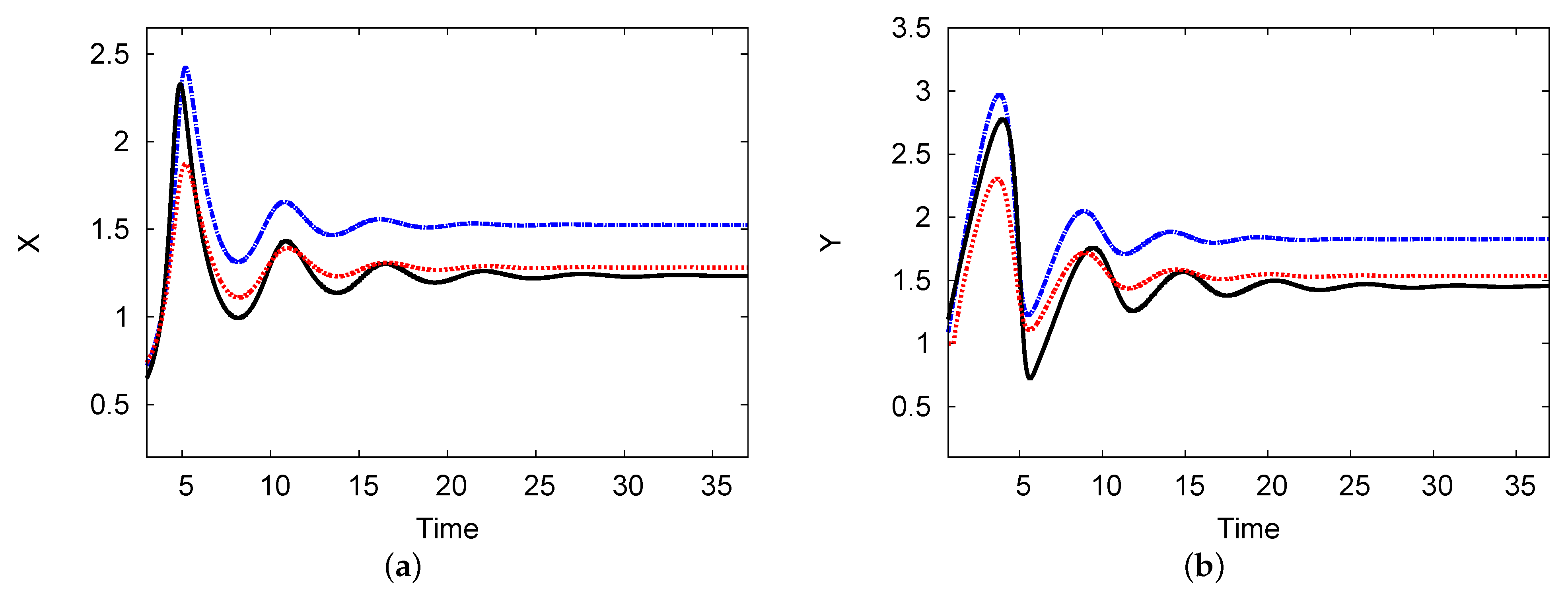
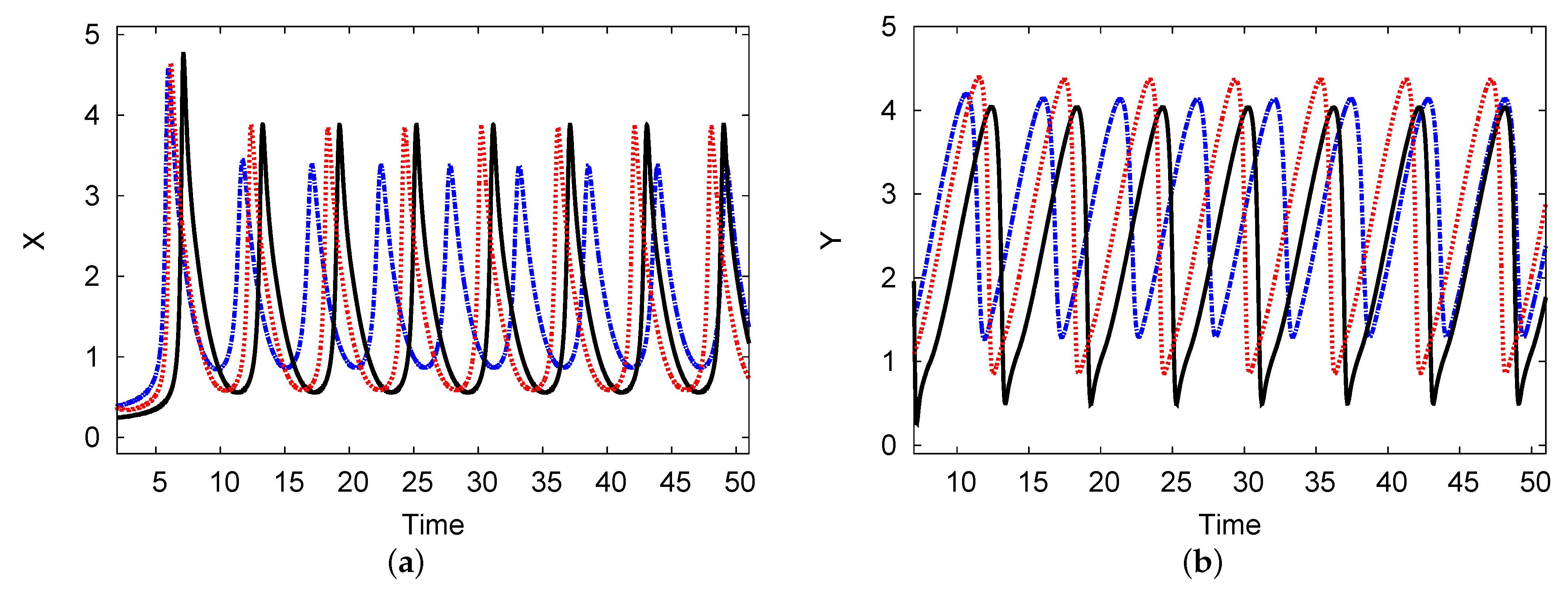
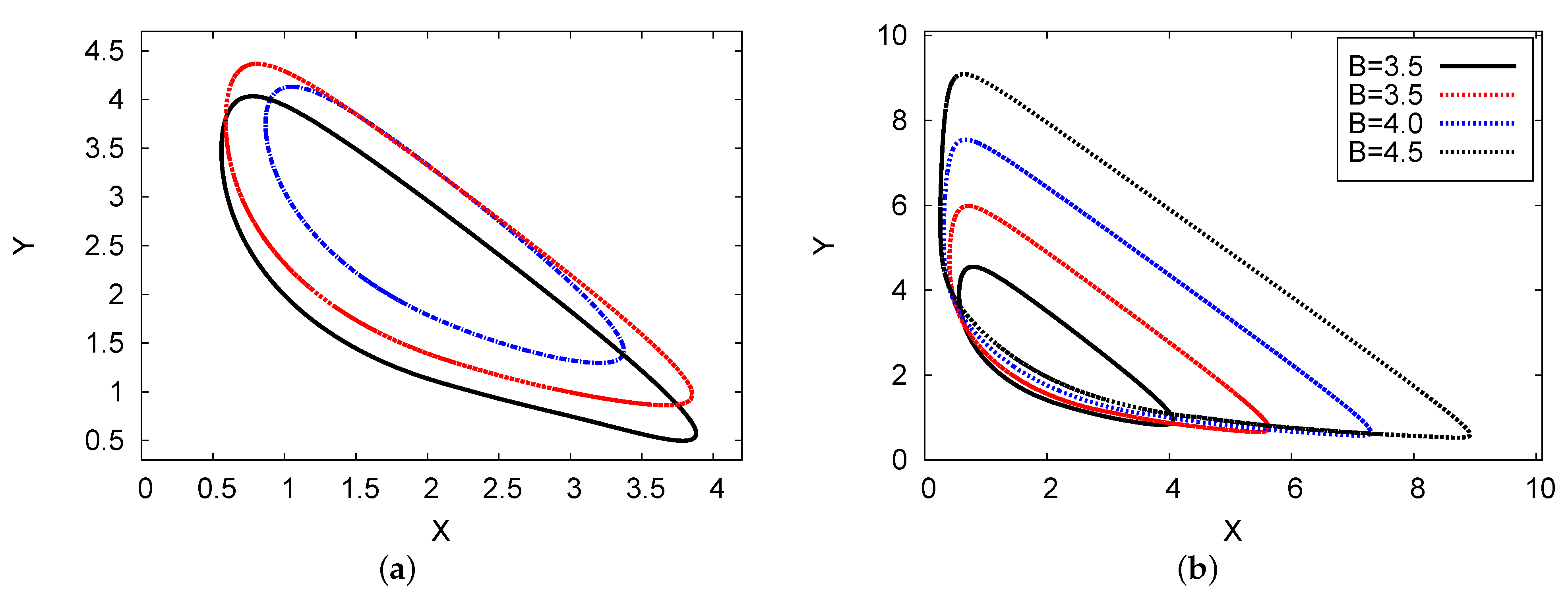
5.2. Bifurcation Diagrams, Periodic Oscillation, and Phase-Plane Map
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alfifi, H.Y.; Marchant, T.R.; Nelson, M.I. Non-smooth feedback control for Belousov-Zhabotinskii reaction-diffusion equations: Semi-analytical solutions. J. Math. Chem. 2016, 57, 157–178. [Google Scholar] [CrossRef] [Green Version]
- Alfifi, H.Y. Semi-analytical solutions for the Brusselator reaction-diffusion model. ANZIM J. 2017, 59, 167–182. [Google Scholar] [CrossRef]
- Marchant, T.R.; Nelson, M.I. Semi-analytical solution for one-and two-dimensional pellet problems. Proc. R. Soc. Lond. 2004, A460, 2381–2394. [Google Scholar] [CrossRef]
- Al Noufaey, K.S.; Marchant, T.R. Semi-analytical solutions for the reversible Selkov model with feedback delay. Appl. Math. Comput. 2014, 232, 49–59. [Google Scholar] [CrossRef] [Green Version]
- Alharthi, M.R.; Marchant, T.R.; Nelson, M.I. Mixed quadratic-cubic autocatalytic reaction-diffusion equations: Semi-analytical solutions. Appl. Math. Model. 2014, 38, 5160–5173. [Google Scholar] [CrossRef]
- Marchant, T.R. Cubic autocatalytic reaction diffusion equations: Semi-analytical solutions. Proc. R. Soc. Lond. 2002, A458, 873–888. [Google Scholar] [CrossRef] [Green Version]
- Merz, W.; Rybka, P. Strong solutions to the Richards equation in the unsaturated zone. J. Math. Anal. Appl. 2010, 371, 741–749. [Google Scholar] [CrossRef] [Green Version]
- Berardi, M.; Difonzo, F. Strong solutions for Richards’ equation with Cauchy conditions and constant pressure gradient. Environ. Fluid Mech. 2020, 20, 165–174. [Google Scholar] [CrossRef]
- Liu, B.; Marchant, T.R. The microwave heating of two-dimensional slabs with small Arrhenius absorptivity. IMA J. Appl. Math. 1999, 62, 137–166. [Google Scholar] [CrossRef]
- Gray, P.; Griffiths, J.F.; Scott, K. Branched-chain reactions in open systems: Theory of the oscillatory ignition limit for the hydrogen+ oxygen reaction in a continuous-flow stirred-tank reactor. Proc. R. Soc. Lond. 1984, A394, 243–258. [Google Scholar]
- Alfifi, H.Y. Semi-analytical solutions for the delayed and diffusive viral infection model with logistic growth. J. Nonlinear Sci. Appl. 2019, 12, 589–601. [Google Scholar] [CrossRef]
- Alfifi, H.Y. Semi analytical solutions for the Diffusive Logistic Equation with Mixed Instantaneous and Delayed Density Dependencel. Adv. Differ. Equ. 2020, 162, 1–15. [Google Scholar]
- Prigogine, I.; Lefever, R. Symmetry Breaking Instabilities in Dissipative Systems. II. J. Chem. Phys. 1968, 48, 1665–1700. [Google Scholar] [CrossRef]
- Adomian, G. The diffusion-Brusselator equation. Comput. Math. Appl. 1995, 29, 1–3. [Google Scholar] [CrossRef] [Green Version]
- Ang, W. The two-dimensional reaction-diffusion Brusselator system: A dual-reciprocity boundary element solution. Eng. Anal. Bound. Elem. 2003, 27, 897–903. [Google Scholar] [CrossRef]
- Mittal, R.; Jiwari, R. Numerical study of two-dimensional reaction-diffusion Brusselator system. Appl. Math. Comput. 2011, 217, 5404–5415. [Google Scholar] [CrossRef]
- Kumar, Y.K.S.; Yildirim, A. A mathematical modeling arising in the chemical systems and its approximate numerical solution. Asia Pac. J. Chem. Eng. 2012, 7, 835–840. [Google Scholar] [CrossRef]
- Twizell, E.; Gumel, A.; Cao, Q. A second-order scheme for the Brusselator reaction-diffusion system. J. Math. Chem. 1999, 26, 297–316. [Google Scholar] [CrossRef]
- Wazwaz, A. The decomposition method applied to systems of partial differential equations and to the reaction-diffusion Brusselator model. Appl. Math. Comput. 2000, 110, 251–264. [Google Scholar] [CrossRef]
- Erneux, T. Applied Delay Differential Equations; Springer: New York, NY, USA, 2009. [Google Scholar]
- Hale, J. Theory of Functional Differential Equations; Springer: New York, NY, USA, 1977. [Google Scholar]
- Tlidi, M.; Gandica, Y.; Sonnino, G.; Averlant, E.; Panajotov, K. Self-Replicating Spots in the Brusselator Model and Extreme Events in the One-Dimensional Case with Delay. Entropy 2016, 18, 64. [Google Scholar] [CrossRef] [Green Version]
- Akhmediev, N.; Kibler, B.; Baronio, F.; Belić, M.; Zhong, W.P.; Zhang, Y.; Chang, W.; Soto-Crespo, J.M.; Vouzas, P.; Grelu, P.; et al. Roadmap on optical rogue waves and extreme events. J. Opt. 2016, 18, 063001. [Google Scholar] [CrossRef] [Green Version]
- Fletcher, C.A. Computational Galerkin Methods; Springer: New York, NY, USA, 1984. [Google Scholar]
- Al Noufaey, K. Stability analysis for Selkov-Schnakenberg reaction-diffusion system. Open Math. 2021, 19, 46–62. [Google Scholar] [CrossRef]
- Alfifi, H.Y.; Marchant, T.R.; Nelson, M.I. Semi-analytical solutions for the 1- and 2-D diffusive Nicholson’s blowflies equation. IMA J. Appl. Math. 2014, 79, 175–199. [Google Scholar] [CrossRef]
- Alfifi, H.Y. The stability and Hopf bifurcation analysis for the delay diffusive neural networks model. AIP Conf. Proc. 2020, 2184, 1–8. [Google Scholar]
- Alfifi, H.Y. Stability and Hopf bifurcation analysis for the diffusive delay logistic population model with spatially heterogeneous environment. Appl. Math. Comput. 2021, in press. [Google Scholar]
- Alfifi, H.Y.; Marchant, T.R. Feedback Control for a Diffusive Delay Logistic Equation: Semi-analytical Solutions. IAENG Appl. Math. 2018, 48, 317–323. [Google Scholar]
- Alfifi, H.Y.; Marchant, T.R.; Nelson, M.I. Generalised diffusive delay logistic equations: Semi-analytical solutions. Dynam. Cont. Dis. Ser. B 2012, 19, 579–596. [Google Scholar]
- Alfifi, H.Y. Semi-analytical solutions for the delayed diffusive food-limited model. In Proceedings of the 2017 7th International Conference on Modeling, Simulation, and Applied Optimization (ICMSAO), Sharjah, United Arab Emirates, 6–7 April 2017; pp. 1–5. [Google Scholar]
- van der Vegt, J.; van der Ven, H. Space—Time Discontinuous Galerkin Finite Element Method with Dynamic Grid Motion for Inviscid Compressible Flows: I. General Formulation. J. Comput. Phys. 2002, 182, 546–585. [Google Scholar] [CrossRef] [Green Version]
- Verwer, J.G.; Hundsdorfer, W.H.; Sommeijer, B. Convergence properties of the Runge-Kutta-Chebyshev method. Numer. Math. 1990, 57, 157–178. [Google Scholar] [CrossRef]
- Smith, G.D. Numerical Solution of Partial Differential Equations: Finite Difference Methods, 3rd ed.; Oxford University Press: New York, NY, USA, 1985. [Google Scholar]


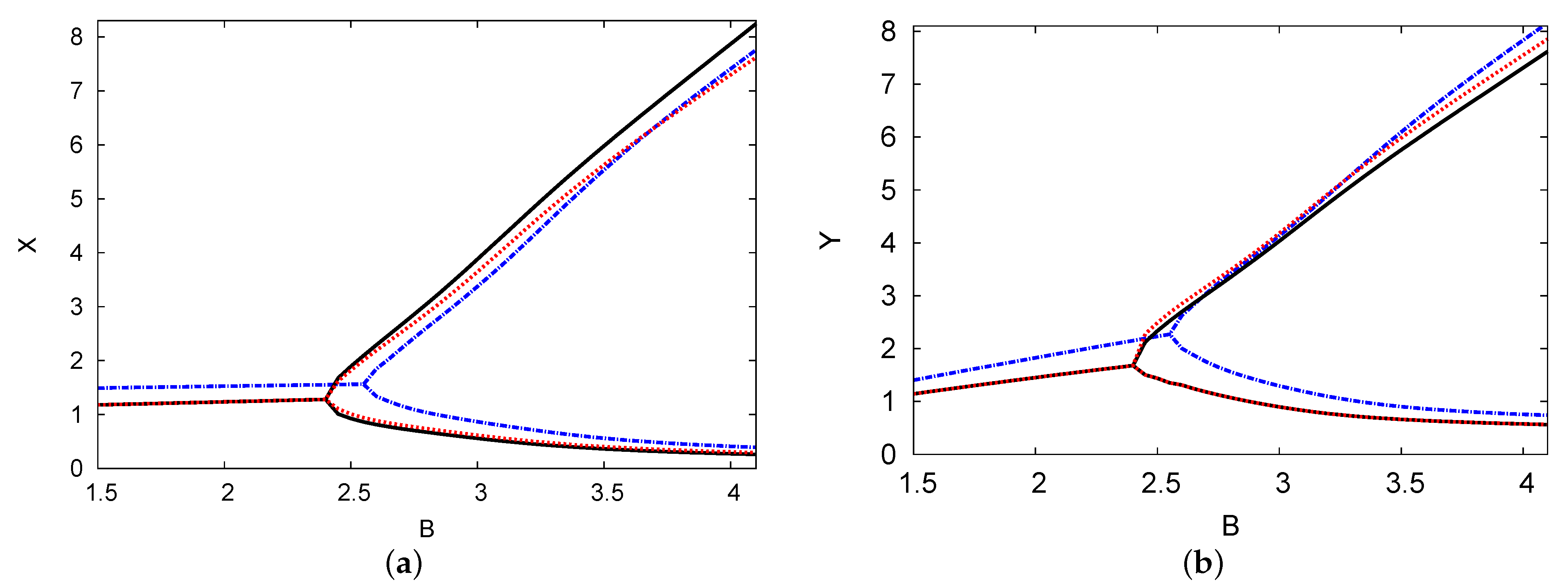

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alfifi, H.Y. Feedback Control for a Diffusive and Delayed Brusselator Model: Semi-Analytical Solutions. Symmetry 2021, 13, 725. https://doi.org/10.3390/sym13040725
Alfifi HY. Feedback Control for a Diffusive and Delayed Brusselator Model: Semi-Analytical Solutions. Symmetry. 2021; 13(4):725. https://doi.org/10.3390/sym13040725
Chicago/Turabian StyleAlfifi, Hassan Yahya. 2021. "Feedback Control for a Diffusive and Delayed Brusselator Model: Semi-Analytical Solutions" Symmetry 13, no. 4: 725. https://doi.org/10.3390/sym13040725
APA StyleAlfifi, H. Y. (2021). Feedback Control for a Diffusive and Delayed Brusselator Model: Semi-Analytical Solutions. Symmetry, 13(4), 725. https://doi.org/10.3390/sym13040725





