Multiphase Phase-Field Lattice Boltzmann Method for Simulation of Soluble Surfactants
Abstract
:1. Introduction
2. Numerical Method
2.1. Proposed Phase-Field Model for Immiscible Fluids Including Surfactants
2.2. Thermodynamic Equilibrium
2.3. Lattice Boltzmann Method
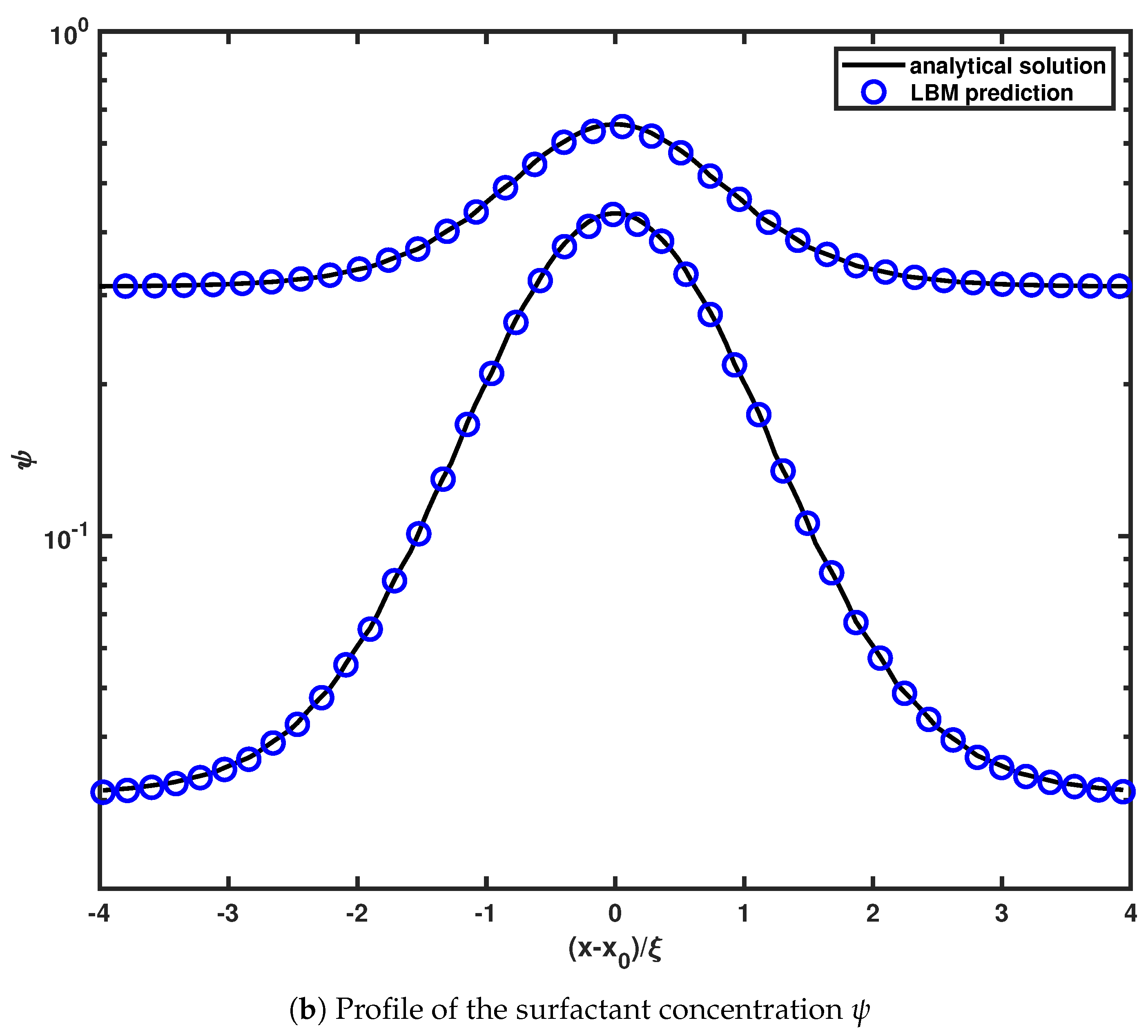
3. Model Validation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LBM | lattice Boltzmann method |
References
- Teigen, K.E.; Song, P.; Lowengrub, J.; Voigt, A. A diffuse-interface method for two-phase flows with soluble surfactants. J. Comput. Phys. 2011, 230, 375–393. [Google Scholar] [CrossRef] [Green Version]
- Sjoblom, J. Emulsions and Emulsion Stability: Surfactant Science Series/61; CRC Press: Boca Raton, FL, USA, 2005; Volume 132. [Google Scholar]
- Stone, H.A.; Stroock, A.D.; Ajdari, A. Engineering flows in small devices: Microfluidics toward a lab-on-a-chip. Annu. Rev. Fluid Mech. 2004, 36, 381–411. [Google Scholar] [CrossRef] [Green Version]
- Baret, J.C.; Kleinschmidt, F.; El Harrak, A.; Griffiths, A.D. Kinetic aspects of emulsion stabilization by surfactants: A microfluidic analysis. Langmuir 2009, 25, 6088–6093. [Google Scholar] [CrossRef] [PubMed]
- Mulqueen, M.; Blankschtein, D. Theoretical and experimental investigation of the equilibrium oil- water interfacial tensions of solutions containing surfactant mixtures. Langmuir 2002, 18, 365–376. [Google Scholar] [CrossRef]
- Zhang, L.; He, L.; Ghadiri, M.; Hassanpour, A. Effect of surfactants on the deformation and break-up of an aqueous drop in oils under high electric field strengths. J. Pet. Sci. Eng. 2015, 125, 38–47. [Google Scholar] [CrossRef] [Green Version]
- Engblom, S.; Do-Quang, M.; Amberg, G.; Tornberg, A.K. On diffuse interface modeling and simulation of surfactants in two-phase fluid flow. Commun. Comput. Phys. 2013, 14, 879–915. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.J.; Li, Z.; Lowengrub, J.; Zhao, H. A level-set method for interfacial flows with surfactant. J. Comput. Phys. 2006, 212, 590–616. [Google Scholar] [CrossRef] [Green Version]
- De Jesus, W.C.; Roma, A.M.; Pivello, M.R.; Villar, M.M.; da Silveira-Neto, A. A 3D front-tracking approach for simulation of a two-phase fluid with insoluble surfactant. J. Comput. Phys. 2015, 281, 403–420. [Google Scholar] [CrossRef]
- Rinaudo, A.; Raffa, G.M.; Scardulla, F.; Pilato, M.; Scardulla, C.; Pasta, S. Biomechanical implications of excessive endograft protrusion into the aortic arch after thoracic endovascular repair. Comput. Biol. Med. 2015, 66, 235–241. [Google Scholar] [CrossRef]
- Mendez, V.; Di Giuseppe, M.; Pasta, S. Comparison of hemodynamic and structural indices of ascending thoracic aortic aneurysm as predicted by 2-way FSI, CFD rigid wall simulation and patient-specific displacement-based FEA. Comput. Biol. Med. 2018, 100, 221–229. [Google Scholar] [CrossRef]
- Seemann, R.; Brinkmann, M.; Pfohl, T.; Herminghaus, S. Droplet based microfluidics. Rep. Prog. Phys. 2011, 75, 016601. [Google Scholar] [CrossRef]
- Teramoto, T.; Yonezawa, F. Droplet growth dynamics in a water/oil/surfactant system. J. Colloid Interface Sci. 2001, 235, 329–333. [Google Scholar] [CrossRef] [PubMed]
- Theissen, O.; Gompper, G. Lattice-Boltzmann study of spontaneous emulsification. Eur. Phys. J. B Condens. Matter Complex Syst. 1999, 11, 91–100. [Google Scholar] [CrossRef]
- Van der Sman, R.; Van der Graaf, S. Diffuse interface model of surfactant adsorption onto flat and droplet interfaces. Rheol. Acta 2006, 46, 3–11. [Google Scholar] [CrossRef]
- Teng, C.H.; Chern, I.L.; Lai, M.C. Simulating binary fluid-surfactant dynamics by a phase field model. Discret. Contin. Dyn. Syst. B 2012, 17, 1289. [Google Scholar] [CrossRef]
- Li, Y.; Kim, J. A comparison study of phase-field models for an immiscible binary mixture with surfactant. Eur. Phys. J. B 2012, 85, 1–9. [Google Scholar] [CrossRef]
- Van der Sman, R.; Meinders, M. Analysis of improved Lattice Boltzmann phase field method for soluble surfactants. Comput. Phys. Commun. 2016, 199, 12–21. [Google Scholar] [CrossRef]
- Gendre, F.; Ricot, D.; Fritz, G.; Sagaut, P. Grid refinement for aeroacoustics in the lattice Boltzmann method: A directional splitting approach. Phys. Rev. E 2017, 96, 023311. [Google Scholar] [CrossRef] [PubMed]
- Gorakifard, M.; Salueña, C.; Cuesta, I.; Far, E.K. Analysis of Aeroacoustic Properties of the Local Radial Point Interpolation Cumulant Lattice Boltzmann Method. Energies 2021, 14, 1443. [Google Scholar] [CrossRef]
- Kian Far, E.; Langer, S. Analysis of the cumulant lattice Boltzmann method for acoustics problems. In Proceedings of the 13th International Conference on Theoretical and Computational Acoustics, Vienna, Austria, 30 July–3 August 2017. [Google Scholar]
- Gorakifard, M.; Salueña, C.; Cuesta, I.; Kian Far, E. Acoustical analysis of fluid structure interaction using the Cumulant lattice Boltzmann method. In Proceedings of the 16th International Conference for Mesoscopic Methods in Engineering and Science, Edinburgh, UK, 23–26 July 2019. [Google Scholar]
- Gorakifard, M.; Cuesta, I.; Salueña, C.; Far, E.K. Acoustic wave propagation and its application to fluid structure interaction using the Cumulant Lattice Boltzmann Method. Comput. Math. Appl. 2021, 87, 91–106. [Google Scholar] [CrossRef]
- Montessori, A.; Lauricella, M.; La Rocca, M.; Succi, S.; Stolovicki, E.; Ziblat, R.; Weitz, D. Regularized lattice Boltzmann multicomponent models for low capillary and Reynolds microfluidics flows. Comput. Fluids 2018, 167, 33–39. [Google Scholar] [CrossRef] [Green Version]
- O’Connor, J.; Day, P.; Mandal, P.; Revell, A. Computational fluid dynamics in the microcirculation and microfluidics: What role can the lattice Boltzmann method play? Integr. Biol. 2016, 8, 589–602. [Google Scholar] [CrossRef] [Green Version]
- Pravinraj, T.; Uma, G.; Umapathy, M. A pseudopotential based lattice Boltzmann modeling of electro wetting-on-dielectric for droplet operations. J. Electrost. 2021, 109, 103547. [Google Scholar] [CrossRef]
- He, Q.; Li, Y.; Huang, W.; Hu, Y.; Li, D.; Wang, Y. Lattice Boltzmann simulations of magnetic particles in a three-dimensional microchannel. Powder Technol. 2020, 373, 555–568. [Google Scholar] [CrossRef]
- Kian Far, E.; Geier, M.; Kutscher, K.; Krafczyk, M. Implicit Large Eddy Simulation of Flow in a Micro-Orifice with the Cumulant Lattice Boltzmann Method. Computation 2017, 5, 23. [Google Scholar] [CrossRef] [Green Version]
- Kian Far, E.; Geier, M.; Kutscher, K.; Konstantin, M. Simulation of micro aggregate breakage in turbulent flows by the cumulant lattice Boltzmann method. Comput. Fluids 2016, 140, 222–231. [Google Scholar] [CrossRef]
- Fattahi, E.; Farhadi, M.; Sedighi, K.; Nemati, H. Lattice Boltzmann simulation of natural convection heat transfer in nanofluids. Int. J. Therm. Sci. 2012, 52, 137–144. [Google Scholar] [CrossRef]
- Fattahi, E.; Farhadi, M.; Sedighi, K. Lattice Boltzmann simulation of natural convection heat transfer in eccentric annulus. Int. J. Therm. Sci. 2010, 49, 2353–2362. [Google Scholar] [CrossRef]
- Kian Far, E.; Shirani, E. Simulation of natural convection heat transfer using the lattice boltzmann method in enclosures. In Proceedings of the 17th Annual Conference of Mechanical Engineering, Tehran, Iran, 16 July 2009. [Google Scholar]
- Fattahi, E.; Pribec, I.; Becker, T. A Novel Lattice Boltzmann Method for Deformable Media. Reactive Flows in Deformable, Complex Media. Math. Forsch. Oberwolfach 2018. [Google Scholar] [CrossRef] [Green Version]
- Kian Far, E.; Shirani, E.; Geller, S. Fluid structure interaction with using of lattice Boltzmann method. In Proceedings of the 13th Annual and 2nd International Fluid Dynamics Conference, Shiraz, Iran, 26–28 October 2010.
- Wang, X.; Ban, X.; He, R.; Wu, D.; Liu, X.; Xu, Y. Fluid-solid boundary handling using pairwise interaction model for non-Newtonian fluid. Symmetry 2018, 10, 94. [Google Scholar] [CrossRef]
- Krafczyk, M.; Tölke, J.; Rank, E.; Schulz, M. Two-dimensional simulation of fluid–structure interaction using lattice-Boltzmann methods. Comput. Struct. 2001, 79, 2031–2037. [Google Scholar] [CrossRef]
- Kian Far, E.; Geier, M.; Krafczyk, M. Simulation of rotating objects in fluids with the cumulant lattice Boltzmann model on sliding meshes. Comput. Math. Appl. 2018. [Google Scholar] [CrossRef]
- Kian Far, E. A sliding mesh LBM approach for the simulation of the rotating objects. In Proceedings of the 13th International Conference for Mesoscopic Methods in Engineering and Science, Hamburg, Germany, 22 July 2016. [Google Scholar]
- Kian Far, E. Simulation of Moving Body in Field Flow and Fluid Structure Interaction with using Lattice Boltzmann Method. Master’s Thesis, Isfahan University of Technology, Isfahan, Iran, 2010. [Google Scholar]
- Kian Far, E. Turbulent flow simulation of dispersion microsystem with Cumulant lattice Boltzmann method. In Proceedings of the Formula X, Manchester, UK, 24 June 2019. [Google Scholar]
- Kian Far, E.; Geier, M.; Kutscher, K.; Krafczyk, M. Distributed cumulant lattice Boltzmann simulation of the dispersion process of ceramic agglomerates. J. Comput. Methods Sci. Eng. 2016, 16, 231–252. [Google Scholar] [CrossRef]
- Fattahi, E.; Waluga, C.; Wohlmuth, B.; Rüde, U.; Manhart, M.; Helmig, R. Lattice Boltzmann methods in porous media simulations: From laminar to turbulent flow. Comput. Fluids 2016, 140, 247–259. [Google Scholar] [CrossRef]
- Mousavi Tilehboni, S.; Fattahi, E.; Hassanzadeh Afrouzi, H.; Farhadi, M. Numerical simulation of droplet detachment from solid walls under gravity force using lattice Boltzmann method. J. Mol. Liq. 2015, 212, 544–556. [Google Scholar] [CrossRef]
- Chen, Z.; Shu, C.; Tan, D.; Niu, X.; Li, Q. Simplified multiphase lattice Boltzmann method for simulating multiphase flows with large density ratios and complex interfaces. Phys. Rev. E 2018, 98, 063314. [Google Scholar] [CrossRef]
- Fei, L.; Yang, J.; Chen, Y.; Mo, H.; Luo, K.H. Mesoscopic simulation of three-dimensional pool boiling based on a phase-change cascaded lattice Boltzmann method. Phys. Fluids 2020, 32, 103312. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, Y. Phase-field modeling droplet dynamics with soluble surfactants. J. Comput. Phys. 2010, 229, 9166–9187. [Google Scholar] [CrossRef]
- Van der Sman, R.; Van der Graaf, S. Emulsion droplet deformation and breakup with lattice Boltzmann model. Comput. Phys. Commun. 2008, 178, 492–504. [Google Scholar] [CrossRef]
- Fard, E.G. A Cumulant LBM approach for Large Eddy Simulation of Dispersion Microsystems. Ph.D. Thesis, Technische Universität Braunschweig, Braunschweig, Germany, 2015. [Google Scholar]






| Samples | Given Interfacial Tension | Given Bulk Surfactant Concentration | Error |
|---|---|---|---|
| 1 | 0.0389 | 0.1 | 2% |
| 2 | 0.0364 | 0.3 | 1.3% |
| 3 | 0.0330 | 0.5 | 0.1% |
| 4 | 0.0308 | 0.6 | 0.6% |
| 5 | 0.0279 | 0.7 | 2.1% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kian Far, E.; Gorakifard, M.; Fattahi, E. Multiphase Phase-Field Lattice Boltzmann Method for Simulation of Soluble Surfactants. Symmetry 2021, 13, 1019. https://doi.org/10.3390/sym13061019
Kian Far E, Gorakifard M, Fattahi E. Multiphase Phase-Field Lattice Boltzmann Method for Simulation of Soluble Surfactants. Symmetry. 2021; 13(6):1019. https://doi.org/10.3390/sym13061019
Chicago/Turabian StyleKian Far, Ehsan, Mohsen Gorakifard, and Ehsan Fattahi. 2021. "Multiphase Phase-Field Lattice Boltzmann Method for Simulation of Soluble Surfactants" Symmetry 13, no. 6: 1019. https://doi.org/10.3390/sym13061019





