Abundant Traveling Wave and Numerical Solutions of Weakly Dispersive Long Waves Model
Abstract
:1. Introduction
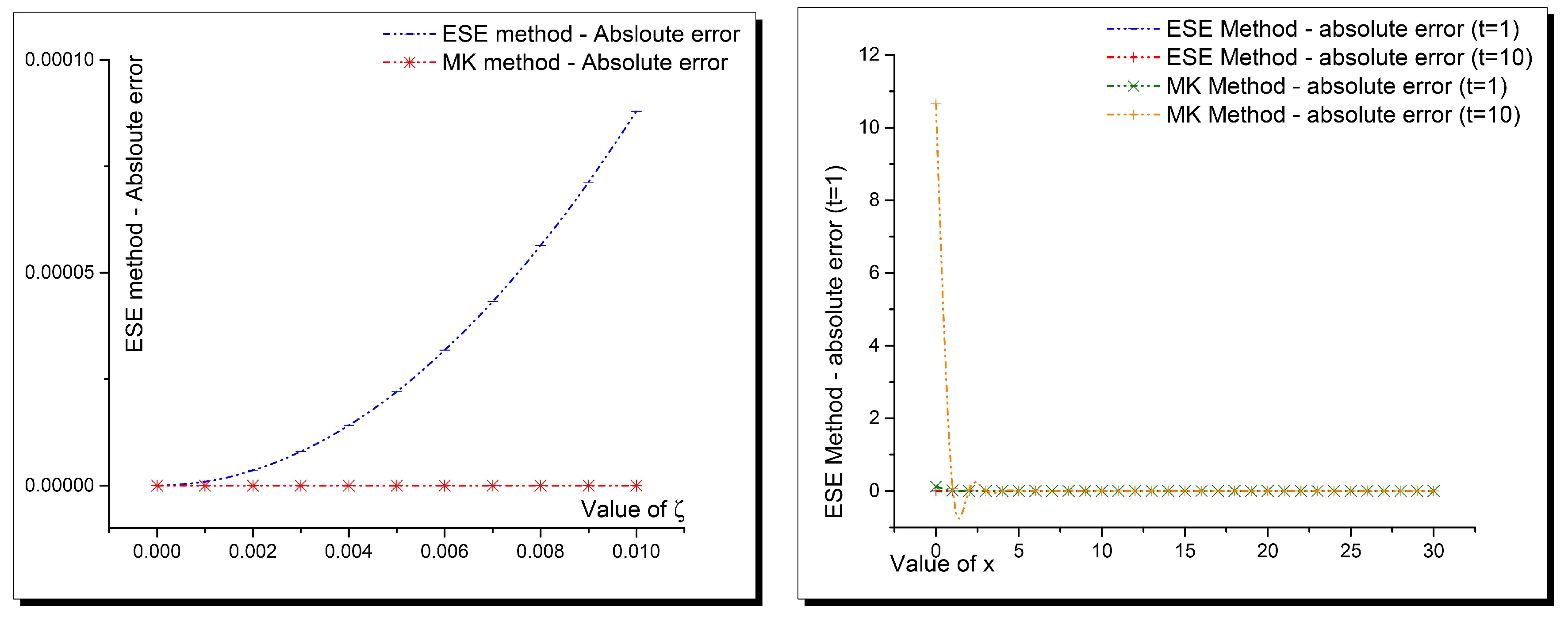
2. Accuracy of Computational Solutions
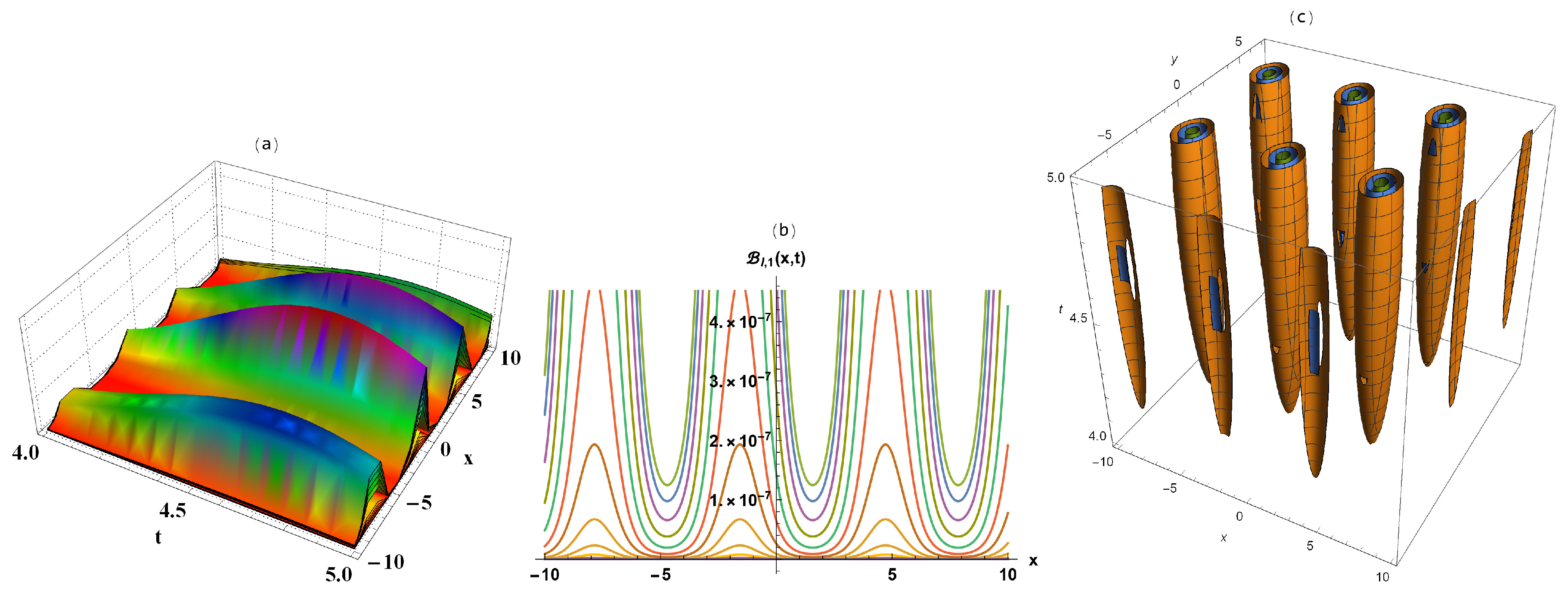
2.1. MDA Method’s Solutions
Semi-Analytical Solutions
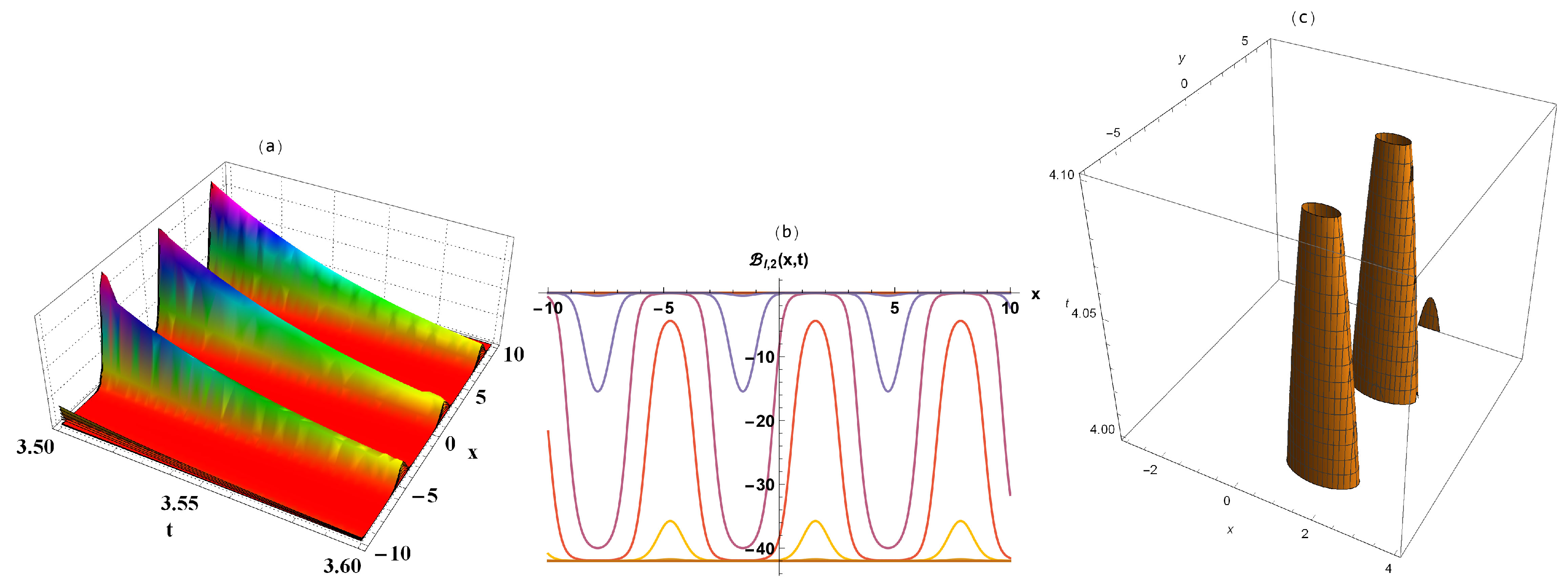
2.2. MK Method’s Solutions
Semi-Analytical Solutions
- Applying the AD method for Equation (2) with the following initial and boundary conditions , gives the following solutionsThus, the semi-analytical solutions of the (2 + 1)-D KP-BBM equation are given by
- Applying the variational iteration method for Equation (1) with the following initial condition gives the following solutions:
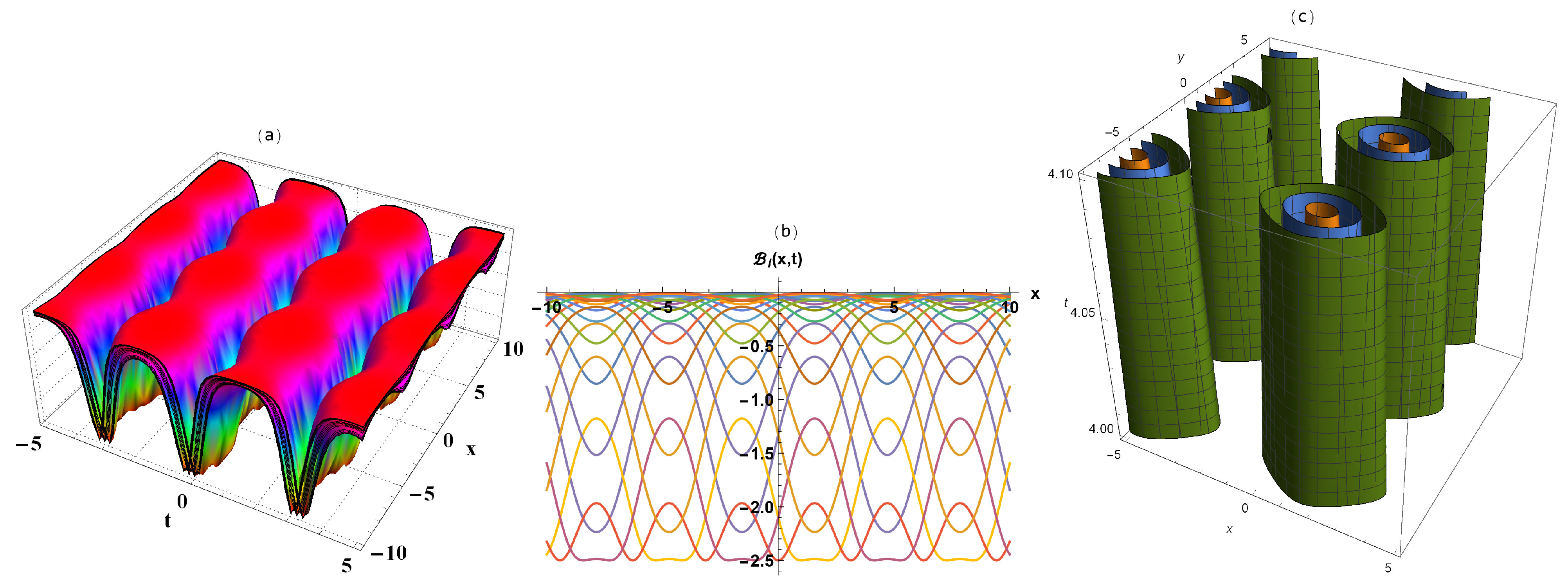
3. Interpretation of Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gao, X.Y.; Guo, Y.J.; Shan, W.R. Bilinear forms through the binary Bell polynomials, N solitons and Bäcklund transformations of the Boussinesq–Burgers system for the shallow water waves in a lake or near an ocean beach. Commun. Theor. Phys. 2020, 72, 095002. [Google Scholar] [CrossRef]
- Liu, J.G.; Feng, Y.Y.; Zhang, H.Y. Exploration of the algebraic traveling wave solutions of a higher order model. Eng. Comput. 2020. [Google Scholar] [CrossRef]
- Pandey, A.K. The effects of surface tension on modulational instability in full-dispersion water-wave models. Eur. J. Mech. B/Fluids 2019, 77, 177–182. [Google Scholar] [CrossRef]
- Crompton, O.; Sytsma, A.; Thompson, S. Emulation of the Saint Venant equations enables rapid and accurate predictions of infiltration and overland flow velocity on spatially heterogeneous surfaces. Water Resour. Res. 2019, 55, 7108–7129. [Google Scholar] [CrossRef]
- Madhusudanan, A.; Illingworth, S.J.; Marusic, I. Coherent large-scale structures from the linearized Navier–Stokes equations. J. Fluid Mech. 2019, 873, 89–109. [Google Scholar] [CrossRef]
- Prakash, A.; Prakasha, D.G.; Veeresha, P. A reliable algorithm for time-fractional Navier-Stokes equations via Laplace transform. Nonlinear Eng. 2019, 8, 695–701. [Google Scholar] [CrossRef]
- Gazzola, F.; Sperone, G. Steady Navier–Stokes Equations in Planar Domains with Obstacle and Explicit Bounds for Unique Solvability. Arch. Ration. Mech. Anal. 2020, 238, 1283–1347. [Google Scholar] [CrossRef]
- Abdel-Aty, A.H.; Khater, M.M.; Baleanu, D.; Abo-Dahab, S.; Bouslimi, J.; Omri, M. Oblique explicit wave solutions of the fractional biological population (BP) and equal width (EW) models. Adv. Differ. Equ. 2020, 2020, 552. [Google Scholar] [CrossRef]
- Abdel-Aty, A.H.; Khater, M.M.; Baleanu, D.; Khalil, E.; Bouslimi, J.; Omri, M. Abundant distinct types of solutions for the nervous biological fractional FitzHugh–Nagumo equation via three different sorts of schemes. Adv. Differ. Equ. 2020, 2020, 476. [Google Scholar] [CrossRef]
- Khater, M.M.; Baleanu, D. On abundant new solutions of two fractional complex models. Adv. Differ. Equ. 2020, 2020, 268. [Google Scholar] [CrossRef]
- Yue, C.; Khater, M.M.; Attia, R.A.; Lu, D. The plethora of explicit solutions of the fractional KS equation through liquid–gas bubbles mix under the thermodynamic conditions via Atangana–Baleanu derivative operator. Adv. Differ. Equ. 2020, 2020, 62. [Google Scholar] [CrossRef] [Green Version]
- Alfalqi, S.; Khater, M.; Alzaidi, J.; Lu, D. Dynamical Behaviour of the Light Pulses through the Optical Fiber: Two Nonlinear Atangana Conformable Fractional Evolution Equations. J. Math. 2020, 2020. [Google Scholar] [CrossRef]
- Khater, M.; Zheng, Q.; Qin, H.; Attia, R.A. On Highly Dimensional Elastic and Nonelastic Interaction between Internal Waves in Straight and Varying Cross-Section Channels. Math. Probl. Eng. 2020, 2020. [Google Scholar] [CrossRef]
- Khater, M.M.; Park, C.; Lu, D. Two effective computational schemes for a prototype of an excitable system. AIP Adv. 2020, 10, 105120. [Google Scholar] [CrossRef]
- Abdel-Aty, A.H.; Khater, M.M.; Dutta, H.; Bouslimi, J.; Omri, M. Computational solutions of the HIV-1 infection of CD4+ T-cells fractional mathematical model that causes acquired immunodeficiency syndrome (AIDS) with the effect of antiviral drug therapy. Chaos Solitons Fractals 2020, 139, 110092. [Google Scholar] [CrossRef] [PubMed]
- Khater, M.; Chu, Y.M.; Attia, R.A.; Inc, M.; Lu, D. On the Analytical and Numerical Solutions in the Quantum Magnetoplasmas: The Atangana Conformable Derivative (2 + 1)-ZK Equation with Power-Law Nonlinearity. Adv. Math. Phys. 2020, 2020. [Google Scholar] [CrossRef]
- Khater, M.M.; Attia, R.A.; Park, C.; Lu, D. On the numerical investigation of the interaction in plasma between (high & low) frequency of (Langmuir & ion-acoustic) waves. Results Phys. 2020, 18, 103317. [Google Scholar]
- Nadeem, M.; Li, F.; Ahmad, H. Modified Laplace variational iteration method for solving fourth-order parabolic partial differential equation with variable coefficients. Comput. Math. Appl. 2019, 78, 2052–2062. [Google Scholar] [CrossRef]
- Khater, M.M.; Attia, R.A.; Abdel-Aty, A.H.; Alharbi, W.; Lu, D. Abundant analytical and numerical solutions of the fractional microbiological densities model in bacteria cell as a result of diffusion mechanisms. Chaos Solitons Fractals 2020, 136, 109824. [Google Scholar] [CrossRef]
- Qin, H.; Khater, M.; Attia, R.A. Inelastic Interaction and Blowup New Solutions of Nonlinear and Dispersive Long Gravity Waves. J. Funct. Spaces 2020, 2020. [Google Scholar] [CrossRef]
- Manafian, J.; Murad, M.A.S.; Alizadeh, A.; Jafarmadar, S. M-lump, interaction between lumps and stripe solitons solutions to the (2 + 1)-dimensional KP-BBM equation. Eur. Phys. J. Plus 2020, 135, 167. [Google Scholar] [CrossRef]
- Tanwar, D.V.; Wazwaz, A.M. Lie symmetries, optimal system and dynamics of exact solutions of (2 + 1)-dimensional KP-BBM equation. Phys. Scr. 2020, 95, 065220. [Google Scholar] [CrossRef]
- Adem, K.R.; Khalique, C.M. Exact solutions and conservation laws of a (2 + 1)-dimensional nonlinear KP-BBM equation. In Abstract and Applied Analysis; Hindawi: London, UK, 2013; Volume 2013. [Google Scholar]
- Kudryashov, N.A.; Loguinova, N.B. Extended simplest equation method for nonlinear differential equations. Appl. Math. Comput. 2008, 205, 396–402. [Google Scholar] [CrossRef]
- Bilige, S.; Chaolu, T. An extended simplest equation method and its application to several forms of the fifth-order KdV equation. Appl. Math. Comput. 2010, 216, 3146–3153. [Google Scholar] [CrossRef]
- Hosseini, K.; Ansari, R. New exact solutions of nonlinear conformable time-fractional Boussinesq equations using the modified Kudryashov method. Waves Random Complex Media 2017, 27, 628–636. [Google Scholar] [CrossRef]
- Kumar, D.; Seadawy, A.R.; Joardar, A.K. Modified Kudryashov method via new exact solutions for some conformable fractional differential equations arising in mathematical biology. Chin. J. Phys. 2018, 56, 75–85. [Google Scholar] [CrossRef]
- Baleanu, D.; Aydogn, S.M.; Mohammadi, H.; Rezapour, S. On modelling of epidemic childhood diseases with the Caputo-Fabrizio derivative by using the Laplace Adomian decomposition method. Alex. Eng. J. 2020, 59, 3029–3039. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Accelerating the convergence of Adomian decomposition method (ADM). J. Comput. Sci. 2019, 31, 54–59. [Google Scholar] [CrossRef]
- Anjum, N.; He, J.H. Laplace transform: Making the variational iteration method easier. Appl. Math. Lett. 2019, 92, 134–138. [Google Scholar] [CrossRef]
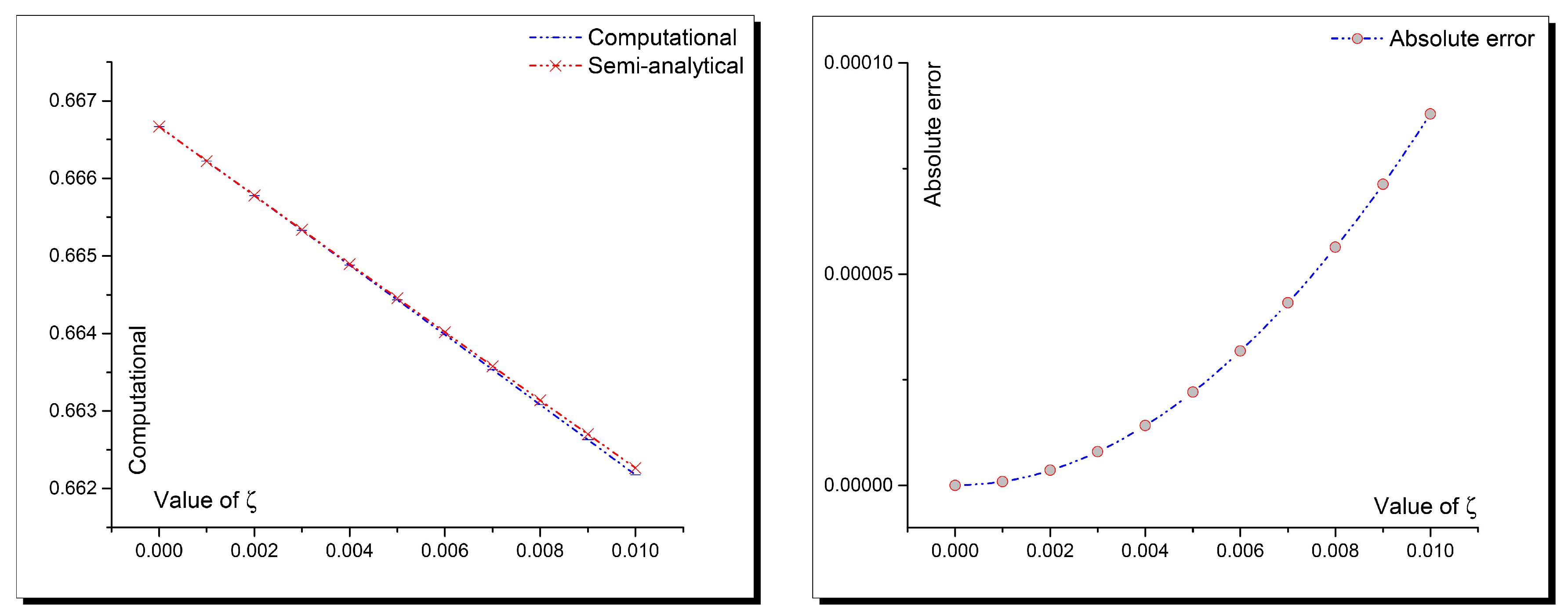



| Value of ℘ | Computational | Semi-Analytical | Absolute Error |
|---|---|---|---|
| 0 | 0.666666667 | 0.666666667 | 0 |
| 0.001 | 0.666221778 | 0.666222666 | 8.87902 |
| 0.002 | 0.665776004 | 0.665779552 | 3.54766 |
| 0.003 | 0.665329347 | 0.66533732 | 7.97339 |
| 0.004 | 0.664881809 | 0.664895969 | 1.41592 |
| 0.005 | 0.664433395 | 0.664455494 | 2.20992 |
| 0.006 | 0.663984107 | 0.664015894 | 3.17875 |
| 0.007 | 0.663533947 | 0.663577166 | 4.32184 |
| 0.008 | 0.66308292 | 0.663139306 | 5.63859 |
| 0.009 | 0.662631027 | 0.662702312 | 7.12843 |
| 0.01 | 0.662178273 | 0.662266181 | 8.79078 |
| Value of x | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 9.435 | 0.0001206 | 0.0001469 | 0.0001731 | 0.0001994 | 0.0002257 | 0.000252 | 0.0002783 | 0.00030459 | 0.0003309 |
| 1 | 9.697 | 1.018 | 1.066 | 1.114 | 1.162 | 1.21 | 1.258 | 1.307 | 1.3546 | 1.4028 |
| 2 | 1.256 | 1.265 | 1.274 | 1.283 | 1.291 | 1.3 | 1.309 | 1.318 | 1.3266 | 1.3354 |
| 3 | 1.69 | 1.691 | 1.693 | 1.694 | 1.696 | 1.698 | 1.699 | 1.701 | 1.7026 | 1.7042 |
| 4 | 2.285 | 2.285 | 2.285 | 2.286 | 2.286 | 2.286 | 2.287 | 2.287 | 2.2872 | 2.2875 |
| 5 | 3.092 | 3.092 | 3.092 | 3.092 | 3.092 | 3.092 | 3.092 | 3.092 | 3.0922 | 3.0923 |
| 6 | 4.184 | 4.184 | 4.184 | 4.184 | 4.184 | 4.184 | 4.184 | 4.184 | 4.1843 | 4.1843 |
| 7 | 5.663 | 5.663 | 5.663 | 5.663 | 5.663 | 5.663 | 5.663 | 5.663 | 5.6627 | 5.6627 |
| 8 | 7.664 | 7.664 | 7.664 | 7.664 | 7.664 | 7.664 | 7.664 | 7.664 | 7.6636 | 7.6636 |
| 9 | 1.037 | 1.037 | 1.037 | 1.037 | 1.037 | 1.037 | 1.037 | 1.037 | 1.0372 | 1.0372 |
| 10 | 1.404 | 1.404 | 1.404 | 1.404 | 1.404 | 1.404 | 1.404 | 1.404 | 1.4036 | 1.4036 |
| 11 | 1.9 | 1.9 | 1.9 | 1.9 | 1.9 | 1.9 | 1.9 | 1.9 | 1.8996 | 1.8996 |
| 12 | 2.571 | 2.571 | 2.571 | 2.571 | 2.571 | 2.571 | 2.571 | 2.571 | 2.5709 | 2.5709 |
| 13 | 3.479 | 3.479 | 3.479 | 3.479 | 3.479 | 3.479 | 3.479 | 3.479 | 3.4793 | 3.4793 |
| 14 | 4.709 | 4.709 | 4.709 | 4.709 | 4.709 | 4.709 | 4.709 | 4.709 | 4.7087 | 4.7087 |
| 15 | 6.373 | 6.373 | 6.373 | 6.373 | 6.373 | 6.373 | 6.373 | 6.373 | 6.3725 | 6.3725 |
| 16 | 8.624 | 8.624 | 8.624 | 8.624 | 8.624 | 8.624 | 8.624 | 8.624 | 8.6243 | 8.6243 |
| 17 | 1.167 | 1.167 | 1.167 | 1.167 | 1.167 | 1.167 | 1.167 | 1.167 | 1.1672 | 1.1672 |
| 18 | 1.58 | 1.58 | 1.58 | 1.58 | 1.58 | 1.58 | 1.58 | 1.58 | 1.5796 | 1.5796 |
| 19 | 2.138 | 2.138 | 2.138 | 2.138 | 2.138 | 2.138 | 2.138 | 2.138 | 2.1377 | 2.1377 |
| 20 | 2.893 | 2.893 | 2.893 | 2.893 | 2.893 | 2.893 | 2.893 | 2.893 | 2.8931 | 2.8931 |
| 21 | 3.915 | 3.915 | 3.915 | 3.915 | 3.915 | 3.915 | 3.915 | 3.915 | 3.9154 | 3.9154 |
| 22 | 5.299 | 5.299 | 5.299 | 5.299 | 5.299 | 5.299 | 5.299 | 5.299 | 5.2989 | 5.2989 |
| 23 | 7.171 | 7.171 | 7.171 | 7.171 | 7.171 | 7.171 | 7.171 | 7.171 | 7.1713 | 7.1713 |
| 24 | 9.705 | 9.705 | 9.705 | 9.705 | 9.705 | 9.705 | 9.705 | 9.705 | 9.7054 | 9.7054 |
| 25 | 1.313 | 1.313 | 1.313 | 1.313 | 1.313 | 1.313 | 1.313 | 1.313 | 1.3135 | 1.3135 |
| 26 | 1.778 | 1.778 | 1.778 | 1.778 | 1.778 | 1.778 | 1.778 | 1.778 | 1.7776 | 1.7776 |
| 27 | 2.406 | 2.406 | 2.406 | 2.406 | 2.406 | 2.406 | 2.406 | 2.406 | 2.4057 | 2.4057 |
| 28 | 3.256 | 3.256 | 3.256 | 3.256 | 3.256 | 3.256 | 3.256 | 3.256 | 3.2558 | 3.2558 |
| 29 | 4.406 | 4.406 | 4.406 | 4.406 | 4.406 | 4.406 | 4.406 | 4.406 | 4.4062 | 4.4062 |
| 30 | 5.963 | 5.963 | 5.963 | 5.963 | 5.963 | 5.963 | 5.963 | 5.963 | 5.9632 | 5.9632 |
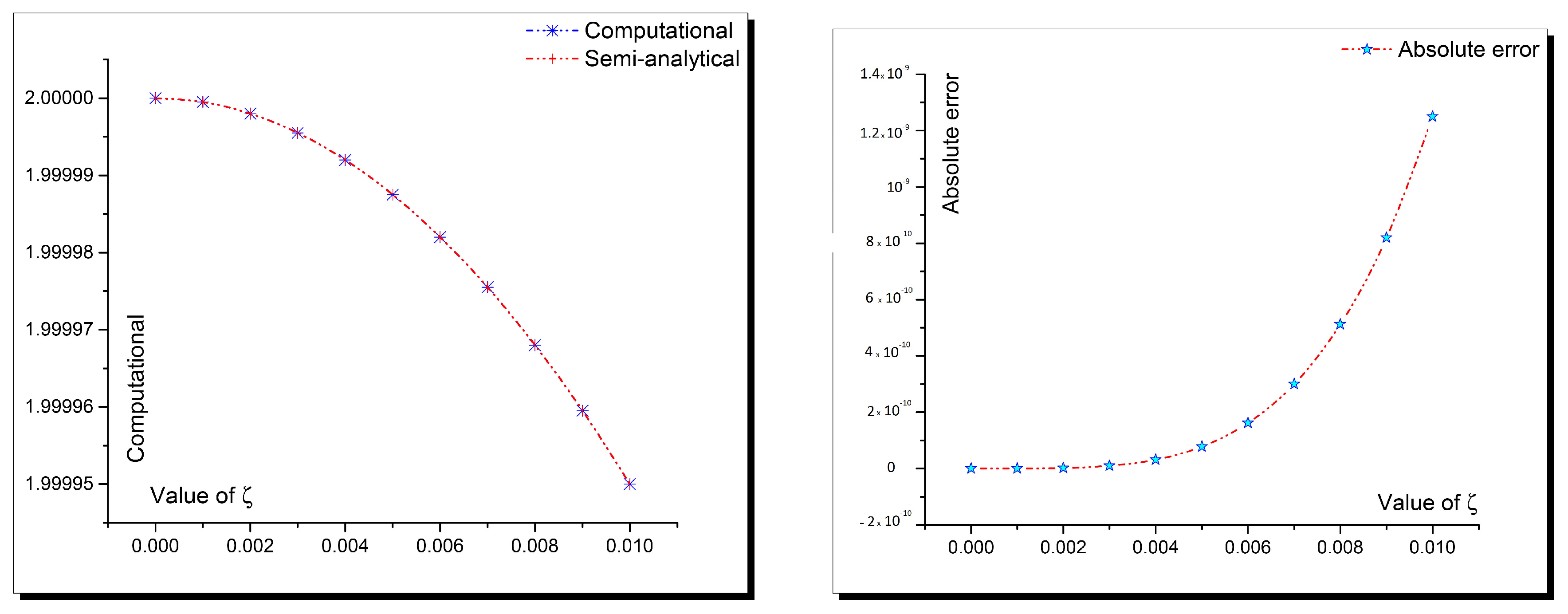
| Value of ℘ | Computational | Semi-Analytical | Absolute Error |
|---|---|---|---|
| 0 | 2 | 2 | 0 |
| 0.001 | 1.9999995 | 1.9999995 | 1.25011 |
| 0.002 | 1.999998 | 1.999998 | 2.0004 |
| 0.003 | 1.9999955 | 1.9999955 | 1.01248 |
| 0.004 | 1.999992 | 1.999992 | 3.20004 |
| 0.005 | 1.9999875 | 1.9999875 | 7.81248 |
| 0.006 | 1.999982 | 1.999982 | 1.62 |
| 0.007 | 1.9999755 | 1.999975501 | 3.00126 |
| 0.008 | 1.999968 | 1.999968001 | 5.12002 |
| 0.009 | 1.999959501 | 1.999959501 | 8.20129 |
| 0.01 | 1.999950001 | 1.999950002 | 1.25001 |
| Value of x | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.1248386 | 0.242138 | 0.2554887 | 0.0684811 | 0.4152942 | 1.2922469 | 2.6587865 | 4.6113225 | 7.24626454 | 10.6600221 |
| 1 | 0.0186997 | 0.0402194 | 0.0625657 | 0.0837456 | 0.1017657 | 0.1146328 | 0.1203537 | 0.1169351 | 0.10238377 | 0.07470652 |
| 2 | 0.0025576 | 0.0053241 | 0.0082615 | 0.0113314 | 0.0144959 | 0.0177167 | 0.0209557 | 0.0241746 | 0.02733544 | 0.03039995 |
| 3 | 0.0003461 | 0.0007039 | 0.0010728 | 0.0014519 | 0.0018407 | 0.0022383 | 0.0026442 | 0.0030575 | 0.00347755 | 0.00390366 |
| 4 | 4.681 | 9.423 | 0.0001422 | 0.0001908 | 0.00024 | 0.0002897 | 0.00034 | 0.0003908 | 0.00044211 | 0.00049393 |
| 5 | 6.333 | 1.27 | 1.909 | 2.552 | 3.197 | 3.846 | 4.497 | 5.151 | 5.8086 | 6.4687 |
| 6 | 8.57 | 1.716 | 2.576 | 3.437 | 4.3 | 5.165 | 6.031 | 6.899 | 7.768 | 8.6387 |
| 7 | 1.16 | 2.32 | 3.482 | 4.644 | 5.806 | 6.97 | 8.134 | 9.3 | 1.0465 | 1.1632 |
| 8 | 1.57 | 3.139 | 4.71 | 6.28 | 7.851 | 9.423 | 1.099 | 1.257 | 1.414 | 1.5712 |
| 9 | 2.124 | 4.248 | 6.373 | 8.498 | 1.062 | 1.275 | 1.487 | 1.7 | 1.9124 | 2.125 |
| 10 | 2.875 | 5.749 | 8.624 | 1.15 | 1.437 | 1.725 | 2.012 | 2.3 | 2.5875 | 2.8751 |
| 11 | 3.89 | 7.781 | 1.167 | 1.556 | 1.945 | 2.334 | 2.723 | 3.112 | 3.5016 | 3.8906 |
| 12 | 5.265 | 1.053 | 1.58 | 2.106 | 2.633 | 3.159 | 3.686 | 4.212 | 4.7387 | 5.2652 |
| 13 | 7.126 | 1.425 | 2.138 | 2.85 | 3.563 | 4.275 | 4.988 | 5.7 | 6.4131 | 7.1256 |
| 14 | 9.643 | 1.929 | 2.893 | 3.857 | 4.822 | 5.786 | 6.75 | 7.715 | 8.6791 | 9.6434 |
| 15 | 1.305 | 2.61 | 3.915 | 5.22 | 6.525 | 7.831 | 9.136 | 1.044 | 1.1746 | 1.3051 |
| 16 | 1.766 | 3.533 | 5.299 | 7.065 | 8.831 | 1.06 | 1.236 | 1.413 | 1.5896 | 1.7663 |
| 17 | 2.39 | 4.781 | 7.171 | 9.561 | 1.195 | 1.434 | 1.673 | 1.912 | 2.1513 | 2.3904 |
| 18 | 3.235 | 6.47 | 9.705 | 1.294 | 1.618 | 1.941 | 2.265 | 2.588 | 2.9115 | 3.235 |
| 19 | 4.378 | 8.756 | 1.313 | 1.751 | 2.189 | 2.627 | 3.065 | 3.502 | 3.9403 | 4.3781 |
| 20 | 5.925 | 1.185 | 1.778 | 2.37 | 2.963 | 3.555 | 4.148 | 4.74 | 5.3326 | 5.9251 |
| 21 | 8.019 | 1.604 | 2.406 | 3.208 | 4.009 | 4.811 | 5.613 | 6.415 | 7.2169 | 8.0188 |
| 22 | 1.085 | 2.17 | 3.256 | 4.341 | 5.426 | 6.511 | 7.597 | 8.682 | 9.767 | 1.0852 |
| 23 | 1.469 | 2.937 | 4.406 | 5.875 | 7.343 | 8.812 | 1.028 | 1.175 | 1.3218 | 1.4687 |
| 24 | 1.988 | 3.975 | 5.963 | 7.951 | 9.938 | 1.193 | 1.391 | 1.59 | 1.7889 | 1.9877 |
| 25 | 2.69 | 5.38 | 8.07 | 1.076 | 1.345 | 1.614 | 1.883 | 2.152 | 2.421 | 2.69 |
| 26 | 3.64 | 7.281 | 1.092 | 1.456 | 1.82 | 2.184 | 2.548 | 2.912 | 3.2765 | 3.6405 |
| 27 | 4.928 | 9.855 | 1.478 | 1.971 | 2.464 | 2.956 | 3.449 | 3.942 | 4.4343 | 4.927 |
| 28 | 6.667 | 1.333 | 2 | 2.667 | 3.334 | 4.001 | 4.667 | 5.334 | 6.001 | 6.6678 |
| 29 | 9.024 | 1.805 | 2.707 | 3.61 | 4.512 | 5.414 | 6.317 | 7.219 | 8.1216 | 9.0238 |
| 30 | 1.221 | 2.443 | 3.664 | 4.886 | 6.106 | 7.328 | 8.549 | 9.769 | 1.0992 | 1.2213 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Akinyemi, L.; Lu, D.; Khater, M.M.A. Abundant Traveling Wave and Numerical Solutions of Weakly Dispersive Long Waves Model. Symmetry 2021, 13, 1085. https://doi.org/10.3390/sym13061085
Li W, Akinyemi L, Lu D, Khater MMA. Abundant Traveling Wave and Numerical Solutions of Weakly Dispersive Long Waves Model. Symmetry. 2021; 13(6):1085. https://doi.org/10.3390/sym13061085
Chicago/Turabian StyleLi, Wu, Lanre Akinyemi, Dianchen Lu, and Mostafa M. A. Khater. 2021. "Abundant Traveling Wave and Numerical Solutions of Weakly Dispersive Long Waves Model" Symmetry 13, no. 6: 1085. https://doi.org/10.3390/sym13061085







