Ensemble Empirical Mode Decomposition with Adaptive Noise with Convolution Based Gated Recurrent Neural Network: A New Deep Learning Model for South Asian High Intensity Forecasting

Abstract

The intensity variation of the South Asian high (SAH) plays an important role in the formation and extinction of many kinds of mesoscale systems, including tropical cyclones, southwest vortices in the Asian summer monsoon (ASM) region, and the precipitation in the whole Asia Europe region, and the SAH has a vortex symmetrical structure; its dynamic field also has the symmetry form. Not enough previous studies focus on the variation of SAH daily intensity. The purpose of this study is to establish a day-to-day prediction model of the SAH intensity, which can accurately predict not only the interannual variation but also the day-to-day variation of the SAH. Focusing on the summer period when the SAH is the strongest, this paper selects the geopotential height data between 1948 and 2020 from NCEP to construct the SAH intensity datasets. Compared with the classical deep learning methods of various kinds of efficient time series prediction model, we ultimately combine the Ensemble Empirical Mode Decomposition with Adaptive Noise (CEEMDAN) method, which has the ability to deal with the nonlinear and unstable single system, with the Permutation Entropy (PE) method, which can extract the SAH intensity feature of IMF decomposed by CEEMDAN, and the Convolution-based Gated Recurrent Neural Network (ConvGRU) model is used to train, test, and predict the intensity of the SAH. The prediction results show that the combination of CEEMDAN and ConvGRU can have a higher accuracy and more stable prediction ability than the traditional deep learning model. After removing the redundant features in the time series, the prediction accuracy of the SAH intensity is higher than that of the classical model, which proves that the method has good applicability for the prediction of nonlinear systems in the atmosphere.

1. Introduction

1.1. Research Background

The South Asian High (SAH) is the largest anticyclone in summer and a dominant system in Asia and the dominant circulation feature spanning Southeast Asia to Afghanistan during the summer season (e.g., [1,2,3]), and the intra-seasonal and annual intensity variation of SAH has significant impacts on global heavy precipitation [4,5,6,7] and temperature anomaly [7,8], and it is closely related to extreme weather events, especially the transport of chemical composition in the upper troposphere and lower stratosphere (UTLS) region [9,10,11,12]. Many weather and climate change systems in the field of meteorology and ocean provide a reliable theoretical basis and feasibility for the prediction of the SAH intensity. However, there are not enough studies to explore the day-to-day intensity change of the SAH. Therefore, we need further studies predicting the intensity variation of the SAH and its impact on extreme weather.

In addition, accurate prediction of the intensity of the SAH can provide a better basis for the prediction technology of various nonlinear systems in the atmosphere and ocean, and it is of great significance for the prediction of global weather and climate change. The intensity variations of almost all atmospheric and oceanic systems, such as the El Niño–Southern Oscillation (ENSO), North Atlantic Oscillation (NAO) index, and Tropical Cyclone (TC) intensity, are characterized by strong uncertainty and are hard to predict [13,14,15,16,17,18,19]; precious studies proved that the intensity of the SAH shows obvious characteristics of interannual and interannual variation [12,20,21]. Based on the trend of the SAH, we will further forecast and capture its intra-seasonal variation characteristics.

At present, there are plenty of studies on the prediction of nonlinear systems in the atmosphere [22,23,24,25]. The main research methods are the traditional numerical model and machine learning prediction method, and there are plenty of defects of traditional mathematical statistical methods like autoregression (AR), moving average (MA), and autoregressive integrated moving average (ARIMA) in the forecasting of weather phenomena and various indexes [26,27,28,29,30,31,32,33]. For example, these models cannot effectively capture the spatial characteristics of various meteorological elements and cannot make a timely response to abrupt weather conditions. The numerical prediction model needs to solve an extremely complex mathematical model, which is expensive and requires huge computing power and a high amount of calculation and time. Due to the rapid change of climate and environment, these traditional methods could not respond to the variation quickly, such as the prediction of rainstorms, TC in a few hours, and large-scale vortex systems such as the SAH [34,35,36,37].

With the development of the big data era, the deep learning method in machine learning has been widely used in the research of various weather systems in the atmosphere and ocean, and many neural network methods have been proven to be better than atmospheric models in forecasting weather and climate phenomena [16,38,39,40,41,42,43]. Neural networks such as the Recurrent Neural Network (RNN) and Convolutional Neural Network (CNN) have been applied to forecast weather and climate indices and achieved remarkable results [13,44,45,46].

1.2. Related Works

In the application of a single or traditional deep learning model, the adjustment of model parameters and the change of training set can often bring relatively accurate results. For example, the Long–Short Term Memory (LSTM) encoder–decoder framework proposed by Sutskever et al. [47] provides a general framework for sequence-to-sequence learning. One LSTM connected by training time is used for the input sequence and the other for the output sequence. Karevan et al. [48] utilize the LSTM model to obtain a data-driven forecasting model, which was applied to the weather forecasting task and achieved high performance. Ham et al. [13] proposed a new CNN model to predict the ENSO events by better predicting the detailed zonal distribution of sea surface temperature, overcoming the defects of the dynamic model and advancing the prediction of ENSO events by one and a half years. Wang et al. [49] used a three-dimensional convolutional neural network (3D-CNN) to learn the implicit correlation between spatial distribution characteristics and TC intensity changes, which significantly improved the accuracy of TC intensity prediction. However, with global warming and the rise of sea levels, the factors that affect all kinds of weather and climate systems present complex and changeable characteristics. For example, the variation of the SAH intensity and location are also closely related to the change of temperature and precipitation of the Qinghai Tibet Plateau (e.g., [21,50,51]). Therefore, in the case of a complex and changeable background field, the change of a nonlinear system presents the characteristics of more difficult prediction and more uncertain factors.

For the single model, training can no longer better improve the accuracy of various nonlinear systems in the atmosphere and the results of numerical prediction models; in order to solve these problems, hybrid models and improved models in deep learning are constantly being explored and proposed. Compared with the single time series model and convolution feature extraction model, the application of composite models in the atmosphere and ocean has achieved more obvious results. For example, the Convolutional and Long–Short Term Memory (ConvLSTM) model proposed by Shi et al. [52] can accurately extract the spatio-temporal characteristics of radar echo step precipitation, and prediction is more accurate than model prediction. CloudLSTM proposed by Zhang et al. [53] predicts the data stream of the geospatial point cloud data source and shows the significant advantage of the deep learning method in series prediction with the strength of air index prediction. Yuan et al. [12] modified the long-term memory and applied it to the prediction of the North Atlantic Oscillation (NAO) index. In the prediction of tropical cyclone (TC), Chen et al. [54] proposed a CNN + LSTM method, which can consider the temporal and spatial relationship between the variables of typhoon formation and extract the spatial relationship of typhoon formation characteristics better than the numerical forecast models. Hsieh et al. [55] improved the average accuracy of total rainfall forecasting during the typhoon period by 80% by combining an artificial neural network (ANN) with multiple regression analysis (MRA). Many research and experimental results also show that the deep learning combined with the mathematical method can achieve good results in the spatiotemporal prediction of a nonlinear system and is superior to the traditional statistical and climate models. There are many precedents for the application of the signal processing method in time series forecasting. Some scientific fields include Neeraj et al. [56], using the Single Spectrum Analysis Long–Short Term Memory (SSA-LSTM) model to forecast the power load, which achieves higher forecasting accuracy than most traditional methods in machine learning (Stylianos et al. [57]). Using the Single Spectrum Analysis (SSA) with Artificial Neural networks (ANN) combined with the hybrid method to predict the time series of road traffic volume can improve the prediction accuracy of the traditional neural network. In the field of meteorology, Guo et al. [58] utilize the signal denoising method Empirical Mode Decomposition (EMD) combined with CNN + LSTM in deep learning to predict the ENSO index and achieved better results than the statistical method and traditional single deep learning model. Additionally, the SAH, as an atmospheric vortex system, has a good similarity with the ENSO index, and also has nonlinear characteristics. The SAH is affected by meteorological factors such as temperature, humidity, and wind speed (e.g., [57,58]). Therefore, we can use the traditional time series model to predict the SAH intensity index. The SAH is also one of the most important synoptic scale systems in the atmospheric circulation. Accurately predicting the intensity of the SAH is one of the important areas that are worthy of research and exploration by using the most advanced model algorithm.

1.3. Research Significance

Therefore, this paper uses the latest signal data processing method combined with the improved deep learning method to predict the SAH intensity index. Because the Gated Recurrent Neural Network (GRU) has a simpler structure than LSTM in the process of single time series, in order to achieve more efficient training efficiency, we combined it with the improved ConvLSTM method, using the latest signal denoising method Ensemble Empirical Mode Decomposition with Adaptive Noise (CEEMDAN) combined with the Convolutional-based Gated Recurrent Neural Network (ConvGRU) deep learning model to predict the SAH intensity index. In the future, the improved method can be applied to the field of nonlinear dynamic systems.

In this paper, we propose a new time series prediction model, which mainly focuses on the change characteristics of vortex intensity to predict the intensity change of the SAH. The SAH intensity index data set uses the potential height field data of the National Centers for Environmental Prediction and National Center for Atmospheric Research (NCEP/NCAR) to construct the research data set, and then the high-frequency signal of the time series is eliminated, that is, the noise in the intensity index is removed by CEEMDAN method. The reconstructed SAH intensity signal is added to the new deep learning model ConvGRU for training and prediction. Compared with the traditional machine learning methods, the advantages and disadvantages between them are compared, and the stability and science of the new model for forecasting weather and climate nonlinear system are evaluated. It provides reference value for the construction and optimization of the nonlinear system prediction model.

The structure of this article is as follows: in the second section, we first describe how to construct the data set, and then introduce the data processing method, model method, and model evaluation method used in this article; in the third section, we mainly compare and analyze the prediction results of each model and point out that the accuracy of the results obtained by CEEMDAN + ConvGRU model is higher, and then compare the stability of the model with the accuracy of the results to evaluate the learning ability. The fourth section summarizes the conclusions and prospects for future research.

2. Data and Method

2.1. Data Description

The SAH is one of the most powerful vortexes in the atmosphere, and its intensity can be described by various meteorological elements in the dynamic field. Geopotential height (GPH) is the best expression of a dynamic field that has a symmetrical structure. It is also the most commonly used method to express the intensity of the SAH. In order to construct a suitable data sequence and further predict the change of the SAH intensity, we selected the GPH of the National Centers for Environmental Prediction and National Center for Atmospheric Research (NCEP/NCAR) data in June, July, and August (JJA) from 1948 to 2020 as the intensity change dataset of the South Asian high (SAH). We used the central GPH as the benchmark data of the intensity of the South Asian high (the maximum of GPH at 100 hPa). In addition, since the SAH is the most powerful vortex at 100 hPa (e.g., [1,2,13]), we took the maximum value of day-to-day GPH at 100 hPa as the intensity data set of this study. The unit of GPH is potential meters (gpm). According to the existing database of potential height, we constructed a 73 × 92, i.e., a total of 6716 days of time series data.

Because the intensity variation of the SAH is affected by many meteorological factors and weather phenomena in the atmosphere and ocean, the prediction of the South Asian high could be attributed to a simple time series problem when we applied deep learning methods. When we calculated the intensity variation of the SAH as its benchmark data, the effect of other meteorological factors on its intensity variation also existed. However, when we selected the influence of other meteorological factors on the SAH intensity, the correlation between them was relatively low, and the multivariate training model had no positive effect on the prediction results.

2.2. Model and Methods

2.2.1. Ensemble Empirical Mode Decomposition with Adaptive Noise (CEEMDAN) and Permutation Entropy (PE)

Ensemble Empirical Mode Decomposition with Adaptive Noise (CEEMDAN) is an improved Empirical Mode Decomposition (EMD) and Ensemble Empirical Mode Decomposition (EEMD) method that is proposed by Torres et al. [57]; EMD has the advantages of strong adaptability and good completeness, which are proposed by Huang et al. [59], and it has been proven to be a better signal processing method than wavelet decomposition in many practical experiments and projects. However, modal aliasing seriously affects the decomposition accuracy of EMD. EEMD eliminates the mode aliasing of EMD, but the residual noise is still in the signal [60,61,62]. CEEMDAN solves the problems of modal confusion and residual noise in the reconstruction sequence. Its algorithm can not only eliminate the residual noise by adding white adaptive noise in each decomposition stage to make the reconstruction error tend to zero, but can also solve the non-stationary problem by decomposing the load signal into Intrinsic Mode Function (IMF) components with different frequencies [63,64,65].

Some theoretical and mathematical foundations needed to be further outlined when we introduced the CEEMDAN method.

(1) We first generated the SAH intensity variation data set, which must contain the white noise:

$${\mathrm{x}}^i\left(t\right)=x\left(t\right)+w^i\left(t\right)$$

(1)

Here, $w^i\left(t\right)\left(\mathrm{i}=1, 2, \cdots , I\right)$ is the noise satisfying the Gaussian distribution, and $I$ is the total number of samples in the intensity set.

(2) EMD was performed on ${\mathrm{x}}^i\left(t\right)$ to obtain the 1st-order Intrinsic Mode Functions (IMF) component of each sample $IM{F}_1^i$. Its mean value was taken as the 1st-order IMF component of $x\left(t\right)$:

$${\widetilde{IMF}}_1\left(t\right)=\frac{1}{I}{{\displaystyle \sum }}_{i=1}^{I}IM{F}_1^i.$$

(2)

(3) Then, the first order residuals and second order IMF components were calculated. The formulation of the first-order residual and the second-order IMF component were, respectively:

$$r_1\left(t\right)=x\left(t\right)-{\widetilde{IMF}}_1\left(t\right)$$

(3)

$${\widetilde{IMF}}_2\left(t\right)=\frac{1}{I}{\displaystyle \sum }_{i=1}^I{E}_1\left\{r_1\left(t\right)+{\epsilon }_1{E}_1\left[w^i\left(t\right)\right]\right\}$$

(4)

where $E_i(·)$ represents the $i$ order IMF component of the signal, and ${\epsilon }_i$ is the parameter controlling the white noise.

(4) Then, we calculated $k\left(k=2, 3,\dots ,K\right)$ ($K$ is the highest order of IMF component) order residual, $k+1$ order of IMF component. The k order residual and the $k+1$ order IMF component were, respectively:

$$r_k\left(t\right)=r_{k-1}\left(t\right)-{\widetilde{IMF}}_k\left(t\right)$$

(5)

$${\widetilde{IMF}}_{k+1}\left(t\right)=\frac{1}{I}{\displaystyle \sum }_{i=1}^I{E}_1\left\{r_k\left(t\right)+{\epsilon }_k{E}_k\left[w^i\left(t\right)\right]\right\}$$

(6)

(5) Step (4) was repeated until the residual could no longer be decomposed, and the judgment criterion was that the number of extreme points of the residual is not more than two.

$$R\left(t\right)=x\left(t\right)-{\displaystyle \sum }_{k=2}^K{\widetilde{IMF}}_k\left(t\right)$$

(7)

Then, the original signal x (T) of the SAH intensity was finally decomposed into:

$$x\left(t\right)={\displaystyle \sum }_{k=2}^K{\widetilde{IMF}}_k\left(t\right)+R\left(t\right)$$

(8)

After introducing the EEMD processing steps, we also needed to judge and divide the threshold value of the decomposed IMF, which means we had to select the appropriate IMF to reconstruct the original signal so as to improve the robustness of the original SAH intensity.

The basic principle of Permutation Entropy (PE) is shown below:

With the development of entropy theory, permutation entropy (PE) has been proposed [66], which has the characteristics of less computation and strong robustness. It can be used to detect the randomness, complexity, and vibration signal mutation of the time series. Entropy can be used to describe the uncertainty of data information, while PE can accurately describe the mutation of complex time series and is highly sensitive to dynamic data variation [67,68]. The value change of PE can reflect the different operating states of the system so as to achieve the purpose of anomaly detection of the time series [69,70,71]. The algorithm process is as follows:

(1) We first assumed the time series $\left\{x\left(i\right),i=1, 2,\cdots ,N\right\}$ of length $N$; a new reconstruction matrix $M$ was obtained after phase space reconstruction was carried out:

$$M=\left[\begin{array}{c}M\left(1\right)\\ \begin{array}{c}M\left(2\right)\\ \begin{array}{c}⋮\\ \begin{array}{c}M\left(j\right)\\ \begin{array}{c}⋮\\ M\left(Q\right)\end{array}\end{array}\end{array}\end{array}\end{array}\right]=\left[\begin{array}{ccc}\begin{array}{cc}x\left(1\right)& x\left(1+t\right)\\ x\left(2\right)& x\left(2+t\right)\end{array}& \begin{array}{c}\cdots \\ \cdots \end{array}& \begin{array}{c}x\left(1+\left(m-1\right)t\right)\\ x\left(2+\left(m-1\right)t\right)\end{array}\\ \begin{array}{cc}⋮& ⋮\end{array}& & ⋮\\ \begin{array}{cc}x\left(j\right)& x\left(j+t\right)\\ ⋮& ⋮\\ x\left(Q\right)& x\left(Q+t\right)\end{array}& \begin{array}{c}\cdots \\ \\ \cdots \end{array}& \begin{array}{c}x\left(j+\left(m-1\right)t\right)\\ ⋮\\ x\left(Q+\left(m-1\right)t\right)\end{array}\end{array}\right]$$

(9)

where $j=1, 2,\cdots ,Q; m$ is the embedding dimension; $t$ represents the time delay; $Q+\left(m-1\right)t=n$.

(2) Then, the $j$ formed was rearranged as $M\left(j\right)=\left\{x\left(j\right)x\left(j+t\right)x\left(j+\left(m-1\right)t\right)\right\}$, which is the reconstruction component in the matrix $M$ in ascending order, i.e.,:

$$\begin{array}{c}M\left(j\right)=\{x\left(j+\left(i_1-1\right)t\right)\le x\left(j+\left(i_2-1\right)t\right)\le \cdots \\ \le x\left(j+\left(i_m-1\right)t\right)\}\end{array}$$

(10)

where $i_1, i_2,\cdots , i_m$ are the positions of the elements in the column of the $M\left(j\right)$ component.

(3) If there was a $x\left(j+\left(i_e-1\right)t\right)=x\left(j+\left(i_c-1\right)t\right)$, according to the value of $e$ and $c$, they needed to be sorted in order from largest to smallest, which means when the $e$ is greater than $c$, $x\left(j+\left(i_e-1\right)t\right)\ge x\left(j+\left(i_c-1\right)t\right)$, and vice versa. Therefore, a corresponding position sequence could be obtained for any component $M\left(j\right)$ contained in the reconstruction matrix $M:$

$$S\left(j\right)=\left(i_1,i_2,\cdots ,i_m\right)\left(j=1,2,\dots ,q\right)$$

(11)

(4) Among them, $q\le m!, S\left(j\right)$ is one of a kind of code sequence from $m!$. Different number codes of $m$ have different permutations as much as $m!$, which means there are $m!$ different sequences of symbols.

Then, the probability of the occurrence of each code sequence was calculated, $P_1,P_2,\cdots ,P_q,{{\displaystyle \sum }}_{j=1}^q{P}_j=1$. In this case, the permutation entropy of the signal time series $\left\{x\left(i\right),i=1,2,\cdots ,N\right\}$ could be defined according to Shannon’s entropy:

$$L_{\mathrm{PE}}\left(m\right)=-{\displaystyle \sum }_{j=1}^q{P}_j\ln P_j$$

(12)

When $P_j=\frac{1}{m}$, L_$L_{\mathrm{PE}}\left(m\right)$ received the maximum value $\ln \left(m!\right)$. With the help of $\ln \left(m!\right)$, the PE of $L_{\mathrm{PE}}\left(m\right)$ was normalized:

$$L_{\mathrm{PE}}=\frac{L_{\mathrm{PE}}\left(m\right)}{\ln \left(m!\right)}$$

(13)

where $0\le L_{\mathrm{PE}}\le 1$.

(5) Ultimately, the value of $L_{\mathrm{PE}}$ indicated the degree of randomness of the one-dimensional time series. The larger $L_{\mathrm{PE}}$, the stronger the randomness of the time series. In contrast, it indicated that the regularity of the time was stronger.

According to the original strength signal provided by the GPH datasets and the criteria of PE, the threshold can range from 0 to 1, and the threshold we selected was 0.9, as the intensity value of the SAH is relatively large, which can reach tens of thousands in magnitude. Therefore, the threshold we chose was as large as possible, which could retain the authenticity of the original signal and the correct solution of the predicted value as much as possible.

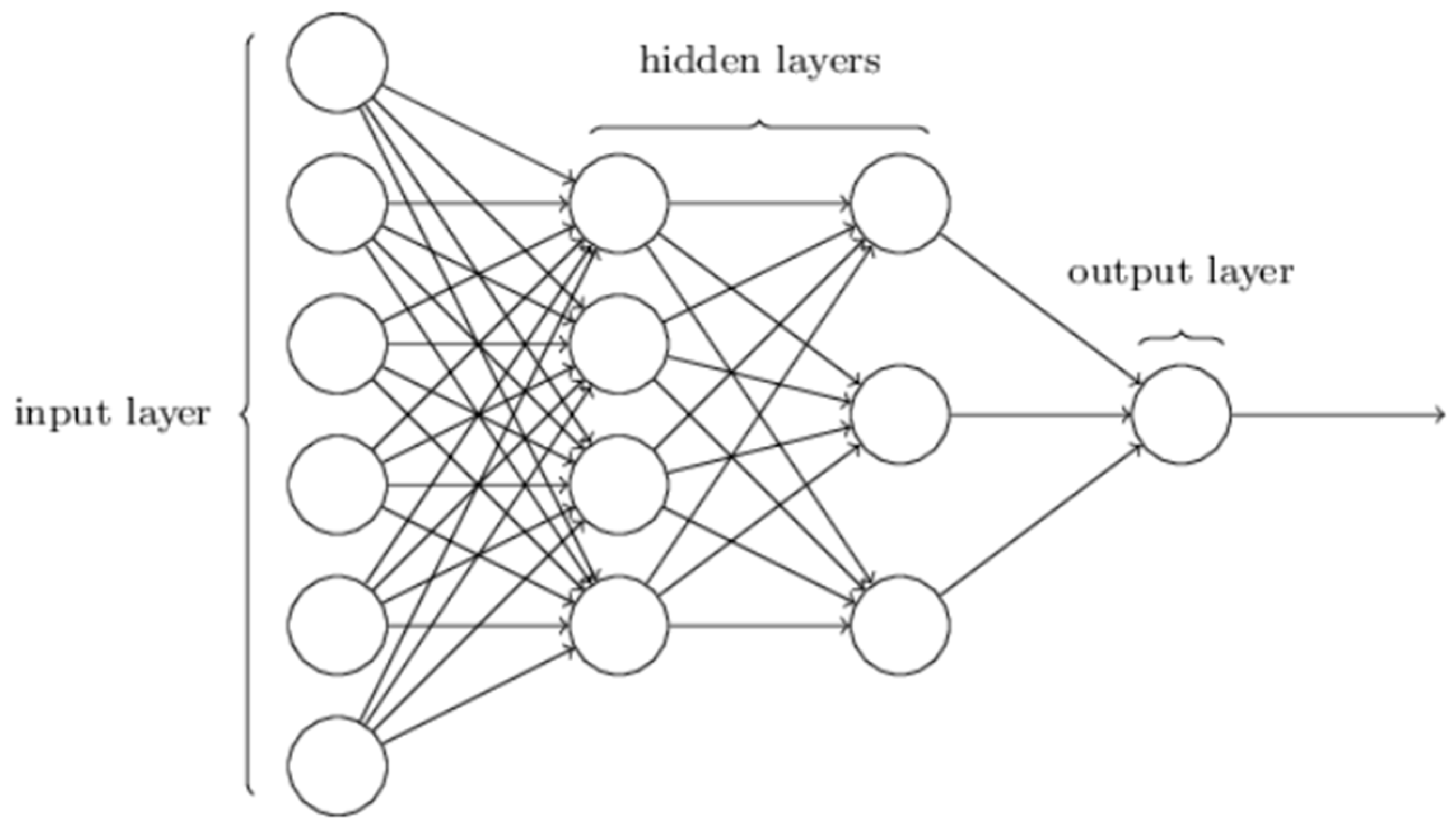
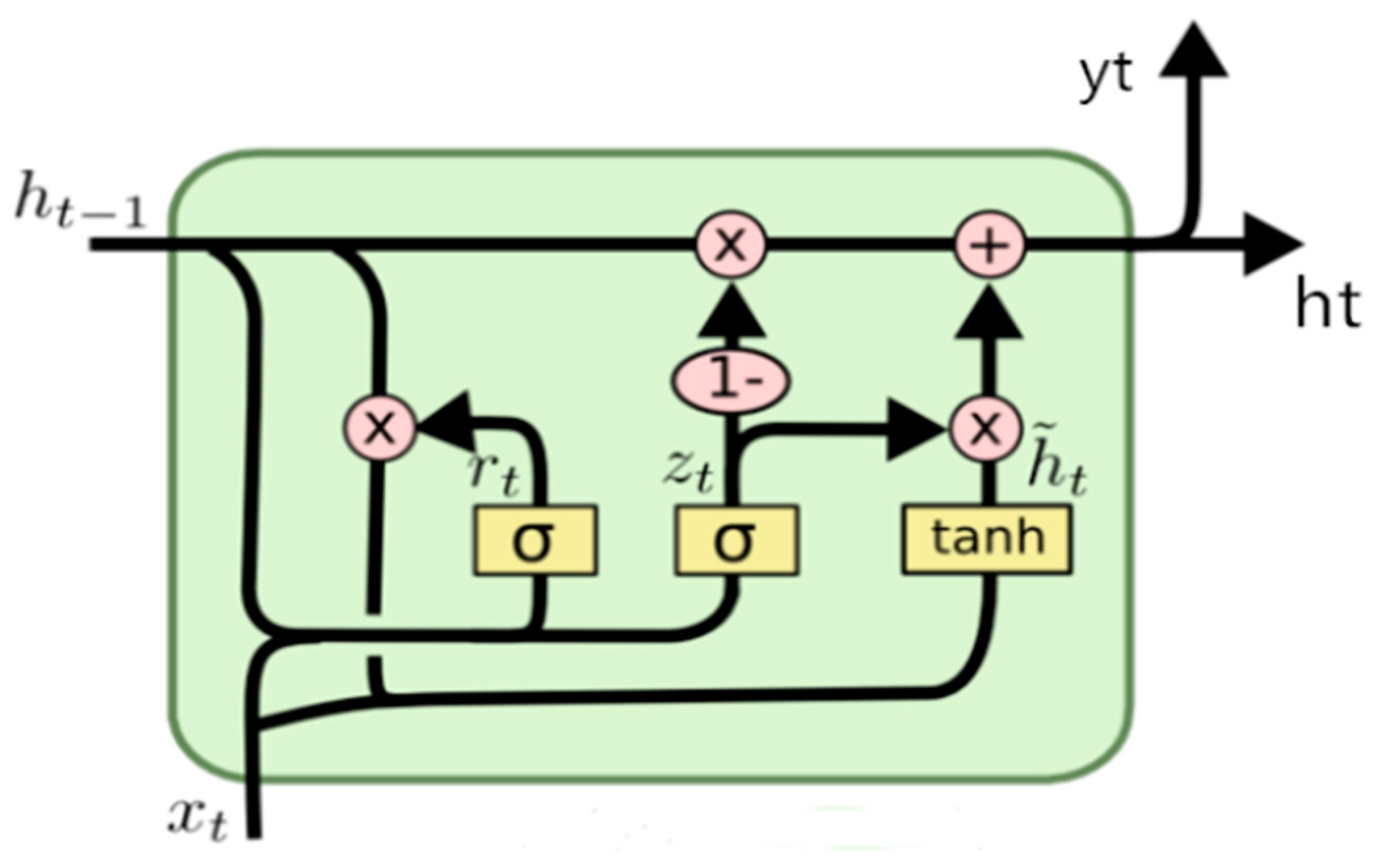
2.2.2. Multi-Layer Perceptron (MLP), Recurrent Neural Network (RNN), and Gated Recurrent Neural Network (GRU)

The Multi-layer Perceptron (MLP), also known as the Artificial Neural Network (ANN), can have multiple hidden layers in addition to input and output layers. Due to its excellent nonlinear mapping ability, high parallelism, and global optimization, MLP has made great achievements in image processing, predictive time series system, pattern recognition, and many areas of scientific computing. The simplest MLP needs to have a hidden layer, namely the input layer, the hidden layer, and the output layer, which can also be called a simple neural network. The MLP structure is shown in Figure 1. In this MLP model for our research, the input x feature connected to the neurons in the hidden layer, and the neurons in the hidden layer connected to the neurons in the input layer. The layers of the multilayer perceptron were fully connected, which means that all neurons in the upper layer were connected to all neurons in the lower layer.

Because the existence of the MLP hidden layer increases the number of super parameters, the training process with slow convergence needed to deal with a large amount of computation in the case study of SAH intensity prediction. In the traditional MLP real valued model, the data input that a single neuron can receive is a single real number. When it carries out multi-dimensional signal input, it usually cannot achieve satisfactory results. In addition, there is no standard method to determine the number of neurons in MLP. At present, the commonly used cross validation has high complexity and is limited by the amount of data.

Considering the computational efficiency, accuracy, and lack of generalization ability of MLP, the Recurrent Neural Network (RNN) was used to predict the time series of the SAH intensity in this study and its structure is shown in Figure 2. RNN is a very powerful neural network used to process and predict the neural network model of sequence data due to its wide use in scenarios where input data are dependent and sequential, that is, the previous input is related to the next input. The intensity variation time series of the SAH was consistent with this kind of series pattern. The biggest difference between RNN and MLP is that RNN can “remember” the previous information and apply it to calculate the current output, which makes the nodes between hidden layers connected. Additionally, it can also consider the time correlation between events with more distance in the time dimension, which has a good prediction effect for the time series with great correlation.

However, due to the gradient disappearance problem, RNN can only have short-term memory, but has the problem of “long-term dependence”. The variants of RNN, such as Long–Short Term Memory (LSTM) and the Gated Recurrent Neural Network (GRU), are widely used in various fields. LSTM is improved on the basis of RNN. Differently from the loop layer in the basic structure of RNN, LSTM uses three “gates” to control the state and output at different times, namely the “input gate”, “output gate”, and “forgetting gate”. LSTM combines short-term memory with long-term memory through a “gate” structure, which can alleviate the problem of gradient disappearance. GRU is improved on the basis of LSTM, which simplifies the structure of LSTM while maintaining the same effect as LSTM. Compared with the three gates of the LSTM structure, GRU simplifies it to two gates: the “update gate” and “reset gate”. GRU couples the output gate and forgetting gate into the update gate. The function of the “update gate” is to control how much information can be brought into the current state in the previous state. The function of the “reset gate” is to control how much information can be written into the current state in the previous state. Similar to LSTM, GRU also retains the existing information and adds filtered information on the basis of the existing information content. The model has the storage function. The difference is that GRU eliminates the memory control in LSTM and simplifies the computation of LSTM. Both LSTM and GRU maintain long-term dependence by adding an internal gating mechanism. Their circular structure is only dependent on all the past states. Accordingly, the current state may also be dependent on future information.

The internal structure of GRU is shown in Figure 3. $h_{t-1}$ is the last time state; $x_t$ and $h_t$ are the input and output value of GRU model at the current time; $r_t$ and $z_t$ are the reset gate and update gate of GRU, respectively. ${\tilde{h}}_t$ is the output candidate value after reset gate processing.

2.2.3. Innovation Model: Convolutional-Based GRU Network (ConvGRU) with CEEMDAN

Spatiotemporal data analysis is a hot field of artificial intelligence combined with meteorological data. Spatiotemporal data analysis has become a key research issue with the development of big data computing. Under the background of ocean meteorological big data, the application of spatiotemporal data analysis has achieved remarkable results in all kinds of systems affecting climate. Therefore, when we analyzed the SAH intensity data, we also considered the spatial distribution characteristics of data distribution, which can better extract the overall characteristics of the time series. The convolutional neural network (CNN) is a common model structure in machine learning. It has achieved good results in image classification, semantic segmentation, and machine translation. The traditional CNN structure includes four layers: the convolution layer, pooling layer, full connection layer, and output layer. As we explained earlier, GRU is very powerful in processing time series data. However, if time series data can be transformed into two-dimensional data by the time step method, that is, if we change the data from 10-time steps to a 2 * 5 grid in this study, convolution operation will be more effective for time series feature extraction based on GRU. After the strength change data processed by reshaping enters the input layer, the convolution layer extracts data features through the hidden layer and outputs them. In this process, there may be multiple hidden layers. The more layers, the deeper the network depth. The final output is as the input of GRU.

Therefore, according to the methods above and their superiority, we proposed a new method that combines the advantages of the convolutional GRU network and CEEMDAN. ConvGRU can predict the intensity of the SAH, which is also capable when handling other time series problems.

Moreover, we mainly introduced the process of ConvLSTM.

First, the main purpose of the update gate is to control the amount of state information flowing into the current state at the previous time; the calculation formula is as follows:

$$z_t^j=\sigma {\left(W_z{x}_t+U_z{h}_{t-1}\right)}^j$$

(14)

The main function of the reset gate is to control the degree of forgetting of the node state information at the previous time; the calculation formula is as follows:

$$r_t^j=\sigma {\left(W_r{x}_t+U_r{h}_{t-1}\right)}^j$$

(15)

where $z_t^j$ and $r_t^j$ are the results of the update gate and reset gate; $\sigma$ is the nonlinear activation function; $h_{t-1}$ is the result of the previous moment from update gate and reset gate; $x_t$ is the input radar echo image sequence; $W_z$, $W_r$, $U_z$, and $U_r$ are the convolution kernel; $j$ is the number of layers; $t$ is the input sequence. The current state was obtained by the following formula:

$$h_t^j=\left(1-z_t^j\right)h_{t-1}^j+z_t^j{h}_t^{j^{\prime }}=\left(1-z_t^j\right)h_{t-1}^j+z_t^j\left\{\tan h{\left[W_{x_t}+U\left(r_t\odot h_{t-1}\right)\right]}^j\right\}$$

(16)

where $\odot$ denotes the multiplication of elements. Compared with GRU, the Convolution-based Gated Recurrent Neural Network (ConvGRU) has stronger learning ability, so this paper used the convolution-based GRU for modeling after CEEMDAN data processing, and its basic calculation formula was as follows:

$$Z_t=\sigma \left(W_{xz}\ast X_t+W_{hz}\ast H_{t-1}\right)$$

(17)

$$R_t=\sigma \left(W_{xr}\ast X_t+W_{hr}\ast H_{t-1}\right)$$

(18)

$$H_t^{\prime }=f\left(W_{xh}\ast X_t+R_t\circ \left(W_{hh}\ast H_{t-1}\right)\right)$$

(19)

$$H_t=\left(1-Z_t\right)\circ H_t^{\prime }+Z_t\circ H_{t-1}$$

(20)

In order to simplify the formula, the deviation part was omitted; $\ast$ denotes convolution operation; $\circ$ denotes Hadamard product [72]; $H_t$, $R_t$, $Z_t$, and $H_t^{\prime }$ denote the memory state, reset gate, update gate, and the new information, respectively; $X_t$ is the input; $f$ is the activation function, which is a relu with leakage correction with a negative slope of 0.2 [73]. $H$ and $W$ are the height and width of the state and input tensors. When a new input comes to the network, the reset gate controlled whether to clear the previous state or not, and the update gate controlled the amount of new information entering the state.

2.2.4. Innovation Method and Strategy

Similar to ConvLSTM proposed by Shi et al. [52], we used convolution combined with the GRU deep learning method to build a deep learning network. The average GPH horizontal distribution is shown in Figure 4. Since the well-known convolutional neural network needs the input of two-dimensional variables, ConvGRU needs the input two-dimensional array of time with the shape of M × N to extract the spatiotemporal information through the convolution kernel of K × L. We first needed to extract the time step. Because the intensity variation of the SAH is constructed by itself, the time series is a one-dimensional variable. We first determined the length of convolution kernel as the scale of 1 × L. Then, the timing information $X_t$ was divided into 10 steps according to the time step. That is to say, the intensity time series of JJA of the SAH each year were divided into the dimensions of shape (82, 10). Since the time step of 10 could be divided into a grid matrix of 2 × 5, the observation value we input at any time could be expressed as 10 is equal to 2 × 5. The prediction of space-time series became the feature extraction of space-time series combined with time step. The advantage of convolution will play a role in the prediction of time series.

The structure of the proposed CEEMDAN + ConvGRU model is shown in Figure 5. We first selected the time series from 1948 to 2020, a total of 73 years of data; each year contains three months, a total of 92 days of data. The data set was divided into the training set and test set. The training set contained the data of the first 60 years, and the data of the last 13 years was used for test training to verify the prediction accuracy of the model. Firstly, we decomposed the time series by CEEMDAN, calculated the PE of each IMF component, and reconstructed the PE that meets the conditions. The reconstructed time series were trained and predicted by ConvGRU, and the predicted results were compared with the SAH intensity series before reconstruction. Ultimately, we drew the corresponding conclusion.

2.2.5. Evaluation of Multi-Model

Mean absolute error (MAE), mean absolute percentage error (MAPE), and root mean square error (RMSE) are widely used in deep learning to measure the error between the real field ${\widehat{y}}_j$ and the predicted value $y_j$, which are defined as follows:

$$\mathrm{MAE}=\frac{1}{N}{\displaystyle \sum }_{j=0}^N\left|{\widehat{y}}_j-y_j\right|$$

(21)

$$\mathrm{MAPE}=\frac{1}{N}{\displaystyle \sum }_{j=0}^N\left|\frac{{\widehat{y}}_j-y_j}{{\widehat{y}}_j}\right|$$

(22)

$$\mathrm{RMSE}=\sqrt{\frac{1}{N}{\displaystyle \sum }_{j=0}^N{\left({\widehat{y}}_j-y_j\right)}^2}$$

(23)

The smaller the values of MAE, MAPE, and RMSE, the higher the accuracy of the prediction model. This study took advantage of these regression evaluation indexes to evaluate the prediction results of MLP, RNN, GRU, ConvGRU, and CEEMDAN + ConvGRU models one by one. The difference between the predicted SAH intensity and the true intensity of each model was compared, which means that the value of the three indicators and the training effect in the process of model training was recorded. The error bar statistics of the multiple training effects for each model were made by MAE, and the stability of each model was further obtained by MAE.

3. Results

3.1. Division of Dataset

The data period selected in this study is 1948–2020, a total of 73 years of data. According to the standard in Section 2.1, we constructed the standard database of SAH intensity with the value of 100 hPa maximum potential height and calculated the time series data of SAH intensity during 1948–2020 JJA. Figure 6 shows the time series data of SAH intensity change. It can be seen that there is no obvious interannual trend in SAH intensity change data, but the intensity change within the year shows the change rule first increasing and then decreasing. Because we selected SAH intensity data in June, July, and August of each year, the time was discontinuous. Therefore, we processed and divided the data of each year according to the data processing method in Section 2.2.4. As shown in

Table 1. Statistical parameter of training and test data sets of SAH intensity, including the number of each divided data sets (note that due to the select number of timesteps is ten, so the daily number of JJA reduced to 92 minus 10 m which is equal to 82). The maximum, minimum, and mean intensity values of each data set are shown.

Data (After Dispose)	Number (Year × Day)	Max Intensity (gpm)	Min Intensity (gpm)	Mean Intensity (gpm)
Training	60 × 82 = 4920	17,038.00	16,692.00	16,871.99
Testing	13 × 82 = 1066	17,005.25	16,732.00	16,893.31

, we divided the data into two parts: the training set and test set. Since 92 days of data were selected every year, it became 82 data after processing into 10 time steps. The data of the first 60 years were used as the training set, and the data of the last 13 years were used as the test set. It can be seen from

Table 2. Permutation Entropy (PE) value corresponding to each Intrinsic Mode Function (IMF) decomposed by ensemble empirical mode decomposition with adaptive noise (CEEMDAN).

Number of IMF	Value of PE
IMF1	0.97838
IMF2	0.80366
IMF3	0.65887
IMF4	0.54547
IMF5	0.46347
IMF6	0.42903
IMF7	0.41028
IMF8	0.39685
IMF9	0.38806
IMF10	0.38830
IMF11	0.0

that there are 4920 data in the large training set and 1066 data in the test set. The maximum value, minimum value, and average value of the data with statistical significance were calculated, respectively. The results show that the average values of the training set and the test set are very close, and their variation ranges are highly consistent.

Due to the large value of the original intensity time series, we needed to do standardized processing before we input it into the deep learning model. The data standardization interval we selected was [0, 1]. That is, the maximum value of the data was converted to 1, the minimum value of the data was converted to 0, and the rest of the strength was between 0 and 1. The normalized intensity data is shown in Figure 7. It can be seen that the normalized data set still does not illustrate an obvious interannual trend. We divided the normalized data into two parts: the training set and test set. In Figure 7, the red line segment represents the sixty-year training data set from 1948 to 2007, and the blue line segment represents the thirteen-year test data set from 2008 to 2020.

3.2. Model Training and Analysis

After the residual was divided into the training set and test set, the CEEMDAN method was used to decompose the original data into multiple IMFs and then calculate the PF value of each IMF. The purpose was to select the appropriate signal to reconstruct the data and further reduce the noise in SAH intensity data. According to (1)~(4) in Section 2.2.1, we decomposed 11 IMFs in the original signal to the greatest extent. Finally, according to Formula (5) in Section 2.2.1, the difference between the intensity values of each time point of the original model and the intensity values of each point of all decomposed IMFs was calculated, and then the residual signal was obtained. From Figure 8, it can be seen that each IMF time series we decomposed changes from day to day. The 12 panels represent 11 IMFs and one residual signal, which are finally decomposed from the original signal by CEEMDAN. Note that the value of the final residual signal is small, while it retains the vibration frequency of the original signal well. Therefore, it also needs to be added into the reconstructed signal.

The value of SAH intensity is extremely large before normalization; in order to keep the true value of the original signal as much as possible and to effectively remove the noise in the data set, we selected the threshold value of PF as much as possible to ensure that the reconstructed signal and the original signal will not have a large error. Table 2 shows PE values of IMF after CEEMDAN decomposition. It can be seen that the PE value of the decomposed IMFs is quite different, and the PE value of IMF1 is as high as 0.97, which indicates that the mode has higher complexity and mutation characteristics compared with the original signal. The PE of IMF2 was reduced to 0.80, which has no significant effect on the original signal. Therefore, we determined the PE selection threshold as 0.9 and 0.8, respectively. Firstly, we compare the variance and standard deviation of reconstructed intensity time series data and original data under different thresholds. The standard deviation and variance of the original data were 56.90 and 3237.85, respectively. When the threshold value was 0.8, the imf1–imf9 and residual signal were selected according to PE value in Table 2 to reconstruct the data. The standard deviation and variance of the reconstructed data are 3004.86 and 54.82, respectively. When the threshold value was 0.9, the imf1–imf10 and residual signal were selected according to the PE value in Table 2 to reconstruct the data. The standard deviation and variance of the reconstructed data are 3149.69 and 56.12, respectively. Because both standard deviation and variance can indicate the degree of deviation from average value of a group of data, the lower the threshold value, the lower the deviation degree of the data, but the greater the difference between the two values and the original signal will be, and the more likely the data are to be distorted. In order to ensure the authenticity and feasibility of the input training model data, the PF threshold selected in this study was 0.9. That is, we eliminated the data of imf1 and used the sum of the daily intensity of the decomposed imf1–imf10 and residual signals reconstructing the data set to be trained and predicted in the innovation model.

Figure 9 shows the original SAH intensity signal and the reconstructed signal of IMFs after PE value screening. It can be seen that the reconstructed signal is smoother than the original signal, and there is no obvious difference between the two values. It shows that the data processing method of CEEMDAN+ PE can effectively eliminate the interference of high frequency noise in the original signal and reduce the complexity of the original signal. Next, we needed to add the reconstructed data set to the new deep learning model Convolutional-based Gated Recurrent Neural Network (ConvGRU) for training and verify the prediction effect of the model.

Before we input the data into the model training, the ConvGRU input data needed to include the time step, length, width, and characteristics of the data. Therefore, according to the method in Section 2.2.4, we first divided the data into annual time series and then processed the annual time series in time steps. The first 10-time steps were used to predict the intensity of the SAH on the next day. Therefore, the input data was the intensity of the SAH in the first 10 days of each year, and the daily change of SAH intensity was also predicted. In order to construct more data sets, we set the sliding window step size of training to 1, so we could still obtain 82 different data sets even if we performed 10-time step interception of 92-day data every year. In order to test the accuracy and stability of the prediction results obtained by combining the reconstructed data set with the ConvGRU model, we input the original data into different deep learning models for synchronous training. Before we applied the new model to the SAH intensity prediction, there were some traditional deep learning methods we needed to explore and compare. The models of comparative experiments include MLP, RNN, GRU, and ConvGRU. Compared with the construction of input data of ConvGRU, the input data of other deep learning models are relatively simple. As for the data input to be processed into 10-time steps and the data output of 1-time step, it was enough. Finally, we predicted the change of SAH intensity in the next 13 years according to the model training effect in the first 60 years. Because the time series was too long, we only intercepted five years (2016–2020) for comparative discussion. Figure 10 shows the time series of the changes of SAH intensity predicted by MLP, ConvGRU, and CEEMDAN + ConvGRU and the original SAH intensity. As we expected, the original data was the closest to the prediction results of our proposed model CEEMDAN + ConvGRU, and the coverage of both was also the largest. The prediction results of the other two models had local prominent features.

Before comparing the results of different deep learning methods and CEEMDAN + ConvGRU methods, we will briefly explain the main time series prediction steps of RNN and GRU methods so as to more reasonably explain the differences between them.

The calculation of the RNN model is divided into two steps: the first step is to calculate the hidden layer $a$ in the $t$ time step; the second step is to calculate the predicted value $y$ in the $t$ time step:

$$a^{\langle t\rangle }=\tanh \left(W_{ax}{x}^{\langle t\rangle }+W_{aa}{a}^{\langle t-1\rangle }+b_a\right)$$

(24)

$${\widehat{y}}^{\langle t\rangle }=softmax\left(W_{ya}{a}^{\langle t\rangle }+b_y\right)$$

(25)

where $W_{ax}$ and $W_{aa}$, the two groups of parameters can be combined with the current data of active $a$ and $x$ in the previous layer, respectively, and can also be combined into one and calculated with the connection of $x$ and $a$.

$$a^{\langle t\rangle }=\tanh \left(W_a\left[a^{\langle t-1\rangle },x^{\langle t\rangle }\right]+b_a\right)$$

(26)

From the structure of RNN, we can know that the output value of RNN at the next time is affected by the input value of the previous time, and in some cases, the output value may be affected by the input value of the later time, so the result will be more accurate. The specific process is that the first element in the time series is input into RNN, and the hidden unit h receives data from two aspects, namely, the value $h_{t-1}$ of the hidden unit at the previous time and the current input data $x_t$, and calculates the output of the current time through the value of the hidden unit. The input $x_{t-1}$ at time $t-1$ can affect the output at time t through the loop structure.

However, gradient explosion and gradient disappearance occur easily during the process of training RNN, which leads to the low transitivity of the gradient in training, that is, the gradient cannot be transferred when handling a long sequence. Therefore, RNN cannot detect the influence of long sequence sometimes. Gradient explosion problem refers to the fact that in RNN, every step of gradient update may accumulate errors, and eventually the gradient becomes very large so that the RNN weights are greatly updated, and the program will receive Nan error. GRU is an improved method of RNN; the mathematical expression used by GRU neurons is as below:

$$r_t=\sigma \left(w_r\left[h_{t-1},x_t\right]\right)$$

(27)

$$z_t=\sigma \left(w_z\left[h_{t-1},x_t\right]\right)$$

(28)

$${\tilde{h}}_t=\tanh \left(w_{\tilde{h}}\left[r_t{h}_{t-1},x_t\right]\right)$$

(29)

$$h_t=\left(1-z_t\right)h_{t-1}+z_t{\tilde{h}}_t$$

(30)

$$y_t=\sigma \left(w_o{h}_t\right)$$

(31)

where $w_r$ is the weight of the reset gate; $w_z$ is the weight of the update gate; $\tan \mathrm{h}$ is the hyperbolic tangent function; $\sigma$ is the sigmoid function, and $w_z$, $w_r$, $w_h$, and $w_0$ are the parameters that need to be trained.

Because the quantitative information cannot be obtained from the prediction graph of the time series, in order to quantify the difference between the prediction results of each model, we used mean absolute error (MAE), mean absolute percentage error (MAPE), and root mean square error (RMSE) to evaluate the prediction results of each model. The evaluation expression of the three regression predictions has been given in Section 2.2.5. Note that our quantified forecast time series includes all forecast years (2008–2020) for a total of 13 years. Figure 11 shows the prediction and evaluation indicators of all models. It demonstrates that for the results of RMSE, Mae, and MAPE, the prediction results of the CEEMDAN + ConvGRU model are obviously different from those of other models. Compared with the traditional deep learning model, RNN, GRU, and other neural networks have obvious advantages over MLP. However, the results of time series prediction also show that this kind of deep learning model has some bottlenecks, that is, with the continuous simplification and optimization of the model, the prediction results do not improve significantly. This study focused on the process of time series processing, and combined with the optimal deep learning method, the prediction accuracy has been significantly improved. The quantitative results showed that the MAPE of CEEMDAN + ConvGRU model was 4.54%, while that of MLP, RNN, GRU, and ConvGRU were 8.14%, 6.83%, 6.46%, and 6.31%, respectively. In addition, MAE values of MLP, RNN, GRU, ConvGRU, and CEEMDAN + ConvGRU models were 13.74, 11.53, 10.91, 10.66, and 7.61, respectively; RMSE values were 17.22, 14.64, 13.70, 13.40, and 9.70, respectively. Three evaluation indexes show that the new model has better prediction results.

Based on the above results, we compared the prediction results of nonlinear systems in the atmosphere by using the deep learning method and mainly selected the forecast results of the ENSO event, Tropical Cyclone (TC) intensity, precipitation, and many other scientific fields. Table 3 shows the results of different deep learning methods in predicting weather systems in the atmosphere, and the results of mixed deep learning methods have higher prediction accuracy.

As we can see from Table 3, compared with the prediction and classification results of a single deep learning model, the accuracy of the hybrid model is often significantly improved. The data-based mathematical processing methods also have great potential among them. For example, the analysis of the typhoon development trend and El Niño are more effective after adding the EEMD and PCA methods. For the hybrid deep learning model, we can see that in the process of nonlinear system processing, it is better to extract features first and combine with traditional algorithms to obtain higher accuracy [74,75,76,77]. For example, CNN-LSTM and PredRNN are typical successful models. Demertzis et al. [78] also pointed out that the Ensemble Approach (ENAP) has better prediction and is a more stable and robust model, because the overall behavior of multiple models has less noise than the corresponding single model. According to Demertzis et al. [78], ENAP should include the process of determining the optimal model. Firstly, the traditional time series prediction models RNN and GRU were used to predict. In order to improve the prediction effect, the convolution method was used to extract the characteristics of the time series, and after the improvement of the most advanced ConvLSTM precipitation prediction method, ConvGRU is used to train and predict. In the process of prediction, there was a large amount of noise in the intensity of the SAH, we added the optimal method of signal processing to the model to filter the noise. Above is the process of using a hybrid model to improve the accuracy.

Table 3. The main idea, the accuracy or improvement degree of experimental results, and the main models in the prediction research area of nonlinear systems, which are related to SAH intensity prediction.

Tasks	Models	Main Idea	Accuracy or Degree of Improvement
Multi-year ENSO forecasts [14]	CNN	Forecasting ENSO events and the detailed zonal distribution of sea surface temperatures compared to dynamical forecast models	Lead times of up to 1.5 years
El Niño Index Prediction [58]	EEMD-CNN-LSTM	Provide accurate El Niño index predictions by comparing different deep learning models.	Improve the accuracy of MAE = 0.33
Precipitation Nowcasting [52]	Convolutional LSTM Network	Build an end-to-end trainable model for the precipitation nowcasting problem	Captures spatiotemporal correlations better and consistently outperforms FC-LSTM
Precipitation Nowcasting [74]	Trajectory GRU	A benchmark for precipitation nowcasting and evaluation protocols.	MSE, MAE, B-MSE, and B-MAE improved more than previous models
TC Intensity prediction [76]	RNN	Predict the TC intensity by designing a data-driven intensity prediction model	The error is 5.1 m/s−1 in 24 h, and it is better than some widely used dynamic models
TC Intensity prediction [54]	CNN-LSTM	Design a spatio-temporal model based on a hybrid network of 2D-CNN, 3D-CNN, and LSTM	Better than the numerical forecast models and traditional ML models.
TC genesis prediction [77]	AdaBoost	A model is used to determine whether a mesoscale convective system (MCS) would evolve into a tropical cyclone.	Achieve a high 97.2% F1-score accuracy
Predictive of spatiotemporal sequences [79]	PredRNN: RNN + ST-LSTM	Spatiotemporal predictive learning can memorize both spatial appearances and temporal variations.	It shows superior predicting power both spatially and temporally
Automatic Oceanic Eddy Detection [42]	PCA+CNN+SVM	Detect eddies automatically and remotely by extracting higher-level features and then fuse multi-scale features to identify eddies, regardless of their structures and scales.	Achieving a 97.8 ± 1% accuracy of detection

Table 3. The main idea, the accuracy or improvement degree of experimental results, and the main models in the prediction research area of nonlinear systems, which are related to SAH intensity prediction.

Tasks	Models	Main Idea	Accuracy or Degree of Improvement
Multi-year ENSO forecasts [14]	CNN	Forecasting ENSO events and the detailed zonal distribution of sea surface temperatures compared to dynamical forecast models	Lead times of up to 1.5 years
El Niño Index Prediction [58]	EEMD-CNN-LSTM	Provide accurate El Niño index predictions by comparing different deep learning models.	Improve the accuracy of MAE = 0.33
Precipitation Nowcasting [52]	Convolutional LSTM Network	Build an end-to-end trainable model for the precipitation nowcasting problem	Captures spatiotemporal correlations better and consistently outperforms FC-LSTM
Precipitation Nowcasting [74]	Trajectory GRU	A benchmark for precipitation nowcasting and evaluation protocols.	MSE, MAE, B-MSE, and B-MAE improved more than previous models
TC Intensity prediction [76]	RNN	Predict the TC intensity by designing a data-driven intensity prediction model	The error is 5.1 m/s−1 in 24 h, and it is better than some widely used dynamic models
TC Intensity prediction [54]	CNN-LSTM	Design a spatio-temporal model based on a hybrid network of 2D-CNN, 3D-CNN, and LSTM	Better than the numerical forecast models and traditional ML models.
TC genesis prediction [77]	AdaBoost	A model is used to determine whether a mesoscale convective system (MCS) would evolve into a tropical cyclone.	Achieve a high 97.2% F1-score accuracy
Predictive of spatiotemporal sequences [79]	PredRNN: RNN + ST-LSTM	Spatiotemporal predictive learning can memorize both spatial appearances and temporal variations.	It shows superior predicting power both spatially and temporally
Automatic Oceanic Eddy Detection [42]	PCA+CNN+SVM	Detect eddies automatically and remotely by extracting higher-level features and then fuse multi-scale features to identify eddies, regardless of their structures and scales.	Achieving a 97.8 ± 1% accuracy of detection

From the prediction of other nonlinear systems in the atmosphere, including the intensity prediction of the vortex system with a symmetrical structure, the hybrid model and the improved model can always have higher accuracy than the traditional deep learning model. The original data processing based on the mathematical signal processing method can also improve the accuracy of prediction results to a certain extent. Therefore, it was feasible and scientific for us to adopt the most advanced screening mechanism of CEEMDAN combined with PE. Finally, the combination of the mathematical processing method and deep learning method ConvGRU was used to extract the signal features better and get more accurate results.

3.3. Model Evaluation

In order to evaluate the stability of each model after analyzing the training and prediction effect of the model, due to the high complexity of deep learning method and the long time series, we often obtained the phenomenon of gradient explosion or gradient disappearance in the process of training. Therefore, the stability of the model and the adjustment of the parameters in the model were particularly important. We first normalized the SAH intensity data and input the normalized data into the training model. The most important step of the deep learning method in the training process is to minimize the loss function and prevent the gradient from exploding or disappearing. We selected the most commonly used optimization function Adam in deep learning, and the loss function was MAE. Then, we chose a different learning rate to train the model; the choice of learning rate included 0.01, 0.1, 0.2, and other growth means; adjusted the number of iterations and batch size in the training process to ensure that the optimal model was trained in the shortest time; and increased the epoch times until the training loss and verification loss of our model training process ere no longer reduced. According to different training models, different learning rates were selected for repeated training to achieve the best effect. At the same time, the MAE values of the model in the process of adjusting different parameters were recorded to further judge the stability of the model.

Figure 12 shows the scatter plot of the predicted SAH intensity and the real SAH intensity. We can see that the correlation between the predicted results and the real results is still the highest in the CEEMDAN + ConvGRU model, which was as high as 0.98. However, the correlation of MLP, RNN, GRU, and ConvGRU models was 0.92, 0.96, 0.95, and 0.96, respectively, which is relatively low and has not been greatly improved with the optimization of the model. From the point of view of the concentration degree of scatter diagram, our proposed CEEMDAN + ConvGRU model still has the highest concentration degree. However, the prediction results of the MLP model were relatively divergent.

After analyzing the relative concentration degree of the prediction results and the real values of each model, we needed to calculate the MAE of the prediction results of each model under different parameter training conditions and then get the stability of the training results of each model and the scientific conclusion. As shown in Figure 13, the box diagram reflects the dispersion of MAE of multiple training results of each model. The upper edge, lower edge, median, 25% median, and 75% median of each group of MAE data are shown. The results show that the proposed CEEMDAN+ ConvGRU model has higher stability and better performance than the traditional deep learning model, and is more suitable for predicting SAH intensity.

4. Discussion

(1)

The dynamic field and the corresponding chemical field of SAH have obvious symmetrical distribution. Taking the center of the anticyclone as the axis, the distribution of chemical substances in the stratosphere and troposphere is constrained by the anticyclone in the center symmetric direction. This is a common feature of the distribution of vortices and matter in the atmosphere. The prediction of SAH intensity can provide some reference for the atmospheric vortex systems of various scales, such as the prediction of tropical cyclone intensity.

(2)

Due to almost all systems in the atmosphere and ocean having nonlinear characteristics, the new CEEMDAN + ConvGRU model can the predict SAH intensity index well and may also be suitable for the prediction of other weather and climate systems. For example, the previous research and the prediction of extreme vortex intensity, weather and climate phenomena such as ENSO, NAO, AO, and other weather and climate phenomena, that is, the prediction of the index, which can be verified and compared with the innovation method. This method provides a new theoretical approach and scientific basis for the prediction of various intensity indices in the atmosphere.

(3)

In the prediction process of this study, we transform the time series characteristics of SAH time series into spatial characteristics for research. Compared with the prediction of El Niño [23], considering the temporal and spatial characteristics of its elements has a certain reference value. The time series can better capture the influence of the previous time series while predicting a single time step. In the process of forecasting, the spatial–temporal distribution characteristics of SAH-related elements are added to the forecasting model to make a multi-dimensional forecast, which has a high value for the prediction of all kinds of weather systems.

(4)

Heavy rainfall is one of the important and difficult points in modern numerical forecasting. SAH intensity has a significant impact on the distribution of water vapor and has a strong positive feedback on heavy rainfall in Asia. There is a teleconnection relationship between precipitation and SAH intensity. The prediction of the SAH intensity index can further accurately quantify the impact of heavy precipitation in Asia and provide a theoretical basis for the numerical prediction system.

(5)

The change of SAH intensity has a serious impact on extreme weather phenomena and disaster weather in Asia, especially typhoons in most parts of China and the Ozone (O₃) trough in the Tibetan Plateau. The CEEMDAN + ConvGRU model can accurately predict the day-to-day variation of SAH intensity, which can provide a theoretical basis for the study of such extreme weather. Adding it into the model and new deep learning method can improve the prediction results of numerical forecasts.

(6)

In the region of different noise reduction processing methods, we also make an effective fusion of signal processing methods and deep learning methods in mathematics. Compared with the traditional methods, it has more feasibility for data processing. The most advanced methods such as CEEMDAN can be applied to the field of artificial intelligence and atmospheric science, which is worthy of discussion. Therefore, this research also provides a solid basis for other prediction fields in the atmosphere.

(7)

In the deep learning method, we combine the convolution network with GRU, which not only considers the time series features, but also extracts the spatial features of time series by using the step-by-step method. It has a certain guiding significance in the prediction of nonlinear system. Recent hybrid supervised–unsupervised techniques can be used to improve the performance of the proposed method in future works; for example, Ieracitano et al. [80] used autoencoder (AE) and MLP to classify the electrospun nanofibers, and the accuracy was as high as 92.5%; Benvenuto et al. [81] used the hybrid method of supervised–unsupervised learning to classify and predict the solar flares, and the result shows that the hybrid method is better than other supervised methods. We can learn from these methods to improve the accuracy and reduce the complexity of the model in future works.

5. Conclusions

In this study, a new time series data analysis method Ensemble Empirical Mode Decomposition with Adaptive Noise (CEEMDAN) combined with the deep learning method Convolutional and Gated Recurrent Neural Network (ConvGRU) is proposed to predict the intensity of South Asian High (SAH). Using the ConvLSTM neural network model, which has achieved good results in precipitation prediction [52], we simplified the network structure to the ConvGRU model, which made a high-quality and proper prediction of SAH intensity. Firstly, after the time series model decomposed enough Intrinsic Mode Functions (IMFs) and residual components through the CEEMDAN method, the decomposed IMF was detected by Permutation Entropy (PE) method, and then the abnormal IMF was excluded by the selected criterion 0.9. The selected IMF and residual components were reconstructed into new SAH intensity series data, and then the reconstructed data were added to the ConvGRU model for training and prediction. The prediction results show that the CEEMDAN + ConvGRU model proposed by us has higher accuracy and a more stable training effect than the traditional deep learning method.

(a)

In general, the ConvGRU training model is simpler than ConvLSTM, the training time is faster, and it is aimed at the nonlinear system in the atmosphere. The annual effect of the intensity variation of the SAH is not significant enough. As variants of the Recurrent Neural Network (RNN), the Gated Recurrent Neural Network (GRU) and Long–Short Time Memory (LSTM) can capture the effective information in the long-term sequence, and GRU has a simpler structure than LSTM, which also has a faster effect on the training of SAH intensity time series. Differently from the previous training and prediction methods of the time series, such as RNN and the one-dimensional convolutional neural network (CNN), we transformed the one-dimensional structure into a two-dimensional structure through time-step processing for each year’s SAH intensity data and then added two-dimensional convolutional network to the training model to better extract the change characteristics of the time series.

(b)

In addition, differently from the traditional deep learning models such as Multi-layer Perceptron (MLP), RNN, GRU, and ConvGRU, we used the CEEMDAN and PE method to eliminate the noise in the time series and obtain more robust data. After that, the randomness and complexity of time series were reduced, so the time series prediction data combined with the method had higher accuracy and a more stable training effect.

(c)

Ultimately, the method of conforming to the model provides a new idea for the prediction of time series. Because of the nonlinear variation characteristics of various weather systems in the atmosphere, influenced by various weather and meteorological elements, there are strong characteristics of mutation and randomness. Therefore, the research considers the processing and prediction of the time series of atmospheric systems to be very important.

However, the study has some limitations. For example, in the prediction process of this study, we only considered a single variable factor, namely SAH intensity, but did not consider the weather factors that affect SAH intensity, such as the height of convection, the change of surface temperature, and so on. In future research, we can add these factors to the model to consider the prediction results of multivariate model input and the advantages and disadvantages of a single variable so as to further improve the prediction accuracy of SAH intensity.

Moreover, when studying the variation of SAH intensity, there is no comparison with the actual weather phenomenon, which cannot provide a direct forecast conclusion for numerical prediction. Since many of the atmospheric vortex systems are similar to the SAH and have symmetrical structures, we can consider adding different vortices in future studies, such as polar vortices, typhoons, etc. We can make a further comparative study between the prediction results and such extreme weather phenomena, make a certain explanation for the correlation between them, and strengthen the ability to predict extreme weather time and the O₃ trough.

Ultimately, the deep learning method is still worthy of improvement, and recent hybrid supervised–unsupervised techniques can be used to improve the performance of the proposed method. For example, the Trajectory GRU (TrajGRU) model that is proposed by Shi et al. [74] is a new forecasting benchmark model for short-time precipitation forecasting; SAH intensity prediction may improve by using this benchmark model. Convolutional Residual-Attention, which is proposed by Yan et al. [44], can also be used in time series prediction, and it has a prominent performance in precipitation forecasting. While using the time series analysis, we do not make better use of the spatial characteristics of the SAH and only focus on the characteristics of intensity time series. In the future, we can select the most advanced neural network for spatial feature extraction and add the spatial characteristics of anticyclone, such as the characteristics of flow field, to the intensity prediction, which may not only be able to predict the intensity of the SAH, but also other structural characteristics. Combining the prediction of chemical distribution and SAH structure characteristics can provide a theoretical basis for the study of chemical transport and atmospheric chemistry.