Derivative-Free Iterative Methods with Some Kurchatov-Type Accelerating Parameters for Solving Nonlinear Systems
Abstract
:1. Introduction
2. Some New Iterative Schemes with Memory
3. Numerical Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ortega, J.M.; Rheinbolt, W.C. Iterative Solution of Nonlinear Equations in Several Variables; Academic Press: New York, NY, USA, 1970. [Google Scholar]
- Torres-Hernandez, A.; Brambila-Paz, F.; Iturrará-Viveros, U.; Caballero-Cruz, R. Fractioaal Newton–Raphson method accelerated with Aitken’s method. Axioms 2021, 10, 47. [Google Scholar] [CrossRef]
- Gdawiec, K.; Kotarski, W.; Lisowska, A. Newton’s method with fractional derivatives and various iteration processes via visual analysis. Numer. Algorithms 2021, 86, 953–1010. [Google Scholar] [CrossRef]
- Akgül, A.; Cordero, A.; Torregrosa, J.R. A fractional Newton method with 2αth-order of convergence and its sability. Appl. Math. Lett. 2019, 98, 344–351. [Google Scholar] [CrossRef]
- Cordero, A.; Girona, I.; Torregrosa, J.R. A variant of Chebyshev’s method with 3αth-order of convergence by using fractional derivatives. Symmetry 2019, 11, 1017. [Google Scholar] [CrossRef] [Green Version]
- Behl, R.; Bhalla, S.; Magreñán, Á.A.; Kumar, S. An efficient high order iterative scheme for large nonlinear systems with dynamics. J. Comp. Appl. Math. 2020, 113249. [Google Scholar] [CrossRef]
- Geum, Y.H.; Kim, Y.I.; Magreñán, Á.A. A biparametric extension of King’s fourth-order methods and their dynamics. Appl. Math. Comput. 2016, 282, 254–275. [Google Scholar] [CrossRef]
- Schwandt, H. A symmetric iterative interval method for systems of nonlinear equations. Computing 1984, 33, 153–164. [Google Scholar] [CrossRef]
- Barco, M.A.; Prince, G.E. New symmetry solution techniques for first-order non-linear PDEs. Appl. Math. Comput. 2001, 124, 169–196. [Google Scholar] [CrossRef]
- Traub, J.F. Iterative Methods for the Solution of Equations; Prentice-Hall: Hoboken, NJ, USA, 1964. [Google Scholar]
- Grau-Sánchez, M.; Grau, À.; Noguera, M. Ostrowski type methods for solving systems of nonlinear equations. Appl. Math. Comput. 2011, 218, 2377–2385. [Google Scholar] [CrossRef]
- Petković, M.S.; Sharma, J.R. On some efficient derivative-free iterative methods with memory for solving systems of nonlinear equations. Numer. Algorithms 2016, 71, 457–474. [Google Scholar] [CrossRef]
- Ahmad, F.; Soleymani, F.; Haghani, F.K.; Serra-Capizzano, S. Higher order derivative-free iterative methods with and without memory for systems of nonlinear equations. Appl. Math. Comput. 2017, 314, 199–211. [Google Scholar] [CrossRef]
- Kansal, M.; Cordero, A.; Bhalla, S.; Torregrosa, J.R. Memory in a new variant of king’s family for solving nonlinear sytstems. Mathematics 2020, 8, 1251. [Google Scholar] [CrossRef]
- Kurchatov, V.A. On a method of linear interpolation for the solution of functional equations. Dokl. Akad. Nauk SSSR 1971, 198, 524–526. [Google Scholar]
- Chicharro, F.I.; Cordero, A.; Garrido, N.; Torregrosa, J.R. On the improvement of the order of convergence of iterative methods for solving nonlinear systems by means of memory. Appl. Math. Lett. 2020, 104, 106277. [Google Scholar] [CrossRef]
- Cordero, A.; Soleymani, F.; Torregrosa, J.R.; Khaksar Haghani, F. A family of Kurchatov-type methods and its stability. Appl. Math. Comput. 2017, 294, 264–279. [Google Scholar] [CrossRef] [Green Version]
- Argyros, I.K.; Ren, H. On the Kurchatov method for solving equations under weak conditions. Appl. Math. Comput. 2016, 273, 98–113. [Google Scholar] [CrossRef]
- Candela, V.; Peris, R. A class of third order iterative Kurchatov-Steffensen(derivative free) methods for solving nonlinear equations. Appl. Math. Comput. 2019, 350, 93–104. [Google Scholar] [CrossRef]
- Weerakoon, S.; Fernando, T.G.I. A variant of Newton’s method with accelerated third-order convergence. Appl. Math. Lett. 2000, 13, 87–93. [Google Scholar] [CrossRef]
- Ahmad, F.; Rehman, S.U.; Ullah, M.Z.; Aljahdali, H.M.; Ahmad, S.; Alshomrani, A.S.; Carrasco, J.A.; Ahmad, S.; Sivasankaran, S. Frozen Jocabian multistep iterative method for solving nonlinear IVPs and BVPs. Complexity 2017, 2017, 9407656. [Google Scholar] [CrossRef]
- Narang, M.; Bhatia, S.; Kanwar, V. New efficient derivative free family of seventh-order methods for solving systems of nonlinear equations. Numer. Algorithms 2017, 76, 283–307. [Google Scholar] [CrossRef]
- Petković, M.S.; Yun, B.I. Sigmoid-like functions and root finding methods. Appl. Math. Comput. 2008, 204, 784–793. [Google Scholar] [CrossRef]
- Yun, B.I. A non-iterative method for solving nonlinear equations. Appl. Math. Comput. 2008, 198, 691–699. [Google Scholar] [CrossRef]
- Yun, B.I. Iterative methods for solving nonliear equations with finitely any roots in an interval. J. Comput. Appl. Math. 2012, 236, 3308–3318. [Google Scholar] [CrossRef] [Green Version]
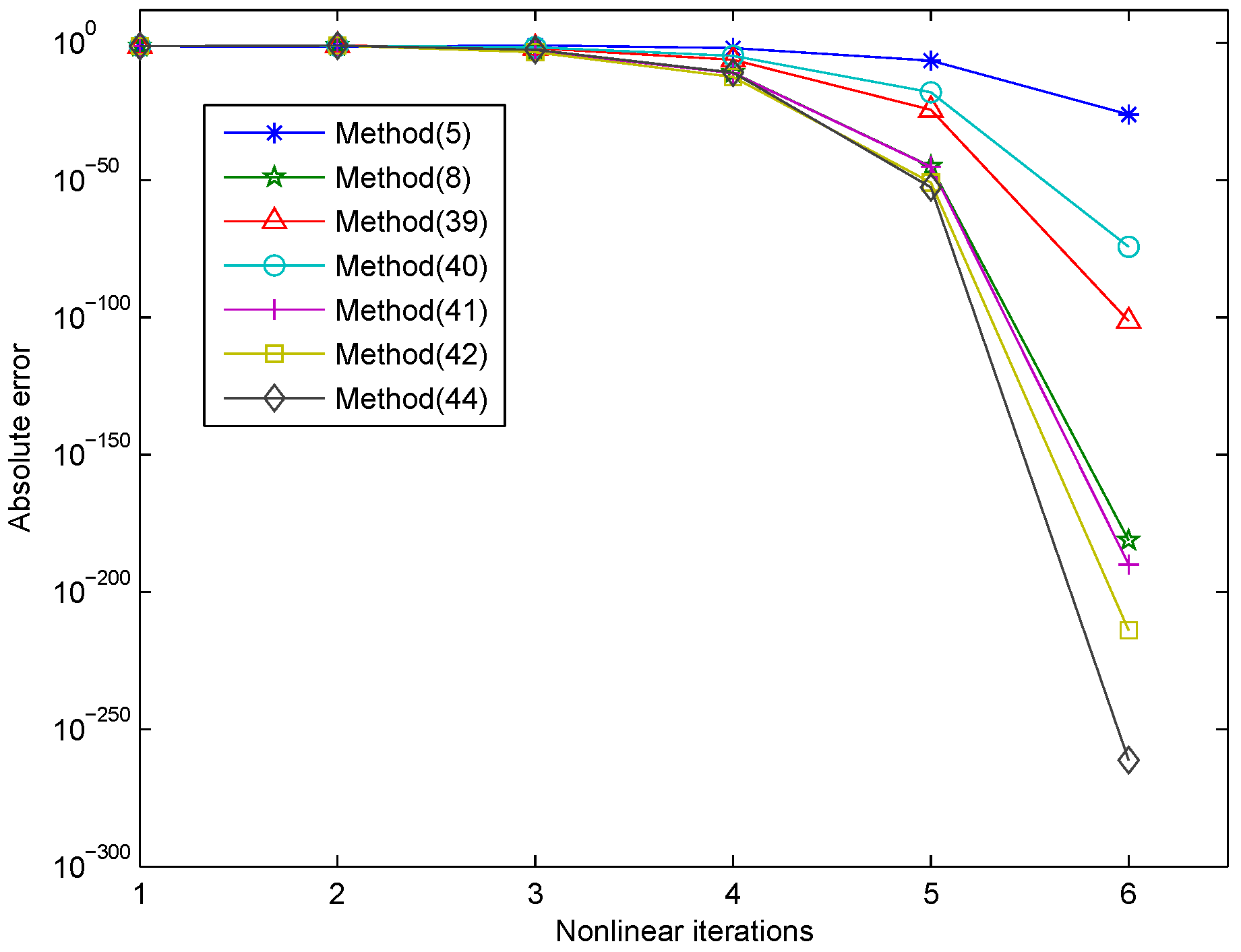

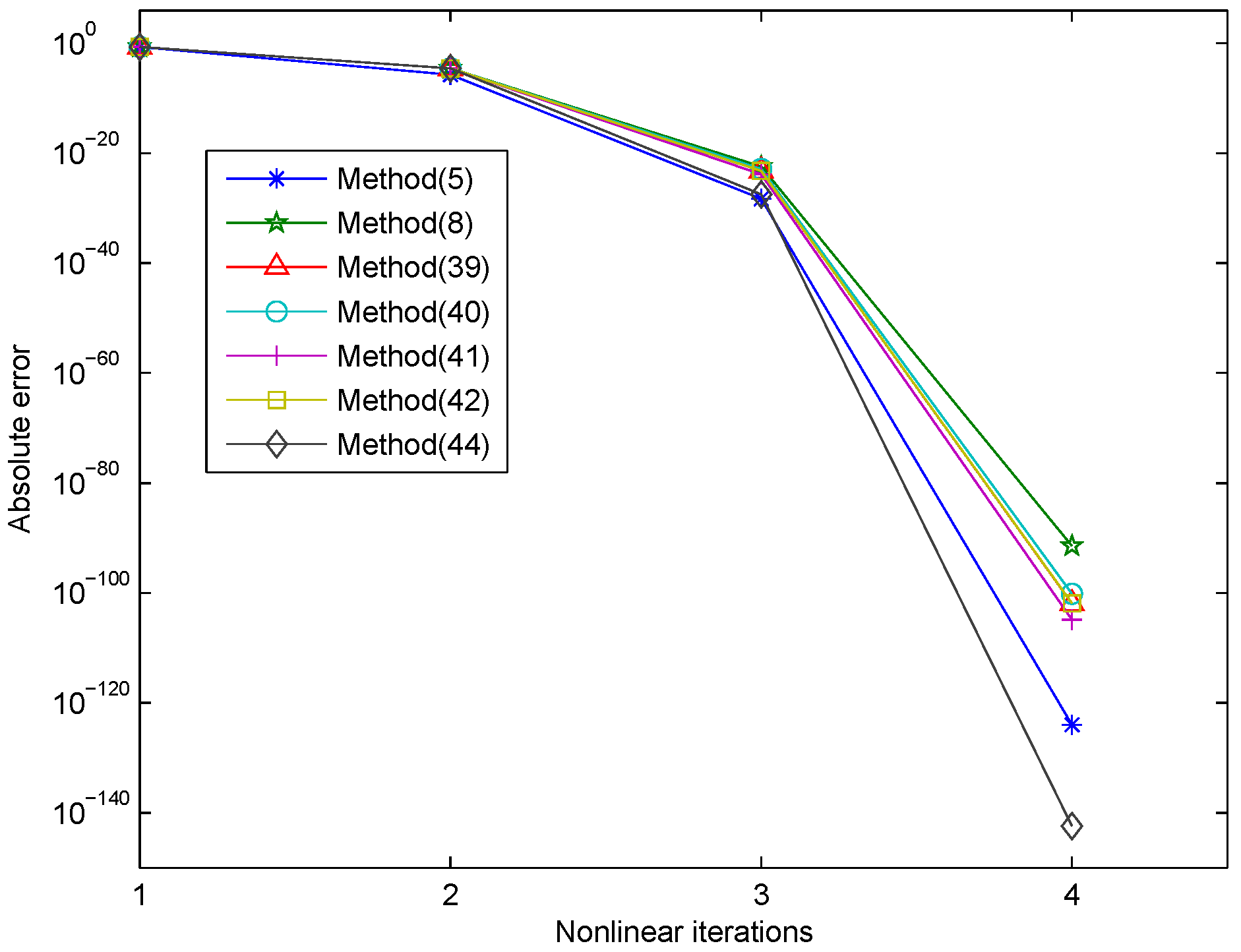
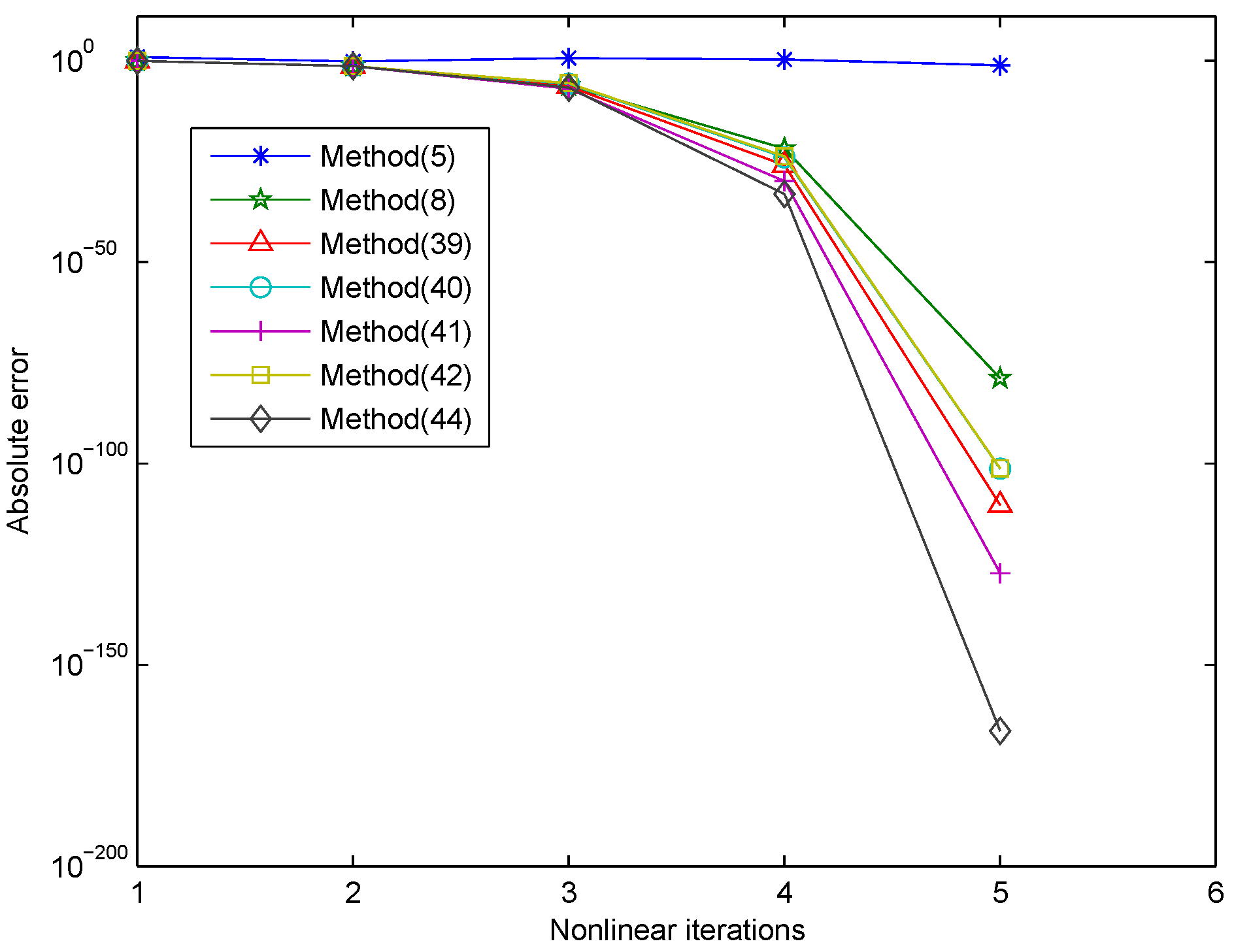
| Methods | NI | EV | EF | ACOC | e-Time |
|---|---|---|---|---|---|
| (5) | 7 | 4.577 × | 1.648 × | 4.22419 | 15.537 |
| (8) | 6 | 6.536 × | 5.328 × | 3.97864 | 15.428 |
| (39) | 6 | 5.041 × | 6.013 × | 4.23649 | 15.943 |
| (40) | 7 | 1.645 × | 1.562 × | 4.23601 | 18.111 |
| (41) | 6 | 9.817 × | 3.228 × | 4.23669 | 14.180 |
| (42) | 6 | 1.114 × | 3.614 × | 4.23381 | 15.319 |
| (43) | 6 | 5.202 × | 1.988 × | 5.00000 | 20.280 |
| (44) | 6 | 6.070 × | 4.302 × | 5.00000 | 20.623 |
| (45) | 6 | 5.833 × | 3.526 × | 5.00000 | 19.000 |
| Methods | NI | EV | EF | ACOC | e-Time |
|---|---|---|---|---|---|
| (5) | 12 | 5.059 × | 3.088 × | 4.23598 | 39.998 |
| (8) | 7 | 3.408 × | 3.497 × | 3.99832 | 12.776 |
| (39) | 7 | 2.323 × | 9.941 × | 4.23562 | 14.242 |
| (40) | 7 | 2.484 × | 1.108 × | 4.23561 | 14.851 |
| (41) | 6 | 8.864 × | 2.159 × | 4.24093 | 10.966 |
| (42) | 6 | 1.014 × | 5.896 × | 4.23542 | 10.764 |
| (43) | 7 | 7.681 × | 2.609 × | 4.99965 | 25.256 |
| (44) | 6 | 3.898 × | 1.470 × | 5.00000 | 14.492 |
| (45) | 6 | 1.791 × | 1.796 × | 5.00000 | 13.135 |
| Methods | NI | EV | EF | ACOC | e-Time |
|---|---|---|---|---|---|
| (5) | 4 | 9.478 × | 1.079 × | 4.23909 | 1.154 |
| (8) | 5 | 6.828 × | 1.072 × | 4.03695 | 1.669 |
| (39) | 4 | 1.172 × | 1.181 × | 4.20358 | 1.294 |
| (40) | 4 | 6.850 × | 7.002 × | 4.20758 | 1.372 |
| (41) | 4 | 1.353 × | 1.369 × | 4.19837 | 1.372 |
| (42) | 4 | 1.329 × | 2.014 × | 4.20446 | 1.357 |
| (43) | 4 | 3.818 × | 2.243 × | 5.00784 | 1.700 |
| (44) | 4 | 1.427 × | 1.637 × | 5.00409 | 1.794 |
| (45) | 4 | 1.841 × | 5.854 × | 5.00505 | 1.762 |
| Methods | NI | EV | EF | ACOC | e-Time |
|---|---|---|---|---|---|
| (5) | 8 | 1.932 × | 3.291 × | 4.26779 | 9.750 |
| (8) | 6 | 6.690 × | 1.315 × | 3.54607 | 9.094 |
| (39) | 5 | 4.488 × | 4.446 × | 4.32150 | 7.410 |
| (40) | 5 | 4.697 × | 1.137 × | 4.23216 | 7.488 |
| (41) | 5 | 5.905 × | 4.505 × | 4.24952 | 7.534 |
| (42) | 5 | 5.803 × | 2.515 × | 4.27379 | 7.566 |
| (43) | 5 | 1.956 × | 6.081 × | 5.04097 | 9.687 |
| (44) | 5 | 3.845 × | 1.974 × | 5.05028 | 9.672 |
| (45) | 5 | 1.104 × | 7.583 × | 4.29476 | 9.703 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Jin, Y.; Zhao, Y. Derivative-Free Iterative Methods with Some Kurchatov-Type Accelerating Parameters for Solving Nonlinear Systems. Symmetry 2021, 13, 943. https://doi.org/10.3390/sym13060943
Wang X, Jin Y, Zhao Y. Derivative-Free Iterative Methods with Some Kurchatov-Type Accelerating Parameters for Solving Nonlinear Systems. Symmetry. 2021; 13(6):943. https://doi.org/10.3390/sym13060943
Chicago/Turabian StyleWang, Xiaofeng, Yingfanghua Jin, and Yali Zhao. 2021. "Derivative-Free Iterative Methods with Some Kurchatov-Type Accelerating Parameters for Solving Nonlinear Systems" Symmetry 13, no. 6: 943. https://doi.org/10.3390/sym13060943
APA StyleWang, X., Jin, Y., & Zhao, Y. (2021). Derivative-Free Iterative Methods with Some Kurchatov-Type Accelerating Parameters for Solving Nonlinear Systems. Symmetry, 13(6), 943. https://doi.org/10.3390/sym13060943





