Derivative-Free Iterative Methods with Some Kurchatov-Type Accelerating Parameters for Solving Nonlinear Systems

Abstract

Some Kurchatov-type accelerating parameters are used to construct some derivative-free iterative methods with memory for solving nonlinear systems. New iterative methods are developed from an initial scheme without memory with order of convergence three. New methods have the convergence order $2+\sqrt{5}\approx 4.236$ and 5, respectively. The application of new methods can solve standard nonlinear systems and nonlinear ordinary differential equations (ODEs) in numerical experiments. Numerical results support the theoretical results.

1. Introduction

Many real-world problems that arise in various scientific fields are modeled by mathematically interesting nonlinear systems $F\left(x\right)=0$. Symmetries and conservation laws are powerful tools for studying explicit solutions of nonlinear systems. Finding the solution of nonlinear systems is an important problem in the area of mathematics, where $F:D\subseteq {\mathbb{R}}^n\to {\mathbb{R}}^n$. Iterative method is a kind of efficient method for solving nonlinear systems. Optimization and acceleration of iterative methods can be achieved by applying symmetries. Newton’s method [1] is the oldest method for solving nonlinear systems, which is quadratically convergent assuming that initial approximation is close enough to the root. Based on Newton’s method, some high-order iterative method have been proposed in the literature. For example, Torres-Hernandez et al. [2], Gdawiec et al. [3], Akgül et al. [4] and Cordero et al. [5] developed some variants of Newton’s method by using fractional derivatives. Behl et al. [6] and Geum et al. [7] proposed some high-order iterative methods and their dynamics are investigated. Schwandt [8] proposed a symmetric iterative method for solving nonlinear systems. Barco et al. [9] obtained the local solutions of partial differential equations by symmetry approach. Derivative-free method is a kind of variant of Newton’s method, which can solve the solution of non-differentiable nonlinear systems. One of the celebrated derivative-free iterative methods is Traub’s method [10], which is given by

$$z^{(j+1)}=z^{\left(j\right)}-{[s^{\left(j\right)}, z^{\left(j\right)}; F]}^{-1}F\left(z^{\left(j\right)}\right),$$

(1)

where $s^{\left(j\right)}= z^{\left(j\right)}+B F\left(z^{\left(j\right)}\right)$, B is a nonzero arbitrary parameter and ${[s^{\left(j\right)},z^{\left(j\right)};F]}^{-1}$ is the inverse of the first-order divided difference operator $[s^{\left(j\right)},z^{\left(j\right)};F]$. The first-order divided difference operator $[.,.;F]:D\times D\subset {\mathbb{R}}^n\times {\mathbb{R}}^n\to L\left({\mathbb{R}}^n\right)$ is an $n\times n$ matrix, which is defined by [11]:

$$[z+h,z;F]={\int }_0^1{F}^{\prime }(z+th)dt,\forall (z,h)\in {\mathbb{R}}^n\times {\mathbb{R}}^n,$$

(2)

where $h=s-z$. Developing the Taylor’s expansion of $F^{\prime }(z+th)$ on the point z, we obtain

$${\int }_0^1{F}^{\prime }(z+th)dt=F^{\prime }\left(z\right)+\frac{1}{2}{F}^{″}\left(z\right)h+\frac{1}{6}{F}^{‴}\left(z\right)h^2+O\left[h^3\right].$$

(3)

In the process of computation, the first-order divided difference operator $[s^{\left(j\right)},z^{\left(j\right)}; F]$ is calculated by [11]

$${[s^{\left(j\right)},z^{\left(j\right)}; F]}_{ik}=\frac{F_i(s_1^{\left(j\right)}\cdots ,s_{k-1}^{\left(j\right)},s_k^{\left(j\right)},z_{k+1}^{\left(j\right)},\cdots ,z_m^{\left(j\right)})-F_i(s_1^{\left(j\right)}\cdots ,s_{k-1}^{\left(j\right)},z_k^{\left(j\right)},z_{k+1}^{\left(j\right)},\cdots ,z_m^{\left(j\right)})}{(s_k^{\left(j\right)}-z_k^{\left(j\right)})},$$

(4)

where $1\le i,k\le m.$

Based on Traub’s method, many derivative-free methods have been studied in the literature [12,13,14,15,16,17,18,19]. Derivative-free methods can be divided into two groups: iterative method with memory and iterative method without memory. Iterative method with memory is superior to iterative method without memory in terms of computational efficiency and stability. To date, very few derivative-free methods with memory for solving nonlinear systems have been proposed in the literature. Recently, Petković and Sharma [12] designed the following derivative-free method with memory for solving nonlinear systems by using the variable parameter method

$$\left\{\begin{array}{c}{s}^{\left(j\right)}=z^{\left(j\right)}-B^{\left(j\right)}F\left(z^{\left(j\right)}\right),\\ t^{\left(j\right)}=z^{\left(j\right)}-{[s^{\left(j\right)},z^{\left(j\right)};F]}^{-1}F\left(z^{\left(j\right)}\right),\\ z^{(j+1)}=t^{\left(j\right)}-(aI+G^{\left(j\right)}((3-2a)I+(a-2)G^{\left(j\right)})){[s^{\left(j\right)},z^{\left(j\right)};F]}^{-1}F\left(t^{\left(j\right)}\right),\end{array}\right.$$

(5)

where $B^{\left(j\right)}=-{[s^{(j-1)},z^{(j-1)};F]}^{-1}$ is called variable parameter, $G^{\left(j\right)}={[s^{\left(j\right)},z^{\left(j\right)};F]}^{-1}[w^{\left(j\right)},t^{\left(j\right)};F]$, $w^{\left(j\right)}=t^{\left(j\right)}+cF\left(t^{\left(j\right)}\right)$ and $c\in R-0$. Method (5) has the convergence order $2+\sqrt{5}\approx 4.236$, when the parameter $a\ne 3$. Using the same variable parameter $B^{\left(j\right)}$ as method (5), Ahmad et al. [13] and Kansal et al. [14] proposed some high order iterative methods with memory for solving nonlinear systems. Using the Kurchatov’s divided difference operator [15], Chicharro et al. [16] designed two derivative-free methods with memory for solving nonlinear systems. Firstly, they constructed the following third-order iterative method without memory

$$\left\{\begin{array}{c}{s}^{\left(j\right)} =z^{\left(j\right)}+BF\left(z^{\left(j\right)}\right),\\ t^{\left(j\right)} =z^{\left(j\right)}-{[s^{\left(j\right)},z^{\left(j\right)};F]}^{-1}F\left(z^{\left(j\right)}\right),\\ z^{(j+1)}=t^{\left(j\right)}-{[s^{\left(j\right)},t^{\left(j\right)};F]}^{-1}F\left(t^{\left(j\right)}\right),\end{array}\right.$$

(6)

which satisfies the following error equation

$${\epsilon }^{(j+1)}=A_2^2{(I+B{F}^{\prime }\left(\zeta \right))}^2{\left({\epsilon }^{\left(j\right)}\right)}^3+O\left({\left({\epsilon }^{\left(j\right)}\right)}^4\right),$$

(7)

where ${\epsilon }^{\left(j\right)}=z^{\left(j\right)}-\zeta$, $\zeta$ is the zero of nonlinear function F and $A_j=\frac{1}{j!}{F}^{\prime }{\left(\zeta \right)}^{-1}{F}^{\left(j\right)}\left(\zeta \right)$, $(j=1,2,\cdots ,n).$ Replacing the constant parameter B with $B^{\left(j\right)}=-{[2z^{\left(j\right)}-z^{(j-1)},z^{(j-1)};F]}^{-1}$ in method (6), they obtained the following fourth-order method with memory

$$\left\{\begin{array}{c}{s}^{\left(j\right)} =z^{\left(j\right)}-{[2z^{\left(j\right)}-z^{(j-1)},z^{(j-1)};F]}^{-1}F\left(z^{\left(j\right)}\right),\\ t^{\left(j\right)} =z^{\left(j\right)}-{[s^{\left(j\right)},z^{\left(j\right)};F]}^{-1}F\left(z^{\left(j\right)}\right),\\ z^{(j+1)}=t^{\left(j\right)}-{[s^{\left(j\right)},t^{\left(j\right)};F]}^{-1}F\left(t^{\left(j\right)}\right),\end{array}\right.$$

(8)

where the first-order divided difference operator $[2z^{\left(j\right)}-z^{(j-1)},z^{(j-1)};F]$ is called Kurchatov’s divided difference operator. Using the Kurchatov’s divided difference operator to design the variable parameter, Cordero et al. [17], Argyros et al. [18] and Candela et al. [19] proposed some efficient Kurchatov-type methods. Variable parameters can be designed by different schemes, which usually uses iterative sequences from the current and previous steps.

In this paper, we design some new variable parameters by using some new Kurchatov-type divided difference operators. This paper is organized as follows. Some new Kurchatov-type divided difference operators are used to construct iterative schemes with memory for the numerical solution of nonlinear systems in Section 2. The main advantage of the new Kurchatov-type divided difference operators is that it has less errors than the Kurchatov’s first-order operator $[2z^{\left(j\right)}-z^{(j-1)},z^{(j-1)};F]$. The order of the basic method (6) is increased from 3 to $(2+\sqrt{5})\approx 4.236$ and 5, respectively. The application of new methods to solve standard nonlinear systems and nonlinear ordinary differential equations (ODEs) is made in numerical experiments. Numerical experiments are made in Section 3. A short summary is given in Section 4.

2. Some New Iterative Schemes with Memory

If $I+B{F}^{\prime }\left(\zeta \right)\ne 0$ in (7), the convergence order of method (6) is three. Letting $B=-{F^{\prime }\left(\zeta \right)}^{-1}$, the order of convergence of method (6) can be improved. However, $F^{\prime }\left(\zeta \right)$ is unknown in practice. In order to improve the order of convergence of method (6), we could choose a variable parameter $B^{\left(j\right)}$ to replace constant parameter B. The variable parameter $B^{\left(j\right)}$ should satisfy $li{m}_{j\to \infty }{B}^{\left(j\right)}=-{F^{\prime }\left(\zeta \right)}^{-1}$. Using the Kurchatov’s divided difference operator $[2z^{\left(j\right)}-z^{(j-1)},z^{(j-1)};F]$ to approach $F^{\prime }\left(\zeta \right)$, Chicharro et al. [16] designed the iterative method (8) with a variable parameter $B^{\left(j\right)}=-{[2z^{\left(j\right)}-z^{(j-1)},z^{(j-1)};F]}^{-1}$. The Kurchatov’s divided difference operator $[2z^{\left(j\right)}-z^{(j-1)},z^{(j-1)};F]$ satisfies

$$\underset{j\to \infty }{lim}[2z^{\left(j\right)}-z^{(j-1)},z^{(j-1)};F]=F^{\prime }\left(\zeta \right),$$

(9)

where iterative sequence $\left\{z^{\left(j\right)}\right\}\to \zeta$ as $j\to \infty$.

To obtain some more effective iterative methods, we design some new Kurchatov-type first-order divided difference operators to construct the accelerating parameter $B^{\left(j\right)}$. If $j\to \infty$, then iterative sequences generated by iterative method (7) satisfy $\left\{t^{\left(j\right)}\right\}\to \zeta$, $\left\{z^{\left(j\right)}\right\}\to \zeta$ and $\left\{s^{\left(j\right)}\right\}\to \zeta$. Using $t^{\left(j\right)},z^{\left(j\right)}$ and $s^{\left(j\right)}$, we can design some first-order divided difference operators to approach $F^{\prime }\left(\zeta \right)$.

Scheme 1.

Using$t^{(j-1)}$and$z^{\left(j\right)}$, we design the first-order divided difference operator$[2t^{(j-1)}-z^{\left(j\right)},z^{\left(j\right)};F]$and obtain the following variable parameter

$$B^{\left(j\right)}=-{[2t^{(j-1)}-z^{\left(j\right)},z^{\left(j\right)};F]}^{-1}.$$

(10)

Using (2) and (3), we have

$$[2t^{(j-1)}-z^{\left(j\right)},z^{\left(j\right)};F]={\int }_0^1{F}^{\prime }(z^{\left(j\right)}+xh)dx=F^{\prime }\left(z^{\left(j\right)}\right)+F^{″}\left(z^{\left(j\right)}\right)h+\frac{2}{3}{F}^{‴}\left(z^{\left(j\right)}\right)h^2+O\left(h^3\right),$$

(11)

where$h=2(t^{(j-1)}-z^{\left(j\right)})$.

Using Taylor’s expansion around$\zeta$and taking into account$F\left(\zeta \right)=0$, we have

$$F\left(z^{\left(j\right)}\right)=F^{\prime }\left(\zeta \right)[{\epsilon }^{\left(j\right)}+A_2{\left({\epsilon }^{\left(j\right)}\right)}^2+A_3{\left({\epsilon }^{\left(j\right)}\right)}^3]+O\left({\left({\epsilon }^{\left(j\right)}\right)}^4\right),$$

(12)

$$F^{\prime }\left(z^{\left(j\right)}\right)=F^{\prime }\left(\zeta \right)[I+2A_2\left({\epsilon }^{\left(j\right)}\right)+3A_3{\left({\epsilon }^{\left(j\right)}\right)}^2]+O\left({\left({\epsilon }^{\left(j\right)}\right)}^3\right),$$

(13)

$$F^{″}\left(z^{\left(j\right)}\right)=F^{\prime }\left(\zeta \right)[2A_2+6A_3\left({\epsilon }^{\left(j\right)}\right)]+O\left({\left({\epsilon }^{\left(j\right)}\right)}^2\right),$$

(14)

and

$$F^{‴}\left(z^{\left(j\right)}\right)=F^{\prime }\left(\zeta \right)\left[6A_3\right]+O\left({\epsilon }^{\left(j\right)}\right),$$

(15)

where${\epsilon }^{\left(j\right)}=z^{\left(j\right)}-\zeta$.

From (12)–(15), we have

$$[2t^{(j-1)}-z^{\left(j\right)},z^{\left(j\right)};F]=F^{\prime }\left(\zeta \right)[I+2A_2{\epsilon }_t^{(j-1)}+A_3{\left({\epsilon }^{\left(j\right)}\right)}^2$$

$$+4A_3{\left({\epsilon }_t^{(j-1)}\right)}^2-2A_3\left({\epsilon }_t^{(j-1)}\right)\left({\epsilon }^{\left(j\right)}\right)]+O_3({\epsilon }_t^{(j-1)},{\epsilon }^{\left(j\right)}),$$

(16)

where${\epsilon }_t^{(j-1)}=t^{(j-1)}-\zeta$, ${\epsilon }_t^{(j-1)}\to 0$and${\epsilon }^{\left(j\right)}\to 0$as$j\to \infty$.

From (16), we obtain

$$\underset{j\to \infty }{lim}[2t^{(j-1)}-z^{\left(j\right)},z^{\left(j\right)};F]=F^{\prime }\left(\zeta \right).$$

(17)

This means that the first order divided difference operator$[2t^{(j-1)}-z^{\left(j\right)},z^{\left(j\right)};F]$can be used to construct the variable parameter$B^{\left(j\right)}$.

Using$X{X}^{-1}=I$and (17), we obtain

$$B^{\left(j\right)}=-{[2t^{(j-1)}-z^{\left(j\right)},z^{\left(j\right)};F]}^{-1}=-[I-2A_2{\epsilon }_t^{(j-1)}-A_3{\left({\epsilon }^{\left(j\right)}\right)}^2+(2A_2^2-4A_3){\left({\epsilon }_t^{(j-1)}\right)}^2$$

$$+2A_3\left({\epsilon }_t^{(j-1)}\right)\left({\epsilon }^{\left(j\right)}\right)]F^{\prime }{\left(\zeta \right)}^{-1}+O_3({\epsilon }_t^{(j-1)},{\epsilon }^{\left(j\right)})$$

(18)

and

$$I+B^{\left(j\right)}{F}^{\prime }\left(\zeta \right)\sim 2A_2{\epsilon }_t^{(j-1)}+A_3{\left({\epsilon }_z^{\left(j\right)}\right)}^2-(2A_2^2-4A_3){\left({\epsilon }_t^{(j-1)}\right)}^2-2A_3\left({\epsilon }_t^{(j-1)}\right)\left({\epsilon }_z^{\left(j\right)}\right)\sim 2A_2{\epsilon }_t^{(j-1)}$$

$$\sim 2A_2^2(I+B^{(j-1)}{F}^{\prime }\left(\zeta \right)){\left({\epsilon }^{(j-1)}\right)}^2.$$

(19)

In this manuscript, the symbols ∼ and O are used in the following way: if$li{m}_{n\to \infty }(x_n/y_n)=C$and$C\ne 0$, then we have$x_n=O\left(y_n\right)$or$x_n\sim y_n$.

Scheme 2.

Using$t^{(j-1)}$and$z^{\left(j\right)}$, we design another first-order divided difference operator$[2t^{(j-1)}-z^{\left(j\right)},t^{(j-1)};F]$and obtain the following variable parameter

$$B^{\left(j\right)}=-{[2t^{(j-1)}-z^{\left(j\right)},t^{(j-1)};F]}^{-1}.$$

(20)

Using (2) and (3), we get

$$[2t^{(j-1)}-z^{\left(j\right)},t^{(j-1)};F]=F^{\prime }\left(t^{(j-1)}\right)+\frac{F^{″}\left(t^{(j-1)}\right)}{2}h+\frac{F^{‴}\left(t^{(j-1)}\right)}{6}{h}^2+O\left(h^3\right)$$

$$=F^{\prime }\left(\zeta \right)[I+3A_2{\epsilon }_t^{(j-1)}-7A_3{\left({\epsilon }_t^{(j-1)}\right)}^2-3A_3\left({\epsilon }^{\left(j\right)}\right)-5A_3\left({\epsilon }_t^{(j-1)}\right)\left({\epsilon }^{\left(j\right)}\right)]+O_3({\epsilon }_t^{(j-1)},{\epsilon }^{\left(j\right)}),$$

(21)

where$h={\epsilon }_t^{(j-1)}-{\epsilon }^{\left(j\right)}$.

From (21), we get

$$B^{\left(j\right)}=-[I-3A_2{\epsilon }_t^{(j-1)}+(9A_2^2-7A_3){\left({\epsilon }_t^{(j-1)}\right)}^2+3A_3\left({\epsilon }^{\left(j\right)}\right)$$

$$-(5A_3+9A_2{A}_3)\left({\epsilon }_t^{(j-1)}\right)\left({\epsilon }^{\left(j\right)}\right)]F^{\prime }{\left(\zeta \right)}^{-1}+O_3({\epsilon }_t^{(j-1)},{\epsilon }^{\left(j\right)})$$

(22)

and

$$I+B^{\left(j\right)}{F}^{\prime }\left(\zeta \right)\sim 3A_2{\epsilon }_t^{(j-1)}\sim 3A_2^2(I+B^{(j-1)}{F}^{\prime }\left(\epsilon \right)){\left({\epsilon }^{(j-1)}\right)}^2.$$

(23)

Scheme 3.

Using$t^{(j-1)}$and$z^{\left(j\right)}$, we design another first-order divided difference operator$[2z^{\left(j\right)}-t^{(j-1)},z^{\left(j\right)};F]$and obtain the following variable parameter

$$B^{\left(j\right)}=-{[2z^{\left(j\right)}-t^{(j-1)},z^{\left(j\right)};F]}^{-1}.$$

(24)

Using (2) and (3), we get

$$[2z^{\left(j\right)}-t^{(j-1)},z^{\left(j\right)};F]=F^{\prime }\left(z^{\left(j\right)}\right)+\frac{1}{2}{F}^{″}\left(z^{\left(j\right)}\right)h+\frac{1}{6}{F}^{‴}\left(z^{\left(j\right)}\right)h^2+O\left(h^3\right)$$

$$=F^{\prime }\left(\zeta \right)[I+3A_2{\epsilon }^{\left(j\right)}-A_2\left({\epsilon }_t^{(j-1)}\right)-5A_3\left({\epsilon }^{\left(j\right)}\right)\left({\epsilon }_t^{(j-1)}\right)+A_3{\left({\epsilon }_t^{(j-1)}\right)}^2+4A_3{\left({\epsilon }^{\left(j\right)}\right)}^2+O_3({\epsilon }_t^{(j-1)},{\epsilon }^{\left(j\right)}),$$

(25)

where$h={\epsilon }^{\left(j\right)}-{\epsilon }_t^{(j-1)}$.

From (25), we obtain

$$B^{\left(j\right)}=-[I+A_2{\epsilon }_t^{(j-1)}-3A_2{\epsilon }^{\left(j\right)}+(9A_2^2-5A_3)\left({\epsilon }_t^{(j-1)}\right){\epsilon }^{\left(j\right)}+(9A_2^2-4A_3){\left({\epsilon }^{\left(j\right)}\right)}^2$$

$$-(3A_2^2+A_3){\left({\epsilon }_t^{(j-1)}\right)}^2]F^{\prime }{\left(\zeta \right)}^{-1}+O_3({\epsilon }_t^{(j-1)},{\epsilon }^{\left(j\right)}),$$

(26)

and

$$I+B^{\left(j\right)}{F}^{\prime }\left(\zeta \right)\sim A_2{\epsilon }_t^{(j-1)}\sim -A_2^2(I+B^{(j-1)}{F}^{\prime }\left(\zeta \right)){\left({\epsilon }^{(j-1)}\right)}^2.$$

(27)

Scheme 4.

The first-order divided difference operator$[3z^{\left(j\right)}-2t^{(j-1)},z^{\left(j\right)};F]$can be constructed by using$t^{(j-1)}$and$z^{\left(j\right)}$, then we obtain the following variable parameter

$$B^{\left(j\right)}=-{[3z^{\left(j\right)}-2t^{(j-1)},z^{\left(j\right)};F]}^{-1}.$$

(28)

Using (2) and (3), we have

$$[3z^{\left(j\right)}-2t^{(j-1)},z^{\left(j\right)};F]=F^{\prime }\left(z^{\left(j\right)}\right)+F^{″}\left(z^{\left(j\right)}\right)h+\frac{2}{3}{F}^{‴}\left(z^{\left(j\right)}\right)h^2+O\left(h^3\right)$$

$$=F^{\prime }\left(\zeta \right)[I+4A_2{\epsilon }^{\left(j\right)}-2A_2\left({\epsilon }_t^{(j-1)}\right)-14A_3\left({\epsilon }^{\left(j\right)}\right)\left({\epsilon }_t^{(j-1)}\right)$$

$$+4A_3{\left({\epsilon }_t^{(j-1)}\right)}^2+13A_3{\left({\epsilon }^{\left(j\right)}\right)}^2]+O_3({\epsilon }_t^{(j-1)},{\epsilon }^{\left(j\right)}),$$

(29)

where$h=2({\epsilon }^{\left(j\right)}-{\epsilon }_t^{(j-1)})$.

From (29), we get

$$B^{\left(j\right)}=-[I+2A_2{\epsilon }_t^{(j-1)}-4A_2{\epsilon }^{\left(j\right)}+(16A_2^2-14A_3)\left({\epsilon }_t^{(j-1)}\right)\left({\epsilon }^{\left(j\right)}\right)$$

$$+(16A_2^2-13A_3){\left({\epsilon }^{\left(j\right)}\right)}^2+(4A_2^2-4A_3){\left({\epsilon }_t^{(j-1)}\right)}^2]F^{\prime }{\left(\zeta \right)}^{-1}+O_3({\epsilon }_t^{(j-1)},{\epsilon }^{\left(j\right)}),$$

(30)

and

$$I+B^{\left(j\right)}{F}^{\prime }\left(\zeta \right)\sim -2A_2{\epsilon }_t^{(j-1)}\sim -2A_2^2(I+B^{(j-1)}{F}^{\prime }\left(\zeta \right)){\left({\epsilon }^{(j-1)}\right)}^2.$$

(31)

Scheme 5.

Using (11) and (29), we obtain

$$\frac{[3z^{\left(j\right)}-2t^{(j-1)},z^{\left(j\right)};F]+[2t^{(j-1)}-z^{\left(j\right)},z^{\left(j\right)};F]}{2}=F^{\prime }\left(\zeta \right)[I+2A_2{\epsilon }^{\left(j\right)}+7A_3{\left({\epsilon }^{\left(j\right)}\right)}^2$$

$$+4A_3{\left({\epsilon }_t^{(j-1)}\right)}^2-8A_3\left({\epsilon }_t^{(j-1)}\right)\left({\epsilon }^{\left(j\right)}\right)]+O_3({\epsilon }_t^{(j-1)},{\epsilon }^{\left(j\right)}).$$

(32)

Using (32), we design the following variable parameter

$$B^{\left(j\right)}=-{\left(\frac{[3z^{\left(j\right)}-2t^{(j-1)},z^{\left(j\right)};F]+[2t^{(j-1)}-z^{\left(j\right)},z^{\left(j\right)};F]}{2}\right)}^{-1}$$

$$=-[I-2A_2{\epsilon }^{\left(j\right)}+(4A_2^2-7A_3){\left({\epsilon }^{\left(j\right)}\right)}^2-4A_3{\left({\epsilon }_t^{(j-1)}\right)}^2+8A_3\left({\epsilon }_t^{(j-1)}\right)\left({\epsilon }^{\left(j\right)}\right)]F^{\prime }{\left(\zeta \right)}^{-1}+O_3({\epsilon }_t^{(j-1)},{\epsilon }^{\left(j\right)}),$$

(33)

and

$$I+B^{\left(j\right)}{F}^{\prime }\left(\zeta \right)\sim 2A_2{\epsilon }^{\left(j\right)}.$$

(34)

Scheme 6.

Using (11) and (25), we get

$$B^{\left(j\right)}=-{\left(\frac{[2t^{(j-1)}-z^{\left(j\right)},z^{\left(j\right)};F]+2[2z^{\left(j\right)}-t^{(j-1)},z^{\left(j\right)};F]}{3}\right)}^{-1}$$

(35)

and

$$I+B^{\left(j\right)}{F}^{\prime }\left(\zeta \right)\sim 2A_2{\epsilon }^{\left(j\right)}.$$

(36)

Scheme 7.

Using (20) and (25), we design

$$B^{\left(j\right)}=-{\left(\frac{[2t^{(j-1)}-z^{\left(j\right)},t^{(j-1)};F]+3[2z^{\left(j\right)}-t^{(j-1)},z^{\left(j\right)};F]}{4}\right)}^{-1}$$

(37)

and

$$I+B^{\left(j\right)}{F}^{\prime }\left(\zeta \right)\sim 2A_2{\epsilon }^{\left(j\right)}.$$

(38)

The first-order divided difference operators (11), (21), (25) and (29) are called Kurchatov-type divided difference operator. Replacing parameter B of method (6) with Schemes 1–7, respectively, we get seven new iterative methods with memory as follows:

$$\left\{\begin{array}{c}{s}^{\left(j\right)} =z^{\left(j\right)}-{[2t^{(j-1)}-z^{\left(j\right)},z^{\left(j\right)};F]}^{-1}F\left(z^{\left(j\right)}\right),\\ t^{\left(j\right)} =z^{\left(j\right)}-{[s^{\left(j\right)},z^{\left(j\right)};F]}^{-1}F\left(z^{\left(j\right)}\right),\\ z^{(j+1)}=t^{\left(j\right)}-{[s^{\left(j\right)},t^{\left(j\right)};F]}^{-1}F\left(t^{\left(j\right)}\right).\end{array}\right.$$

(39)

$$\left\{\begin{array}{c}{s}^{\left(j\right)} =z^{\left(j\right)}-{[2t^{(j-1)}-z^{\left(j\right)},t^{(j-1)};F]}^{-1}F\left(z^{\left(j\right)}\right),\\ t^{\left(j\right)} =z^{\left(j\right)}-{[s^{\left(j\right)},z^{\left(j\right)};F]}^{-1}F\left(z^{\left(j\right)}\right),\\ z^{(j+1)}=t^{\left(j\right)}-{[s^{\left(j\right)},t^{\left(j\right)};F]}^{-1}F\left(t^{\left(j\right)}\right).\end{array}\right.$$

(40)

$$\left\{\begin{array}{c}{s}^{\left(j\right)} =z^{\left(j\right)}-{[2z^{\left(j\right)}-t^{(j-1)},z^{\left(j\right)};F]}^{-1}F\left(z^{\left(j\right)}\right),\\ t^{\left(j\right)} =z^{\left(j\right)}-{[s^{\left(j\right)},z^{\left(j\right)};F]}^{-1}F\left(z^{\left(j\right)}\right),\\ z^{(j+1)}=t^{\left(j\right)}-{[s^{\left(j\right)},t^{\left(j\right)};F]}^{-1}F\left(t^{\left(j\right)}\right).\end{array}\right.$$

(41)

$$\left\{\begin{array}{c}{s}^{\left(j\right)} =z^{\left(j\right)}-{[3z^{\left(j\right)}-2t^{(j-1)},z^{\left(j\right)};F]}^{-1}F\left(z^{\left(j\right)}\right),\\ t^{\left(j\right)} =z^{\left(j\right)}-{[s^{\left(j\right)},z^{\left(j\right)};F]}^{-1}F\left(z^{\left(j\right)}\right),\\ z^{(j+1)}=t^{\left(j\right)}-{[s^{\left(j\right)},t^{\left(j\right)};F]}^{-1}F\left(t^{\left(j\right)}\right).\end{array}\right.$$

(42)

$$\left\{\begin{array}{c}{s}^{\left(j\right)} =z^{\left(j\right)}-{\left(\frac{[3z^{\left(j\right)}-2t^{(j-1)},z^{\left(j\right)};F]+[2t^{(j-1)}-z^{\left(j\right)},z^{\left(j\right)};F]}{2}\right)}^{-1}F\left(z^{\left(j\right)}\right),\\ t^{\left(j\right)} =z^{\left(j\right)}-{[s^{\left(j\right)},z^{\left(j\right)};F]}^{-1}F\left(z^{\left(j\right)}\right),\\ z^{(j+1)}=t^{\left(j\right)}-{[s^{\left(j\right)},t^{\left(j\right)};F]}^{-1}F\left(t^{\left(j\right)}\right).\end{array}\right.$$

(43)

$$\left\{\begin{array}{c}{s}^{\left(j\right)} =z^{\left(j\right)}-{\left(\frac{[2t^{(j-1)}-z^{\left(j\right)},z^{\left(j\right)};F]+2[2z^{\left(j\right)}-t^{(j-1)},z^{\left(j\right)};F]}{3}\right)}^{-1}F\left(z^{\left(j\right)}\right),\\ t^{\left(j\right)} =z^{\left(j\right)}-{[s^{\left(j\right)},z^{\left(j\right)};F]}^{-1}F\left(z^{\left(j\right)}\right),\\ z^{(j+1)}=t^{\left(j\right)}-{[s^{\left(j\right)},t^{\left(j\right)};F]}^{-1}F\left(t^{\left(j\right)}\right).\end{array}\right.$$

(44)

$$\left\{\begin{array}{c}{s}^{\left(j\right)} =z^{\left(j\right)}-{\left(\frac{[2t^{(j-1)}-z^{\left(j\right)},t^{(j-1)};F]+3[2z^{\left(j\right)}-t^{(j-1)},z^{\left(j\right)};F]}{4}\right)}^{-1}F\left(z^{\left(j\right)}\right),\\ t^{\left(j\right)} =z^{\left(j\right)}-{[s^{\left(j\right)},z^{\left(j\right)};F]}^{-1}F\left(z^{\left(j\right)}\right),\\ z^{(j+1)}=t^{\left(j\right)}-{[s^{\left(j\right)},t^{\left(j\right)};F]}^{-1}F\left(t^{\left(j\right)}\right).\end{array}\right.$$

(45)

The iterative process of the new methods (39)–(45) can be converted to solve linear systems. For example, method (39) can be written by

$$\left\{\begin{array}{c}[2t^{(j-1)}-z^{\left(j\right)},z^{\left(j\right)};F]{\gamma }_1=-F\left(z^{\left(j\right)}\right),s^{\left(j\right)}={\gamma }_1+z^{\left(j\right)},\\ [s^{\left(j\right)},z^{\left(j\right)};F]{\gamma }_2=-F\left(z^{\left(j\right)}\right),t^{\left(j\right)}=z^{\left(j\right)}+{\gamma }_2,\\ [s^{\left(j\right)},t^{\left(j\right)};F]{\gamma }_3=-F\left(t^{\left(j\right)}\right),z^{(j+1)}=t^{\left(j\right)}+{\gamma }_3.\end{array}\right.$$

(46)

Remark 1.

Schemes 1–4 have the same error relations. So, methods (39)–(42) have the same convergence order. Schemes 5–7 have different schemes with the same error relations, methods (43)–(45) have the same convergence order.

The convergence orders of new schemes (39)–(42) are analyzed in the following result.

Theorem 1.

Let $\zeta \in {\mathbb{R}}^n$ be a zero of $F:D\subset {\mathbb{R}}^n\to {\mathbb{R}}^n$ that is sufficiently differentiable function in an open neighborhood D of ζ. Suppose that initial guess $z^{\left(0\right)}$ is close enough to ζ. Then, iterative methods (39)–(42) have the convergence order $2+\sqrt{5}\approx 4.236$ and the order of convergence of methods (43)–(45) is 5.

Proof. 

Let $h^{\left(j\right)}=I+B^{\left(j\right)}{F}^{\prime }\left(\zeta \right)$ in (19), then

$$h^{\left(j\right)}\sim 2A_2^2(I+B^{(j-1)}{F}^{\prime }\left(\zeta \right)){\left({\epsilon }^{(j-1)}\right)}^2\sim 2A_2^2{h}^{(j-1)}{\left({\epsilon }^{(j-1)}\right)}^2$$

$$\sim 4A_2^4\left(h^{(j-2)}\right){\left({\epsilon }^{(j-2)}\right)}^2{\left({\epsilon }^{(j-1)}\right)}^2$$

$$\sim 2^j{A}_2^{2j}\left(h^{\left(0\right)}\right){\left({\epsilon }^{\left(0\right)}\right)}^2{\left({\epsilon }^{\left(1\right)}\right)}^2{\left({\epsilon }^{\left(2\right)}\right)}^2\cdots {\left({\epsilon }^{(j-2)}\right)}^2{\left({\epsilon }^{(j-1)}\right)}^2.$$

(47)

Suppose that the iterative sequence $\left\{z^{\left(j\right)}\right\}$ has the following error relation

$${\epsilon }^{(j+1)}\sim D_{j+1}{\left({\epsilon }^{\left(0\right)}\right)}^{r_{j+1}},0\le j\le n,$$

(48)

where ${\epsilon }^{\left(0\right)}=z^{\left(0\right)}-\zeta$, ${\epsilon }^{(k+1)}=z^{(k+1)}-\zeta$ and $D_{j+1}$ is an asymptotic error constant.

From (7), (47) and (48), we get

$${\epsilon }^{(j+1)}\sim A_2^2{(I+B^{\left(j\right)}{F}^{\prime }\left(\zeta \right))}^2{\left({\epsilon }^{\left(j\right)}\right)}^3$$

$$\sim A_2^2{\left(h^{\left(j\right)}\right)}^2{\left({\epsilon }^{\left(j\right)}\right)}^3$$

$$\sim 2^{2j}{A}_2^{4j+2}{h}_0^2{\left({\epsilon }^{\left(0\right)}\right)}^4{\left(D_1{\left({\epsilon }^{\left(0\right)}\right)}^{r_1}\right)}^4{\left(D_2{\left({\epsilon }^{\left(0\right)}\right)}^{r_2}\right)}^4\cdots {\left(D_{j-2}{\left({\epsilon }^{\left(0\right)}\right)}^{r_{j-2}}\right)}^4{\left(D_{j-1}{\left({\epsilon }^{\left(0\right)}\right)}^{r_{j-1}}\right)}^4{\left(D_j{\left({\epsilon }^{\left(0\right)}\right)}^{r_j}\right)}^3.$$

(49)

Comparing the error ${\epsilon }^{\left(0\right)}$ in (48) and (49), we get

$$r_{j+1}=4+4r_1+4r_2+\cdots +4r_{j-2}+4r_{j-1}+3r_j.$$

(50)

From (50), we have

$$r_{j+1}=4r_j+r_{j-1}.$$

(51)

Letting $\underset{j\to \infty }{lim}(r_{j+1}/r_j)=\underset{j\to \infty }{lim}(r_j/r_{j-1})=R$ and dividing (51) by $r_j$, we get

$$R=4+\frac{1}{R}.$$

(52)

The solution of Equation (52) is $2+\sqrt{5}$. Therefore, method (39) with memory has order $R=2+\sqrt{5}\approx 4.236$. The variable parameters (10), (20), (24) and (28) have the same error relation, so methods (39)–(42) have the same convergence order.

From (7) and (34), we get

$${\epsilon }^{(j+1)}\sim A_2^2{(I+B^{\left(j\right)}{F}^{\prime }\left(\zeta \right))}^2{\left({\epsilon }^{\left(j\right)}\right)}^3\sim 4A_2^4{\left({\epsilon }^{\left(j\right)}\right)}^5.$$

(53)

Therefore, method (43) with memory has convergence order five. The variable parameters Schemes 5–7 have the same error relation, so methods (43)–(45) have the same convergence order. □

3. Numerical Results

Our methods (39)–(45) are compared with Petković’s method (5) and Chicharro’s method (8) for solving nonlinear systems and ODEs. For numerical experiments, Maple 14 with 2048 digits is used. The stopping criterion $\left|\right|z^{\left(j\right)}-z^{(j-1)}\left|\right|<{10}^{-100}$ is used in numerical algorithms. The initial parameter $B^{\left(0\right)}$ is the identity matrix.

Table 1. Convergence behavior of iterative methods for Example 1.

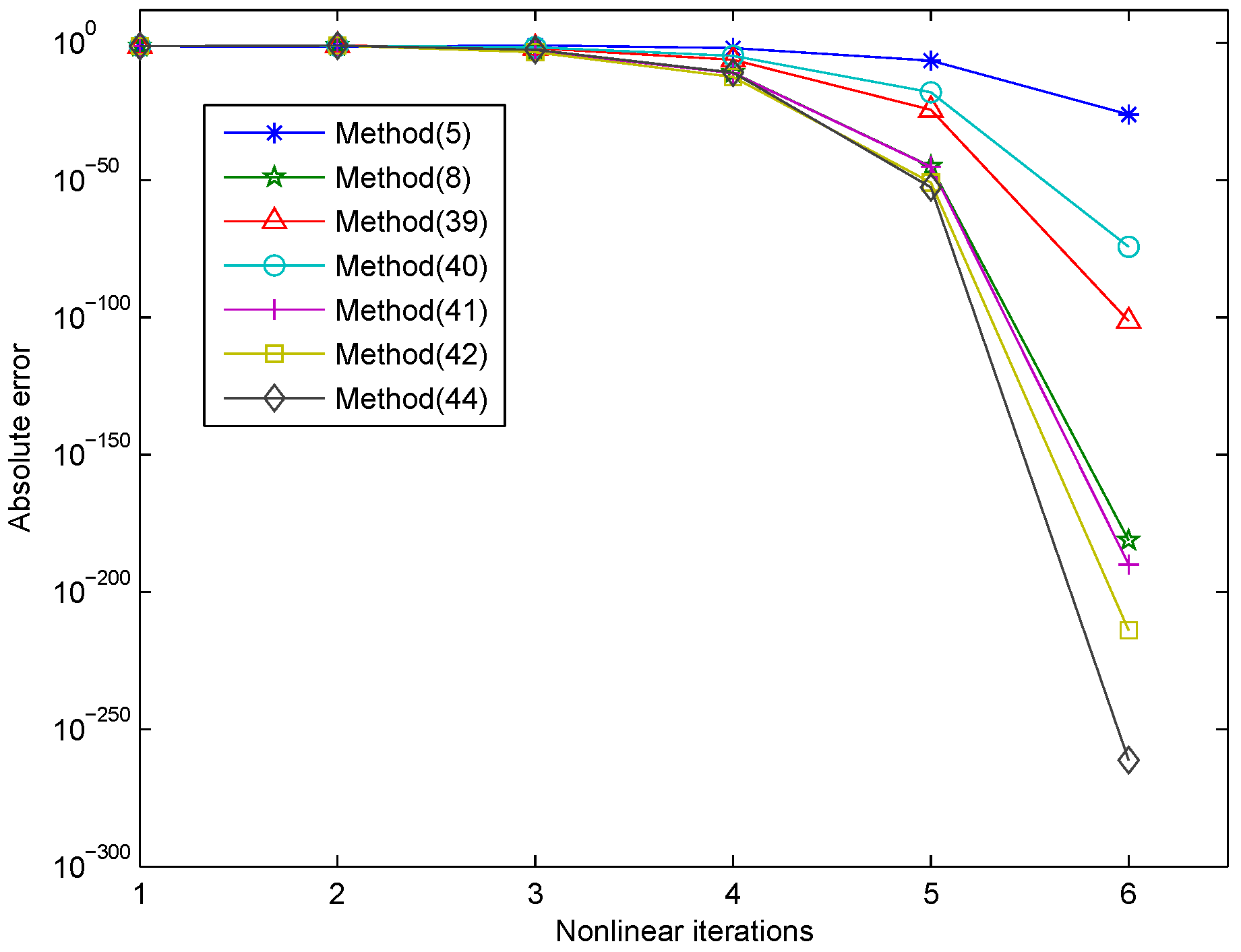
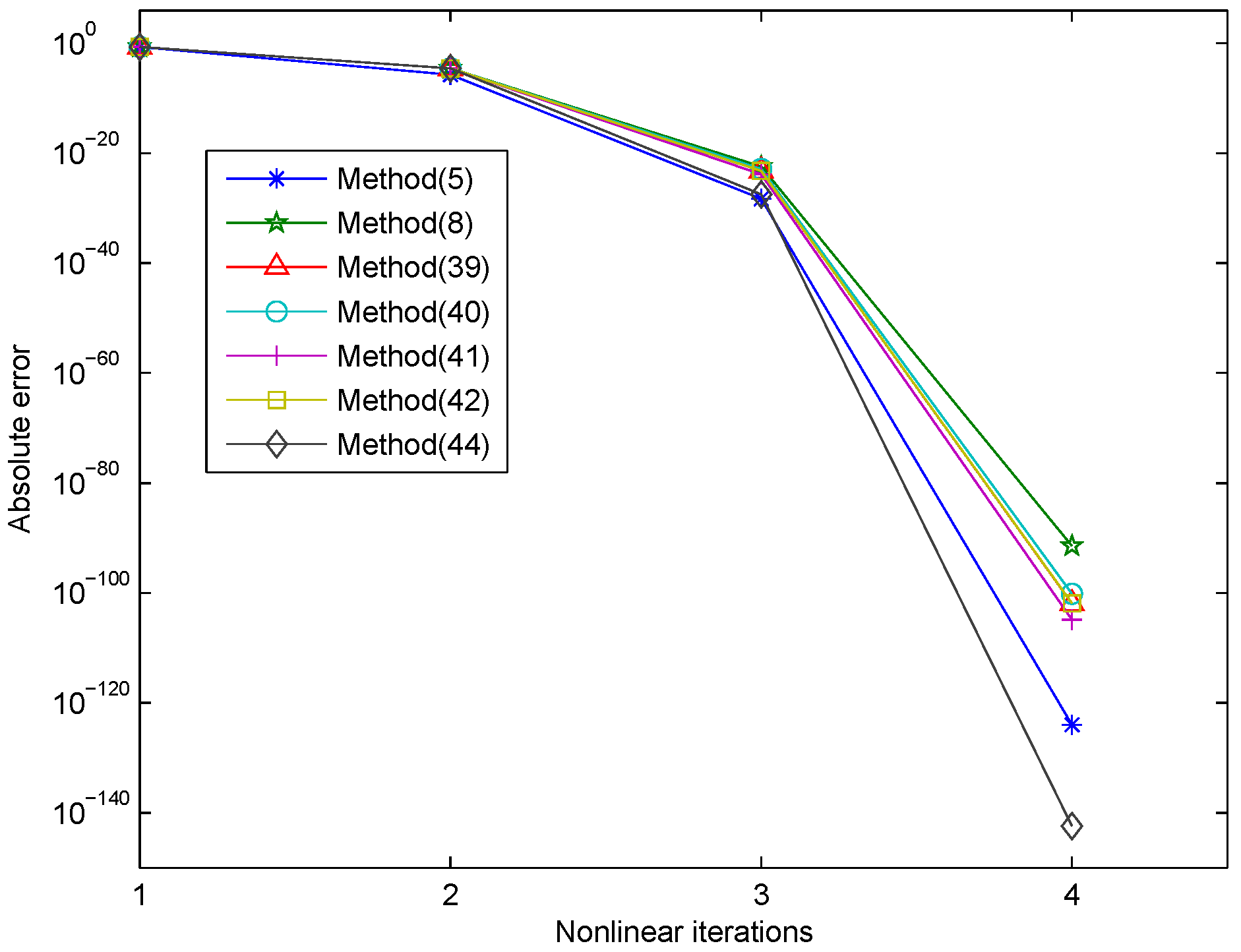
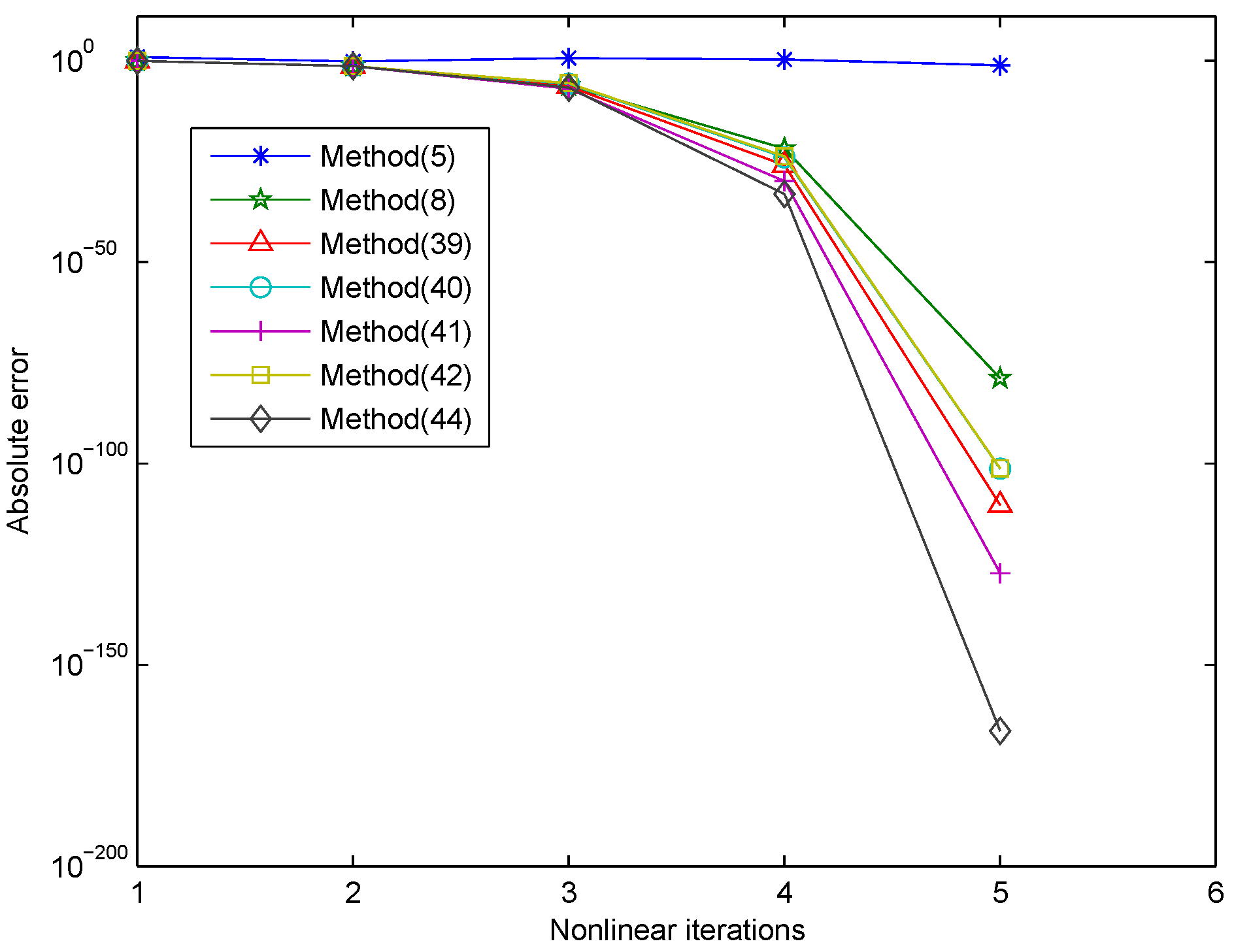
Methods	NI	EV	EF	ACOC	e-Time
(5)	7	4.577 × ${10}^{-103}$	1.648 × ${10}^{-461}$	4.22419	15.537
(8)	6	6.536 × ${10}^{-182}$	5.328 × ${10}^{-726}$	3.97864	15.428
(39)	6	5.041 × ${10}^{-102}$	6.013 × ${10}^{-427}$	4.23649	15.943
(40)	7	1.645 × ${10}^{-313}$	1.562 × ${10}^{-1322}$	4.23601	18.111
(41)	6	9.817 × ${10}^{-191}$	3.228 × ${10}^{-803}$	4.23669	14.180
(42)	6	1.114 × ${10}^{-214}$	3.614 × ${10}^{-904}$	4.23381	15.319
(43)	6	5.202 × ${10}^{-262}$	1.988 × ${10}^{-1304}$	5.00000	20.280
(44)	6	6.070 × ${10}^{-262}$	4.302 × ${10}^{-1304}$	5.00000	20.623
(45)	6	5.833 × ${10}^{-262}$	3.526 × ${10}^{-1304}$	5.00000	19.000

,

Table 2. Convergence behavior of iterative methods for Example 2.

Methods	NI	EV	EF	ACOC	e-Time
(5)	12	5.059 × ${10}^{-417}$	3.088 × ${10}^{-1759}$	4.23598	39.998
(8)	7	3.408 × ${10}^{-299}$	3.497 × ${10}^{-1191}$	3.99832	12.776
(39)	7	2.323 × ${10}^{-288}$	9.941 × ${10}^{-1214}$	4.23562	14.242
(40)	7	2.484 × ${10}^{-298}$	1.108 × ${10}^{-1255}$	4.23561	14.851
(41)	6	8.864 × ${10}^{-134}$	2.159 × ${10}^{-559}$	4.24093	10.966
(42)	6	1.014 × ${10}^{-130}$	5.896 × ${10}^{-546}$	4.23542	10.764
(43)	7	7.681 × ${10}^{-176}$	2.609 × ${10}^{-870}$	4.99965	25.256
(44)	6	3.898 × ${10}^{-472}$	1.470 × ${10}^{-2046}$	5.00000	14.492
(45)	6	1.791 × ${10}^{-386}$	1.796 × ${10}^{-1923}$	5.00000	13.135

,

Table 3. Convergence behavior of iterative methods for Example 3.

Methods	NI	EV	EF	ACOC	e-Time
(5)	4	9.478 × ${10}^{-125}$	1.079 × ${10}^{-530}$	4.23909	1.154
(8)	5	6.828 × ${10}^{-371}$	1.072 × ${10}^{-1483}$	4.03695	1.669
(39)	4	1.172 × ${10}^{-102}$	1.181 × ${10}^{-436}$	4.20358	1.294
(40)	4	6.850 × ${10}^{-101}$	7.002 × ${10}^{-429}$	4.20758	1.372
(41)	4	1.353 × ${10}^{-105}$	1.369 × ${10}^{-449}$	4.19837	1.372
(42)	4	1.329 × ${10}^{-102}$	2.014 × ${10}^{-436}$	4.20446	1.357
(43)	4	3.818 × ${10}^{-143}$	2.243 × ${10}^{-718}$	5.00784	1.700
(44)	4	1.427 × ${10}^{-143}$	1.637 × ${10}^{-720}$	5.00409	1.794
(45)	4	1.841 × ${10}^{-143}$	5.854 × ${10}^{-720}$	5.00505	1.762

and

Table 4. Convergence behavior of iterative methods for Example 4.

Methods	NI	EV	EF	ACOC	e-Time
(5)	8	1.932 × ${10}^{-132}$	3.291 × ${10}^{-559}$	4.26779	9.750
(8)	6	6.690 × ${10}^{-282}$	1.315 × ${10}^{-1002}$	3.54607	9.094
(39)	5	4.488 × ${10}^{-111}$	4.446 × ${10}^{-468}$	4.32150	7.410
(40)	5	4.697 × ${10}^{-102}$	1.137 × ${10}^{-429}$	4.23216	7.488
(41)	5	5.905 × ${10}^{-128}$	4.505 × ${10}^{-540}$	4.24952	7.534
(42)	5	5.803 × ${10}^{-102}$	2.515 × ${10}^{-429}$	4.27379	7.566
(43)	5	1.956 × ${10}^{-146}$	6.081 × ${10}^{-730}$	5.04097	9.687
(44)	5	3.845 × ${10}^{-167}$	1.974 × ${10}^{-833}$	5.05028	9.672
(45)	5	1.104 × ${10}^{-121}$	7.583 × ${10}^{-517}$	4.29476	9.703

give the numerical results and the following information: NI means the number of iterations, EF means function values at the last step, EV represents the error values of $\left|\right|z^{\left(j\right)}-z^{(j-1)}\left|\right|$, $e-Time$ represents the CPU time (in second) and ACOC [20] is the approximated computational order of convergence. Figure 1, Figure 2, Figure 3 and Figure 4 show the iterative processes of different methods for solving nonlinear systems.

Example 1.

$$1-2\left(\sum _{j=1,j\ne i}^{15}{z}_j^2\right)+arctan{z}_i=0, i=1,2,\cdots 15.$$

The solution $\zeta \approx {\{0.2074, \cdots ,0.2074\}}^T$ is obtained by the initial guess $z^{\left(0\right)}={\{0.038,\cdots 0.038\}}^T.$

The iterative processes of different methods for solving Example 1 are shown by Figure 1. Figure 1 shows that our method (44) has higher computational accuracy than other methods.

Example 2.

$$z_i-cos(2z_i-\sum _{j=1}^{15}{z}_j)=0,i=1,2,\cdots 15,$$

The solution $\zeta \approx {\{0.939822,0.939822\cdots ,0.939822\}}^T$ is obtained by initial guess $z^{\left(0\right)}={\{0.5,0.5,\cdots ,0.5\}}^T$.

The iterative processes of different methods for solving Example 2 are shown by Figure 2. Figure 2 shows that our method (44) has higher computational accuracy than other methods. Methods (41) and (42) have the similar convergence behavior.

Example 3.

Boundary-value problem [21]:

$$\begin{array}{c}{u}^{″}\left(z\right)+e^{u\left(z\right)}=0,z\in [0,1],\\ u\left(0\right)=0,u\left(1\right)=1.\end{array}$$

Using difference method, the second derivative of this problem is discretized by

$$\begin{array}{c}{u}_j^{″}=\frac{u_{j+1}-2u_j+u_{j-1}}{h^2},j=1,2,3,\cdots ,n-1,\end{array}$$

The interval $[0,1]$ is divided into n smaller intervals with end points $0=z_0<z_1<\cdots <z_{n-1}<z_n=1$. The partition is regular, this is ▵$z_j=1/n$ for all j. We obtain the nonlinear systems as follows:

$$\begin{array}{c}{u}_{j-1}-2u_j+u_{j+1}+h^2{e}^{u_j}=0,j=1,2,3,\dots ,n-1.\end{array}$$

For $n=6,$ the solution ${\{0.07748,0.12494,0.14093,\dots ,0.07748\}}^T$ is founded by the initial value is $z^{\left(0\right)}={(0.3,\cdots 0.3)}^T.$ The numerical results are displayed in Table 3.

The iterative processes of different methods for solving Example 3 are shown by Figure 3. Figure 3 show that our method (44) has higher computational accuracy than other methods. Methods (39), (40) and (41) have the similar convergence behavior for Example 3.

Example 4.

Boundary-value problem [22]:

$$\begin{array}{c}{u}^{″}\left(z\right)-u{\left(z\right)}^3-sin\left(u^{\prime }{\left(z\right)}^2\right)=0,z\in [0,1],\\ u\left(0\right)=0,u\left(1\right)=1.\end{array}$$

The first derivative is discretized by

$$\begin{array}{c}{u}_j^{\prime }=\frac{u_{j+1}-u_{j-1}}{2h},j=1,2,3,\cdots ,n-1.\end{array}$$

We get the following nonlinear systems by using the same discretization method as Example 3

$$\begin{array}{c}{u}_{j-1}-2u_j+u_{j+1}-h^2{u}_j^3-h^{2}sin\left({\left(\frac{u_{j-1}-u_{j+1}}{2h}\right)}^2\right)=0,j=1,2,3,\dots ,n-1.\end{array}$$

For $n=8$, the solution ${\{0.0846,0.1767,0.2776,\dots ,0.8159\}}^T$ is founded by the initial guess $z^{\left(0\right)}={(0.97,\cdots 0.97)}^T.$ Table 4 shows the numerical results.

Table 1, Table 2, Table 3 and Table 4 show that our iterative methods (43)–(45) with memory are superior to Petković’s method (5) and Chicharro’s method (8) with memory in terms of convergence order and iterative methods (40)–(41) cost less computing time than other methods. Methods (43)–(45) have the similar computational accuracy, so we omit methods (43) and (45) in Figure 1, Figure 2, Figure 3 and Figure 4. Figure 1, Figure 2, Figure 3 and Figure 4 show that our methods (44) have higher computational accuracy than other methods.

The iterative processes of different methods for solving Example 4 are shown by Figure 4. Figure 4 shows that our method (44) has higher computational accuracy than other methods.

4. Conclusions

In this paper, we proposed four new Kurchatov-type first-order divided operators. Using these new Kurchatov-type first-order divided operators, we designed some new accelerating parameters and constructed seven derivative-free iterative methods with memory for solving nonlinear systems. The local convergence order of Chicharro’s method without memory (6) was improved from 3 to $2+\sqrt{5}\approx 4.236$ and 5, respectively. Numerical results support the theoretical results. We should note that the main objective of this paper was to develop a high-order method and prove the local convergence order of new methods. The initial approximation must be close enough to zero of the nonlinear function. If the initial approximation is far from the zero of nonlinear function, then the iterative sequence generated by iterative method converges slowly or diverges. Therefore, the choice of good initial approximations is very important to iterative methods. Some strategies for finding sufficiently good initial approximation have been proposed [23,24,25]. Finding good initial approximation for multipoint iterative method needs further research.