Stationary Distribution and Extinction in a Stochastic SIQR Epidemic Model Incorporating Media Coverage and Markovian Switching
Abstract
:1. Introduction
2. Preliminaries
3. Existence and Uniqueness of the Global Positive Solution
4. Existence of Ergodic Stationary Distribution of Model (2)
5. Extinction of Model (2)
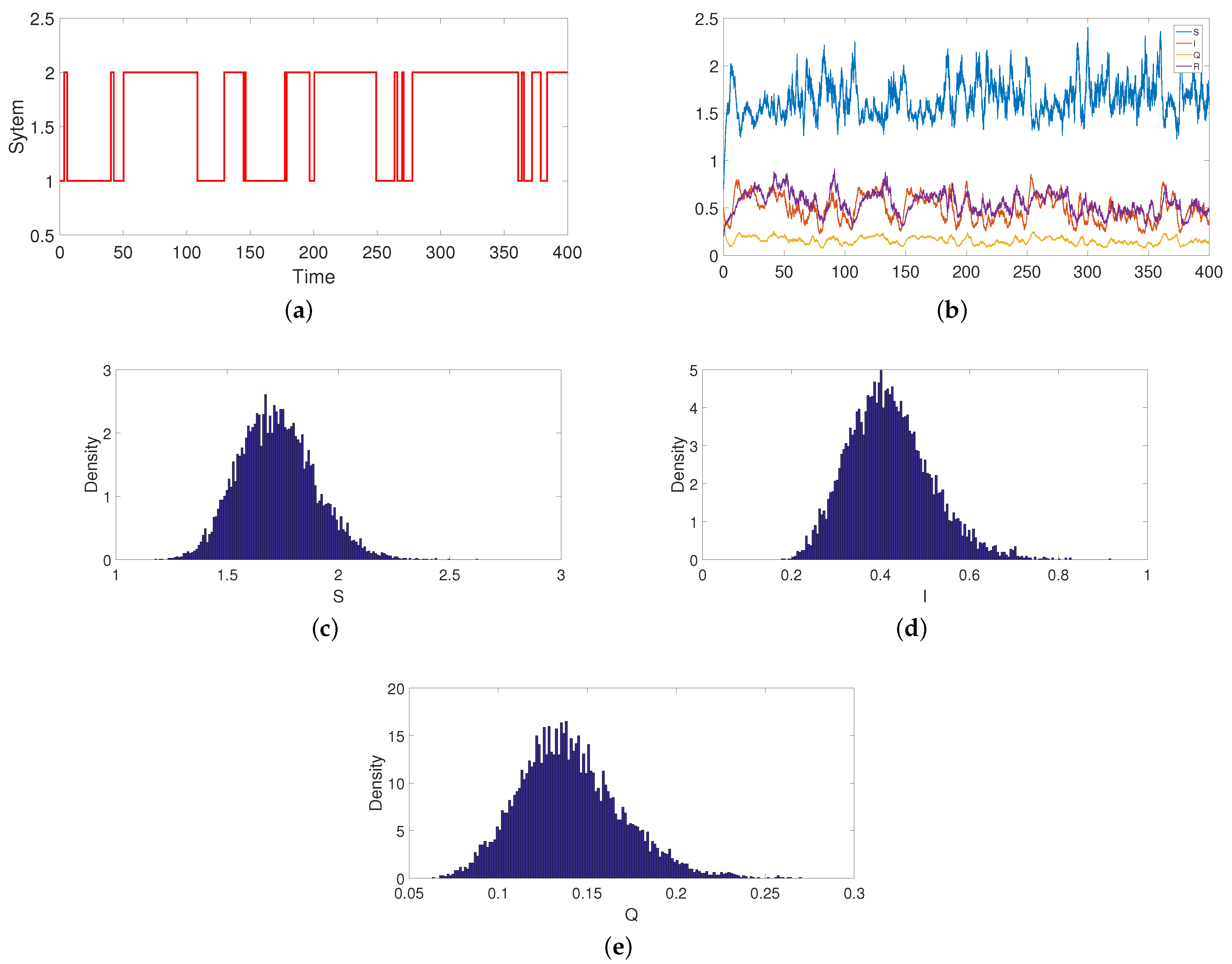
6. Numerical Simulations
7. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ariful Kabir, K.M.; Kugaa, K.; Tanimotoc, J. Analysis of SIR epidemic model with information spreading of awareness. Chaos Solitons Fractals 2019, 119, 118–125. [Google Scholar] [CrossRef]
- Chen, F. A susceptible-infected epidemic model with voluntary vaccinations. J. Math. Biol. 2006, 53, 253–272. [Google Scholar] [CrossRef] [PubMed]
- Cao, X.; Jin, Z. Epidemic threshold and ergodicity of an SIS model in switched networks. J. Math. Anal. Appl. 2019, 479, 1182–1194. [Google Scholar] [CrossRef]
- Guo, X.; Luo, J. Stationary distribution and extinction of SIR model with nonlinear incidence under Markovian switching. Phys. A Stat. Mech. Its Appl. 2018, 505, 471–481. [Google Scholar] [CrossRef]
- Li, J.; Ma, Z. Qualitative analysis of SIS epidemic model with vaccination and varying total population size. Math. Comput. Model. 2002, 35, 1235–1243. [Google Scholar] [CrossRef]
- Li, G.; Xu, X.; Zhang, M.; Liu, Q. Densely connected network for impulse noise removal. Pattern Anal. Appl. 2020, 23, 1263–1275. [Google Scholar] [CrossRef]
- Meng, X.; Chen, L.; Wu, B. A delay SIR epidemic model with pulse vaccination and incubation times. Nonlinear Anal. Real World Appl. 2010, 11, 88–98. [Google Scholar] [CrossRef]
- Shim, E.; Feng, Z.; Martcheva, M.; Chavez, C. An age-structured epidemic model of rotavirus with vaccination. J. Math. Biol. 2006, 53, 719–746. [Google Scholar] [CrossRef]
- Xu, P.; Wu, S.; Huang, J. Ergodicity of stochastic damped higher-order KdV equation driven by white noise. Appl. Math. Lett. 2020, 110, 106575. [Google Scholar] [CrossRef]
- Zhang, Y.; Fan, K.; Gao, S.; Liu, Y.; Chen, S. Ergodic stationary distribution of a stochastic SIRS epidemic model incorporating media coverage and saturated incidence rate. Phys. A Stat. Mech. Its Appl. 2019, 514, 671–685. [Google Scholar] [CrossRef]
- Zhao, Y.; Jiang, D. The threshold of a stochastic SIS epidemic model with vaccination. Appl. Math. Comput. 2014, 243, 718–727. [Google Scholar] [CrossRef]
- Cui, J.; Tao, X.; Zhu, H. An SIS infection model incorporating media coverage. Rocky Mt. J. Math. 2008, 38, 1323–1334. [Google Scholar] [CrossRef]
- Ma, M.; Liu, S.; Li, J. Does media coverage influence the spread of drug addiction? Commun. Nonlinear Sci. Numer. Simul. 2017, 50, 169–179. [Google Scholar] [CrossRef]
- Misra, A.; Sharma, A.; Shukla, J. Modeling and analysis of effects of awraencess programs by media on the spread of infectious diaeases. Math. Comput. Model. 2011, 53, 1221–1228. [Google Scholar] [CrossRef]
- Zhang, T.; Meng, X. Stability analysis of a chemostat model with maintenance energy. Appl. Math. Lett. 2017, 68, 1–7. [Google Scholar] [CrossRef]
- Liu, M.; He, X.; Yu, J. Dynamics of a stochastic regime-switching predator-prey model with harvesting and distributed delays. Nonlinear Anal. Hybrid Syst. 2018, 28, 87–104. [Google Scholar] [CrossRef]
- Liu, Q.; Jiang, D.; Shi, N. Threshold behavior in a stochastic SIQR epidemic model with standard and regime switching. Appl. Math. Comput. 2018, 316, 310–325. [Google Scholar]
- Lv, X.; Wang, L.; Meng, X. Global analysis of a new nonlinear stochastic differential competition system with impulsive effect. Adv. Differ. Equ. 2017, 2017, 296. [Google Scholar] [CrossRef] [Green Version]
- Qi, H.; Zhang, S.; Meng, X.; Dong, H. Periodic solution and ergodic stationary distribution of two stochastic SIQS epidemic systems. Phys. A Stat. Mech. Its Appl. 2018, 508, 223–241. [Google Scholar] [CrossRef]
- Yu, X.; Sun, Y.; Zhang, T. Persistence and ergodicity of a stochastic single species model with Allee effect under regime switching. Commun. Nonlinear Sci. Numer. Simul. 2018, 59, 359–374. [Google Scholar] [CrossRef]
- Can, C.; Zhang, W. On observability and detectability of continuous-time stochastic Markov jump systems. J. Syst. Sci. Complex. 2015, 28, 830–847. [Google Scholar]
- Khasminskii, R. Stochastic Stability of Differential Equation; Springer: Berlin, Germany, 2011. [Google Scholar]
- Ma, H.; Jia, Y. Stability analysis for stochastics differential equations with infinite Markovian switchings. J. Math. Anal. Appl. 2016, 435, 593–605. [Google Scholar] [CrossRef]
- Lipster, R. A strong law of large numbers for local martingales. Stochastics 1980, 3, 217–228. [Google Scholar]
- Mao, X. Stationary distribution of stochastic population systems. Syst. Control Lett. 2011, 60, 398–405. [Google Scholar] [CrossRef] [Green Version]
- Mao, X.; Marion, G.; Renshaw, E. Environmental brownian noise suppresses explosions in population dynamics. Stoch. Process. Appl. 2002, 97, 95–110. [Google Scholar] [CrossRef]
- Kabir, K.A.; Tanimoto, J. Analysis of epidemic outbreaks in two-layer networks with different structures for information spreading and disease diffusion. Commun. Nonlinear Sci. Numer. Simul. 2019, 72, 565–574. [Google Scholar] [CrossRef]
- Kabir, K.A.; Tanimoto, J. Vaccination strategies in a two-layer SIR/V–UA epidemic model with costly information and buzz effect. Commun. Nonlinear Sci. Numer. Simul. 2019, 76, 92–108. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, Y.; Jiao, J.; Zhang, Q.; Zhang, Y.; Ren, X. Stationary Distribution and Extinction in a Stochastic SIQR Epidemic Model Incorporating Media Coverage and Markovian Switching. Symmetry 2021, 13, 1122. https://doi.org/10.3390/sym13071122
Ding Y, Jiao J, Zhang Q, Zhang Y, Ren X. Stationary Distribution and Extinction in a Stochastic SIQR Epidemic Model Incorporating Media Coverage and Markovian Switching. Symmetry. 2021; 13(7):1122. https://doi.org/10.3390/sym13071122
Chicago/Turabian StyleDing, Yanlin, Jianjun Jiao, Qianhong Zhang, Yongxin Zhang, and Xinzhi Ren. 2021. "Stationary Distribution and Extinction in a Stochastic SIQR Epidemic Model Incorporating Media Coverage and Markovian Switching" Symmetry 13, no. 7: 1122. https://doi.org/10.3390/sym13071122
APA StyleDing, Y., Jiao, J., Zhang, Q., Zhang, Y., & Ren, X. (2021). Stationary Distribution and Extinction in a Stochastic SIQR Epidemic Model Incorporating Media Coverage and Markovian Switching. Symmetry, 13(7), 1122. https://doi.org/10.3390/sym13071122




