A Special Multigrid Strategy on Non-Uniform Grids for Solving 3D Convection–Diffusion Problems with Boundary/Interior Layers
Abstract
:1. Introduction
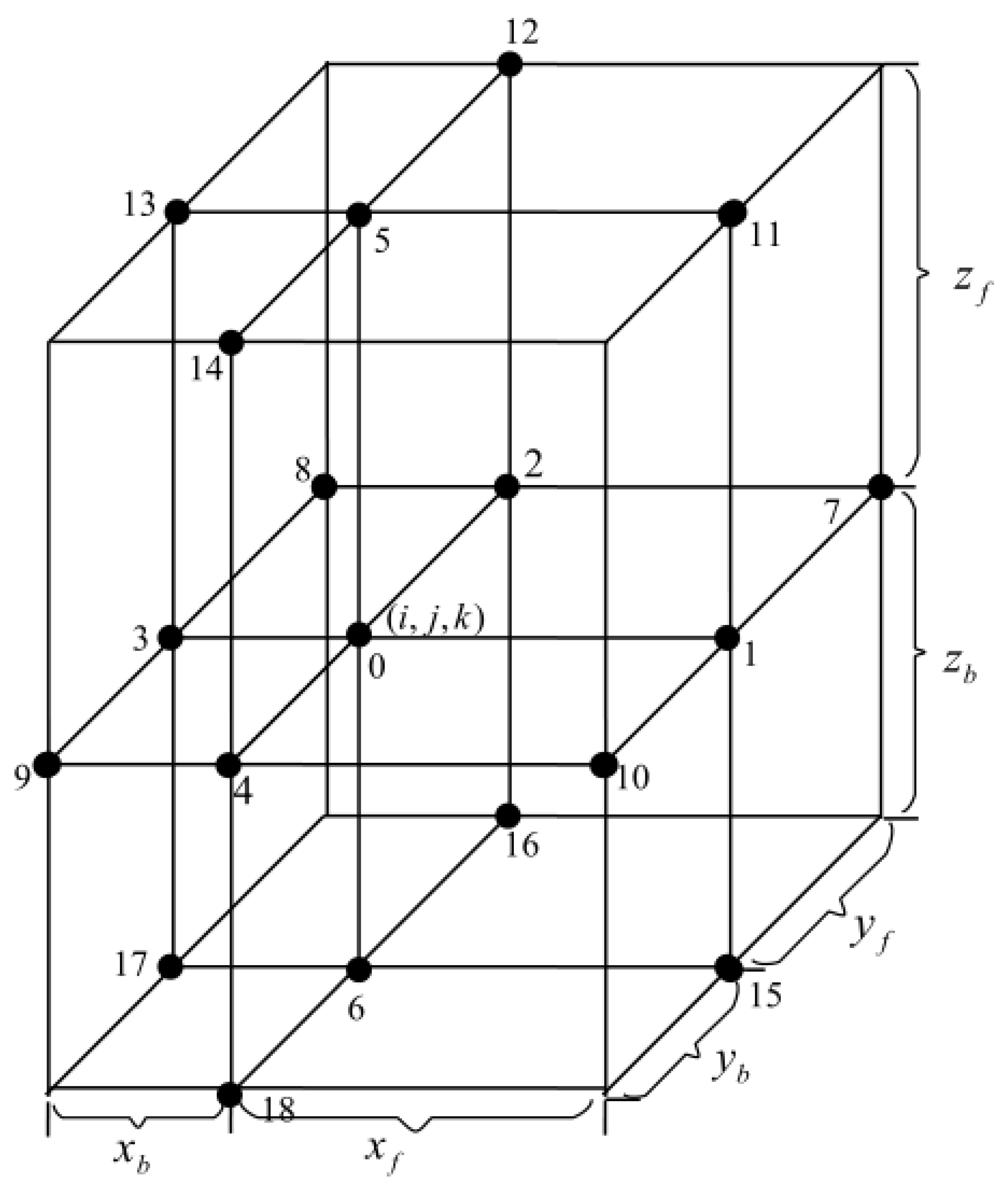
2. HOC Scheme on Non-Uniform Grids
3. Partial Semi-Coarsening Multigrid Method
3.1. Restriction Operator
3.2. Interpolation Operator
3.3. Relaxation Operator
4. Numerical Experiments
4.1. Problem 1
4.2. Problem 2
4.3. Problem 3
4.4. Problem 4
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 2D | two-dimensional |
| 3D | three-dimensional |
| HOC | high-order compact |
| unknown function | |
| p | convective coefficient on the x-axis |
| q | convective coefficient on the y-axis |
| r | convective coefficient on the z-axis |
| f | the forcing function |
| x | spatial coordinate on the x-axis |
| y | spatial coordinate on the y-axis |
| z | spatial coordinate on the z-axis |
| computational domain | |
| domain boundary | |
| CPU | computing time |
| computational domain on the x-axis, | |
| computational domain on the y-axis, | |
| computational domain on the z-axis, | |
| discrete point coordinate on the x-axis | |
| discrete point coordinate on the y-axis | |
| discrete point coordinate on the z-axis | |
| number of discrete grids on the x-axis | |
| number of discrete grids on the y-axis | |
| number of discrete grids on the z-axis | |
| i | discrete grid index on the x-axis on the fine grid |
| j | discrete grid index on the y-axis on the fine grid |
| k | discrete grid index on the z-axis on the fine grid |
| discrete grid index on the x-axis on the coarse grid | |
| discrete grid index on the y-axis on the coarse grid | |
| discrete grid index on the z-axis on the coarse grid | |
| backward step length on the x-axis | |
| forward step length on the x-axis | |
| backward step lengths on the y-axis | |
| forward step lengths on the y-axis | |
| backward step lengths on the z-axis | |
| forward step lengths on the z-axis | |
| the first and second order central difference operator on the x-axis | |
| the first and second order central difference operator on the y-axis | |
| the first and second order central difference operator on the z-axis | |
| r | residual on the fine grid |
| residual on the coarse grid | |
| area of the i-th subregion | |
| pre-smoothing times | |
| post-smoothing times | |
| Error | maximum absolute error |
| Num | numbers of multigrid iterations |
| Order | convergence order |
| log | base 10 logarithmic function |
| Re | Reynolds number |
| boundary or interior layer parameters | |
| diffusion coefficient | |
| grids stretching parameters on the x-axis | |
| grids stretching parameters on the y-axis | |
| grids stretching parameters on the z-axis |
Appendix A. Details of the Finite Difference Operators
Appendix B. Restriction Operator on a Non-Uniform Grid When Nx = Ny = Nz
Appendix C. Interpolation Operator on a Non-Uniform Grid When Nx = Ny = Nz
References
- Batchelor, G.K. An Introduction to Fluid Dynamics; Cambridge University Press: Cambridge, UK, 1967. [Google Scholar]
- Blazek, J. Computational Fluid Dynamics: Principles and Applications; Butterworth-Heinemann: Oxford, UK, 2005. [Google Scholar]
- Zhang, J. An explicit fourth-order compact finite difference scheme for three-dimensional convection–diffusion equation. Commun. Numer. Methods Eng. 1998, 14, 263–280. [Google Scholar] [CrossRef]
- Zhang, J.; Ge, L.; Gupta, M.M. Fourth order compact difference schemes for 3D convection diffusion eqution with boundary layers on non-uniform grid. Neural Parallel Sci. Comput. 2000, 8, 373–392. [Google Scholar]
- Ge, Y.; Cao, F. A high order compact difference scheme and multigrid method for solving the 3D convection diffusion equation on non-uniform grids. In Proceedings of the 2012 Fourth International Conference on Computational and Information Sciences (ICCIS’12), Chongqing, China, 17–19 August 2012; pp. 714–717. [Google Scholar] [CrossRef]
- Dai, R.; Wang, Y.; Zhang, J. Fast and high accuracy multiscale multigrid method with multiple coarse grid updating strategy for the 3D convection–diffusion equation. Comput. Math. Appl. 2013, 66, 542–559. [Google Scholar] [CrossRef]
- Ge, Y.; Cao, F.; Zhang, J. A transformation-free HOC scheme and multigrid method for solving the 3D Poisson equation on non-uniform grids. J. Comput. Phys. 2013, 234, 199–216. [Google Scholar] [CrossRef]
- Gupta, M.M.; Manohar, R.P.; Stephenson, J.W. A single cell high order scheme for the convection–diffusion equation with variable coefficients. Int. J. Numer. Meth. Fluids 1984, 4, 641–651. [Google Scholar] [CrossRef]
- Ge, L.; Zhang, J. High accuracy iterative solution of convection diffusion equation with boundary layers on non-uniform grids. J. Comput. Phys. 2001, 171, 560–578. [Google Scholar] [CrossRef] [Green Version]
- Radhakrishna Pillai, A.C. Fourth-order exponential finite difference methods for boundary value problems of convective diffusion type. Int. J. Numer. Meth. Fluids 2001, 37, 87–106. [Google Scholar] [CrossRef]
- Kalita, J.C.; Dass, A.K.; Dalal, D.C. A transformation-free HOC scheme for steady convection–diffusion on non-uniform grids. Int. J. Numer. Meth. Fluids 2004, 44, 33–53. [Google Scholar] [CrossRef]
- Tian, Z.F.; Dai, S.Q. High-order compact exponential finite difference methods for convection–diffusion type problems. J. Comput. Phys. 2007, 220, 952–974. [Google Scholar] [CrossRef]
- Farrell, P.A.; Hegarty, A.F.; Miller, J.J.H.; O’Rordan, E.; Shishkin, G.I. Robust Computational Techniques for Boundary Layers; Champan & Hall/CRC: Boca, Raton, FL, USA, 2000. [Google Scholar]
- Zhang, J.; Sun, H.; Zhao, J. High order compact scheme with multigrid local mesh refinement procedure for convection diffusion problems. Comput. Methods Appl. Mech. Eng. 2002, 191, 4661–4674. [Google Scholar] [CrossRef]
- Shanab, R.A.; Seddek, L.F.; Mohamed, S.A. Non-uniform HOC scheme for the 3D convection–diffusion equation. Appl. Comput. Math. 2013, 2, 64–77. [Google Scholar] [CrossRef] [Green Version]
- Brandt, A. Multi-level adaptive solutions to boundary-value problems. Math. Comp. 1977, 31, 333–390. [Google Scholar] [CrossRef]
- Li, M.; Zheng, Z.; Pan, K. Extrapolation multiscale multigrid method for solving 2D Poisson equation with sixth order compact scheme. J. Appl. Math. Comput. 2019, 60, 589–604. [Google Scholar] [CrossRef]
- Gupta, M.M.; Kouatchou, J.; Zhang, J. Comparison of second- and fourth-order discretization for multigrid Poisson solvers. J. Comput. Phys. 1997, 132, 226–232. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J. Multigrid method and fourth-order compact scheme for 2D Poisson equation with unequal mesh-size discretization. J. Comput. Phys. 2002, 179, 170–179. [Google Scholar] [CrossRef] [Green Version]
- Ge, Y. Multigrid method and fourth-order compact difference discretization scheme with unequal meshsizes for 3D Poisson equation. J. Comput. Phys. 2010, 229, 6381–6391. [Google Scholar] [CrossRef]
- Gupta, M.M.; Kouatchou, J.; Zhang, J. A compact multigrid solver for convection–diffusion equations. J. Comput. Phys. 1997, 132, 123–129. [Google Scholar] [CrossRef]
- Ge, Y.; Cao, F. Multigrid method based on the transformation-free HOC scheme on non-uniform grids for 2D convection diffusion problems. J. Comput. Phys. 2011, 230, 4051–4070. [Google Scholar] [CrossRef]
- Cao, F.; Ge, Y.; Sun, H.-W. Partial semi-coarsening multigrid method based on the HOC scheme on non-uniform grids for the convection–diffusion problems. Int. J. Comput. Math. 2017, 94, 2356–2372. [Google Scholar] [CrossRef]
- Medina, A.C.; Schmid, R. Solution of high order compact discretized 3D elliptic partial differential equations by an accelerated multigrid method. J. Comput. Appl. Math. 2019, 350, 343–352. [Google Scholar] [CrossRef]
- Wesseling, P. An Introduction to Multigrid Methods; Wiley: Chichester, UK, 1992. [Google Scholar]
- Mulder, W.A. A new multigrid approach to convection problems. J. Comput. Phys. 1989, 83, 303–317. [Google Scholar] [CrossRef]
- Liu, C.; Liu, Z. Multigrid mapping and box relaxation for simulation of the whole process of flow transition in 3D boundary layers. J. Comput. Phys. 1995, 119, 325–341. [Google Scholar] [CrossRef]
- Liu, C. Multilevel Adaptive Methods in Computational Fluid Dynamics. Ph.D Thesis, University of Colorado Denver, Denver, CO, USA, 1989. [Google Scholar]
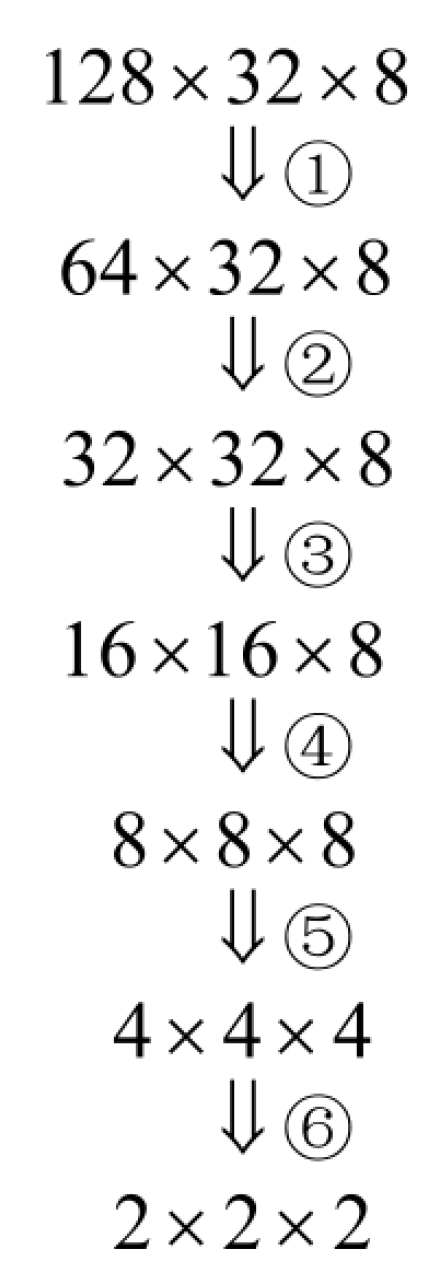
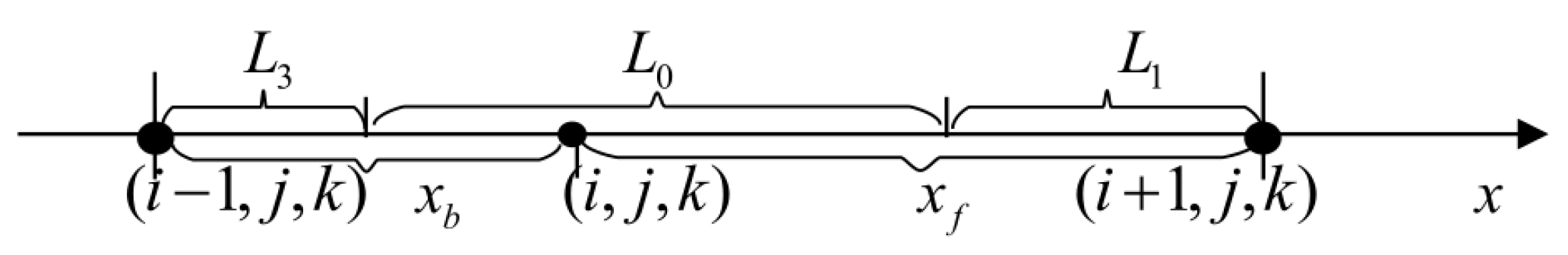




| Full-Coarsening Grids [5] | Partial Semi-Coarsening Grids | ||||||
|---|---|---|---|---|---|---|---|
| Num | CPU | Error | Num | CPU | Error | ||
| 11 | 5.023 | 2.175 | 11 | 5.023 | 2.175 | ||
| 9 | 1.482 | 2.476 | |||||
| 6 | 0.296 | 5.240 | |||||
| 6 | 0.125 | 1.831 | |||||
| 11 | 0.999 | 2.732 | 11 | 0.999 | 2.732 | ||
| 7 | 0.250 | 2.784 | |||||
| 5 | 0.063 | 4.211 | |||||
| 10 | 0.141 | 7.539 | 10 | 0.141 | 7.539 | ||
| 11 | 0.047 | 7.606 | |||||
| Full-Coarsening Grids [5] | Partial Semi-Coarsening Grids | ||||||
|---|---|---|---|---|---|---|---|
| Num | CPU | Error | Num | CPU | Error | ||
| 12 | 8.658 | 1.533 | 12 | 8.658 | 1.533 | ||
| 9 | 2.215 | 1.533 | |||||
| 6 | 0.499 | 1.568 | |||||
| 5 | 0.140 | 2.434 | |||||
| 12 | 1.076 | 2.690 | 12 | 1.076 | 2.690 | ||
| 8 | 0.234 | 2.827 | |||||
| 6 | 0.078 | 2.950 | |||||
| Full-Coarsening Grids [5] | Partial Semi-Coarsening Grids | ||||||
|---|---|---|---|---|---|---|---|
| Num | CPU | Error | Num | CPU | Error | ||
| 13 | 25.370 | 3.875 | 13 | 25.370 | 3.875 | ||
| 15 | 7.066 | 3.944 | |||||
| 7 | 0.733 | 4.357 | |||||
| 5 | 0.140 | 3.860 | |||||
| 11 | 1.950 | 6.095 | 11 | 1.950 | 6.095 | ||
| 6 | 0.312 | 6.564 | |||||
| 5 | 0.094 | 5.897 | |||||
| 6 | 0.156 | 1.196 | 6 | 0.156 | 1.196 | ||
| 4 | 0.047 | 1.271 | |||||
| Full-Coarsening Grids [5] | Partial Semi-Coarsening Grids | ||||||
|---|---|---|---|---|---|---|---|
| Num | CPU | Error | Num | CPU | Error | ||
| 10 | 11.500 | 3.828 | 10 | 11.500 | 3.828 | ||
| 6 | 1.911 | 4.102 | |||||
| 6 | 0.480 | 4.082 | |||||
| 6 | 0.120 | 3.885 | |||||
| 8 | 1.181 | 9.275 | 8 | 1.181 | 9.275 | ||
| 6 | 0.234 | 9.232 | |||||
| 6 | 0.094 | 8.737 | |||||
| Full-Coarsening Grids [5] | Partial Semi-Coarsening Grids | ||||||
|---|---|---|---|---|---|---|---|
| Num | CPU | Error | Num | CPU | Error | ||
| 19 | 24.320 | 3.827 | 19 | 24.320 | 3.827 | ||
| 12 | 8.615 | 3.853 | |||||
| 11 | 3.089 | 4.175 | |||||
| 11 | 1.373 | 4.741 | |||||
| 13 | 1.684 | 6.652 | 13 | 1.684 | 6.652 | ||
| 11 | 0.764 | 7.116 | |||||
| 11 | 0.327 | 7.382 | |||||
| 10 | 0.156 | 1.515 | 10 | 0.156 | 1.515 | ||
| 10 | 0.079 | 1.558 | |||||
| Full-Coarsening Grids [5] | Partial Semi-Coarsening Grids | ||||||
|---|---|---|---|---|---|---|---|
| Num | CPU | Error | Num | CPU | Error | ||
| 34 | 42.870 | 7.505 | 34 | 42.870 | 7.505 | ||
| 17 | 10.890 | 7.856 | |||||
| 16 | 4.012 | 7.968 | |||||
| 16 | 1.856 | 8.067 | |||||
| 18 | 2.287 | 1.916 | 18 | 2.287 | 1.916 | ||
| 16 | 0.983 | 1.923 | |||||
| 16 | 0.453 | 1.905 | |||||
| Uniform Grid | Non-Uniform Grid | |||||||
|---|---|---|---|---|---|---|---|---|
| Num | CPU | Error | Order | Num | CPU | Error | Order | |
| 6 | 0.203 | 4.096 | 6 | 0.203 | 4.452 | |||
| 7 | 2.028 | 2.615 | 3.97 | 8 | 2.153 | 2.748 | 4.02 | |
| 7 | 16.110 | 1.646 | 3.99 | 11 | 23.910 | 1.712 | 4.00 | |
| 6 | 0.234 | 6.348 | 6 | 0.223 | 2.921 | |||
| 7 | 2.122 | 4.279 | 3.89 | 10 | 2.852 | 1.784 | 4.03 | |
| 7 | 17.510 | 2.730 | 3.97 | 15 | 36.230 | 1.111 | 4.01 | |
| 6 | 0.171 | 7.759 | 6 | 0.218 | 8.423 | |||
| 6 | 1.419 | 1.585 | 2.29 | 12 | 2.591 | 4.989 | 4.08 | |
| 6 | 10.220 | 1.474 | 3.43 | 26 | 43.180 | 3.076 | 4.02 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, T.; Zhang, L.; Cao, F.; Ge, Y. A Special Multigrid Strategy on Non-Uniform Grids for Solving 3D Convection–Diffusion Problems with Boundary/Interior Layers. Symmetry 2021, 13, 1123. https://doi.org/10.3390/sym13071123
Ma T, Zhang L, Cao F, Ge Y. A Special Multigrid Strategy on Non-Uniform Grids for Solving 3D Convection–Diffusion Problems with Boundary/Interior Layers. Symmetry. 2021; 13(7):1123. https://doi.org/10.3390/sym13071123
Chicago/Turabian StyleMa, Tianlong, Lin Zhang, Fujun Cao, and Yongbin Ge. 2021. "A Special Multigrid Strategy on Non-Uniform Grids for Solving 3D Convection–Diffusion Problems with Boundary/Interior Layers" Symmetry 13, no. 7: 1123. https://doi.org/10.3390/sym13071123
APA StyleMa, T., Zhang, L., Cao, F., & Ge, Y. (2021). A Special Multigrid Strategy on Non-Uniform Grids for Solving 3D Convection–Diffusion Problems with Boundary/Interior Layers. Symmetry, 13(7), 1123. https://doi.org/10.3390/sym13071123






