Identification of Road Profile Parameters from Vehicle Suspension Dynamics for Control of Damping

Abstract

Concept of symmetry covers physical link between road profile form, vehicle dynamic characteristics, and speed conjunction. Symmetry frame between these items is asymmetric itself and has no direct expression, but it affects a vibration level on the vehicle and driving comfort. Usually, we can change only the vehicle’s speed to achieve desired vibrations level of the driver and passengers. Recently, vehicle dynamic characteristics can be changed depending on its damping system structure, but these solutions are limited by construction and control possibilities and evidently represented by symmetric dependency between road input and the resulting acceleration of the vehicle. The main limitation of this process is to have a reliable value of the existing road profile that is mainly defined by road category but unpredictable for each road distance. Functional road profile calculations are provided in this article, where power spectral density (further-PSD) and waviness of the road play the main role in delineating road profile parameters. Furthermore, the transfer function system was created using full car dynamic model analysis. Values on vehicle suspension’s effects on acceleration were obtained from vehicle speed and road roughness. Acceleration values and transfer function were used to calculate PSD value quickly and practically. This calculated result can be formed as a control value to the vehicle damping control. In addition, the provided methodology became useful to determine road quality for adjustment of vehicle suspension parameters and set safe driving characteristics, which became part of driver assistant systems or autonomous driving mode.

1. Introduction

Ride quality, vehicle handling, fuel consumption, and tire wear depend on road quality [1]. Road impact to vehicle and vehicle impact to the road degradation creates a symmetric entity with the reference frame represented by dynamic features of the vehicle. Bad road condition and potholes cause damage to vehicles, and regular monitoring of road quality is required to avoid the high costs of damage the vehicles [2]. Detailed information about road profile is key for transport authorities maintaining adequate ride quality for vehicles, vehicle designers and engineers developing suspension systems. Bad road profile requires a smart suspension system from passive to semi-active [3,4,5,6,7] and active control [8,9,10,11] in automotive technology. So far, a universal solution for vibrations control has not been achieved, but the possibility of controlling vehicle dynamic response allows for the adjustment of drivers’ and passengers’ felt vibrations [12]. Due to road irregularities’ unpredictability, controlling the dynamic properties of the vehicle suspension becomes a complex task consisting of: (i) road irregularities’ value reading process, (ii) generation of the control signals, and (iii) control of the regulation process [13]. Then, although vibrations control has its solutions, reading of the irregularities becomes a real challenge. Despite that, there are ways to read road profile. Different methods and equipment to measure the road surface characteristics are briefly discussed in [14,15,16]. They can be divided into three categories: system response-based estimation, direct measurement, and non-contact measurement [17,18]. A dozen various inexpensive response-based methods of road profile recognition are reviewed and presented in [19]. Some of them use accelerometers mounted in different places and transfer functions for profile reconstruction or roughness estimation [19,20,21,22]. There are papers where an accelerometer is used for control of smart suspension [6,23,24]. Research where road surface waviness used to control damping has not been published yet.

At the same time, we have found various roughness or ride quality indices used in literature, i.e., international roughness index (IRI), ride quality index (RQI), whole-body vibration (a_wz), ride number (RN) and others [14,15,16,25]. Some of them are associated with standards [15]. Standard ISO 8608:2016, which defines road surface profiles [26], provides two essential parameters: the degree of roughness G_d(n₀) or G_d(Ω₀) identified as power spectral density (further-PSD) of the vertical road profile displacement, and the waviness w. The main usefulness of road waviness value for the transportation community consists of [27]: (i) it modulates power distribution of the road elevation spectrum; (ii) short wavelengths (with w < 2) affect road surface, while long wavelengths (w > 2) affect the whole structure. On the other hand, they negatively influence vehicle handling and ride comfort. Waviness has a much higher impact on the total power than a degree of roughness G_d alone, but vehicle velocity v and waviness w modulate PSD of the vertical vibrations as v^w−1. Also, the root mean square (further-RMS) value of particular vibration responses as well as IRI are proportional to v^(w−1)/2 [28,29].

Use of acceleration value from wheel hub in our case is based on the possibility of collecting acceleration data practically by mounting the general purpose accelerometer (bandwidth not less than 1 Hz to 30 Hz, measurement range up to 50 m/s²) on the lower end of the shock absorber. While the accelerometer is an inertial sensor, it requires no extra reference point to install it. Choice of waviness (w) as an essential road profile parameter better reflects real road surface and is possible to define with fewer efforts practically.

In contrast to the majority of existing publications, we are using “two-split” and “three-line” models to obtain three “waviness” values in the desired frequency range. Our research proves that this approach can be used to control damping parameters of car suspension. Moreover, it allows for realizing precise and smooth control of the damper damping coefficient, while [21] uses values of G_d and w. Their approach reproduces the generated road profiles according to the assigned types very well, but using such a method to control shock absorbers will be insufficient since the damping coefficient cannot vary smoothly. The damping coefficient will be adjusted only when the profile value will exceed a certain range. Another group of scientists [30] used linear fitting in ten octaves. They showed good road classification for two-wheeled vehicles. However, this is not appropriate for controlling the damping coefficient due to the huge matrix of possible combinations.

As stated in [19], many studies use a quarter-vehicle model and passive suspension system, while transfer function and other methods mostly use the passive system. We plan to control our developed (semi-)active suspension using information obtained from a segment of passed road profile.

This paper provides a methodology to detect road profile characteristics from acceleration values, which can easily be detected for in-situ mounted sensors. It is possible to estimate the power spectral density of road profile from wheel hub acceleration using transfer functions. Obtained PSD allows for the adjustment of vehicle driving mode in the case of driver assistant systems or fully automated drive mode, set damping parameters for adjustable shock absorbers or provide driving hints for the driver. This data processing with derived transfer function is fast and requires lower processing power than methods presented in [6,30]. Therefore, it can be processed on board or even by an internal shock absorber processor. The methodology of data extraction is deeply related to the concept of symmetry due to our approach of implementing direct data transformation using polynomial; therefore, acceleration values can be processed backwards from vehicle body vibration trough a symmetric transformation procedure. Vehicle body and wheel hub vibrations are related with defined transfer functions. The provided methodology based on extraction of waviness values uses parameters from a full-car dynamic model, which already compared with experimental data [31].

2. Materials and Methods

The proposed methodology of road profile waviness is classified by obtained accelerations of a hub of each wheel, and requires some mathematical manipulation, which is provided below in the text. The road profile here is generated using the provided methodology, which ensures concordance of obtained profile to the real road surface of the corresponding category. A generation of longitudinal road profiles based on sums of various length sinusoidal waves with different amplitudes and phases has been applied by many authors [32,33,34,35,36,37,38]. The one-sided PSD spectrum was split into N equal parts according to frequency, and for each is generated a harmonic sample with central frequency, spectral amplitude. Random values of phase angles ${\phi }_i$ were uniformly distributed in the range from 0 to 2π. To create artificial road profile samples were superimposed in the spatial domain according to Equations (1) and (2):

$$z(x)={\displaystyle \sum _{i=1}^{N=\left({\mathsf{\Omega }}_{\mathrm{U}}-{\mathsf{\Omega }}_{\mathrm{L}}\right)/\mathsf{\Delta }\mathsf{\Omega }}{Z}_i\cos \left({\mathsf{\Omega }}_{i}x+{\phi }_i\right) \mathrm{with}}$$

(1)

$$Z_i=\sqrt{2G_{\mathrm{d}}({\mathsf{\Omega }}_i)\mathsf{\Delta }\mathsf{\Omega }}.$$

(2)

where G_d(Ω_i) is displacement PSD at angular spatial frequency Ω_i, $Z_i$ is the amplitude of ith harmonic, ${\mathsf{\Omega }}_{\mathrm{U}}, {\mathsf{\Omega }}_{\mathrm{L}}$ are upper and lower angular spatial frequencies in the PSD spectrum [rad/m], $\mathsf{\Delta }\mathsf{\Omega }$ is the width of each frequency band, and ${\mathsf{\Omega }}_i={\mathsf{\Omega }}_{\mathrm{L}}+\left(i-1\right)\mathsf{\Delta }\mathsf{\Omega }$ is the angular spatial frequency of ith harmonic or ith frequency band. In our case, the number of harmonic samples was N = 1000. For general on-road measurements, recommended lower and upper limits of angular spatial frequencies (=2πn) are 2π × 0.01 rad/m and 2π × 10 rad/m, respectively [26].

The required step size of road distance x, according to the data sampling theorem [39], is equal to $\mathsf{\Delta }x\le \frac{2\pi }{2{\mathsf{\Omega }}_{\mathrm{U}}}=0.05 \mathrm{m}.$ A smoother profile could be achieved by minimising steps. However, it only increases the required computational efforts. To get more various road profiles, instead of the linear fitting

$$G_{\mathrm{d}}(\mathsf{\Omega })=G_{\mathrm{d}}({\mathsf{\Omega }}_0){\left(\mathsf{\Omega }/{\mathsf{\Omega }}_0\right)}^{-w}$$

(3)

recommended by ISO standard [26] in Equation (2), we used two split fittings provided in [40]:

$$G_{\mathrm{d}}({\mathsf{\Omega }}_i)=\{\begin{array}{ccc}{G}_{\mathrm{d}}({\mathsf{\Omega }}_0){\mathsf{\Omega }}_i^{-w_1}& \mathrm{for}& {\mathsf{\Omega }}_i\le {\mathsf{\Omega }}_1\\ G_{\mathrm{d}}({\mathsf{\Omega }}_0){\mathsf{\Omega }}_i^{-w_2}& \mathrm{for}& {\mathsf{\Omega }}_1<{\mathsf{\Omega }}_i\le {\mathsf{\Omega }}_2\\ G_{\mathrm{d}}({\mathsf{\Omega }}_0){\mathsf{\Omega }}_i^{-w_3}& \mathrm{for}& {\mathsf{\Omega }}_2<{\mathsf{\Omega }}_i\end{array}$$

(4)

The degree of roughness G_d(Ω₀) is PSD value at the reference angular spatial frequency. The extreme spatial frequencies ${\mathsf{\Omega }}_1=2\pi \times 0.21$ rad/m and ${\mathsf{\Omega }}_2=2\pi \times 1.22$ rad/m produced a minimal error describing the Swedish road network [40]. A new random set of initial phases was generated at each $2\pi /{\mathsf{\Omega }}_{\mathrm{L}}$ distance to avoid a replication of the road profile. Additionally, we used the Welch type windowing function with the value of exponent equal to 10 to minimise the appearance of abrupt shifts at the connections between profile segments [41]. The road profiles were calculated through written MATLAB™ code. The profile for the right vehicle side (both front and rear wheel) was formed by reversing the order of the left side profile related to the vehicle. For comparison, identical sequences of random numbers were used to generate each profile.

Our developed dynamic model of the whole car [31] was used to simulate vehicle passing these profiles. The model included ten masses (car’s mass, four wheels’ masses, masses of four passengers and baggage box) and moments of inertia about the X and Y axes. Twelve generalised coordinates defined the behaviour of the modelled car: vertical axis coordinate—Z; rotation angles about X and Y axes—${\phi }_x$ and ${\phi }_y$; $z_1, z_2, z_3, z_4$ are the vertical coordinates of wheels; $z_{13}, z_{14}, z_{15}, z_{16}$ are coordinates of the centres of mass of the driver and passengers, and $z_{18}$ is coordinate of the centre of baggage’s mass. The model was build using Lagrange’s equation of the second type. These equations were solved analytically, and after differentiating, we obtained the final system, consisting of the equations, presented in this form:

$$\begin{array}{l}{a}_{ii}{\dot{q}}_i+b_{i1}{\dot{q}}_1+b_{i2}{\dot{q}}_2+\dots +b_{in}{\dot{q}}_n+c_{i1}{q}_1+c_{i2}{q}_2+\dots +c_{in}{q}_n=\\ =d_{i1}{\eta }_1+d_{i2}{\eta }_2+d_{i3}{\eta }_3+d_{i4}{\eta }_4+d_{i1}^{*}{\dot{\eta }}_1+d_{i2}^{*}{\dot{\eta }}_2+d_{i3}^{*}{\dot{\eta }}_3+d_{i4}^{*}{\dot{\eta }}_4.\end{array}$$

(5)

where a, b, c, d, d* (with corresponding indexes) are coefficients of equations, derived from matrixes of stiffness, dissipation and inertia; $q_i$ is generalised coordinate, in respect to which differentiation was applied during the building of a system of equations; n is the number of generalised coordinates; and ${\eta }_1, {\eta }_2, {\eta }_3, {\eta }_4$ are coordinates along which the system of the car is excited kinematically. Each overdot is a shorthand for a time derivative. The rear wheels are excited with the same road profile as the front wheels, with corresponding shifts by a distance equal to the distance between the front and rear wheel centres.

The research was performed by simulating the car, Range Rover Evoque, with the driver and front passenger but without rear passengers or baggage (all parameters presented in supplementary materials Table S1). The second derivative of the ${\ddot{z}}_1, {\ddot{z}}_2, {\ddot{z}}_3, {\ddot{z}}_4$ coordinates was taken as road generated acceleration values from road excitation for further analysis. Road PSD was estimated on the relationship between the road surface and vehicle acceleration via a transfer function:

$${\mathrm{PSD}}_{\mathrm{road}}(.)=\frac{{\mathrm{PSD}}_{\mathrm{acc}}(.)}{H(.)},$$

(6)

where H(.) and PSD_road(.) or PSD_acc(.) are the transfer function and PSD for a frequency Ω or n due to road profile or wheel accelerations, respectively. Waviness values were extracted from PSD spectra using the straight line for logarithmic values in the ranges specified for each waviness. To evaluate road surface PSD estimation quality, we used the normalised root mean squared error parameter (NRMSE). This is given by the RMS error between the estimated value $\widehat{y}$ and true value y, normalised to the RMS of road roughness true value, and expressed as a percentage [42]:

$$\mathrm{NRMSE}=\frac{\mathrm{RMS}(\widehat{y}-y)}{\mathrm{RMS}(y)}100\%.$$

(7)

3. Results and Discussion

Initially, the samples of road profile with various $w_1, w_2, w_3$ waviness values and with the ISO road class B parameter $G_{\mathrm{d}}({\mathsf{\Omega }}_0)=4\times {10}^{-6} {\mathrm{m}}^3, {\mathsf{\Omega }}_0=1 \mathrm{rad}/\mathrm{m}$ [26] have been generated. Simulated datasets were named using the naming rule as “prw₁w₂w₃”, where w_i can have the values of 1, 2 and 3. The length of each generated profile was 1000 m. Displacement PSD (G_d) spectra of profiles passing at speed v were obtained using fast Fourier transformation (FFT) with a 50% overlapping Hamming window of length $N=2\times floor(1000[\mathrm{m}]/v[\mathrm{m}/\mathrm{s}]/\mathsf{\Delta }t[\mathrm{s}]/2)$ points (with buffer size 1000 m) and time step ∆t = 0.01 s (sampling frequency 100 Hz). Implemented here, floor is the function rounding toward negative infinity. As is recommended by ISO standard [26], the smoothed PSD spectra of pr222 profile at car speed v = 20, 50, 70, 90 or 130 km/h are shown in Figure 1. From PSD spectra were estimated three cases of waviness values:

(1)

Using Equation (4) without smoothing; w₁ in frequency range from 0.0557 to 0.21 cycles/m; w₂ in frequency range from 0.21 cycles/m up to 1.22 cycles/m or max value; w₃ in frequency range from 1.22 cycles/m up to max value.

(2)

Using Equation (4) but after smoothing.

(3)

After smoothing along a straight line using Equation (3), starting from octave with lower cut-off frequency 0.0557 cycles/m and centre frequency 0.0625 cycles/m up to octave with max value.

Waviness values estimated from pr222 profile at various speed using Hamming, Hanning, Bartlett or rectangular window in FFT are presented in

Table 1. Estimated waviness values of pr222 profile when FFT buffer size is 1000 m and 100 m.

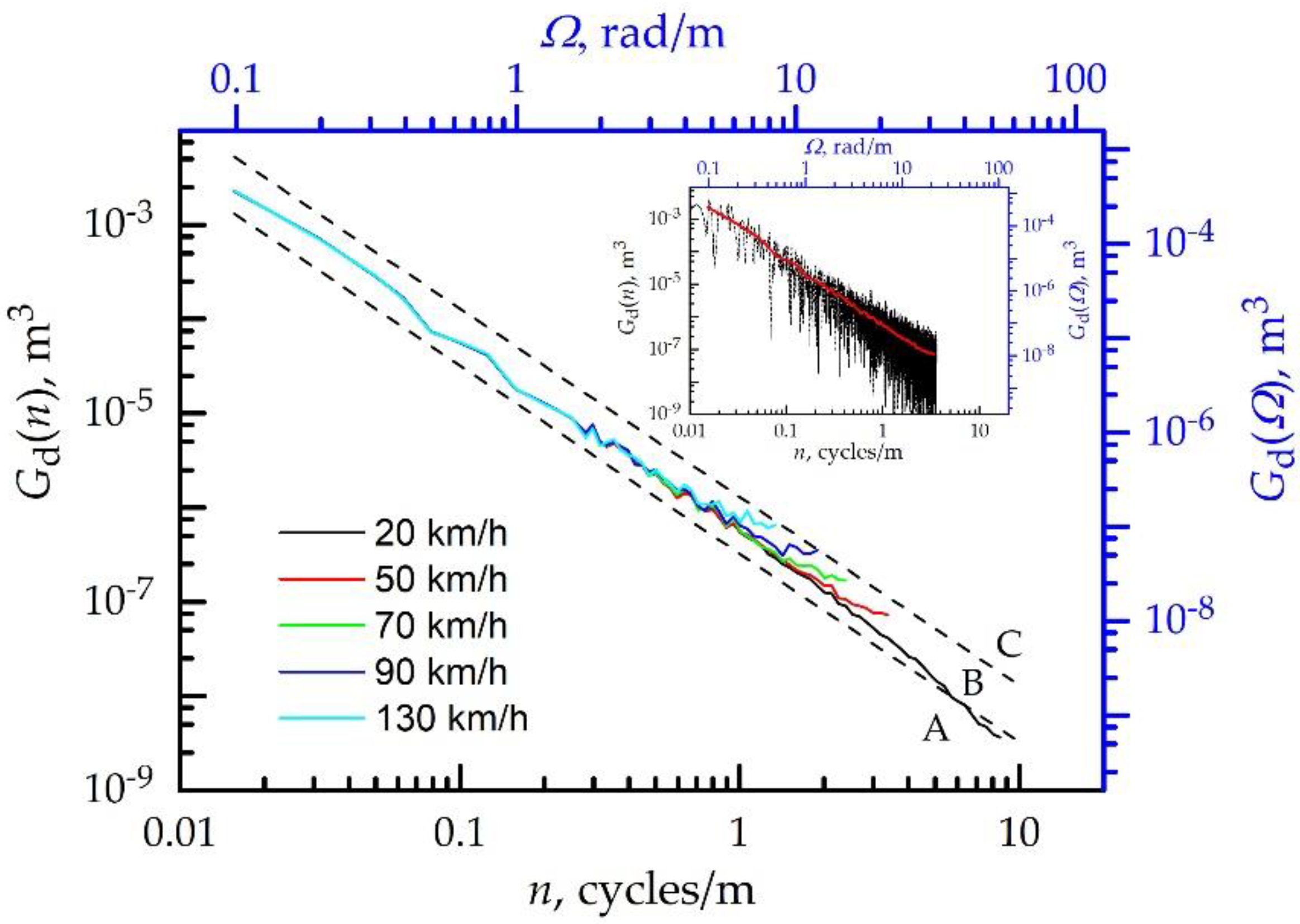
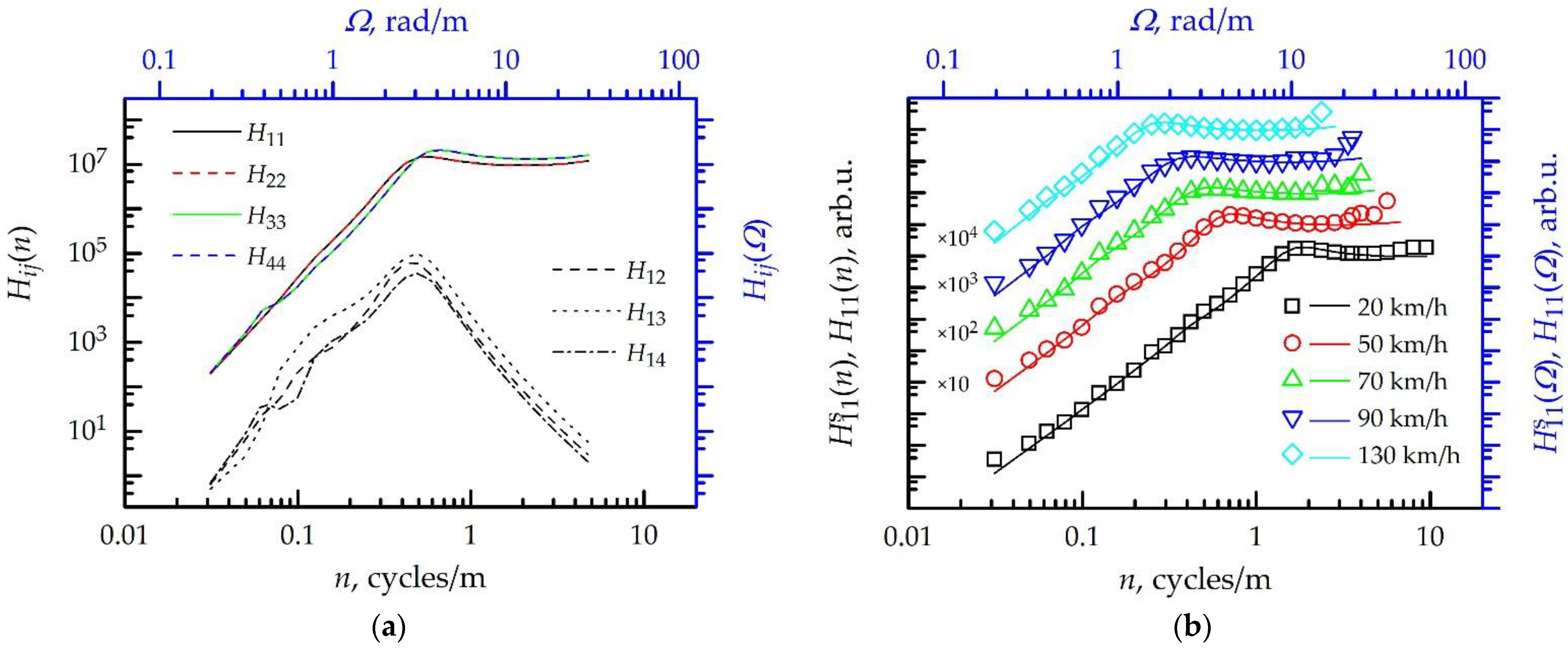
Speed, km/h (N; x, m)	Window	w1, w2, w3 (Case 1)		w1, w2, w3 (Case 2)		w (Case 3)
		Buffer		Buffer		Buffer
		1000 m	100 m	1000 m	100 m	1000 m	100 m
20 (18000; 1000) (1800; 100)	Hamming	2.5, 2.1, 2.4	2.4, 2.0, 2.4	2.3, 2.0, 2.4	2.1, 1.9, 2.3	2.1	2.1
	Hanning	2.5, 2.1, 2.4	2.5, 2.0, 2.4	2.3, 2.0, 2.4	2.1, 1.9, 2.3	2.1	2.1
	Bartlett	2.5, 2.1, 2.4	2.4, 2.0, 2.5	2.3, 2.0, 2.4	2.1, 1.9, 2.4	2.1	2.1
	Rectangular	2.1, 2.0, 2.4	2.2, 2.0, 2.3	2.1, 2.0, 2.4	2.0, 1.9, 2.2	2.1	2.0
50 (7200; 1000) (720; 100)	Hamming	2.5, 2.1, 1.5	2.4, 1.9, 1.6	2.3, 2.0, 1.7	2.1, 1.9, 1.7	1.9	1.9
	Hanning	2.6, 2.1, 1.6	2.4, 1.9, 1.6	2.3, 2.0, 1.7	2.1, 1.9, 1.7	1.9	1.9
	Bartlett	2.5, 2.1, 1.5	2.4, 1.9, 1.6	2.3, 2.0, 1.7	2.1, 1.9, 1.7	1.9	1.9
	Rectangular	2.1, 2.0, 1.5	2.2, 2.0, 1.6	2.1, 2.0, 1.7	2.0, 1.9, 1.6	1.9	1.9
70 (5142; 999.8) (514; 99.94)	Hamming	2.5, 2.0, 1.2	2.4, 1.9, 1.4	2.3, 1.9, 1.1	2.1, 1.8, 1.3	1.9	1.9
	Hanning	2.5, 2.0, 1.2	2.5, 1.9, 1.4	2.3, 1.9, 1.1	2.1, 1.8, 1.3	1.9	1.9
	Bartlett	2.4, 2.0, 1.2	2.4, 1.9, 1.4	2.3, 1.9, 1.1	2.2, 1.9, 1.3	1.9	1.9
	Rectangular	2.1, 2.1, 1.2	2.3, 2.0, 1.3	2.1, 1.9, 1.2	2.0, 1.8, 1.2	1.9	1.8
90 (4000; 1000) (400; 100)	Hamming	2.6, 1.9, 0.3	2.4, 1.9, 0.5	2.3, 1.9, 0.4	2.1, 1.8, 0.8	1.8	1.8
	Hanning	2.6, 2.0, 0.4	2.5, 1.9, 0.6	2.3, 1.9, 0.3	2.2, 1.8, 0.8	1.8	1.8
	Bartlett	2.6, 1.9, 0.2	2.4, 1.9, 0.5	2.3, 1.8, 0.4	2.2, 1.8, 0.8	1.8	1.8
	Rectangular	2.2, 1.9, 0.3	2.3, 1.9, 0.8	2.1, 1.9, 0.7	2.0, 1.8, 0.8	1.8	1.8
130 (2768; 999.6) (276; 99.67)	Hamming	2.5, 1.7, −3.0	2.4, 1.7, −0.1	2.3, 1.7, --	2.1, 1.6, --	1.8	1.8
	Hanning	2.5, 1.7, −3.2	2.4, 1.7, 0.0	2.3, 1.7, --	2.2, 1.6, --	1.8	1.8
	Bartlett	2.5, 1.7, −3.4	2.4, 1.7, −0.4	2.3, 1.7, --	2.2, 1.6, --	1.8	1.8
	Rectangular	2.1, 1.8, 0.2	2.2, 1.8, −1.3	2.1, 1.7, --	1.9, 1.6, --	1.8	1.8

. Increasing speed from 20 km/h to 130 km/h, the maximum frequency of one-sided PSD spectra decreases from 8.99 cycles/m down to 1.38 cycles/m. At the same time, powers of higher frequencies (see Figure 1) increase and this influences the decrease of waviness values w₂, w₃ (case 1 and 2) and w (case 3), increasing speed. Values of w₃ without smoothing could be negative due to approximation of few points in the much-dispersed area (see inset of Figure 1, and columns of Table 1 with the header “1000 m”) or not extracted at all such as when buffer size is 100 m. Values of w₁ without smoothing are a bit higher than after smoothing. This could be explained by the fact that lower and higher frequencies are accounted for during the smoothing procedure. The smallest waviness deviations from theoretical values of ISO recommended ones are obtained using a rectangular window and smoothing procedure.

Similar tendencies are observed, and mean waviness values in the distance of 1000 m are estimated with a buffer size of 100 m (see columns of Table 1 with the header “100 m”). However, a more detailed analysis of other profiles showed that the rectangular window gives the worst results only in some cases (see Tables S2–S4) but has the smallest error while others vary from case to case, which means the maximum difference between the values used to generate the profile and those extracted. It should be noted that a decrease of FFT buffer size increases the variation of waviness, but mean values remain close to the ones used in generation.

Our previous investigation showed that the straight-line approximation of PSD of the road profile proposed by ISO standard doesn’t contribute suitable information required to control damping parameters of car suspension [43]. In the light of previous observations, the third waviness index is not suitable for the control coefficient of damping of the suspension. Moreover, from the optimal damping coefficient calculations for various profiles in our previous research [31], we observed that the changing of the w₃ value influences only tens of the damping coefficient. Thus, we are using only values of w₁ and w₂ waviness and rectangular window in FFT calculation. Our aim is to get waviness value, not PSD; therefore, we are not using smoothing. Additionally, to minimise the calculation resources, it is possible to use, for example, MatLab function pwelch with a shorter vector of chosen frequencies.

Our next step is to obtain information about the passing road profile segment, and to evaluate PSD and extract waviness w₁ and w₂. One should choose which is optimal from all road profile generation methods, requiring less computational resources and shorter passed distance, being more precise. This procedure demands a separate detailed study that is not our aim. We estimated PSD of road profile from wheel acceleration values using transfer functions obtained from the full-car model. Using Cramer’s method and applying the principle of superposition to the system in the form of Equation (5), we can obtain the theoretical transfer functions for four accelerations for each wheel hub ${\ddot{z}}_i$ for each displacement input ${\eta }_j$:

$$H_{ij}(.)={\left|s^2\frac{z_i(s)}{{\eta }_j(s)}\right|}^2,$$

(8)

where Laplace’s complex variable $s=\sqrt{-1}\mathsf{\Omega }v=\sqrt{-1}2\pi nv$. A more detailed form of H₁₁ is presented in the supplementary material Equation (S1). Calculated acceleration transfer functions H_ii and cross-transfer functions of first point H_1j at 70 km/h are presented in Figure 2a. As can be expected, transfer functions are the same for front left and front right wheels or for the rear left and rear right wheels. Meantime cross-transfer function impacts are more than two orders of magnitude smaller. Consequently, it is enough to use only the H_ii transfer function for further calculations. Comparison of the simulation transfer function $H_{11}^{\mathrm{s}}$, evaluated using Equation (6) and PSD of input (displacement) and output (acceleration) of one wheel in our full-car model simulation, and theoretical transfer function varying car speed are shown in Figure 2b. One can observe good agreement between them in the frequency range interesting us. NRMSE of simulated and theoretical transfer functions at all velocities is less than 65% for all range values and decreases to 8% for a range from 0.21 to 1.22 cycles/m. Thus, using the transfer function at chosen frequency range in restoring road profile from wheel hub accelerations or without smoothing, one could expect precise results.

The transfer function method has some disadvantages. Usually, it is used with constant speed (a small-time span or buffer length can eliminate). In addition, few potholes on the road surface can significantly change estimated values for the segment. The provided methods, described in [44,45,46], can minimise road pothole impact to real road PSD values.

Any other method could be used for road PSD profile restoring from wheel hub acceleration values. For example, another possible way to identify the road profile, knowing the dynamic responses of the car (the chassis acceleration and deflection of the suspension), is a new fast and simple technique, called independent component analysis (ICA), based on the so-called inverse problem [47]. The advantages of the ICA are that the identification of road excitation is simpler and faster compared to the other estimation techniques. Also, it is robust to the sprung mass variation. Furthermore, the addition of noise has a negligible effect on the estimation process. Therefore, there is no need to use a more complex full-car model to estimate the road profile [47].

Finally, we verified how waviness values extracted from PSD spectra of recovered road profile do meet values obtained from PSD spectra of generated road profile. Recovering road roughness data from generated PSD spectra expresses the concept of symmetry in the research idea and methodology. Minimal and maximal values of both w₁, w₂ waviness and maximal NRMSE value of each profile at various speeds are presented in

Table 2. Extreme waviness values and maximum NRMSE.

Profile and Waviness		Speed, km/h
		20			50			70			90			130
		Min Max NRMSE			Min Max NRMSE			Min Max NRMSE			Min Max NRMSE			Min Max NRMSE
pr111	w1	2.3	5.7	197	2.6	6.5	214	2.0	5.5	212	2.3	6.0	251	1.4	5.1	216
	w2	0.7	1.7	50	0.8	2.2	64	0.4	1.5	46	0.5	1.4	49	−0.3	0.8	70
pr112	w1	−0.3	4.6	129	−0.4	4.1	128	0.2	3.7	93	1.1	3.1	104	−0.7	3.1	74
	w2	0.7	1.5	35	0.6	1.7	32	0.5	1.4	32	0.6	1.4	26	0.3	1.6	36
pr122	w1	−0.2	4.3	118	0.4	3.7	112	0.0	3.3	91	1.1	3.1	101	−0.8	3.1	75
	w2	1.7	2.5	14	1.6	2.7	17	1.6	2.4	15	1.4	2.4	13	0.9	2.4	17
pr132	w1	−0.1	4.2	114	0.4	3.7	109	0.0	3.2	92	1.1	3.1	100	−0.3	3.1	72
	w2	2.6	3.5	9	2.3	3.6	12	2.2	3.2	9	1.8	2.9	11	1.0	2.4	18
pr212	w1	0.7	4.6	57	0.2	4.3	62	0.7	4.2	56	1.2	3.6	47	0.3	3.8	40
	w2	0.7	1.4	36	0.7	1.6	34	0.5	1.4	32	0.6	1.4	27	0.4	1.5	35
pr222	w1	0.4	4.6	53	0.3	4.2	56	0.6	3.8	56	1.1	3.6	46	0.1	3.9	39
	w2	1.7	2.4	15	1.6	2.7	18	1.4	2.4	16	1.4	2.4	13	1.0	2.3	16
pr232	w1	0.7	4.4	50	0.3	4.1	57	0.6	3.6	56	1.1	3.6	45	0.1	3.9	38
	w2	2.6	3.4	10	2.2	3.6	13	2.2	3.2	9	1.8	2.9	12	1.1	2.4	18
pr312	w1	1.8	5.5	30	1.7	5.2	36	1.6	4.6	30	1.5	4.3	32	1.4	4.7	28
	w2	0.8	1.4	29	0.6	1.6	27	0.6	1.4	25	0.7	1.4	21	0.5	1.5	27
pr322	w1	1.8	5.1	29	1.4	4.9	35	1.5	4.5	30	1.3	4.2	33	1.4	4.8	28
	w2	1.8	2.4	13	1.6	2.6	15	1.5	2.4	12	1.6	2.4	12	1.2	2.2	16
pr332	w1	1.7	4.7	27	1.4	5.0	36	1.5	4.6	31	1.2	4.2	33	1.4	4.8	27
	w2	2.6	3.4	9	2.3	3.6	14	2.2	3.3	12	1.9	2.8	12	1.3	2.3	20
pr333	w1	1.9	4.6	24	1.8	4.6	26	1.7	4.7	26	1.6	4.5	27	1.9	4.5	28
	w2	2.7	3.5	8	2.6	3.5	13	2.6	3.5	13	2.6	3.5	13	2.4	3.4	15

(estimated using rectangular window without smoothing in FFT, buffer 100 m).

4. Conclusions

Provided analysis of vehicle suspension and wheel hub accelerations revealed an apparent possibility of extracting road characteristics from sensor data reliably. Sensing road parameters just with a simple technique opens new horizons in infrastructure observation using background data streamed from passing cars, detecting defect information, damage depth, and development in the time domain. This information will be useful for car producers as a method of vehicle operation monitoring in terms of safety and lifetime for the entire car body.

As the main achievement of this research, we should claim successful deciphering of accelerometer data into road category according to ISO classification and set damping characteristics of the vehicle suspension system. The created methodology with transfer function implementation in fast data processing provides a green light for in-situ mounted low computing power systems. Such installation inside shock-absorbers will transfer road characteristics to the central vehicle safety block and set shock absorber damping values to minimise vibration values of the vehicle body. These values, provided in Table 2, became extremely important in the case of driver assistant systems and autonomous driving systems.

Results of this research are still begging for continuation, because randomly distributed hills and holes on road surface requires a more detailed analysis of sensor signals; recent papers cover only standard defined road surface analysis.

Future research will evaluate non-standard road artefact evaluation and data fusion with a navigation system and issue the commands for vehicle suspension from obtained sensor data.