Multiple Attribute Decision Making Based on Linguistic Generalized Weighted Heronian Mean

Abstract

In actual multiple attribute decision making, people often use language to evaluate attributes of the object, and sometimes there are associations between the attributes. Therefore, the study of multiple attribute decision making with language as attributes and associations between attributes is of great theoretical significance and practical value. The Heronian mean is not only an operator which reflects the associations between attributes, but also has excellent properties, including idempotency, monotonicity, boundedness, parameter symmetry, and alternate symmetry. In this paper, firstly a new linguistic generalized weighted Heronian mean (LGWHM) was provided, and its properties including idempotency, monotonicity, boundedness, and limit were studied. Then, a new three-parameter linguistic generalized weighted Heronian mean (TPLGWHM) and its idempotency, monotonicity, and boundedness properties were proposed. Finally, multi-attribute decision making methods based on the new linguistic generalized weighted Heronian mean were given, and an example was analyzed and compared with other methods.

1. Introduction

Multiple attribute decision making is a significant branch of contemporary decision-making theory. Its theory and method are widely used in many fields of management science and engineering [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28]. It usually uses the existing decision information to sort and choose a set of (limited) alternatives in a certain way. There are two core problems: One is how to ascertain the attribute weight when the attribute values are aggregated; the other is how to concentrate the attribute values, that is, how to determine the attribute value aggregation function (also known as integration operator) [29]. Scholars have given many integration operators and extended them to uncertain environments such as linguistic environment and fuzzy environment. Generalized mean is an important operator. Dyckhoff and Pedrycz [30] proposed the generalized mean as connective operators for fuzzy set theory which easily allows for modeling the degree of compensation in a natural manner including the arithmetic and geometric means, as well as the maximum and minimum operators as special cases. The generalized mean can reflect the preference of decision makers and consider decision information from the overall perspective; thus, the research of generalized mean has attracted the attention of scholars.

In multiple attribute decision making, people often like to directly use language such as “excellent”, “good”, “medium”, and “poor” to evaluate some attributes of the evaluation object; thus, the study of information integration operator with language as attribute value is very significant. At present, great achievements have been made in the research of language integration operators. Rodriguez [31] presented the concept of a hesitant fuzzy linguistic term set, and gave a multiple criteria linguistic decision model. Experts provide their evaluation through the introduction of language expression in the model. Xu [32] gave an overview of multi-granularity linguistic group decision making from the aspects of transformation function and decision making process. Liu [33] extended the traditional geometric average, ordered geometric average and mixed geometric average to intuitionistic uncertain linguistic environment, and proposed three intuitionistic uncertain linguistic geometric average integration operators and two intuitionistic uncertain linguistic multi-attribute decision-making methods.

The traditional analysis theory of multiple attribute decision making usually assumes that the attributes are independent of each other, but in the actual multiple attribute decision making problems, there is sometimes a certain correlation between the attributes. For example, when selecting equipment according to the three attributes of price, quality and after-sales service, the price of equipment with high quality and after-sales service is not cheap. Each attribute has an effect on the other two attributes. Therefore, in the selection or construction of aggregation operator, for the aggregation problem of attributes with correlation relationship, it is often necessary to take this correlation factor into consideration, so as to make the decision-making more reasonable and objective. In fact, the Bonferroni mean, Heronian mean, and their generalization in the fuzzy environment, intuitionistic fuzzy environment, hesitant fuzzy environment, and linguistic environment are the main aggregation operators that can reflect the interaction between attributes. Liu [34] defined the three-parameter Heronian mean operator and the three-parameter weighted Heronian mean operator and extended them to linguistic environment. Yu [3] provided some new integration operators for intuitionistic fuzzy information, investigated properties of the proposed operators, and introduced an approach for multi-criteria decision making based on the intuitionistic fuzzy geometric weighed Heronian mean. Yin [35] proposed a new dynamic evaluation method considering the interaction between attributes of enterprise learning merit. Zhang, Zhang, Huang, and Wang [36] used Heronian mean information aggregation technology to fuse picture fuzzy numbers and proposed new picture fuzzy aggregation operators.

Therefore, it is of great significance to study the multiple attribute decision making with language as attributes and associations between attributes. Moreover, in actual decision-making, decision-makers need to evaluate decision-making objects from multiple perspectives, considering not only the interaction between attributes, but also the overall information of decision objects, as well as the risk preference of decision makers. Thus, in this paper, we proposed a new linguistic generalized weighted Heronian mean (LGWHM) operator, which has the advantages of both generalized mean and Heronian mean operator, and can reflect the information integrity, and attribute relevance and decision-maker’s risk preference. Considering the multi-association between input variables, we further propose a new three-parameter linguistic generalized weighted Heronian mean (TPLGWHM). On these bases, multiple attribute decision making methods based on the new linguistic generalized weighted Heronian mean are given, and an example is analyzed and compared with other methods.

The remaining of this article is formed as below. In Section 2, a number of basic concepts are presented. In Section 3, a novel linguistic generalized weighted Heronian mean (LGWHM) is provided, and its idempotency, monotonicity, boundedness, and limit properties are studied. Then a new three-parameter linguistic generalized weighted Heronian mean (TPLGWHM) and its idempotency, monotonicity, and boundedness properties are proposed. In Section 4, multi-attribute decision making methods based on the new linguistic generalized weighted Heronian mean are given, and an example is analyzed and compared with other methods. The conclusions are given in Section 5.

2. Preliminaries

Let $\mathrm{H}=\left\{{\mathsf{\xi }}_0,{\mathsf{\xi }}_1,\cdots ,{\mathsf{\xi }}_{\mathrm{t}}\right\}$ be a linguistic term set. The number of its elements is generally odd, that is, t is even. The number of its elements is called granularity, and ${\mathsf{\xi }}_{\mathrm{i}}$is the linguistic evaluation value of information, which satisfies the following four properties [37]:

(1) The elements in$\mathrm{H}$ are ordered, that is, if $i>j$, then ${\xi }_i>{\xi }_j$ (that is, ${\xi }_i$ is better than ${\xi }_j$);

(2) There is a negative operator, i.e., $\mathrm{neg}\left({\xi }_j\right)={\xi }_i$, where $i=t-j$;

(3) If ${\xi }_i\ge {\xi }_j$, then $\max \left\{{\xi }_i,{\xi }_j\right\}={\xi }_i$;

(4) If ${\xi }_i\le {\xi }_j$, then $\min \left\{{\xi }_i,{\xi }_j\right\}={\xi }_i$.

In general, $\mathrm{t}$is taken as a smaller even number, usually no more than 8. For example, $\mathrm{H}=\left\{{\mathsf{\xi }}_0,{\mathsf{\xi }}_1,{\mathsf{\xi }}_2,{\mathsf{\xi }}_3,{\mathsf{\xi }}_4\right\}$ means {poor, bad, medium, good, better}, or $\mathrm{H}=\left\{{\mathsf{\xi }}_0,{\mathsf{\xi }}_1,{\mathsf{\xi }}_2,{\mathsf{\xi }}_3,{\mathsf{\xi }}_4,{\mathsf{\xi }}_5,{\mathsf{\xi }}_6,{\mathsf{\xi }}_7,{\mathsf{\xi }}_8\right\}$ means {extremely poor, very poor, poor, slightly poor, medium, slightly good, good, very good, excellent}.

For the linguistic term set $\mathrm{H}=\left\{{\mathsf{\xi }}_1,{\mathsf{\xi }}_2,\cdots ,{\mathsf{\xi }}_{\mathrm{t}}\right\}$, its element ${\mathsf{\xi }}_{\mathrm{i}}$is strictly incremented by subscript. In practical application, in order to avoid the loss of information, Xu [38] extended the discrete linguistic term set to continuous form, and obtained a new continuous linguistic term set, called extended language term set: $\overline{\mathrm{H}}=\left\{{\mathsf{\xi }}_{\mathsf{\beta }}\right|{\mathsf{\xi }}_{-\mathrm{p}}\le {\mathsf{\xi }}_{\mathsf{\beta }}\le {\mathsf{\xi }}_{\mathrm{p}},\mathsf{\beta }\in \left[-\mathrm{p},\mathrm{p}\right]\}$, where $\mathrm{p}$ is a sufficiently large positive integer. If ${\mathsf{\xi }}_{\mathsf{\beta }}\in H$, then ${\mathsf{\xi }}_{\mathsf{\beta }}$ is the original linguistic term, otherwise ${\mathsf{\xi }}_{\mathsf{\beta }}$ is called virtual linguistic term. The extended language term set also increases strictly according to the subscript. In addition, unless otherwise stated, the following language terms are all elements of the expanded language terms set.

Xu [38,39] provided the following operation rules of language variables:

${\xi }_l⊞{\xi }_m={\xi }_{l+m}; \lambda {\xi }_l={\xi }_{\lambda l}; {\left({\xi }_l\right)}^{\lambda }={\xi }_{l^{\lambda }}; {\xi }_l⊠{\xi }_m={\xi }_{lm};{\xi }_l\boxminus {\xi }_m={\xi }_{l-m};{\xi }_l\oslash {\xi }_m={\xi }_{l/m}$,

and further provided the following operation rules:

Let ${\xi }_l,{\xi }_m,{\xi }_k\in H$, then ${\xi }_l⊞{\xi }_m={\xi }_m⊞{\xi }_l; {\xi }_l⊠{\xi }_m={\xi }_m⊠{\xi }_l; ({\xi }_l⊞{\xi }_m)⊞{\xi }_k={\xi }_l⊞({\xi }_m⊞{\xi }_k);\lambda ({\xi }_l⊞{\xi }_m)=\lambda {\xi }_m⊞\lambda {\xi }_l$; $({\xi }_l⊠{\xi }_m)⊠{\xi }_k={\xi }_l⊠({\xi }_m⊠{\xi }_k);$ ${\lambda }_1{\xi }_l⊞{\lambda }_2{\xi }_l=\left({\lambda }_1+{\lambda }_2\right){\xi }_l;$ ${({\xi }_l⊠{\xi }_m)}^{\lambda }={\xi }_l^{\lambda }⊠{\xi }_m^{\lambda }; {\xi }_l^{{\lambda }_1}⊠{\xi }_l^{{\lambda }_2}={\xi }_l^{{\lambda }_1+{\lambda }_2}$.

3. The New Linguistic Generalized Weighted Heronian Mean

First, we provide linguistic Heronian mean.

Definition 1.

[34] Let ${\xi }_1,{\xi }_2,\cdots ,{\xi }_n$be a group of language terms, $\mu ,\nu \ge 0$. Then the linguistic Heronian mean (LHM) aggregation operator is:

$$LH{M}^{\mu ,\nu }({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)={\left(\frac{2}{n(n+1)}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=i}^n{\left({\xi }_i\right)}^{\mu }{\left({\xi }_j\right)}^{\nu }}}\right)}^{\frac{1}{\mu +\nu }}.$$

Remark. 

$LH{M}^{\mu ,\nu }\left({\xi }_1,{\xi }_2,\cdots ,{\xi }_n\right)$ has idempotency, monotonicity, boundedness, parameter symmetry properties, and alternate symmetry.

Theorem 1.

[34] Let ${\xi }_i=h_{{\theta }_i}\left(i=1,2,\cdots ,n\right)$ be a group of language terms, $\mu ,\nu \ge 0$, then:

$$LH{M}^{\mu ,\nu }({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)=h_{{\left(\frac{2}{n(n+1)}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=i}^n{\left({\theta }_i\right)}^{\mu }{\left({\theta }_j\right)}^{\nu }}}\right)}^{\frac{1}{\mu +\nu }}}.$$

In order to provide some properties of the new linguistic generalized weighted Heronian mean, we first provide the following two lemmas.

Lemma 1.

[40] Let $y_l\ge 0, l=1,2,\cdots ,n,$and then the generalized mean aggregation operator:

$$WP(y_1,y_2,\cdots ,y_n)={\left({\displaystyle \sum _{l=1}^n{w}_i{y}_i^t}\right)}^{1/t}$$

which is monotonically increasing with respect to the parameter $t$ and increasing with respect to each independent variable.

Lemma 2.

[40] Let $y_i\ge 0, i=1,2,\cdots ,n.$Then the generalized mean aggregation operator:

$$WP(y_1,y_2,\cdots ,y_n)={\left({\displaystyle \sum _{i=1}^n{w}_i{y}_i^t}\right)}^{1/t}$$

which has the following limit properties:

$$\begin{array}{l}(1) \underset{t\to 0}{\lim }{\left({\sum }_{i=1}^n{w}_i{y}_i^t\right)}^{1/t}={\prod }_{i=1}^n{y}_i^{w_i}, \\ (2) \underset{t\to +\infty }{\lim }{\left({\sum }_{i=1}^n{w}_i{y}_i^t\right)}^{1/t}=\max \left\{y_1,y_2,\cdots ,y_n\right\},\\ (3) \underset{t\to -\infty }{\lim }{\left({\sum }_{i=1}^n{w}_i{y}_i^t\right)}^{1/t}=\min \left\{y_1,y_2,\cdots ,y_n\right\}.\end{array}$$

Definition 2.

Let ${\xi }_1,{\xi }_2,\cdots ,{\xi }_n$ be a group of language terms. If $p,q\ne 0$, then:

$$LGH{M}^{p,q}({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)={\left[\frac{2}{n(n+1)}\underset{i,j=1,j=i}{\overset{n}{⊞}}{\left(\frac{\mu }{\mu +\nu }{\xi }_i^p⊞\frac{\nu }{\mu +\nu }{\xi }_j^p\right)}^{q/p}\right]}^{1/q},$$

which is called the linguistic generalized Heronian mean(LGHM) aggregation operator.

Theorem 2.

Let ${\xi }_l=h_{{\theta }_l}\left(l=1,2,\cdots ,n\right)$ be a group of language terms. If $p,q\ne 0$, then:

$$LGH{M}^{p,q}({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)=h_{{\left[\frac{2}{n(n+1)}{\displaystyle \sum _{i,j=1,j=i}^n{\left(\frac{\mu {\theta }_i^p+\nu {\theta }_j^p}{\mu +\nu }\right)}^{q/p}}\right]}^{1/q}}.$$

Proof. 

According to the operation rules of language variables, we find: ${\xi }_i^p=h_{{\theta }_i{}^p}$, ${\xi }_j^p=h_{{\theta }_j{}^p}$. Then:

$$\frac{\mu }{\mu +\nu }{\xi }_i^p⊞\frac{\nu }{\mu +\nu }{\xi }_j^p=h_{\frac{\mu {\theta }_i^p+\nu {\theta }_j^p}{\mu +\nu }}.$$

Thus:

$$\underset{i,j=1,j=i}{\overset{n}{⊞}}{\left(\frac{\mu }{\mu +\nu }{\xi }_i^p⊞\frac{\nu }{\mu +\nu }{\xi }_j^p\right)}^{q/p}=h_{{\displaystyle \sum _{i,j=1,j=i}^n{\left(\frac{\mu {\theta }_i^p+\nu {\theta }_j^p}{\mu +\nu }\right)}^{q/p}}}.$$

Therefore:

$${\left[\frac{2}{n(n+1)}\underset{i,j=1,j=i}{\overset{n}{⊞}}{\left(\frac{\mu }{\mu +\nu }{\xi }_i^p⊞\frac{\nu }{\mu +\nu }{\xi }_j^p\right)}^{q/p}\right]}^{1/q}=h_{{\left[\frac{2}{n(n+1)}{\displaystyle \sum _{i,j=1,j=i}^n{\left(\frac{\mu {\theta }_i^p+\nu {\theta }_j^p}{\mu +\nu }\right)}^{q/p}}\right]}^{1/q}},$$

that is:

$$LGH{M}^{p,q}({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)=h_{{\left[\frac{2}{n(n+1)}{\displaystyle \sum _{i,j=1,j=i}^n{\left(\frac{\mu {\theta }_i^p+\nu {\theta }_j^p}{\mu +\nu }\right)}^{q/p}}\right]}^{1/q}}.$$

The proof is complete. □

Theorem 3.

$LGHM$ operator has the following properties:

(1) Idempotency. If ${\xi }_i=\zeta \left(i=1,2,\cdots ,n\right),$ then $LGH{M}^{p,q}(\varsigma ,\varsigma ,\cdots ,\varsigma )=\varsigma$.

In fact, if $\varsigma =h_{\theta }$, then:

$$\begin{array}{l}LGH{M}^{p,q}(\varsigma ,\varsigma ,\cdots ,\varsigma )={\left[\frac{2}{n(n+1)}\underset{i,j=1,j=i}{\overset{n}{⊞}}{\left(\frac{\mu }{\mu +\nu }{\varsigma }_{}^p⊞\frac{\nu }{\mu +\nu }{\varsigma }_{}^p\right)}^{q/p}\right]}^{1/q}\\ =h_{{\left[\frac{2}{n(n+1)}{\displaystyle \sum _{i,j=1,j=i}^n{\left(\frac{\mu }{\mu +\nu }{\theta }_{}^p+\frac{\nu }{\mu +\nu }{\theta }_{}^p\right)}^{q/p}}\right]}^{1/q}}=h_{{\left[{\theta }^q\left(\frac{2}{n(n+1)}{\displaystyle \sum _{i,j=1,j=i}^n{\left(\frac{\mu }{\mu +\nu }+\frac{\nu }{\mu +\nu }\right)}^{q/p}}\right)\right]}^{1/q}}=h_{\theta }=\varsigma \end{array}.$$

That is, $LGHM$ operator is idempotent.

(2) Monotonicity. If ${\xi }_i\le {\varsigma }_i,{ \xi }_i=h_{{\theta }_i}\left(i=1,2,\cdots ,n\right), p,q\ge 0,$then:

$$LGH{M}^{p,q}({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)\le LGH{M}^{p,q}({\varsigma }_1,{\varsigma }_2,\cdots ,{\varsigma }_n).$$

Proof. 

Let $f({\theta }_1,{\theta }_2,\cdots ,{\theta }_n)\triangleq {\left[\frac{2}{n(n+1)}{\displaystyle \sum _{i,j=1,j=i}^n{\left(\frac{\mu }{\mu +\nu }{\theta }_i^p+\frac{\nu }{\mu +\nu }{\theta }_j^p\right)}^{q/p}}\right]}^{1/q}$, and then by:

$$\begin{array}{l}\frac{\partial f}{\partial {\theta }_i}\\ ={\left[\frac{2}{qn(n+1)}{\displaystyle \sum _{i,j=1,j=i}^n{\left(\frac{\mu }{\mu +\nu }{\theta }_i^p+\frac{\nu }{\mu +\nu }{\theta }_j^p\right)}^{q/p}}\right]}^{1/q-1}\left[\frac{q}{p}{\displaystyle \sum _{i,j=1,j=i}^n{\left(\frac{\mu }{\mu +\nu }{\theta }_i^p+\frac{\nu }{\mu +\nu }{\theta }_j^p\right)}^{q/p-1}}\right]\frac{p\mu {\theta }_i^{p-1}}{\mu +\nu }\\ =\frac{\mu q{\theta }_i^{p-1}}{\mu +\nu }{\left[\frac{2}{qn(n+1)}{\displaystyle \sum _{i,j=1,j=i}^n{\left(\frac{\mu }{\mu +\nu }{\theta }_i^p+\frac{\mu }{\mu +\nu }{\theta }_j^p\right)}^{q/p}}\right]}^{1/q-1}\left[{\displaystyle \sum _{i,j=1,j=i}^n{\left(\frac{\mu }{\mu +\nu }{\theta }_i^p+\frac{\nu }{\mu +\nu }{\theta }_j^p\right)}^{q/p-1}}\right]\\ \ge 0.\end{array}$$

We know that the function $f({\theta }_1,{\theta }_2,\cdots ,{\theta }_n)$ is monotonically increasing with respect to each independent variable. According to the property (1) of language term set in preliminaries, we can know that, for any ${\xi }_i\le {\varsigma }_i\left(i=1,2,\cdots ,n\right),$ there is:

$$LGH{M}^{p,q}({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)\le LGH{M}^{p,q}({\varsigma }_1,{\varsigma }_2,\cdots ,{\varsigma }_n).\square$$

(3) Boundedness.$\min \{{\xi }_1,{\xi }_2,\cdots ,{\xi }_n\}\le LGH{M}^{p,q}({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)\le \max \{{\xi }_1,{\xi }_2,\cdots ,{\xi }_n\}$.

Proof. 

Without losing generality, let $\min \left\{{\xi }_1,{\xi }_2,\cdots ,{\xi }_n\right\}={\xi }_1$, $\max \left\{{\xi }_1,{\xi }_2,\cdots ,{\xi }_n\right\}={\xi }_n$, and then we can know from the proof of monotonicity of $LGHM$ operator that $LGHM$ operator is increasing with respect to each independent variable ${\xi }_i\left(i=1,2,\cdots ,n\right)$, so there is:

$$LGH{M}^{p,q}({\xi }_1,{\xi }_1,\cdots ,{\xi }_1)\le LGH{M}^{p,q}({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)\le LGH{M}^{p,q}({\xi }_n,{\xi }_n,\cdots ,{\xi }_n).$$

From the idempotency of $LGHM$ operator, we can see that:

$$LGH{M}^{p,q}({\xi }_1,{\xi }_1,\cdots ,{\xi }_1)={\xi }_1, LGH{M}^{p,q}({\xi }_n,{\xi }_n,\cdots ,{\xi }_n)={\xi }_n.$$

So:

$${\xi }_1\le LGH{M}^{p,q}({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)\le {\xi }_n$$

That is:

$$\min \{{\xi }_1,{\xi }_2,\cdots ,{\xi }_n\}\le LGH{M}^{p,q}({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)\le \max \{{\xi }_1,{\xi }_2,\cdots ,{\xi }_n\}.$$

The proof is complete. □

The relationship between $LGH{M}^{p,q}({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)$ operator and linguistic geometric Heronian mean is provided as follows.

Theorem 4.

Let ${\xi }_l=h_{{\theta }_l}\left(l=1,2,\cdots ,n\right)$ be a group of language terms. If $p,q\ne 0$, then:

$$\begin{array}{l}\underset{q\to 0}{\lim }LGH{M}^{p,q}({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)\triangleq LGH{M}^{p,}{}^0({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)\\ =\underset{q\to 0}{\lim }{\left[\frac{2}{n(n+1)}\underset{i,j=1,j=i}{\overset{n}{⊞}}{\left(\frac{\mu }{\mu +\nu }{\xi }_i^p⊞\frac{\nu }{\mu +\nu }{\xi }_j^p\right)}^{q/p}\right]}^{1/q}=h_{{\left[{\displaystyle \prod _{i,j=1,j=i}^n{\left(\frac{\mu }{\mu +\nu }{\theta }_i^p+\frac{\nu }{\mu +\nu }{\theta }_j^p\right)}^{1/p}}\right]}^{\frac{2}{n(n+1)}}}\end{array}.$$

In particular, if we set $p=1$, then:

$$LGH{M}^{1,0}({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)=h_{{\left({\displaystyle \prod _{i,j=1,j=i}^n\frac{\mu }{\mu +\nu }{x}_i+\frac{\nu }{\mu +\nu }{x}_j}\right)}^{\frac{2}{n(n+1)}}}.$$

Proof. 

According to Lemma 2, we attain:

$$\begin{array}{l}\underset{q\to 0}{\lim }LGH{M}^{p,q}({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)=\underset{q\to 0}{\lim }{\left[\frac{2}{n(n+1)}\underset{i,j=1,j=i}{\overset{n}{⊞}}{\left(\frac{\mu }{\mu +\nu }{\xi }_i^p⊞\frac{\mu }{\mu +\nu }{\xi }_j^p\right)}^{q/p}\right]}^{1/q}\\ =\underset{q\to 0}{\lim }{h}_{{\left[\frac{2}{n(n+1)}{\displaystyle \sum _{i,j=1,j=i}^n{\left(\frac{\mu }{\mu +\nu }{\theta }_i^p+\frac{\nu }{\mu +\nu }{\theta }_j^p\right)}^{q/p}}\right]}^{1/q}}\end{array}.$$

Then:

$$\begin{array}{l}\underset{q\to 0}{\lim }{\left[\frac{1}{n(n+1)}{\displaystyle \sum _{i,j=1,j=i}^n{\left(\frac{\mu }{\mu +\nu }{\theta }_i^p+\frac{\nu }{\mu +\nu }{\theta }_j^p\right)}^{q/p}}\right]}^{1/q}\\ =\underset{q\to 0}{\lim }\exp \frac{\left[\ln {\displaystyle \sum _{i,j=1,j=i}^n{\left(\frac{\mu }{\mu +\nu }{\theta }_i^p+\frac{\nu }{\mu +\nu }{\theta }_j^p\right)}^{q/p}}-\ln n(n+1)\right]}{q}\end{array}.$$

Moreover:

$$\begin{array}{l}\underset{q\to 0}{\lim }\frac{\left[\ln {\displaystyle \sum _{i,j=1,j=i}^n{\left(\frac{\mu }{\mu +\nu }{\theta }_i^p+\frac{\nu }{\mu +\nu }{\theta }_j^p\right)}^{q/p}}-\ln n(n+1)\right]}{q}=\underset{q\to 0}{\lim }\frac{{\left[{\displaystyle \sum _{i,j=1,j=i}^n{\left(\frac{\mu }{\mu +\nu }{\theta }_i^p+\frac{\nu }{\mu +\nu }{\theta }_j^p\right)}^{q/p}}\right]}^{\prime }}{{\displaystyle \sum _{i,j=1,j=i}^n{\left(\frac{\mu }{\mu +\nu }{\theta }_i^p+\frac{\nu }{\mu +\nu }{\theta }_j^p\right)}^{q/p}}}\\ =\underset{q\to 0}{\lim }\frac{{\displaystyle \sum _{i,j=1,j=i}^n{\left(\frac{\mu }{\mu +\nu }{\theta }_i^p+\frac{\nu }{\mu +\nu }{\theta }_j^p\right)}^{q/p}\ln {\left(\frac{\mu }{\mu +\nu }{\theta }_i^p+\frac{\nu }{\mu +\nu }{\theta }_j^p\right)}^{1/p}}}{{\displaystyle \sum _{i,j=1,j=i}^n{\left(\frac{\mu }{\mu +\nu }{\theta }_i^p+\frac{\nu }{\mu +\nu }{\theta }_j^p\right)}^{q/p}}}\\ =\frac{2}{n(n+1)}{\displaystyle \sum _{i,j=1,j=i}^n\ln {\left(\frac{\mu }{\mu +\nu }{\theta }_i^p+\frac{\nu }{\mu +\nu }{\theta }_j^p\right)}^{1/p}}=\ln {\left[{\displaystyle \prod _{i,j=1,j=i}^n{\left(\frac{\mu }{\mu +\nu }{\theta }_i^p+\frac{\nu }{\mu +\nu }{\theta }_j^p\right)}^{1/p}}\right]}^{\frac{2}{n(n+1)}}\end{array}$$

then, we have:

$$\underset{q\to 0}{\lim }LGH{M}^{p,q}({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)=h_{{\left[{\displaystyle \prod _{i,j=1,j=i}^n{\left(\frac{\mu }{\mu +\nu }{\theta }_i^p+\frac{\nu }{\mu +\nu }{\theta }_j^p\right)}^{1/p}}\right]}^{\frac{2}{n(n+1)}}}.$$

The proof is complete. □

Remark. 

$LGH{M}^{1,0}({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)$is the linguistic geometric Heronian mean.

Next, we provide a new linguistic generalized weighted Heronian mean aggregation operator.

Definition 3.

Let ${\xi }_1,{\xi }_2,\cdots ,{\xi }_n$ be a group of language terms, $let p,q\ne 0$, and let $w_l\left(l=1,2,\cdots ,n\right)$ be the weight of ${\xi }_l$, where $w_l\ge 0, {\sum }_{l=1}^n{w}_l=1$. Then:

$$LGWH{M}^{p,q}({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)={\left[\frac{1}{\lambda }\underset{i,j=1,j=i}{\overset{n}{⊞}}{\left(w_i{\xi }_i^p⊞w_j{\xi }_j^p\right)}^{q/p}\right]}^{1/q}$$

is called the linguistic generalized weighted Heronian mean aggregation operator, where:

$$\lambda ={\displaystyle \sum _{i,j=1,j=i}^n{\left(w_i+w_j\right)}^{q/p}}.$$

Theorem 5.

Let ${\xi }_l=h_{{\theta }_l}\left(l=1,2,\cdots ,n\right)$ be a group of language terms, $let p,q\ne 0$, and let $w_l\left(l=1,2,\cdots ,n\right)$ be the weight of ${\xi }_l,$ where $w_l\ge 0, {\sum }_{l=1}^n{w}_l=1$. Then:

$$LGWH{M}^{p,q}({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)=h_{{\left[\frac{1}{\lambda }{\displaystyle \sum _{i,j=1,j=i}^n{\left(w_i{\theta }_i^p+w_j{\theta }_j^p\right)}^{q/p}}\right]}^{1/q}},$$

where:$\lambda ={\displaystyle \sum _{i,j=1,j=i}^n{\left(w_i+w_j\right)}^{q/p}}$.

Proof. 

According to the operation rules of language variables, we find: ${\xi }_i^p=h_{{\theta }_i{}^p}$, ${\xi }_j^p=h_{{\theta }_j{}^p}$. then:

$$w_i{\xi }_i^p⊞w_j{\xi }_j^p=h_{w_i{\theta }_i^p+w_j{\theta }_j^p}.$$

Thus:

$$\underset{i,j=1,j=i}{\overset{n}{⊞}}{\left(w_i{\xi }_i^p⊞w_j{\xi }_j^p\right)}^{q/p}=h_{{\displaystyle \sum _{i,j=1,j=i}^n{\left(w_i{\theta }_i^p+w_j{\theta }_j^p\right)}^{q/p}}}.$$

Therefore:

$${\left[\frac{1}{\lambda }\underset{i,j=1,j=i}{\overset{n}{⊞}}{\left(w_i{\xi }_i^p⊞w_j{\xi }_j^p\right)}^{q/p}\right]}^{1/q}=h_{{\left[\frac{1}{\lambda }{\displaystyle \sum _{i,j=1,j=i}^n{\left(w_i{\theta }_i^p+w_j{\theta }_j^p\right)}^{q/p}}\right]}^{1/q}},$$

that is:

$$LGWH{M}^{p,q}({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)=h_{{\left[\frac{1}{\lambda }{\displaystyle \sum _{i,j=1,j=i}^n{\left(w_i{\theta }_i^p+w_j{\theta }_j^p\right)}^{q/p}}\right]}^{1/q}}.$$

The proof is complete. □

Theorem 6.

$LGWHM$ operator has the following properties:

(1) Idempotency. If ${\xi }_i=\zeta \left(i=1,2,\cdots ,n\right),$ then $LGWH{M}^{p,q}(\varsigma ,\varsigma ,\cdots ,\varsigma )=\varsigma$.

In fact, let $\varsigma =h_{\theta }$, then:

$$\begin{array}{l}LGWH{M}^{p,q}(\varsigma ,\varsigma ,\cdots ,\varsigma )={\left[\frac{1}{\lambda }\underset{i,j=1,j=i}{\overset{n}{⊞}}{\left(w_i{\varsigma }_{}^p⊞w_j{\varsigma }_{}^p\right)}^{q/p}\right]}^{1/q}=h_{{\left[\frac{1}{\lambda }{\displaystyle \sum _{i,j=1,j=i}^n{\left(w_i{\theta }_{}^p+w_j{\theta }_{}^p\right)}^{q/p}}\right]}^{1/q}}\\ =h_{{\left[{\theta }^q\left(\frac{1}{\lambda }{\displaystyle \sum _{i,j=1,j=i}^n{\left(w_i+w_j\right)}^{q/p}}\right)\right]}^{1/q}}=h_{\theta }=\varsigma \end{array}.$$

That is, $LGWHM$operator is idempotent.

(2) Monotonicity. If ${\xi }_i\le {\varsigma }_i,{ \xi }_i=h_{{\theta }_i}\left(i=1,2,\cdots ,n\right), p,q\ge 0,$then:

$$LGWH{M}^{p,q}({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)\le LGWH{M}^{p,q}({\varsigma }_1,{\varsigma }_2,\cdots ,{\varsigma }_n).$$

Proof. 

Let $f({\theta }_1,{\theta }_2,\cdots ,{\theta }_n)\triangleq {\left[\frac{1}{\lambda }{\displaystyle \sum _{i,j=1,j=i}^n{\left(w_i{\theta }_i^p+w_j{\theta }_j^p\right)}^{q/p}}\right]}^{1/q}$, and then by:

$$\begin{array}{l}\frac{\partial f}{\partial {\theta }_i}={\left[\frac{1}{\lambda q}{\displaystyle \sum _{i,j=1,j=i}^n{\left(w_i{\theta }_i^p+w_j{\theta }_j^p\right)}^{q/p}}\right]}^{1/q-1}\left[\frac{q}{p}{\displaystyle \sum _{i,j=1,j=i}^n{\left(w_i{\theta }_i^p+w_j{\theta }_j^p\right)}^{q/p-1}}\right]\left(p{w}_i{\theta }_i^{p-1}\right)\\ =q{w}_i{\theta }_i^{p-1}{\left[\frac{1}{\lambda q}{\displaystyle \sum _{i,j=1,j=i}^n{\left(w_i{\theta }_i^p+w_j{\theta }_j^p\right)}^{q/p}}\right]}^{1/q-1}\left[{\displaystyle \sum _{i,j=1,j=i}^n{\left(w_i{\theta }_i^p+w_j{\theta }_j^p\right)}^{q/p-1}}\right]\ge 0\end{array},$$

we know that the function $f({\theta }_1,{\theta }_2,\cdots ,{\theta }_n)$ is monotonically increasing with respect to each independent variable. According to the property (1) of language term set in preliminaries, we can know that, for any ${\xi }_i\le {\varsigma }_i\left(i=1,2,\cdots ,n\right),$there is:

$$LGWH{M}^{p,q}({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)\le LGWH{M}^{p,q}({\varsigma }_1,{\varsigma }_2,\cdots ,{\varsigma }_n).$$

The proof is complete. □

(3) Boundedness. $\min \{{\xi }_1,{\xi }_2,\cdots ,{\xi }_n\}\le LGWH{M}^{p,q}({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)\le \max \{{\xi }_1,{\xi }_2,\cdots ,{\xi }_n\}$.

Proof. 

Without losing generality, let $\min \{{\xi }_1,{\xi }_2,\cdots ,{\xi }_n\}={\xi }_1$,$\max \{{\xi }_1,{\xi }_2,\cdots ,{\xi }_n\}={\xi }_n$, and then we can know from the proof of monotonicity of $LGWHM$ operator that $LGWHM$ operator is increasing with respect to each independent variable ${\xi }_i\left(i=1,2,\cdots ,n\right)$, so there is:

$$LGWH{M}^{p,q}({\xi }_1,{\xi }_1,\cdots ,{\xi }_1)\le LGWH{M}^{p,q}({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)\le LGWH{M}^{p,q}({\xi }_n,{\xi }_n,\cdots ,{\xi }_n).$$

From the idempotency of $LGWHM$ operator, we can see that:

$$LGWH{M}^{p,q}({\xi }_1,{\xi }_1,\cdots ,{\xi }_1)={\xi }_1, LGWH{M}^{p,q}({\xi }_n,{\xi }_n,\cdots ,{\xi }_n)={\xi }_n.$$

So:

$${\xi }_1\le LGWH{M}^{p,q}({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)\le {\xi }_n.$$

that is:

$$\min \{{\xi }_1,{\xi }_2,\cdots ,{\xi }_n\}\le LGWH{M}^{p,q}({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)\le \max \{{\xi }_1,{\xi }_2,\cdots ,{\xi }_n\}.$$

The proof is complete. □

The relationship between $LGWH{M}^{p,q}({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)$ operator and linguistic geometric Heronian mean is provided as follows.

Theorem 7.

Let ${\xi }_l=h_{{\theta }_l}\left(l=1,2,\cdots ,n\right)$ be a group of language terms, $let p,q\ne 0$, and let $w_l\left(l=1,2,\cdots ,n\right)$ be the weight of ${\xi }_l,$ where $w_l\ge 0, {\sum }_{l=1}^n{w}_l=1$. Then:

$$\begin{array}{l}\underset{q\to 0}{\lim }LGWH{M}^{p,q}({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)\triangleq LGWH{M}^{p,}{}^0({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)\\ =\underset{q\to 0}{\lim }{\left[\frac{1}{\lambda }\underset{i,j=1,j=i}{\overset{n}{⊞}}{\left(w_i{\xi }_i^p⊞w_j{\xi }_j^p\right)}^{q/p}\right]}^{1/q}=h_{{\left[{\displaystyle \prod _{i,j=1,j=i}^n{\left(\frac{w_i}{w_i+w_j}{\theta }_i^p+\frac{w_j}{w_i+w_j}{\theta }_j^p\right)}^{1/p}}\right]}^{\frac{2}{n(n+1)}}}\end{array}.$$

In particular, if we set $p=1$, then:

$$LGWH{M}^{1,0}({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)=h_{{\left({\displaystyle \prod _{i,j=1,j=i}^n\frac{w_i}{w_i+w_j}{\theta }_i+\frac{w_j}{w_i+w_j}{\theta }_j}\right)}^{\frac{2}{n(n+1)}}}.$$

Proof. 

According to Lemma 2, we have:

$$\begin{array}{l}\underset{q\to 0}{\lim }LGWH{M}^{p,q}({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)=\underset{q\to 0}{\lim }{\left[\frac{1}{\lambda }\underset{i,j=1,j=i}{\overset{n}{⊞}}{\left(w_i{\xi }_i^p⊞w_j{\xi }_j^p\right)}^{q/p}\right]}^{1/q}\\ =\underset{q\to 0}{\lim }{h}_{{\left[\frac{1}{\lambda }{\displaystyle \sum _{i,j=1,j=i}^n{\left(w_i{\theta }_i^p+w_j{\theta }_j^p\right)}^{q/p}}\right]}^{1/q}}.\end{array}$$

Then:

$$\underset{q\to 0}{\lim }{\left[\frac{1}{\lambda }{\displaystyle \sum _{i,j=1,j=i}^n{\left(w_i{\theta }_i^p+w_j{\theta }_j^p\right)}^{q/p}}\right]}^{1/q}=\underset{q\to 0}{\lim }\exp \frac{\left[\ln {\displaystyle \sum _{i,j=1,j=i}^n{\left(w_i{\theta }_i^p+w_j{\theta }_j^p\right)}^{q/p}}-\ln \lambda \right]}{q}.$$

Moreover:

$$\begin{array}{l}\underset{q\to 0}{\lim }\frac{\left[\ln {\displaystyle \sum _{i,j=1,j=i}^n{\left(w_i{\theta }_i^p+w_j{\theta }_j^p\right)}^{q/p}}-\ln \lambda \right]}{q}=\underset{q\to 0}{\lim }\left\{\frac{{\left[{\displaystyle \sum _{i,j=1,j=i}^n{\left(w_i{\theta }_i^p+w_j{\theta }_j^p\right)}^{q/p}}\right]}^{\prime }}{{\displaystyle \sum _{i,j=1,j=i}^n{\left(w_i{\theta }_i^p+w_j{\theta }_j^p\right)}^{q/p}}}-\frac{{\lambda }^{\prime }}{\lambda }\right\}\\ =\underset{q\to 0}{\lim }\frac{{\displaystyle \sum _{i,j=1,j=i}^n{\left(w_i{\theta }_i^p+w_j{\theta }_j^p\right)}^{q/p}\ln {\left(w_i{\theta }_i^p+w_j{\theta }_j^p\right)}^{1/p}}}{{\displaystyle \sum _{i,j=1,j=i}^n{\left(w_i{\theta }_i^p+w_j{\theta }_j^p\right)}^{q/p}}}-\underset{q\to 0}{\lim }\frac{{\displaystyle \sum _{i,j=1,j=i}^n{\left(w_i+w_j\right)}^{q/p}\ln {\left(w_i+w_j\right)}^{1/p}}}{\lambda }\\ =\frac{2}{n(n+1)}\left[{\displaystyle \sum _{i,j=1,j=i}^n\ln {\left(w_i{\theta }_i^p+w_j{\theta }_j^p\right)}^{1/p}}-{\displaystyle \sum _{i,j=1,j=i}^n\ln {\left(w_i+w_j\right)}^{1/p}}\right]\\ =\frac{2}{n(n+1)}\left[{\displaystyle \sum _{i,j=1,j=i}^n\ln {\left(\frac{w_i{\theta }_i^p+w_j{\theta }_j^p}{w_i+w_j}\right)}^{1/p}}\right]=\frac{2}{n(n+1)}\left[{\displaystyle \sum _{i,j=1,j=i}^n\ln {\left(\frac{w_i}{w_i+w_j}{\theta }_i^p+\frac{w_j}{w_i+w_j}{\theta }_j^p\right)}^{1/p}}\right]\\ =\ln {\left[{\displaystyle \prod _{i,j=1,j=i}^n{\left(\frac{w_i}{w_i+w_j}{\theta }_i^p+\frac{w_j}{w_i+w_j}{\theta }_j^p\right)}^{1/p}}\right]}^{\frac{2}{n(n+1)}},\end{array}$$

then, we attain:

$$\underset{q\to 0}{\lim }LGWH{M}^{p,q}({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)=s_{{\left[{\displaystyle \prod _{i,j=1,j=i}^n{\left(\frac{w_i}{w_i+w_j}{\theta }_i^p+\frac{w_j}{w_i+w_j}{\theta }_j^p\right)}^{1/p}}\right]}^{\frac{2}{n(n+1)}}}.$$

The proof is complete. □

Remark. 

$LGWH{M}^{1,0}({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)$is the linguistic weighted geometric Heronian mean.

Next, we provide a new three-parameter linguistic generalized Heronian mean aggregation operator.

Definition 4.

Let ${\xi }_1,{\xi }_2,\cdots ,{\xi }_n$ be a group of language terms. If $p,q\ne 0$, and $\mu , \nu , \omega >0$, then:

$$\begin{array}{l}TPLGH{M}^{p,q}({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)\\ ={\left[\frac{6}{n(n+1)(n+2)}\underset{i,j,k=1,k=j=i}{\overset{n}{⊞}}{\left(\frac{\mu }{\mu +\nu +\omega }{\xi }_i^p⊞\frac{\nu }{\mu +\nu +\omega }{\xi }_j^p⊞\frac{\omega }{\mu +\nu +\omega }{\xi }_k^p\right)}^{q/p}\right]}^{1/q}\end{array}$$

is called the three-parameter linguistic generalized Heronian mean(TPLGH)aggregation operator.

Theorem 8.

Let ${\xi }_l=h_{{\theta }_l}\left(l=1,2,\cdots ,n\right)$ be a group of language terms. If $p,q\ne 0$, and $\mu , \nu , \omega >0$, then:

$$TPLGH{M}^{p,q}({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)=h_{{\left[\frac{6}{n(n+1)(n+2)}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=i}^n{\displaystyle \sum _{k=j}^n{\left(\frac{\mu }{\mu +\nu +\omega }{\theta }_i^p+\frac{\nu }{\mu +\nu +\omega }{\theta }_j^p+\frac{\omega }{\mu +\nu +\omega }{\theta }_k^p\right)}^{q/p}}}}\right]}^{1/q}}.$$

Theorem 9.

$TPLGHM$ operator has the following properties:

(1) Idempotency. If ${\xi }_l=\zeta \left(l=1,2,\cdots ,n\right)$, then $TPLGH{M}^{p,q}(\zeta ,\zeta ,\cdots ,\zeta )=\zeta$.

(2) Monotonicity. If ${\xi }_i\le {\zeta }_i$, ${\xi }_i=s_{{\theta }_i}$, ${\theta }_i\ge 0 \left(i=1,2,\cdots ,n\right),$ $p,q\ge 0,$ then

$$TPLGH{M}^{p,q}({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)\le TPLGH{M}^{p,q}({\zeta }_1,{\zeta }_2,\cdots ,{\zeta }_n).$$

(3) Boundedness. $\min \{{\xi }_1,{\xi }_2,\cdots ,{\xi }_n\}\le TPLGH{M}^{p,q}({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)\le \max \{{\xi }_1,{\xi }_2,\cdots ,{\xi }_n\}$.

Theorem 10.

Let ${\xi }_l=h_{{\theta }_l}\left(l=1,2,\cdots ,n\right)$ be a group of language terms. If$p,q\ne 0$, and $\mu , \nu , \omega >0$, then:

$$\begin{array}{l}\underset{q\to 0}{\lim }TPLGH{M}^{p,q}({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)\triangleq TPLGH{M}^{p,}{}^0({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)\\ =\underset{q\to 0}{\lim }{\left[\frac{6}{n(n+1)(n+2)}\underset{\begin{array}{l}i,j,k=1,\\ j=i=k\end{array}}{\overset{n}{⊞}}{\left(\frac{\mu }{\mu +\nu +\omega }{\xi }_i^p⊞\frac{\nu }{\mu +\nu +\omega }{\xi }_j^p⊞\frac{\omega }{\mu +\nu +\omega }{\xi }_k^p\right)}^{q/p}\right]}^{1/q}\\ =h_{{\left[{\displaystyle \prod _{\begin{array}{l}i,j,k=1,\\ j=i=k\end{array}}^n{\left(\frac{\mu }{\mu +\nu +\omega }{\theta }_i^p+\frac{\nu }{\mu +\nu +\omega }{\theta }_j^p+\frac{\omega }{\mu +\nu +\omega }{\theta }_k^p\right)}^{1/p}}\right]}^{\frac{6}{n(n+1)(n+2)}}}\end{array}.$$

In particular, if we set $p=1$, then:

$$TPLGH{M}^{1,}{}^0({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)=h_{{\left[{\displaystyle \prod _{\begin{array}{l}i,j,k=1,\\ j=i=k\end{array}}^n\left(\frac{\mu }{\mu +\nu +\omega }{\theta }_i+\frac{\nu }{\mu +\nu +\omega }{\theta }_j+\frac{\omega }{\mu +\nu +\omega }{\theta }_k\right)}\right]}^{\frac{6}{n(n+1)(n+2)}}}.$$

Definition 5.

Let ${\xi }_1,{\xi }_2,\cdots ,{\xi }_n$ be a group of language terms, let$p,q\ne 0$, and let $w_l\left(l=1,2,\cdots ,n\right)$ be the weight of ${\xi }_l$, where $w_l\ge 0, {\sum }_{l=1}^n{w}_l=1$. Then:

$$TPLGWH{M}^{p,q}({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)={\left[\frac{1}{\lambda }\underset{i,j,k=1,k=j=i}{\overset{n}{⊞}}{\left(w_i{\xi }_i^p⊞w_j{\xi }_j^p⊞w_k{\xi }_k^p\right)}^{q/p}\right]}^{1/q}$$

is called the three-parameter linguistic generalized weighted Heronian mean aggregation operator, where$\lambda ={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=i}^n{\displaystyle \sum _{k=j}^n{\left(w_i+w_j+w_k\right)}^{{}^{q/p}}}}}$.

Theorem 11.

Let ${\xi }_l=h_{{\theta }_l}\left(l=1,2,\cdots ,n\right)$ be a group of language terms, let$p,q\ne 0$, and let $w_l\left(l=1,2,\cdots ,n\right)$ be the weight of ${\xi }_l$, where $w_l\ge 0, {\sum }_{l=1}^n{w}_l=1$. Then:

$$TPLGWH{M}^{p,q}({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)=h_{{\left[\frac{1}{\lambda }{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=i}^n{\displaystyle \sum _{k=j}^n{\left(w_i{\theta }_i^p+w_j{\theta }_j^p+w_k{\theta }_k^p\right)}^{q/p}}}}\right]}^{1/q}}$$

where $\lambda ={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=i}^n{\displaystyle \sum _{k=j}^n{\left(w_i+w_j+w_k\right)}^{{}^{q/p}}}}}$.

Theorem 12.

$TPLGWHM$ operator has the following properties:

(1) Idempotency. If ${\xi }_l=\zeta \left(l=1,2,\cdots ,n\right)$, then $TPLGWH{M}^{p,q}(\zeta ,\zeta ,\cdots ,\zeta )=\zeta$.

(2) Monotonicity. If ${\xi }_i\le {\zeta }_i$, ${\xi }_i=h_{{\theta }_i}$, ${\theta }_i\ge 0 \left(i=1,2,\cdots ,n\right),$$p,q\ge 0,$ then:

$$TPLGWH{M}^{p,q}({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)\le TPLGWH{M}^{p,q}({\zeta }_1,{\zeta }_2,\cdots ,{\zeta }_n).$$

(3) Boundedness. $\min \{{\xi }_1,{\xi }_2,\cdots ,{\xi }_n\}\le TPLGWH{M}^{p,q}({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)\le \max \{{\xi }_1,{\xi }_2,\cdots ,{\xi }_n\}$.

The proof of the above three properties is similar to Theorem 6.

Theorem 13.

Let ${\xi }_l=h_{{\theta }_l}\left(l=1,2,\cdots ,n\right)$ be a group of language terms, $let p,q\ne 0$, and let $w_l\left(l=1,2,\cdots ,n\right)$ be the weight of ${\xi }_l,$where $w_l\ge 0, {\sum }_{l=1}^n{w}_l=1$. Then:

$$\begin{array}{l}\underset{q\to 0}{\lim }TPLGWH{M}^{p,q}({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)\triangleq TPLGWH{M}^{p,}{}^0({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)\\ =\underset{q\to 0}{\lim }{\left[\frac{1}{\lambda }\underset{i,j,k=1,j=i=k}{\overset{n}{⊞}}{\left(w_i{\xi }_i^p⊞w_j{\xi }_j^p⊞w_k{\xi }_k^p\right)}^{q/p}\right]}^{1/q}\\ =h_{{\left[{\displaystyle \prod _{i,j,k=1,j=i=k}^n{\left(\frac{w_i}{w_i+w_j+w_k}{\theta }_i^p+\frac{w_j}{w_i+w_j+w_k}{\theta }_j^p+\frac{w_k}{w_i+w_j+w_k}{\theta }_k^p\right)}^{1/p}}\right]}^{\frac{6}{n(n+1)(n+2)}}}\end{array}.$$

In particular, if we set $p=1$, then:

$$TPLGWH{M}^{1,}{}^0({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)=h_{{\left[{\displaystyle \prod _{i,j,k=1,j=i=k}^n\left(\frac{w_i}{w_i+w_j+w_k}{\theta }_i+\frac{w_j}{w_i+w_j+w_k}{\theta }_j+\frac{w_k}{w_i+w_j+w_k}{\theta }_k\right)}\right]}^{\frac{6}{n(n+1)(n+2)}}}.$$

4. Multiple Attribute Decision Making Methods Based on the Proposed Operators

The multiple attribute decision making methods based on the proposed operators were provided. Then the methods were analyzed by an example, which were compared with the existing multiple attribute decision making methods. The effectiveness of the proposed methods was illustrated, and the influence of parameters $p,q$ on the decision making results was analyzed.

4.1. Multiple Attribute Decision Making Based on the Proposed Operators

Let the scheme set be $\mathrm{X}=\left\{x_1,x_2,\cdots x_m\right\},$ attribute set be $\mathrm{U}=\left\{u_1,u_2,\cdots u_n\right\},$ and attribute weight vector be $\mathsf{\omega }=\left({\omega }_1,{\omega }_2,\cdots ,{\omega }_n\right),{ \mathsf{\omega }}_j\ge 0, {\sum }_{j=1}^n{\omega }_j=1.$

Step 1. The attribute value of scheme $x_i$ with respect to attribute $u_j$ is ${\xi }_{ij}$, which is given by the decision maker. ${\xi }_{ij}$ is language variable and the decision attribute matrix is $A={({\xi }_{ij})}_{mn},{\xi }_{ij}\ge 0,{\xi }_{ij}\in S(i=1,2,3,\dots ,m, j=1,2,3,\dots ,n)$.

Step 2. According to the new linguistic generalized weighted Heronian mean (LGWHM):

$$LGWH{M}^{p,q}({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)=h_{{\left[\frac{1}{\lambda }{\displaystyle \sum _{i,j=1,j=i}^n{\left(w_i{\theta }_i^p+w_j{\theta }_j^p\right)}^{q/p}}\right]}^{1/q}}$$

or the new three-parameter linguistic generalized weighted Heronian mean (TPLGWHM):

$$TPLGWH{M}^{p,q}({\xi }_1,{\xi }_2,\cdots ,{\xi }_n)=h_{{\left[\frac{1}{\lambda }{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=i}^n{\displaystyle \sum _{k=j}^n{\left(w_i{\theta }_i^p+w_j{\theta }_j^p+w_k{\theta }_k^p\right)}^{q/p}}}}\right]}^{1/q}}$$

the comprehensive evaluation value of each scheme is calculated.

Step 3. The comprehensive evaluation values of each scheme are sorted, and the decision results are provided.

4.2. An Illustrative Example

In order to illustrate the effectiveness of the decision-making methods given in this paper, the example in reference [34] was used for illustration, and the decision results were compared with the existing multiple attribute decision making methods.

Example. 

A unit made six assessment indicators for cadre selection: ideological and moral character $\left(u_1\right)$, work attitude $\left(u_2\right)$, work style $\left(u_3\right)$, cultural level and knowledge structure $\left(u_4\right)$, leadership ability $\left(u_5\right)$ and development ability $\left(u_6\right)$, and the weight vector is $\omega =\left(0.22,0.11,0.19,0.10,0.16,0.22\right)$. According to the six indexes mentioned above, the experts evaluated five candidates $x_i\left(i=1,2,3,4,5\right)$ with the linguistic scale $H=\left\{h_{-4}, h_{-3}, h_{-2}, h_{-1}, h_0,h_1, h_2, h_3, h_4\right\}$, and gave the linguistic decision matrix.

Table 1. Decision matrix.

	${\mathit{u}}_1$	${\mathit{u}}_2$	${\mathit{u}}_3$	${\mathit{u}}_4$	${\mathit{u}}_5$	${\mathit{u}}_6$
$x_1$	$h_3$	$h_1$	$h_{-1}$	$h_4$	$h_2$	$h_4$
$x_2$	$h_4$	$h_2$	$h_0$	$h_2$	$h_4$	$h_1$
$x_3$	$h_3$	$h_4$	$h_2$	$h_1$	$h_4$	$h_0$
$x_4$	$h_4$	$h_2$	$h_4$	$h_2$	$h_0$	$h_3$
$x_5$	$h_2$	$h_4$	$h_4$	$h_3$	$h_0$	$h_2$

is the decision matrix. Try to identify the best candidate.

A person’s ideological and moral character, work attitude, work style, cultural level and knowledge structure, leadership ability and development ability are not independent of each other, but interact with each other. For example, ideological and moral character has a positive impact on work attitude and work style, and work attitude has a promoting effect on work style and development ability. Similarly, one can analyze that each attribute has an impact on other attributes [34]. Therefore, the new linguistic generalized weighted Heronian mean operator given in this paper was considered for information aggregation.

1. First, we discussed the case of multiple attribute decision making based on the new linguistic generalized weighted Heronian mean (LGWHM).

We took different values of parameters $p$ and $q$, and calculated corresponding comprehensive attribute value of each scheme with the LGWHM operator.

Then we ranked the schemes according to the comprehensive attribute values. The results are shown in

Table 2. Ranking results for different $p,q$.

	$\mathit{h}({\mathit{x}}_1)$	$\mathit{h}({\mathit{x}}_2)$	$\mathit{h}({\mathit{x}}_3)$	$\mathit{h}({\mathit{x}}_4)$	$\mathit{h}({\mathit{x}}_5)$	Ranking Results
$p=1,q=1$	$h_{2.1800}$	$h_{2.1600}$	$h_{2.2200}$	$h_{2.7200}$	$h_{2.3800}$	$x_4>x_5>x_3>x_1>x_2$
$p=1,q=3$	$h_{2.8500}$	$h_{2.7414}$	$h_{2.5578}$	$h_{3.2178}$	$h_{2.6290}$	$x_4>x_1>x_2>x_5>x_3$
$p=1,q=10$	$h_{3.5159}$	$h_{3.4914}$	$h_{2.8557}$	$h_{3.6772}$	$h_{3.0237}$	$x_4>x_1>x_2>x_5>x_3$
$p=3,q=3$	$h_{3.0228}$	$h_{2.9708}$	$h_{2.9178}$	$h_{3.2352}$	$h_{2.9403}$	$x_4>x_1>x_2>x_5>x_3$
$p=10,q=1$	$h_{2.9539}$	$h_{2.7306}$	$h_{2.8810}$	$h_{3.0444}$	$h_{2.9679}$	$x_4>x_5>x_1>x_3>x_2$
$p=10,q=3$	$h_{3.2533}$	$h_{3.1872}$	$h_{3.2176}$	$h_{3.3449}$	$h_{3.2339}$	$x_4>x_1>x_5>x_3>x_2$
$p=10,q=10$	$h_{3.5830}$	$h_{3.6313}$	$h_{3.5251}$	$h_{3.6699}$	$h_{3.5534}$	$x_4>x_2>x_1>x_5>x_3$

.

It can be seen from Table 2 that when $p$ and $q$ took different values, the ranking results were relatively stable, and the best scheme remained unchanged. However, with the change of parameters $p$ and $q$, the ranking results of schemes also changed.

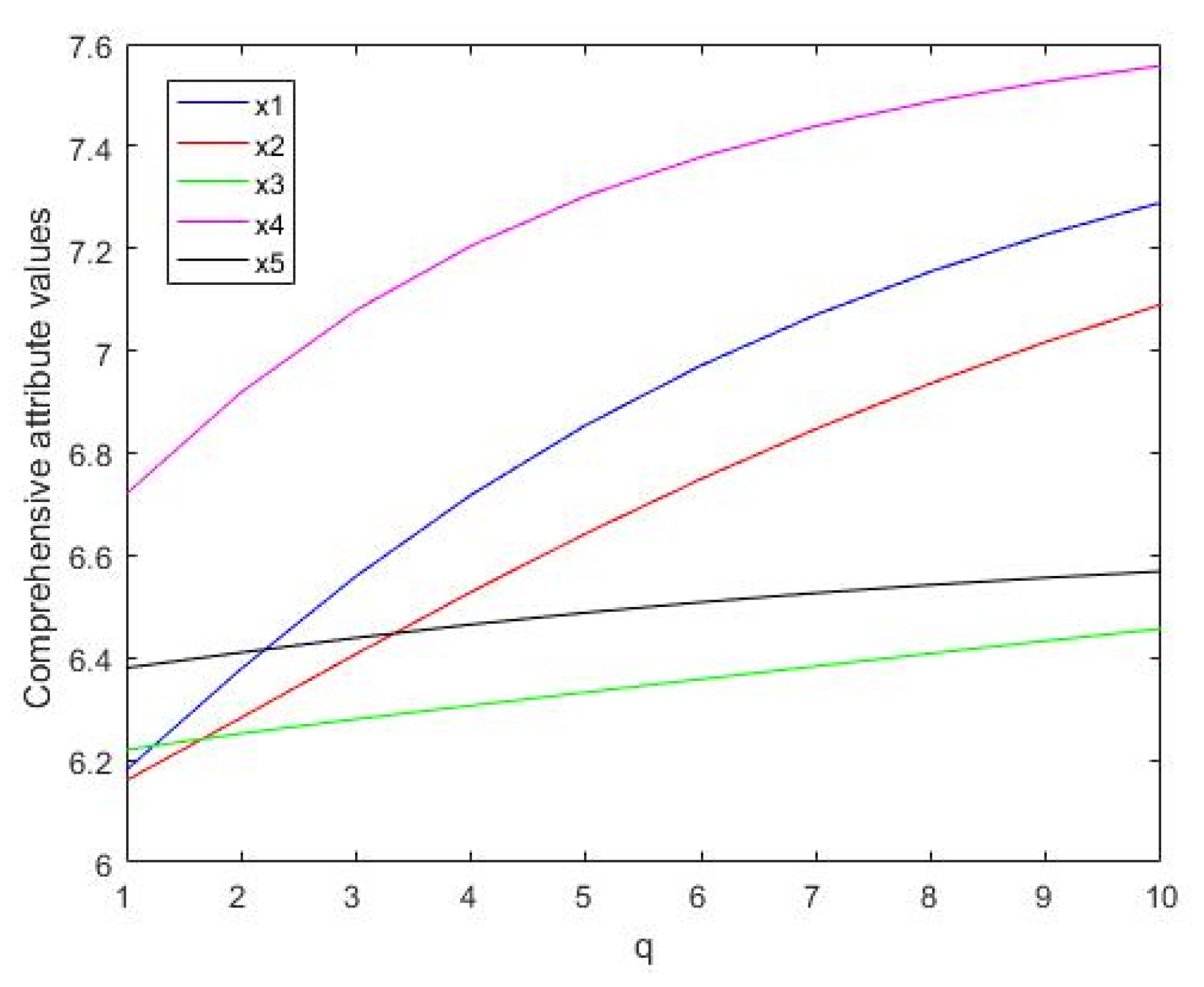
We fixed the value of parameter $p\left(p=1\right)$ and $q$ was taken from 1 to 10. The change of comprehensive attribute value of each scheme based on LGWHM is shown in Figure 1. We fixed the value of parameter $q\left(q=1\right)$ and $p$ was taken from 1 to 10. The change of comprehensive attribute value of each scheme based on LGWHM is shown in Figure 2. To facilitate drawing, we adjusted the granularity to a positive number, that is, the granularity was adjusted from 0 to 8.

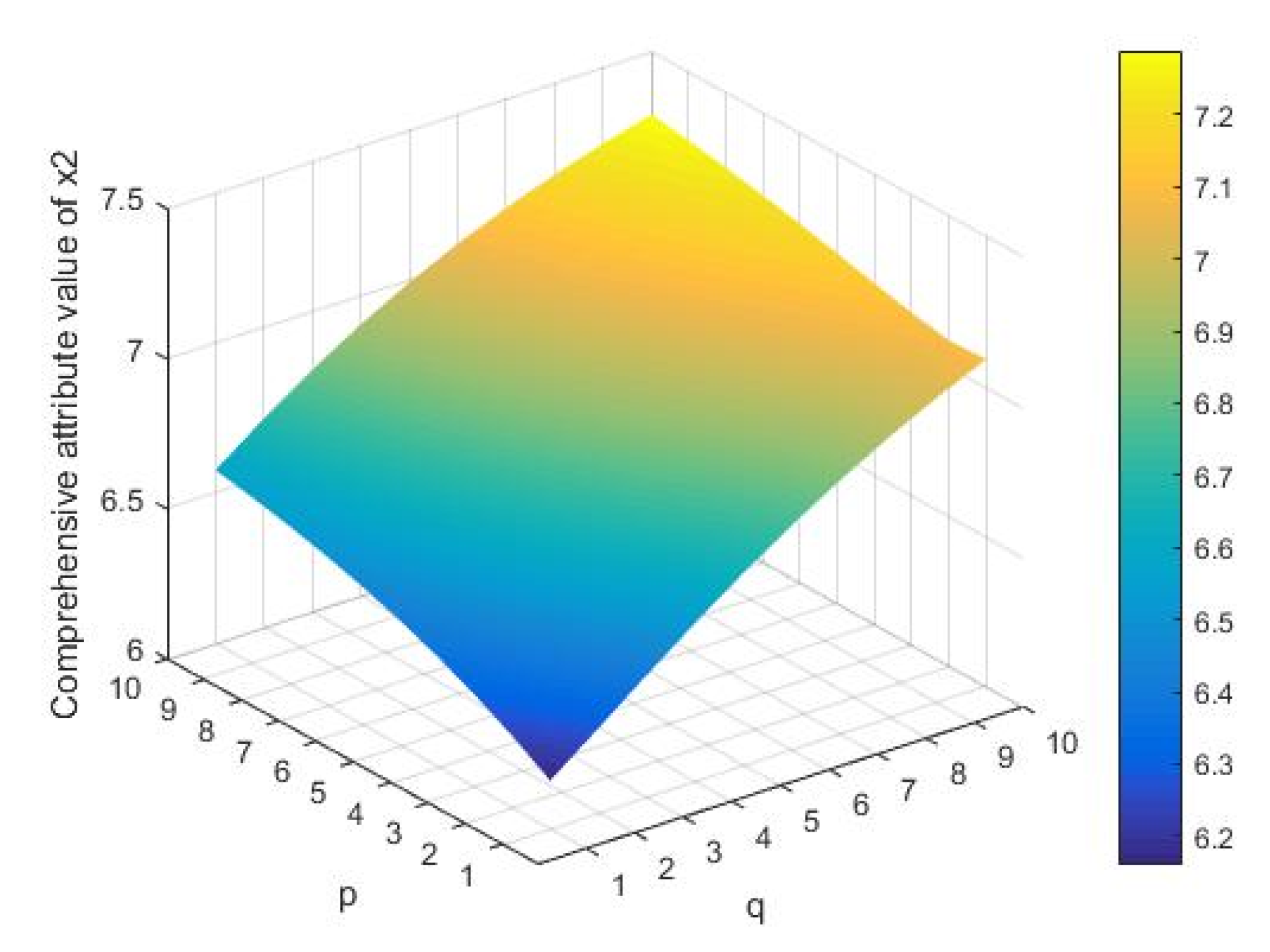
When p and q changed, the comprehensive attribute values of the four schemes based on LGWHM changed, as shown in Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7. To facilitate drawing, we adjusted the granularity to a positive number, that is, the granularity was adjusted from 0 to 8.

2. Second, we discussed the case of multiple attribute decision making based on the three-parameter linguistic generalized weighted Heronian mean (TPLGWHM).

We took different values of parameters $p$ and $q$, and calculated corresponding comprehensive attribute value of each scheme with the TPLGWHM operator.

Then we ranked the schemes according to the comprehensive attribute values. The results are shown in

Table 3. Ranking results for different $p,q$.

	$\mathit{h}({\mathit{x}}_1)$	$\mathit{h}({\mathit{x}}_2)$	$\mathit{h}({\mathit{x}}_3)$	$\mathit{h}({\mathit{x}}_4)$	$\mathit{h}({\mathit{x}}_5)$	Ranking Results
$p=1,q=1$	$h_{2.1800}$	$h_{2.1600}$	$h_{2.2200}$	$h_{2.7200}$	$h_{2.3800}$	$x_4>x_5>x_3>x_1>x_2$
$p=1,q=3$	$h_{2.7274}$	$h_{2.6224}$	$h_{2.4915}$	$h_{3.1189}$	$h_{2.5779}$	$x_4>x_1>x_2>x_5>x_3$
$p=1,q=10$	$h_{3.3890}$	$h_{3.3480}$	$h_{2.8010}$	$h_{3.5931}$	$h_{2.9371}$	$x_4>x_1>x_2>x_5>x_3$
$p=3,q=3$	$h_{3.0228}$	$h_{2.9708}$	$h_{2.9178}$	$h_{3.2352}$	$h_{2.9403}$	$x_4>x_1>x_2>x_5>x_3$
$p=10,q=1$	$h_{3.1574}$	$h_{2.9918}$	$h_{3.1094}$	$h_{3.2543}$	$h_{3.1569}$	$x_4>x_1>x_5>x_3>x_2$
$p=10,q=3$	$h_{3.3522}$	$h_{3.3111}$	$h_{3.3136}$	$h_{3.4427}$	$h_{3.3253}$	$x_4>x_1>x_5>x_3>x_2$
$p=10,q=10$	$h_{3.5830}$	$h_{3.6313}$	$h_{3.5251}$	$h_{3.6699}$	$h_{3.5534}$	$x_4>x_2>x_1>x_5>x_3$

.

It can be seen from Table 3 that when $p$ and $q$ took different values, the ranking results were relatively stable, and the best scheme remained unchanged. However, with the change of parameters p and q, the ranking results of schemes also changed.

We fixed the value of parameter $p\left(p=1\right)$ and $q$ was taken from 1 to 10. The change of comprehensive attribute value of each scheme based on TPLGWHM is shown in Figure 8. We fixed the value of parameter $q\left(q=1\right)$ and $p$ was taken from 1 to 10. The change of comprehensive attribute value of each scheme based on TPLGWHM is shown in Figure 9. To facilitate drawing, we adjusted the granularity to a positive number, that is, the granularity was adjusted from 0 to 8.

When $p$ and $q$ changed, the comprehensive attribute values of the four schemes based on TPLGWHM changed as shown in Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14. To facilitate drawing, we adjusted the granularity to a positive number, that is, the granularity was adjusted from 0 to 8.

3. Finally, the flexibility and robustness of the proposed methods were discussed.

From Table 2 and Table 3 and Figure 1, Figure 2, Figure 8 and Figure 9, we can see that when $p$ and $q$ took different values, the ranking results were relatively stable, and the best scheme remained unchanged. These showed that the proposed methods had good robustness.

However, with the change of parameters $p$ and $q$, the ranking results of schemes also changed. When the parameters $p$ and $q$ took the same values, the ranking results of method based on LGWHM and method based on TPLGWHM were not exactly the same, and the comprehensive attribute values were different. The main reason was that method based on LGWHM considered the relationship between two input variables, and the method based on TPLGWHM considered the relationship between three input variables. With the increase of parameters p and q, the comprehensive attribute values became larger. These showed that the proposed methods had good flexibility. In actual decision-making, the parameters can be selected according to the risk preference of the decision-maker. The decision-maker who takes a gloomy view could select smaller parameters, and the optimistic decision-maker could select larger parameters.

To sum up, the results illustrate the flexibility and robustness of the proposed methods. So, the proposed methods are effective and feasible, and sufficient to deal with practical MADM problems.

4.3. Comparative Analysis

In this section, the proposed methods were compared with the existing multiple attribute decision making methods. Using the above example, we chose the method based on extended ordered weighted averaging (EOWA) operator, and the method introduced by Liu [34] based on the three-parameter linguistic weighted Heronian mean (TPLWHM) operator to compare with the methods proposed in this paper. The comparison results are shown in

Table 4. Comparison results.

Methods	Comprehensive Attribute Values	Ranking Results
The method based on EOWA operator	$h\left(x_1\right)=h_{2.0300},$$h\left(x_2\right)=h_{2.0600},$$h\left(x_3\right)=h_{2.2500}$$h\left(x_4\right)=h_{2.4100},$$h\left(x_5\right)=h_{2.4100}$	$x_4\sim x_5>x_3>x_2>x_1$
Liu’s [34] method based on TPLWHM operator ($p=q=r=1$)	$h\left(x_1\right)=h_{2.4056},$$h\left(x_2\right)=h_{2.3378},$$h\left(x_3\right)=h_{2.3258}$$h\left(x_4\right)=h_{2.8754},$$h\left(x_5\right)=h_{2.4550}$	$x_4>x_5>x_1>x_2>x_3$
The proposed method based on LGWHM operator ($p=1,q=1$)	$h\left(x_1\right)=h_{2.1800},$$h\left(x_2\right)=h_{2.1600},$$h\left(x_3\right)=h_{2.2200}$$h\left(x_4\right)=h_{2.7200},$$h\left(x_5\right)=h_{2.3800}$	$x_4>x_5>x_3>x_1>x_2$
The proposed method based on LGWHM operator ($p=10,q=1$)	$h\left(x_2\right)=h_{2.7306},$$h\left(x_3\right)=h_{2.8810}$$h\left(x_4\right)=h_{3.0444},$$h\left(x_5\right)=h_{2.9679}$	$x_4>x_5>x_1>x_3>x_2$
The proposed method based on TPLGWHM operator ($p=1,q=1$)	$h\left(x_1\right)=h_{2.1800},$$h\left(x_2\right)=h_{2.1600},$$h\left(x_3\right)=h_{2.2200}$$h\left(x_4\right)=h_{2.7200},$$h\left(x_5\right)=h_{2.3800}$	$x_4>x_5>x_3>x_1>x_2$
The proposed method based on TPLGWHM operator ($p=10,q=1$)	$h\left(x_1\right)=h_{3.1574},$$h\left(x_2\right)=h_{2.9918},$$h\left(x_3\right)=h_{3.1094}$$h\left(x_4\right)=h_{3.2543},$$h\left(x_5\right)=h_{3.1569}$	$x_4>x_1>x_5>x_3>x_2$

.

From Table 4, we can see the following results:

(1) Using the method based on EOWA operator for decision-making, the comprehensive attribute values of schemes 4 and 5 were the same. Therefore, the method based on EOWA operator could not rank the alternatives effectively in this example;

(2) The ranking result obtained by the proposed method based on LGWHM ($p=q=1$) was different from that derived by method based on TPLWHM ($p=q=r=1$) in reference [34]. Although both of them were based on the Heronian mean, the proposed method based on LGWHM had the characteristics of generalized mean operator;

(3) The ranking result obtained by the proposed method based on TPLGWHM ($p=q=1$) was different from that derived by method based on TPLWHM ($p=q=r=1$) in reference [34]. Although both of them were based on the Heronian mean, the proposed method based on LGWHM had the characteristics of generalized mean operator;

(4) When the parameters $p$ and $q$ took the same values, the ranking result of the proposed method based on LGWHM and that of the proposed method based on TPLGWHM were not exactly the same. When $p=10, q=1$, the ranking result obtained by the proposed method based on LGWHM was $x_4>x_5>x_1>x_3>x_2$, and that derived by the proposed method based on TPLGWHM was $x_4>x_1>x_5>x_3>x_2$. The main reason was that the method based on LGWHM considered the relationship between two input variables, and the method based on TPLGWHM considered the relationship between three input variables;

(5) According to the risk preference of different decision makers, different parameters could be selected. Therefore, the method presented in this paper had more extensive application.

5. Conclusions

In this paper, a new linguistic generalized weighted Heronian mean (LGWHM) and a new three-parameter linguistic generalized weighted Heronian mean (TPLGWHM) were proposed, and a series of properties were studied. On these bases, multiple attribute decision making methods based on the new linguistic generalized weighted Heronian mean were given, and an example was analyzed and compared with other methods. This paper further generalized the Heronian mean and extended multiple attribute decision making. In the future, we will further study the generalization of the proposed operators, and make a profound study of their flexibility and robustness. Lastly, we propose an open problem, which was inspired by a reviewer’s comment.

Open problem. Is there a measurement/criterion such that the decision result produced by using the TPGWHM is better than the result generated by the LWHM?