Nonlocal Symmetry, Painlevé Integrable and Interaction Solutions for CKdV Equations

Abstract

In this paper, we provide a method to construct nonlocal symmetry of nonlinear partial differential equation (PDE), and apply it to the CKdV (CKdV) equations. In order to localize the nonlocal symmetry of the CKdV equations, we introduce two suitable auxiliary dependent variables. Then the nonlocal symmetries are localized to Lie point symmetries and the CKdV equations are extended to a closed enlarged system with auxiliary dependent variables. Via solving initial-value problems, a finite symmetry transformation for the closed system is derived. Furthermore, by applying similarity reduction method to the enlarged system, the Painlevé integral property of the CKdV equations are proved by the Painlevé analysis of the reduced ODE (Ordinary differential equation), and the new interaction solutions between kink, bright soliton and cnoidal waves are given. The corresponding dynamical evolution graphs are depicted to present the property of interaction solutions. Moreover, With the help of Maple, we obtain the numerical analysis of the CKdV equations. combining with the two and three-dimensional graphs, we further analyze the shapes and properties of solutions u and v.

1. Introduction and Motivation

Symmetry plays an important role in the construction of solutions for nonlinear (PDE), a continuous symmetry of a PDE system is a transformation that leaves invariant for the solution manifold of the system, i.e., it maps any solution of the system into a solution of the same system. As one of the main methods for studying differential equations, the Lie symmetry method has received extensive attention and has been developing vigorously since it was proposed by Sophus Lie [1]. The Lie symmetry method can not only obtain new solutions from old ones, but also reduce the dimensions of partial differential equations (PDEs) [2,3,4]. Once the reduction equations are derived, one can derive the Painlevé integral property through the reduced ODE and get several types of exact solutions. Nonlocal symmetry as a generalization of the symmetry was first studied by Vinogradov and Krasil’shchik in 1980 [5], which has close relationship with the integrable models. Compared with Lie point symmetry, the construction process of nonlocal symmetry is more complicated, but once the nonlocal symmetry of the equation is obtained, new types of symmetry reductions and exact solutions of some PDEs will also be obtained. Therefore, a variety of methods for constructing nonlocal symmetry have been proposed. For instance, Galas obtained the nonlocal symmetry from the pseudopotential [6]. Bluman, Euler et al. constructed nonlocal symmetry of PDEs by using potential system [7,8,9,10]. Lou and Hu started from the recursion operator and its inverse to construct the nonlocal symmetry for PDEs [11]. Lou, Hu and Chen derived the nonlocal symmetry from the Bäcklund transformation [12]. Lou and Reyes derived an infinite number of nonlocal symmetry of PDEs from a parameter dependent symmetry without using recursion operator [13,14]. Gao, Lou and Tang found that Painlevé analysis can be applied to obtain nonlocal symmetry corresponding to the residues with respect to the singular manifold of the truncated Painlevé expansion, which is also called residual symmetry [15]. Xin and Chen obtained the nonlocal symmetries from the auxiliary system (Lax pair) of PDEs [16,17].

This paper is motivated by Reference [16]; we start from the Lax pairs of the following CKdV equations

$$\begin{array}{c}{u}_t-\frac{1}{2}{u}_{xxx}+\frac{3}{2}{v}_{xxx}-3(u-v)u_x+6u{v}_x=0,\hfill \\ v_t-\frac{1}{2}{v}_{xxx}+\frac{3}{2}{u}_{xxx}-3(v-u)v_x+6u_{x}v=0,\hfill \end{array}$$

(1)

with $u=u(x,t),v=v(x,t)$. By improving the classic Lie group method, along with altering the assumptions for symmetries, the local and nonlocal symmetries of Equation (1) are both derived firstly (Theorem 1). Since nonlocal symmetry cannot be applied to symmetry reduction directly, thus, a problem emerged of how to localize the nonlocal symmetry into local ones and how to use the obtained local symmetry to study the properties of the original PDEs.

Solving the above two problems is another innovative point of this article. Here, we give a method to localize the nonlocal symmetries by introducing the auxiliary potential variables, then the nonlocal symmetries are localized to Lie point symmetries of the extended system. When the prolonged system is regarded as a potential system, the nonlocal symmetries of the original equations can be obtained by calculating the Lie point symmetry of the entire system.

After localization the nonlocal symmetries, we employ the finite symmetry transformations theorem [6], and solving the initial value problems of the local symmetries, the corresponding finite symmetry transformations are derived (Theorem 2). That is to say, if we know the simple solution of Equation (1), then, by Theorem 2, other solutions for Equation (1) will be obtained. Moreover, we are interested in using standard Lie point symmetry approach to study the similarity reductions of the prolonged system. Then, one can not only study the Painlevé integral property of the CKdV Equation (1), but also construct some new interaction solutions for Equation (1) via localization procedures related with the nonlocal symmetry. This kind of solutions among different types of nonlinear excitation is hardly studied by other methods. This method not only can be applied in constant coefficient but also variable coefficient nonlinear systems [18,19,20,21,22,23,24,25,26].

The CKdV Equation (1) was first presented in Reference [27] to discuss the symmetry invariant and symmetry breaking soliton solutions of AB-KdV equations, which can be used to describe many physical phenomena, such as the internal-gravity-wave motion in a shallow stratified liquid [28], the atmospheric and oceanic blocking phenomena [29], etc. Equation (1) is integrable, which can be derived from the reduction of the Hirota-Satsuma systems [30,31,32,33], and the Lax pairs are as follows

$${\psi }_{xx}=P_1\psi =\left(\begin{array}{cc}-u& 0\\ 0& -v\end{array}\right)\psi ,$$

(2)

$${\psi }_t=P_2\psi =\left(\begin{array}{cc}\frac{1}{2}{(3v-u)}_x+(u-3v){\partial }_x& 0\\ 0& \frac{1}{2}{(3u-v)}_x+(v-3u){\partial }_x\end{array}\right)\psi ,$$

(3)

where

$$\psi =\left(\begin{array}{c}{\psi }_1\\ {\psi }_2\end{array}\right),$$

and the compatibility condition is

$$P_{1t}-P_{2x}+[P_1,P_2]=0.$$

Enlightened by References [34,35], the rest contents are arranged as follows: In Section 2, we list some important definitions, theorems and provide a general method to construct nonlocal symmetry of nonlinear PDE. In Section 3, we apply the mehtod provided in Section 2 to study the nonlocal symmetries of the CKdV equations. In Section 4, by introducing potential variables to extend the original system, the nonlocal symmetries are transformed into the Lie point symmetries, and the corresponding finite transformation groups are given with Lie’s first theorem. In Section 5, two types of symmetry reductions of Equation (1) are discussed, the Painlevé property, interaction solutions and numerical analysis of Equation (1) are also derived. A short conclusion and further researches are included in the last Section.

2. Preliminaries

Firstly, we list some important definitions and theorems [7] which will be used later.

Definition 1.

A one-parameter Lie group of point transformations

$$\begin{array}{c}{\left(x^{*}\right)}^i=f^i(x,u;ϵ),\hfill \\ {\left(u^{*}\right)}^{\mu }=g^{\mu }(x,u;ϵ),\hfill \end{array}$$

(4)

leaves the following PDE system

$$\begin{array}{c}{R}^{\sigma }(x,u,\partial u,\dots ,{\partial }^{k}u)=0,(x=(x^1,\dots ,x^n),u\left(x\right)=(u^{\left(1\right)}\left(x\right),\dots ,u^{\left(m\right)}\left(x\right))),\hfill \end{array}$$

(5)

invariant if and only if its kth extension

$$\begin{array}{c}{X}^{\left(k\right)}={\xi }^i(x,u)\frac{\partial }{\partial x^i}+{\eta }^{\mu }(x,u)\frac{\partial }{\partial u^{\mu }}+{\eta }_i^{\left(1\right)\mu }(x,u,\partial u)\frac{\partial }{\partial u_i^{\mu }}+\cdots +{\eta }_{i_1\dots i_k}^{\left(k\right)\mu }(x,u,\partial u,\dots ,{\partial }^{k}u)\frac{\partial }{\partial u_{i_1\dots i_k}^{\mu }}\hfill \end{array}$$

(6)

leaves invariant the solution manifold of (5) in $(x,u,\partial u,\dots ,{\partial }^{k}u)$, i.e., it maps any family of solution surfaces of PDE system (5). In this case, the one-parameter Lie group of point transformations (4) is called a point symmetry of the PDE system (5).

Definition 2.

A symmetry $\sigma =\sigma \left(u\right)$ of a PDE system (5), is defined as a solution of its linearized equation,

$$\begin{array}{c}{R}^{\prime }\sigma \equiv \frac{d}{dϵ}R(u+ϵ\sigma ){|}_{ϵ=0},\hfill \end{array}$$

(7)

which means (7) is invariant under the transformation

$$\begin{array}{c}u\to u+ϵ\sigma ,\hfill \end{array}$$

(8)

with the infinitesimal parameter ϵ.

Definition 3.

For PDE system (5), we define

$$V={\xi }^n(x,u)\frac{\partial }{\partial x^n}+{\eta }^m(x,u)\frac{\partial }{\partial u^m},$$

(9)

be the infinitesimal generator of the Lie group of point transformations (4).

Definition 4.

For PDE system (5), if we derive the infinitesimal generators (9) of classical Lie point symmetries, then the corresponding finite symmetry transformations are given as the solution of the initial value problem

$$\begin{array}{c}\frac{d\widehat{x}}{dϵ}=\xi (\widehat{x},\widehat{t},\widehat{u}),\widehat{x}(ϵ=0)=x,\hfill \\ \frac{d\widehat{t}}{dϵ}=\tau (\widehat{x},\widehat{t},\widehat{u}),\widehat{t}(ϵ=0)=t,\hfill \\ \frac{d\widehat{u_i}}{dϵ}={\eta }^{u_i}(\widehat{x},\widehat{t},\widehat{u}),\widehat{u_i}(ϵ=0)=u_i.\hfill \end{array}$$

(10)

Method for Seeking Nonlocal Symmetries

In this subsection, we give the concrete steps to construct nonlocal symmetry for system (5). For simplicity, we consider the case $n=2,m=1$, i.e., $(x^1,x^2)=(x,t)$.

Step 1. According to Definition 2, we write the symmetry equation of the system (5).

Step 2. Choosing the appropriate auxiliary systems. Usually, we can use the Lax pair, Bäcklund transformation, potential system, pseudo-potential, etc. and the general forms are as follows,

$$\begin{array}{cc}\begin{array}{c}{R}_{\alpha }(x,y,t,u,u_x,u_t,\dots ,{\psi }_x,{\psi }_t,\hfill \\ {\psi }_{xx},{\psi }_{xt},{\psi }_{tt},\dots ,{\psi }_{\lambda x},{\psi }_{\mu t})=0,\hfill \end{array}& \alpha \in {\mathbb{Z}}^{+}\end{array}$$

(11)

where $\psi =({\psi }^1,{\psi }^2,\dots ,{\psi }^{\beta })$ denote $\beta$ auxiliary variables and ${\psi }_{\lambda x}$ denote $\lambda$th-order partial derivatives of x, ${\psi }_{\mu t}$ denote $\mu$th-order partial derivatives of t.

Let $U\simeq \mathbb{R}$ be the space representing the single coordinate u, the space $U_1$ is isomorphic to ${\mathbb{R}}^2$ with coordinates $(u_x,u_t)$. Similarly, $U_2\simeq {\mathbb{R}}^3$ has the coordinates representing the second order partial derivatives of u, and in general, $U_k\simeq {\mathbb{R}}^{k+1}$, since there are $k+1$ distinct k-th order partial derivatives of u. Finally, the space $U^{\left(k\right)}=U\times U_1\times \cdots \times U_k$ with coordinates $U^{\left(k\right)}=(u;u_x,u_t;u_{xx},u_{xt},u_{tt};\cdots )$.

Step 3. Extending the original space $X\times U$ to the prolonged space $X\times U^{\left(n\right)}$ with coordinates$(x,t,u,u,u_x,u_t,\dots )$. ${\tilde{V}}^{\left(n\right)}$ denotes the n-th prolongation of V, which is a vector field on the n-jet space $X\times U^{\left(n\right)}$ with the following form

$${\tilde{V}}^{\left(n\right)}=\sum _{i=1}^2{\xi }^i\frac{\partial }{\partial x^i}+\sum _L{\eta }^L\frac{\partial }{\partial u_L}.$$

(12)

then, we introduce the new variables into the coefficient function, and the transformed coefficient function ${\xi }^i,{\eta }^L$ depend on the variables $(x,t,u,\cdots ,\psi ,\psi ,{\psi }_x,{\psi }_t,\dots ,{\psi }_{\lambda x},{\psi }_{\mu t})$, ${\eta }^0=\eta$ and ${\eta }^L$ have the form,

$${\eta }^L=D_{L}u-\sum _{i=1}^2{u}_L{D}_L{\xi }^i.$$

(13)

Step 4. In order to construct the nonlocal symmetries, we need to solve the following equations

$${\tilde{V}}^{(n)}{\mathsf{\Delta }}_v(x,u^{(n)})\left|{}_{\genfrac{}{}{0pt}{}{{\mathsf{\Delta }}_v(x,u^{(n)})=0}{Equation\left(3\right)}}\right.=0.$$

(14)

Through the system (14), we obtain the coefficients of ${\partial }^{k}u,{\psi }_{\lambda x},{\psi }_{\mu t}$ and let them equal to zero, which leads to a large number of determined equations for the coefficient functions ${\xi }^i$ and ${\eta }^L$. Solving the determined equations with $Maple$, the local and nonlocal symmetry can be derived.

Next, take a CKdV equations as an example to illustrate the above processes. In this paper, we choose the Lax pair as the auxiliary system.

3. The Nonlocal Symmetry of the CKdV Equations

In order to construct nonlocal symmetry of the CKdV Equation (1), the first step is to write the symmetry equations by Definition 2.

The symmetry

$$\begin{array}{c}\sigma \equiv \left(\begin{array}{c}{\sigma }_1\\ {\sigma }_2\end{array}\right),\hfill \end{array}$$

(15)

of CKdV (1) is defined as a solution of the following linearized system

$$\begin{array}{c}{\sigma }_{1t}-\frac{1}{2}{\sigma }_{1xxx}+\frac{3}{2}{\sigma }_{2xxx}-3{\sigma }_1{u}_x-3u{\sigma }_{1x}+3{\sigma }_2{u}_x+3v{\sigma }_{1x}+6{\sigma }_1{v}_x+6u{\sigma }_{2x}=0,\hfill \\ {\sigma }_{2t}-\frac{1}{2}{\sigma }_{2xxx}+\frac{3}{2}{\sigma }_{1xxx}-3{\sigma }_2{v}_x-3v{\sigma }_{2x}+3{\sigma }_1{v}_x+3u{\sigma }_{2x}+6B{\sigma }_{1x}+6{\sigma }_2{u}_x=0.\hfill \end{array}$$

(16)

Namely, (15) is form invariant under the transformation.

$$\begin{array}{c}\left(\begin{array}{c}u\\ v\end{array}\right)\to \left(\begin{array}{c}u\\ v\end{array}\right)+ϵ\left(\begin{array}{c}{\sigma }_1\\ {\sigma }_2\end{array}\right)\hfill \end{array}$$

(17)

Similar to the standard Lie symmetry method, the symmetries ${\sigma }_1$, ${\sigma }_2$ can be written as

$$\begin{array}{c}{\sigma }_1=\overline{X}{u}_x+\overline{T}{u}_t-\overline{U},{\sigma }_2=\overline{X}{v}_x+\overline{T}{v}_t-\overline{V}.\hfill \end{array}$$

(18)

However, there exists the essential difference with Lie symmetry. According to the second step, we assume $\overline{X},\overline{T},\overline{U},\overline{V}$ are functions of $x,t,u,v,{\psi }_1,{\psi }_2,{\psi }_{1x},{\psi }_{2x}$.

To proceed, using the third step, solving the determined equations, we derive the following nonlocal symmetry theorem of the CKdV Equation (1).

Theorem 1.

The CKdV Equation (1) possesses the following nonlocal symmetries

$$\begin{array}{c}{\sigma }_1=(c_{1}x+c_3)u_x+(3c_{1}t+c_2)u_t+2c_{1}u-2c_4{\psi }_1{\psi }_{2x}-6c_4{\psi }_2{\psi }_{1x},\hfill \\ {\sigma }_2=(c_{1}x+c_3)v_x+(3c_{1}t+c_2)v_t-6c_4{\psi }_1{\psi }_{2x}-2c_4{\psi }_2{\psi }_{1x}+2c_{1}v,\hfill \end{array}$$

(19)

where $c_i(i=1,\dots ,4)$ is arbitrary constant.

Via the forth step, we give the specific proof of the Theorem 1 as follows.

Proof. 

Substituting Equation (18) into Equation (16), eliminating $u_t$, $v_t$, and ${\psi }_{1xx}$, ${\psi }_{1t}$, ${\psi }_{2xx}$, ${\psi }_{2t}$ in terms of the Lax pairs (2) and (3), we derive a system of determining equations for the functions $\overline{X}$, $\overline{T}$, $\overline{U}$, $\overline{V}$, which can be solved by symbolic computing tool $Maple$ to give

$$\begin{array}{c}\overline{T}=3c_{1}t+c_2,\overline{U}=2c_4{\psi }_1{\psi }_{2x}+6c_4{\psi }_2{\psi }_{1x}-2c_{1}u,\hfill \\ \overline{X}=c_{1}x+c_3,\overline{V}=6c_4{\psi }_1{\psi }_{2x}+2c_4{\psi }_2{\psi }_{1x}-2c_{1}v.\hfill \end{array}$$

(20)

Substituting Equation (20) into Equation (18), we derive the exact form of ${\sigma }_1,{\sigma }_2$ are expression (19). □

Remark 1.

The prolongation of vector fields shows that the symmetries ${\sigma }_1,{\sigma }_2$ are neither classical Lie point symmetries nor Lie-Bäcklund symmetries because they depend not only on the variables $x,t,u,v$ but also on the auxiliary variables and their high order partial derivatives. More results may be obtained if we assume the coefficients ${\xi }^i,{\eta }^L$ have integral terms of the auxiliary variable i.e., they are the functions of $(x,t,u,\cdots ,\int \psi dx,\cdots )$.

However, if we rewrite the symmetry Equation (19) as two parts

$$\begin{array}{c}{\sigma }_{11}=(c_{1}x+c_3)u_x+(3c_{1}t+c_2)u_t+2c_{1}u,\hfill \\ {\sigma }_{21}=(c_{1}x+c_3)v_x+(3c_{1}t+c_2)v_t+2c_{1}v,\hfill \end{array}$$

(21)

and

$$\begin{array}{c}{\sigma }_{12}=-2c_4{\psi }_1{\psi }_{2x}-6c_4{\psi }_2{\psi }_{1x},\hfill \\ {\sigma }_{22}=-6c_4{\psi }_1{\psi }_{2x}-2c_4{\psi }_2{\psi }_{1x}.\hfill \end{array}$$

(22)

we find that ${\sigma }_{11},{\sigma }_{21}$ in the expressions (22) denote the classical Lie symmetries and ${\sigma }_{12},{\sigma }_{22}$ denote the nonlocal symmetries of the CKdV equations respectivly. For simplicity, letting $c_1=0,c_2=0,c_3=0,c_4=1$ in (19), we obtain the following nonlocal symmetries for Equation (1)

$$\begin{array}{c}{\sigma }_1=-2{\psi }_1{\psi }_{2x}-6{\psi }_2{\psi }_{1x},\hfill \\ {\sigma }_2=-6{\psi }_1{\psi }_{2x}-2{\psi }_2{\psi }_{1x}.\hfill \end{array}$$

(23)

4. Localization of the Nonlocal Symmetry

As we know, nonlocal symmetry cannot be applied to construct explicit solutions for PDEs directly, but once it is localized, especially as Lie point symmetry, we can further use the obtained results to explore the properties of the equations. According to this idea, we introduce two auxiliary variables ${\psi }_3={\psi }_{1x},{\psi }_4={\psi }_{2x}$ to extend the original system, the closed prolonged system of the CKdV equations become

$$\begin{array}{c}{u}_t-\frac{1}{2}{u}_{xxx}+\frac{3}{2}{v}_{xxx}-3(u-v)u_x+6u{v}_x=0,\hfill \\ v_t-\frac{1}{2}{v}_{xxx}+\frac{3}{2}{u}_{xxx}-3(v-u)v_x+6u_{x}v=0,\hfill \\ {\psi }_{1xx}=-u{\psi }_1,{\psi }_{2xx}=-v{\psi }_2,\hfill \\ {\psi }_{1t}=\frac{3}{2}{\psi }_1{v}_x-\frac{1}{2}{\psi }_1{u}_x+(u-3v){\psi }_{1x},\hfill \\ {\psi }_{2t}=\frac{3}{2}{\psi }_2{u}_x-\frac{1}{2}{\psi }_2{u}_x+(v-3u){\psi }_{2x},\hfill \\ {\psi }_3={\psi }_{1x},{\psi }_4={\psi }_{2x}.\hfill \end{array}$$

(24)

According to the Definition 2, the symmetries equations of system (24) are as follows

$$\begin{array}{c}{\sigma }_{3xx}+{\sigma }_1{\psi }_1+u{\sigma }_3=0,\hfill \\ {\sigma }_{4xx}+{\sigma }_2{\psi }_2+v{\sigma }_4=0,\hfill \\ {\sigma }_{3t}-\frac{3}{2}{\sigma }_3{v}_x+8{\psi }_1^2{\psi }_{2xx}-8{\psi }_1{\psi }_{1x}{\psi }_{2x}+\frac{1}{2}{\sigma }_3{u}_x-u{\sigma }_{3x}+3v{\sigma }_{3x}=0,\hfill \\ {\sigma }_{4t}-\frac{3}{2}{\sigma }_4{u}_x+8{\psi }_2^2{\psi }_{1xx}-8{\psi }_2{\psi }_{1x}{\psi }_{2x}+\frac{1}{2}{\sigma }_4{v}_x-B{\sigma }_{4x}+3u{\sigma }_{4x}=0,\hfill \\ {\sigma }_5-{\sigma }_{3x}=0,{\sigma }_6-{\sigma }_{4x}=0,\hfill \end{array}$$

(25)

with ${\sigma }_1$ and ${\sigma }_2$ being given by (23), ${\psi }_1$, ${\psi }_2$, ${\psi }_3$ and ${\psi }_4$ satisfying the following transformations

$$\begin{array}{c}{\psi }_1\to {\psi }_1+ϵ{\sigma }_3,{\psi }_2\to {\psi }_2+ϵ{\sigma }_4,\hfill \\ {\psi }_3\to {\psi }_3+ϵ{\sigma }_5,{\psi }_4\to {\psi }_4+ϵ{\sigma }_6.\hfill \end{array}$$

Solving Equations (16) and (25) leads to

$$\begin{array}{c}{\sigma }_3={\psi }_{1}f,{\sigma }_4={\psi }_{2}f,\hfill \end{array}$$

(26)

with f satisfying

$$\begin{array}{c}{f}_x=2{\psi }_1{\psi }_2,\hfill \\ f_t=2v{\psi }_1{\psi }_2+2u{\psi }_1{\psi }_2+8{\psi }_{1x}{\psi }_{2x},\hfill \end{array}$$

(27)

and the symmetry equations for f are

$$\begin{array}{c}{\sigma }_{7x}=2({\sigma }_3{\psi }_2+{\psi }_1{\sigma }_4),\hfill \\ {\sigma }_{7t}-2{\psi }_1{\psi }_2({\sigma }_2+{\sigma }_1)-2v({\sigma }_3{\psi }_2+{\psi }_1{\sigma }_4)-2u({\sigma }_3{\psi }_2+{\psi }_1{\sigma }_4)-8({\sigma }_{3x}{\psi }_{2x}+{\psi }_{1x}{\sigma }_{4x})=0.\hfill \end{array}$$

(28)

What is more interesting is that the auxiliary-dependent variable f satisfies the Schwartzian form of the CKdV equations

$$\begin{array}{c}(C{C}_x+C_t)(S+C)=0,\hfill \end{array}$$

(29)

with

$$C=\frac{f_t}{f_x},S=\frac{f_{xxx}}{f_x}-\frac{3}{2}{\left(\frac{f_{xx}}{f_x}\right)}^2.$$

The Schwarzian form (29) is invariant under the Möbious transformation

$$f\stackrel{}{\to }\frac{a+bf}{c+df}(ad\ne bc).$$

That is to say, Equation (29) bears three symmetries ${\sigma }^f=d_1$, ${\sigma }^f=d_{2}f$ and ${\sigma }^f=d_3{f}^2$ with arbitrary constants $d_1$, $d_2$ and $d_3$.

Here, if take

$$\begin{array}{c}{\sigma }^7={\sigma }^f=f^2,\hfill \end{array}$$

(30)

one can see that the nonlocal symmetries (23) in the original spaces $\{x,t,A,B,{\psi }_1,{\psi }_2\}$ can be localized to Lie point symmetries

$$\begin{array}{c}{\sigma }_1=-2{\psi }_1{\psi }_{2x}-6{\psi }_2{\psi }_{1x},\hfill \\ {\sigma }_2=-6{\psi }_1{\psi }_{2x}-2{\psi }_2{\psi }_{1x},\hfill \\ {\sigma }_3={\psi }_{1}f,{\sigma }_4={\psi }_{2}f,\hfill \\ {\sigma }_5={\psi }_{3}f+2{\psi }_1^2{\psi }_2,{\sigma }_6={\psi }_{4}f+2{\psi }_1{\psi }_2^2,\hfill \\ {\sigma }_7=f^2.\hfill \end{array}$$

(31)

In the extend spaces $\{x,t,u,v,{\psi }_1,{\psi }_2,{\psi }_3,{\psi }_4,f\}$, the corresponding vector is

$$\begin{array}{c}\widehat{V}=-2({\psi }_1{\psi }_{2x}+3{\psi }_2{\psi }_{1x})\frac{\partial }{\partial u}-2(3{\psi }_1{\psi }_{2x}+{\psi }_2{\psi }_{1x})\frac{\partial }{\partial v}+{\psi }_{1}f\frac{\partial }{\partial {\psi }_1}+{\psi }_{2}f\frac{\partial }{\partial {\psi }_2}+({\psi }_{3}f+2{\psi }_1^2{\psi }_2)\frac{\partial }{\partial {\psi }_3}\hfill \\ +({\psi }_{4}f+2{\psi }_1{\psi }_2^2)\frac{\partial }{\partial {\psi }_4}+f^2\frac{\partial }{\partial f}.\hfill \end{array}$$

According to Definition 4, we obtain the following symmetry group transformation Theorem.

Theorem 2.

If $u,v,{\psi }_1,{\psi }_2,{\psi }_3,{\psi }_4,f$ are solutions of the prolonged system, so are $\widehat{u},\widehat{v},\widehat{{\psi }_1},\widehat{{\psi }_2},$ $\widehat{{\psi }_3},\widehat{{\psi }_4},\widehat{f}$

$$\begin{array}{c}\widehat{u}=u+\frac{2ϵ{\psi }_1{\psi }_4}{1+ϵf}+\frac{6ϵ{\psi }_2{\psi }_3}{1+ϵf}-\frac{8{ϵ}^2{\psi }_1^2{\psi }_2^2}{{(1+ϵf)}^2},\hfill \\ \widehat{v}=v+\frac{6ϵ{\psi }_1{\psi }_4}{1+ϵf}+\frac{2ϵ{\psi }_2{\psi }_3}{1+ϵf}-\frac{8{ϵ}^2{\psi }_1^2{\psi }_2^2}{{(1+ϵf)}^2},\hfill \\ \widehat{{\psi }_1}=\frac{{\psi }_1}{1+ϵf},\widehat{{\psi }_2}=\frac{{\psi }_2}{1+ϵf},\hfill \\ \widehat{{\psi }_3}=\frac{{\psi }_3}{1+ϵf}-\frac{2ϵ{\psi }_1^2{\psi }_2}{{(1+ϵf)}^2},\widehat{{\psi }_4}=\frac{{\psi }_4}{1+ϵf}-\frac{2ϵ{\psi }_1{\psi }_2^2}{{(1+ϵf)}^2},\hfill \\ \widehat{f}=\frac{f}{1+ϵf},\hfill \end{array}$$

(32)

where ϵ is an arbitrary group parameter.

Proof. 

Letting ${\psi }_3={\psi }_{1x},{\psi }_4={\psi }_{2x}$, via Definition 4, by solving the following initial value problems:

$$\begin{array}{cc}\frac{\mathrm{d}\widehat{u}\left(ϵ\right)}{\mathrm{d}ϵ}=2({\widehat{\psi }}_1{\widehat{\psi }}_4+3{\widehat{\psi }}_2{\widehat{\psi }}_3),\hfill & \widehat{u}\left(0\right)=u,\hfill \\ \frac{\mathrm{d}\widehat{v}\left(ϵ\right)}{\mathrm{d}ϵ}=2(3{\widehat{\psi }}_1{\widehat{\psi }}_4+{\widehat{\psi }}_2{\widehat{\psi }}_3),\hfill & \widehat{v}\left(0\right)=v,\hfill \\ \frac{\mathrm{d}{\widehat{\psi }}_1\left(ϵ\right)}{\mathrm{d}ϵ}=-{\widehat{\psi }}_1\widehat{f},\hfill & {\psi }_1\left(0\right)={\psi }_1,\hfill \\ \frac{\mathrm{d}{\widehat{\psi }}_2\left(ϵ\right)}{\mathrm{d}ϵ}=-{\widehat{\psi }}_2\widehat{f},\hfill & {\widehat{\psi }}_2\left(0\right)={\psi }_2,\hfill \\ \frac{\mathrm{d}{\widehat{\psi }}_3\left(ϵ\right)}{\mathrm{d}ϵ}=-{\widehat{\psi }}_3\widehat{f}-2{\widehat{\psi }}_1^2{\psi }_2,\hfill & \widehat{{\psi }_3}\left(0\right)={\psi }_3,\hfill \\ \frac{\mathrm{d}{\widehat{\psi }}_4\left(ϵ\right)}{\mathrm{d}ϵ}=-{\widehat{\psi }}_4\widehat{f}-2{\widehat{\psi }}_1{\widehat{\psi }}_2^2,\hfill & \widehat{{\psi }_4}\left(0\right)={\psi }_4,\hfill \\ \frac{\mathrm{d}\widehat{f}\left(ϵ\right)}{\mathrm{d}ϵ}=-\widehat{f^2}\left(ϵ\right),\hfill & \widehat{f}\left(0\right)=f,\hfill \end{array}$$

(33)

one can easily derive the solutions of the system (33) given in Theorem 3. □

From Theorem 2, we can get a pair of new solutions $\widehat{u},\widehat{v}$ from given solutions $u,v$ for Equation (1) through the finite symmetry transformations (32). It should be mentioned that the last expression in (32) is nothing but the Möbious transformation of the Schwartz form (29).

To proceed, we study the Lie point symmetries for the prolonged systems (24) and (27) of this section. By employing the classical Lie symmetry method, we first suppose the vector of the symmetries has the following form

$$\begin{array}{c}V=X\frac{\partial }{\partial x}+T\frac{\partial }{\partial t}+U\frac{\partial }{\partial u}+V\frac{\partial }{\partial v}+{\mathsf{\Psi }}_1\frac{\partial }{\partial {\psi }_1}+{\mathsf{\Psi }}_2\frac{\partial }{\partial {\psi }_2}+{\mathsf{\Psi }}_3\frac{\partial }{\partial {\psi }_3}+{\mathsf{\Psi }}_4\frac{\partial }{\partial {\psi }_4}+F\frac{\partial }{\partial f},\hfill \end{array}$$

(34)

where $X,T,U,V,{\mathsf{\Psi }}_1,{\mathsf{\Psi }}_2,{\mathsf{\Psi }}_3,{\mathsf{\Psi }}_4,F$ are functions of $x,t,u,v,{\psi }_1,{\psi }_2,{\psi }_3,{\psi }_4$ and f. In other words, the closed system is invariant under the following infinitesimal transformations

$$\begin{array}{c}(x,t,u,v,{\psi }_1,{\psi }_2,{\psi }_3,{\psi }_4,f)\to \hfill \\ (x+ϵX,t+ϵT,u+ϵU,v+ϵV,{\psi }_1+ϵ{\mathsf{\Psi }}_1,{\psi }_2+ϵ{\mathsf{\Psi }}_2,{\psi }_3+ϵ{\mathsf{\Psi }}_3,{\psi }_4+ϵ{\mathsf{\Psi }}_4,f+ϵf)\hfill \end{array}$$

with

$$\begin{array}{c}{\sigma }^1=X{u}_x+T{u}_t-U,{\sigma }^2=X{v}_x+T{v}_t-V,{\sigma }^3=X{\psi }_{1x}+T{\psi }_{1t}-{\mathsf{\Psi }}_1,\hfill \\ {\sigma }^4=X{\psi }_{2x}+T{\psi }_{2t}-{\mathsf{\Psi }}_2,{\sigma }^5=X{\psi }_{3x}+T{\psi }_{3t}-{\mathsf{\Psi }}_3,{\sigma }^6=X{\psi }_{4x}+T{\psi }_{4t}-{\mathsf{\Psi }}_4,\hfill \\ {\sigma }^7=X{f}_x+T{f}_t-F.\hfill \end{array}$$

(35)

Inserting the above ${\sigma }^i$ (i = 1, …, 7) into the linearized equations of the prolonged systems, i.e., (16), (25) and (28), eliminating $u_t,v_t,{\psi }_{1xx},{\psi }_{1t},{\psi }_{2xx}$, ${\psi }_{2t},f_x,f_t$, and collecting the coefficients of the independent partial derivatives of dependent variables $u,v$, we derive a system of overdetermined linear equations for the infinitesimals $X,T,U,V,{\mathsf{\Psi }}_1,{\mathsf{\Psi }}_2,{\mathsf{\Psi }}_3,{\mathsf{\Psi }}_4,F$. Solving the determining equations will lead to

$$\begin{array}{c}X=c_{1}x+c_3,T=3c_{1}t+c_2,U=-2(c_4{\psi }_1{\psi }_4+3c_4{\psi }_2{\psi }_3+c_{1}u),\hfill \\ V=-2(3c_4{\psi }_1{\psi }_4+c_4{\psi }_2{\psi }_3+c_{1}v),{\mathsf{\Psi }}_1=(c_{4}f+c_5){\psi }_1,\hfill \\ {\mathsf{\Psi }}_2=(c_{4}f+c_6){\psi }_2,{\mathsf{\Psi }}_3=2c_4{\psi }_1^2{\psi }_2+(c_{4}f-c_1+c_5){\psi }_3,\hfill \\ {\mathsf{\Psi }}_4=2c_4{\psi }_1{\psi }_2^2+(c_{4}f-c_1+c_6){\psi }_4,F=(c_{4}f+c_1+c_5+c_6)f+c_7,\hfill \end{array}$$

(36)

where $c_i$, $(i=1,\cdots ,7)$ is arbitrary constant.

For convenience, we restate and summarize the above content in theorem as follows.

Theorem 3.

The prolonged CKdV equations possess the following Lie point symmetries

$$\begin{array}{c}{\sigma }^1=(c_{1}x+c_3)u_x+(3c_{1}t+c_2)u_t+2(c_4{\psi }_1{\psi }_4+3c_4{\psi }_2{\psi }_3+c_{1}u),\hfill \\ {\sigma }^2=(c_{1}x+c_3)v_x+(3c_{1}t+c_2)v_t+2(3c_4{\psi }_1{\psi }_4+c_4{\psi }_2{\psi }_3+c_{1}v),\hfill \\ {\sigma }^3=(c_{1}x+c_3){\psi }_{1x}+(3c_{1}t+c_2){\psi }_{1t}-(c_{4}f+c_5){\psi }_1,\hfill \\ {\sigma }^4=(c_{1}x+c_3){\psi }_{2x}+(3c_{1}t+c_2){\psi }_{2t}-(c_{4}f+c_6){\psi }_2,\hfill \\ {\sigma }^5=(c_{1}x+c_3){\psi }_{3x}+(3c_{1}t+c_2){\psi }_{3t}-2c_4{\psi }_1^2{\psi }_2+(c_{4}f-c_1+c_5){\psi }_3,\hfill \\ {\sigma }^6=(c_{1}x+c_3){\psi }_{4x}+(3c_{1}t+c_2){\psi }_{4t}-2c_4{\psi }_1{\psi }_2^2+(c_{4}f-c_1+c_6){\psi }_4,\hfill \\ {\sigma }^7=(c_{1}x+c_3)f_x+(3c_{1}t+c_2)f_t-(c_{4}f+c_1+c_5+c_6)f+c_7.\hfill \end{array}$$

(37)

When setting $c_i=0(i=1,\dots ,7,i\ne 4)$, and $c_4=1$, the above symmetries (36) degenerate into Equation (23).

5. Symmetry Reduction to the CKdV Equation

For nonlinear partial differential equation(NPDE), we are interested in studying its exact solutions by different methods, and then to analysis the physical properties which contains. Currently, there are lots of methods to construct exact solutions for NPDE [36,37,38,39], in this section, we mainly construct some kind of group invariant solutions for the CKdV equations by classical Lie symmetry method. Firstly, we need to solve the symmetry constraint conditions ${\sigma }^i=0(i=1,\dots ,7)$ defined by (35) with (36), which is equivalent to solving the following characteristic equations

$$\begin{array}{c}\frac{dx}{X}=\frac{dt}{T}=\frac{du}{U}=\frac{dv}{V}=\frac{d{\psi }_1}{{\mathsf{\Psi }}_1}=\frac{d{\psi }_2}{{\mathsf{\Psi }}_2}=\frac{d{\psi }_3}{{\mathsf{\Psi }}_3}=\frac{d{\psi }_4}{{\mathsf{\Psi }}_4}=\frac{df}{F},\hfill \end{array}$$

(38)

we obtain two nontrivial similar reductions and several substantial invariant solutions listed below.

Next, we discuss the similarity reductions for (1) under the following two cases: $c_1\ne 0$ and $c_1=0$, then the Painlevé integrable property and two kinds of nontrivial group invariant solutions of Equation (1) listed in the follows.

5.1. Symmetry Reduction and Painlevé Integrable to the CKdV Equations

In this section, we will consider the symmetry reduction of Equation (1) in case of $c_1\ne 0$, and obtain the Painlevé integrability of Equation (1) through the Painlevé integrability of the reduced ordinary differential equation.

Reduction 1.

$c_1\ne 0$.

Without loss of generality, we assume $c_2=c_3=c_5=c_6=0$. By solving the characteristic Equation (38) and letting $\frac{c_1^2-4c_4{c}_7}{144c_1^2}=k^2$, the following two sub-cases of $k\ne 0$ and $k=0$ need to be considered.

Case 1.

$k\ne 0$. The similarity solutions are as follows

$$\begin{array}{c}u=\frac{U\left(z\right)}{t^{\frac{2}{3}}}+\frac{2c_4}{9c_1^2{k}^2{t}^{\frac{2}{3}}}exp(-\frac{2}{3}F\left(z\right))\{c_4{\mathsf{\Psi }}_1^2\left(z\right){\mathsf{\Psi }}_2^2\left(z\right)\frac{1}{{(2cosh{\left(t_1\right)}^2-1)}^2}-\frac{3c_{1}ktanh\left(t_1\right)({\mathsf{\Psi }}_1\left(z\right){\mathsf{\Psi }}_4\left(z\right)+3{\mathsf{\Psi }}_2\left(z\right){\mathsf{\Psi }}_3\left(z\right))}{tanh{\left(t_1\right)}^2+1)}\},\hfill \\ v=\frac{V\left(z\right)}{t^{\frac{2}{3}}}+\frac{2c_4}{9c_1^2{k}^2{t}^{\frac{2}{3}}}exp(-\frac{2}{3}F\left(z\right))\{c_4{\mathsf{\Psi }}_1^2\left(z\right){\mathsf{\Psi }}_2^2\left(z\right)\frac{1}{{(2cosh{\left(t_1\right)}^2-1)}^2}-\frac{3c_{1}ktanh\left(t_1\right)(3{\mathsf{\Psi }}_1\left(z\right){\mathsf{\Psi }}_4\left(z\right)+{\mathsf{\Psi }}_2\left(z\right){\mathsf{\Psi }}_3\left(z\right))}{tanh{\left(t_1\right)}^2+1)}\},\hfill \\ {\psi }_1=\frac{{\mathsf{\Psi }}_1\left(z\right)exp(-\frac{1}{6}F\left(z\right))}{t^{\frac{1}{6}}(2cosh{\left(t_1\right)}^2-1)},{\psi }_2=\frac{{\mathsf{\Psi }}_2\left(z\right)exp(-\frac{1}{6}F\left(z\right))}{t^{\frac{1}{6}}(2cosh{\left(t_1\right)}^2-1)},f=-\frac{c_1(12tanh\left(2t_1\right)k+1)}{2c_4},\hfill \\ {\psi }_3=\frac{1}{3}exp(-\frac{1}{2}F\left(z\right))(\frac{6{\mathsf{\Psi }}_3\left(z\right)}{\sqrt{t}}sech\left(2t_1\right)+\frac{2c_4{\mathsf{\Psi }}_2\left(z\right){\mathsf{\Psi }}_1^2\left(z\right)sinh\left(t_1\right)cosh\left(t_1\right)}{\sqrt{t}k{c}_1{(sinh{\left(t_1\right)}^2+cosh{\left(t_1\right)}^2)}^2}),\hfill \\ {\psi }_4=\frac{1}{3}exp(-\frac{1}{2}F\left(z\right))(\frac{6{\mathsf{\Psi }}_4\left(z\right)}{\sqrt{t}}sech\left(2t_1\right)+\frac{2c_4{\mathsf{\Psi }}_1\left(z\right){\mathsf{\Psi }}_2^2\left(z\right)sinh\left(t_1\right)cosh\left(t_1\right)}{\sqrt{t}k{c}_1{(sinh{\left(t_1\right)}^2+cosh{\left(t_1\right)}^2)}^2}),\hfill \end{array}$$

(39)

with $t_1=k(lnt+F\left(z\right))$ and $z=x{t}^{-\frac{1}{3}}$.

Substituting (39) into the extended equations, we obtain

$$\begin{array}{c}{\mathsf{\Psi }}_3\left(z\right)=-\frac{1}{6}exp\left(\frac{1}{3}F\left(z\right)\right)({\mathsf{\Psi }}_1\left(z\right)F_z\left(z\right)-6{\mathsf{\Psi }}_{1z}\left(z\right),\hfill \\ {\mathsf{\Psi }}_4\left(z\right)=-\frac{1}{c_4{\mathsf{\Psi }}_1^2\left(z\right)}exp\left(\frac{2}{3}F\left(z\right)\right)c_1{k}^2({\mathsf{\Psi }}_1\left(z\right)F_z^2\left(z\right)-6{\mathsf{\Psi }}_{1z}\left(z\right)F_z\left(z\right)+6{\mathsf{\Psi }}_1\left(z\right)F_{zz}\left(z\right)),\hfill \\ U\left(z\right)=-\frac{1}{36}(F_z^2\left(z\right)-6F_{zz}\left(z\right))-\frac{1}{{\mathsf{\Psi }}_1\left(z\right)}(4k^2{\mathsf{\Psi }}_1\left(z\right)F_z^2\left(z\right)+{\mathsf{\Psi }}_{1zz}\left(z\right))+\frac{1}{3{\mathsf{\Psi }}_1\left(z\right)}{\mathsf{\Psi }}_{1z}\left(z\right)F_z\left(z\right)),\hfill \\ V\left(z\right)=-\frac{1}{36}((144k^2+1)F_z^2\left(z\right)+18F_{zz}\left(z\right))+\frac{1}{3{\mathsf{\Psi }}_1\left(z\right)}({\mathsf{\Psi }}_{1z}\left(z\right)F_z\left(z\right)+3{\mathsf{\Psi }}_{1zz})\hfill \\ -\frac{2{\mathsf{\Psi }}_{1z}}{F_z\left(z\right){\mathsf{\Psi }}_1^2}({\mathsf{\Psi }}_{1z}\left(z\right)F_z\left(z\right)-{\mathsf{\Psi }}_1\left(z\right)F_{zz}\left(z\right)),\hfill \\ {\mathsf{\Psi }}_1\left(z\right)=\sqrt{-\frac{6F_z\left(z\right)c_1}{c_4}}kexp(\int Q_1\left(z\right)dz),{\mathsf{\Psi }}_2\left(z\right)=\sqrt{-\frac{6F_z\left(z\right)c_1}{c_4}}kexp(-\int Q\left(z\right)dz),\hfill \end{array}$$

(40)

where $F_1\left(z\right)=F_z\left(z\right),Q_1\left(z\right)=Q_z\left(z\right)$ satisfy the following equations

$$\begin{array}{c}6F_{1zz}{F}_1\left(z\right)-48k^2{F}_1^4\left(z\right)+36Q_1^2\left(z\right)F_1^2\left(z\right)-2z{F}_1^2\left(z\right)-9F_{1z}^2+6F_1\left(z\right)=0,\hfill \\ 6Q_{1zz}\left(z\right)F_1\left(z\right)+Q_1\left(z\right)(4z{F}_1\left(z\right)-48Q_1^2\left(z\right)F_1\left(z\right)-9)=0.\hfill \end{array}$$

(41)

Solving the second equation of system (41) leads to

$$\begin{array}{c}{F}_1\left(z\right)=-\frac{9}{2}\frac{Q_1\left(z\right)}{24Q_1^3\left(z\right)-2z{Q}_1\left(z\right)-3Q_{1zz}\left(z\right)}.\hfill \end{array}$$

(42)

Substituting the expression (42) into the first equation of system (41), we derive a fourth-order ordinary differential equation of $Q\left(z\right)$. Then, we use the Ablowitz–Ramani–Segur (ARS) algorithm to test the Painlevé property of Equation (41). The dominant behavior for the first equation of (41) around $(z-z_0)$ is $Q_1\left(z\right)\sim \frac{Q_0\left(z\right)}{{(z-z_0)}^r}$, where $Q_0\left(z\right)$ and $z_0$ are arbitrary constants. Via the Leading terms analysis leads to the following two branches:

$$Q_1\left(z\right)\sim \frac{\frac{1}{2}}{{(z-z_0)}^r},Q_1\left(z\right)\sim \frac{-\frac{1}{2}}{{(z-z_0)}^r},$$

and the resonant points $\{-1,1,4,5\}$. After boring calculation, it indicates the system (41) is Painlevé integrable. By the relationship of partial differential equation and the corresponding reduction equation [40], we know that Equation (1) is Painlevé integrable.

Case 2.

$k=0$. The similarity solutions are as follows

$$\begin{array}{c}u=\frac{U\left(z\right)}{t^{\frac{2}{3}}}-\frac{8c_4^2{\mathsf{\Psi }}_1^2\left(z\right){\mathsf{\Psi }}_2^2\left(z\right)}{9t^{\frac{2}{3}}{c}_1^2{t}_1^2}+\frac{2c_4(3{\mathsf{\Psi }}_3\left(z\right){\mathsf{\Psi }}_2\left(z\right)+{\mathsf{\Psi }}_4\left(z\right){\mathsf{\Psi }}_1\left(z\right))}{3t^{\frac{2}{3}}{c}_1{t}_1},\hfill \\ v=\frac{V\left(z\right)}{t^{\frac{2}{3}}}-\frac{8c_4^2{\mathsf{\Psi }}_1^2\left(z\right){\mathsf{\Psi }}_2^2\left(z\right)}{9t^{\frac{2}{3}}{c}_1^2{t}_1^2}+\frac{2c_4({\mathsf{\Psi }}_3\left(z\right){\mathsf{\Psi }}_2\left(z\right)+3{\mathsf{\Psi }}_4\left(z\right){\mathsf{\Psi }}_1\left(z\right))}{3t^{\frac{2}{3}}{c}_1{t}_1},\hfill \\ {\psi }_1=\frac{{\mathsf{\Psi }}_1\left(z\right)}{t^{\frac{1}{6}}{t}_1},{\psi }_2=\frac{{\mathsf{\Psi }}_2\left(z\right)}{t^{\frac{1}{6}}{t}_1},f=-\frac{c_1(t_1+6)}{2c_4{t}_1},\hfill \\ {\psi }_3=-\frac{2c_4{\mathsf{\Psi }}_1^2\left(z\right){\mathsf{\Psi }}_2\left(z\right)}{3c_1{t}_1^2\sqrt{t}}+\frac{{\mathsf{\Psi }}_3\left(z\right)}{t_1\sqrt{t}},{\psi }_4=-\frac{2c_4{\mathsf{\Psi }}_1\left(z\right){\mathsf{\Psi }}_2^2\left(z\right)}{3c_1{t}_1^2\sqrt{t}}+\frac{{\mathsf{\Psi }}_4\left(z\right)}{t_1\sqrt{t}}.\hfill \end{array}$$

(43)

Substituting (43) into the extended equations, we obtain

$$\begin{array}{c}U\left(z\right)=-\frac{{\mathsf{\Psi }}_{1zz}\left(z\right)}{{\psi }_1\left(z\right)},V\left(z\right)=-\frac{{\mathsf{\Psi }}_{2zz}\left(z\right)}{{\psi }_2\left(z\right)},{\mathsf{\Psi }}_1\left(z\right)=\frac{\sqrt{6c_1{F}_1\left(z\right)}exp(\int Q_1\left(z\right)dz)}{2\sqrt{c_4}},\hfill \\ {\mathsf{\Psi }}_2\left(z\right)=\frac{\sqrt{6c_1{F}_1\left(z\right)}exp(-\int Q_1\left(z\right)dz)}{2\sqrt{c_4}},{\mathsf{\Psi }}_3\left(z\right)={\mathsf{\Psi }}_{1z}\left(z\right),{\mathsf{\Psi }}_4\left(z\right)={\mathsf{\Psi }}_{2z}\left(z\right),\hfill \end{array}$$

where $F_1\left(z\right)=F_z\left(z\right)$ and $Q_1\left(z\right)=Q_z\left(z\right)$ satisfy the following equations

$$\begin{array}{c}6F_1\left(z\right)F_{1zz}\left(z\right)+36F_1^2\left(z\right)Q_1^2\left(z\right)-2z{F}_1^2\left(z\right)-9F_{1z}^2\left(z\right)+6F_1\left(z\right)=0,\hfill \\ 6F_1\left(z\right)Q_{1zz}\left(z\right)-48Q_1\left(z\right)F_1\left(z\right)Q_1^2\left(z\right)+4z{F}_1\left(z\right)-9Q_1\left(z\right)=0.\hfill \end{array}$$

(44)

For the system (44), applying the same method as subcase 1, we also derive the following two branches

$$Q_1\left(z\right)\sim \frac{\frac{1}{2}}{{(z-z_0)}^r},Q_1\left(z\right)\sim \frac{-\frac{1}{2}}{{(z-z_0)}^r},$$

and the resonant points $\{-1,1,4,5\}$. Furthermore, the Painlevé integrable of system (44) can be obtained and the same property of Equation (1) is also guaranteed.

5.2. Symmetry Reduction and Group Invariant Solutions to the CKdV Equation

In this section, we consider the symmetry reduction of Equation (1) in case of $c_1=0$, and get two kinds of group invariant solutions.

Reduction 2.

$c_1=0$.

For simplicity, we take $c_2=1$ and let $\frac{{(c_5+c_6)}^2}{4}-c_4{c}_7=l^2$. Then, the following two subcases need to be discussed.

Case 3.

$l\ne 0$. It leads to the following similarity solutions

$$\begin{array}{c}u=U\left(z\right)-\frac{2c_4}{l}({\mathsf{\Psi }}_1\left(z\right){\mathsf{\Psi }}_4\left(z\right)+3{\mathsf{\Psi }}_2\left(z\right){\mathsf{\Psi }}_3\left(z\right))tanh{t}_1-\frac{8c_4^2}{l^2}{\mathsf{\Psi }}_1^2{\mathsf{\Psi }}_2^2{sech}^2{t}_1,\hfill \\ v=V\left(z\right)-\frac{2c_4}{l}(3{\mathsf{\Psi }}_1\left(z\right){\mathsf{\Psi }}_4\left(z\right)+{\mathsf{\Psi }}_2\left(z\right){\mathsf{\Psi }}_3\left(z\right))tanh{t}_1-\frac{8c_4^2}{l^2}{\mathsf{\Psi }}_1^2{\mathsf{\Psi }}_2^2{sech}^2{t}_1,\hfill \\ {\psi }_1=-{\mathsf{\Psi }}_1\left(z\right)exp(\frac{t(c_5-c_6)}{2})sech{t}_1,{\psi }_2=-{\mathsf{\Psi }}_2\left(z\right)exp(\frac{(c_5-c_6)t}{2})sech{t}_1,\hfill \\ {\psi }_3=-\frac{2exp(\frac{(c_5-c_6)t}{2})}{l}2c_4{\mathsf{\Psi }}_1^2\left(z\right){\mathsf{\Psi }}_2\left(z\right)tanh\left(t_1\right)+2exp(\frac{t(c_5-c_6)}{2}){\mathsf{\Psi }}_{3}sech{t}_1,\hfill \\ f=\frac{1}{2c_4}(2ltanh{t}_1-c_5-c_6),\hfill \end{array}$$

(45)

where $t_1=l(F\left(z\right)+t)$, and $z=x-c_{3}t$ are similarity variables.

Substituting (45) into the extended system, we derive

$$\begin{array}{c}U\left(z\right)=\frac{4c_4^2{\mathsf{\Psi }}_1^2\left(z\right){\mathsf{\Psi }}_2^2\left(z\right)}{l^2}-\frac{{\mathsf{\Psi }}_{1zz}\left(z\right)}{{\mathsf{\Psi }}_1\left(z\right)},V\left(z\right)=\frac{4c_4^2{\mathsf{\Psi }}_1^2\left(z\right){\mathsf{\Psi }}_2^2\left(z\right)}{l^2}-\frac{{\mathsf{\Psi }}_{2zz}\left(z\right)}{{\mathsf{\Psi }}_2\left(z\right)},\hfill \\ {\mathsf{\Psi }}_1\left(z\right)=\frac{l}{2}\sqrt{\frac{2F_1\left(z\right)}{c_4}}exp(\int Q_1\left(z\right)dz),{\mathsf{\Psi }}_2\left(z\right)=\frac{l}{2}\sqrt{\frac{2F_1\left(z\right)}{c_4}}exp(\int -Q_1\left(z\right)dz),\hfill \\ {\mathsf{\Psi }}_3\left(z\right)={\mathsf{\Psi }}_{1z}\left(z\right),{\mathsf{\Psi }}_4\left(z\right)={\mathsf{\Psi }}_{2z}\left(z\right),\hfill \\ F_1\left(z\right)=\frac{6Q_1\left(z\right)}{32Q_1^3\left(z\right)-8c_3{Q}_1\left(z\right)-4Q_{1zz}\left(z\right)+c_5-c_6},\hfill \end{array}$$

(46)

where $Q_1\left(z\right)=Q_z\left(z\right)$ satisfies the following elliptic equation

$$\begin{array}{c}{Q}_{1z}^2\left(z\right)=a_0+a_1{Q}_1\left(z\right)+a_2{Q}_1^2\left(z\right)+a_3{Q}_1^3\left(z\right)+a_4{Q}_1^4\left(z\right),\hfill \end{array}$$

(47)

with $\{a_0=-\frac{4l^2}{a_3^2},a_1=\frac{1}{2}(c_5-c_6),a_2=-2c_3,a_4=4\}$ or $\{a_0=0,a_1=\frac{c_6-c_5}{4},a_2=-2c_3,a_3=\frac{c_5-c_6}{2c_3}+\frac{2l^2}{c_3(c_5-c_6)}\}$.

Since $Q_1\left(z\right)$ in Equation (47) can be expressed as different types of Jacobian elliptic functions, we can derive the interactions solutions between soliton and many kinds of cnoidal periodic waves through the (45) and (46). In order to show this soliton and cnodial waves more clearly, we take a special solution of Equation (47) as

$$\begin{array}{c}{Q}_1\left(z\right)={\mu }_1+{\mu }_2\mathrm{JacobiSN}(\mathrm{z},\mathrm{m}).\hfill \end{array}$$

(48)

Substituting Equation (48) into (47) leads to

$$\begin{array}{c}{a}_3=-16{\mu }_1,c_3=2{\mu }_2^2-12{\mu }_1^2+\frac{1}{2},c_6=32{\mu }_1^3-16{\mu }_1{\mu }_2^2+c_5-4{\mu }_1,\hfill \\ l=8{\mu }_1\sqrt{-4{\mu }_1^4+4{\mu }_1^2{\mu }_2^2+{\mu }_1^2-{\mu }_2^2},m=2{\mu }_2.\hfill \end{array}$$

(49)

Substituting expressions (49) into (47) and (46), we obtain the exact forms of $F_1\left(z\right),$${\mathsf{\Psi }}_1\left(z\right),{\mathsf{\Psi }}_2\left(z\right),{\mathsf{\Psi }}_3\left(z\right),{\mathsf{\Psi }}_4\left(z\right)$, $U\left(z\right),V\left(z\right)$, and then we put them into the first two expressions of Equation (45), we will get the exact solutions of u and v. The result is omitted here because of its prolixity, but the corresponding images of u and v are as follows with the parameters {${\mu }_1=2,{\mu }_2=1,c3=-2,c_5=-1,c_6=-\frac{1}{3},l=-10$}.

At the same time, we give the numerical solution of u at $x=0$ as follows.

With the help of $Maple$, we give the numerical analysis of u at $x=0$. By taking the value of time t at some key points, the result of numerical analysis is almost completely consistent with the two-dimensional graph Figure 1a of the exact solution. From

Table 1. Numerical analysis of u at $x=0$.

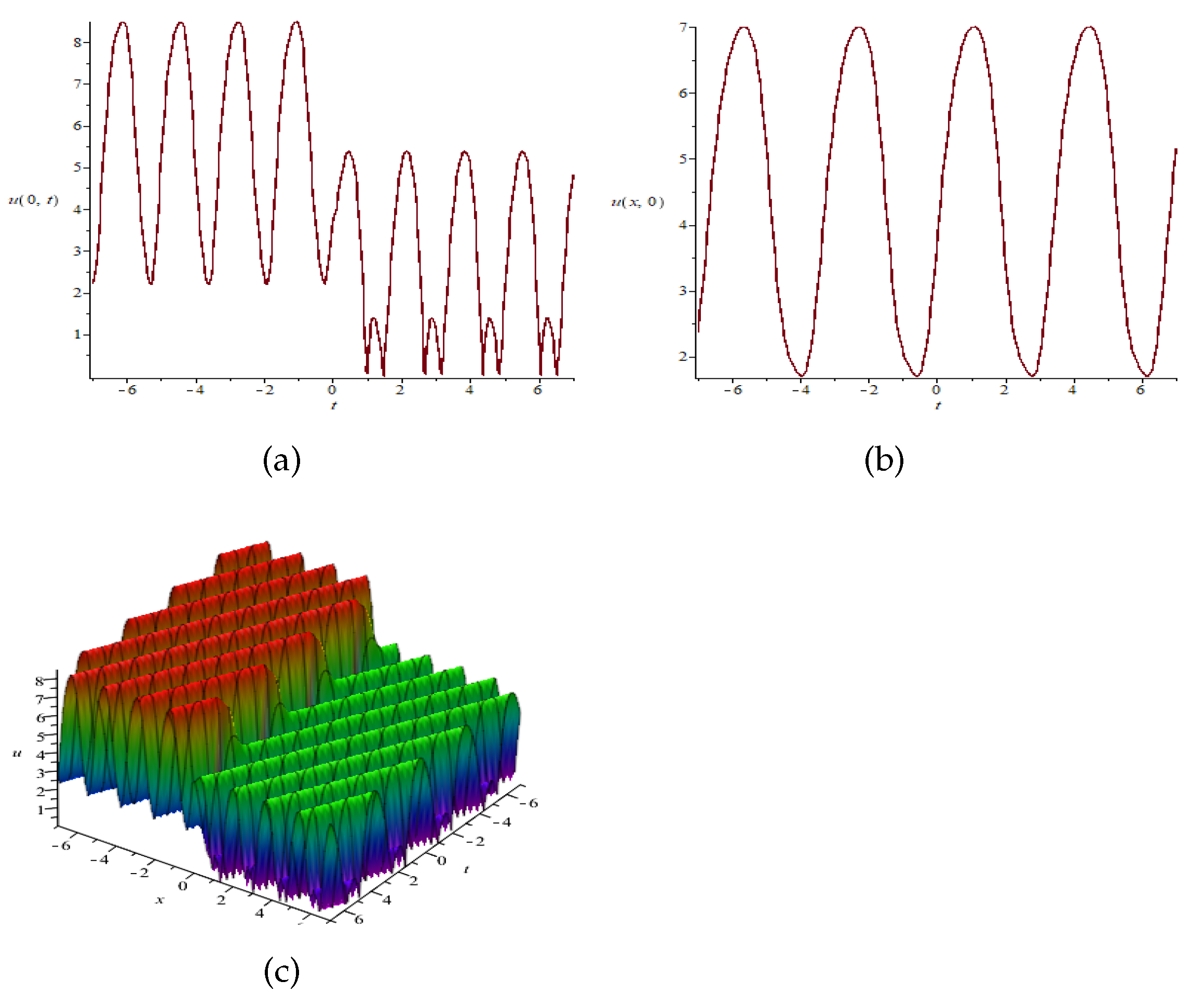
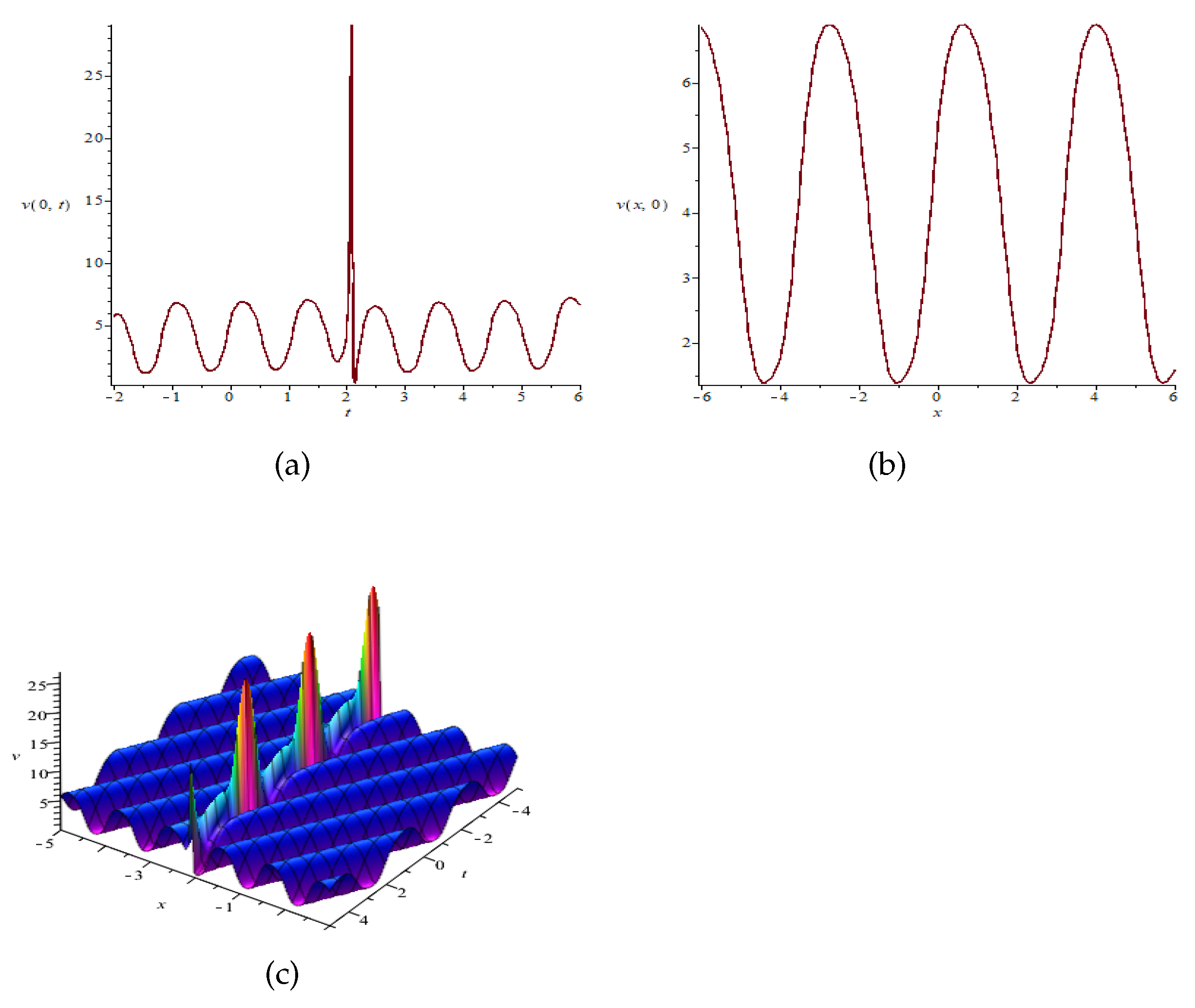
x	0	0	0	0	0	0	0	0	0
t	−7	−6.2354	−6	−5.2777	−4	−3.5919	−2.8640	−2	−1.9063
u	2.21334	8.33976	8.31707	2.21344	5.06270	2.21352	8.33954	2.38391	2.21331
x	0	0	0	0	0	0	0	0	0
t	−1.1783	−1	−0.2516	0.5049	1	1.2401	1.4742	2	2.1255
u	8.33943	8.45273	2.21235	5.35937	0.01779	1.3420	0.017117	5.07370	5.35921
x	0	0	0	0	0	0	0	0	0
t	2.6881	2.9258	3	3.1599	3.8113	4	4.3715	4.5250	4.8492
u	0.01816	1.34208	1.10875	0.01761	5.35924	5.02672	0.01780	1.34188	0.01737
x	0	0	0	0	0	0	0	0	0
t	5	5.4971	6	6.0573	6.3030	6.5315
u	1.82085	5.35929	0.98980	0.01704	1.33029	0.01664

, we can see that the value of u changes periodically from $t=-7$ to $t=-0.2516$, the value at the highest point is approximately 8.34 and the value at the lowest point is approximately 2.21. When $t=0.5049$, the value of u suddenly becomes smaller, and then it varies periodically. Combining the two-dimensional and three-dimensional graph, we know that the soliton and the periodic wave interact at this moment to form a kink soliton solution, and the collision between soliton and periodic wave is an elastic collision. Namely, the shape of the wave does not change before and after collision.

At the same time, we give the numerical solution of v at $x=0$ as follows.

Similar to Table 1, the numerical analysis of v at $x=0$ also be derived. By taking the value of time t at some key points, the numerical analysis is almost completely consistent with the two-dimensional graph Figure 2a of the exact solution. From

Table 2. Numerical analysis of v at $x=0$.

x	0	0	0	0	0	0	0	0	0
t	−2	−2.0035	−1.5320	−1	−0.9694	−0.3412	0.3051	0.7705	1
u	5.59065	5.54969	1.35679	6.55527	6.69761	1.35605	6.69981	1.46356	2.96166
x	0	0	0	0	0	0	0	0	0
t	1.2234	1.8534	2	2.0883	2.1418	2.4900	2.9770	3	3.6751
u	6.69693	2.09575	4.69652	29.07161	0.039392	6.53238	1.35676	1.28513	6.64508
x	0	0	0	0	0	0	0	0	0
t	4	4.1479	4.6155	5	5.2619	5.7031
u	2.45604	1.38254	6.69679	4.68181	1.50911	6.69698

, we can see that the value of v reaches the maximum at $t=2$, which is close to 29.07. That is the result of the interaction between the soliton and the elliptical periodic wave. The collision is an elastic collision. Since, when $t=-2$ to 1.2234 and $t=2$ to 5.7031, the values of v present a periodic characteristic, the maximum value is 6.70, and the minimum value is 1.36.

Similarly, we can get the change of u with time t at different positions of x, and the change rule is consistent with that at $x=0$.

Case 4.

$l=0$. It leads to the following similarity solutions

$$\begin{array}{c}u=U\left(z\right)-8c_4^2\frac{{\mathsf{\Psi }}_1^2\left(z\right){\mathsf{\Psi }}_2^2\left(z\right)}{t_1^2}+\frac{2c_4}{t_1}({\mathsf{\Psi }}_1\left(z\right){\mathsf{\Psi }}_4\left(z\right)+3{\mathsf{\Psi }}_2\left(z\right){\mathsf{\Psi }}_3\left(z\right)),\hfill \\ v=V\left(z\right)-8c_4^2\frac{{\mathsf{\Psi }}_1^2\left(z\right){\mathsf{\Psi }}_2^2\left(z\right)}{t_1^2}+\frac{2c_4}{t_1}(3{\mathsf{\Psi }}_1\left(z\right){\mathsf{\Psi }}_4\left(z\right)+{\mathsf{\Psi }}_2\left(z\right){\mathsf{\Psi }}_3\left(z\right)),\hfill \\ {\psi }_1=\frac{{\mathsf{\Psi }}_1\left(z\right)}{t_1}exp(\frac{t(c_5-c_6)}{2}),{\psi }_2=\frac{{\mathsf{\Psi }}_2\left(z\right)}{t_1}exp(\frac{t(c_6-c_5)}{2}),\hfill \\ {\psi }_3=-\frac{2c_4{\mathsf{\Psi }}_1^2\left(z\right){\mathsf{\Psi }}_2\left(z\right)exp(\frac{t(c_5-c_6)}{2})}{t_1^2}+\frac{exp(\frac{t(c_5-c_6)}{2}){\mathsf{\Psi }}_3\left(z\right)}{t_1},\hfill \\ {\psi }_4=-\frac{2c_4{\mathsf{\Psi }}_1\left(z\right){\mathsf{\Psi }}_2^2\left(z\right)exp(\frac{t(c_6-c_5)}{2})}{t_1^2}+\frac{exp(\frac{t(c_6-c_5)}{2}){\mathsf{\Psi }}_4\left(z\right)}{t_1},\hfill \\ f=-\frac{(c_5+c_6)(t+F\left(z\right))+2}{2c_4{t}_1},\hfill \end{array}$$

(50)

where $t_1=t+F\left(z\right)$ and $z=x-c_{3}t$.

Substituting the expressions (50) into the prolonged system, we derive

$$\begin{array}{c}U\left(z\right)=-\frac{{\psi }_{1zz}}{{\mathsf{\Psi }}_1},V\left(z\right)=-\frac{{\psi }_{2zz}}{{\mathsf{\Psi }}_2},{\mathsf{\Psi }}_1\left(z\right)=\frac{1}{2}\frac{2F_1\left(z\right)}{c_4}exp(\int Q_1\left(z\right)dz),\hfill \\ {\mathsf{\Psi }}_2\left(z\right)=\frac{1}{2}\frac{2F_1\left(z\right)}{c_4}exp(\int -Q_1\left(z\right)dz),{\mathsf{\Psi }}_3\left(z\right)={\mathsf{\Psi }}_{1z}\left(z\right),{\mathsf{\Psi }}_4\left(z\right)={\mathsf{\Psi }}_{2z}\left(z\right),\hfill \\ F_1\left(z\right)=\frac{6Q_1\left(z\right)}{32Q_1^3\left(z\right)-8c_3{Q}_1\left(z\right)-4Q_{1zz}\left(z\right)+c_5-c_6},\hfill \end{array}$$

(51)

and $Q_1\left(z\right)$ satisfies elliptic equation

$$Q_{1z}^2\left(z\right)=b_0+b_1{Q}_1\left(z\right)+b_2{Q}_1^2\left(z\right)+b_3{Q}_1^3\left(z\right)+b_4{Q}_1^4\left(z\right),$$

with $\{a_0=0,a_1=\frac{c_6-c_5}{4},a_2=-2c_3,a_3=\frac{c_5-c_6}{2c_3},a_4=4\}$, or $\{a_0=0,a_1=\frac{c_5-c_6}{2},a_2=-2c_3,a_3=a_3,a_4=4\}.$

For this subcase, according to the method of subcase 3, one can also get the interaction solutions of u and v, which reflect the interactions between Jacobian elliptic function and rational function.

6. Conclusions and Further Researches

In this paper, we provide the basic method to construct the nonlocal symmetry of nonlinear PDE, employ this method to derive the local and nonlocal symmetries of Equation (1), give the corresponding finite symmetry transformations theorem, and discuss the similarity reductions of the prolonged system. Furthermore, the Painlevé integral property and two types of new exact solutions are presented, which include the special interaction solutions between the soliton and the cnoidal periodic wave, and the soliton with rational function solution. This kind of solution can be easily applicable to the analysis of physically interesting processes. Besides, we also give the numerical analysis of the CKdV equations, which can verify the properties of exact solution.

For the provided method in this paper, we only consider the Lax pairs as the auxiliary system. However, if we choose the Bäcklund transformation, potential system, pseudo-potential as the auxiliary system, maybe, we can obtain different nonlocal symmetries.

Meanwhile, there is an other interesting thing that the CKdV Equation (1) have close relationship with the AB-KdV. If we let $u=A,v=B=A^{\widehat{P}\widehat{T}}=A(-x,-t)$ (where $\widehat{P}$ and $\widehat{T}$ are the usual parity and time-reversal operators respectively) and put the above assumption into Equation (1), then (1) will be reduced to the following integrable nonlocal AB-KdV equations

$$\begin{array}{c}{A}_t-\frac{1}{2}{A}_{xxx}+\frac{3}{2}{B}_{xxx}-3(A-B)A_x+6A{B}_x=0,B=A^{\widehat{P}\widehat{T}}=A(-x,-t).\hfill \end{array}$$

(52)

Therefore, for the symmetry reduction 1 and 2, $Q\left(z\right)=0$ leads to ${\mathsf{\Psi }}_1={\mathsf{\Psi }}_2$, then we can further deduce $u=v$ and derive the PT (Parity and Time) symmetric exact solution for the AB-KdV equation by the transformations of $x=-x,t=-t$.

Based on the above facts, we consider whether all of the coupled equations can be reduced to a corresponding nonlocal AB equation. If so, whether we can get some new types of solutions of nonlocal equations by solving the corresponding local equations will be discussed in our future work.