Bateson and Wright on Number and Quantity: How to Not Separate Thinking from Its Relational Context

Abstract

As part of his explication of the epistemological error made in separating thinking from its ecological context, Bateson distinguished counts from measurements. With no reference to Bateson, the measurement theory and practice of Benjamin Wright also recognizes that number and quantity are different logical types. Describing the confusion of counts and measures as schizophrenic, like Bateson, Wright, a physicist and certified psychoanalyst, showed mathematically that convergent stochastic processes informing counts are predictable in ways that facilitate methodical measurements. Wright’s methods experimentally evaluate the complex symmetries of nonlinear and stochastic numeric patterns as a basis for estimating interval quantities. These methods also retain connections with locally situated concrete expressions, mediating the data display by contextualizing it in relation to the abstractly communicable and navigable quantitative unit and its uncertainty. Decades of successful use of Wright’s methods in research and practice are augmented in recent collaborations of metrology engineers and psychometricians who are systematically distinguishing numeric counts from measured quantities in new classes of knowledge infrastructure. Situating Wright’s work in the context of Bateson’s ideas may be useful for infrastructuring new political, economic, and scientific outcomes.

1. Multilevel Meanings and Logical Types

Difficulties in communication posed by the simultaneous presence of multiple levels of meaning in language have been a perennial topic of investigation for philosophers, logicians, anthropologists, and, more recently, theorists in the areas of complex adaptive systems, autopoiesis, organizational research, and knowledge infrastructure. The odd capacity for statements about statements to be meaningless even when they are grammatically correct (as in the viciously circular, “This statement is false”) led Russell [1,2] to develop a theory of logical types as a means of distinguishing levels of propositions. Bateson [3] cites Russell along with Wittgenstein, Carnap, Whorf, and his own early work as examples of the need to avoid confusion by separating and balancing concrete denotative statements about observations, abstract metalinguistic statements about words, and formal metacommunicative statements about statements.

In their account of these sequences of nested symmetries, Russell and others assume a Cartesian, dualist perspective of externally imposed control as the only viable means of respecting logical type structures. Bateson and others, however, take an agent-based perspective that lends itself to an alternative internally derived capacity for devising infrastructural standards akin to those of natural language. The utility and meaningfulness of these standards and their adaptive capacities in the face of otherwise unmanageable complexity may provide otherwise unattainable motivations for investing in their construction.

Ecologically speaking, Bateson contends, a fundamental epistemological error is made when cognitive operations are separated from the structural relationships in which they are immanent (i.e., when the symmetry of adjacent levels of complexity is ignored). Thus, referring denotatively to something learned (“the cat is on the mat”) is very different from a metalinguistic statement about what was learned (“the word ‘cat’ cannot scratch”). Metacommunicative statements about statements, in turn, assert theories about learning (“my telling you where to find your cat was friendly”). Paradoxical sentences (“This statement is false”) present what seems to be a factual denotative observation but are simultaneously metacommunicative, because they refer back to themselves in a statement about a statement. Symmetry is violated despite the grammatically correct syntax.

Cross-level confusions such as these are ubiquitous in existing knowledge infrastructures. They can even be said to form a fundamental component in the modern cultural worldview. They have been incorporated unintentionally, as a result of seeming to have no obvious alternative, into the background assumptions, policies, and procedures of contemporary market, governmental, educational, healthcare, and research institutions. These mixed messages continue unabated, in general, even though their root causes have been successfully addressed for decades in specific instances of theory and practice.

Important aspects of these solutions were anticipated by Bateson but came to fruition in the work of Benjamin Wright, a physicist and psychoanalyst who made a number of fundamental contributions in measurement modelling, experimental approaches to instrument calibration, parameter estimation, fit analysis, software development, professional development, and applications across multiple fields [4,5]. After describing the problem of how confused logical types are implicated in mixed messages, Bateson’s distinction between numeric counts and quantitative measures will be shown to set the stage for Wright’s expansion on that theme. Specifically, the problem being addressed concerns the epistemological confusion of numeric counts and measured quantities, and the solution offered consists of improved measurement implemented via metrological infrastructures functioning at multiple levels of complexity. The specific contribution made by this article is situating measurements and instruments calibrated to reference standards in the context of larger epistemological issues; this connection opens up new possibilities for meeting the highly challenging technical demand for new forms of analysis and information technology that are as locally grounded as they are temporally and spatially mobile and abstract [6,7,8].

2. The Schizophrenia of Symmetry Violations Ignoring Logical Types

Cross-level fallacies falsely generalize parts to wholes, or vice versa [9]. When wholes are greater than the sums of their parts, and exist at a higher order level of complexity, valid generalizations must be based in persistent isomorphisms demonstrably exhibiting shared functional relationships [10]. Ignoring cross-level fallacies results in a kind of schizophrenia, where messages confusing two levels of meaning put the listener in an unresolvable double bind.

Concurring with Bateson and generalizing his double bind concept to the pervasive incorporation of cross-level fallacies in communications, Deleuze and Guattari [11] suggest that “…society is schizophrenizing at the level of its infrastructure” (p. 361). Brown [12] diagnoses the problem as one in which “schizophrenic literalism equates symbol and original object so as to retain the original object, to avoid object-loss.” Star and Ruhleder [6] similarly point out that cross-level fallacies’ “discontinuities have the same conceptual importance for the relationship between information infrastructure and organizational transformation that Bateson’s work on the double bind had for the psychology of schizophrenia.”

Repeated experiences with cross-level fallacies in psychological research during the 1950s and 1960s played a central role in Benjamin D. Wright’s (1926–2015) insights into how to avoid them. Wright [4,5] was a certified psychoanalyst [13,14] and former physicist [15] whose experience with computers and mathematical modelling made him an early leader in educational and psychological research [16,17]. Significantly, that work involved children with schizophrenia [18,19].

Working with a UNIVAC I, Wright [16] wrote a combined factor analysis and regression program. In his role as a consultant to Chicago-area marketing firms, Wright was “doing 10 to 20 factor analyses a week,” with some clients that “did the same study every couple of weeks for years,” running “one study a hundred times with the same instruments.” Doing this work, Wright [20] said he was in “considerable distress,” feeling like a “con man” and “a crook.” As a physicist, he sought reproducible measures read from instruments calibrated in interval units traceable to consensus standards. As a psychoanalyst, Wright was concerned with human meaning. Fearing that he was satisfying neither his scientific nor his human values, Wright [20] joked about “going to the psychoanalyst to have my schizophrenia mended week by week.”

Bateson’s [21] sense of the schizophrenic double bind involves situations in which an implacable authority demands rigid conformity with idealized structures that cannot be realized within the existing constraints of a given situation. This is the kind of situation in which Wright found himself, and that situation remains today the context in which those employing commonly used statistical methods in psychology and the social sciences still find themselves.

The double bind is one in which the value of mathematical abstraction is asserted and desired; at the same time, the methods employed for realizing that value are completely inadequate to the task. Everyone is well aware of the truth of the point made by both Bateson and Wright, that numeric counts are not measured quantities: it is plain and obvious that someone holding ten rocks may not possess as much rock mass as another person holding one rock. The same principle plainly applies in the context of data from tests and surveys, such that counts of correct or agreeable answers to easy questions are not quantitatively equivalent to identical counts of correct or agreeable answers to difficult questions. The practicality, convenience, and scientific rigor of measurement models quantifying constructs in ways facilitating the equating of easy and hard tests have been documented and validated for decades, although have not yet been integrated into mainstream conceptions of measurement.

Even so, the resolution of the double bind Wright helped to create is widely applied in dozens of fields and thousands of papers published over the last 50 years (as can be readily established via searches of Google Scholar for “Rasch” in association with any of the following: analysis, measurement, scaling, model). This resolution has not, however, been incorporated into mainstream methods or the background assumptions and infrastructures of research and practice.

Much of the discord in today’s political, economic, organizational, and environmental world exhibits the characteristics of a schizophrenic double bind [11,22,23,24]. Practical difficulties in formulating clear theoretical and methodological applications of the double bind concept in psychological counseling [25,26,27,28,29,30] do not remove the systemic need for resolution of the cross-level fallacies embedded within knowledge infrastructures. Star [31] frames the problem, asking,

In the absence of a central authority or standardized protocol, how is robustness of findings (and decision making) achieved? The answer from the scientific community is complex and twofold: they create objects that are both plastic and coherent through a collective course of action.

In this context, the question arises as to the general feasibility of a systematic experimental solution to the problem of pervasive cross-level fallacies in communication. What collective courses of action resolve double binds in communication by creating objects that adapt to local circumstances without compromising their coherent comparability?

3. Separating and Balancing Levels of Reference

Ever since the publication of Russell’s 1908 article on logical types [1], writers working in a wide range of different fields have recognized the need to closely attend to the distinctions among them. In the context of living systems, “every discussion should begin with an identification of the level of reference, and the discourse should not change to another level without a specific statement that this is occurring” [32]. When developing information technology, “for systems that provide electronic support for computer-supported cooperative work, only those applications which simultaneously take into account both the formal, computational level and the informal, workplace/cultural level are successful” [6]. Therefore, “Multilevel thinking, grounded in historical and spatiotemporal context, is thus a necessity, not an option” [33] (p. 355).

In support of multilevel thinking, Van de Vijver and colleagues [34] offer advanced multilevel analytic methods, Palmgren [35] extends Russell’s [1] results on the mathematical logic of a functional reducibility axiom, whereas Lee and colleagues [36] describe the conceptualization of psychological constructs in a multilevel approach to individual creativity. The availability of tools and concepts such as these for making and sustaining cross-level distinctions has not, however, led to the development of broad-scale infrastructures incorporating those distinctions.

The difficulty is one of perceiving and taking hold of a fundamental but implicit characteristic of the social environments in which we exist. Bateson [3] and others [37] note that contextual frame shifts across levels of complexity are not usually made explicit in everyday discourse. Common usage simply moves words across levels without attending to the implicit shifts in meaning across frames. Sometimes funny jokes and meaningful metaphors can be made from these kinds of dissonances, but far too often the disconnection leads only to miscommunications. Adopting Bateson’s [3] terms, the question taken up here is how we might devise infrastructural standards distinguishing between denotative statements about learning something, metalinguistic statements of learning about learning, and metacommunicative theories of learning, where statements are about statements.

For a science of complexity or a science of polycontextual metapatterns based on Bateson’s work [38,39,40] to realize its mission, knowledge infrastructures must operationalize metalinguistic awareness. Promising preliminary efforts in this direction [7,8,41,42,43,44,45,46,47,48,49,50] overlook an essential set of opportunities and challenges of decisive importance.

Krippendorff [51] provides an important hint in a new direction when he identifies an unresolved issue in Bateson’s use of Russell’s theory of types. Krippendorff suggests that the omission of self-determination and autonomy from Bateson’s sense of logical type distinctions demands the development of a new, more constructive and intentional, “theory that allows circularities to enter and that can then explain, among other things, why belief in the Theory of Logical Types reifies itself in all kinds of hierarchies whose experiential consequence almost always is oppression.”

4. Numeric Counts vs. Quantitative Measures

A theory of that kind, one that includes self-determination and autonomy, follows from recognizing and leveraging patterns in the way things come into words. Two primary patterns are of interest. The older pattern dates to the origins of language and involves words associated with semantically well-formed conceptual determinations, where a class of things in the world (cats, for instance) with consistently identifiable features has a name easily learned by all speakers of the language. These word–thing–concept assemblages, or semiotic triangles, have a generality and universality to them that makes habitual usage and transparent representations possible. Usage typically distinguishes levels of meaning appropriately, such that double bind confusions and cross-level fallacies may be found in humorous jokes, poetic metaphors, and deceitful prevarications, but are not deliberately distributed throughout messaging systems.

A more recently emerged pattern, however, involves words associated with things that are neither consistently identifiable in the world nor clearly determined concepts. This class of words often involves numbers treated as meaningful in the same way that the word “cat” is, and in the same way that the number words for meters and hours are, but which plainly and obviously cannot and do not actually support that kind of generality. This class of words concerns scores from educational tests and ratings from assessments and surveys. In classrooms, hospitals, workplaces, the media, and elsewhere, counts of correct answers, sums of ratings, and associated percentages are treated as meaningful, even though their signification is inherently restricted to the context defined by the particular questions answered. Common usage incorrectly assumes that the denotative factuality of numeric counts and scores translates automatically into quantitative measures. Denotatively meaningful counts of correct test answers are fallaciously applied at the metalinguistic level as representations of performance. They are similarly also used at the metacommunicative level to justify instructional, admissions, and graduation decisions, even in the absence of metalinguistic significance and an experimentally substantiated theoretical rationale.

The cross-level transference of scores whose meaning depends strictly on the specific content of particular questions asked of particular people results in the kinds of vicious circularities and schizophrenic double binds reported by Wright [20] concerning his use of factor and regression analyses of test scores. Problems associated with this kind of cross-level fallacy also have been observed in recent years as a consequence of the No Child Left Behind education act in the United States. [52]. These problems can potentially be rectified by closely attending to how things come into words. A bottom-up focus on Bateson’s sense of process may provide means for obtaining new and liberating experiential consequences from the Theory of Logical Types, instead of the oppressive consequences noted by Krippendorf [51].

4.1. Bateson on Convergent Stochastic Sequences

Bateson [53] identified the source of the problem when he recognized that “…quantity and pattern are of different logical type and do not readily fit together in the same thinking.” This is because “Not all numbers are the products of counting…smaller…commoner numbers…are… recognized as patterns in a single glance” [53]. Additionally, “…we get numbers by counting or pattern recognition while we get quantities by measurement”.

Bateson does not turn the problem around to ask how patterns in counting might explain the genesis of quantities, but he [53] does, however, devote considerable attention to the “generative process whereby the classes are created before they can be named”. He (p. 216) follows Mittelstaedt in characterizing “a whole genus of methods of perfecting an adaptive act” in terms of feedback from a class of self-correcting practices, and in characterizing another genus of methods in terms of performance calibrations: “…in these cases, ‘calibration’ is related to ‘feedback’ as higher logical type is related to lower.”

Bateson [53] also identifies convergent “stochastic sequences” in the forms of feedback encountered in genetics and learning. This feedback is what makes prediction of future events possible. Although Bateson does not develop his thinking in this direction, he implies that these sequences should cohere in stochastic games of trial and error. These games inform a calibration language of measurement naming quantities embodied in metalinguistic instruments read in standardized units and predicted by metacommunicative theory. Devine [54] independently makes the same point, saying that:

The computational mechanics approach [to stochastic processes] recognises that, where a noisy pattern in a string of characters is observed as a time or spatial sequence, there is the possibility that future members of the sequence can be predicted. The approach shows that one does not need to know the whole past to optimally predict the future of an observed stochastic sequence, but only what causal state the sequence comes from. All members of the set of pasts that generate the same stochastic future belong to the same causal state.

Rasch’s [55,56] stochastic models for measurement are based on the same principle of reproducible patterns of invariance estimated from what are conceived as inherently incomplete samples of data collected in the past. These patterns are hypothesized to take various forms specified in a class of models as being structured by causal relationships retaining characteristic identities as repeatable constructs across samples of things, people, or processes measured, and across samples of questions, indicators, or items comprising the measuring instruments [57,58,59,60,61,62,63,64,65,66,67].

Probabilistic models for measurement have been characterized in terms of complex adaptive systems [68], but are more commonly treated as scaling algorithms in the fields of psychometrics, educational measurement, survey research, etc. [69,70,71,72,73,74,75,76,77]. Recent collaborations of psychometricians and metrologists [65,78,79,80,81,82,83,84,85,86] are reaching beyond the usual analytic perspective to posit the viability of distributed interconnected ecosystem relations. These researchers suggest that systematic distinctions between numeric counts and measured quantities can be built into knowledge infrastructures in the same way that the standard kilogram unit for measuring mass has been globally adopted. Separating and balancing the utility of each logical type by providing the contextualization and maximizing their meaningfulness requires incorporating consensus standard methods for explicit experimental tests of, and theoretical justifications for, unit definitions and instrument calibrations.

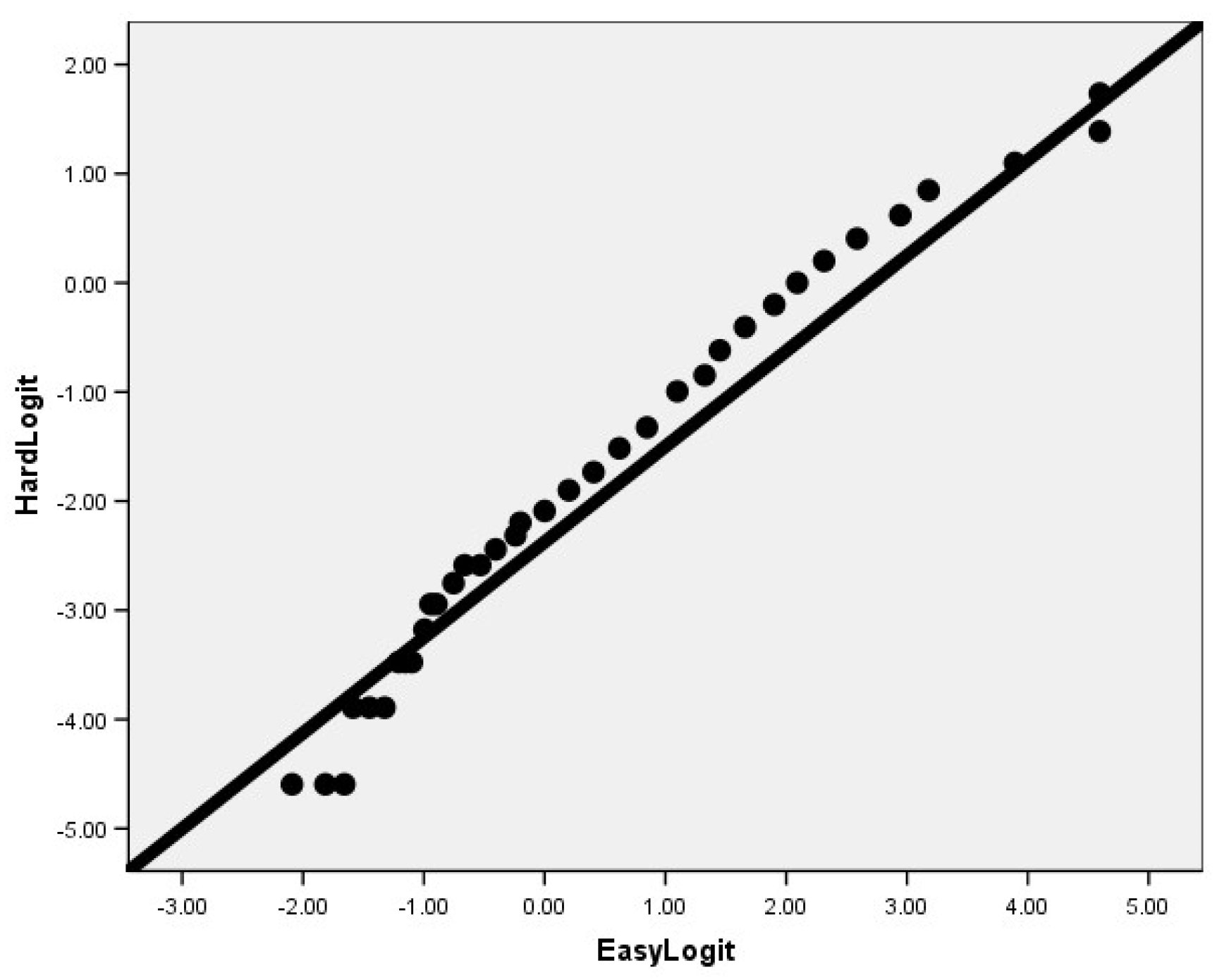
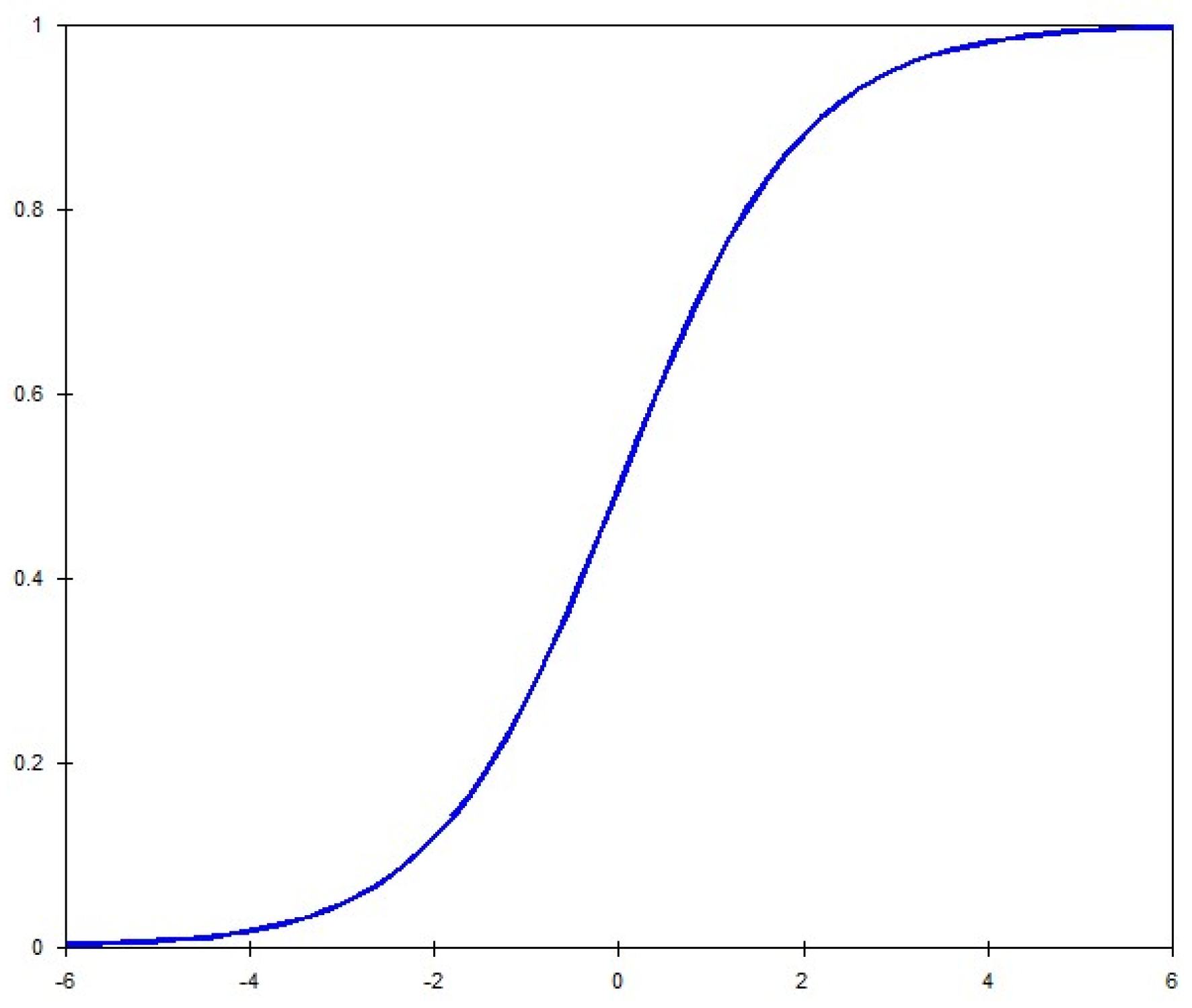
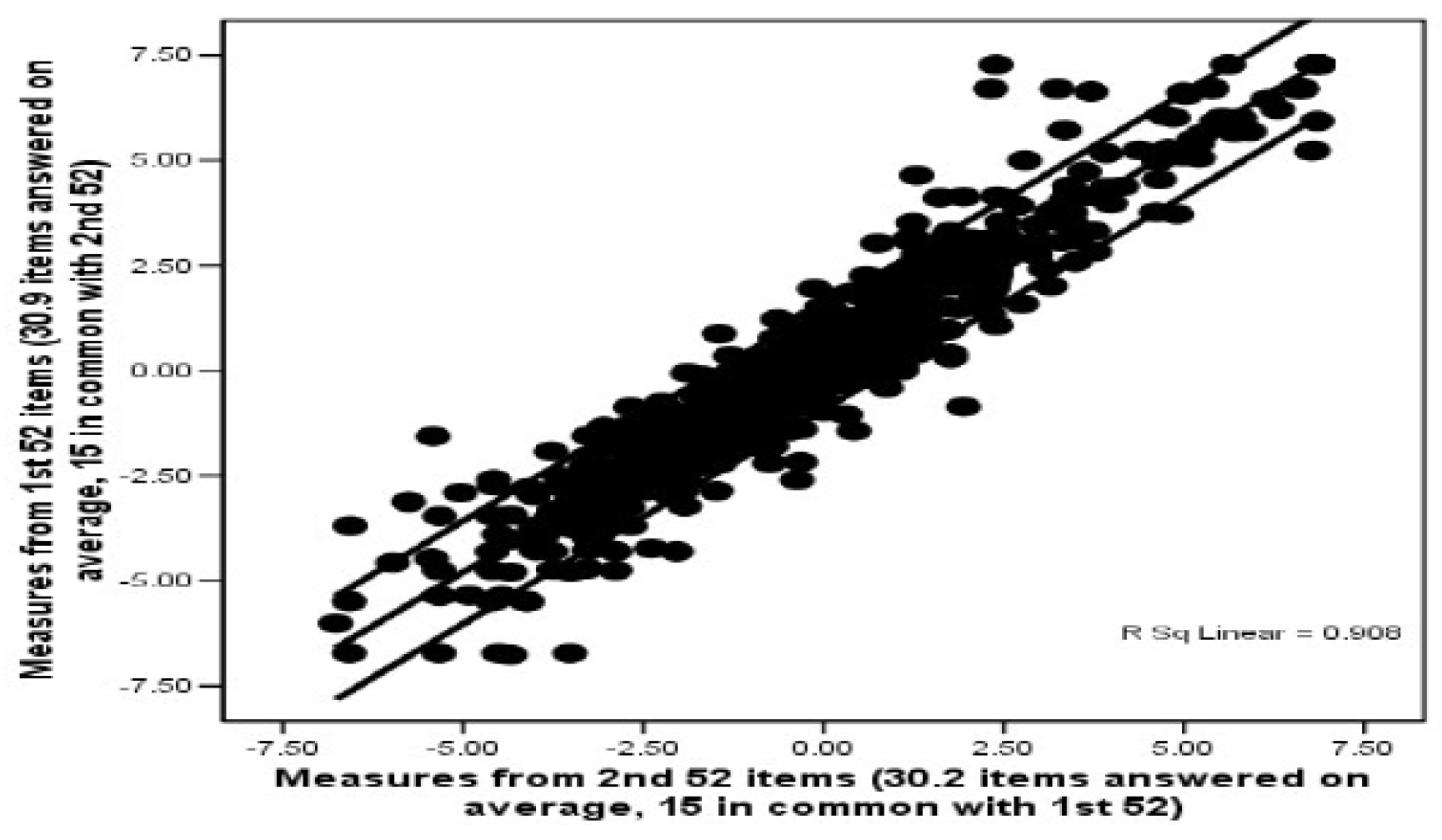
4.2. Wright’s Expansions on Rasch’s Stochastic Models for Measurement

Echoing Bateson’s language of the predictability obtained from convergent stochastic sequences, Wright [76] couches the advantages of Rasch’s models in terms of their support for inferential processes of learning from the data in hand to predict future data not yet obtained. Moving beyond a merely analytic process of statistical inference, Wright [76] speaks to the need and the basis for stable units of measurement, as in the history of the economics of taxation and trade informed by instruments read in universally accessible common metrics.

Wright’s position is supported by mathematical proofs of Rasch’s [55] parameter separability theorem and decades of experimental evidence [87,88,89]. Rasch’s models satisfy the axioms of conjoint additivity [90], and employ observed scores as minimally sufficient (i.e., both necessary and sufficient) estimators of the model parameters [91,92,93,94]. Statistical sufficiency is key here. Following Fisher [95,96], estimates that contain the complete information available in the data are necessary to models positing separable parameters [92]. Sufficiency is established mathematically as defining a set of invariant rules that is “an essentially complete subclass of the class of invariant rules” [97,98].

Insight into what this means can be gained by picking up where Bateson left off in his realizations that counting patterns are of a different logical type than quantities, and that feedback patterns aggregate to calibrate performances at a discontinuous new level of complexity. Wright [94,99,100,101] describes how patterns in counts can be experimentally evaluated relative to a probabilistic model requiring structural invariance and sufficient statistics to support or refute the hypothesis that a construct can be measured in an interval unit quantity. Where Bateson [53] stops with a distinction between being able to possess exactly three tomatoes but never being able to have exactly three gallons of water, Wright [76,77,94,99,100,101] shows how to derive what we want (measures and quantities) from what we have (counts and numbers).

Counts of events, such as correct answers to questions, or counts of categorical ratings, are typically interpreted as indicating the presence or absence of some social or psychological trait, an ability, knowledge, performance capacity, or behavior. Identical scores (summed counts or ratings) from the same items are interpreted as meaning the same thing, even if they may in fact conceal quite different patterns. Scores are known to be interpretable only in terms of an ordinal scale, one in which higher numbers mean more (typically), but with no associated capacity for determining how much more. Despite this caveat, ordinal scores are nonetheless routinely employed in statistical comparisons assuming interval units [73,101,102,103], contributing to the widespread promulgation of cross-level fallacies in knowledge infrastructures.

Wright [100] implicitly expands on Bateson’s point concerning the difference between counts and quantities. He notes that oranges vary in size and juice content in such a way that it is not possible to tell how many oranges it will take to obtain two glasses (about a pint, or almost 500 mL) of juice. “Sometimes it’s only three. Other times it can take six.” He finds that oranges are about half juice, by weight, and because “a pint’s a pound the whole world round,” a pint of orange juice will typically be produced by two pounds (about 1 kg) of oranges. His grocery store sells oranges in four-pound bags; therefore, he knows to take out half of the oranges in the bag to obtain a pint of orange juice.

The same principle applies to the difference between counts and quantities in any science. Figure 1 and Figure 2 illustrate the practical difference between the kinds of comparisons supported by counts and measures. Figure 1 shows how the meanings of counts are restricted to the frame of reference defined by a particular group of persons responding to a particular group of questions. Imagine that a group of people all answer every question on a long test or survey, each item is scored as a count of correct or agreeable responses, and the items are then divided into two groups. One group is made up of all the highest scoring items, and the other is made up of all the lowest scoring questions. Each person then has two scores, one from the easy questions, and another from the hard ones.

Figure 1 is a plot of these pairs of scores, expressed as percentages of the maximum possible. Two points, at 0 and 100, are on the identity line, showing that the same score is obtained on both instruments. When someone obtains the highest possible score of 100 on the hard questions, they also obtain the highest possible score on the easiest questions. Conversely, when someone obtains the lowest possible score of 0 on the easy questions, they also obtain a 0 on the hard ones. However, by definition, in between these extremes, everyone will have higher scores on the easy questions than on the hard ones.

In keeping with the ordinal status of the scores, the distance between adjacent scores changes depending on where they are positioned between 0 and 100. The relation between score changes, such that 1–1 and 99–99 indicate close correspondences, but the entire range of 25 to 100 on the hard questions spans only 80 to 100 on the easy questions. The same kind of relationship would be obtained if responses from a group of people were scored, divided into high and low groups, and pairs of scores were then assigned to all of the items and plotted.

Figure 2 shows what happens when something as simple as taking the log-odds of the response probabilities is used to estimate measures. Here, there is a nearly linear relationship between the pairs of measures from the two instruments, providing a basis for equating them to a common unit. More sophisticated estimation methods provide closer correspondences than this simple approximation [104]. Even so, Figure 2 illustrates why, as noted by Narens and Luce [105], Stevens was justified in adding log-interval scales as a fifth type in his measurement taxonomy (the others being nominal, ordinal, interval, and ratio).

Figure 1 shows the meaning of the same count to change nonlinearly from the easy questions to the hard ones. In addition, the unit size changes within each set of scores, so there is no way to identify a common score structure across them. Figure 2, however, shows that the two instruments could be scaled to a shared unit by estimating the item locations together via the common sample. Once they are equated and anchored at fixed values, the easy and hard questions, or any combination of subsets of them, can be administered to estimate measures in a stable, comparable quantitative metric [106,107].

Adaptive instrument administrations of this kind can be accomplished via paper and pencil or electronic self-scoring forms that report numeric patterns contextualized by measured quantities, along with uncertainty estimates. These forms provide immediate feedback at the point of use with no need for data computerization or analysis [108,109]. The universal availability of such instruments traceable to common metrics is essential to the creation of effective knowledge infrastructures separating forms of information by logical type.

Figure 3 shows the ogival relation between numeric scores and measured quantities, given data in a complete person-by-item matrix where everyone answers all questions. As can also be discerned in Figure 1, it is apparent in Figure 3 that, relative to their corresponding logits, scores at the extremes are packed more closely together than scores in the middle of the range. The same small percentage change on the vertical axis near 0 or 100 percent translates into a large logit difference relative to the smaller logit differences observed in the middle of the scale for the same percentage change.

Figure 4 and Figure 5 show that linearly comparable results are obtained across samples of items and persons. Specifically, the structural invariance of the construct measured retains its characteristic properties in the manner required for the definition of meaningful quantity. Independent samples of items measuring the same construct will result in linear and highly correlated pairs of measurements, as shown in Figure 4. Conversely, independent samples of persons participating in the same construct will result in linear and highly correlated pairs of item calibrations, as shown in Figure 5.

Finally, Figure 6 illustrates an example of the extent to which theoretical predictions implemented via an explanatory model of item components are borne out by empirical calibrations. Far from being rare exceptions to the rule in psychological and social measurement, as claimed by Sijtsma [111], these kinds of results and the principles informing them have been in wide circulation for decades [60,61,62,63,65,66,67,112,113,114,115,116]. These models and their results should be more routinely incorporated in a metrological context for standard research and practice.

4.3. The Difference That Makes a Difference as a Model Separating Logical Types

A key accommodation of the nonlinearity and scale-dependence of numeric counts became built into a wide range of measurement applications in a number of fields by Likert’s [117] observation that the middle range of the logistic ogive in Figure 3 is approximately linear. This assertion of the near-equivalence of counts and measures for complete data in this range provided an inexpensive and pragmatic alternative to Thurstone’s [118] more difficult methods that focused on calibrating instruments not affected in their measuring function by the particulars of who is measured. It also led to the systematic incorporation of unresolvable double binds in the messaging systems of virtually all major institutions. That is, the policies and practices of education, healthcare, government, and business all rely on nonlinear and ordinal numeric counts and percentages that are presented and treated as though they are linear, interval measured quantities.

What makes this a schizophrenic double bind? Just this: everyone involved is perfectly well aware that these counts of concrete events and entities (my ten small rocks or ten correct answers to easy questions, versus your five large rocks or five correct answers to difficult questions) are not quantitatively comparable, but everyone nonetheless plays along and acts as if they are. We restrict comparisons to responses to the same set of questions as one way of covering over our complicity in the maintenance of the illusion. This results in the uncontrolled proliferation of thousands of different, incomparable ways of purportedly measuring the same thing. Everyone accepts this as a necessity that must be accommodated—although it is nothing of the sort.

The schizophrenic dissonance of these so-called metrics is in no way incontrovertibly written in stone as an absolutely unrevisable linguistic formula. Following on from the emergence of key developments in measurement theory and practice in the 1960s, two highly reputable measurement theoreticians wrote in 1986 that (a) the same structure serving as a basis for measuring mass, length, duration, and charge also serves as a basis for measuring probabilities, and (b) that this broad scope of fundamental measurement theory’s applicability was “widely accepted” [105]. However, if measurement approaches avoiding the epistemological error of confusing counts for quantities were “widely accepted” by 1986, why are communications infrastructures dependent on psychological and social measurements still so fragmented? Why have systematic implementations of the structures commonly found to hold across physical and psychosocial measurements not been devised so as to better inform the management of outcomes?

The answers to these questions likely involve the extreme difficulty of thinking, acting, and organizing in relation to multiple levels of complexity. As Wright concludes, the difference between counting right answers and constructing measures is the same as the difference between counting and weighing oranges. However, neither Wright nor Bateson ever mentions the infrastructural issues involved in making it possible to weigh oranges in a quality assured quantity value traceable to a global metrological standard. It is true that, just as one person with three oranges might have as much orange juice as someone else with six, so, too, might one person correctly answering three hard questions have more reading ability as someone else correctly answering six easier questions. However, this point alone contributes nothing to envisioning, planning, incentivizing, resourcing, or staffing the development of the infrastructure needed to perform a measurement of reading ability, for instance, as universally interpretable as the measurement of mass.

An alternative examination of the counts–quantities situation is provided by Pendrill and Fisher [84], who apply engineering and psychometric models to numeric count estimates obtained from members of a South American indigenous culture lacking number words greater than three. The results clearly support Bateson’s sense of the relation of counting to pattern recognition by demonstrating how intuitive visualizations approximate numeric tallies and so provide a basis for estimating quantitative measures. However, Pendrill and Fisher expand the consideration of the problem to a level of generality supporting the viability of a new class of metrological knowledge infrastructure standards.

The process begins by positing and testing the hypothesis that the only difference that makes a difference is the one between the ability of the person and the difficulty of the question. Of course, questions must be written and administered in ways that provide a reasonable basis for conducting these kinds of data tests [75,119]. Model fit may not be tenable when questions do not all tap the same construct, and when the specific question answered cannot be inferred from the response. Key to this instrument design process, therefore, is close attention to a theoretical rationale concerning what the construct is, how it varies from less to more, how the questions asked cause responses to manifest a particular invariance, and how the evidence accrued will warrant quantitative inferences.

When questions focus on specific cognitive or behavioral processes that can be inferred from the responses, and when the questions vary in their difficulty or agreeability across a wide range, response probabilities often consistently and monotonically increase from less to more. When enough questions are asked to reduce uncertainty to a small fraction of the observed variation [110,120], reproducible invariances can be reliably measured. Consistent reproduction of a unidimensional construct across persons and items results in the fit of data to the model, such that the log-odds of the probability P of a correct response to item i by person n depends only on the difference between the person measure B and the item calibration D:

ln(P_ni/(1 − P_ni)) = B_n − D_i

(1)

This model states a key difference that makes a difference in conceptually and operationally distinguishing numeric counts’ level of logical type from that of measured quantities. The more able the person is, the more likely a correct response will be observed on any item, within the range of uncertainty. The more difficult an item is, the less likely a correct response will be observed, from any person, within the range of uncertainty.

Given model fit and an explanatory theory predicting item calibrations, ordinal numeric counts can be re-expressed as interval-measured quantities meaningfully interpreted in terms of differences that make a difference. Fit to the model provides empirical substantiation of the existence of unit quantities that stand as consistent, repeatable, and comparable differences. An explanatory theory successfully predicting the scale locations of items based on features systematically varied across them enables qualitative annotations to and interpretations of the quantitative scale [75,119].

Although this model unrealistically posits an unachievable ideal, it does so in the good company of the Pythagorean theorem, Newton’s laws, and many other mathematical formulations of regularly reproducible patterns exhibiting the stability needed for predicting the future. Furthermore, the model, similarly to the Pythagorean, Newtonian, and many other examples from the history of science, also accommodates local idiosyncrasies in the context of an abstract standard explained by a predictive theory. The goal, therefore, is not to impose an artificially homogenized sameness but to instead contextualize individuals’ creative improvisations to make them negotiable in the moment, in the manner of everyday language.

Extensive experience with models of these kinds in dozens of fields has resulted in sophisticated methods of parameter estimation, instrument equating, item banking, model fit analysis, reporting, etc. Given the patterns of human development over time, and of healing processes across a wide range of conditions, existing educational and healthcare institutions are already designed around intuitions of the self-organizing invariant structures modeled and measured via Rasch’s models. Seeing how one or more instruments designed to measure variation in a specific construct align item contents across samples is a convincing display of evidence as to construct stability [87,121,122,123]. These kinds of patterns led to a large study of reading comprehension in the 1970s involving 350,000 students in all 50 U.S. states, calibrating and equating seven major reading tests [124,125]. This work eventually led to the development of a theoretical model explaining item variation and the deployment of a reading comprehension metric [66,67,126] now reported annually for over 32 million students in the U.S. alone.

5. Discussion

In accord with Bateson, Wright [127] maintains that “As long as primitive counts and raw scores are routinely mistaken for measures…there is no hope of…a reliable or useful science.” Wright and Linacre [101] point out that attention to the difference between counts and measures in psychological measurement is not new. Thorndike called for the relevant methods in 1904, and Thurstone devised approximate solutions in the 1920s. As was also shown by Luce and Tukey [128] for their new form of fundamental measurement, Rasch’s solution, formulated as an extension of Maxwell’s analysis of Newton’s second law of motion, is both necessary and sufficient, no matter what science is involved [90,91,92,93,94,129,130,131].

This is as it should be if we aspire to knowledge infrastructures incorporating fair comparisons living up to the meaning of the balance scale as a symbol of justice. If observed counts summarize all of the available information for each person responding (or object rated, etc.), then those counts represent a pattern supporting the estimation of a quantity and associated uncertainty. Wright [77] says:

Inverse probability reconceives our raw observations as a probable consequence of a relevant stochastic process with a useful formulation. The apparent determinism of formulae like F = MA depends on the prior construction of relatively precise measures of F and M… The first step from raw observation to inference is to identify the stochastic process by which an inverse probability can be defined. Bernoulli’s binomial distribution is the simplest process. The compound Poisson is the stochastic parent of all such measuring distributions.

The history of science can be seen as multiple instances of situations in which repeated observations of data patterns invariantly structured as independent reproductions of the same phenomenon led to explanatory predictive models and the calibration of instruments measuring in standard units [89,131]. From this perspective, experimental evidence of patterns of structural invariance in numeric counts supports meaningful expression in an explanatory model comprising a conceptual determination useful for calibrating instruments measuring in interval units.

When the process is completed and a useful abstraction has become a habitually used labor-saving tool in the economy of language, rediscovering how meaningfulness was achieved and distributed becomes a difficult process. Science and technology studies, however, repeatedly arrive at conclusions focusing on problems of logical types, cross-level fallacies, and levels of meaning [6,42,47,132,133,134,135,136]. No efforts to date in this area, however, have capitalized on Bateson’s logical type distinctions between counting and measurement in developing knowledge infrastructures that include quantitative social and psychological data.

Developments in this direction follow Finkelstein [137,138], who presented measurement and measurement systems in terms of symbolically represented information. Metrological psychometrics research is explicitly oriented toward clear separations of denotative numeric and metalinguistic quantitative logical types [65,78,79,80,81,82,83,84,85,86,139]. Quantity is furthermore defined in metacommunicative theoretical terms as requiring explanatory construct models [60,61,62,63,67,126].

Logical type distinctions of these kinds can be made across a potentially infinite array of levels. Transitions across levels of cognitive and moral reasoning have long been a focus of scaling research in developmental psychology [70,140,141,142,143,144,145]. Probabilistic models for measurement have been used to show how different methods of numerically scoring developmental levels can be equated to common metric quantities.

A logical type distinction between numeric counts and measured quantities should be made not only in the bottom-up calibration of instruments, but also in the top-down reporting of measurements [139]. Formative applications of measures in education and healthcare benefit from response-level data reports communicating feedback on unique individual patterns in the context of the expected learning progression, developmental sequence, or healing trajectory. No data ever fit a model perfectly, but the point is usefulness, not truth [55,146]. Given a well-studied construct and well-calibrated instrumentation measuring to a reasonably small degree of uncertainty, even markedly inconsistent response patterns may convey important information useful to teachers’ instructional planning, or clinicians’ treatment planning.

In education, therefore, individualized instruction should not be based only on quantitative measures and associated uncertainties indicating where the student is positioned along the learning progression. It should also take into account evidence of special weaknesses and strengths, as shown in the numeric pattern of responses scored correct and incorrect [147,148,149,150]. Notable directions for ongoing research in this area break out separate but interrelated investigations taking place at these levels:

• Denotative data reports for formative feedback on concrete responses mapping individualized growth;
• Metalinguistic Wright maps used in psychometric scaling evaluations and abstract instrument calibrations;
• Metacommunicative construct maps and specification equations illustrating explanatory models and formal predictive theories.

All three of these areas are supported by various software packages, such as the BEAR Assessment System Software [151,152,153,154,155], ConQuest [156], RUMM [157], Winsteps [158], various R statistics packages [159], and others.

6. Conclusions

Probabilistic models for measurement inform a multilevel context operationalizing a science of data, instruments, and theory implementing Bateson’s emphasis on differences that make a difference. By hypothesizing a pragmatic ideal condition in which nothing influences a person’s response to a question but the difference between their ability and the difficulty of the challenges posed, Rasch makes Bateson’s maxim testable in a wide range of situations.

Wright laid out the means for understanding Rasch’s models in ways conforming to Bateson’s distinctions between the levels of complexity in meaning. Number is not quantity, and counting is not measurement; therefore, knowledge infrastructures of all kinds treating numeric counts as quantitative measures are compromised by avoidable cross-level fallacies and schizophrenic double binds. However, patterns in numeric counts can be—and are—used to test hypotheses of quantitative structure useful in constructing measures. Knowledge infrastructures respecting the limits of different logical types are not only possible, but have, in limited instances, already been created [67,78,123,126].

These infrastructures satisfy Whitehead’s [160] recognition that “Civilization advances by extending the number of important operations which we can perform without thinking about them” (p. 61). Given the complexity of the problem, it is unreasonable to expect individuals to master the technical matters involved. This insight contradicts those, such as Kahneman [161], who recommend learning to think slower instead of allowing language’s fast automatic associations to play out. Whitehead [160] held that this position, “that we should cultivate the habit of thinking of what we are doing,” is “a profoundly erroneous truism.” Developmental psychology [162,163,164,165,166] and social studies of science [167,168,169] have arrived at much the same conclusion, noting that individual intelligence is often a function of the infrastructural scaffolding provided by linguistic and scientific standards. When these standards do not include the concepts and words needed for dealing with the concrete problems of the day, individuals and institutions must inevitably fail.

The cultural schizophrenia caused by communications routinely comprising mixed messages has led to dire and unsustainable consequences, globally. There are many who say immediate transformative efforts must be mounted in response to the urgency of the potentially catastrophic crises humanity faces. Few, if any, of those urging transformative programs speak to the most vital differences that matter in making a difference, those involving logical type distinctions sustained not at the level of individual skill and inclination, but at the institutional level of infrastructural standards.

This shift of focus from persuading and educating individuals to altering the environments they inhabit has been described as the difference between modernizing and ecologizing [167,168,169]. However, even when relational sociocognitive ecologies are conceived and examined [6,45,46,49,170,171], the value ascribed to metrology by Latour [172,173] is never connected with the corresponding need for new forms of computability addressing the design challenge of achieving results that are “both socially situated and abstract enough to travel across time and space” [6]. The focus on individuals is so deeply ingrained into the fabric of institutionalized assumptions and norms that it prevails even when shifting the environmental infrastructure is the ostensible object of inquiry [139].

Fears that repressive methods will be used to control populations, as has happened so often in the past, justify cautious evaluations of new proposals for innovative efforts to improve the human condition. Taking Scott’s [174] suggestion of conceiving information infrastructures on the model of language converges with Hayek’s [175] agreement with Whitehead [160] concerning the advancement of civilization, and with Hayek’s associated suggestion that totalitarian impulses be countered by co-locating information and decision makers together in context, as noted by Hawken [176] (p. 21). This co-location opens up key opportunities for experimental trial and error approaches supporting noncoercive self-determination.

These opportunities are not easily obtained. The biological concept of ecosystem resilience, for instance, has been unenthusiastically received by social theorists because it appears to favor adaptive responses supporting the persistence of the status quo, and not the adaptive emergence of new forms of social life [177]. Similarly, ethnographic studies of culture often assume infrastructures function only to give material form to political realities that are uncritically taken to be permanent and stable [178]. Bottom-up approaches to conceptual speciation events, where new things come into words, may then provide an attractive alternative that informs infrastructuring as a kind of ontological experimentation [179].

Incorporating logical type distinctions in knowledge infrastructures may inspire more confidence in the capacity to balance tradition with creativity. In light of the connections between Bateson’s and Wright’s ideas on the differences between counting numbers and measured quantities, methodical sensitivity to cross-level fallacies and multiple levels of meaning may become an essential component of ontologically oriented infrastructure experiments deliberately intended to shape politics and power via participatory processes.

Perhaps clearer ways of formulating new classes of responses to these challenges will be found by recognizing and working with, instead of against, logical type discontinuities. As Oppenheimer [180] recognized, “all sciences arise as refinements, corrections, and adaptations of common sense.” Similarly, Bohr [181] noted that mathematical models provide “a refinement of general language.” Nersessian [182] shows how scientific research extends ordinary everyday cognitive practices. Gadamer [183] points out that the distinction between number and the noetic order of existence comprises “the world of ideas from which science is derived and which alone makes science possible” (pp. 35–36).

Bateson diagnosed the schizophrenic double-bind and cross-level fallacies built into knowledge infrastructures, emphasizing that counts are not measures. Wright expanded on Rasch’s mathematics to develop methods separating and balancing numeric counts and measured quantities, in the process extricating himself from what he perceived to be a schizophrenic situation. A psychometric metrology of emergent, bottom-up, self-organizing processes based in Bateson’s, Rasch’s, and Wright’s works may provide the kind of experimental infrastructuring needed for generalized development of new kinds of outcomes for the wide array of institutions currently incorporating logical type confusions in their communications.