2.1. Phase and Modulus Retrieval of Normally Located Object
Most of the modern methods of phase retrieval are, a further development of the algorithms created 30–40 years ago (see the literature cited in [
20,
24] and [
31,
32,
33]). These algorithms are presented in many articles and monographs and continue to be improved. They assume that the registration of the field intensity distribution on the detector explicitly determines the modulus of the Fourier image of the field on the object in a certain range of the spatial frequencies.
The algorithms contain 4 basic operations on the complex object function
: (a) the Fourier transform
, (b) replacing its modulus with the experimentally obtained value
, (c) the inverse Fourier transform
and (d) the
transform of the function
, that is a priori information about the object. The result of these transformations is a new function
defined in the same domain as
. If
and
coincide with the specified precision, then the goal is achieved. A priori information (
) can be the measurement of the field modulus directly behind the object or in any other plane, the shape of the object, that is, equality to zero of the field on the object plane outside a definite area, non-negative values of the field, etc.
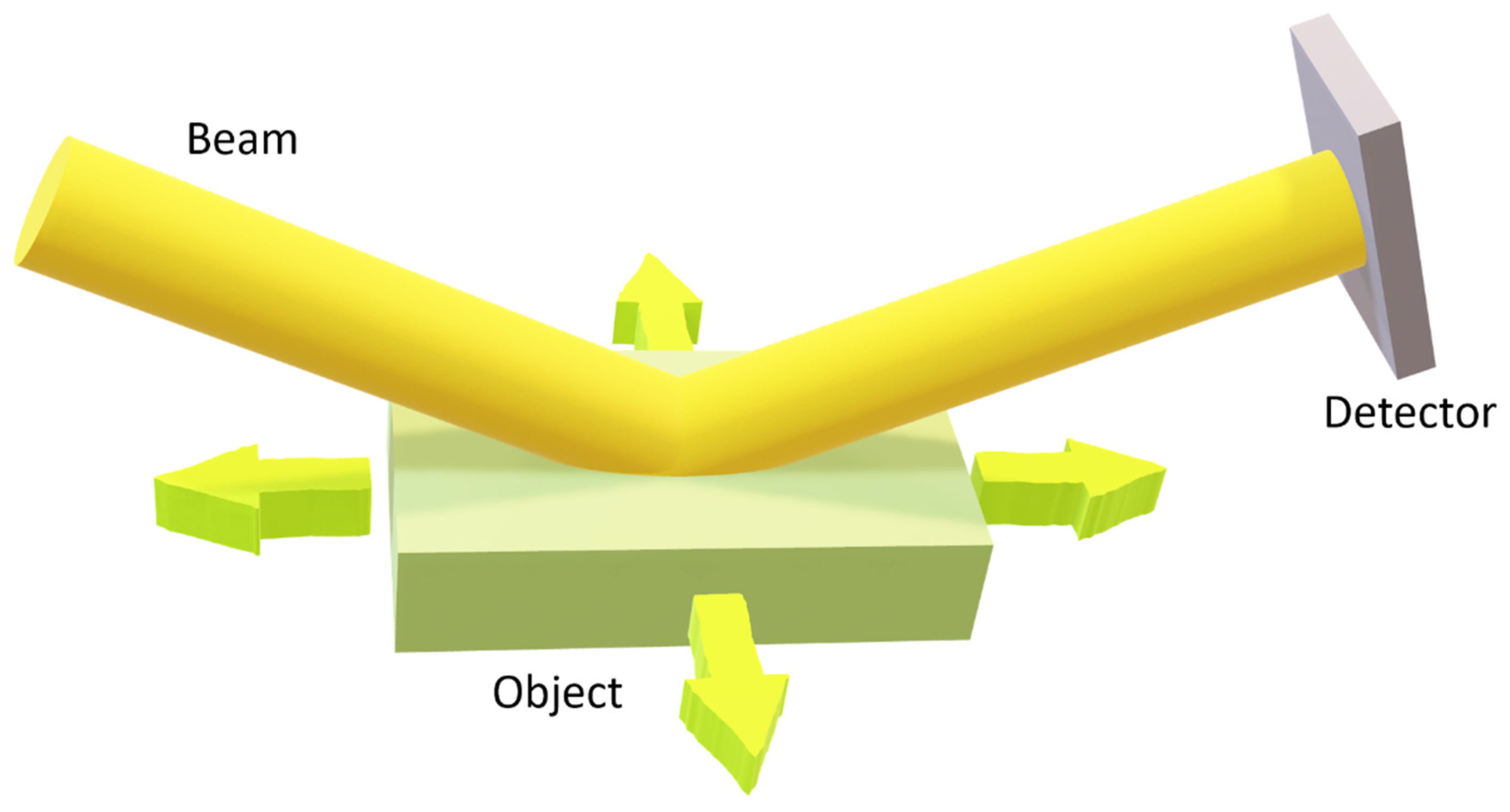
The diagram of a typical diffraction-resolved lensless imaging microscope contains a coherent radiation source illuminating a transparent object located in the
plane (see
Figure 2). Unlike conventional microscopes, there are no optical elements between the object and the detector. The laser illuminating the object on the left and the computer processing the data from the detector are not shown in the diagram.
Let us show the role of the Fourier transform using the example of an angular spectrum that describes the propagation of coherent radiation from an object
to a detector
(see
Figure 2) and is an exact, and consequently, nonparaxial solution of the wave equation. It defines the wave field in a half-space through spatial harmonics in the object plane:
where
is the wave number,
is the Fourier transform of the field distribution
in the object plane. Papers [
29,
34,
35,
36] are devoted to the analysis of this expression and its connection with other forms of the diffraction integral. Here we will consider only issues related to modeling the propagation of non-paraxial beams in the problems of image phase reconstruction and ptychography.
Assume that the detector recording the intensity is in the far zone of the object, i.e., in the Fourier plane, where:
is the size of the object, and the aperture angle
is assumed to be fixed. Considering (2) under condition (3) and using the stationary phase method [
37], it is easy to make sure that the field at the detector takes the form:
Expression (4), obtained from the exact solution (2) of the Helmholtz wave equation, shows that in the far zone the spatial distribution of the field is expressed through the Fourier transform of the field on the object plane . Moreover, when the coordinate on the detector changes from 0 to , the corresponding spatial harmonic changes from 0 to . In other words, there are no harmonics in the far field. In the general case, this expresses the fact that the limiting spatial resolution in the far zone is determined by the wavelength , regardless of the type of optical system.
In practice, in phase retrieval algorithms (see review [
31]), to avoid the computational complexity of exact Expression (4), a simpler one is used—the Fresnel integral, which follows from exact Expression (2) at small aperture angles
:
that in the far field (3) has the form:
Let us compare the obtained expression (6) with the exact value of the field in the far zone (4). Comparison of the arguments of the Fourier transform of the initial distribution
shows that the use of the Fresnel integral in the far zone (6) for calculating the field at the detector is possible only for
, i.e.,
and aperture
. Otherwise, we would be talking about the harmonics of the initial distribution
which, according to (4), are not contained in the far zone at all. Adding to this the requirement that the phase factors in (4) and (6) coincide, we obtain the condition for the applicability of the Fresnel integral in the far field (3), (see [
38]):
A more detailed theoretical discussion of the issue is available in review [
39].
Thus, the angular spectrum approximation (4), as well as the paraxial approximation (6), in the far zone lead to the aforementioned connection between the field intensity distribution at the detector and the Fourier transform module of the field in the object plane. Namely, the intensity on the detector is algebraically expressed through the Fourier transform of the field amplitude on the object.
2.2. Angular Spectrum and Oblique Object
Consider the propagation of reflected directional monochromatic radiation from a tilted opaque object as shown in
Figure 3. The surface of the object is located on plane
in the half-plane
, the detector is on the
plane at
. The plane
is inclined to the plane
at an angle of
, and to the plane of the detector at an angle of
. Without loss of generality, one can suggest
. This can be achieved by choosing the appropriate coordinate system. Then, we will assume that the radiation is described by the scalar function
, which is a solution of the Helmholtz equation:
We also assume that the radiation propagates in the direction of increasing
from left to right being a superposition
of the plane waves (“angular spectrum method”) with transverse momentum
One can see that the function
is the Fourier transform of the function
. The fact that the plane wave (10) propagates in the direction of increasing
is expressed by the plus sign in front of the square root in the exponent. Let us denote unit vectors along the
,
,
,
axes as
,
,
,
, respectively. Then the 3D wave vector is
. The plane of the object divides the space into a conditionally upper half-space, where
and the lower one, where
. We denote the quantities referring to the upper half-space by the “
” sign at the bottom, and the lower half-space by the “
” sign at the bottom. Occurrence of the wave
in the positive half-space is formulated as the condition:
where
is the real part, since
is complex in general case. Considering that
we express (11) through the angles:
where, for convenience, we introduced the dimensionless parameter
. Then, the symbol “~” at the top will denote quantities divided by
. We introduce new notation: complex angles
and
that satisfy the conditions:
From Equations (13) and (14) we can express
through the angles
and
:
Using Equation (13), the condition (12) can be written as:
For
the vector
is real. Then, the angle
is equal to the angle of inclination
to the plane of the object, and the angle
is equal to the angle of inclination
to the
axis (see
Figure 3). For all angles
, the condition (16) is equivalent to the condition
, that means a wave, either leaving the object in the upper half-space for
, or surface wave moving along the object from top to bottom at
. The angular spectrum
can be represented as an integral of plane waves (9) and as a product of the slow and fast parts:
In what follows, we will be interested in the evolution of the slow part
more suitable for numerical calculations. The slow part of the plane wave looks like this:
Suppose that the field of the exit wave of the object is known — it is the function
defined on the plane
. To obtain the field on the detector
we will find an arbitrary harmonic
:
Substituting
into (18) we get:
From Equations (19) and (20) we obtain the equations connecting
and
:
Using Equation (14), we rewrite Equations (21) and (22) in the form:
It follows from Equations (24) and (15) that:
Thus, for each harmonic
there are two solutions. One of them, according to Equations (25) and (16), corresponds to a plane wave in the upper half-space, where
, and the other to a plane wave in the lower half-space, where
. Since we consider the object to be opaque, we can assume that the wave with
corresponds to the reflected wave, and the wave in the lower half-space with
does not exist. Therefore, choose
:
It is easy to see that the imaginary part
and
is non-negative for all
. From Equation (21),
and Equation (26) we obtain:
According to Equation (18), it follows that waves with complex
would decay exponentially with increasing
and
, so that the information about the corresponding frequencies
does not reach the detector. Therefore, an unambiguous reconstruction of the
field from the
field needs
:
Let us suppose that
and
are the size of the smallest detail of the object
along the directions
and
, correspondingly (see
Figure 4). Then the spectrum is restricted by the Nyquist theorem:
Condition (29) is satisfied for all
from Equation (31) when:
In what follows, we will assume that the object is non-crystalline, and its surface changes on a scale larger than the wavelength, and
,
. Then, with taking into account
the expression (32) takes the form:
This inequality can be rewritten by introducing the dimensionless parameter
:
Expanding by small parameters
and
and taking into account only the first terms, we can get:
And, for the angle
we obtain:
Expression (36), up to a factor of 2, coincides with the definition of the
-parameter from [
40]. Thus, we can assume that Formula (34) generalizes Formula (36), obtained in [
40] using the paraxial approximation
,
.
Now we can write out the final expression for the field
in the form of angular spectrum:
where
satisfies (26). From Equation (21) it follows that:
Taking the uniqueness condition (29), we obtain the field at the detector:
The real limits of integration in Equation (39) are limited by the spectrum
according to (31). Equation (39) means that the Fourier transforms of the object
and the detector
are related by:
Please note that to obtain (40) we did not use the paraxial approximation. Therefore, the result is valid for the cases of long distances and large numerical apertures. Since the dependence is nonlinear (see Equation (21)), the computation of from involves three "heavy" numerical operations–Fast Fourier Transform, interpolation, and Inverse Fast Fourier Transform.
2.3. Far-Field Solution
For the phase retrieval of the X-ray region of the spectrum, the far diffraction zone is usually used since the necessary condition for oversampling is satisfied in the far zone.
Let us find a solution for the far zone. Since the object is set to be in the region
, we assume that the edge of the object closest to the detector has a coordinate
. For convenience, instead of
and
coordinates, we will use the dimensionless parameters
and
. Since the object begins at
we introduce the Fourier transform of the object
beginning from
. According to (37):
and the field on the detector in terms
according to Equations (37) and (41) is:
The derivatives
up to the second order can be written as:
If the inequality (29) is fulfilled, then derivatives (43) and (44) are finite. With using the stationary phase approximation at
with fixed
and
we obtain:
From Equations (43) and (45) the stationary point is:
Then the second derivatives at the stationary point are:
Using Equations (26) and (46), we can find
at the stationary point:
Finally, for the field at the detector in the far zone, we obtain:
Defining the beginning of the object on
axis as
and the distance from the object to the detector as
, we can get a familiar formula:
It is easy to show that the function
is not one-to-one. There are infinitely large values of
and
, for which
has the same values. Therefore, for further analysis, it will be more convenient for us to use the aperture coordinates, which we define as follows:
In aperture coordinates, Equations (50) and (51) take the form:
In this form, the function already one-to-one depends on and .
The far-field criterion for a tilted object is also of interest, but it is outside the scope of this work. It is obvious that a use of the far-field criterion for a vertical object (3) is sufficient here.
2.5. Frequency Domain of the Detector
The frequency domain
is determined by inequalities (31) and, under the assumption of smoothness
at distances of the order of the wavelength, is a subset of the domain
. Consider the function
from Equation (26). According to (43) the stationary point
is reached when
=
. It is easy to check that
at the considered angles
. Therefore, the inner part of the
domain does not contain the stationary point
. In addition, the second derivative
is negative definite, since it follows from Equations (44), (25) and (16) that the eigenvalues
are negative and equal to
and
. Thus, the minimum and maximum values of
are on the domain boundary
. It is also necessary to take into account that the radical part in (26) must be nonnegative. Therefore, there are several cases, depending on the area of intersection of the rectangular region (31) and the circle of unit radius centered at the point
:
| Condition | (57) |
| . |
|
. |
|
|
| |
Thus, Equation (57) exhausts all possible cases and allows you to analytically find the domain
. The pixel size
can be chosen based on the maximum modulus
:
| Condition | (58) |
| . |
|
. |
|
|
| |
To determine , it is enough to substitute into Equation (58). Considering that it makes no sense to choose , since this no longer expands the frequency domain, we get .
2.6. Spatial Domain of the Detector
According to (39) and (41), the field at the detector may be expressed as:
Since the size of the region on the plane
is
, the steps of numerical integration in (59), according to Nyquist’s theorem, are
. For numerical integration over
to be successful, the phase change in the exponent in (59) should not exceed
at step
:
Expressing in this inequality
in terms of
according to (38), we obtain:
Substituting
in (61) and using the notation
and
, we get:
Expression (63) is valid for any
and
, in particular for
,
:
and for
,
:
Adding inequalities (64) and (65) we obtain:
Inequality (65) obviously implies the inequality:
Inequalities (60)–(67) are obtained under the assumption that
is the point closest to the object. But absolutely similar inequalities can be obtained for any point of the object, including for the upper (far from the detector) edge of the object. The right-hand side in inequality (66) corresponds to the size of the diffraction spot from the point at position
. The total size of the domain
is actually equal to the size of the diffraction spot from the entire object and, therefore, should be the sum of half of the diffraction spot from the near edge of the object at a distance
, the projection of the length of the object onto the detector
and half of the diffraction spot from the far edge of the object at a distance
. As a result, you should accept:
For the minimum coordinate
, similar reasoning leads to the fact that it is necessary to take the projection of the lower edge
minus half of its diffraction spot. This corresponds exactly to the right-hand side of (67):
Similarly, for
we get:
From Equations (68) and (69) it follows that the center of the detector domain turned out to be displaced along the
axis relative to the center of the object domain by the value:
We believe that it is more convenient for calculations to have a detector domain whose center has the same
and
coordinates as the center of the object. Therefore, let’s increase
so that the new domain overlaps the old one and at the same time its center is on the same axis with the center of the object domain. To do this, obviously, you need to add
to
and we get the final result:
2.7. Frequency Domain of the Detector in the Far Field
In the far field, we will use aperture coordinates (52)–(54), which give an unambiguous relationship between the spatial frequency
of the field on the object and the sine of the aperture angles
and
. According to (55), the field
is equal to the product of the fast part
and the slow part
Typically, applications compute the slow part . Therefore, we define for it the frequency and spatial domains in coordinates and .
Let’s designate pixels of this domain as
and
, and sizes as
and
. The frequency domain can be determined by noting that the change in the detector coordinates to
and
is associated with a change in the corresponding frequencies on the object
and
. This connection is easy to find by differentiating (56):
Let us reverse expression (76) and obtain the required relationship:
Changing by one pixel in the object domain
must change at least one pixel in the detector domain
or
. Therefore, at least one of the two inequalities must hold:
or
Minimizing the left-hand side of inequality (78) with the condition
, we obtain:
Similarly, for
we get:
or
Hence, minimizing the left-hand side of (82), we obtain:
Finally, for the far field aperture pixel sizes, we get:
A rectangular grating symmetrical about the optical axis in aperture coordinates is mapped onto the detector plane
in the form of a pincushion grating with the maximum cell density in the center. Therefore, the pixels in the
plane can be chosen equal: