Adaptive Fuzzy Fault-Tolerant Control against Time-Varying Faults via a New Sliding Mode Observer Method

Abstract

In this study, the problem of observer-based adaptive sliding mode control is discussed for nonlinear systems with sensor and actuator faults. The time-varying actuator degradation factor and external disturbance are considered in the system simultaneously. In this study, the original system is described as a new normal system by combining the state vector, sensor faults, and external disturbance into a new state vector. For the augmented system, a new sliding mode observer is designed, where a discontinuous term is introduced such that the effects of sensor and actuator faults and external disturbance will be eliminated. In addition, based on a tricky design of the observer, the time-varying actuator degradation factor term is developed in the error system. On the basis of the state estimation, an integral-type adaptive fuzzy sliding mode controller is constructed to ensure the stability of the closed-loop system. Finally, the effectiveness of the proposed control methods can be illustrated with a numerical example.

1. Introduction

In industrial processes, actuator and/or sensor always occur with various components faults due to unexpected physical constraints and reasons [1,2,3,4]. In order to maintain the reliability of the overall control systems, fault detection and isolation (FDI) and fault-tolerant control (FTC) have received increasing research attention during the past decade [5,6,7,8]. The design scheme of FDI is to generate a residual signal to judge whether the faults occur and provide a solution to determine the location of the faults [9,10,11]. However, in practice, it is difficult to obtain the exact information of the fault. In this sense, the fault estimate has been developed and has become an ideal design basis of FTC [12,13]. In recent years, a great number of fault estimation methods have been reported in the existing literature, for instance, nonlinear observer method, adaptive learning observer method, filter-based estimation method and differential geometry methods, etc. [14,15,16].

Consequent to the in-depth study of SMO by researchers, combined with fuzzy and adaptive technologies [17,18,19], sliding mode observers have been widely used in motors, aerial vehicle, and other fields [20,21,22,23,24]. Among these existing fault estimation approaches, sliding mode observer (SMO) [25,26,27] refers to one of the most popular nonlinear observer methods, where the fault is reconstructed by the so-called equivalent output error injection principle [14]. In this research forefront, a few fault estimation SMO results have been developed for various systems by the researchers [11,28]. In [29], a fault estimation SMO was developed for mismatched nonlinear systems with unknown disturbances, where an adaptive law was designed to update the sliding mode gain online. In [30], the authors proposed a cascaded SMO method to cope with the fault estimation problem for the case in which the first Markov matrix of the system is not a full rank. In [31,32], based on a descriptor system augmentation strategy, the authors proposed a new type of extended SMO approach, which was applied to Ito stochastic systems and Markovian jump systems, respectively.

Sliding mode control is a very effective control method, and some new ideas have been put forward recently by researchers [33,34]. Hou et al. [35] solved the chattering problem common in the sliding mode control for the servo motor system by designing a new continuous terminal sliding mode control algorithm. In [36], an optimization problem based on non-negative constraints was defined for time-varying delay systems, to obtain sliding mode surface parameters and simplify the stability analysis process. In [37], the nonlinear function with sliding variable was introduced by the approach law, which alleviates the chattering phenomenon and improves the tracking performance.

However, it should be pointed out that most existing fault estimation results are concerned only about actuator faults or sensor faults. Moreover, most of the reported work has been focused on only additive actuator fault, while multiplicative type actuator fault (also called fault degradation factor) has received little research attention. In fact, in many practical control systems such as satellite systems, the multiplicative actuator faults may always occur with a time-varying characterization. However, the existing SMO methods in the aforementioned literature cannot be applied directly to solve this design problem due to technical constraints, and only additive actuator faults are therefore considered. It is thus desirable to develop a new effective SMO approach to investigate this problem.

In this paper, we aimed to research the fault estimation and FTC design problem for the continuous-time nonlinear system, where sensor fault, external disturbance, time-varying multiplicative actuator faults, and unknown nonlinearity are considered simultaneously in a unified framework. A new type of SMO based on a system augmentation scheme is developed for the investigated plant. The designed observer can estimate state vector, sensor faults, and external disturbance, which thus possesses a more extensive estimation performance, compared to the traditional SMO method. Moreover, due to the tricky structure of the observer, the time-varying actuator degradation factor in the derived error system can be eliminated. Based on the state estimation of the SMO, an adaptive integral-type sliding control law is designed to ensure the asymptotic stability of the overall fault control systems, where an adaptive fuzzy updating law is involved with the controller gain to approximate the unknown nonlinearity of the plant. Finally, a simulation example is given to verify the effectiveness of the proposed FTC methods. The structure of this article is as follows: Section 2 gives the system model, hypothesis, and related theory. Section 3 designs the observer and controller and analyzes the stability and the accessibility of sliding mode motion. Section 4 provides a simulation example. Section 5 summarizes the whole paper.

Notation: The n-dimensional Euclidean space is defined by ${\mathbf{R}}^n$. The set of all $m\times n$ real matrices is represented as ${\mathbf{R}}^{m\times n}$. Positive-definite (negative-definite) matrix A is defined by $A>0(<0)$. An identity matrix is defined by $I_n$ (n is the dimension of matrix I); diag$\{\dots \}$ denotes a block diagonal matrix.

2. Problem Formulation and Preliminaries

2.1. Problem Statement

Consider the following uncertainty nonlinear system subject to time-varying actuator fault, sensor fault, and external disturbance:

$$\begin{array}{cc}\hfill \dot{x}\left(t\right)=& Ax\left(t\right)+B(\rho \left(t\right)u\left(t\right)+f_a\left(t\right))+Ef\left(x\right)+D_{x}d\left(t\right)\hfill \\ \hfill y\left(t\right)=& Cx\left(t\right)+D_s{f}_s\left(t\right)+D_{y}d\left(t\right).\hfill \end{array}$$

(1)

where $x\left(t\right)\in {\mathbf{R}}^n$, $u\left(t\right)\in {\mathbf{R}}^m$, $f_a\left(t\right)\in {\mathbf{R}}^m$, $f\left(x\right)\in {\mathbf{R}}^{n_f}$, $d\left(t\right)\in {\mathbf{R}}^{n_d}$, $y\left(t\right)\in {\mathbf{R}}^p$, $f_s\left(t\right)\in {\mathbf{R}}^q$, $\rho \left(t\right)=\mathrm{diag}\left\{{\rho }_1\left(t\right),{\rho }_2\left(t\right),\dots ,{\rho }_h\left(t\right)\right\}$, ${\rho }_h\left(t\right)$($h=1,2,...,m$) represent the immeasurable system state, control input, unknown stuck actuator fault, unknown smooth nonlinear function, unknown external disturbance, measurable output, unknown sensor fault, unknown time-varying actuator efficiency factor, hth actuator, respectively. It is assumed that $0\le {\underline{\rho }}_h\le {\rho }_h\left(t\right)\le {\overline{\rho }}_h\le 1$, for $h=1,2,\dots ,m$, where ${\underline{\rho }}_h$ and ${\overline{\rho }}_h$ are the known constants. Then, defining that $\mathrm{diag}\left\{{\overline{\rho }}_1,{\overline{\rho }}_2,\dots ,{\overline{\rho }}_h\right\}=\overline{\rho }$, $\mathrm{diag}\{{\underline{\rho }}_1,{\underline{\rho }}_2,\dots ,{\underline{\rho }}_h\}=\underline{\rho }$, the following cases of hth actuator failure are considered:

$$\begin{array}{c}\hfill \left\{\begin{array}{ccc}Case1:\hfill & {\rho }_h\left(t\right)=1,\hfill & \mathrm{the}h\mathrm{th}\mathrm{actuator}\mathrm{has}\mathrm{no}\mathrm{fault};\hfill \\ Case2:\hfill & {\rho }_h\left(t\right)=0,\hfill & \mathrm{the}h\mathrm{th}\mathrm{actuator}\mathrm{is}\mathrm{outage};\hfill \\ Case3:\hfill & {\rho }_h\left(t\right)\in (0,1),\hfill & \mathrm{the}h\mathrm{th}\mathrm{actuator}\mathrm{is}\mathrm{partial}\mathrm{lo}-\hfill \\ & & \mathrm{ss}\mathrm{of}\mathrm{effectiveness};\hfill \\ Case4:\hfill & f_{ah}\left(t\right)\ne 0,\hfill & \mathrm{the}h\mathrm{th}\mathrm{actuator}\mathrm{undergoes}\hfill \\ & & \mathrm{stuck}\mathrm{fault}.\hfill \end{array}\right.\end{array}$$

For the given system matrices $A,B,C,D_s,D_x,D_y,E$, the matrix E is supposed to satisfy that $E=B{B}_f$ in this paper. Without loss of generality, we suppose that the pair $(A,B)$ is controllable, and the pair $(A,C)$ is observable. In order to study the problem of the redundancy actuator fault, we assume that $\mathrm{rank}\left(B\right)=l\le m$. Thus, we have $B=B_1{B}_2$, where $B_1\in {\mathbf{R}}^{n\times l}$ and $B_2\in {\mathbf{R}}^{l\times m}$. Then, the state equation of the original system (1) can be rewritten as

$$\begin{array}{c}\hfill \dot{x}\left(t\right)=Ax\left(t\right)+B_1{B}_2(\rho \left(t\right)u\left(t\right)+f_a\left(t\right))+Ef\left(x\right)+D_{x}d\left(t\right).\end{array}$$

(2)

Remark 1.

Different from the existing results of the simultaneous actuator fault and sensor fault in [38], the fault problem in this paper is more complex. The time-varying actuator faults including loss of effectiveness fault, outage fault, and stuck fault, combined with bias sensor fault, are first studied simultaneously. Due to the more general character of actuator fault, the traditional observer-based controllers are unable to provide the desired estimation and control performance; this is also the difficulty in FTC design.

In this paper, we give the following assumptions:

Assumption 1.

The stuck actuator fault $f_a\left(t\right)$, bias sensor fault $f_s\left(t\right)$ and external disturbance $d\left(t\right)$ are supposed to satisfy that

$$\begin{array}{cc}\hfill & \parallel f_a\left(t\right)\parallel \le f_{a1},\parallel {\dot{f}}_s\left(t\right)\parallel \le f_{s1},\parallel f_s\left(t\right)\parallel \le f_{s2},\hfill \\ \hfill & \parallel \dot{d}\left(t\right)\parallel \le d_1,\parallel d\left(t\right)\parallel \le d_2\hfill \end{array}$$

(3)

where $f_{a1},f_{s1},f_{s2},d_1,d_2$ are unknown scalars.

Assumption 2

([32]). It is assumed that the actuators satisfy the redundancy condition: $\mathrm{rank}\left(B_2\right)=\mathrm{rank}\left(B_2\rho \left(t\right)\right)=l$.

Assumption 3.

The system matrix dimensions satisfy: $\mathit{rank}\left(B_1\right)=\mathit{rank}\left(C{B}_1\right)=l$, and a scalar σ can be found such that

$$\begin{array}{c}\hfill \mathit{rank}\left[\begin{array}{cc}\sigma I+A& D_x\\ C& D_y\end{array}\right]=n+n_d.\end{array}$$

(4)

Remark 2.

Assumption 1 is proposed for proofing the stability of closed-loop systems and the accessibility of sliding mode motion in Section 3, which is an important condition for scaling. Compared to the traditional methods in [39], Assumption 2 will relax the restriction that the norm bound of the external disturbance, stuck actuator fault, and bias sensor fault, which will be applicable to a larger class of practical systems. Assumption 3 is a necessary condition in the process of designing a controller.

2.2. Fuzzy Logic Systems

The fuzzy IF–THEN rules of fuzzy logic systems (FLSs) are given as follows [40]:

$$\begin{array}{cc}\hfill R^i:& \mathrm{If}{x}_1\left(t\right)\mathrm{is}{F}_{1i}\mathrm{and}{x}_2\left(t\right)\mathrm{is}{F}_{2i},\cdots ,\mathrm{and}{x}_n\left(t\right)\mathrm{is}{F}_{ni},\hfill \\ \hfill & \mathrm{then}\overline{y}\left(t\right)\mathrm{is}{G}_i\hfill \end{array}$$

where $x\left(t\right)={[x_1\left(t\right),x_2\left(t\right),\dots ,x_n\left(t\right)]}^T$ and $\overline{y}\left(t\right)$ represent the input and output of the FLS, respectively. $F_{\iota i}$ and $G_{\iota i}$ are fuzzy sets $(\iota =1,2,...,n)$. $i=1,2,\cdots ,N$ (N is the number of the fuzzy rules). Obviously, the FLS can be represented as follows:

$$\begin{array}{c}\hfill \overline{y}\left(x\right)=\frac{{\sum }_{i=1}^N{\overline{y}}_i\left({\prod }_{\iota =1}^n{\mu }_{F_{\iota i}}\left(x_{\iota }\right)\right)}{{\sum }_{i=1}^N\left({\prod }_{\iota =1}^n{\mu }_{F_{\iota i}}\left(x_{\iota }\right)\right)}\end{array}$$

(5)

where ${\mu }_{F_{\iota i}}\left(x\left(t\right)\right)$ is the membership functions, and ${\overline{y}}_i$ is the point at which ${\mu }_{G_i}=max\left\{{\mu }_{G_i}\right\}$, and it is assumed that ${\mu }_{G_i}\left({\overline{y}}_i\right)=1$. Define the following fuzzy basis functions:

$$\begin{array}{c}\hfill {\phi }_i\left(x\right)=\frac{{\prod }_{\iota =1}^n{\mu }_{F_{\iota i}}\left(x_{\iota }\right)}{{\sum }_{i=1}^N{\prod }_{\iota =1}^n{\mu }_{F_{\iota i}}\left(x_{\iota }\right)},i=1,2,...,N.\end{array}$$

(6)

Denoting $\theta ={[{\overline{y}}_1,{\overline{y}}_2,\dots ,{\overline{y}}_N]}^T$ and $\phi \left(x\right)={[{\phi }_1\left(x\right),{\phi }_2\left(x\right),\dots ,{\phi }_N\left(x\right)]}^T$. Then, (5) can be rewritten as

$$\begin{array}{c}\hfill \overline{y}\left(x\right)={\theta }^T\phi \left(x\right).\end{array}$$

(7)

Lemma 1

([41]). For any continuous function, $f\left(x\right)$ defined over a compact set Ω and any given positive constant ${\delta }_0$, there exists θ such that

$$\begin{array}{c}\hfill \underset{x\in \Omega }{sup}|f\left(x\right)-{\theta }^T\phi \left(x\right)|\le {\delta }_0.\end{array}$$

(8)

Since $x\left(t\right)$ is not measurable, the function $f\left(x\right)$ can be represented by the following FLSs:

$$\begin{array}{cc}\hfill f\left(x\right)& ={\theta }^T\phi \left(x\right)+{\delta }_f\left(t\right)\hfill \\ \hfill & ={\theta }^T\phi \left(\widehat{x}\right)+{\theta }^T(\phi \left(x\right)-\phi \left(\widehat{x}\right))+{\delta }_f\left(t\right)\hfill \end{array}$$

(9)

where ${\delta }_f\left(t\right)$ is the approximation error. Then, the reconstruction error $\delta \left(t\right)$ can be obtained

$$\begin{array}{c}\hfill \delta \left(t\right)={\theta }^T(\phi \left(x\right)-\phi \left(\widehat{x}\right))+{\delta }_f\left(t\right).\end{array}$$

(10)

In general, $\delta \left(t\right)$ is assumed to be bounded with

$$\begin{array}{c}\hfill \parallel \delta \left(t\right)\parallel \le \overline{\delta },\end{array}$$

(11)

where $\overline{\delta }>0$ is an unknown constant.

To design the adaptive law for the unknown vector $\theta$, we supposed that $\theta >0$ throughout the paper, which is not to lose the generality and also used in the FTC problems of fuzzy logical systems ([41]).

3. Main Results

3.1. Observer Design

Consider the following augmented system:

$$\begin{array}{cc}\hfill \dot{\overline{x}}\left(t\right)& =\overline{A}\overline{x}\left(t\right)+{\overline{B}}_1{B}_2\rho \left(t\right)u\left(t\right)+{\overline{B}}_1{B}_2{B}_{f}f\left(x\right)+\overline{D}\overline{\omega }\left(t\right)\hfill \\ \hfill y\left(t\right)& =\overline{C}\overline{x}\left(t\right)\hfill \end{array}$$

(12)

where

$$\begin{array}{cc}\hfill \overline{x}\left(t\right)& =\left[\begin{array}{c}x\left(t\right)\\ d\left(t\right)\\ D_s{f}_s\left(t\right)\end{array}\right],\overline{\omega }\left(t\right)=\left[\begin{array}{c}{f}_a\left(t\right)\\ \sigma d\left(t\right)+\dot{d}\left(t\right)\\ \sigma f_s\left(t\right)+{\dot{f}}_s\left(t\right)\end{array}\right],\hfill \\ \hfill \overline{A}& =\left[\begin{array}{ccc}A& D_x& 0\\ 0& -\sigma I_{nd}& 0\\ 0& 0& -\sigma I_p\end{array}\right],{\overline{B}}_1=\left[\begin{array}{c}{B}_1\\ 0\\ 0\end{array}\right],\hfill \\ \hfill \overline{D}& =\left[\begin{array}{ccc}B& 0& 0\\ 0& I& 0\\ 0& 0& D_s\end{array}\right],\overline{C}=\left[\begin{array}{ccc}C& D_y& I_p\end{array}\right],\hfill \\ \hfill \overline{n}& =n+n_d+p,0<\sigma <1.\hfill \end{array}$$

(13)

From Assumption 3, we have

$$\begin{array}{c}\hfill \mathrm{rank}\left(\overline{C}{\overline{B}}_1\right)=\mathrm{rank}\left(C{B}_1\right)=l.\end{array}$$

(14)

Hence, $\overline{C}{\overline{B}}_1$ is fully column rank. Then, we define that

$$\begin{array}{cc}\hfill H=& {\overline{B}}_1{\left({\left(\overline{C}{\overline{B}}_1\right)}^T\overline{C}{\overline{B}}_1\right)}^{-1}{\left(\overline{C}{\overline{B}}_1\right)}^T\hfill \\ \hfill & +\zeta [I-\overline{C}{\overline{B}}_1{\left({\left(\overline{C}{\overline{B}}_1\right)}^T\overline{C}{\overline{B}}_1\right)}^{-1}{\left(\overline{C}{\overline{B}}_1\right)}^T],\hfill \end{array}$$

(15)

where $\zeta \in {\mathbf{R}}^{\overline{n}\times p}$ is a free matrix to be selected. Before the design of fault-tolerant observer, we define the following matrices:

$$\begin{array}{cc}\hfill A_0& =\overline{A}-H\overline{C}\overline{A},L_2=(A_0-L_1\overline{C})H,\hfill \\ \hfill L_s& =(I-H\overline{C})\overline{D},L=L_1+L_2\hfill \end{array}$$

(16)

where $L_1\in {\mathbf{R}}^{\overline{n}\times p}$ is the gain matrix to be designed later. Now, we introduce the following lemma for the existence of $L_1$, which will be used in the observer design.

Lemma 2.

The pair $(A_0,\overline{C})$ is detectable if there exists a matrix ζ such that $(I-H\overline{C})$ is invertible.

Proof. 

Since $(I-H\overline{C})$ can be invertible through selecting an appropriate matrix $\zeta$, the matrix $\left[\begin{array}{cc}I-H\overline{C}& sH\\ 0& I_p\end{array}\right]$ is of full column rank for ∀$s\in {\mathbf{R}}^{+}$. Then, it can be obtained that

$$\begin{array}{cc}\hfill \mathrm{rank}\left[\begin{array}{c}sI-A_0\\ \overline{C}\end{array}\right]& =\mathrm{rank}\left(\left[\begin{array}{cc}I-H\overline{C}& sH\\ 0& I_p\end{array}\right]\left[\begin{array}{c}sI-\overline{A}\\ \overline{C}\end{array}\right]\right)\hfill \\ \hfill & =\mathrm{rank}\left[\begin{array}{c}sI-\overline{A}\\ \overline{C}\end{array}\right]\hfill \\ \hfill & =\mathrm{rank}\left[\begin{array}{ccc}sI-A& -D_x& 0\\ 0& (s+\sigma )I_d& 0\\ 0& 0& (s+\sigma )I_p\\ C& D_y& I_p\end{array}\right]\hfill \\ \hfill & =\mathrm{rank}\left[\begin{array}{cc}sI+A& D_x\\ 0& (s+\sigma )I_d\\ C& D_y\end{array}\right]+p.\hfill \end{array}$$

(17)

Since the pair $(A,C)$ is detectable, when $s\ne -\sigma$, it is obvious that

$$\begin{array}{cc}\hfill & \mathrm{rank}\left[\begin{array}{cc}sI+A& D_x\\ 0& (s+\sigma )I_d\\ C& D_y\end{array}\right]\hfill \\ \hfill =& \mathrm{rank}\left[\begin{array}{c}sI+A\\ C\end{array}\right]+n_d=n+n_d.\hfill \end{array}$$

(18)

When $s=-\sigma$, the following equation holds from Assumption 3

$$\begin{array}{cc}\hfill & \mathrm{rank}\left[\begin{array}{cc}sI+A& D_x\\ 0& (s+\sigma )I_d\\ C& D_y\end{array}\right]\hfill \\ \hfill =& \mathrm{rank}\left[\begin{array}{cc}-\sigma I+A& D_x\\ C& D_y\end{array}\right]=n+n_d.\hfill \end{array}$$

(19)

Summarizing the analysis above, we have

$$\begin{array}{c}\hfill \mathrm{rank}\left[\begin{array}{c}sI-A_0\\ \overline{C}\end{array}\right]=n+n_d+p=\overline{n}.\end{array}$$

(20)

Consequently, the pair $(A_0,\overline{C})$ is detectable. It completes the proof. □

Then, the following sliding mode observer for system (12) is developed:

$$\begin{array}{cc}\hfill \dot{z}\left(t\right)& =(A_0-L_1\overline{C})z\left(t\right)+Ly\left(t\right)+L_s{u}_s\left(t\right)\hfill \\ \hfill \widehat{\overline{x}}\left(t\right)& =z\left(t\right)+Hy\left(t\right)\hfill \end{array}$$

(21)

where $z\left(t\right)\in {\mathbf{R}}^{\overline{n}}$; $\widehat{\overline{x}}\left(t\right)={[\widehat{x}\left(t\right),\widehat{d}\left(t\right),D_s{\widehat{f}}_s\left(t\right)]}^T$ is the estimation of $\overline{x}\left(t\right)$; $u_s\left(t\right){\mathbf{R}}^{\overline{n}}$ is the discontinue input to be designed; the matrices $A_0,L_1,L,L_s,H$ are defined in (16). Then, we have

$$\begin{array}{cc}\hfill \dot{\widehat{\overline{x}}}\left(t\right)=& (A_0-L_1\overline{C})z\left(t\right)+Ly\left(t\right)+L_s{u}_s\left(t\right)+H\overline{C}\dot{\overline{x}}\hfill \\ \hfill =& (A_0-L_1\overline{C})\widehat{\overline{x}}\left(t\right)-(A_0-L_1\overline{C})Hy\left(t\right)+L_{1}y\left(t\right)\hfill \\ \hfill & +L_{2}y\left(t\right)+L_s{u}_s\left(t\right)+H\overline{C}\dot{\overline{x}}\hfill \\ \hfill =& (A_0-L_1\overline{C})\widehat{\overline{x}}\left(t\right)+L_1\overline{C}\overline{x}\left(t\right)+L_s{u}_s\left(t\right)+H\overline{C}\dot{\overline{x}}.\hfill \end{array}$$

(22)

The augment system (12) can be rewritten as

$$\begin{array}{cc}\hfill \dot{\overline{x}}\left(t\right)=& (A_0-L_1\overline{C})\overline{x}\left(t\right)+{\overline{B}}_1{B}_2\rho \left(t\right)u\left(t\right)+{\overline{B}}_1{B}_2{B}_{f}f\left(x\right)\hfill \\ \hfill & +H\overline{C}\overline{A}\overline{x}\left(t\right)+L_1\overline{C}\overline{x}\left(t\right)+\overline{D}\overline{\omega }\left(t\right)\hfill \\ \hfill =& (A_0-L_1\overline{C})\overline{x}\left(t\right)+L_s\overline{\omega }\left(t\right)+L_1\overline{C}\overline{x}\left(t\right)+H\overline{C}\overline{D}\overline{\omega }\left(t\right)\hfill \\ \hfill & +H\overline{C}({\overline{B}}_1{B}_2{B}_{f}f\left(x\right)+\overline{A}\overline{x}\left(t\right)+{\overline{B}}_1{B}_2\rho \left(t\right)u\left(t\right))\hfill \\ \hfill =& (A_0-L_1\overline{C})\overline{x}\left(t\right)+L_s\overline{\omega }\left(t\right)+L_1\overline{C}\overline{x}\left(t\right)+H\overline{C}\dot{\overline{x}}.\hfill \end{array}$$

(23)

Define that $\overline{e}\left(t\right)=\widehat{\overline{x}}\left(t\right)-\overline{x}\left(t\right)$, we have

$$\begin{array}{c}\hfill \dot{\overline{e}}\left(t\right)=(A_0-L_1\overline{C})\overline{e}\left(t\right)+(I-H\overline{C})\overline{D}(u_s\left(t\right)-\overline{\omega }\left(t\right)).\end{array}$$

(24)

Remark 3.

It can be seen that the effect of the time-varying actuator degradation has been removed in the error dynamics (24) by using an interesting matrix parameter design of H. This will help us to employ the sliding mode observer (SMO) technology to obtain the estimation of the system state $\widehat{x}\left(t\right)$.

Since the constants $f_{a1},f_{s1},f_{s2},d_1,d_2$ are unknown in Assumption 1, we introduce a positive constant $\psi$ such that

$$\begin{array}{c}\hfill f_{a1}+f_{s1}+\sigma f_{s2}+d_1+\sigma d_2\le \psi \end{array}$$

(25)

where $\sigma$ is given in (13). It can be seen that $\psi$ is also unknown in (25), so we will substitute the estimation $\widehat{\psi }\left(t\right)$ for $\psi$ in the observer design, and the adaptive law for $\psi$ is presented,

$$\begin{array}{c}\hfill \dot{\widehat{\psi }}\left(t\right)=c_e\parallel s_e\left(t\right)\parallel ,\widehat{\psi }\left(0\right)\ge 0\end{array}$$

(26)

where $s_e\left(t\right)$ is defined in (27), and $c_e$ is the adaptive gain parameter.

Now, the sliding mode is defined as follows:

$$\begin{array}{c}\hfill s_e\left(t\right)={\overline{D}}^T{(I-H\overline{C})}^{T}P\overline{e}\left(t\right)\end{array}$$

(27)

where $s_e\left(t\right)\in {\mathbf{R}}^{\overline{n}}$, and $P>0$ is the Lyapunov matrix such that

$$\begin{array}{c}\hfill {\overline{D}}^T{(I-H\overline{C})}^{T}P=R\overline{C}\end{array}$$

(28)

where the parameter matrix $R\in {\mathbf{R}}^{(m+n_d+q)\times p}$ is to be determined. Then, we design the discontinuous input $u_s\left(t\right)$ as follows:

$$\begin{array}{c}\hfill u_s\left(t\right)=-(\epsilon +\widehat{\psi }\left(t\right))sgn\left(s_e\left(t\right)\right).\end{array}$$

(29)

where $\epsilon$ is a positive constant designed later.

3.2. Controller Design

Let $u\left(t\right)=B_2^T\tilde{u}\left(t\right)$, we have

$$\begin{array}{cc}\hfill \dot{x}\left(t\right)=& Ax\left(t\right)+B_1{B}_2\rho \left(t\right)B_2^T\tilde{u}\left(t\right)+B_1{B}_2{f}_a\left(t\right)\hfill \\ \hfill & +Ef\left(x\right)+Dd\left(t\right).\hfill \end{array}$$

(30)

In the following part a Lemma is presented.

Lemma 3.

For the nonsingular matrix $B_2\rho \left(t\right)B_2^T$ in (30), a positive scalar μ can be found such that $B_2\rho \left(t\right)B_2^T\ge \mu I_l$.

Proof. 

Based on Assumption 3, we have

$$\begin{array}{c}\hfill \mathrm{rank}\left(\rho \left(t\right)\right)\ge \mathrm{rank}\left(B_2\rho \left(t\right)\right)=l\end{array}$$

(31)

that is, $m(m\ge l)$ actuators do not surfer outage. Without loss of generality, the first l actuators are assumed to kept from outage, and ${\rho }_o\left(t\right),{\rho }_a\left(t\right)\in {\mathbf{R}}^{m\times m}$ are defined as follows

$$\begin{array}{cc}\hfill {\rho }_o\left(t\right)& =\mathrm{diag}\{{\rho }_1^{1/2}\left(t\right),{\rho }_2^{1/2}\left(t\right),...,{\rho }_l^{1/2}\left(t\right),0,...0\},\hfill \\ \hfill {\rho }_a\left(t\right)& =\mathrm{diag}\{{\rho }_1^{1/2}\left(t\right),{\rho }_2^{1/2}\left(t\right),...,{\rho }_l^{1/2}\left(t\right),{\rho }_1^{1/2}\left(t\right),...{\rho }_1^{1/2}\left(t\right)\},\hfill \end{array}$$

(32)

where $0<{\rho }_h\left(t\right)\le 1$ with $h=1,2,...,l$. So we have

$$\begin{array}{c}\hfill \mathrm{rank}\left(B_2{\rho }_o\left(t\right)\right)=\mathrm{rank}\left(B_2{\rho }_o\left(t\right){\rho }_a\left(t\right)\right)=\mathrm{rank}\left(B_2\rho \left(t\right)\right)=l.\end{array}$$

(33)

Obviously,

$$\begin{array}{c}\hfill \mathrm{rank}\left(B_2\rho \left(t\right)B_2^T\right)=\mathrm{rank}\left(B_2{\rho }_o\left(t\right){\rho }_o\left(t\right)B_2^T\right)=l.\end{array}$$

(34)

Consequently, the matrix $B_2\rho \left(t\right)B_2^T$ is invertible. Then, we have

$$\begin{array}{cc}\hfill & B_2\rho \left(t\right)B_2^T-B_2\underline{\rho }{B}_2^T=B_2(\rho \left(t\right)-\underline{\rho })B_2^T\ge 0\hfill \\ \hfill & B_2\underline{\rho }{B}_2^T-\mu I_l\ge 0\hfill \end{array}$$

(35)

where $\mu ={\lambda }_{min}\left(B_2\underline{\rho }{B}_2^T\right)$. Hence, we have

$$\begin{array}{c}\hfill B_2\rho \left(t\right)B_2^T\ge \mu I_l.\end{array}$$

(36)

It completes the proof. □

Then, the following integral sliding surface is constructed

$$\begin{array}{c}\hfill s\left(t\right)=F{y}_c\left(t\right)+{\int }_0^{t}K\widehat{x}\left(t\right)d\left(t\right)\end{array}$$

(37)

where

$$\begin{array}{cc}\hfill y_c\left(t\right)& =y\left(t\right)-D_s{\widehat{f}}_s\left(t\right)-D_y\widehat{d}\left(t\right),\hfill \\ \hfill F& ={\left({\left(C{B}_1\right)}^{T}C{B}_1\right)}^{-1}{\left(C{B}_1\right)}^T\hfill \end{array}$$

(38)

and $K\in {\mathbf{R}}^{l\times n}$ is designed later. $D_s{\widehat{f}}_s\left(t\right)$ and $\widehat{d}\left(t\right)$ can obtained in the observer (21) that

$$\begin{array}{c}\hfill D_s{\widehat{f}}_s\left(t\right)=[0,0,I_p]\widehat{\overline{x}}\left(t\right),\widehat{d}\left(t\right)=[0,I_{nd},0]\widehat{\overline{x}}\left(t\right).\end{array}$$

(39)

Denoting $e_{fs}\left(t\right)={\widehat{f}}_s\left(t\right)-f_s\left(t\right)$, $e_d\left(t\right)=\widehat{d}\left(t\right)-d\left(t\right)$, we have

$$\begin{array}{cc}\hfill \dot{s}\left(t\right)=& FC\dot{x}\left(t\right)-F{D}_s{\dot{e}}_{fs}\left(t\right)-F{D}_y{\dot{e}}_d\left(t\right)+K\widehat{x}\left(t\right)\hfill \\ \hfill =& FC(Ax\left(t\right)+B_1{B}_2\rho \left(t\right)B_2\tilde{u}\left(t\right)+B_1{B}_2{f}_a\left(t\right)+Ef\left(x\right))\hfill \\ \hfill & +FC{D}_{x}d\left(t\right)-F{D}_s{\dot{e}}_{fs}\left(t\right)-F{D}_y{\dot{e}}_d\left(t\right)+K\widehat{x}\left(t\right)\hfill \\ \hfill =& FCAx\left(t\right)+B_2\rho \left(t\right)B_2\tilde{u}\left(t\right)+B_2{f}_a\left(t\right)+B_2{B}_{f}f\left(x\right)\hfill \\ \hfill & +FC{D}_{x}d\left(t\right)-F{D}_s{\dot{e}}_{fs}\left(t\right)-F{D}_y{\dot{e}}_d\left(t\right)+K\widehat{x}\left(t\right).\hfill \end{array}$$

(40)

It can be seen that $B_2\rho \left(t\right)B_2^T$ is invertible according to Lemma 1. Therefore, the equivalent control law in the sliding mode can be obtained from $\dot{s}\left(t\right)=0$ that

$$\begin{array}{cc}\hfill {\tilde{u}}_{eq}\left(t\right)=& -{\left(B_2\rho \left(t\right)B_2^T\right)}^{-1}[FCAx\left(t\right)+B_2{f}_a\left(t\right)+B_2{B}_{f}f\left(t\right)\hfill \\ \hfill & +FC{D}_{x}d\left(t\right)-F{D}_s{\dot{e}}_{fs}\left(t\right)-F{D}_y{\dot{e}}_d\left(t\right)+K\widehat{x}\left(t\right)].\hfill \end{array}$$

(41)

Substituting (41) into (30), the sliding mode dynamics can be obtained as follows:

$$\begin{array}{cc}\hfill \dot{x}\left(t\right)=& (A-B_{1}FCA-B_{1}K)x\left(t\right)-B_{1}K{I}_e\overline{e}\left(t\right)\hfill \\ \hfill & +B_{1}F(D_s{\dot{e}}_{fs}\left(t\right)+D_y{\dot{e}}_d\left(t\right))+(D_x-B_{1}FC{D}_x)d\left(t\right)\hfill \\ \hfill =& (A_a-B_{1}K)x\left(t\right)-B_{1}K{I}_e\overline{e}\left(t\right)+B_{\Phi }\Phi \left(t\right)\hfill \end{array}$$

(42)

where $A_a=A-B_{1}FCA$, $I_e=\left[\begin{array}{cc}{I}_n& 0\end{array}\right]$, $B_{\Phi }=\left[\begin{array}{ccc}{B}_{1}F{D}_s& B_{1}F{D}_y& D_x-B_{1}FC{D}_x\end{array}\right]$, $\Phi \left(t\right)={\left[\begin{array}{ccc}{\dot{e}}_{fs}^T\left(t\right)& {\dot{e}}_d^T\left(t\right)& d^T\left(t\right)\end{array}\right]}^T$.

According to Assumption 2, it can be shown that ${\dot{e}}_{fs}\left(t\right),{\dot{e}}_d\left(t\right)$ are bounded, and they will both converge to 0. In addition, the disturbance $d\left(t\right)$ has also been assumed in the sense of $L_2$ norm in (1). Therefore, we assume $\Phi \left(t\right)\in L_2[0,\infty ]$.

In the following theorem, the stability condition for the overall closed-loop system is given.

Theorem 1.

Given a positive scalar γ, the closed-loop system (24) and (42) is robust stable with an $H_{\infty }$ performance γ, that is ${\parallel x\left(t\right)\parallel }^2+\parallel \overline{e}{\left(t\right)\parallel }^2\le {\gamma }^2{\parallel \Phi \left(t\right)\parallel }^2$, if there exist symmetric positive definite matrices $P\in {\mathbf{R}}^{\overline{n}\times \overline{n}},Q\in {\mathbf{R}}^{n\times n}$, matrices $X\in {\mathbf{R}}^{n\times n}$, $Y\in {\mathbf{R}}^{\overline{n}\times p}$, $R\in {\mathbf{R}}^{(m+q)\times p}$ such that

$$\begin{array}{cc}\hfill & \Omega =\left[\begin{array}{ccc}{\Omega }_{11}+I& -X{I}_e& Q{B}_{\Phi }\\ & {\Omega }_{22}+I& 0\\ & *& -{\gamma }^{2}I\end{array}\right]<0\hfill \end{array}$$

(43)

$$\begin{array}{cc}\hfill & D^T{(I-H\overline{C})}^{T}P=R\overline{C}\hfill \end{array}$$

(44)

where

$$\begin{array}{cc}\hfill {\Omega }_{11}& =Q{A}_a+A_a^{T}Q-X-X^T,\hfill \\ \hfill {\Omega }_{22}& =P{A}_0+A_0^{T}P-Y\overline{C}-{\overline{C}}^T{Y}^T.\hfill \end{array}$$

(45)

The proportional gain $L_1$ in (24) and K in (42) can be calculated as

$$\begin{array}{c}\hfill L_1=P^{-1}Y,K={\left(B_1^T{B}_1\right)}^{-1}{B}_1^T{Q}^{-1}X.\end{array}$$

(46)

Proof. 

First, we define the error variable $\tilde{\psi }\left(t\right)=\widehat{\psi }\left(t\right)-\psi$, where $\psi$ and $\widehat{\psi }\left(t\right)$ are defined in (25) and (26), respectively. Choose the following Lyapunov function:

$$\begin{array}{c}\hfill V\left(t\right)=V_x\left(t\right)+V_e\left(t\right)+V_{\psi }\left(t\right)\end{array}$$

(47)

where

$$\begin{array}{c}\hfill V_x\left(t\right)=x^T\left(t\right)Qx\left(t\right),V_e\left(t\right)={\overline{e}}^{T}P\overline{e},V_{\psi }\left(t\right)=\frac{{\tilde{\psi }}^2\left(t\right)}{c_e}.\end{array}$$

(48)

Then, we have

$$\begin{array}{cc}\hfill {\dot{V}}_x\left(t\right)=& x^T\left(t\right)[{(A_a-B_{1}K)}^{T}Q+Q(A_a-B_{1}K)]x\left(t\right)\hfill \\ \hfill & -2x^T\left(t\right)Q{B}_{1}K{I}_e\overline{e}\left(t\right)+2x^T\left(t\right)Q{\overline{B}}_{\Phi }\Phi \left(t\right)\hfill \\ \hfill {\dot{V}}_e\left(t\right)=& {\overline{e}}^T\left(t\right)[P(A_0-L_1\overline{C})+{(A_0-L_1\overline{C})}^{T}P]\overline{e}\left(t\right)\hfill \\ \hfill & +2{\overline{e}}^T\left(t\right)P(I-H\overline{C})\overline{D}(u_s\left(t\right)-\overline{f}\left(t\right))\hfill \\ \hfill {\dot{V}}_{\psi }\left(t\right)=& \frac{2\tilde{\psi }\left(t\right)\dot{\tilde{\psi }}\left(t\right)}{c_e}.\hfill \end{array}$$

(49)

Since $\dot{\tilde{\psi }}\left(t\right)=\dot{\widehat{\psi }}\left(t\right)$, it can be derived from the adaptive law (26) and (27) that

$$\begin{array}{cc}\hfill & 2{\overline{e}}^T\left(t\right)P(I-H\overline{C})\overline{D}(u_s\left(t\right)-\overline{f}\left(t\right))+\frac{2\tilde{\psi }\left(t\right)\dot{\tilde{\psi }}\left(t\right)}{c_e}\hfill \\ \hfill \le & -2s_e^T\left(t\right)(\epsilon +\widehat{\psi }\left(t\right))\mathrm{sgn}\left(s_e\left(t\right)\right)+2\parallel s_e\left(t\right)\parallel \parallel \overline{f}\left(t\right)\parallel +\frac{2\tilde{\psi }\left(t\right)\dot{\widehat{\psi }}\left(t\right)}{c_e}\hfill \\ \hfill \le & -2\parallel s_e\left(t\right)\parallel (\epsilon +\widehat{\psi }\left(t\right))+\frac{2\tilde{\psi }\left(t\right)\dot{\widehat{\psi }}\left(t\right)}{c_e}\hfill \\ \hfill & +2\parallel s_e\left(t\right)\parallel (f_{a1}+f_{s1}+\sigma f_{s2}+d_1+\sigma d_2)\hfill \\ \hfill \le & -2\epsilon \parallel s_e\left(t\right)\parallel -2\parallel s_e\left(t\right)\parallel \tilde{\psi }\left(t\right)+\frac{2\tilde{\psi }\left(t\right)\dot{\widehat{\psi }}\left(t\right)}{c_e}\hfill \\ \hfill \le & -2\epsilon \parallel s_e\left(t\right)\parallel .\hfill \end{array}$$

(50)

Let $Q{B}_{1}K=X$ and $P{L}_1=Y$, when $\Phi \left(t\right)=0$, after some algebraic manipulation, it can be obtained from (49) and (50) that

$$\begin{array}{cc}\hfill \dot{V}\left(t\right)=& {\dot{V}}_x\left(t\right)+{\dot{V}}_e\left(t\right)+{\dot{V}}_{\psi }\left(t\right)\hfill \\ \hfill \le & x^T\left(t\right)[Q(A_a-B_{1}K)+{(A_a-B_{1}K)}^{T}Q]x\left(t\right)\hfill \\ \hfill & -2x^T\left(t\right)Q{B}_{1}K{I}_e\overline{e}\left(t\right)+{\overline{e}}^T\left(t\right)[P(A_0-L_1\overline{C})\hfill \\ \hfill & +{(A_0-L_1\overline{C})}^{T}P]\overline{e}\left(t\right)-\epsilon \parallel s_e\left(t\right)\parallel \hfill \\ \hfill \le & {\left[\begin{array}{c}x\left(t\right)\\ \overline{e}\left(t\right)\end{array}\right]}^T\left[\begin{array}{cc}{\Omega }_{11}& -X{I}_e\\ *& {\Omega }_{22}\end{array}\right]\left[\begin{array}{c}x\left(t\right)\\ \overline{e}\left(t\right)\end{array}\right].\hfill \end{array}$$

(51)

If we can obtain the feasible solutions to (43), then it can be concluded that $\dot{V}\left(t\right)<0$ in (51). Therefore, system (24) and (42) is asymptotically stable when $\Phi \left(t\right)=0$.

Now we will consider the $H_{\infty }$ performance under zero initial conditions that

$$\begin{array}{cc}\hfill J=& {\int }_0^{\infty }(x^T\left(t\right)x\left(t\right)+{\overline{e}}^T\left(t\right)\overline{e}\left(t\right)-{\gamma }^2{\Phi }^T\left(t\right)\Phi \left(t\right))dt\hfill \\ \hfill \le & {\int }_0^{\infty }(x^T\left(t\right)x\left(t\right)+{\overline{e}}^T\left(t\right)\overline{e}\left(t\right)-{\gamma }^2{\Phi }^T\left(t\right)\Phi \left(t\right)\hfill \\ \hfill & +\dot{V}\left(t\right))dt-{\int }_0^{\infty }\dot{V}\left(t\right)dt\hfill \\ \hfill \le & {\int }_0^{\infty }(x^T\left(t\right)x\left(t\right)+{\overline{e}}^T\left(t\right)\overline{e}\left(t\right)-{\gamma }^2{\Phi }^T\left(t\right)\Phi \left(t\right)\hfill \\ \hfill & +\dot{V}\left(t\right))dt-V(\infty )+V\left(0\right)\hfill \\ \hfill \le & {\int }_0^{\infty }(x^T\left(t\right)x\left(t\right)+{\overline{e}}^T\left(t\right)\overline{e}\left(t\right)-{\gamma }^2{\Phi }^T\left(t\right)\Phi \left(t\right)+\dot{V}\left(t\right))dt.\hfill \end{array}$$

(52)

From (49) and (50), we have

$$\begin{array}{cc}\hfill & x^T\left(t\right)x\left(t\right)+{\overline{e}}^T\left(t\right)\overline{e}\left(t\right)-{\gamma }^2{\Phi }^T\left(t\right)\Phi \left(t\right)+\dot{V}\left(t\right)\hfill \\ \hfill \le & \left[\begin{array}{ccc}{x}^T\left(t\right)& {\overline{e}}^T\left(t\right)& {\Phi }^T\left(t\right)\end{array}\right]\Omega {\left[\begin{array}{ccc}{x}^T\left(t\right)& {\overline{e}}^T\left(t\right)& {\Phi }^T\left(t\right)\end{array}\right]}^T\hfill \\ \hfill <& 0\hfill \end{array}$$

(53)

where $\Omega$ is defined in (43). From (52) and (53), it can be obtained that $J<0$, and the $H_{\infty }$ performance has been established.

Since $B_1$ is of full column rank, $B_1^T{B}_1$ is nonsingular. Hence, we have $K={\left(B_1^T{B}_1\right)}^{-1}{B}_1^T{Q}^{-1}X$. It completes the proof. □

Remark 4.

It is evident that there is linear matrix equality in Theorem 1, and the LMI toolbox can not be used directly. According to the algorithm in [41], (44) can be taken as

$$\begin{array}{cc}\hfill & \mathrm{Trace}\left[{(D^T{(I-H\overline{C})}^{T}P-R\overline{C})}^T(D^T{(I-H\overline{C})}^{T}P-R\overline{C})\right]\hfill \\ \hfill & =0.\hfill \end{array}$$

Thus, the following inequality can be obtained:

$$\begin{array}{c}\hfill {(D^T{(I-H\overline{C})}^{T}P-R\overline{C})}^T(D^T{(I-H\overline{C})}^{T}P-R\overline{C})<\eta I_{\overline{n}}\end{array}$$

(54)

where ${\eta }_i$ is a parameter to be designed. By the Schur complement, it is derived that

$$\begin{array}{c}\hfill \left[\begin{array}{cc}-\eta I_{\overline{n}}& {(D^T{(I-H\overline{C})}^{T}P-R\overline{C})}^T\\ *& -I_{m+n_d+q}\\ \end{array}\right]<0.\end{array}$$

(55)

Then, the following minimization problem is equivalent to Theorem 1:

$$\begin{array}{c}\hfill \min \eta \\ \hfill \mathrm{subject}\mathrm{to}\left(43\right)\mathrm{and}\left(55\right)\end{array}$$

(56)

which can be solved by the LMI toolbox in MATLAB directly.

Using pseudo-inverse can be, in some cases, not trivial. Ref. [42] encountered the same problem as solving (46) in solving the pole assignment problem, which divided the problem into two stages to solve and simplified the calculation process. This method can be considered to solve the case in which it is difficult to calculate the pseudo-inverse matrix. Ref. [43] proposes a new control specification for solving pole assignment based on LMI, and we will consider using this method to solve the LMI problem in this paper in a subsequent work.

3.3. Reachability Analysis of Sliding Motion

In the following section, the reachability of the sliding surfaces $s\left(t\right)$ in (37) is analyzed.

Before designing the sliding mode control law $u\left(t\right)$, we present the following adaptive laws:

$$\begin{array}{cc}\hfill {\dot{\widehat{\theta }}}_h\left(t\right)& =c_{\theta h}\parallel s\left(t\right)\parallel \parallel B_2{B}_f\parallel {\phi }_h\left(\widehat{x}\right),\widehat{\theta }\left(0\right)\ge 0,h=1,2,...,N,\hfill \\ \hfill \dot{\widehat{\overline{\delta }}}\left(t\right)& =c_{\delta }\parallel s\left(t\right)\parallel \parallel B_2{B}_f\parallel ,\widehat{\overline{\delta }}\left(0\right)\ge 0,\hfill \\ \hfill \dot{\widehat{\xi }}\left(t\right)& =c_{\xi }\parallel s\left(t\right)\parallel ,\widehat{\xi }\left(0\right)\ge 0,\hfill \end{array}$$

(57)

where $c_{\theta h},c_{\delta },c_{\xi }$ are the positive adaptive gains to be designed, and $\widehat{\xi }\left(t\right)$ is the estimation of $\xi$ such that

$$\begin{array}{cc}\hfill & \parallel B_2{f}_a\left(t\right)\parallel +\parallel FC{D}_{x}d\left(t\right)\parallel +\parallel F{D}_s\dot{f_s}\left(t\right)\parallel \hfill \\ \hfill +& \parallel F{D}_y\dot{d}\left(t\right)\parallel +\parallel FCA{e}_x\left(t\right)\parallel \le \xi .\hfill \end{array}$$

(58)

Obviously, we have ${\widehat{\theta }}_h\left(t\right),\widehat{\overline{\delta }}\left(t\right),\widehat{\xi }\left(t\right)\ge 0$. The sliding mode law $\tilde{u}\left(t\right)$ is designed as

$$\begin{array}{cc}\hfill \tilde{u}\left(t\right)=& -\frac{1}{\mu }(\eta +\zeta \left(t\right)+\widehat{\xi }\left(t\right)+\sum _{h=1}^N{\widehat{\theta }}_h\left(t\right)\phi \left(\widehat{x}\left(t\right)\right)\hfill \\ \hfill & +\widehat{\overline{\delta }}\left(t\right))sgn\left(s\left(t\right)\right),\hfill \end{array}$$

(59)

where $\eta >0$ will be designed later.

$$\begin{array}{c}\hfill \zeta \left(t\right)=\parallel FCA\widehat{x}\left(t\right)\parallel +\parallel K\widehat{x}\left(t\right)\parallel +\parallel F{D}_s{\dot{\widehat{f}}}_s\left(t\right)\parallel +\parallel F{D}_y\dot{\widehat{d}}\left(t\right)\parallel .\end{array}$$

(60)

Remark 5.

In order to illustrate the computational effort of solving the LMI, we proposed the following through MATLAB LMI Toolbox:

1. 

Select a suitable free matrix ς and a scalar σ, which satisfies Equation (4), such that $(I-H\overline{C})$ is invertible;

2. 

Design an appropriate Equation (29), define suitable matrices $H,A_0,L_s,L_2,L$, and solve the minimization problem Equation (56);

3. 

Design adaptive law Equation (57), Equation (65), and sliding mode law Equation (59).

By analyzing the reachability of sliding motion, we have the following theorem:

Theorem 2.

If there exist matrices $0<P^T=P\in {\mathbf{R}}^{\overline{n}\times \overline{n}}$, $0<Q^T=Q\in {\mathbf{R}}^{n\times n}$, and matrices $R\in {\mathbf{R}}^{(m+n_d+q)\times p}$, $X\in {\mathbf{R}}^{n\times n}$, $Y\in {\mathbf{R}}^{\overline{n}\times p}$, such that (43) and (44) hold. Based on the input $u\left(t\right)$ defined in (59), the system state of (42) can be driven onto the sliding surface $s\left(t\right)=0$ in finite time.

Proof. 

First, denoting that

$$\begin{array}{cc}\hfill {\tilde{\theta }}_h\left(t\right)& ={\widehat{\theta }}_h\left(t\right)-{\theta }_h,h=1,2,...,N,\hfill \\ \hfill \tilde{\xi }\left(t\right)& =\widehat{\xi }\left(t\right)-\xi ,\tilde{\overline{\delta }}\left(t\right)=\widehat{\overline{\delta }}\left(t\right)-\overline{\delta }.\hfill \end{array}$$

(61)

Then, we define that

$$\begin{array}{c}\hfill V_0\left(t\right)=V_s\left(t\right)+V_{\xi }\left(t\right)+V_{\theta }\left(t\right)+V_{\delta }\left(t\right)\end{array}$$

(62)

where

$$\begin{array}{cc}\hfill V_s\left(t\right)& =\frac{1}{2}{s}^T\left(t\right)s\left(t\right),V_{\theta }\left(t\right)=\sum _{h=1}^N\frac{{\tilde{\theta }}_h^2\left(t\right)}{2c_{\theta h}},\hfill \\ \hfill V_{\xi }\left(t\right)& =\frac{{\tilde{\xi }}^2\left(t\right)}{2c_{\xi }},V_{\delta }\left(t\right)=\frac{{\tilde{\overline{\delta }}}^2\left(t\right)}{2c_{\delta }}\hfill \end{array}$$

(63)

We have

$$\begin{array}{cc}\hfill & {\dot{V}}_s\left(t\right)=s^T\left(t\right)\dot{s}\left(t\right)\hfill \\ \hfill =& s^T\left(t\right)[FCAx\left(t\right)+B_{2}d\left(t\right)+B_2\rho \left(t\right)B_2^T\tilde{u}\left(t\right)+K\widehat{x}\left(t\right)]\hfill \\ \hfill \le & \parallel s\left(t\right)\parallel [\parallel FCAx\left(t\right)\parallel +\parallel B_2\parallel \parallel d\left(t\right)\parallel +\parallel K\widehat{x}\left(t\right)\parallel ]\hfill \\ \hfill & -s^T\left(t\right)B_2\rho \left(t\right)B_2^T\phi \left(t\right)sgn\left(s\left(t\right)\right)\hfill \\ \hfill \le & \parallel s\left(t\right)\parallel [\parallel FCAx\left(t\right)\parallel +\parallel B_2\parallel \parallel d\left(t\right)\parallel +\parallel K\widehat{x}\left(t\right)\parallel ]\hfill \\ \hfill & -s^T\left(t\right)B_2\underline{\rho }{B}_2^T\phi \left(t\right)sgn\left(s\left(t\right)\right)\hfill \\ \hfill \le & \parallel s\left(t\right)\parallel [\parallel FCAx\left(t\right)\parallel +\parallel B_2\parallel \parallel d\left(t\right)\parallel +\parallel K\widehat{x}\left(t\right)\parallel ]-\mu \left|s\left(t\right)\right|\phi \left(t\right)\hfill \\ \hfill \le & \parallel s\left(t\right)\parallel [\parallel FCA\widehat{x}\left(t\right)\parallel +\parallel FCA{e}_x\left(t\right)\parallel +\parallel B_2\parallel \parallel d\left(t\right)\parallel +\parallel K\widehat{x}\left(t\right)\parallel ]\hfill \\ \hfill & -\left|s\left(t\right)\right|(\parallel FCA\widehat{x}\left(t\right)\parallel +\parallel FCA{B}_n\parallel \frac{ϵ\left(t\right)}{\sqrt{{\lambda }_{min}\left(P\right)}}\hfill \\ \hfill & +\parallel B\parallel \overline{d}+\parallel K\widehat{x}\left(t\right)\parallel +\eta )\hfill \\ \hfill \le & -\eta \parallel s\left(t\right)\parallel .\hfill \end{array}$$

(64)

The proof is completed. □

Remark 6.

Specifically, when the unknown actuator efficiency factor is constant as $\rho \left(t\right)=\rho$, the estimation of the ρ can be given in the proposed methods, and the stabilization of the closed-loop system can be also guaranteed simultaneously.

Now, the adaptive law for ${\rho }_h$ is given by

$$\begin{array}{cc}\hfill {\dot{\widehat{\rho }}}_h\left(t\right)& ={\mathrm{Proj}}_{[{\underline{\rho }}_h,{\overline{\rho }}_h]}\left\{L_h\left(t\right)\right\}\hfill \\ \hfill & =\left\{\begin{array}{cc}0,\hfill & \mathrm{if}{\widehat{\rho }}_h\left(t\right)={\underline{\rho }}_h,\mathrm{and}{L}_h\left(t\right)\le 0\hfill \\ \hfill & \mathrm{or}{\widehat{\rho }}_h\left(t\right)={\overline{\rho }}_h,\mathrm{and}{L}_h\left(t\right)\ge 0\hfill \\ L_h\left(t\right),\hfill & \mathrm{otherwise}\hfill \end{array}\right.\hfill \end{array}$$

(65)

where

$$\begin{array}{c}\hfill L_h\left(t\right)=c_h{s}^T\left(t\right)B_2^{\left(h\right)}{\left(B_2^{\left(h\right)}\right)}^T\tilde{u}\left(t\right)\end{array}$$

(66)

where $B_2^h$ is the hth column of $B_2$. The SMC law $\tilde{u}\left(t\right)$ is designed in (59).

Theorem 3.

If there exist symmetric positive definite matrices $P\in {\mathbf{R}}^{\overline{n}\times \overline{n}}$, $Q\in {\mathbf{R}}^{n\times n}$, matrices $R\in {\mathbf{R}}^{(m+q)\times p}$, $X\in {\mathbf{R}}^{n\times n}$, $Y\in {\mathbf{R}}^{\overline{n}\times p}$, such that (43) and (44) hold. Under the control input $u\left(t\right)$ in (59), the trajectory $x\left(t\right)$ of the closed-loop system (42) will be driven onto the sliding surface $s\left(t\right)=0$ in finite time.

Proof. 

Define that

$$\begin{array}{c}\hfill {\tilde{\rho }}_h\left(t\right)={\widehat{\rho }}_h\left(t\right)-{\rho }_h,V_s=0.5s^T\left(t\right)s\left(t\right)+\sum _{h=1}^m\frac{{\tilde{\rho }}_h^2\left(t\right)}{c_h}.\end{array}$$

(67)

Then, we have

$$\begin{array}{cc}\hfill {\dot{V}}_s\left(t\right)=& s^T\left(t\right)\dot{s}\left(t\right)+\sum _{h=1}^m\frac{{\tilde{\rho }}_h\left(t\right){\dot{\tilde{\rho }}}_h\left(t\right)}{c_h}\hfill \\ \hfill \le & \parallel s\left(t\right)\parallel [\parallel FCAx\left(t\right)\parallel +\parallel B_2\parallel \parallel d\left(t\right)\parallel +\parallel K\widehat{x}\left(t\right)\parallel ]\hfill \\ \hfill & -\frac{1}{\mu }{s}^T\left(t\right)B_2\rho B_2^T{\phi }_1\left(t\right)sgn\left(s\left(t\right)\right)+\sum _{h=1}^m\frac{{\tilde{\rho }}_h\left(t\right){\dot{\widehat{\rho }}}_h\left(t\right)}{c_h}\hfill \\ \hfill \le & \parallel s\left(t\right)\parallel [\parallel FCAx\left(t\right)\parallel +\parallel B_2\parallel \parallel d\left(t\right)\parallel +\parallel K\widehat{x}\left(t\right)\parallel ]\hfill \\ \hfill & -\frac{1}{\mu }{s}^T\left(t\right)B_2\widehat{\rho }\left(t\right)B_2^T{\phi }_1\left(t\right)sgn\left(s\left(t\right)\right)\hfill \\ \hfill & +\sum _{h=1}^m\frac{{\tilde{\rho }}_h\left(t\right){\dot{\widehat{\rho }}}_h\left(t\right)}{c_h}-s^T\left(t\right)B_2\tilde{\rho }\left(t\right)B_2^T\tilde{u}\left(t\right)\hfill \\ \hfill \le & -\eta \parallel s\left(t\right)\parallel -\sum _{h=1}^m\frac{{\tilde{\rho }}_h\left(t\right)L_h}{c_h}+\sum _{h=1}^m\frac{{\tilde{\rho }}_h\left(t\right){\dot{\widehat{\rho }}}_h\left(t\right)}{c_h}\hfill \\ \hfill \le & -\eta \parallel s\left(t\right)\parallel .\hfill \end{array}$$

(68)

The proof is completed. □

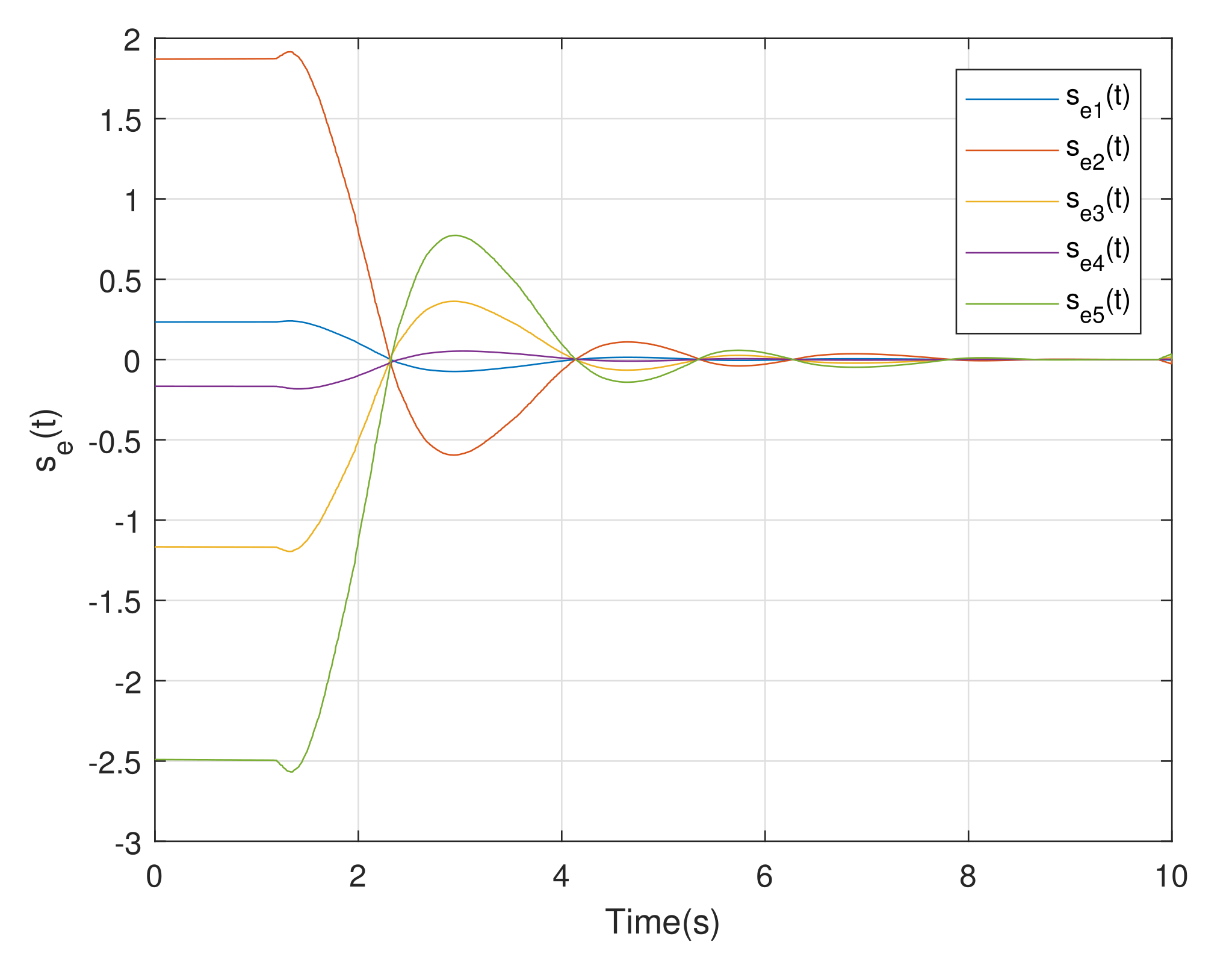
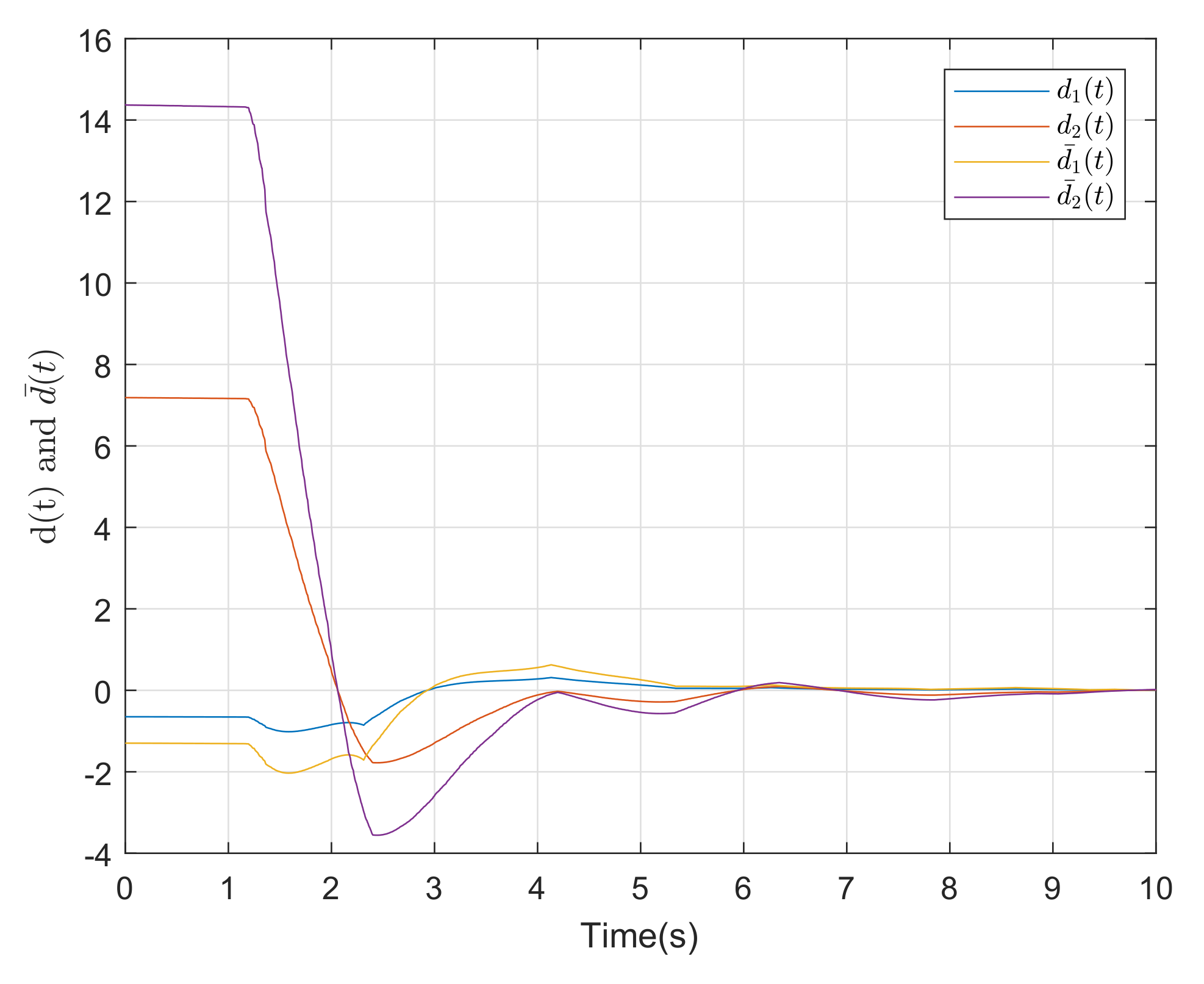
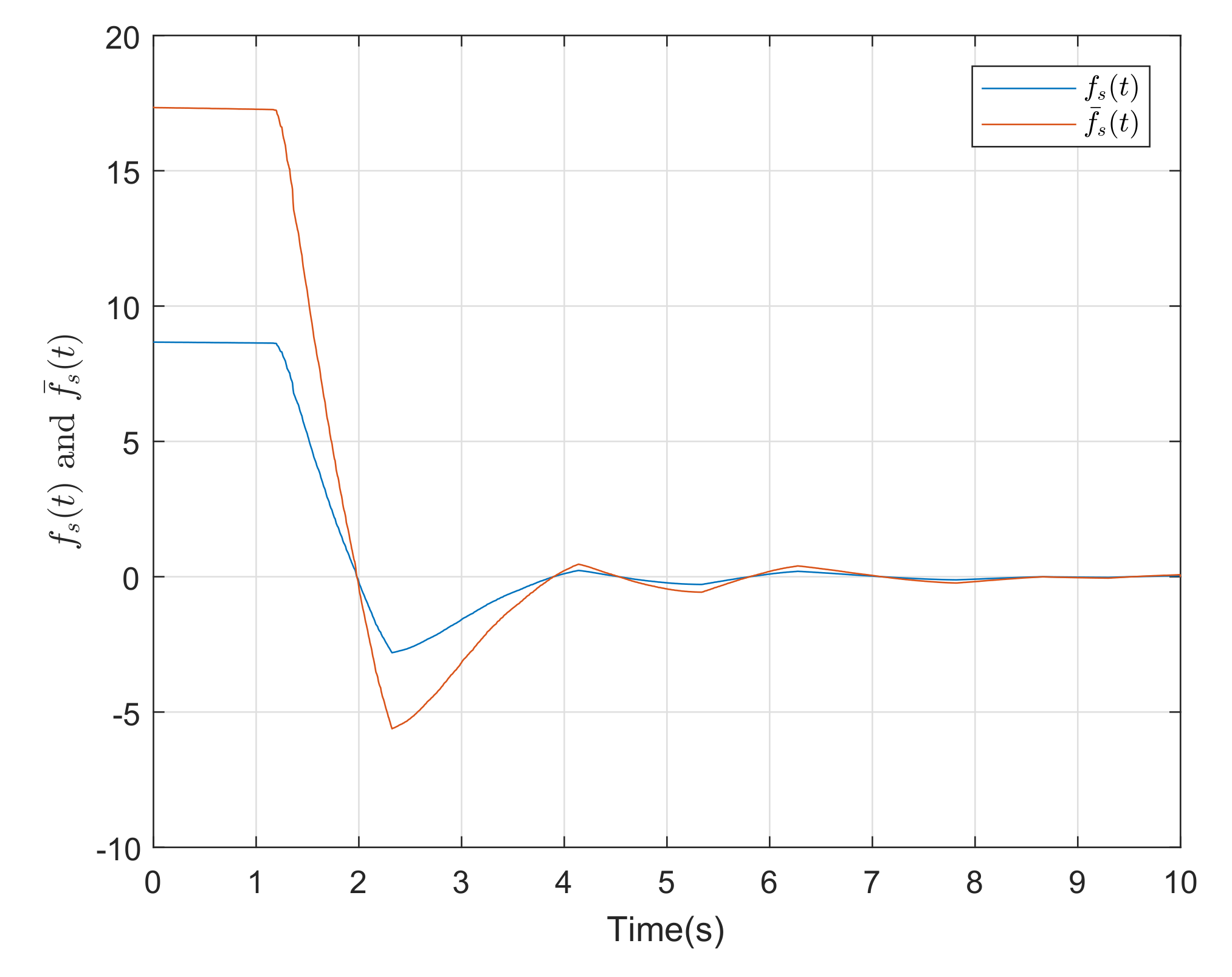
4. Simulation Example

In this section, a numerical example is given and the correctness of the theorem is verified. Consider an uncertain nonlinear system subject to time-varying actuator fault, sensor fault, and external disturbance as form (1), where

$$\begin{array}{cc}\hfill A& =\left[\begin{array}{cc}-1& 1\\ -8& -1\end{array}\right],B=\left[\begin{array}{cc}-1& 0\\ -5& -4\end{array}\right],\hfill \\ \hfill C& =\left[\begin{array}{cc}0.14& 0.1\\ -1& 2\end{array}\right],B_1=\left[\begin{array}{cc}-1& 0\\ -5& -4\end{array}\right],\hfill \\ \hfill B_2& =\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right],D_s=\left[\begin{array}{c}2\\ 1\end{array}\right],B_f=\left[\begin{array}{c}1\\ 2\end{array}\right],\hfill \\ \hfill D_x& =\left[\begin{array}{cc}2& 1\\ 0& 1\end{array}\right],D_y=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right],E=B{B}_f=\left[\begin{array}{c}-1\\ -13\end{array}\right]\hfill \end{array}$$

with $n=2$, $m=2$, $p=2$, $l=2$, $q=1$, $n_d=2$, $\sigma =0.2$, $\overline{n}=n+n_d=4$. It can be checked that $\left(A,B\right)$ is controllable, and $\left(A,C\right)$ is observable. Let $f\left(x\right)=sin\left(x_1\left(t\right)\right)$, $\sigma =0.2$, $f_a\left(t\right)=\left[\begin{array}{c}1\\ 1\end{array}\right]$ denote the stuck actuator fault.

• Observer Design: In the first step, the fault-tolerant observer is designed given the following matrices:

  $$H=\left[\begin{array}{cc}5.2763& 0.8476\\ 2.6131& 0.9185\\ 0& 0\\ 0& 0\\ 0& 0\\ 0& 0\end{array}\right]$$

  $$A_0=\left[\begin{array}{cccccc}3.3368& 3.3318& 3.2731& -0.9444& 1.0552& 0.1695\\ 1.6441& 1.6511& 1.6281& -0.3620& 0.5226& 0.1837\\ 0& 0& -0.2& 0& 0& 0\\ 0& 0& 0& -0.2& 0& 0\\ 0& 0& 0& 0& -0.2& 0\\ 0& 0& 0& 0& 0& -0.2\end{array}\right]$$

  $$L_s=\left[\begin{array}{ccccc}1.11396& 8.8916& -5.2763& -0.8476& -11.4002\\ 0.5457& 4.3937& -2.6131& -0.9185& -6.1448\\ 0& 0& 1& 0& 0\\ 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 2\\ 0& 0& 0& 0& 1\end{array}\right]$$

  $$L_2=\left[\begin{array}{cc}-257676& -160190\\ -202696& -128852\\ -36008& -24683\\ 87374& 57837\\ 87818& 57410\\ 43079& 28139\end{array}\right],L=\left[\begin{array}{cc}5323& 54247\\ 4321& 42672\\ 855& 7580\\ -1972& 18394\\ -1946& 18488\\ -953& 9069\end{array}\right]$$
• Design of controller $u_s\left(t\right)$: Next, we design the sliding mode function (27). According to (24) and the adaptive gain $c_e=0.1$, the discontinuous input $u_s\left(t\right)$ is given by

  $$\begin{array}{cc}& s_e\left(t\right)=\hfill \\ \hfill & \left[\begin{array}{cccccc}-2.3389& 9.0417& 14.3679& 3.8213& 14.1294& 4.0084\\ -29.7330& 95.3811& 116.8905& 43.4552& 116.2150& 43.5985\\ 3.6878& -1.8811& 19.6842& -1.7707& 18.8433& -5.1520\\ -15.3572& 26.7646& -14.2582& 18.1904& -14.3375& 14.4901\\ -22.5776& 52.2656& 19.5038& 25.2978& 24.8239& 25.2804\end{array}\right]\overline{e}\left(t\right)\hfill \\ \hfill & \dot{\widehat{\psi }}\left(t\right)=0.1∥s_e\left(t\right)∥\hfill \\ \hfill & u_s\left(t\right)=-\left(0.2+\widehat{\psi }\left(t\right)\right)\mathrm{sgn}\left(s_e\left(t\right)\right)\hfill \end{array}$$
• Design of controller: The state feedback gain matrix K as

  $$K=\left[\begin{array}{cc}-3005& 401\\ 4762& -1179\end{array}\right]$$

  and the matrix F is

  $$F=\left[\begin{array}{cc}-5.2631& 0.2631\\ 0& -1.2500\end{array}\right]$$

The simulation results for system (2) are shown in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6 below. The trajectory of error vector $\overline{e}\left(t\right)$ is shown in Figure 1. Figure 1 illustrates a comparison between the actual state of the system and the state estimated by the observer, and the error is asymptotically stable. The trajectories of output error sliding surface $s_e\left(t\right)$ and discontinuous term $u_s\left(t\right)$ are shown in Figure 2 and Figure 3, respectively. As shown in Figure 4, the state of the system is asymptotically stable, thus verifying that the sliding surface and controller are effective. It can be seen from Figure 3 that the system can reach the sliding surface in a short time, which is basically consistent with the theoretical analysis. The sliding variables (40) and the sliding mode controllers (59) are very close to zero after 8s. The comparisons of state vector $x\left(t\right)$, external disturbance $d\left(t\right)$, and sensor fault $f_s\left(t\right)$ and their estimations are illustrated in Figure 4, Figure 5 and Figure 6, respectively. It can be seen that the proposed FTC approach can ensure the asymptotical stability of the closed-loop fault system.

The study in [44] investigates an adaptive fuzzy output feedback fault-tolerant optimal control problem for a class of single-input and single-output nonlinear systems. The comparison of the performance of the two controllers is given in

Table 1. The performance indexes of our method and [8].

Performance Indexes	Convergence Time (s)	Steady-State Error
Our method	8	0.002
The controller in [8]	14	0.04

using the same data of Example. By comparison, it can be found that our method is better than the adaptive fuzzy sliding-mode controller (59) in terms of convergence time and steady-state error.

5. Conclusions

In this study, the adaptive fuzzy FTC problem was addressed for a class of nonlinear systems with actuator fault, sensor fault, and external disturbance. By augmenting the original plant into a normal system, a new SMO was designed to obtain the estimation of the state vectors and faults information. Based on the state estimation, an integral-type SMC strategy was developed to stabilize the closed-loop fault system. The advantage of this study is providing an observer that can simultaneously estimate state vectors, sensor faults, and external disturbances and has a wider estimation range than the traditional SMO. In addition, the effect of the time-varying actuator degradation in the error system can be eliminated because of the structure of the observer. However, there are some limitations in this article. For example, the proposed method is complicated in practical application and cannot be directly applied to descriptor systems. Future work will focus on extending the designed methods (small-gain theorem [44,45]) to more complicated systems such as switched systems and stochastic systems.