Adaptive Fuzzy Fault-Tolerant Control against Time-Varying Faults via a New Sliding Mode Observer Method
Abstract
:1. Introduction
2. Problem Formulation and Preliminaries
2.1. Problem Statement
2.2. Fuzzy Logic Systems
3. Main Results
3.1. Observer Design
3.2. Controller Design
3.3. Reachability Analysis of Sliding Motion
- 1.
- Select a suitable free matrix ς and a scalar σ, which satisfies Equation (4), such that is invertible;
- 2.
- 3.
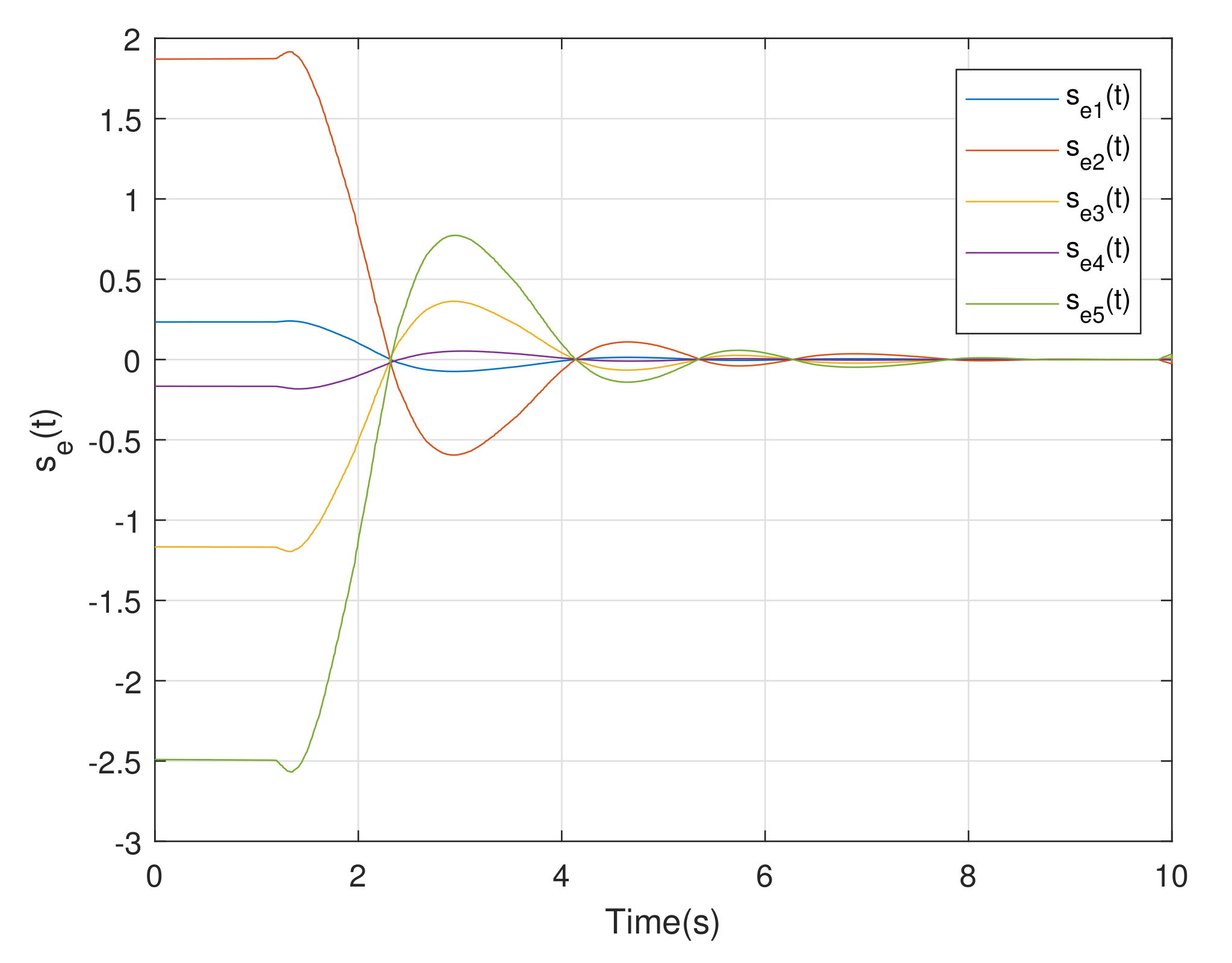
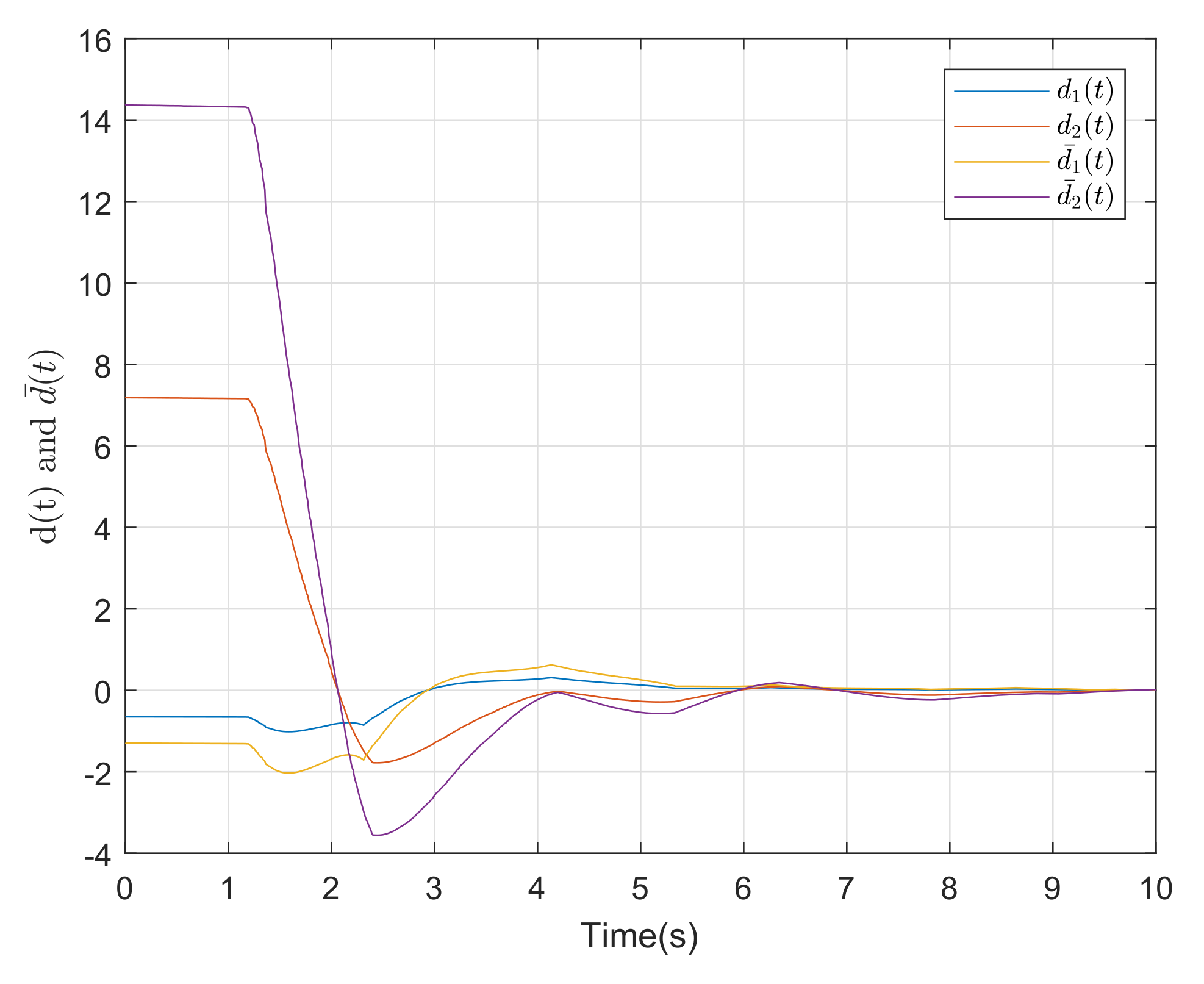
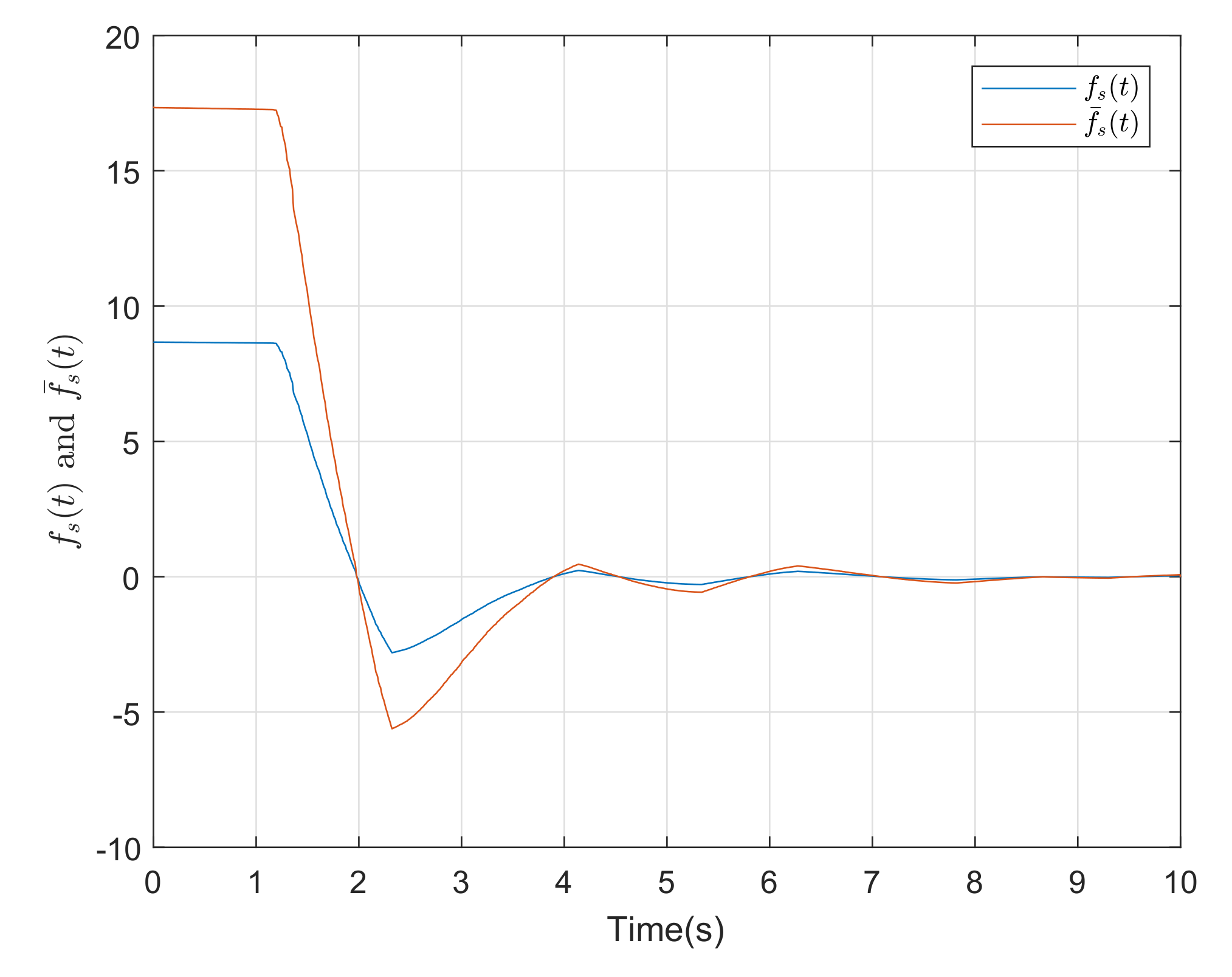
4. Simulation Example
- Observer Design: In the first step, the fault-tolerant observer is designed given the following matrices:
- Design of controller: The state feedback gain matrix K asand the matrix F is
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gao, Z.; Ding, S.X. State and Disturbance Estimator for Time-Delay Systems With Application to Fault Estimation and Signal Compensation. IEEE Trans. Signal Process. 2007, 55, 5541–5551. [Google Scholar]
- Wu, L.; Ho, D.W. Fuzzy filter design for Itô stochastic systems with application to sensor fault detection. IEEE Trans. Fuzzy Syst. 2009, 17, 233–242. [Google Scholar]
- Liu, X.; Gao, Z.; Chen, M.Z. Takagi-Sugeno Fuzzy Model Based Fault Estimation and Signal Compensation with Application to Wind Turbines. IEEE Trans. Ind. Electron. 2017, 64, 5678–5689. [Google Scholar] [CrossRef]
- Liu, X.; Gao, Z. Integrated fault estimation and fault-tolerant control for stochastic systems with Brownian motions. Int. J. Robust Nonlinear Control 2018, 28, 1915–1941. [Google Scholar] [CrossRef]
- Liu, X.; Han, J.; Wei, X.; Zhang, H.; Hu, X. Intermediate variable observer based fault estimation and fault-tolerant control for nonlinear stochastic system with exogenous disturbance. J. Frankl. Inst. 2020, 357, 5380–5401. [Google Scholar] [CrossRef]
- Zhang, K.; Jiang, B.; Staroswiecki, M. Dynamic output feedback-fault tolerant controller design for Takagi–Sugeno fuzzy systems with actuator faults. IEEE Trans. Fuzzy Syst. 2010, 18, 194–201. [Google Scholar] [CrossRef]
- Wang, X.; Yang, G.H. Fault-Tolerant Consensus Tracking Control for Linear Multiagent Systems Under Switching Directed Network. IEEE Trans. Cybern. 2020, 50, 1921–1930. [Google Scholar] [CrossRef]
- Li, Y.; Sun, K.; Tong, S. Observer-Based Adaptive Fuzzy Fault-Tolerant Optimal Control for SISO Nonlinear Systems. IEEE Trans. Cybern. 2019, 49, 649–661. [Google Scholar] [CrossRef]
- Tariq, M.F.; Khan, A.Q.; Abid, M.; Mustafa, G. Data-Driven Robust Fault Detection and Isolation of Three-Phase Induction Motor. Automatica 2019, 66, 4707–4715. [Google Scholar] [CrossRef]
- Deng, C.; Yang, G.H. Distributed adaptive fault-tolerant control approach to cooperative output regulation for linear multi-agent systems. Automatica 2019, 103, 62–68. [Google Scholar] [CrossRef]
- Yang, H.; Yin, S. Reduced order sliding mode observer-based fault estimation for Markov jump systems. IEEE Trans Autom. Control 2019, 64, 4733–4740. [Google Scholar] [CrossRef]
- Jiang, B.; Zhang, K.; Shi, P. Integrated fault estimation and accommodation design for discrete-time Takagi-Sugeno fuzzy systems with actuator faults. IEEE Trans. Fuzzy Syst. 2011, 19, 291–304. [Google Scholar] [CrossRef] [Green Version]
- Allahverdi, F.; Ramezani, A.; Forouzanfar, M. Sensor fault detection and isolation for a class of uncertain nonlinear system using sliding mode observers. Automatica 2020, 61, 219–228. [Google Scholar] [CrossRef]
- Li, Z.; Chen, X. Adaptive actuator fault compensation and disturbance rejection scheme for spacecraft. Int. J. Control Autom. Syst. 2021, 357, 5380–5401. [Google Scholar]
- Casavola, A.; Famularo, D.; Franzè, G. A robust deconvolution scheme for fault detection and isolation of uncertain linear systems: An LMI approach. Automatica 2005, 41, 1463–1472. [Google Scholar] [CrossRef]
- Karimi, H.R. Robust synchronization and fault detection of uncertain master-slave systems with mixed time-varying delays and nonlinear perturbations. Int. J. Control Autom. Syst. 2011, 9, 671–680. [Google Scholar] [CrossRef] [Green Version]
- Lin, B.; Su, X.; Li, X. Fuzzy Sliding Mode Control for Active Suspension System with Proportional Differential Sliding Mode Observer: Fuzzy SMC for active suspension system with PD sliding mode observer. Asian J. Control 2019, 21, 264–276. [Google Scholar] [CrossRef] [Green Version]
- Piltan, F.; Prosvirin, A.E.; Jeong, I.; Im, K.; Kim, J.M. Rolling-element bearing fault diagnosis using advanced machine learning-based observer. Appl. Sci. 2019, 9, 5404. [Google Scholar] [CrossRef] [Green Version]
- Zheng, W.; Xia, B.; Wang, W.; Lai, Y.; Wang, M.; Wang, H. State of charge estimation for power lithium-Ion battery using a fuzzy logic sliding mode Observer. Energies 2019, 12, 2491. [Google Scholar] [CrossRef] [Green Version]
- Xu, W.; Qu, S.; Zhao, L.; Zhang, H. An improved adaptive sliding mode observer for middle- and high-speed rotor tracking. IEEE Trans. Power Electron. 2009, 36, 1043–1053. [Google Scholar] [CrossRef]
- Gong, C.; Hu, Y.; Gao, J.; Wang, Y.; Yan, L. An improved delay-suppressed sliding mode observer for sensorless vector-controlled PMSM. IEEE Trans. Ind. Electron. 2019, 67, 5913–5923. [Google Scholar] [CrossRef]
- Cai, W.; She, J.; Wu, M.; Ohyama, Y. Disturbance suppression for quadrotor UAV using sliding-mode-observer-based equivalent-input-disturbance approach. ISA Trans. 2019, 92, 286–297. [Google Scholar] [CrossRef] [PubMed]
- Lopac, N.; Bulic, N.; Vrkic, N. Sliding mode observer-based load angle estimation for salient-pole wound rotor synchronous generators. Energies 2019, 12, 1609. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Zhang, X.; Wu, X.; Tan, G.; Chen, X. Sensorless control for IPMSM based on adaptive super-twisting sliding-mode observer and improved phase-locked loop. Energies 2019, 12, 1225. [Google Scholar] [CrossRef] [Green Version]
- Xiong, Y.; Saif, M. Sliding mode observer for nonlinear uncertain systems. IEEE Trans. Autom. Control 2001, 46, 2012–2017. [Google Scholar] [CrossRef]
- Apaza-Perez, W.A.; Moreno, J.A.; Fridman, L. Global Sliding Mode Observers for Some Uncertain Mechanical Systems. IEEE Trans. Autom. Control 2020, 65, 1348–1355. [Google Scholar] [CrossRef]
- Li, J.; Yang, G.H. Fuzzy Descriptor Sliding Mode Observer Design: A Canonical Form-Based Method. IEEE Trans. Fuzzy Syst. 2020, 28, 2048–2062. [Google Scholar] [CrossRef]
- Nguyen, N.P.; Hong, S.K. Fault diagnosis and fault-tolerant control scheme for quadcopter UAVs with a total loss of actuator. Energies 2019, 12, 1139. [Google Scholar] [CrossRef] [Green Version]
- Huang, S.N.; Tan, K.K. Fault detection, isolation, and accommodation control in robotic systems. IEEE Trans. Autom. Sci. Eng. 2008, 5, 480–489. [Google Scholar] [CrossRef]
- Aslam, M.S.; Ullah, R.; Dai, X.; Sheng, A. Event-triggered scheme for fault detection and isolation of non-linear system with time-varying delay. IET Control Theory Appl. 2020, 14, 2429–2438. [Google Scholar] [CrossRef]
- Li, H.; Gao, H.; Shi, P.; Zhao, X. Fault-tolerant control of Markovian jump stochastic systems via the augmented sliding mode observer approach. Automatica 2014, 50, 1825–1834. [Google Scholar] [CrossRef]
- Liu, M.; Shi, P. Sensor fault estimation and tolerant control for Itô stochastic systems with a descriptor sliding mode approach. Automatica 2013, 49, 1242–1250. [Google Scholar] [CrossRef]
- Jin, Z.; Wang, Z.; Li, J. Input-to-state stability of the nonlinear fuzzy systems via small-gain theorem and decentralized sliding mode control. IEEE Trans. Fuzzy Syst. 2021. [Google Scholar] [CrossRef]
- Zhang, Y.; Jin, Z.; Zhang, Q. Impulse elimination of the Takagi-Sugeno fuzzy singular system via sliding mode control. IEEE Trans. Fuzzy Syst. 2021. [Google Scholar] [CrossRef]
- Hou, H.; Yu, X.; Xu, L.; Rsetam, K.; Cao, Z. Finite-time continuous terminal sliding mode control of servo motor systems. IEEE Trans. Ind. Electron. 2020, 67, 5647–5656. [Google Scholar] [CrossRef]
- Hou, H.; Yu, X.; Fu, Z. Sliding-mode control of uncertain time-varying systems with state delays: A non-negative constraints approach. IEEE Trans. Syst. Man Cybern. Syst. 2020. [Google Scholar] [CrossRef]
- Hou, H.; Yu, X.; Xu, L.; Chuei, R.; Cao, Z. Discrete-time terminal sliding-mode tracking control with alleviated chattering. IEEE/ASME Trans. Mechatron. 2019, 24, 1808–1817. [Google Scholar] [CrossRef]
- Qian, M.; Yi, H.; Zheng, Z. Integrated fault tolerant attitude control approach for satellite attitude system with sensor faults. Optim. Control Appl. Methods 2020, 41, 555–570. [Google Scholar] [CrossRef]
- Mallavalli, S.; Fekih, A. A fault tolerant tracking control for a quadrotor UAV subject to simultaneous actuator faults and exogenous disturbances. Int. J. Control 2020, 99, 655–668. [Google Scholar] [CrossRef]
- Chen, C.P.; Liu, Y.J.; Wen, G.X. Fuzzy Neural Network-Based Adaptive Control for a Class of Uncertain Nonlinear Stochastic Systems. IEEE Trans. Cybern. 2014, 44, 583–593. [Google Scholar] [CrossRef] [PubMed]
- Feng, X.; Wang, Y. Fault estimation based on sliding mode observer for Takagi-Sugeno fuzzy systems with digital communication constraints. J. Frankl. Inst. 2020, 357, 569–588. [Google Scholar] [CrossRef]
- Richiedei, D.; Tamellin, I. Active control of linear vibrating systems for antiresonance assignment with regional pole placement. J. Sound Vib. 2021, 494, 115858. [Google Scholar] [CrossRef]
- Faria, F.A.; Assunção, E.; Teixeira, M.C.; Cardim, R.; Da Silva, N.A.P. Robust state-derivative pole placement LMI-based designs for linear systems. Int. J. Control 2009, 82, 1–12. [Google Scholar] [CrossRef]
- Jin, Z.; Wang, Z. Input-to-state stability of the nonlinear singular systems via small-gain theorem. Appl. Mathe. Comput. 2020, 402, 126171. [Google Scholar] [CrossRef]
- Liu, T.; Jiang, Z.P. A small-gain approach to robust event-triggered control of nonlinear systems. IEEE Trans. Autom. Control 2015, 60, 2072–2085. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Nie, Y.; Chen, L. Adaptive Fuzzy Fault-Tolerant Control against Time-Varying Faults via a New Sliding Mode Observer Method. Symmetry 2021, 13, 1615. https://doi.org/10.3390/sym13091615
Zhang Y, Nie Y, Chen L. Adaptive Fuzzy Fault-Tolerant Control against Time-Varying Faults via a New Sliding Mode Observer Method. Symmetry. 2021; 13(9):1615. https://doi.org/10.3390/sym13091615
Chicago/Turabian StyleZhang, Yi, Yingying Nie, and Liheng Chen. 2021. "Adaptive Fuzzy Fault-Tolerant Control against Time-Varying Faults via a New Sliding Mode Observer Method" Symmetry 13, no. 9: 1615. https://doi.org/10.3390/sym13091615
APA StyleZhang, Y., Nie, Y., & Chen, L. (2021). Adaptive Fuzzy Fault-Tolerant Control against Time-Varying Faults via a New Sliding Mode Observer Method. Symmetry, 13(9), 1615. https://doi.org/10.3390/sym13091615






