Prediction of Partition Coefficients in SDS Micelles by DFT Calculations
Abstract
:1. Introduction
2. Materials and Methods
2.1. Apparatus and Conditions
2.2. Determination of Partition Coefficients in SDS Micelles
2.3. Computational Determination of Partition Coefficients
2.4. Statistical Analysis
3. Results and Discussion
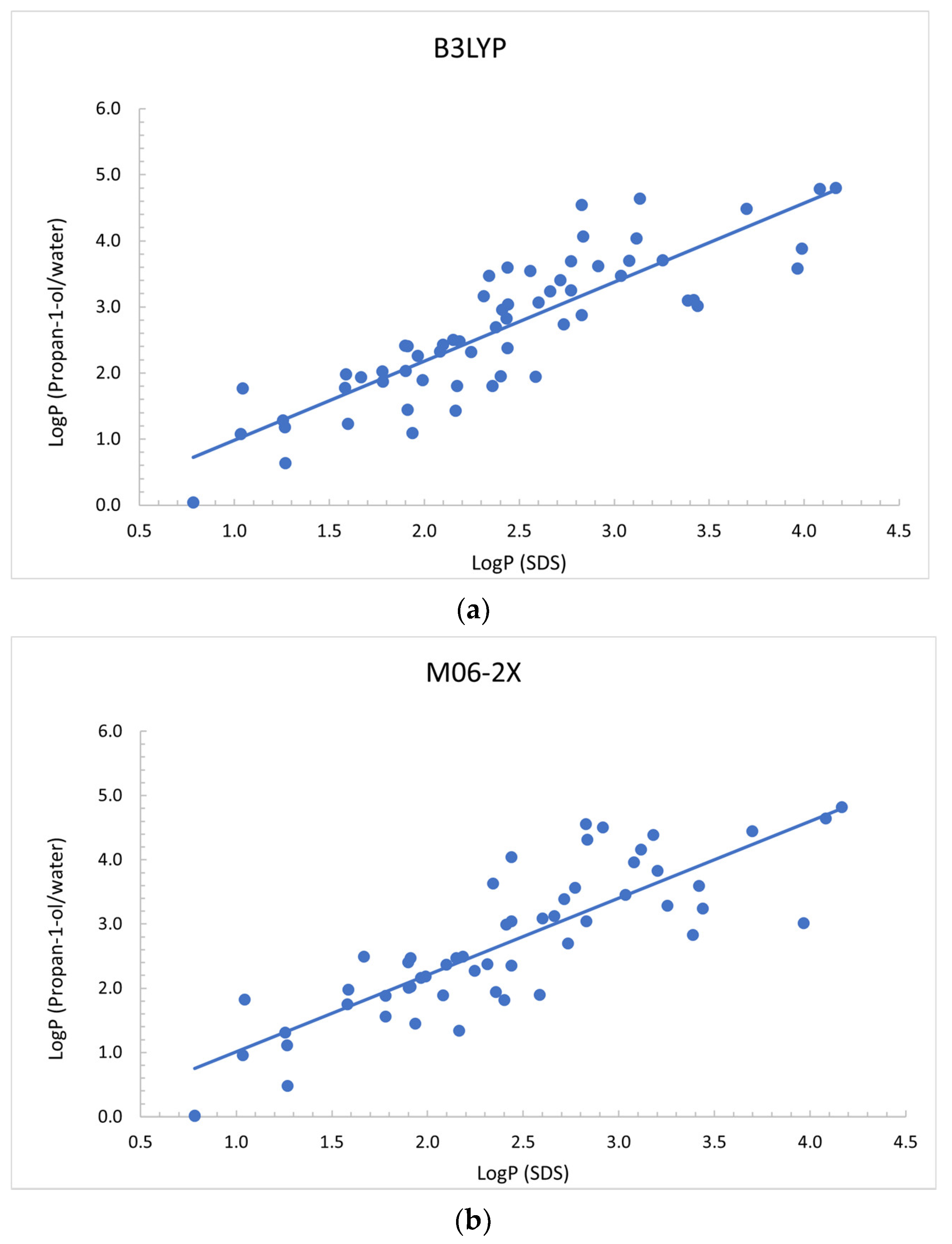
3.1. Identification of Best Solvents for Prediction of Log P in SDS Micelles
3.2. Comparison with Experimental Octanol/Water Partition Coefficients
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bannan, C.C.; Calabró, G.; Kyu, D.Y.; Mobley, D.L. Calculating Partition Coefficients of Small Molecules in Octanol/Water and Cyclohexane/Water. J. Chem. Theory Comput. 2016, 12, 4015–4024. [Google Scholar] [CrossRef] [Green Version]
- Amézqueta, S.; Subirats, X.; Fuguet, E.; Roses, M.; Rafols, C. Octanol-water partition constant. Liquid-Phase Extraction. In Handbooks in Separation Science; Poole, C.F., Ed.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 183–208. [Google Scholar] [CrossRef]
- Koehler, M.G.; Grigoras, S.; Dunn, W.J. The Relationship Between Chemical Structure and the Logarithm of the Partition Coefficient. Quant. Struct. Relatsh. 1988, 7, 150–159. [Google Scholar] [CrossRef]
- Schwarze, M.; Volovych, I.; Wille, S.; Mokrushina, L.; Arlt, W.; Schomacker, R. Partition Coefficients of Itaconates in Aqueous-Micellar Solutions: Measurements and Predictions with COSMO-RS. Ind. Eng. Chem. Res. 2012, 51, 1846–1852. [Google Scholar] [CrossRef]
- Fuguet, E.; Ràfols, C.; Bosch, E.; Abraham, M.H.; Rosés, M. Solute–solvent interactions in micellar electrokinetic chromatography III. Characterization of the selectivity of micellar electrokinetic chromatography Systems. J. Chromatogr. A 2002, 942, 237–248. [Google Scholar] [CrossRef]
- Fuguet, E.; Ràfols, C.; Bosch, E.; Abraham, M.H.; Rosés, M. Erratum to “Solute–solvent interactions in micellar electrokinetic chromatography. III. Characterization of the selectivity of micellar electrokinetic chromatography Systems”. J. Chromatogr. A 2009, 1216, 6877–6879. [Google Scholar] [CrossRef]
- Fuguet, E.; Ràfols, C.; Bosch, E.; Rosés, M. Characterization of the solvation properties of sodium n-dodecyl sulphate micelles in buffered and unbuffered aqueous phases by solvatochromic indicators. Langmuir 2003, 19, 55–62. [Google Scholar] [CrossRef]
- Ingram, T.; Storm, S.; Kloss, L.; Mehling, T.; Jakobtorweihen, S.; Smirnova, I. Prediction of micelle/water and liposome/water partition coefficients based on molecular dynamics simulations, COSMO-RS, and COSMOmic. Langmuir 2013, 29, 3527–3537. [Google Scholar] [CrossRef] [PubMed]
- Ritter, E.; Yordanova, D.; Gerlach, T.; Smirnova, I.; Jakobtorweihen, S. Molecular dynamics simulations of various micelles to predict micelle water partition equilibria with COSMOmic: Influence of micelle size and structure. Fluid Phase Equilibria 2016, 422, 43–55. [Google Scholar] [CrossRef]
- Yordanova, D.; Ritter, E.; Gerlach, T.; Jensen, J.H.; Smirnova, I.; Jakobtorweihen, S. Solute Partitioning in Micelles: Combining Molecular Dynamics Simulations, COSMOmic, and Experiments. J. Phys. Chem. B 2017, 121, 5794–5809. [Google Scholar] [CrossRef]
- Turchi, M.; Kognole, A.A.; Kumar, A.; Cai, Q.; Lian, G.; Mackerell, A.D. Predicting Partition Coefficients of Neutral and Charged Solutes in the Mixed SLES-Fatty Acid Micellar System. J. Phys. Chem. B 2020, 124, 1653–1664. [Google Scholar] [CrossRef]
- Nedyalkova, M.; Madurga, S.; Tobiszewski, M.; Simeonov, V. Calculating the Partition Coefficients of Organic Solvents in Octanol/Water and Octanol/Air. J. Chem. Inf. Model. 2019, 59, 2257–2263. [Google Scholar] [CrossRef] [PubMed]
- Jones, M.R.; Brooks, B.R.; Wilson, A.K. Partition coefficients for the SAMPL5 challenge using transfer free energies. J. Comput.-Aided Mol. Des. 2016, 30, 1129–1138. [Google Scholar] [CrossRef]
- Chou, J.T.; Jurs, P.C. Computer-Assisted Computation of Partition Coefficients from Molecular Structures Using Fragment Constants. J. Chem. Inf. Comput. Sci. 1979, 19, 172–178. [Google Scholar] [CrossRef]
- Ghose, A.K.; Crippen, G.M. Atomic Physicochemical Parameters for Three-Dimensional Structure-Directed Quantitative Structure-Activity Relationships I. Partition Coefficients as a Measure of Hydrophobicity. J. Comput. Chem. 1986, 7, 565–577. [Google Scholar] [CrossRef] [Green Version]
- Tielker, N.; Tomazic, D.; Eberlein, L.; Kast, S.M.; Güssregen, S. The SAMPL6 challenge on predicting octanol–water partition coefficients from EC-RISM theory. J. Comput.-Aided Mol. Des. 2020, 34, 453–461. [Google Scholar] [CrossRef] [Green Version]
- Lyubartsev, A.P.; Jacobsson, S.P.; Sundholm, G.; Laaksonen, A. Solubility of organic compounds in water/octanol systems. A expanded ensemble molecular dynamics simulation study of log P parameters. J. Phys. Chem. B 2001, 105, 7775–7782. [Google Scholar] [CrossRef]
- Hodges, G.; Eadsforth, C.; Bossuyt, B.; Bouvy, A.; Enrici, M.H.; Geurts, M.; Kotthoff, M.; Michie, E.; Miller, D.; Müller, J.; et al. A comparison of log K ow (n-octanol–water partition coefficient) values for non-ionic, anionic, cationic and amphoteric surfactants determined using predictions and experimental methods. Environ. Sci. Eur. 2019, 31, 1–18. [Google Scholar] [CrossRef]
- Klamt, A.; Eckert, F.; Reinisch, J.; Wichmann, K. Prediction of cyclohexane-water distribution coefficients with COSMO-RS on the SAMPL5 data set. J. Comput.-Aided Mol. Des. 2016, 30, 959–967. [Google Scholar] [CrossRef]
- Bannan, C.C.; Burley, K.H.; Chiu, M.; Shirts, M.R.; Gilson, M.K.; Mobley, D.L. Blind prediction of cyclohexane-water distribution coefficients from the SAMPL5 challenge. J. Comput.-Aided Mol. Des. 2016, 30, 927–944. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rustenburg, A.S.; Dancer, J.; Lin, B.; Feng, J.A.; Ortwine, D.F.; Mobley, D.L.; Chodera, J.D. Measuring experimental cyclohexane-water distribution coefficients for the SAMPL5 challenge. J. Comput.-Aided Mol. Des. 2016, 30, 945–958. [Google Scholar] [CrossRef] [Green Version]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Perspective on Foundations of Solvation Modeling: The Electrostatic Contribution to the Free Energy of Solvation. J. Chem. Theory Comput. 2008, 4, 877–887. [Google Scholar] [CrossRef] [PubMed]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. Density-Functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef] [Green Version]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef] [Green Version]
- Fuguet, E.; Ràfols, C.; Rosés, M.; Bosch, E. Critical micelle concentration of surfactants in aqueous buffered and unbuffered systems. J. Anal. Chim. Acta 2005, 548, 95–100. [Google Scholar] [CrossRef]
- Mennucci, B.; Cancès, E.; Tomasi, J. Evaluation of Solvent Effects in Isotropic and Anisotropic Dielectrics and in Ionic Solutions with a Unified Integral Equation Method: Theoretical Bases, Computational Implementation, and Numerical Applications. J. Phys. Chem. B 1997, 101, 10506–10517. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision, C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Hanwell, M.D.; Curtis, D.E.; Lonie, D.C.; Vandermeersch, T.; Zurek, E.; Hutchison, G.R. Avogadro: An advanced semantic chemical editor, visualization, and analysis platform. J. Cheminform. 2012, 4, 17. [Google Scholar] [CrossRef] [Green Version]

| Compound | Log PSDS |
|---|---|
| Ethylbenzene | 2.71 |
| Propylbenzene | 3.20 |
| Butylbenzene | 3.70 |
| 1-phenylethanone | 2.08 |
| 1-phenylpropan-1-one | 2.41 |
| 1-phenylbutan-1-one | 2.77 |
| 1-phenylpentan-1-one | 3.18 |
| 1-phenylheptan-1-one | 4.17 |
| Furan | 1.26 |
| 2-nitroaniline | 2.16 |
| 2,3-benzofuran | 2.44 |
| Diphenylmethanone | 3.25 |
| Benzamide | 1.60 |
| 4-chloroaniline | 2.18 |
| 2,3-dimethylphenol | 2.31 |
| Naphthalen-2-ol | 2.73 |
| 4-aminobenzamide | 1.27 |
| 3-methylphenol | 1.97 |
| 2,4-dimethylphenol | 2.38 |
| Naphthalene | 3.04 |
| Pyrimidine | 0.78 |
| Benzaldehyde | 1.90 |
| 3-chloroaniline | 2.15 |
| Pyrrole | 1.04 |
| 3-nitroaniline | 1.91 |
| 4-chlorophenol | 2.25 |
| Phenol | 1.58 |
| Methylbenzoate | 2.40 |
| Bromobenzene | 2.60 |
| 1,4-xylene | 2.77 |
| Benzene-1,3-diol | 1.27 |
| 2-methylaniline | 1.90 |
| 1-methoxy-2-nitrobenzene | 2.17 |
| N-4-chlorophenylacetamide | 2.43 |
| Aniline | 1.59 |
| Nitrobenzene | 1.99 |
| Chlorobenzene | 2.44 |
| N-phenylacetamide | 1.78 |
| 4-nitroaniline | 1.94 |
| Anisole | 2.10 |
| Benzonitrile | 1.91 |
| 1-ethyl-4-nitrobenzene | 2.83 |
| 1-methoxy-4-nitrobenzene | 2.36 |
| N,N-diethyl-4-nitroaniline | 3.42 |
| Benzyl benzoate | 3.96 |
| Caffeine | 1.67 |
| Corticosterone | 3.99 |
| Cortisone | 3.39 |
| β-Estradiol | 4.08 |
| Estriol | 3.12 |
| Cortisol | 3.44 |
| Hydroquinone | 1.03 |
| Quinoline | 2.59 |
| Atrazine | 2.84 |
| Diuron | 2.92 |
| Fluometuron | 2.56 |
| Isoproturon | 2.83 |
| Linuron | 3.08 |
| Metobromuron | 2.66 |
| Monuron | 2.34 |
| Metoxuron | 2.44 |
| Phenyl urea | 1.78 |
| Propazine | 3.13 |
| Solvent | Dielectric Constant | R2 B3LYP | R2 M06-2X |
|---|---|---|---|
| Heptane | 1.92 | 0.04 | 0.07 |
| Cyclohexane | 2.02 | 0.03 | 0.06 |
| N-dodecane | 2.03 | 0.08 | 0.04 |
| Pyridine | 2.35 | 0.20 | 0.30 |
| Diethyl sulfide | 6.14 | 0.12 | 0.22 |
| Acetic acid | 6.2 | 0.03 | 0.09 |
| Decan-1-ol | 7.53 | 0.26 | 0.34 |
| Octanol | 10.3 | 0.40 | 0.48 |
| Propan-2-ol | 19.26 | 0.68 | 0.68 |
| Acetone | 20.16 | 0.19 | 0.35 |
| Propan-1-ol | 21.03 | 0.73 | 0.69 |
| Methanol | 32.61 | 0.71 | 0.62 |
| 1,2-ethane diol | 40.24 | 0.12 | 0.26 |
| Dimethyl sulfoxide | 46 | 0.13 | 0.23 |
| Formic acid | 58 | 0.06 | 0.10 |
| Solvent | B3LYP | M06-2X |
|---|---|---|
| Propan-1-ol | y = 1.2 x − 0.2 (1.0, 1.4) (−0.7, 0.3) | y = 1.2 x − 0.2 (1.0, 1.4) (−0.7, 0.4) |
| Propan-2-ol | y = 1.1 x − 0.0 (0.9, 1.4) (−0.5, 0.6) | y = 1.3 x − 0.3 (1.0, 1.5) (−0.9, 0.3) |
| Methanol | y = 1.2 x − 0.2 (1.0, 1.4) (−0.7, 0.3) | y = 1.3 x − 0.4 (1.0, 1.6) (−1.1, 0.3) |
| Density Functinal | Slope | R2 | MAE | RMSE | MSE |
|---|---|---|---|---|---|
| B3LYP | 0.67 (0.52, 0.82) | 0.60 | 0.58 | 0.79 | 0.63 |
| M06-2X | 0.71 (0.57, 0.86) | 0.65 | 0.64 | 0.79 | 0.63 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saranjam, L.; Fuguet, E.; Nedyalkova, M.; Simeonov, V.; Mas, F.; Madurga, S. Prediction of Partition Coefficients in SDS Micelles by DFT Calculations. Symmetry 2021, 13, 1750. https://doi.org/10.3390/sym13091750
Saranjam L, Fuguet E, Nedyalkova M, Simeonov V, Mas F, Madurga S. Prediction of Partition Coefficients in SDS Micelles by DFT Calculations. Symmetry. 2021; 13(9):1750. https://doi.org/10.3390/sym13091750
Chicago/Turabian StyleSaranjam, Leila, Elisabet Fuguet, Miroslava Nedyalkova, Vasil Simeonov, Francesc Mas, and Sergio Madurga. 2021. "Prediction of Partition Coefficients in SDS Micelles by DFT Calculations" Symmetry 13, no. 9: 1750. https://doi.org/10.3390/sym13091750
APA StyleSaranjam, L., Fuguet, E., Nedyalkova, M., Simeonov, V., Mas, F., & Madurga, S. (2021). Prediction of Partition Coefficients in SDS Micelles by DFT Calculations. Symmetry, 13(9), 1750. https://doi.org/10.3390/sym13091750










