The Reactivity of Human and Equine Estrogen Quinones towards Purine Nucleosides

Abstract

Conjugated estrogen medicines, which are produced from the urine of pregnant mares for the purpose of menopausal hormone replacement therapy (HRT), contain the sulfate conjugates of estrone, equilin, and equilenin in varying proportions. The latter three steroid sex hormones are highly similar in molecular structure as they only differ in the degree of unsaturation of the sterane ring “B”: the cyclohexene ring in estrone (which is naturally present in both humans and horses) is replaced by more symmetrical cyclohexadiene and benzene rings in the horse-specific (“equine”) hormones equilin and equilenin, respectively. Though the structure of ring “B” has only moderate influence on the estrogenic activity desired in HRT, it might still significantly affect the reactivity in potential carcinogenic pathways. In the present theoretical study, we focus on the interaction of estrogen orthoquinones, formed upon metabolic oxidation of estrogens in breast cells with purine nucleosides. This multistep process results in a purine base loss in the DNA chain (depurination) and the formation of a “depurinating adduct” from the quinone and the base. The point mutations induced in this manner are suggested to manifest in breast cancer development in the long run. We examine six reactions between deoxyadenosine and deoxyguanosine as nucleosides and estrone-3,4-quinone, equilin-3,4-quinone, and equilenin-3,4-quinone as mutagens. We performed DFT calculations to determine the reaction mechanisms and establish a structure–reactivity relationship between the degree of unsaturation of ring “B” and the expected rate of DNA depurination. As quinones might be present in the cytosol in various protonated forms, we introduce the concept of “effective barriers” to account for the different reactivity and different concentrations of quinone derivatives. According to our results, both equine estrogens have the potential to facilitate depurination as the activation barrier of one of the elementary steps (the initial Michael addition in the case of equilenin and the rearomatization step in the case of equilin) significantly decreases compared to that of estrone. We conclude that the appearance of exogenous equine estrogen quinones due to HRT might increase the risk of depurination-induced breast cancer development compared to the exposure to endogenous estrone metabolites. Still, further studies are required to identify the rate-limiting step of depurination under intracellular conditions to reveal whether the decrease in the barriers affects the overall rate of carcinogenesis.

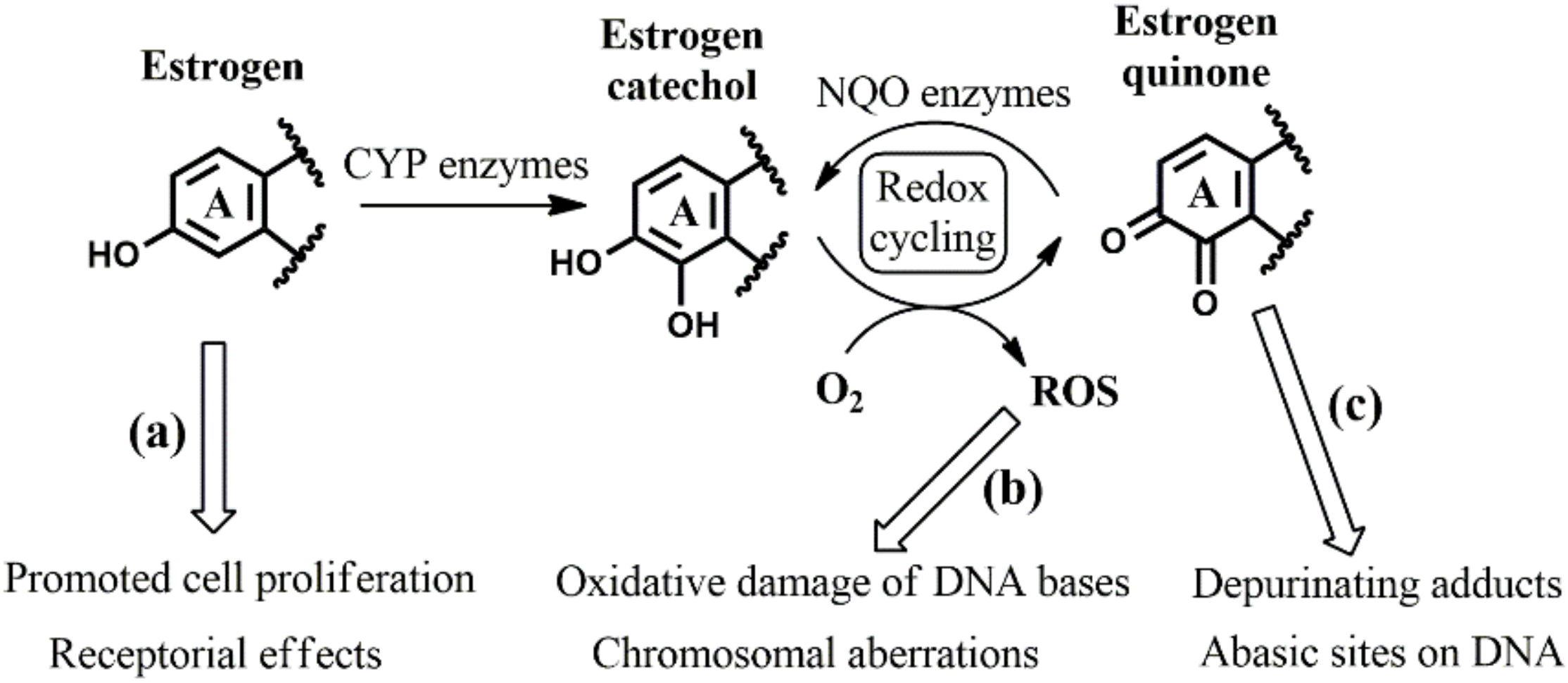
1. Introduction

Estrogens are essential female sex hormones; however, several clinical trials have demonstrated that long-term exposure to estrogens considerably increases the chance of breast cancer development [1,2]. Apart from the cases of natural early menarche or late menopause, this risk factor usually arises due to the application of estrogen hormone replacement therapy (HRT) [3]. As striking evidence for the role of HRT in carcinogenesis, a sudden 6.7% decrease was observed in the incidence rate of breast cancer in the USA following a drop in HRT use in 2002 [4]. Still, the molecular mechanisms behind HRT-induced cancer formation are not fully understood. As HRT medicines commonly contain non-human estrogens, it is a fundamental question whether these components pose an increased risk compared to human-like hormones or whether the undesired side effects of the therapy can simply be traced back to prolonged exposure to estrogens in general [5].

One of the most popular HRT medications is conjugated equine estrogens (CEEs), which are isolated from the urine of pregnant mares and sold under the brand name “Premarin” among others. CEEs consist of the sulfate conjugates of horse-specific “equine estrogens”, equilin (Eq), and equilenin (Eqn), besides those of estrone (E), which is an endogenous estrogen in both humans and horses [6]. The latter three estrogens (referred to generally as “Ex” in the following paragraphs) possess a highly similar molecular structure as they only differ in the degree of unsaturation of ring “B”: the cyclohexene ring of estrone is replaced by more symmetrical cyclohexadiene and benzene rings in equilin and equilenin, respectively (Figure 1). Though Eq and Eqn retain the hormonal activity of E in humans [7,8], this fact does not exclude the possibility of ring-“B”-dependent reactivities on potential carcinogenic pathways [9].

To date, three possible sources of carcinogenesis have been identified in the metabolism of estrogens such as E, Eq, and Eqn (Figure 2). Firstly, the estrogen hormones themselves may induce cancer development by promoting cell proliferation (and hence increase the number the genomic mutations during DNA replication) [10,11] or by acting on certain estrogen receptors that play a role in controlling signal transduction outside the nucleus [12,13] (Figure 2a). Secondly, redox cycling between catechol and quinone metabolites leads to the generation of reactive oxygen species (ROS) [9,14,15,16,17], which are harmful to a variety of cell components, including DNA (Figure 2b). Thirdly, estrogen quinones can also directly react with DNA, resulting in purine base loss from the affected strand (Figure 2c) [18,19,20,21]. In this work, we concentrate on this latter aspect.

It is known that 3,4-orthoquinones (marked as Ex-Q(H) in Figure 3, where Ex is a general term referring to E, Eq, or Eqn, while Q indicates the 3,4-quinone form and “(H)” highlights the presence of a H atom on C1), formed upon the metabolic oxidation of estrone, equilin, and equilenin [21,22,23], are able to cross the nuclear membrane through either passive diffusion or active transport mediated by estrogen receptor alpha [17,24]. In the cell nucleus, these quinones are apt to attack the nucleophilic sites of deoxyadenosine (AR) and deoxyguanosine (GR). This induces a multistep reaction, ending up in the cleavage of the glycosidic C-N bond, which yields a “depurinating adduct”, Ex-QH₂-G or Ex-QH₂-A, and an abasic site in the DNA chain (Figure 3, right) [18]. The latter might be readily converted to a point mutation site by false DNA repair. In the long run, the accumulation of such mutations leads to carcinogenesis.

The importance of this pathway is highlighted by both in vitro and in vivo experiments. For example, the treatment of rat or mouse mammary glands with E-Q(H) resulted in potentially carcinogenic DNA mutations within hours, which was traced back to error-prone base excision repair of the abasic sites formed upon depurination [21]. Even more strikingly, depurinating adducts can be used as tumor biomarkers in humans; namely, increased levels of E-QH₂-G and E-QH₂-A were observed in the urine and serum of breast cancer patients and women at high risk of breast cancer [20].

In order to understand the effect of additional double-bond(s) in ring “B”, the reactivity of estrone, equilin, and equilenin needs to be compared in each elementary step of purine base loss. Such an analysis is difficult to achieve experimentally, as only macroscopic quantities (such as the time course of adduct formation) can be determined in this way; moreover, precise measurements can only be performed on simplified model systems [9,19,25] where the reaction conditions (e.g., pH, distribution of protonated/deprotonated species, reactant concentrations) might significantly deviate from those peculiar to an actual breast cell nucleus. Computational chemistry, on the contrary, enables the detailed examination of any reaction sequence at the level of elementary steps, which has been proven to be especially useful in studying complex reaction mechanisms [26,27,28,29], including biochemical transformations [30,31].

In this work, we use density functional theory to explore the elementary reactions leading to a depurination event. We explore the effect of ring “B” unsaturations on barrier height using the truncated models of estrogen-3,4-quinones and purine nucleosides (Figure 4) as initial molecules. (We note that the modeling of the DNA strands by separated nucleosides is a commonly applied practice in both the experimental and theoretical research of carcinogenesis [18,19]. There is strong experimental evidence that the reactivity of nucleosides closely resembles that of DNA [25].) Altogether, six reactions were studied by pairing each estrogen model (E’-Q(H), Eq’-Q(H), and Eqn’-Q(H)) to each nucleoside model (GR’ and AR’). In the cytosol, quinones might be present in various protonated forms. In order to take the effect of protonation into account, we introduced the concept of effective barriers. Finally, we compared the carcinogenic potential of human and equine estrogens on the quinone-induced depurination pathway.

2. Computational Methods

All calculations were carried out using the Gaussian 16 program [32]. Sample input files and the detailed description of the calculations described below can be found in the Supplementary Materials.

2.1. Molecular Gibbs Free Energies

The geometry of the intermediates of depurination was optimized (in all protonation states conceivable in the intracellular environment) at the B3LYP/6-311++G** level [33,34], applying Grimme’s “D3(BJ)” empirical dispersion correction [35] in all cases. The hydration sphere of molecules was simulated using the CPCM solvent model [36].

Harmonic frequency calculations and thermochemical analyses at 25 °C and 1 atm were performed at the same level of theory. Gibbs free energies (G) presented in the manuscript include all thermochemical corrections of the electronic energy. The absence of imaginary frequencies was confirmed in the computed vibrational spectrum of all intermediates (transition states were characterized by one imaginary frequency).

We note that although biochemical reactions in humans occur at 37 °C instead 25 °C, the compatibility to the experimental reference pK_a data described in the next subsection requires setting T = 25 °C in the computations. Still, we confirmed that the activation barriers and the net Gibbs free energy differences of chemical reactions are practically independent of the temperature in the narrow range of 25–37 °C (see Table S17 in the Supplementary Materials).

2.2. Acidity Constants and the Fraction of the Non-Dominant Protonation State

In aqueous solutions, the equilibrium state between the conjugate acid and the conjugate base form of a given intermediate (e.g., the equilibrium of OH ⇌ O⁻ + H⁺ on a hydroxy group) is reached practically instantaneously. This effect was taken into account by the acidity constant, which determines the protonated and deprotonated fractions at the pH of the cell nucleus, which is estimated to be 7.2 [37].

After optimizing the intermediates in their conjugated acid/base forms, the pK_a values characterizing the basicity of the dominant form (referred to as “Int” below) were calculated based on the following chemical equations:

IntH⁺+Ref_a → Int + Ref_aH⁺  ΔG_a = G(Int) + G(Ref_aH⁺) − G(IntH⁺) − G(Ref_a)

where Ref_aH⁺ denotes a reference acid with an experimentally determined pK_a value, which is close in molecular structure to a given IntH⁺ form. (These acids, selected for the characterization of each intermediate, are listed in Section 2 of the Supplementary Materials, along with the literature pK_a values at 25 °C.)

By definition, the computable Gibbs free energy changes of ΔG_a are related to the known acidities (pK_a(Ref_aH⁺)) and to the acidities to be determined (pK_a(IntH⁺)) as:

$$\Delta G_a=RTln\left({10}^{-p{K}_a\left(\mathit{R}\mathit{e}{\mathit{f}}_{\mathit{a}}{\mathit{H}}^{\mathbf{+}}\right)}\right)-RTln\left({10}^{-p{K}_a\left(\mathit{I}\mathit{n}\mathit{t}{\mathit{H}}^{\mathbf{+}}\right)}\right)$$

Substituting the values of the universal gas constant (R = 0.001986 kcal/molK) and the standard temperature (T = 298.15 K) to the equations above gives

$$p{K}_a\left(\mathit{I}\mathit{n}\mathit{t}{\mathit{H}}^{\mathbf{+}}\right)=p{K}_a\left(\mathit{R}\mathit{e}{\mathit{f}}_{\mathit{a}}{\mathit{H}}^{\mathbf{+}}\right)+0.732 \Delta G_a$$

where the Gibbs free energies are to be substituted in kcal/mol unit.

Having the proper acidity constant at hand, we can obtain the fraction of the protonated IntH⁺ relative to the most abundant Int at pH = 7.2. By definition, the acidity constant (K_a) depends on the fraction to be determined (x_prot) as:

$$K_a\left(\mathit{I}\mathit{n}\mathit{t}{\mathit{H}}^{\mathbf{+}}\right)={10}^{-p{K}_a\left(\mathit{I}\mathit{n}\mathit{t}{\mathit{H}}^{\mathbf{+}}\right)}=\frac{\left[{\mathit{H}}^{\mathbf{+}}\right]\left[\mathit{I}\mathit{n}\mathit{t}\right]}{\left[\mathit{I}\mathit{n}\mathit{t}{\mathit{H}}^{\mathbf{+}}\right]}=\frac{{10}^{-7.2}}{x_{prot}}$$

which gives

$$x_{prot}=\frac{\left[\mathit{I}\mathit{n}\mathit{t}{\mathit{H}}^{\mathbf{+}}\right]}{\left[\mathit{I}\mathit{n}\mathit{t}\right]}={10}^{p{K}_a\left(\mathit{I}\mathit{n}\mathit{t}{\mathit{H}}^{\mathbf{+}}\right)-7.2}$$

We also note that the above formula can be extended to multiply protonated species. For instance, the fraction of a doubly protonated form ($x_{2prot}$) can be written as:

$$x_{2prot}=\frac{\left[\mathit{I}\mathit{n}\mathit{t}{\mathit{H}}_{\mathbf{2}}^{\mathbf{2}\mathbf{+}}\right]}{\left[\mathit{I}\mathit{n}\mathit{t}\right]}=\frac{\left[\mathit{I}\mathit{n}\mathit{t}{\mathit{H}}_{\mathbf{2}}^{\mathbf{2}\mathbf{+}}\right]}{\left[\mathit{I}\mathit{n}\mathit{t}{\mathit{H}}^{\mathbf{+}}\right]}\frac{\left[\mathit{I}\mathit{n}\mathit{t}{\mathit{H}}^{\mathbf{+}}\right]}{\left[\mathit{I}\mathit{n}\mathit{t}\right]}=\left({10}^{p{K}_a\left(\mathit{I}\mathit{n}\mathit{t}{\mathit{H}}_{\mathbf{2}}^{\mathbf{2}\mathbf{+}}\right)-7.2}\right)\left({10}^{p{K}_a\left(\mathit{I}\mathit{n}\mathit{t}{\mathit{H}}^{\mathbf{+}}\right)-7.2}\right)$$

2.3. Activation Gibbs Free Energies (Barriers)

Activation Gibbs free energies (ΔG^‡) were computed based on the canonical transition state theory. The geometry of transition states (TSs) was optimized by searching for first-order saddle points on the potential energy surface at the level of the theory described in Section 2.1. The presence of exactly one imaginary vibrational frequency, corresponding to the reaction coordinate of interest, was confirmed in all cases. The value of activation Gibbs free energy was obtained by subtracting the molecular Gibbs free energy of the initial molecule(s) from that of the transition state:

ΔG^‡ = G(TS) − Σ G(initial molecules)

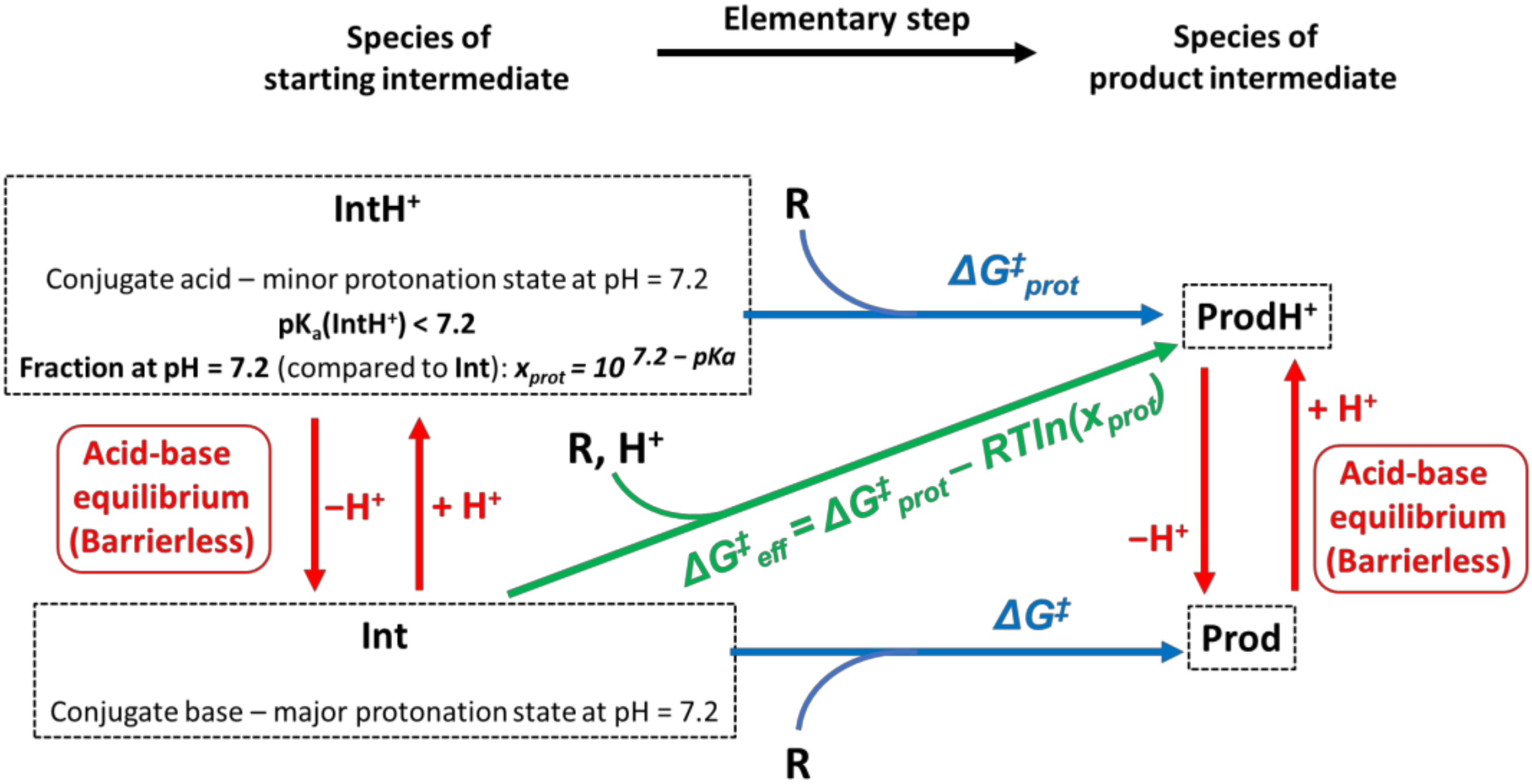
2.4. Effective Activation Gibbs Free Energies (Effective Barriers)

The concept of “effective barriers” is based on the Eyring-Polányi equation [38], which states that the reaction rate (r) of a given elementary step depends exponentially on the activation of Gibbs free energy:

$$r=A{e}^{-\frac{\Delta G^{‡}}{RT}}\left[\mathit{I}\mathit{n}\mathit{t}\right]\left[\mathit{R}\right]$$

where A is a temperature-dependent but otherwise universal pre-exponential factor, while [Int] and [R] refer to the molar concentration of the reacting intermediate and that of its reaction partner (if applicable), respectively.

In the case of the alternative route, where the protonated form of a given “Int” reacts with the same partner (or decays unimolecularly, which mathematically corresponds to [R] = 1) through a barrier of $\Delta G^{‡}{}_{prot}$, the rate can be expressed as:

$$\begin{gathered} r_{prot}=A{e}^{-\frac{\Delta G^{‡}{}_{prot}}{RT}}\left[\mathit{I}\mathit{n}\mathit{t}{\mathit{H}}^{+}\right]\left[\mathit{R}\right]=A{e}^{-\frac{\Delta G^{‡}{}_{prot}}{RT}}{x}_{prot}\left[\mathit{I}\mathit{n}\mathit{t}\right]\left[\mathit{R}\right]=A{e}^{-\frac{\Delta G_{prot}^{‡}}{RT}}{e}^{\frac{RTln\left(x_{prot}\right)}{RT}}\left[\mathit{I}\mathit{n}\mathit{t}\right]\left[\mathit{R}\right] \\ =A{e}^{-\frac{\Delta G^{‡}{}_{eff, prot}}{RT}}\left[\mathit{I}\mathit{n}\mathit{t}\right]\left[\mathit{R}\right] \end{gathered}$$

That is, an effective activation barrier of

$$\Delta G^{‡}{}_{eff, prot}=\Delta G^{‡}{}_{prot}-RTln\left(x_{prot}\right)$$

can be defined, which can be directly compared to the $\Delta G^{‡}$ computed for the reaction with the dominant “Int” species. (Roughly speaking, the term $-RTln\left(x_{prot}\right)$ can be grasped as the Gibbs free energy level of IntH⁺ over Int at the considered physiological pH.)

3. Results and Discussion

First, we are going to discuss the elementary steps of depurination, followed by the introduction of the concept of “effective barriers”, which enables us to take into account the reactivity and relative abundance of variously protonated quinones. Afterward, the effect of ring “B” will be discussed on the various elementary steps of the depurination reaction. Finally, we conclude on the relative carcinogenic potential of E, Eq, and Eqn metabolites based on our findings.

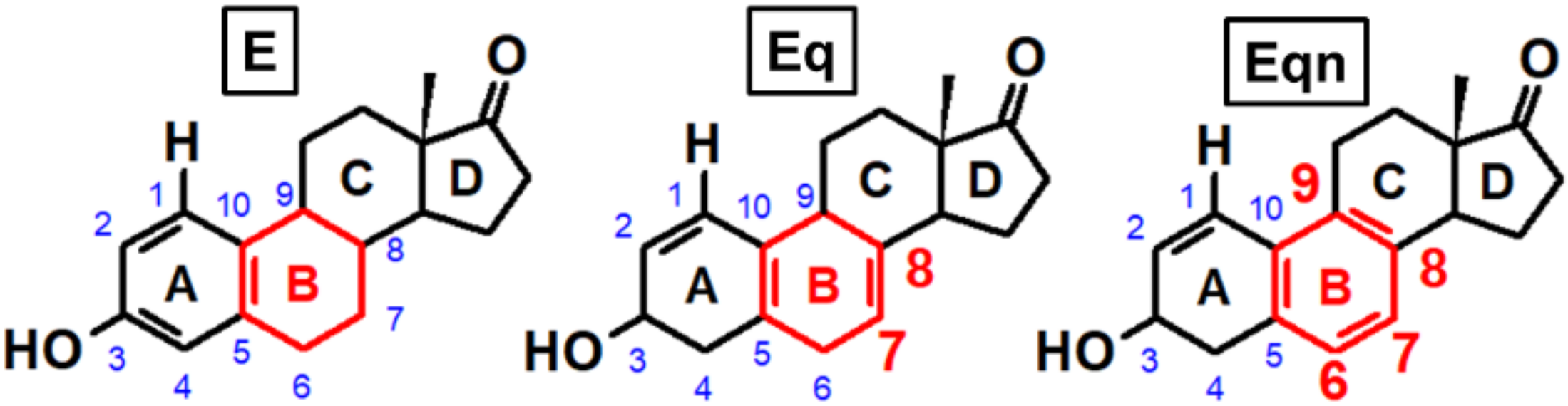
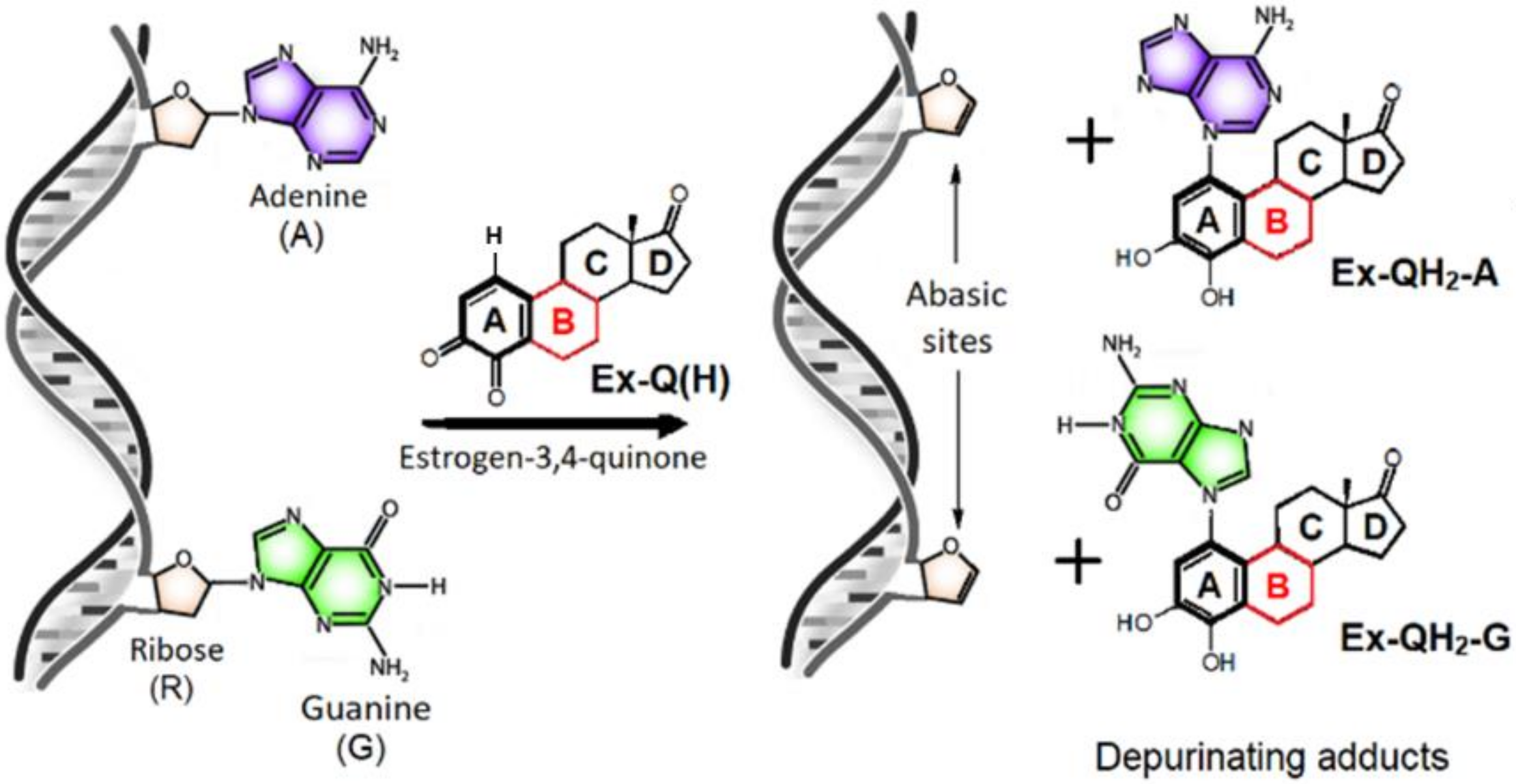
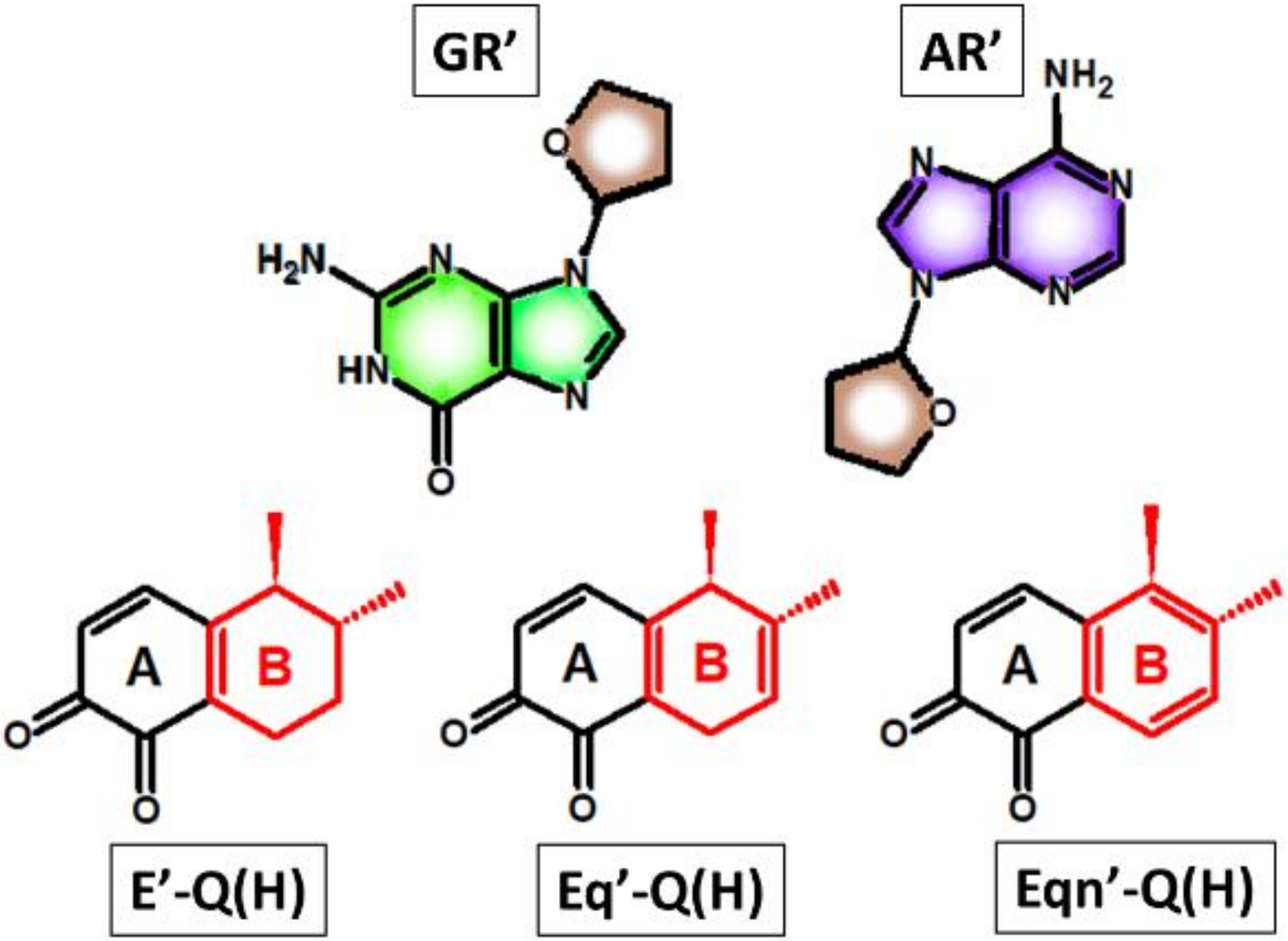
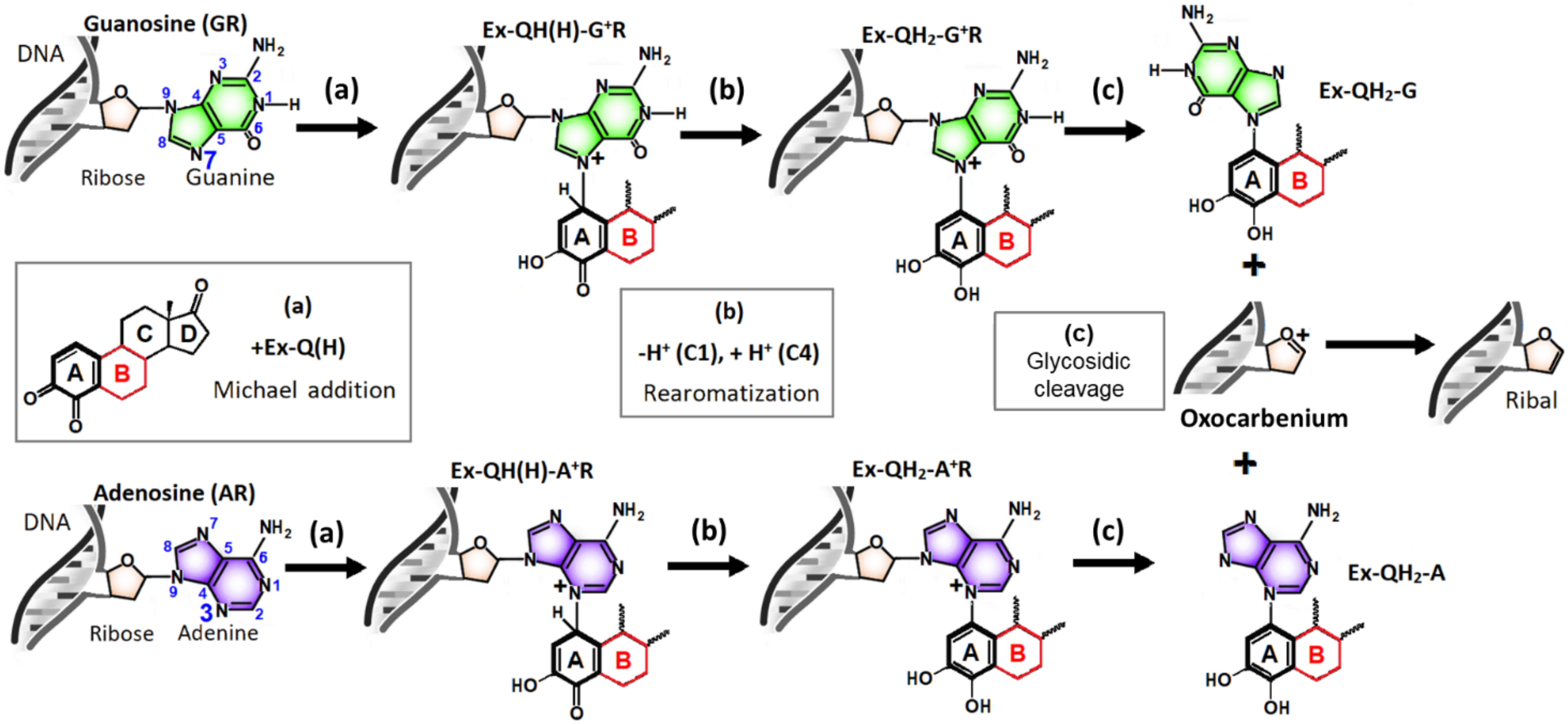
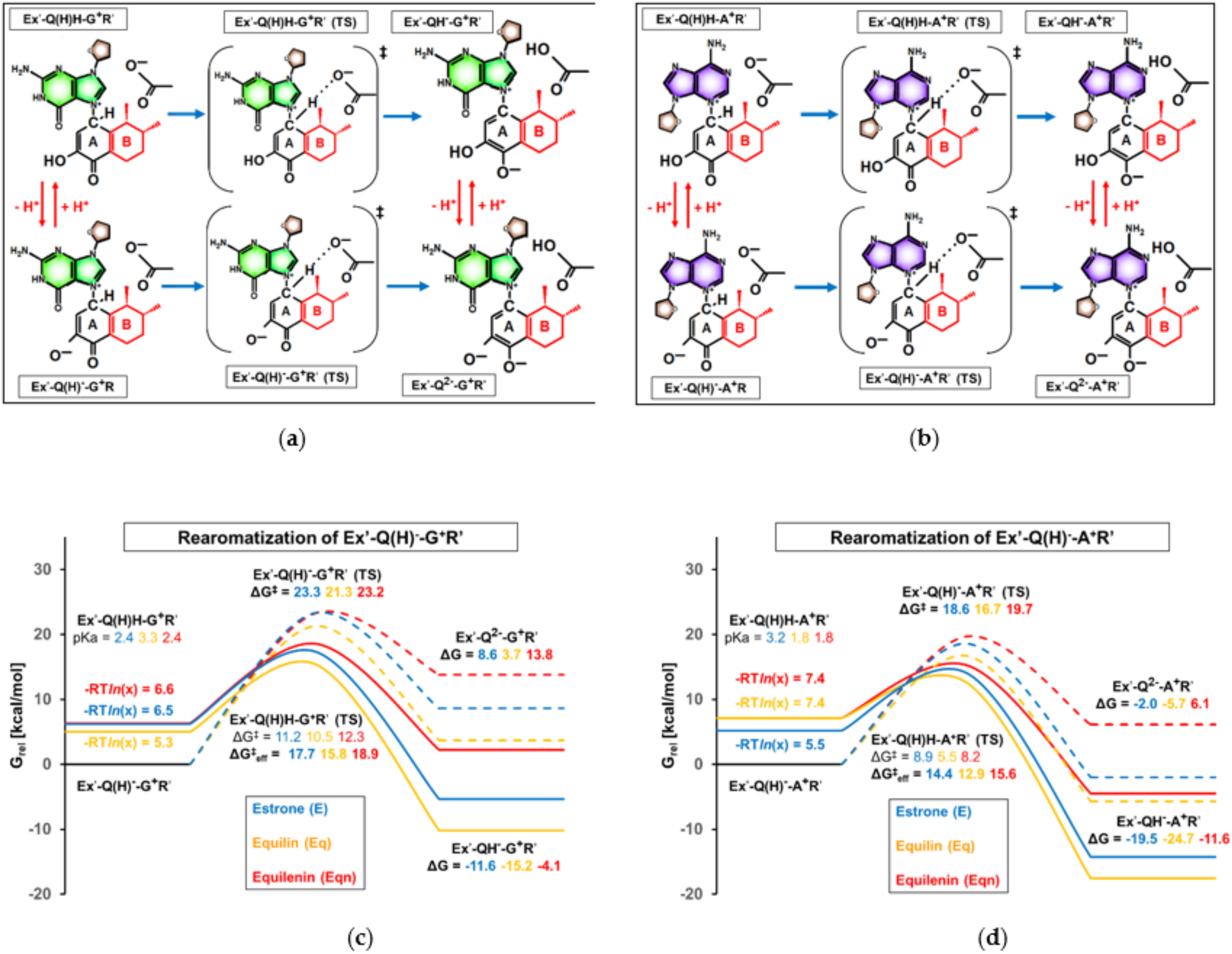
3.1. Identifying the Elementary Steps of Depurination

We relied on previous mechanistic studies [18,19] when drawing the sequence of elementary reactions to be investigated. Accordingly, the first step of the depurination process is a Michael addition, where a lone electron pair of the purine base attacks the estrogen-3,4-quinone at the C1 atom, which creates a covalent bond between C1 and N7 in the case of guanosine or between C1 and N3 in the case of adenosine (Figure 5a). In the second step, a proton is released from C1 to a Brønsted base, which restores the aromaticity in ring “A” (“rearomatization”, Figure 5b). Finally, the glycosidic C–N bond spontaneously breaks, which gives the “depurinating adduct” and a deoxyribose oxocarbenium ring [39] as products (“glycosidic cleavage”, Figure 5c). (The oxocarbenium is subsequently converted to ribal in the DNA chain; however, these final steps proceed independently of the estrogen metabolite reactant.)

By experiments, it is not possible to determine with complete certainty which elementary step serves as a bottleneck in vivo. Even though the loss of deoxyribose from guanosine adducts was found to be rate-limiting in several in vitro model studies [19,25,40,41], it is questionable as to what extent the applied reaction conditions distort the relation among the rates of individual steps. The main issue is the concentration of the reacting species (e.g., the quinone or base partner required for rearomatization), which is somehow arbitrarily set in the referenced experiments as the actual value in the vicinity of the DNA of a breast cell is challenging to estimate. Thus, as the rate-determining step is uncertain and may also vary according to current intracellular concentrations, the effect of unsaturations needs to be investigated in all three elementary reactions. Herein, we calculate the dependence of the activation Gibbs free energies (ΔG^‡; also referred to as “barriers” in the following paragraphs) on the structure of ring “B” and the purine base.

3.2. Accounting for the Distribution of Protonation States: Effective Activation Gibbs Free Energies

An additional issue in the theoretical investigation of carcinogenesis is the hitherto unexplored role of the protonation–deprotonation equilibria of the intermediates shown in Figure 5. In aqueous solutions, the state of dynamic equilibrium between conjugate acid and conjugate base is reached practically instantaneously on functional groups integrated in the hydrogen bond network of water (such as OH ⇌ O⁻ + H⁺ on aromatic hydroxy groups or ≡N + H⁺ ⇌ ≡N-H⁺ on nitrogen atoms possessing a lone electron pair), which then determines the accessibility of a given protonation state at the physiological pH of 7.2. (We note here that the proton loss from C1 required from rearomatization (Figure 5b) cannot be handled by the aforementioned instantaneous equilibrium model as a -C-H unit does not act as a hydrogen bond donor).

As illustrated by Figure 6, it is conceivable that the activation barrier of a given reaction is significantly lower, starting from a non-dominant protonation state, which is typically a conjugate acid (see the frame of IntH⁺ in Figure 6 as an example). In such cases, the kinetics are not only influenced by the barrier itself but also by the fraction of the more reactive protonation state at the nuclear pH of 7.2, which is determined by the acidity constant (pK_a). (Without going into mathematical details, we would like to note here that in experimental mechanistic studies conducted at pH = 4 [18,19,25,40], the relative abundance of protonated forms is artificially high, which should be kept in mind when interpreting the results.) In order to be able to compare the reaction routes starting from different protonation states, effective activation Gibbs free energies ($\Delta G^{‡}{}_{eff}$) were calculated, which take both the barrier and the fraction of the protonated species ($x_{prot}$) into account:

$$\Delta G^{‡}{}_{eff}=\Delta G^{‡}{}_{prot}-RTln\left(x_{prot}\right)$$

where $\Delta G^{‡}{}_{prot}$ stands for the activation Gibbs free energy of the transformation of the non-dominant conjugate acid species, while R, T and $x_{prot}$ denote the universal gas constant and the temperature, respectively. The derivation of the formula and the mathematical relation between acidity (pK_a) and fraction ($x_{prot}$) can be found in the section on computational methods.

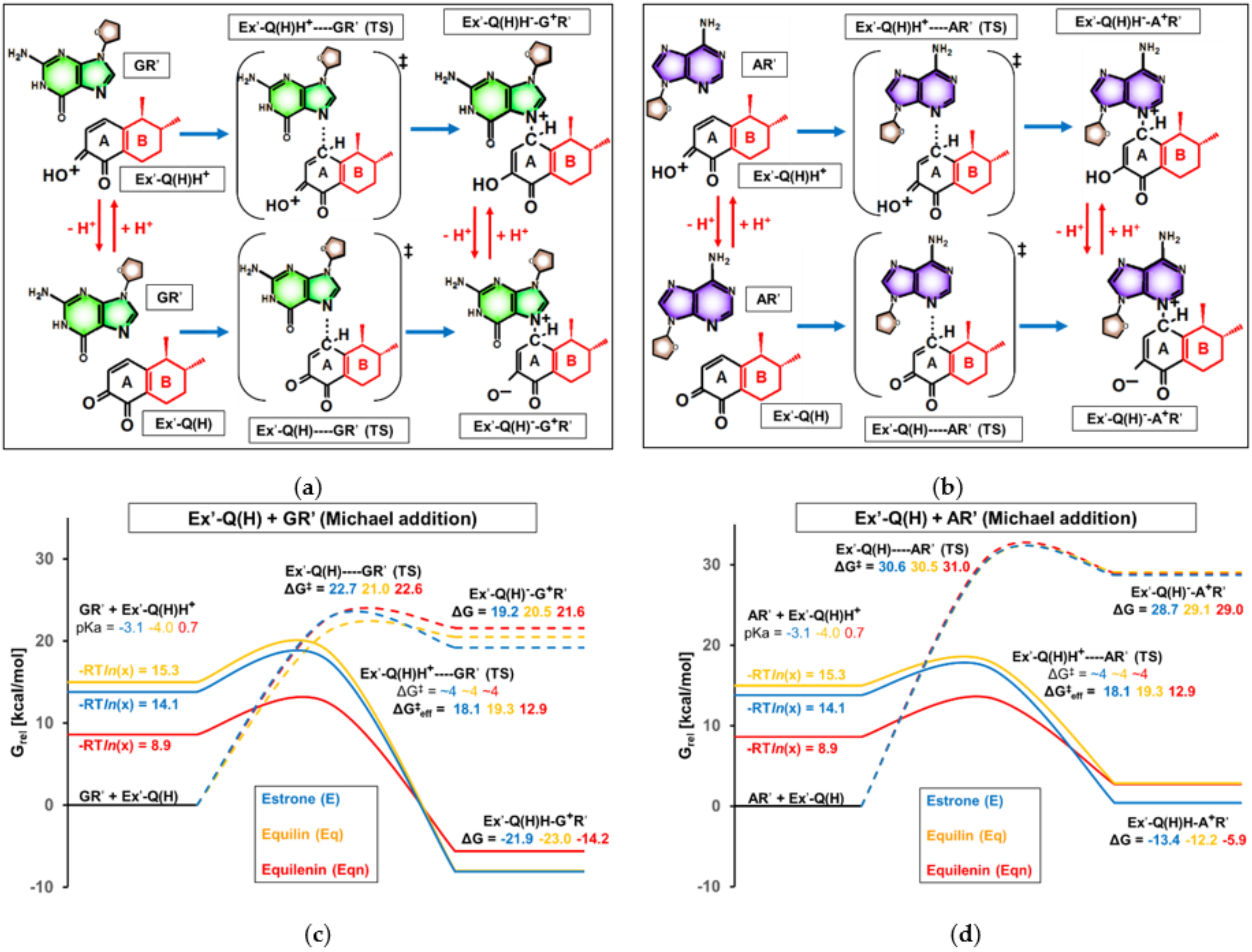
3.3. Effect of Ring “B” on Michael Addition

The process of depurination is initiated by the electrophilic attack of estrogen-3,4-quinone on a guanosine or adenosine site, leading to the formation of a covalent bond between the C1 atom of ring “A” and one of the nitrogen atoms of the purine base. The possible scenarios of this Michael addition step, along with the nomenclature of the involved species and transition states, are depicted in Figure 7a (with guanosine as the base) and Figure 7b (for adenosine as the base). The change in Gibbs free energy levels during the reaction, compared to the initial state of separated quinone and base fragments, is visualized in Figure 7c,d. In the latter figures, the effect of unsaturations on ring “B” can be observed by comparing the Gibbs free energy profiles with estrone, equilin, and equilenin quinones (indicated by blue, orange, and red colors, respectively).

At the beginning of our investigations, we calculated the barrier of the direct reaction between the quinone Ex’-Q(H) and the nucleoside GR’ or AR’ (bottom row in Figure 7a,c). (The nucleosides or nucleoside-derived molecule parts will also be referred to as BxR’ in the Discussion section, where Bx stands for any of the bases of G and A). According to the results shown in Figure 7b,d (see dashed lines), the Gibbs free energy level of transition states Ex’-Q(H)–GR’ (TS) (21–23 kcal/mol) and Ex’-Q(H)–AR’ (TS) (30–31 kcal/mol) are closely independent of ring “B”. However, considering that the high obtained $\Delta G^{‡}$ values indicate a negligible rate of direct Michael addition at biologically relevant temperatures—especially if nanomolar concentrations of estrogen metabolites are present, as expected in the breast cells of HRT patients—the latter finding becomes irrelevant. Thus, it is necessary to take into account the non-dominant protonation states of the reactants, and the barriers with E’, Eq’, and Eqn’ derivatives need to be compared in the kinetically most favorable route of the initial addition step.

In the alternative scenario of Michael addition, the C–N bond formation is preceded by the protonation of the quinone [18] (left column in Figure 7a,b). In the resulting conjugate acid, Ex’-Q(H)H⁺, the electrophilicity of C1 is considerably enhanced, as demonstrated by the resonance structures shown in Figure 8.

In contrast to neutral quinones, Ex’-Q(H)H⁺ species react in Michael addition through very low barriers, owing to the increased positive partial charge of C1. We found that the activation Gibbs free energies (ΔG^‡) required for the formation of Ex’-Q(H)H⁺---BxR’ (TS) were all below 4 kcal/mol (consult the Supplementary Materials for the obtained concrete barrier values). Since 4 kcal/mol is the Eyring-Polányi barrier for diffusion-limited bimolecular reactions in aqueous medium near room temperature [42], we concluded that practically all collisions between Ex’-Q(H)H⁺ and BxR’ lead to chemical reactions, and the latter lower barrier limit of ΔG^‡ = 4 kcal/mol was assumed in all six cases presented in Figure 7c,d.

Of course, as protonated quinones are strong Brønsted acids (pK_a < 1), their fraction in a solution of pH = 7.2 is extremely low. Nevertheless, even if the activation Gibbs free energy of 4 kcal/mol of the diffusion-limited Michael addition is adjusted according to the proportion of the conjugate acids (by the addition of -RTln(x_prot), as visualized on the left side of Figure 6c,d), the Gibbs free energy level of the positively charged transition states Ex’-Q(H)H⁺---BxR’ (TS) remains far below that of the neutral analogs. Accordingly, the effective barriers (ΔG^‡_eff) provided in Figure 7c,d determine the reaction rate of Michael addition.

The addition of one isolated double bond to ring “B” negligibly alters ΔG^‡_eff: a mere 1.2 kcal/mol increase was observed when substituting E’-Q(H) (ΔG^‡_eff = 18.1 kcal/mol for both purine bases) to Eq’-Q(H) (ΔG^‡_eff = 19.3 kcal/mol for both purine bases), which is due to the 0.9 unit difference in the pK_a values of the conjugate acids. Even if we attach importance to the latter minor differences, the equilin derivative can only be shown to be less reactive in Michael addition; that is, Eq does not pose enhanced risk relative to E in this particular step.

Equilenin-3,4-quinone, on the contrary, significantly differs from the estrone quinone in proton affinity. The pK_a value of 0.7 calculated for Eqn’-Q(H)H⁺ indicates that the proportion of the protonated species is orders of magnitude larger than in the case of the human sex hormone metabolite (pK_a = −3.1) under the same conditions. Strikingly, the increased stability of Eqn’-Q(H)H⁺ at neutral pH lowers the Gibbs free energy level by more than 5 kcal/mol compared to E’ (left column of Figure 6c,d). As a result, the Michael addition reactions with equilin-3,4-quinone proceed through a significantly smaller effective barrier (ΔG^‡_eff = 12.9 kcal/mol with both GR’ and AR’) than with the estrone metabolite (ΔG^‡_eff = 18.1 kcal/mol). Importantly, these results suggest that the occurrence of Michael addition to DNA bases is more frequent when exposed to therapeutically applied equilenin instead of an equal amount of natural estrone. Under the conditions where the initial Michael addition step determines the depurination rate, this deviation can result in the acceleration of carcinogenesis by Eqn.

The alteration of pK_a (and thus, ΔG^‡_eff) upon introducing the additional double bonds can be explained by the extensive electron delocalization on the conjugated double bond system peculiar to Eqn’-Q(H)H⁺. This unique delocalization stabilizes the protonated quinone by distributing the positive charge over rings “A” and “B”, which results in an outstandingly high proportion of Eqn’-Q(H)H⁺ at neutral pH and, hence, makes equilenin quinone especially apt to react in Michael addition.

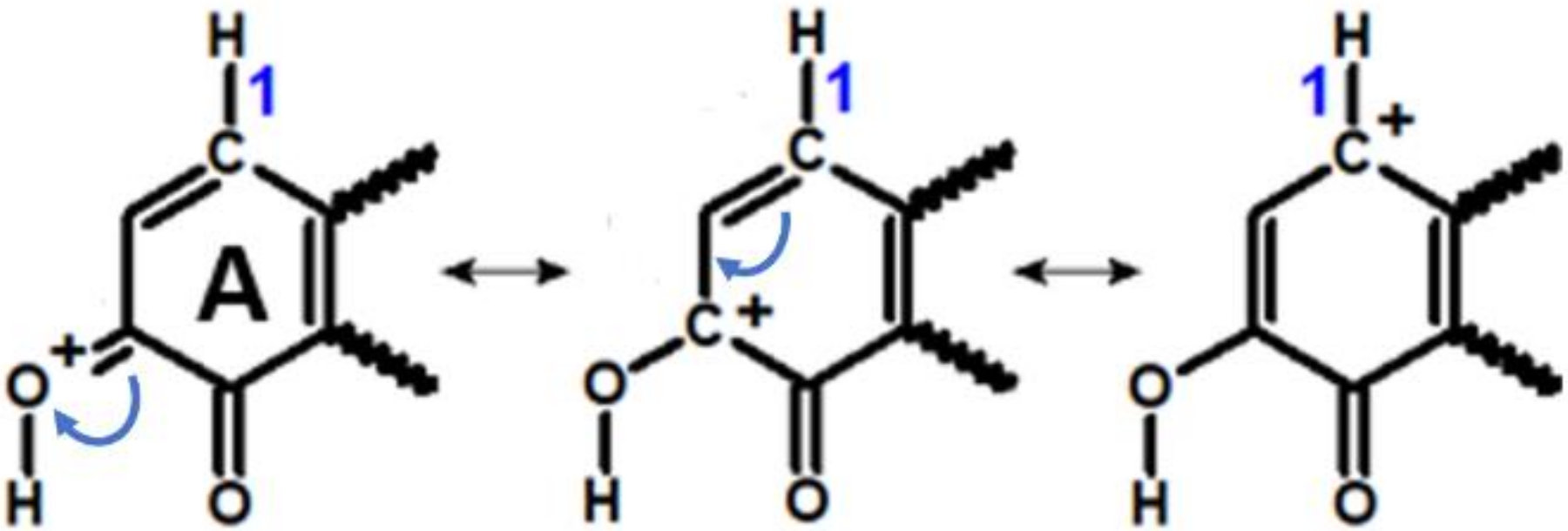
3.4. Effect of Ring “B” on Rearomatization

The formation of the Michael adducts Ex’-Q(H)H-G⁺R’ and Ex’-Q(H)H-A⁺R’ is followed by a deprotonation on C1, which restores the aromaticity of ring “A”. As already been mentioned in the introduction, such a process-in contrast to other proton transfers from O–H or N–H bonds, presented in this work, cannot be handled as a fast equilibrium as the C–H bond is not incorporated into the hydrogen bond network of the aqueous environment. Herein, we model the proton loss by virtually reacting the products of Michael addition with a carboxylate ion (modeled as an acetate ion), which is one of the most abundant Brønsted bases in biological systems.

Even though chemical intuition suggests a facile proton loss from already positively charged structures (top rows of Figure 9a,b), it also has to be taken into account that Ex’-Q(H)H-G⁺R’ and Ex’-Q(H)H-A⁺R’ are not stable at pH = 7.2. Namely, they immediately lose protons from the -OH group (connected to C3) upon their formation, as indicated by the low pK_a values of 1.8–3.3. Accordingly, similar to the previously presented Michael addition step, the rate of rearomatization is either determined by the fraction of protonated forms and the effective barrier or, alternatively, by the barrier of the direct reaction of deprotonated forms Ex’-Q(H)⁻-G⁺R’ and Ex’-Q(H)^--A⁺R’ with the Brønsted base (bottom rows of Figure 9a,b). The possible Gibbs free energy profiles of rearomatization are presented in Figure 9c (with GR’ connected to C1) and Figure 9d (with AR’ connected to C1).

Although the initial states of Figure 9 (Ex’-Q(H)^--Bx⁺R’, Ex’-Q(H)H-Bx⁺R’, as shown in the left columns) are identical to the final states of Figure 7, their relative position on the Gibbs free energy scale differs. Namely, while Figure 7 reflects the thermodynamic relations relative to the separated reactants of Michael addition, Figure 9 arranges the species according to their fraction at pH = 7.2 in the instantaneously formed acid-base equilibrium mixture, which actually influences the reactivity in the subsequent rearomatization step.

As visualized in Figure 9c,d, the deprotonated Michael adducts are less prone to rearomatization than their conjugate acid forms; the barriers corresponding to Ex’-Q(H)^--Bx⁺R’ (TS) (peak of dashed lines in Figure 9c,d) exceed the effective barriers obtained for the respective Ex’-Q(H)H-Bx⁺R’ (TS) analogs (peak of solid lines in Figure 9c,d) by 4–6 kcal/mol. Thus, similarly to the previously discussed Michael addition step, the comparison of ΔG^‡_eff values provides the most relevant information concerning the effect of unsaturations in Eq and Eqn.

Considering the relationship of ΔG^‡_eff values, it can be observed that the effects of cyclohexadiene (Eq’) and benzene (Eqn’) rings are reversed compared to Michael addition: one isolated double bond (Eq’) facilitates, while the condensation of aromaticity (Eqn’) hinders the rearomatization process.

In the case of the rearomatization of the guanosine containing the Michael adduct, both the pK_a-derived correction factor and the barrier of the actual rearomatization show a slight decrease with Eq’ compared to the values for E’ (see the “-RTln(x)” and “ΔG^‡” values near the solid lines in Figure 9c). These differences accumulate to a 1.9 kcal/mol drop in the effective barrier (ΔG^‡_eff is 15.8 kcal/mol with Eq’ and 17.7 kcal/mol with E’). Interestingly, although an even more significant 3 kcal/mol drop in ΔG^‡ occurs in the case of the adenosine analog (ΔG^‡ was calculated to be 5.5 kcal/mol with Eq’ and 8.9 kcal/mol with E’; see Figure 9d, center), the relatively low pK_a of Ex’-Q(H)H-A⁺R’ decreases this difference and only a 1.5 kcal/mol deviation was found in ΔG^‡_eff between the Eq’ (ΔG^‡_eff = 12.9 kcal/mol) and E’ derivatives (ΔG^‡_eff = 14.4 kcal/mol). Nevertheless, it is unequivocal that a double bond in ring “B” provides easier access to “A”-ring aromatic structures and, thus, has the potential to increase the rate of carcinogenesis.

Interestingly, the benzene-type ring “B” of equilenin, which considerably increased the reactivity in Michael addition relative to the cyclohexene ring of estrone, was found to alter the effective barrier of rearomatization by a mere 1 kcal/mol (ΔG^‡_eff was calculated to be 18.9 kcal/mol with GR’ and 15.6 kcal/mol with AR’). What is more, ΔG^‡_eff changed upwards compared to E’ derivatives, which suggests stronger resistance to proton loss.

3.5. Effect of ring “B” on Gylcosidic Cleavage

The final elementary step of the depurination process is the unimolecular decomposition of the rearomatized intermediate to a “depurinating adduct” and a positively charged oxocarbenium ring. The conceivable pathways of this transformation are summarized in Figure 10a,b.

The product of the previous rearomatization step is commonly assumed to be Ex’-QH₂-Bx⁺R’ (see the middle of the left column in Figure 10a,b) [19,25], which would derive from the instantaneous protonation of the Ex’-Q^2--Bx⁺R’ or Ex’-QH^--Bx⁺R’ formed upon rearomatization (Figure 9a–d, product intermediates). Nevertheless, the pK_a values of 2.2–6.9, calculated for Ex’-QH₂-Bx⁺R’, clearly reveal that the dominant species at physiological pH is the overall neutral Ex’-QH^--Bx⁺R’ (Figure 10a,b, bottom left). Thus, we began investigating the glycosidic cleavage by examining the decomposition of Ex’-QH^--Bx⁺R’ → Ex’-QH^--Bx + R’⁺. The resulting Gibbs free energy profiles are visualized in Figure 10c,d.

In spite of our extensive efforts, any attempts to locate a first-order saddle point on the potential energy surface corresponding to the transition state of the dissociation failed, most likely due to the flatness of the surface in the vicinity of the saddle point, which hinders the convergence of conventional transition state search techniques. Based on our experiences and previously reported potential energy surface scans [19], we assumed a monotonous increase of Gibbs free energy in the course of glycosidic cleavage and handled the net Gibbs free energy change as a barrier (ΔG ≈ ΔG^‡). (We note that the latter assumption underestimates the barrier since a considerable amount of entropy is gained from the dissociation of the activated complex [43]. Nevertheless, as this entropy gain should be highly similar for E’, Eq’, and Eqn’, the value of ΔG ≈ ΔG^‡ can be used to compare barriers.)

According to our computations, the effect of ring “B” on the rate of the third elementary step is small. The obtained ΔG values for Eq’ and Eqn’ derivatives deviate, at most, by ±1.2 kcal/mol from ΔGs for E’, which were calculated to be 19.6 kcal/mol (with a G base) and 21.6 kcal/mol (with an A base). Moreover, with the sole exception of Eqn’-QH^--G⁺R’ (ΔG ≈ ΔG^‡ = 18.4 kcal/mol), equine metabolites were found to be slightly less prone to unimolecular decomposition than their estrone analogs.

As the leaving oxocarbenium ion is positively charged, it is reasonable to assume that its release is facilitated by the protonation of Ex’-QH^--Bx⁺R’, which increases the overall charge of the initial intermediate of glycosilic cleavage. The aforementioned conjugate acid Ex’-QH₂-Bx⁺R’, for example, is easily accessible: its Gibbs free energy level (as given by-RTln(x_prot)) is as low as 0.8–6.8 kcal/mol, depending on the estrogen and the purine base (Figure 10e,f, left column). Thus, we studied the decomposition of Ex’-QH₂-Bx⁺R’ as the next step (see dashed lines in Figure 10e,f), which was also based on Gibbs free energy changes (ΔG) as the localization of first-order saddle points was still infeasible.

The thermodynamics of the reactions Ex’-QH₂-Bx⁺R’ → Ex’-QH₂-Bx + R’⁺ (ΔG = 15–16 kcal/mol with a G base, 18–19 kcal/mol with an A base), which are also considered barriers due to the continuous increase of Gibbs free energy during the transformation, are more favorable compared to those with the conjugate base Ex’-QH^--Bx⁺R’. However, as Ex’-QH₂-Bx⁺R’ is a minor species at pH = 7.2, the effective barrier also depends on its pK_a. Interestingly, the highest pK_as (that is, the highest fractions of Ex’-QH₂-Bx⁺R’ in neutral solution) were found in the case of E’, as a result of which the estrone derivatives show the highest reactivity, i.e., the lowest effective barriers, in glycosidic cleavage. The ΔG^‡_eff values of 16.3 kcal/mol (protonation facilitated the decomposition of E’-QH^--G⁺R’; see Figure 10e, right) and 20.5 kcal/mol (protonation facilitated the decomposition of E’-QH^--A⁺R’; see Figure 10f, right) are 3–4 kcal/mol below the analogous effective barriers with equilin and equilenin and are also lower than any of the activation barriers obtained for the direct transformation of the deprotonated species Ex’-QH^--Bx⁺R’. This finding implies that the formation of point mutations by glycosidic cleavage has the highest rate when estrone is present in the adduct, and equine estrogens are less harmful in this aspect.

Since it is known that the non-enzymatic depurination of DNA might involve an additional protonation on the purine base [39], we also decided on extending our investigations into the N-protonated species E’-QH₂-BxH²⁺R’ (Figure 10a,b, top left). The corresponding Gibbs free energy profiles of glycosidic cleavage are depicted by the dotted lines in Figure 10e,f. We observed that the hitherto highly endergonic (ΔG >> 0) unimolecular bond cleavages become closely thermoneutral (ΔG ≈ 0) upon a protonation on N3 (of guanine) or N7 (of adenine). As expected, the more favorable thermodynamics are coupled to more favorable kinetics, which can now be evaluated based on the usual saddle point search: the barriers of the cleavage vary around 10 kcal/mol (with a G base; see the dotted peak in Figure 9e) or around 3 kcal/mol (with an A base; see the dotted peak in Figure 10f).

Still, the barriers need to be adjusted according to the extremely low fraction of the doubly protonated E’-QH₂-BxH²⁺R’ at pH = 7.2. According to the resulting ΔG^‡_eff values, shown next to the dotted peaks in Figure 10e,f, estrone derivatives remain the most reactive (as indicated by the lowest ΔG^‡_eff values of 27.4 kcal/mol with G and 18.5 kcal/mol with A) even after one of the N atoms of the purine base is protonated. This can be traced back to (1) the relatively high catecholic pK_a value characterizing the first protonation of the predominant species and (2) the close independence of the second pK_a value and the barrier of actual glycosidic cleavage from the degree of unsaturation of ring “B”. To conclude our findings on the final elementary step, it can be stated that none of the equine estrogens are apt to increase the reaction rate compared to estrone.

4. Conclusions

Even though conjugated equine estrogen (CEE) medicines have been used in hormone replacement therapy for decades, little is known about the carcinogenic potential of their human exogenous components, such as equilin and equilenin. This paper aimed to compare the reactivity of the latter “equine estrogens” to that of the human endogenous estrone on the pathway of “depurinating adduct” formation from estrogen-3,4-quinones and purine DNA bases, which is considered as one of the most significant estrogen-induced breast carcinogenic routes.

Our quantum chemical analysis on the elementary steps of depurination points to the increased reactivity of equine estrogens:

(1)

in the case of Michael addition of the DNA nucleoside to the quinone metabolite (first elementary step), where a higher rate of orders of magnitude is expected with equilenin-3,4-quinone compared to the analogous estrone derivative. The 5 kcal/mol lower effective activation Gibbs free energy with equilenin can be explained by the relatively high stability of its protonated 3,4-quinone, which serves as the actual reaction partner of adenosine or guanosine.

(2)

in the case of the subsequent rearomatization step (i.e., proton loss from C1 of estrogen), where the proton release is slightly accelerated by the other equine estrogen, equilin. Here, a less significant, 1.5–2 kcal/mol decrease in the effective barrier was observed compared to that calculated for the estrone derivative.

Of course, the deviations described below only manifest an increased rate of carcinogenesis if the given elementary step (Michael addition or rearomatization) determines the reaction rate. Still, as neither of these steps can be stated to be facile under intracellular conditions (mainly due to the uncertain relation of concentrations in the nucleus of breast cells), both above unfavorable effects of equine estrogens should be accounted for in cells exposed to CEE medication.

As a final remark, we would like to emphasize that apart from the height of the rate-determining effective barrier, the amount of available Ex-Q(H) in the nucleus also influences the absolute rate of carcinogenesis. Strictly speaking, the order of reaction rates only corresponds to the reverse order of effective barriers if the initial concentrations of E-Q(H), Eq-Q(H), and Eqn-Q(H) are equal or, at least, comparable. (In other words, an estrogen metabolite with higher ΔG^‡_eff, and hence lower carcinogenic potential, might also produce carcinogenic mutations at an outstandingly high rate if it is present in outstandingly high concentrations.) Determination of the concentration of estrogen-3,4-quinones, which depends on many factors (e.g, proportion of E, Eq, and Eqn in the HRT drug, dosage, bioavailability, metabolic rate of oxidation) falls out of the scope of this paper. Nevertheless, other studies on estrogen metabolism, including our previous paper, where we showed that equine estrogens have an enhanced aptitude to metabolize to 3,4-quinones [44], point to the direction that equine estrogen quinones are not only more reactive towards DNA but also likely more abundant in the nucleus of breast cells exposed to HRT medication.

Taken together with the enhanced aptitude of equine estrogens to metabolize to 3,4-quinones, as reported previously by our research group, it can be inferred that the presence of equilin and/or equilenin might significantly contribute to breast cancer development.

Our results underline the need for long-term (pre)clinical studies that individually evaluate the carcinogenic potential of the components of CEE. Furthermore, we suggest a detailed experimental investigation of the reactions Ex-Q(H) + BxR (where the effect of the initial concentrations, pH, and time course of all relevant intermediate concentrations should be observed) in order to conclude on the rate-limiting step of depurination under the conditions corresponding to an actual breast cell. In this way, it can be decided whether the lower Michael addition and rearomatization barriers obtained for Eqn and Eq, respectively (as described in the above points), truly affect the overall rate of carcinogenesis.

We believe that apart from drawing the above conclusions on hitherto unconsidered risk factors of equine estrogen medications, our present work—including our concept of “effective activation Gibbs free energies”—may also serve as a useful framework for studying the carcinogenic potential of other estrogen hormones or related compounds.