Efficiency Optimization Strategy of Permanent Magnet Synchronous Motor for Electric Vehicles Based on Energy Balance
Abstract
:1. Introduction
2. PMSM Model and Loss Model
3. Efficiency Optimization Strategy
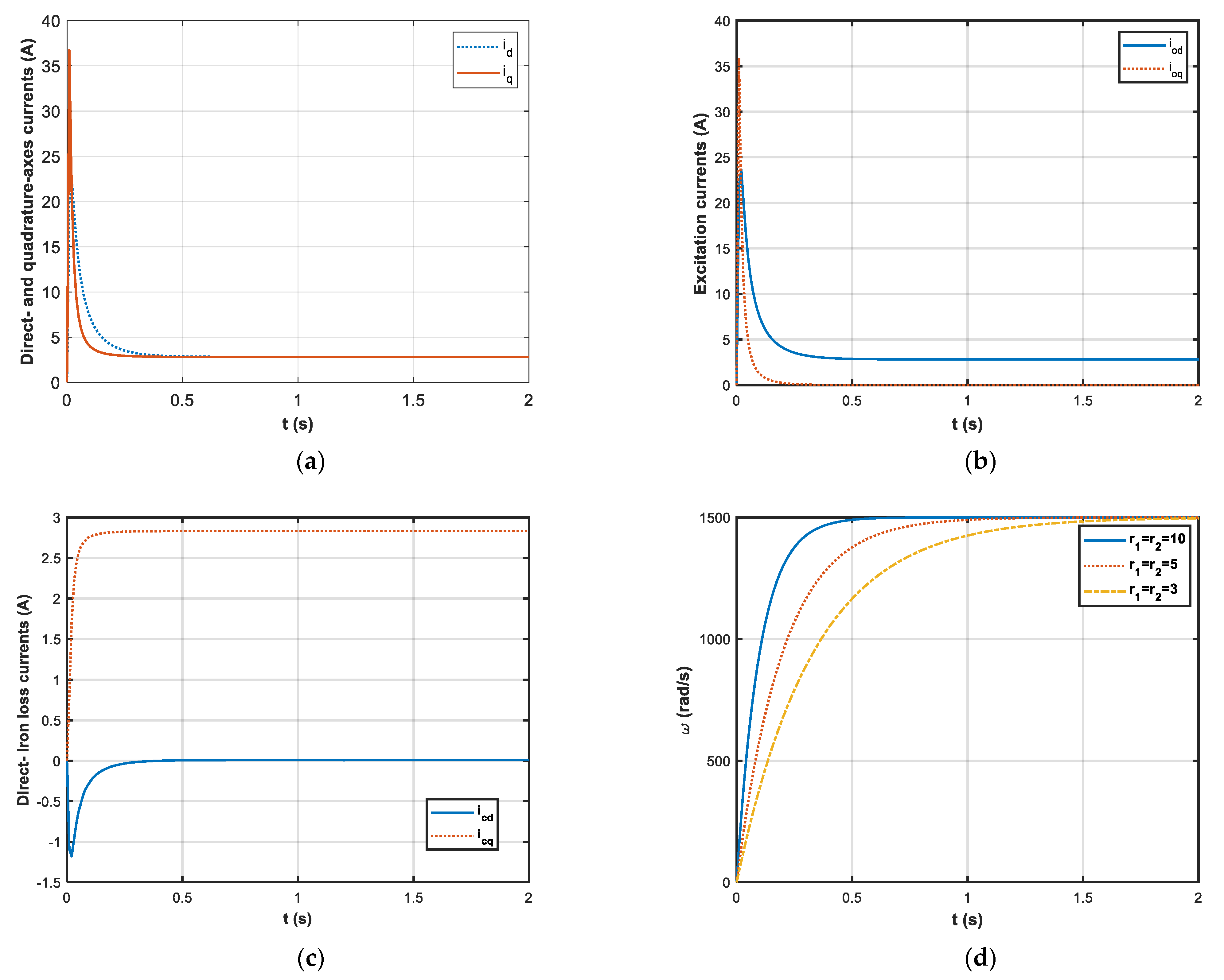
4. Algorithm Realization
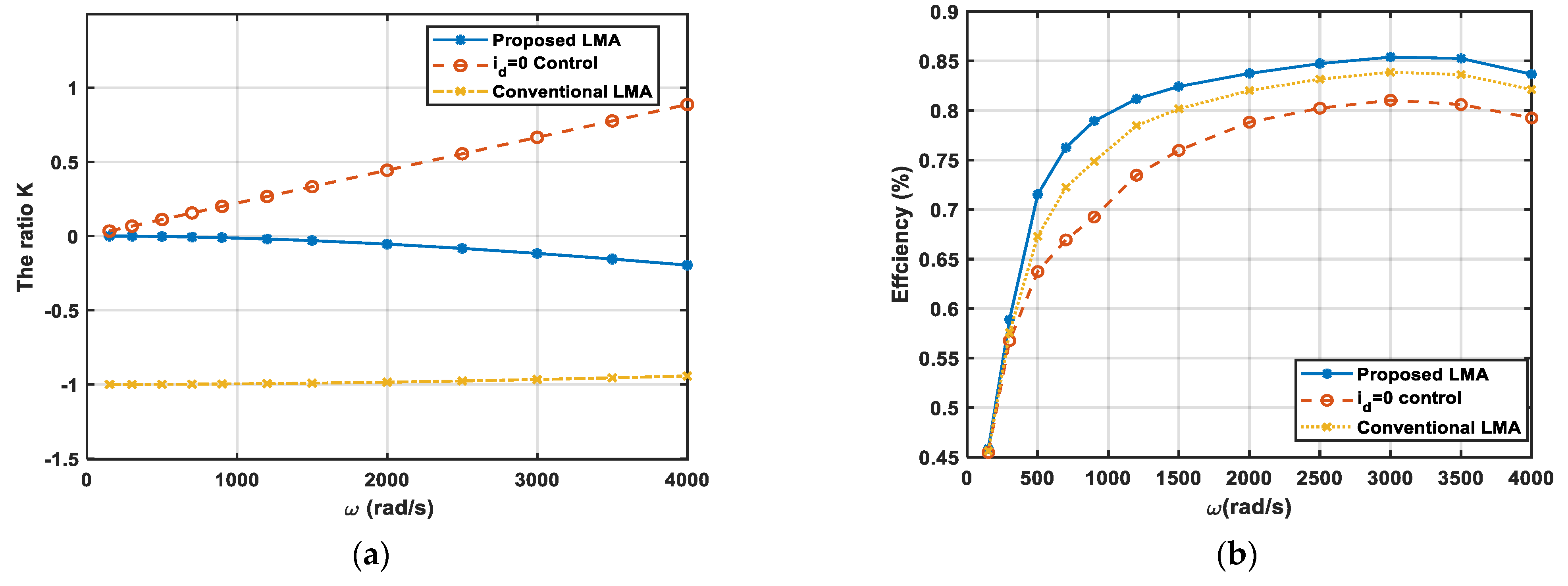
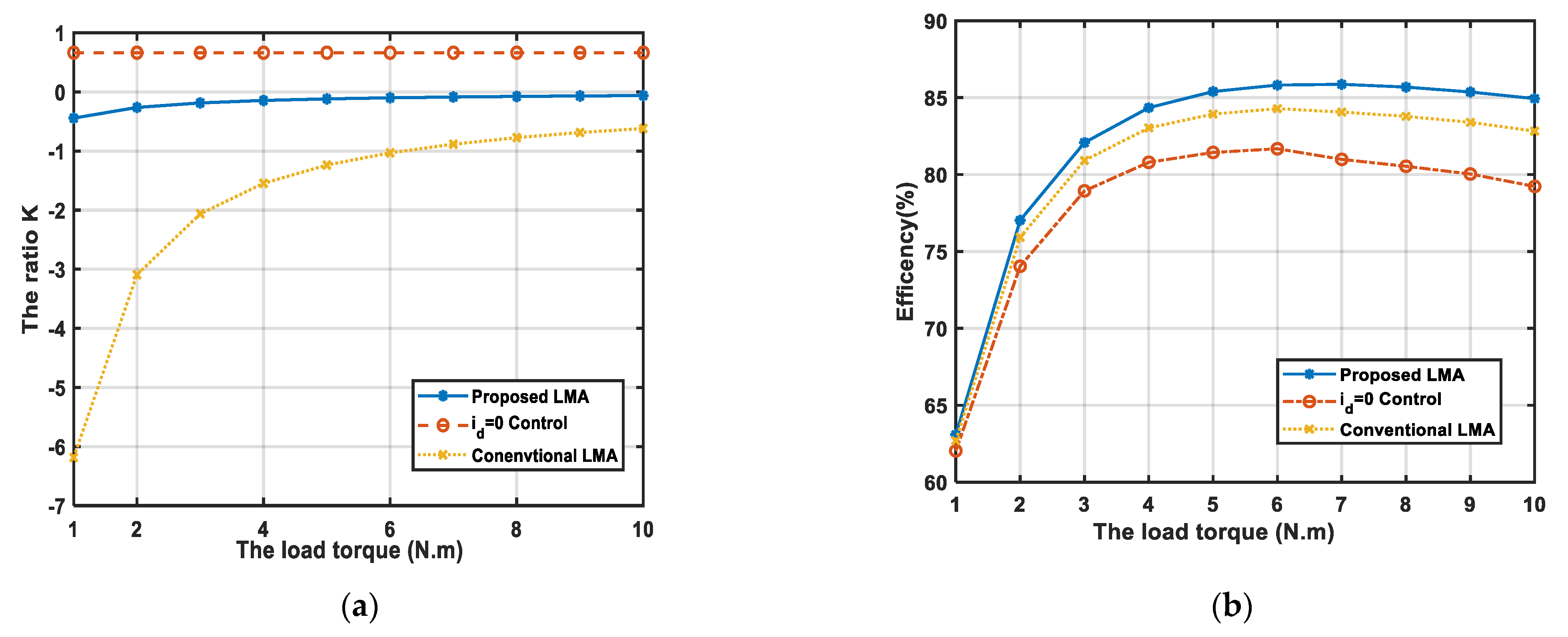
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, W.; Wang, Z.; Drugge, L.; Nybacka, M. Evaluating Model Predictive Path Following and Yaw Stability Controllers for Over-Actuated Autonomous Electric Vehicles. IEEE Trans. Veh. Technol. 2020, 69, 12807–12821. [Google Scholar] [CrossRef]
- Chau, K.T.; Chan, C.C.; Liu, C. Overview of Permanent-Magnet Brushless Drives for Electric and Hybrid Electric Vehicles. IEEE Trans. Ind. Electron. 2008, 55, 2246–2257. [Google Scholar] [CrossRef] [Green Version]
- Rezaei, A.; Burl, J.B.; Rezaei, M.; Zhou, B. Catch Energy Saving Opportunity in Charge-Depletion Mode, a Real-Time Controller for Plug-In Hybrid Electric Vehicles. IEEE Trans. Veh. Technol. 2018, 67, 11234–11237. [Google Scholar] [CrossRef]
- Xu, L.; Li, J.; Ouyang, M. Multi-mode control strategy for fuel cell electric vehicles regarding fuel economy and durability. Int. J. Hydrog. Energy 2014, 39, 2374–2389. [Google Scholar] [CrossRef]
- Emadi, A.; Lee, Y.J.; Rajashekara, K. Power electronics and motor drives in electric, hybrid electric, and plug-in hybrid electric vehicles. IEEE Trans. Ind. Electron. 2008, 55, 2237–2245. [Google Scholar] [CrossRef]
- Haddoun, A.; Mohamed, B.H.E.; Demba, D.; Rachid, A.; Jamel, G.; Kamel, S. A Loss-Minimization DTC Scheme for EV Induction Motors. IEEE Trans. Veh. Technol. 2007, 56, 81–88. [Google Scholar] [CrossRef] [Green Version]
- Uddin, M.; Rebeiro, R. Comparison of Efficiency for a PI and a FLC Based IPMSM Drive Incorporating Loss Minimization Algorithm over Wide Speed Range; Energy Conversion Congress & Expositions: San Jose, CA, USA, 2009. [Google Scholar]
- Zhu, Z.Q.; Howe, D. Electrical machines and drives for electric, hybrid, and fuel cell vehicles. Proc. IEEE 2007, 95, 746–765. [Google Scholar] [CrossRef]
- Rubino, S.; Dordevic, O.; Bojoi, R.; Levi, E. Modular Vector Control of Multi-Three-Phase Permanent Magnet Synchronous Motors. IEEE Trans. Ind. Electron. 2021, 68, 9136–9147. [Google Scholar] [CrossRef]
- Boldea, I.; Tutelea, L.; Parsa, L.; Dorrell, D. Automotive electric propulsion systems with reduced or no permanent magnets: An overview. IEEE Trans. Ind. Electron. 2014, 61, 5696–5711. [Google Scholar] [CrossRef]
- Morimoto, S.; Ooi, S.; Inoue, Y.; Sanada, M. Experimental evaluation of a rare-earth-free PMSM with ferrite magnets for automotive applications. IEEE Trans. Ind. Electron. 2014, 61, 5749–5756. [Google Scholar] [CrossRef]
- Hu, X.; Jiang, J.; Egardt, B.; Cao, D. Advanced power-source integration in hybrid electric vehicles: Multicriteria optimization approach. IEEE Trans. Ind. Electron. 2015, 62, 7847–7858. [Google Scholar] [CrossRef]
- Carpiuc, S.-C. Rotor temperature detection in permanent magnet synchronous machine-based automotive electric traction drives. IEEE Trans. Power Electron. 2017, 32, 2090–2097. [Google Scholar] [CrossRef]
- Mun, J.-M.; Park, G.-J.; Seo, S.; Kim, D.-W.; Kim, Y.-J.; Jung, S.-Y. Design characteristics of IPMSM with wide constant power speed range for EV traction. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar] [CrossRef]
- Lim, M.-S.; Chai, S.-H.; Hong, J.-P. Design of saliency-based sensorless-controlled IPMSM with concentrated winding for EV traction. IEEE Trans. Magn. 2016, 52, 8200504-1–8200504-4. [Google Scholar] [CrossRef]
- Liu, T.; Hu, X.; Li, S.E.; Cao, D. Reinforcement learning optimized look-ahead energy management of a parallel hybrid electric vehicle. IEEE/ASME Trans. Mechatron. 2017, 22, 1497–1507. [Google Scholar] [CrossRef]
- Wei, D.; He, H.; Cao, J. Hybrid electric vehicle electric motors for optimum energy efficiency: A computationally efficient design. Energy 2020, 203, 117779. [Google Scholar] [CrossRef]
- Malekpour, M.; Abarghooee, R.; Terzija, V. Maximum torque per ampere control with direct voltage control for IPMSM drive systems. Int. J. Electr. Power Energy Syst. 2020, 116, 105509. [Google Scholar] [CrossRef]
- Vaez, S. Loss Minimization Control of Interior Permanent Magnet Motor Drives. Ph.D. Dissertation, Queen’s University at Kingston, Kingston, ON, Canada, 1997. [Google Scholar]
- Bose, B.K. A high-performance inverter-fed drive system of an interior permanent magnet synchronous machine. IEEE Trans. Ind. Appl. 1988, 24, 987–997. [Google Scholar] [CrossRef]
- Morimoto, S.; Sanada, M.; Takeda, Y. Wide-speed operation of interior permanent magnet synchronous motors with high-performance current regulato. IEEE Trans. Ind. Appl. 1994, 30, 920–926. [Google Scholar] [CrossRef]
- Lenke, R.U.; Doncker, R.W.D.; Mu-Shin, K. Field weakening control of interior permanent magnet machine using improved current interpolation technique. In Proceedings of the 37th IEEE Power Electronics Specialists Conference, Jeju, Korea, 18–22 June 2016; pp. 1–5. [Google Scholar]
- Kim, J.M.; Sul, S.K. Speed control of interior permanent magnet synchronous motor drive for the flux weakening operation. IEEE Trans. Ind. Appl. 1997, 33, 43–48. [Google Scholar]
- Pan, C.T.; Liaw, J.H. A robust field-weakening control strategy for surface-mounted permanent-magnet motor drives. IEEE Trans. Energy Convers. 2005, 20, 701–709. [Google Scholar] [CrossRef]
- Cheng, N.; Zhang, Y.; Gui, W. Flux weakening control of embedded permanent magnet synchronous motor drive system. Control. Theory Appl. 2013, 28, 717–723. [Google Scholar]
- Bai, Y.; Tang, X.; Wu, G. Flux-weakening speed control of the Interior permanent magnet synchronous motor. Trans. China Electro Tech. Soc. 2011, 26, 54–59. [Google Scholar]
- Cavallaro, C.; Di Tommaso, A.O.; Miceli, R.; Raciti, A.; Galluzzo, G.R.; Trapanese, M. Efficiency enhancement of permanent-magnet synchronous motor drives by online loss minimization approaches. IEEE Trans. Ind. Electron. 2005, 52, 1153–1160. [Google Scholar] [CrossRef] [Green Version]
- Guo, Q.; Zhang, C.; Li, L.; Zhang, J.; Liu, J.; Wang, T. Efficiency optimization control of permanent magnet synchronous motor for electric vehicle. Micromotors 2014, 47, 142–146. [Google Scholar]
- Morimoto, S.; Tong, Y.; Takeda, Y.; Hirasa, T. Loss minimization control of permanent magnet synchronous motor drives. IEEE Trans. Ind. Electron. 2002, 41, 511–517. [Google Scholar] [CrossRef]
- Hang, J.; Wu, H.; Ding, S.; Huang, Y.; Wei, H. Improved Loss Minimization Control for IPMSM Using Equivalent Conversion Method. IEEE Trans. Power Electron. 2021, 36, 1931–1940. [Google Scholar] [CrossRef]
- Pei, W.; Li, C.Z.K.; Cui, N. Hamilton system modeling and passive control for induction motor of electric vehicles by considering iron losses. Control. Theory Appl. 2011, 28, 869–873. [Google Scholar]
- Gonz’alez, H. Development of Control Schemes Based on Energy Shaping for a Class of Nonlinear Systems and Design of a Triphase Inverter Open Prototype for Online Applications in Induction Motors; University of Chile: Santiago, Chile, 2005. (In Spanish) [Google Scholar]
- Yu, J.; Pei, W.; Zhang, C. A Loss-Minimization Port-Controlled Hamilton Scheme of Induction Motor for Electric Vehicles. IEEE/ASME Trans. Mechatron. 2015, 20, 2645–2653. [Google Scholar] [CrossRef]
- Batlle, C.; Cerezo, A.D. Energy based modelling and simulation of the interconnection of a back-to-back converter and a doubly-fed induction machine. In Proceedings of the 2006 American Control Conference Minneapolis, Minneapolis, MN, USA, 14 June 2016; pp. 1851–1856. [Google Scholar]
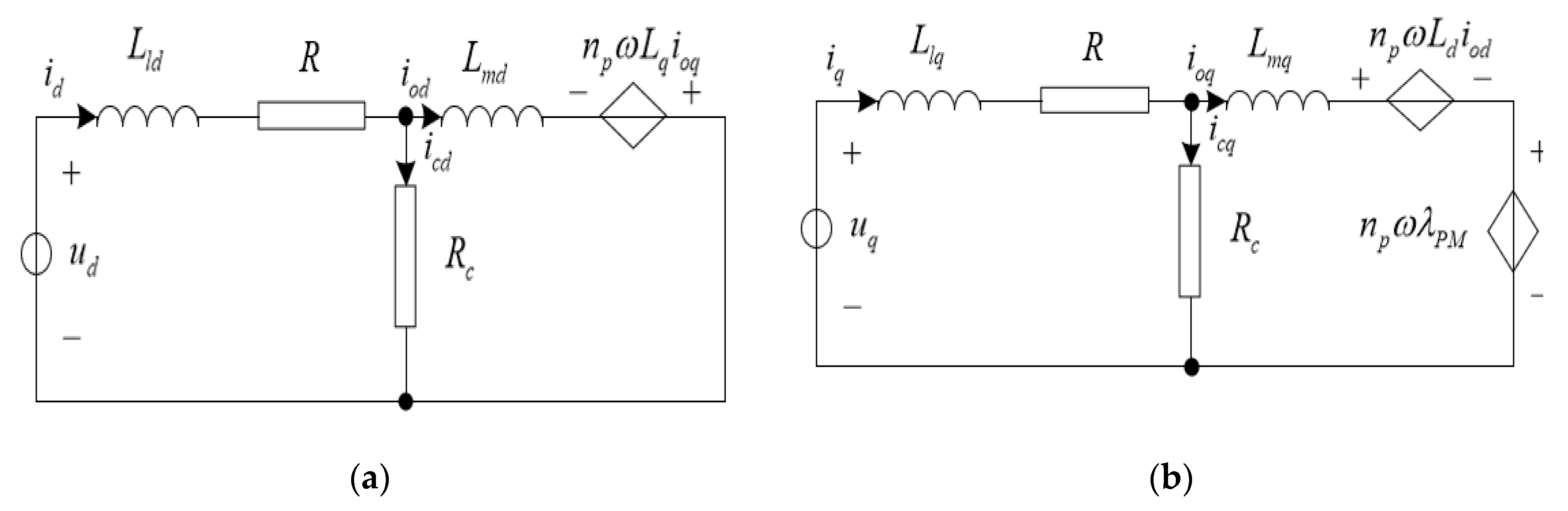
| Parameters | Description |
|---|---|
| id,iq | direct-axis and quadrature-axis current components |
| iod,ioq | direct and quadrature axes excitation current components |
| icd,icq | direct and quadrature axes iron loss current components |
| Ld,Lq | direct and quadrature axes inductance components |
| Lld,Llq | direct and quadrature axes leakage inductance components |
| Lmd,Lmq | direct and quadrature axes excitation inductances |
| R, Rc | stator resistance and core loss resistances |
| J | moment inertia of the motor |
| np | pole pairs of motor |
| rotor mechanical angular speed | |
| ud,uq | direct and quadrature axes voltage |
| λPM | excitation flux of rotor permanent magnet |
| TL | load torque |
| Parameters | Values |
|---|---|
| rated rotor speed (rad/s) | 3000 |
| rated torque TL (N·m) | 5 |
| pole pairs np | 6 |
| stator resistance R (Ω) | 2.21 |
| core loss resistances Rc (Ω) | 200 |
| direct and quadrature inductance Ld, Lq (mH) | 14.77 |
| excitation inductance Lmd, Lmq (mH) | 8 |
| leakage inductance Lld, Llq (mH) | 3.77 |
| moment inertia J (kg·m2) | 0.002 |
| permanent magnet flux λPM (Wb) | 0.084 |
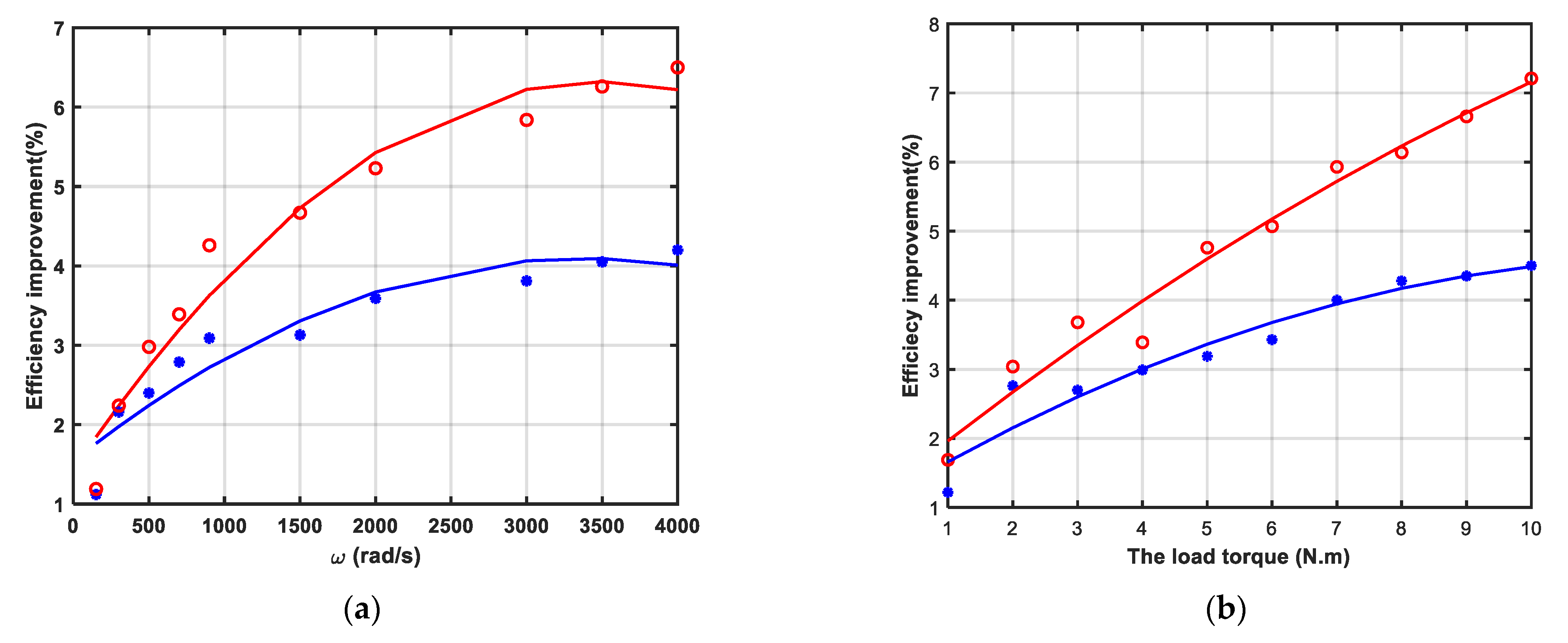
| 3 | 5 | 7 | 9 | 10 | |
|---|---|---|---|---|---|
| (%) | 3.05 | 3.19 | 3.95 | 4.35 | 4.49 |
| (%) | 4.76 | 5.93 | 6.71 | 6.71 | 7.12 |
| ω (rad/s) | 500 | 900 | 1500 | 2000 | 3000 |
|---|---|---|---|---|---|
| (%) | 2.41 | 3.09 | 3.13 | 3.59 | 4.05 |
| (%) | 2.98 | 4.26 | 4.67 | 5.32 | 6.26 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pei, W.; Zhang, Q.; Li, Y. Efficiency Optimization Strategy of Permanent Magnet Synchronous Motor for Electric Vehicles Based on Energy Balance. Symmetry 2022, 14, 164. https://doi.org/10.3390/sym14010164
Pei W, Zhang Q, Li Y. Efficiency Optimization Strategy of Permanent Magnet Synchronous Motor for Electric Vehicles Based on Energy Balance. Symmetry. 2022; 14(1):164. https://doi.org/10.3390/sym14010164
Chicago/Turabian StylePei, Wenhui, Qi Zhang, and Yongjing Li. 2022. "Efficiency Optimization Strategy of Permanent Magnet Synchronous Motor for Electric Vehicles Based on Energy Balance" Symmetry 14, no. 1: 164. https://doi.org/10.3390/sym14010164
APA StylePei, W., Zhang, Q., & Li, Y. (2022). Efficiency Optimization Strategy of Permanent Magnet Synchronous Motor for Electric Vehicles Based on Energy Balance. Symmetry, 14(1), 164. https://doi.org/10.3390/sym14010164








