Photoacoustics Waveform Design for Optimal Signal to Noise Ratio
Abstract
:1. Introduction
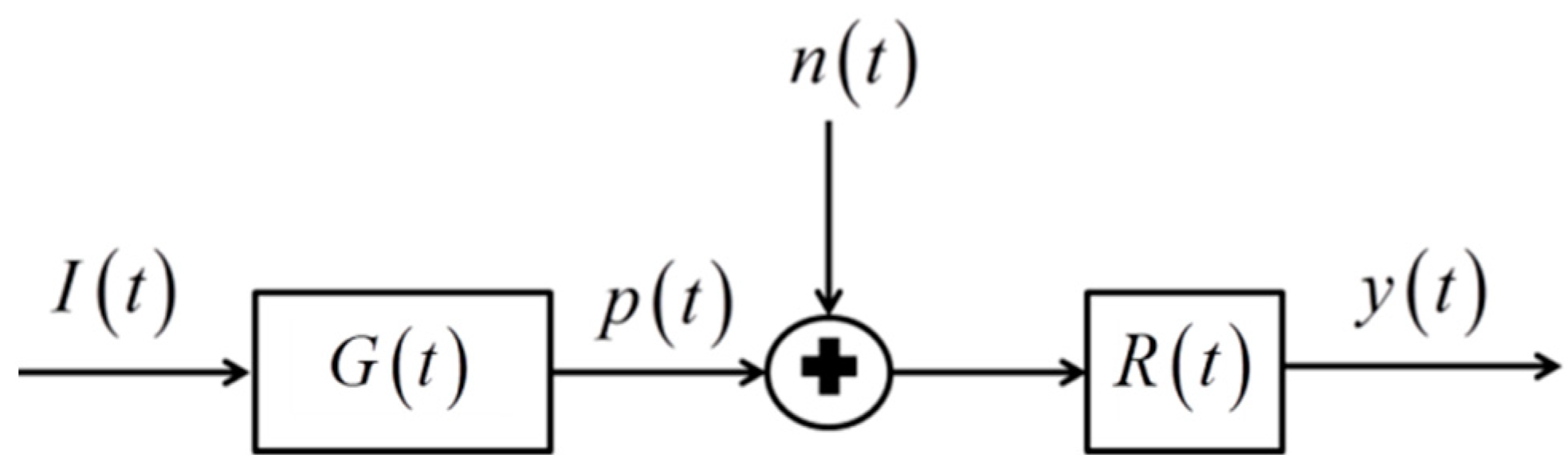
2. Mathematical Statement of the Problem
2.1. Maximizing SNR
2.2. Maximizing SNR under Constraints on the Input
3. Numerical Simulations
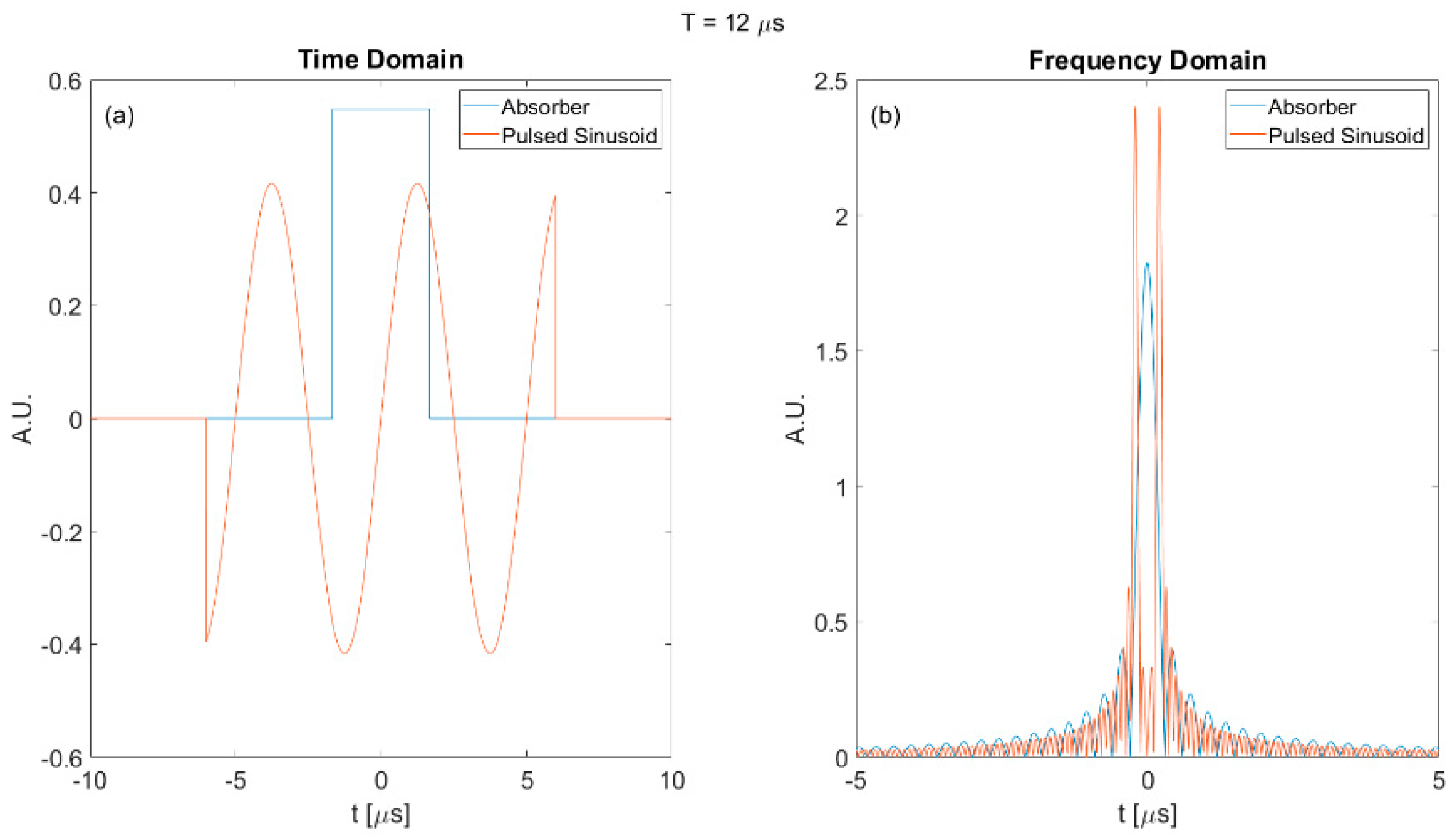
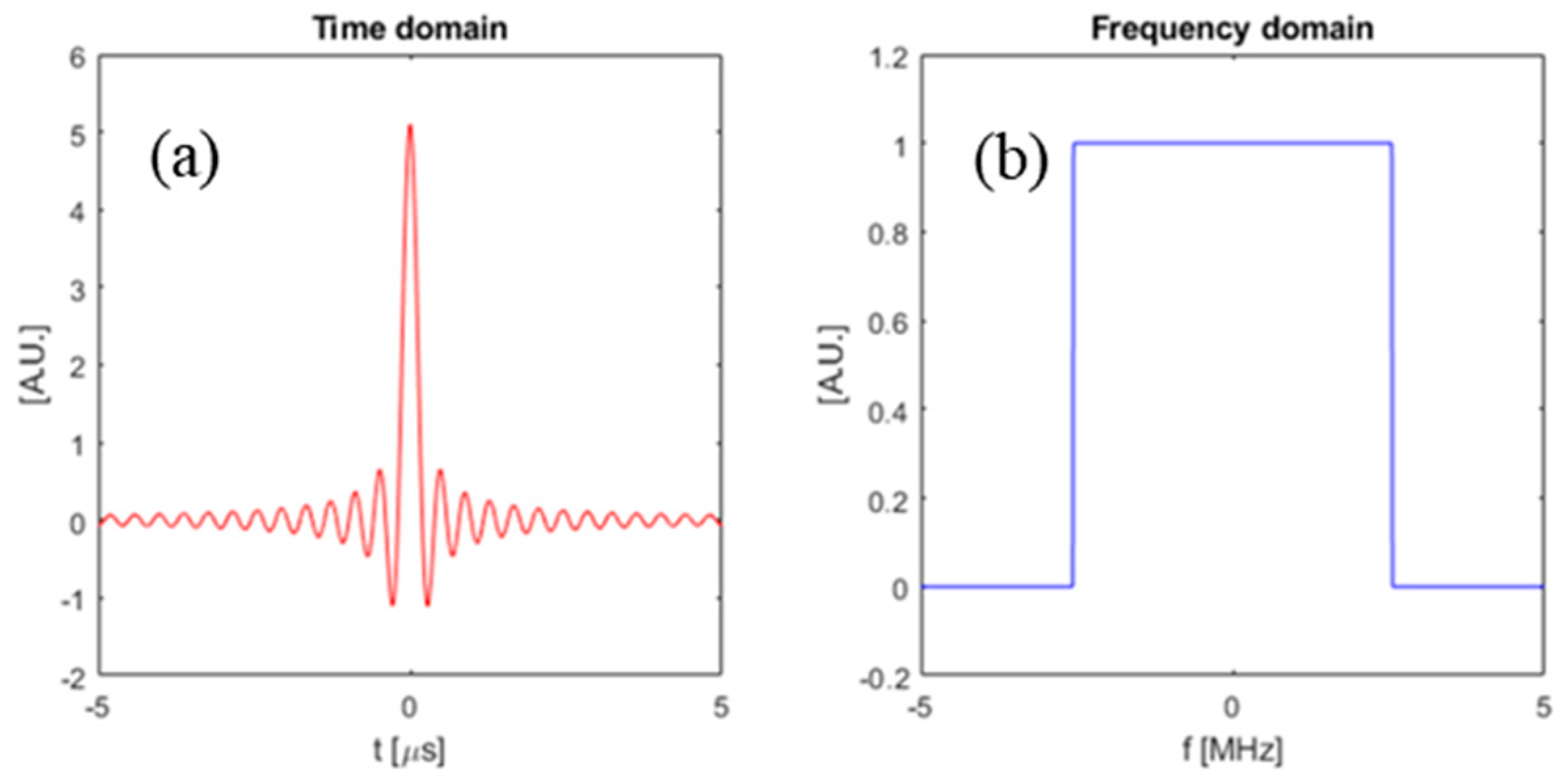
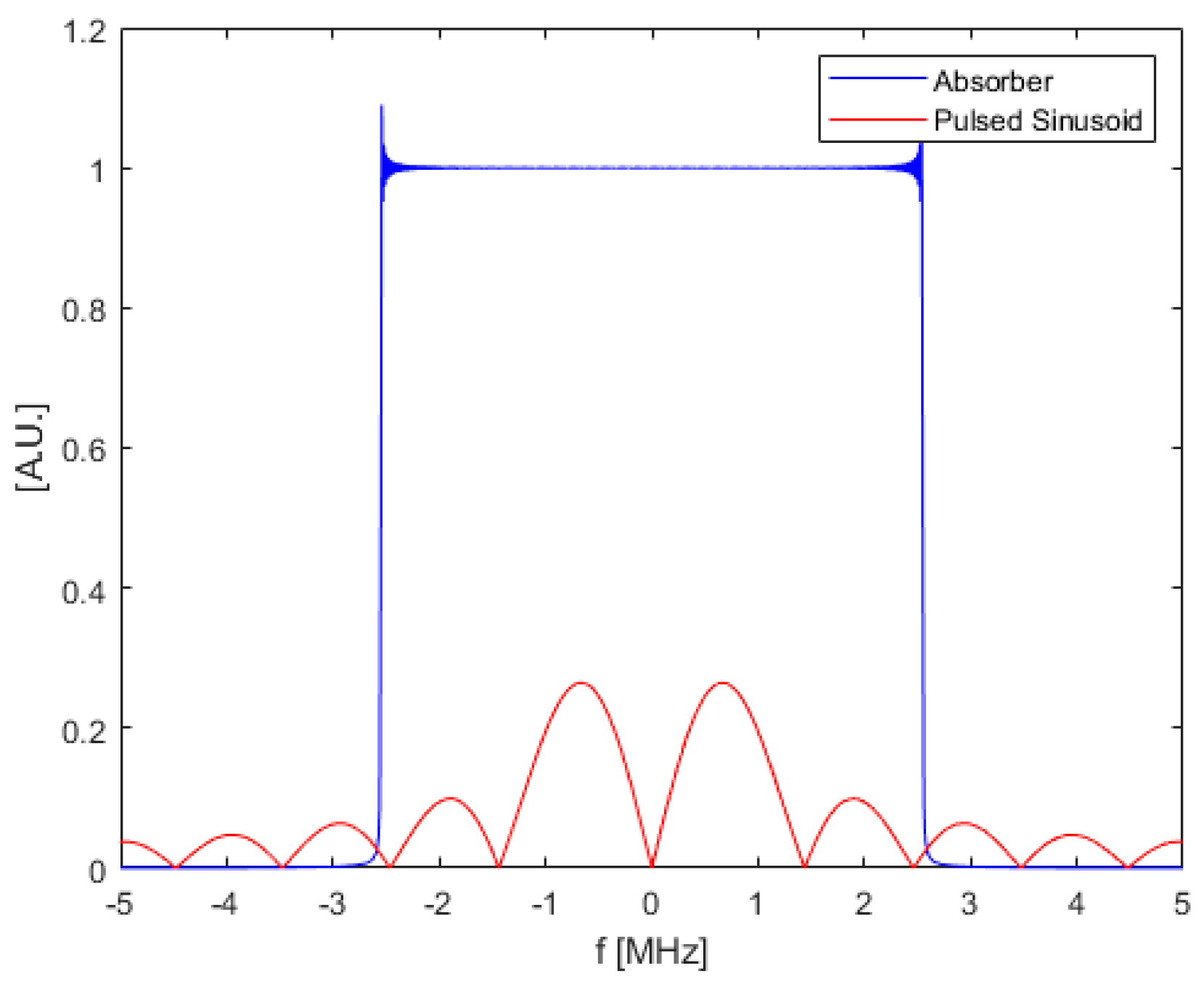
3.1. Bandlimited Absorber
3.2. Square Absorber
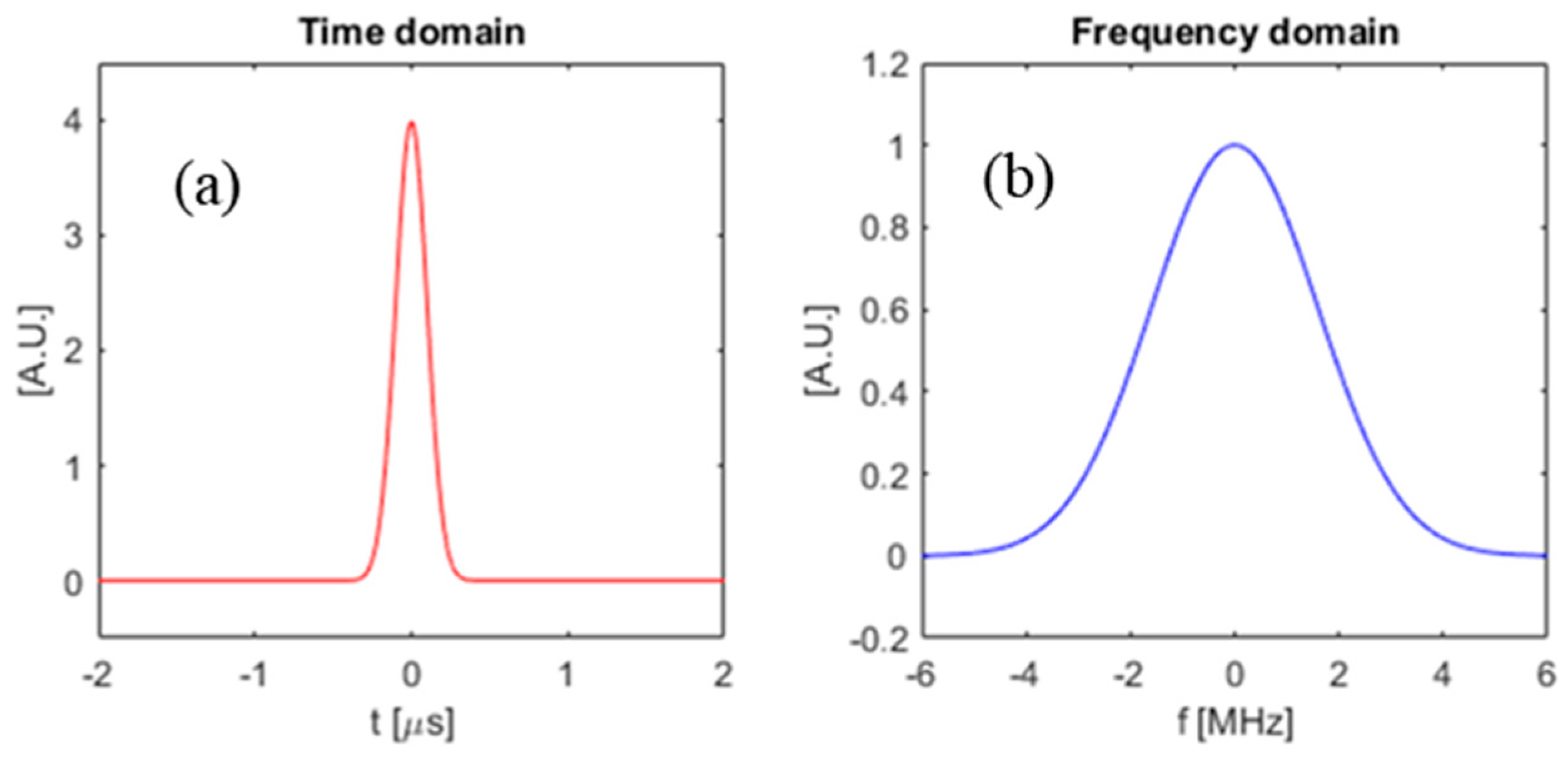
3.3. Gaussian Absorber
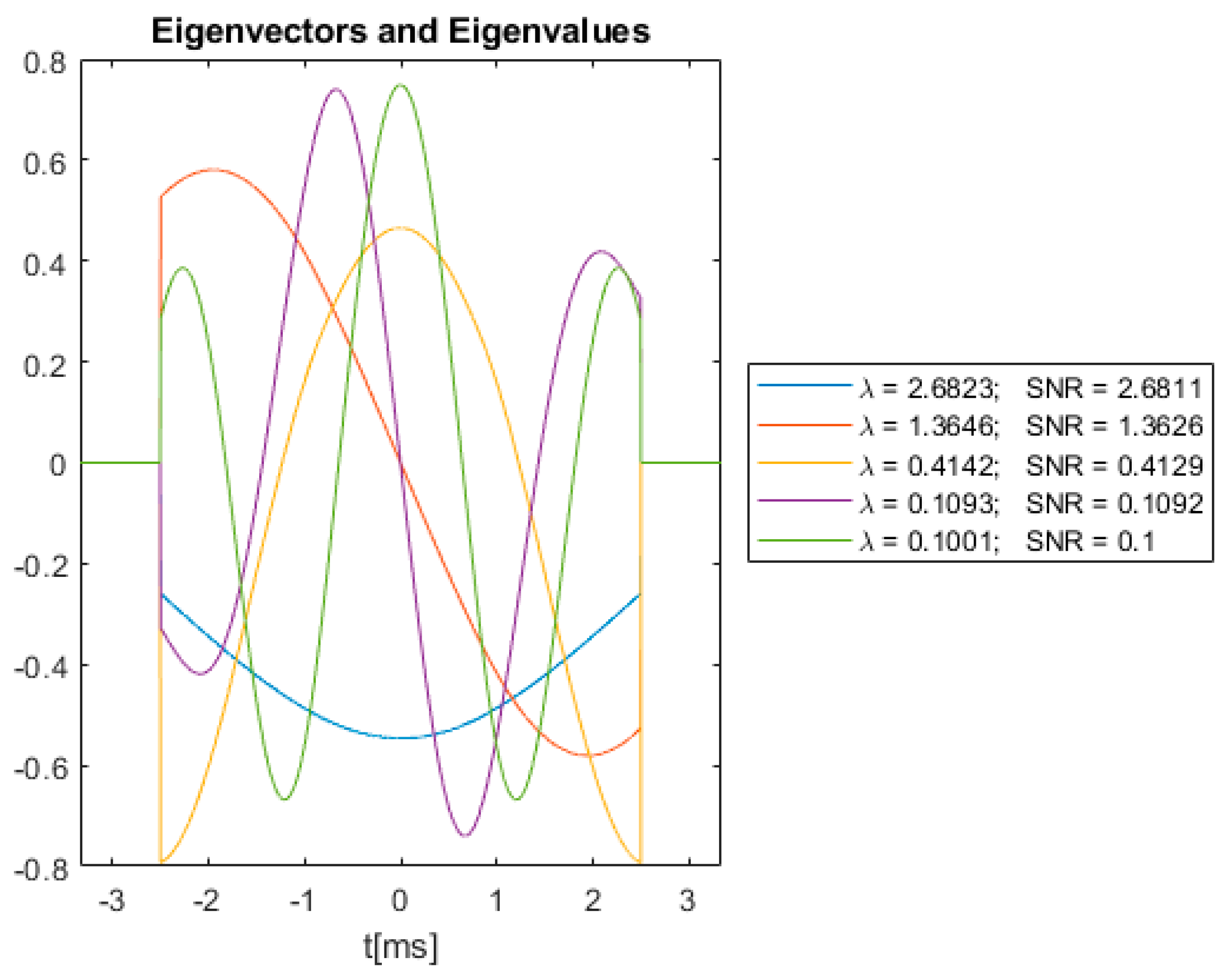
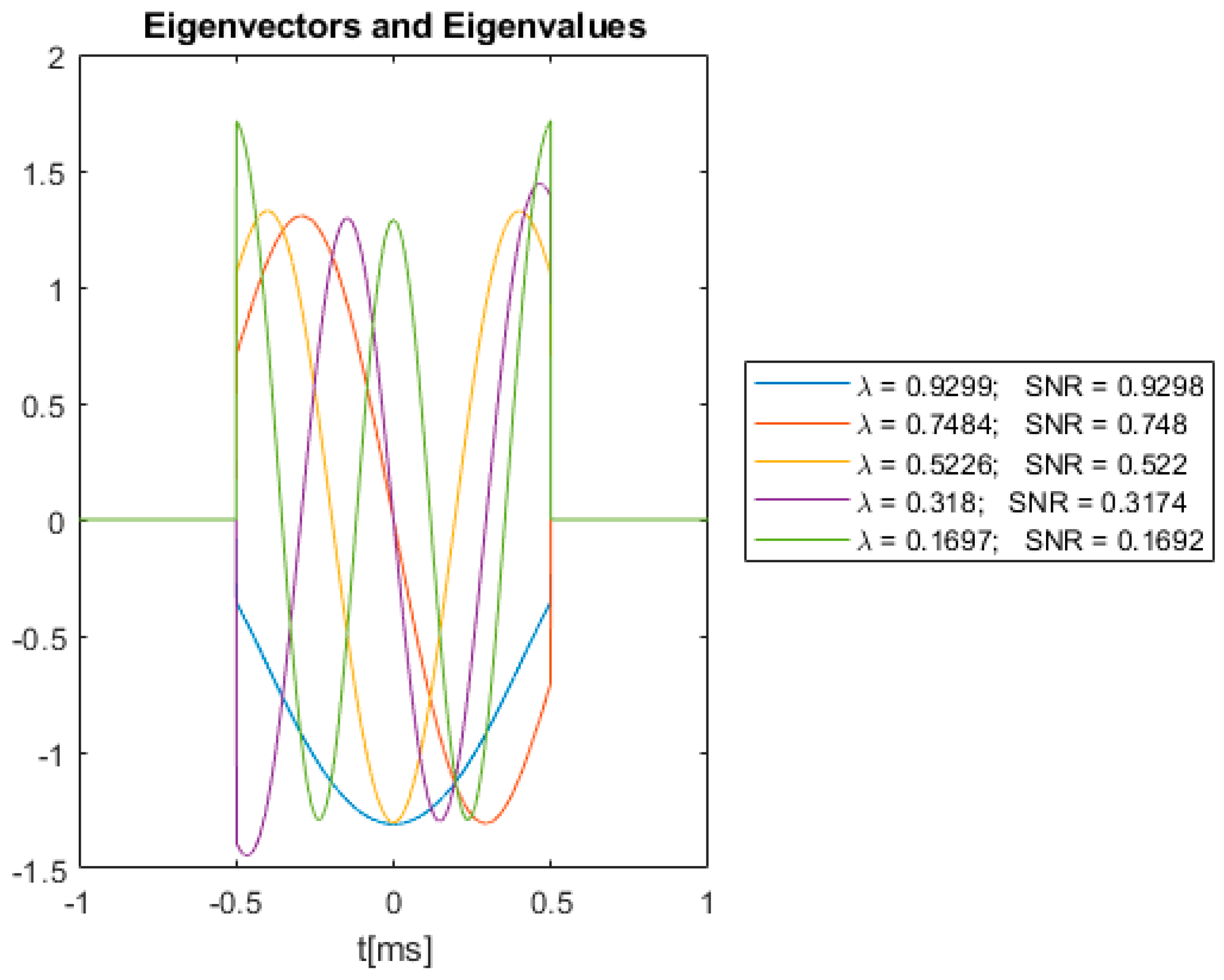
3.4. Optimal SNR and Eigenvalue
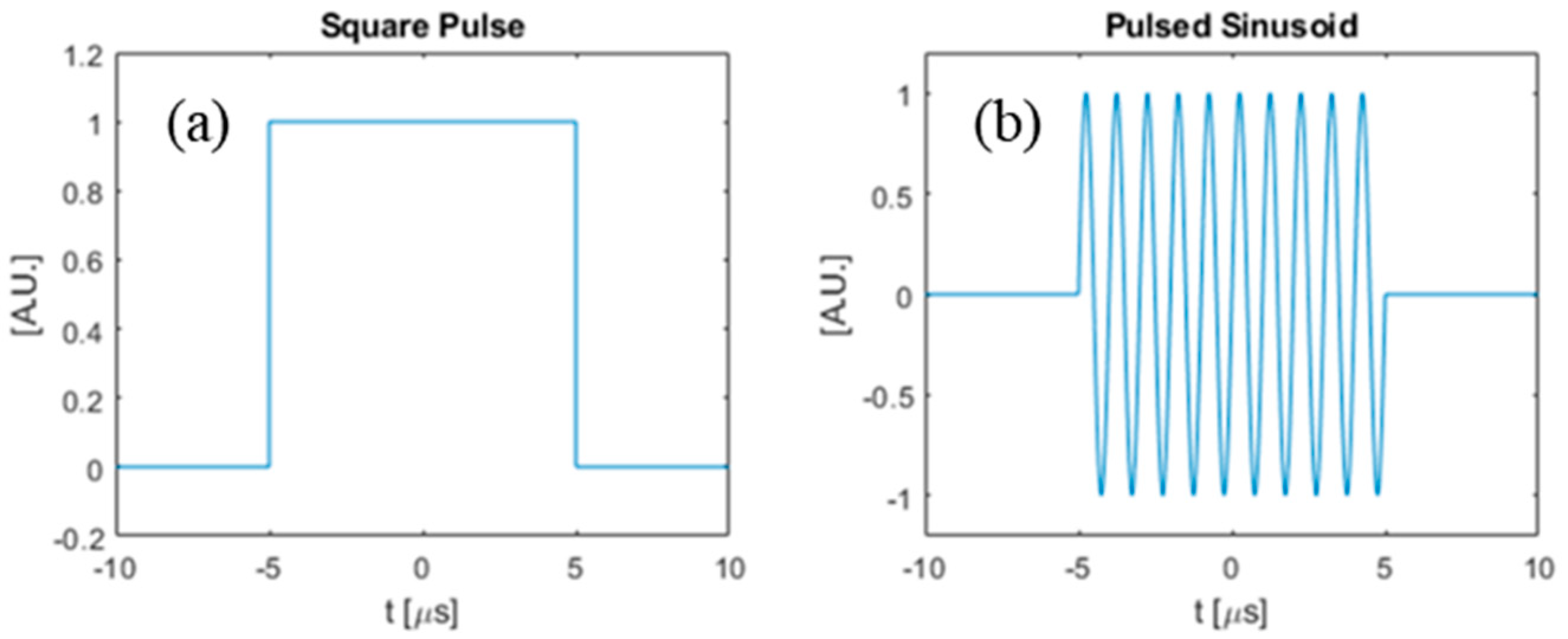
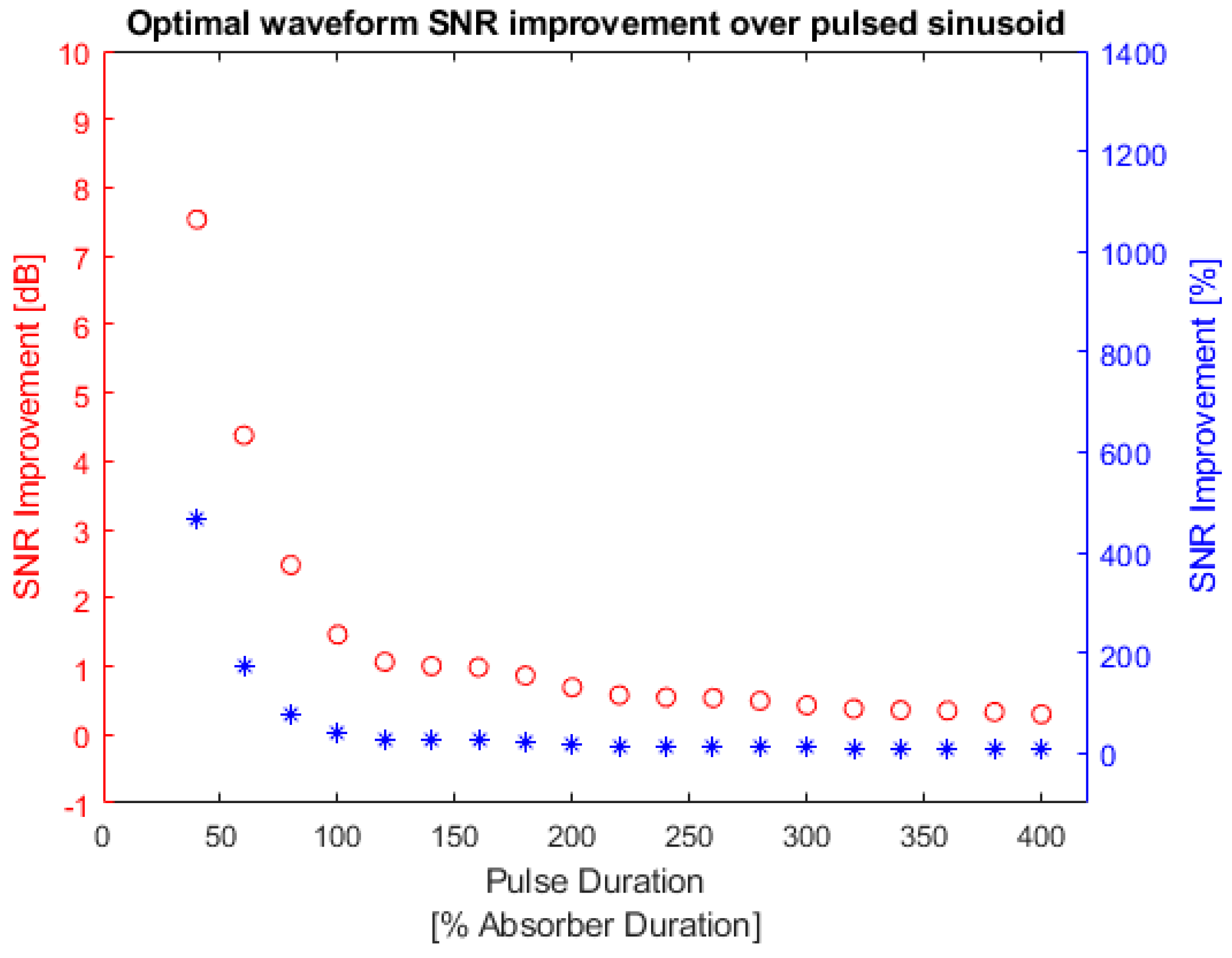
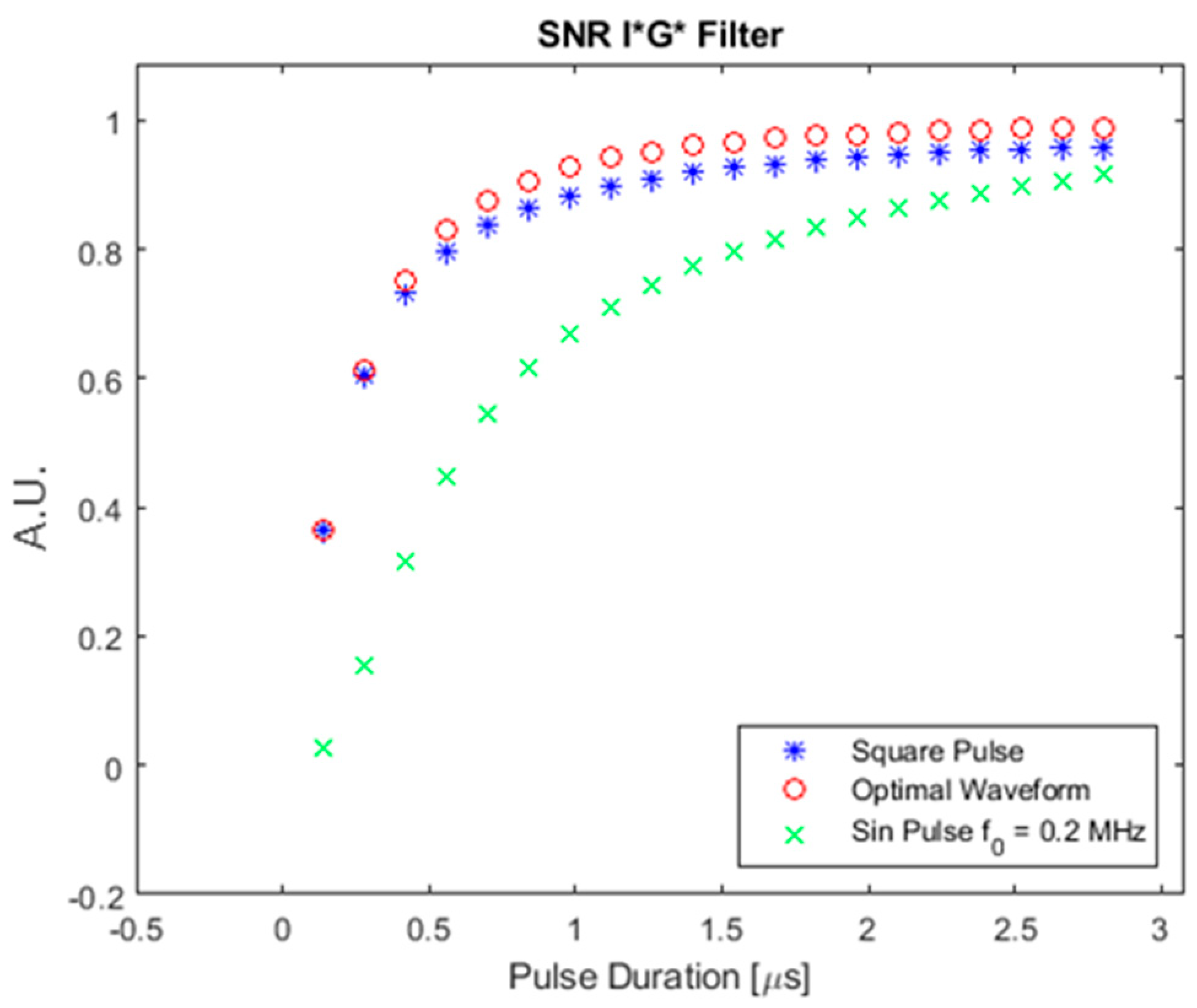
3.5. SNR Comparison between Different Input Waveforms
3.5.1. Bandlimited Absorber SNR
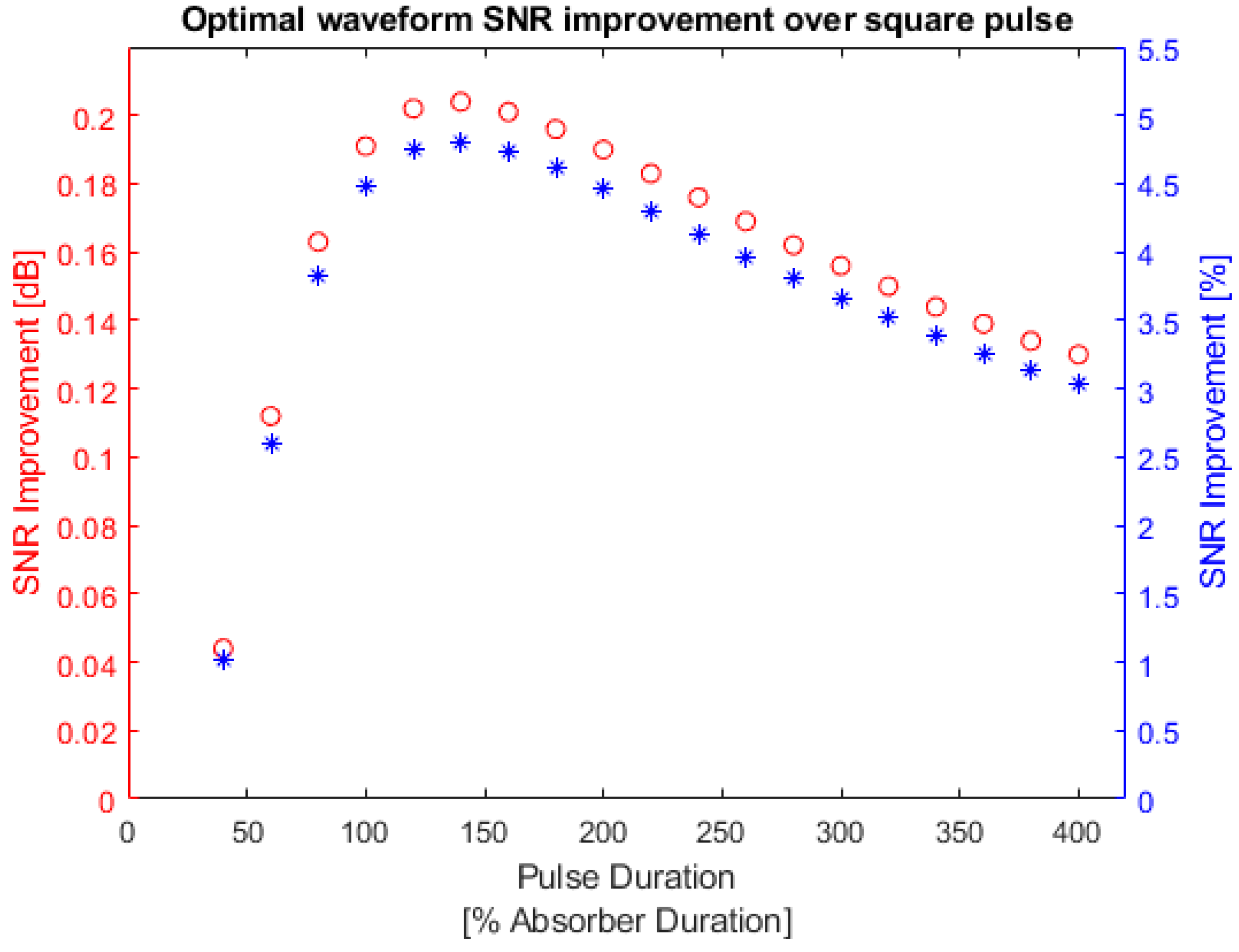
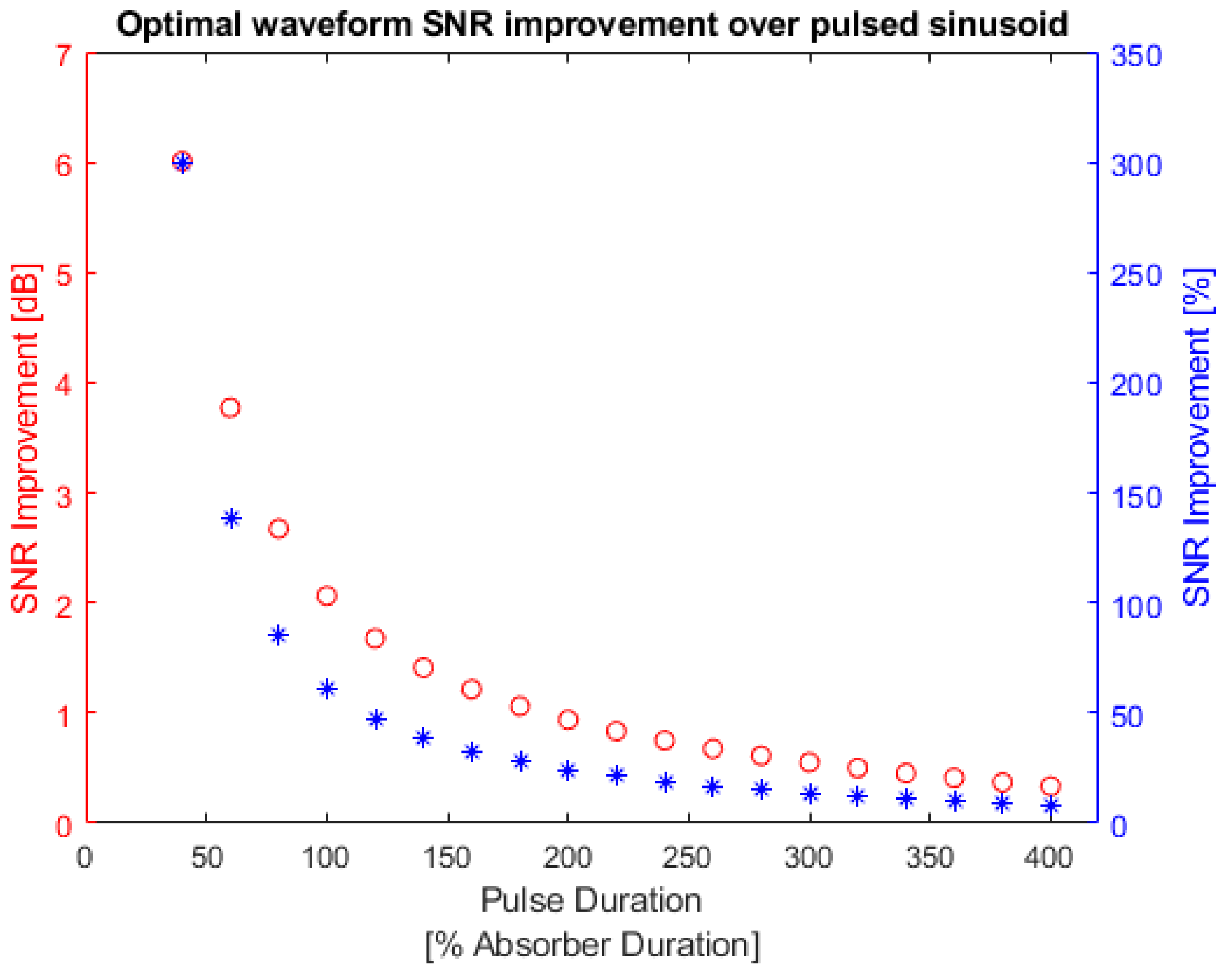
3.5.2. Square Absorber SNR
3.5.3. Gaussian Absorber
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| T (us) | SNR Optimal | SNR Pulse | SNR Improvement (%) | SNR Improvement (dB) |
|---|---|---|---|---|
| 0.157 | 0.658 | 0.676 | 2.59 | 0.114 |
| 0.235 | 0.85 | 0.839 | 1.275 | 0.055 |
| 0.314 | 0.944 | 0.896 | 5.33 | 0.226 |
| 0.392 | 0.982 | 0.903 | 8.73 | 0.363 |
| 0.471 | 0.995 | 0.907 | 9.749 | 0.404 |
| 0.549 | 0.999 | 0.922 | 8.39 | 0.35 |
| 0.627 | 1 | 0.939 | 6.492 | 0.273 |
| 0.706 | 1 | 0.948 | 5.478 | 0.232 |
| 0.784 | 1 | 0.95 | 5.315 | 0.225 |
| 0.863 | 1 | 0.951 | 5.192 | 0.22 |
| 0.941 | 1 | 0.956 | 4.65 | 0.197 |
| 1.02 | 1 | 0.962 | 3.959 | 0.169 |
| 1.098 | 1 | 0.966 | 3.563 | 0.152 |
| 1.176 | 1 | 0.966 | 3.494 | 0.149 |
| 1.255 | 1 | 0.967 | 3.439 | 0.147 |
| 1.333 | 1 | 0.969 | 3.184 | 0.136 |
| 1.412 | 1 | 0.972 | 2.842 | 0.122 |
| 1.49 | 1 | 0.974 | 2.636 | 0.113 |
| 1.569 | 1 | 0.975 | 2.599 | 0.111 |
| T (us) | SNR Optimal | SNR Pulsed Sinusoid | SNR Improvement (%) | SNR Improvement (dB) |
|---|---|---|---|---|
| 0.157 | 0.658 | 0.116 | 466.904 | 7.535 |
| 0.235 | 0.85 | 0.31 | 174.117 | 4.379 |
| 0.314 | 0.944 | 0.533 | 77.093 | 2.482 |
| 0.392 | 0.982 | 0.701 | 40.071 | 1.463 |
| 0.471 | 0.995 | 0.778 | 27.862 | 1.067 |
| 0.549 | 0.999 | 0.793 | 26.016 | 1.004 |
| 0.627 | 1 | 0.797 | 25.465 | 0.985 |
| 0.706 | 1 | 0.82 | 22.035 | 0.865 |
| 0.784 | 1 | 0.853 | 17.327 | 0.694 |
| 0.863 | 1 | 0.876 | 14.257 | 0.579 |
| 0.941 | 1 | 0.882 | 13.366 | 0.545 |
| 1.02 | 1 | 0.884 | 13.135 | 0.536 |
| 1.098 | 1 | 0.892 | 12.114 | 0.497 |
| 1.176 | 1 | 0.906 | 10.428 | 0.431 |
| 1.255 | 1 | 0.917 | 9.115 | 0.379 |
| 1.333 | 1 | 0.921 | 8.632 | 0.36 |
| 1.412 | 1 | 0.922 | 8.475 | 0.353 |
| 1.49 | 1 | 0.926 | 7.979 | 0.333 |
| 1.569 | 1 | 0.934 | 7.119 | 0.299 |
| T (us) | SNR Optimal | SNR Pulse | SNR Improvement (%) | SNR Improvement (dB) |
|---|---|---|---|---|
| 1.333 | 1.156 | 1.156 | 0.033 | 0.001 |
| 2 | 1.604 | 1.6 | 0.246 | 0.011 |
| 2.667 | 1.968 | 1.956 | 0.622 | 0.027 |
| 3.333 | 2.251 | 2.222 | 1.278 | 0.055 |
| 4 | 2.46 | 2.407 | 2.194 | 0.094 |
| 4.667 | 2.618 | 2.54 | 3.079 | 0.132 |
| 5.333 | 2.737 | 2.639 | 3.739 | 0.159 |
| 6 | 2.83 | 2.716 | 4.196 | 0.178 |
| 6.667 | 2.905 | 2.778 | 4.567 | 0.194 |
| 7.333 | 2.963 | 2.828 | 4.754 | 0.202 |
| 8 | 3.011 | 2.87 | 4.896 | 0.208 |
| 8.667 | 3.049 | 2.906 | 4.927 | 0.209 |
| 9.333 | 3.083 | 2.936 | 4.999 | 0.212 |
| 10 | 3.109 | 2.963 | 4.945 | 0.21 |
| 10.667 | 3.133 | 2.986 | 4.922 | 0.209 |
| 11.333 | 3.152 | 3.006 | 4.833 | 0.205 |
| 12 | 3.172 | 3.025 | 4.865 | 0.206 |
| 12.667 | 3.182 | 3.041 | 4.655 | 0.198 |
| 13.333 | 3.196 | 3.055 | 4.596 | 0.195 |
| T (us) | SNR Optimal | SNR Pulsed Sinusoid | SNR Improvement (%) | SNR Improvement (dB) |
|---|---|---|---|---|
| 1.333 | 1.16 | 0.107 | 977.237 | 10.323 |
| 2 | 1.6 | 0.243 | 560.914 | 8.201 |
| 2.667 | 1.97 | 0.432 | 355.3 | 6.583 |
| 3.333 | 2.25 | 0.668 | 237.134 | 5.278 |
| 4 | 2.46 | 0.912 | 169.635 | 4.308 |
| 4.667 | 2.62 | 1.082 | 142.043 | 3.839 |
| 5.333 | 2.74 | 1.08 | 153.568 | 4.041 |
| 6 | 2.83 | 0.881 | 221.326 | 5.069 |
| 6.667 | 2.91 | 0.636 | 356.915 | 6.598 |
| 7.333 | 2.96 | 0.523 | 466.711 | 7.534 |
| 8 | 3.01 | 0.561 | 437.138 | 7.301 |
| 8.667 | 3.05 | 0.675 | 351.491 | 6.546 |
| 9.333 | 3.08 | 0.79 | 290.506 | 5.916 |
| 10 | 3.11 | 0.838 | 270.845 | 5.692 |
| 10.667 | 3.13 | 0.786 | 298.454 | 6.004 |
| 11.333 | 3.15 | 0.665 | 374.279 | 6.76 |
| 12 | 3.17 | 0.563 | 463.317 | 7.508 |
| 12.667 | 3.18 | 0.544 | 485.44 | 7.675 |
| 13.333 | 3.2 | 0.598 | 434.502 | 7.279 |
| T (us) | SNR Optimal | SNR Pulse | SNR Improvement (%) | SNR Improvement (dB) |
|---|---|---|---|---|
| 0.28 | 0.612 | 0.606 | 1.021 | 0.044 |
| 0.42 | 0.751 | 0.732 | 2.606 | 0.112 |
| 0.56 | 0.829 | 0.798 | 3.832 | 0.163 |
| 0.7 | 0.876 | 0.839 | 4.487 | 0.191 |
| 0.84 | 0.907 | 0.866 | 4.755 | 0.202 |
| 0.98 | 0.927 | 0.885 | 4.806 | 0.204 |
| 1.12 | 0.942 | 0.899 | 4.74 | 0.201 |
| 1.26 | 0.952 | 0.91 | 4.615 | 0.196 |
| 1.4 | 0.96 | 0.919 | 4.46 | 0.19 |
| 1.54 | 0.967 | 0.927 | 4.295 | 0.183 |
| 1.68 | 0.971 | 0.933 | 4.128 | 0.176 |
| 1.82 | 0.975 | 0.938 | 3.964 | 0.169 |
| 1.96 | 0.978 | 0.942 | 3.807 | 0.162 |
| 2.1 | 0.981 | 0.946 | 3.657 | 0.156 |
| 2.24 | 0.983 | 0.95 | 3.516 | 0.15 |
| 2.38 | 0.985 | 0.953 | 3.383 | 0.144 |
| 2.52 | 0.986 | 0.955 | 3.258 | 0.139 |
| 2.66 | 0.988 | 0.958 | 3.14 | 0.134 |
| 2.8 | 0.989 | 0.96 | 3.03 | 0.13 |
| T (us) | SNR Optimal | SNR Pulsed Sinusoid | SNR Improvement (%) | SNR Improvement (dB) |
|---|---|---|---|---|
| 0.28 | 1.16 | 0.153 | 299.306 | 6.013 |
| 0.42 | 1.6 | 0.315 | 138.36 | 3.772 |
| 0.56 | 1.97 | 0.448 | 85.065 | 2.673 |
| 0.7 | 2.25 | 0.545 | 60.775 | 2.062 |
| 0.84 | 2.46 | 0.616 | 47.148 | 1.678 |
| 0.98 | 2.62 | 0.67 | 38.404 | 1.411 |
| 1.12 | 2.74 | 0.712 | 32.273 | 1.215 |
| 1.26 | 2.83 | 0.746 | 27.7 | 1.062 |
| 1.4 | 2.91 | 0.774 | 24.133 | 0.939 |
| 1.54 | 2.96 | 0.797 | 21.254 | 0.837 |
| 1.68 | 3.01 | 0.817 | 18.866 | 0.751 |
| 1.82 | 3.05 | 0.835 | 16.844 | 0.676 |
| 1.96 | 3.08 | 0.85 | 15.1 | 0.611 |
| 2.1 | 3.11 | 0.864 | 13.574 | 0.553 |
| 2.24 | 3.13 | 0.876 | 12.219 | 0.501 |
| 2.38 | 3.15 | 0.887 | 11.009 | 0.454 |
| 2.52 | 3.17 | 0.897 | 9.916 | 0.411 |
| 2.66 | 3.18 | 0.907 | 8.922 | 0.371 |
| 2.8 | 3.2 | 0.915 | 8.012 | 0.335 |
Appendix B

References
- Suzuki, K.; Yamashita, Y.; Ohta, K.; Kaneko, M.; Yoshida, M.; Chance, B. Quantitative measurement of optical parameters in normal breasts using time-resolved spectroscopy: In vivo results of 30 Japanese women. J. Biomed. Opt. 1996, 1, 330. [Google Scholar] [CrossRef] [PubMed]
- Wells, P.N.T. Ultrasonic imaging of the human body. Rep. Prog. Phys. 1999, 62, 671–722. [Google Scholar] [CrossRef] [Green Version]
- Kruger, R.A.; Reinecke, D.R.; Kruger, G.A. Thermoacoustic computed tomography–technical considerations. Med. Phys. 1999, 26, 1832–1837. [Google Scholar] [CrossRef] [PubMed]
- Kruger, R.A.; Kopecky, K.K.; Aisen, A.M.; Reinecke, D.R.; Kruger, G.A.; Kiser, W.L. Thermoacoustic CT with Radio Waves: A Medical Imaging Paradigm. Radiology 1999, 211, 275–278. [Google Scholar] [CrossRef] [PubMed]
- Ku, G.; Wang, L.V. Scanning thermoacoustic tomography in biological tissue. Med. Phys. 2000, 27, 1195–1202. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; Wang, L.V. Time-domain reconstruction for thermoacoustic tomography in a spherical geometry. IEEE Trans. Med. Imaging 2002, 21, 814–822. [Google Scholar] [PubMed] [Green Version]
- Xu, M.; Xu, Y.; Wang, L.V. Time-domain reconstruction algorithms and numerical simulations for thermoacoustic tomography in various geometries. IEEE Trans. Biomed. Eng. 2003, 50, 1086–1099. [Google Scholar] [PubMed] [Green Version]
- Telenkov, S.A.; Mandelis, A. Photothermoacoustic imaging of biological tissues: Maximum depth characterization comparison of time and frequency-domain measurements. J. Biomed. Opt. 2009, 14, 044025. [Google Scholar] [CrossRef] [PubMed]
- Telenkov, S.; Mandelis, A. Signal-to-noise analysis of biomedical photoacoustic measurements in time and frequency domains. Rev. Sci. Instrum. 2010, 81, 124901. [Google Scholar] [CrossRef]
- Lashkari, B.; Mandelis, A. Photoacoustic radar imaging signal-to-noise ratio, contrast, and resolution enhancement using nonlinear chirp modulation. Opt. Lett. 2010, 35, 1623–1625. [Google Scholar] [CrossRef] [PubMed]
- Lashkari, B.; Mandelis, A. Comparison between pulsed laser and frequency-domain photoacoustic modalities: Signal-to-noise ratio, contrast, resolution, and maximum depth detectivity. Rev. Sci. Instrum. 2011, 82, 094903. [Google Scholar] [CrossRef] [PubMed]
- Lashkari, B.; Mandelis, A. Linear frequency modulation photoacoustic radar: Optimal bandwidth and signal-to-noise ratio for frequency-domain imaging of turbid media. J. Acoust. Soc. Am. 2011, 130, 1313–1324. [Google Scholar] [CrossRef] [Green Version]
- Telenkov, S.A.; Alwi, R.; Mandelis, A. Photoacoustic correlation signal-to-noise ratio enhancement by coherent averaging and optical waveform optimization. Rev. Sci. Instrum. 2013, 84, 104907. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lashkari, B.; Mandelis, A. Features of the Frequency- and Time-Domain Photoacoustic Modalities. Int. J. Thermophys. 2013, 34, 1398–1404. [Google Scholar] [CrossRef]
- Baddour, N.; Mandelis, A. The Effect of Acoustic Impedance on Subsurface Absorber Geometry Reconstruction using 1D Frequency-Domain Photoacoustics. Photoacoustics 2015, 3, 132–142. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alwi, R.; Telenkov, S.; Mandelis, A.; Leshuk, T.; Gu, F.; Oladepo, S.; Michaelian, K. Silica-coated super paramagnetic iron oxide nanoparticles (SPION) as biocompatible contrast agent in biomedical photoacoustics. Biomed. Opt. Express 2012, 3, 2500–2509. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, X.; Bauer, D.R.; Vollin, J.L.; Manzi, D.G.; Witte, R.S.; Xin, H. Impact of Microwave Pulses on Thermoacoustic Imaging Applications. IEEE Antennas Wirel. Propag. Lett. 2012, 11, 1634–1637. [Google Scholar] [CrossRef]
- Sun, Z.; Baddour, N.; Mandelis, A. Waveform engineering analysis of photoacoustic radar chirp parameters for spatial resolution and SNR optimization. Photoacoustics 2019, 14, 49–66. [Google Scholar] [CrossRef]
- Bell, M.R. Information theory and radar waveform design. IEEE Trans. Inf. Theory 1993, 39, 1578–1597. [Google Scholar] [CrossRef] [Green Version]
- Jangjoo, A.; Lashkari, B.; Sivagurunathan, K.; Mandelis, A.; Baezzat, M.R. Truncated correlation photoacoustic coherence tomography: An axial resolution enhancement imaging modality. Photoacoustics 2021, 23, 100277. [Google Scholar] [CrossRef]
- Zhao, W.; Yu, H.; Wen, Y.; Li, P.; Wang, X.; Wang, F.; Yang, Y.; Liu, L.; Li, W.J. Improving photoacoustic-imaging axial positioning accuracy and signal-to-noise ratio using acoustic echo effect. Sens. Actuators Phys. 2021, 329, 112788. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, L. Adaptive dual-speed ultrasound and photoacoustic computed tomography. Photoacoustics 2022, 27, 100380. [Google Scholar] [CrossRef] [PubMed]
- Kukačka, J.; Metz, S.; Dehner, C.; Muckenhuber, A.; Paul-Yuan, K.; Karlas, A.; Fallenberg, E.M.; Rummeny, E.; Jüstel, D.; Ntziachristos, V. Image processing improvements afford second-generation handheld optoacoustic imaging of breast cancer patients. Photoacoustics 2022, 26, 100343. [Google Scholar] [CrossRef] [PubMed]
- Cebrecos, A.; García-Garrigós, J.J.; Descals, A.; Jiménez, N.; Benlloch, J.M.; Camarena, F. Beamforming for large-area scan and improved SNR in array-based photoacoustic microscopy. Ultrasonics 2021, 111, 106317. [Google Scholar] [CrossRef] [PubMed]
- Gerald, J. Diebold Photoacoustic Monopole Radiation. In Photoacoustic Imaging and Spectroscopy; Optical Science and Engineering; CRC Press: Boca Raton, FL, USA, 2009; pp. 3–17. ISBN 978-1-4200-5991-5. [Google Scholar]
- Klauder, J.R.; Price, A.C.; Darlington, S.; Albersheim, W.J. The Theory and Design of Chirp Radars. Bell Syst. Tech. J. 1960, 39, 745–808. [Google Scholar] [CrossRef]
- Mamou, J.; Ketterling, J.A.; Silverman, R.H. High-frequency Pulse-compression Ultrasound Imaging with an Annular Array. In Acoustical Imaging; Akiyama, I., Ed.; Springer Netherlands: Dordrecht, The Netherlands, 2009; pp. 81–86. [Google Scholar]
- Qin, Y.; Wang, Z.; Ingram, P.; Li, Q.; Witte, R.S. Optimizing Frequency and Pulse Shape for Ultrasound Current Source Density Imaginag. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2012, 59, 2149–2155. [Google Scholar] [PubMed] [Green Version]
- Hague, D.A.; Buck, J.R. The Generalized Sinusoidal Frequency-Modulated Waveform for Active Sonar. IEEE J. Ocean. Eng. 2017, 42, 109–123. [Google Scholar]
- Wang, Y.; Yang, J. Continuous Transmission Frequency Modulation Detection under Variable Sonar-Target Speed Conditions. Sensors 2013, 13, 3549–3567. [Google Scholar] [CrossRef]
- Hassani, S. Mathematical Physics: A Modern Introduction to Its Foundations; Springer Science & Business Media: Berlin, Germany, 2013; ISBN 978-3-319-01195-0. [Google Scholar]
- Islam, M.S.; Chong, U. Noise reduction of continuous wave radar and pulse radar using matched filter and wavelets. EURASIP J. Image Video Process. 2014, 2014, 43. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Z.; Zhao, A.; Hui, J.; Hou, B.; Sotudeh, R.; Niu, F. A Frequency-Domain Adaptive Matched Filter for Active Sonar Detection. Sensors 2017, 17, 1565. [Google Scholar] [CrossRef] [Green Version]
- Hill, C.R.; Bamber, J.C.; Haar, G. Physical Principles of Medical Ultrassonics, 2nd ed.; John Wiley & Sons: Chichester, UK, 2004; ISBN 978-0-470-09396-2. [Google Scholar]
- Telenkov, S.; Mandelis, A.; Lashkari, B.; Forcht, M. Frequency-domain photothermoacoustics: Alternative imaging modality of biological tissues. J. Appl. Phys. 2009, 105, 102029. [Google Scholar] [CrossRef]
- Moh, T.T. Algebra; Series on University Mathematics; Version 5; World Scientific: Singapore, 1992; ISBN 978-981-02-1195-0. [Google Scholar]
- Lou, C.; Nie, L.; Xu, D. Effect of excitation pulse width on thermoacoustic signal characteristics and the corresponding algorithm for optimization of imaging resolution. J. Appl. Phys. 2011, 110, 083101. [Google Scholar] [CrossRef]
- Liu, S.; Zhao, Z.; Zhu, X.; Wang, Z.-L.; Song, J.; Wang, B.; Gong, Y.-B.; Nie, Z.-P.; Liu, Q.H. Analysis of Short Pulse Impacting on Microwave Induced Thermo-Acoustic Tomography. Prog. Electromagn. Res. C 2016, 61, 37–46. [Google Scholar] [CrossRef]
- Qin, T.; Wang, X.; Meng, H.; Qin, Y.; Wan, G.; Witte, R.S.; Xin, H. Performance improvement for thermoacoustic imaging using compressive sensing. In Proceedings of the 2014 IEEE Antennas and Propagation Society International Symposium (APSURSI), Memphis, TN, USA, 6–11 July 2014; pp. 1919–1920. [Google Scholar]










Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baddour, N.; Sun, Z. Photoacoustics Waveform Design for Optimal Signal to Noise Ratio. Symmetry 2022, 14, 2233. https://doi.org/10.3390/sym14112233
Baddour N, Sun Z. Photoacoustics Waveform Design for Optimal Signal to Noise Ratio. Symmetry. 2022; 14(11):2233. https://doi.org/10.3390/sym14112233
Chicago/Turabian StyleBaddour, Natalie, and Zuwen Sun. 2022. "Photoacoustics Waveform Design for Optimal Signal to Noise Ratio" Symmetry 14, no. 11: 2233. https://doi.org/10.3390/sym14112233





