Generating Many Majorana Corner Modes and Multiple Phase Transitions in Floquet Second-Order Topological Superconductors
Abstract
:1. Introduction
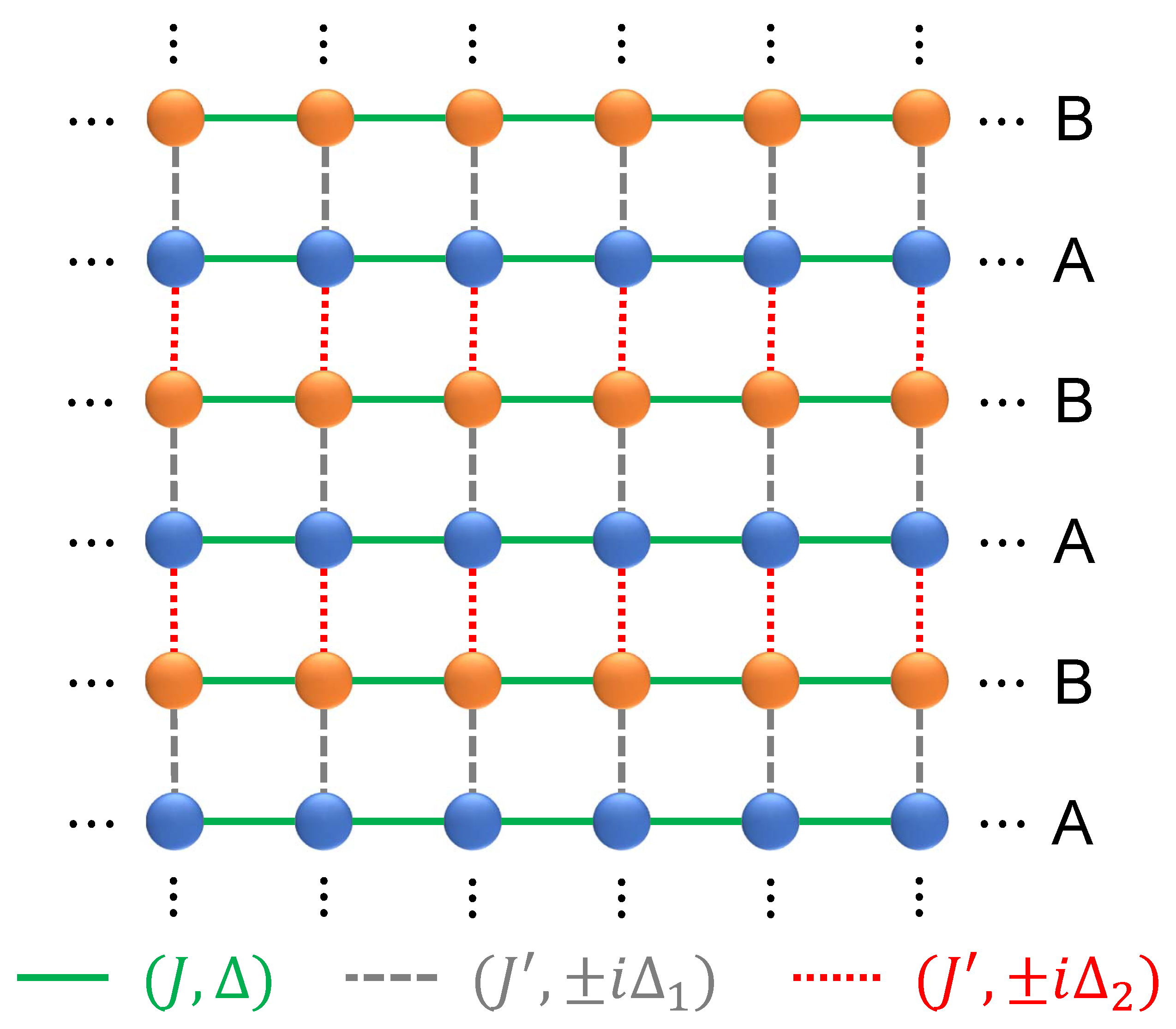
2. Model
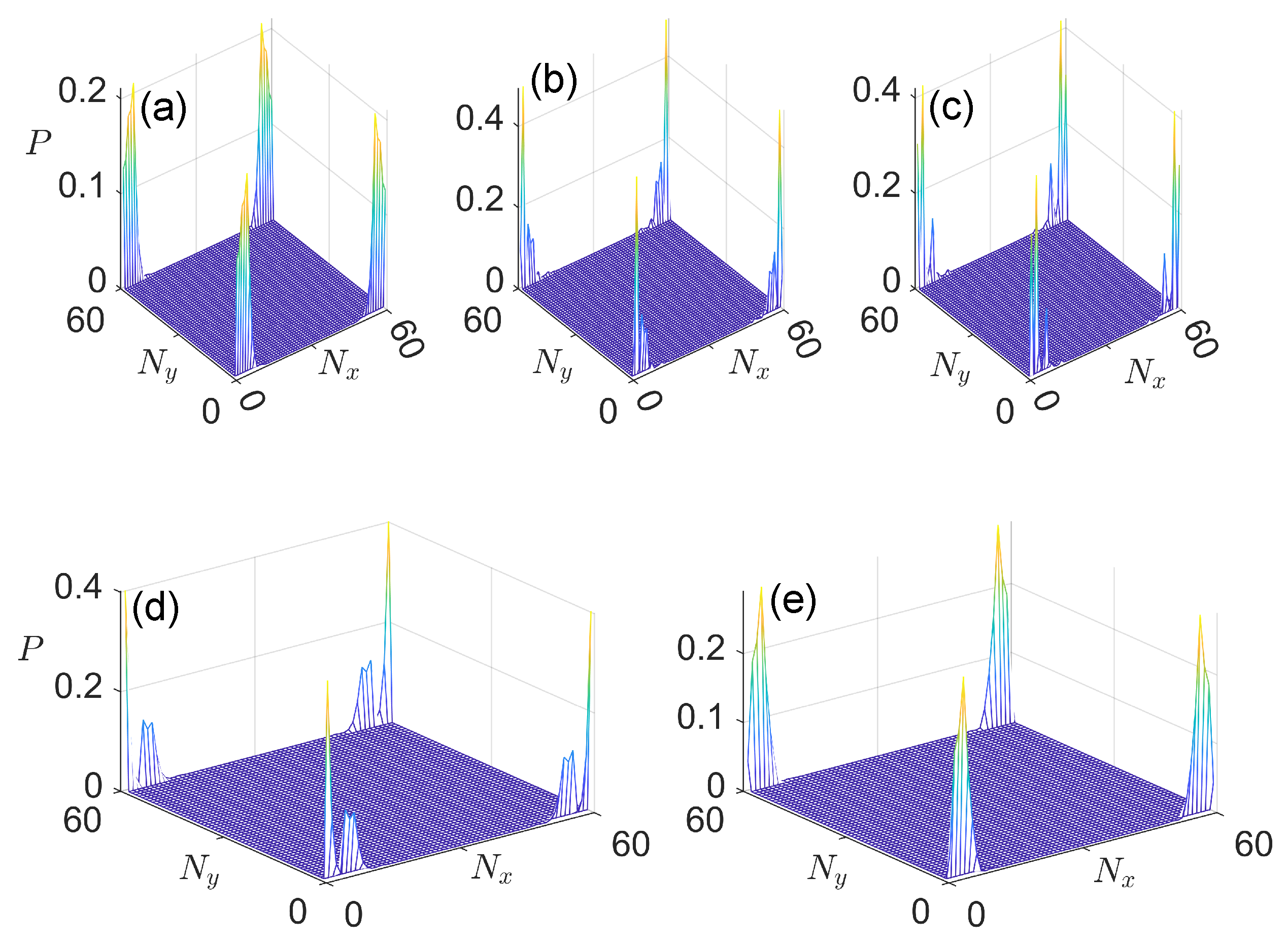
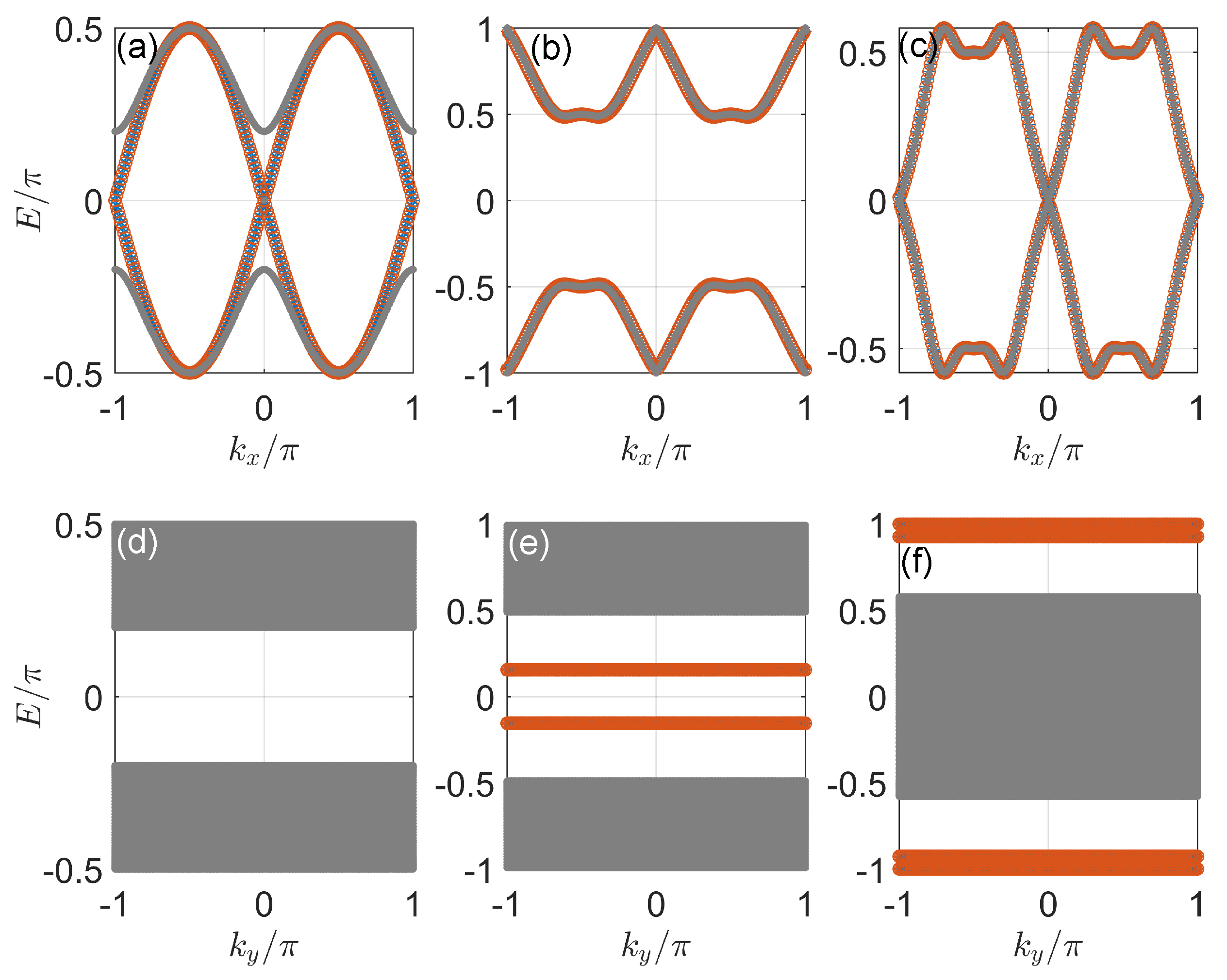
3. Results
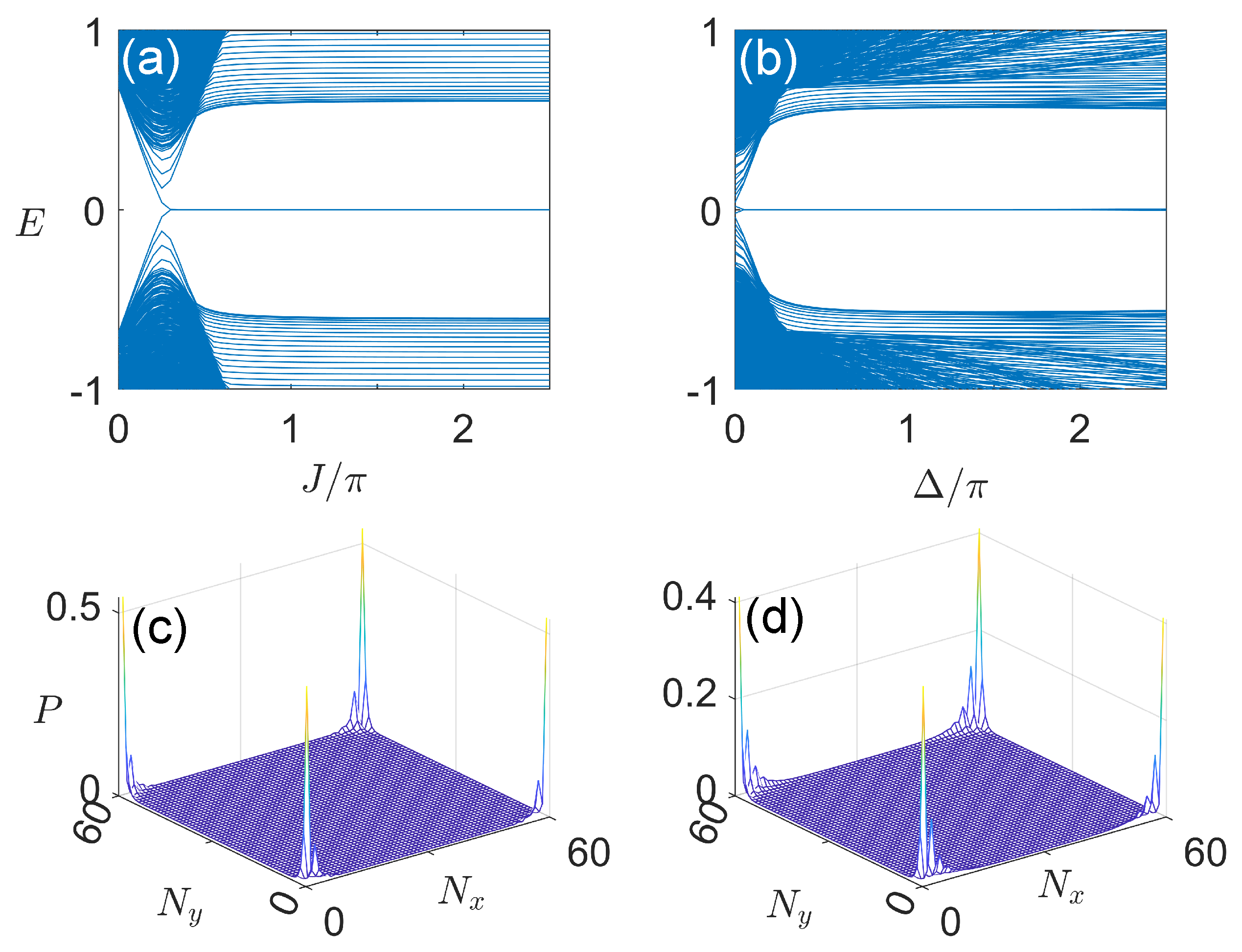
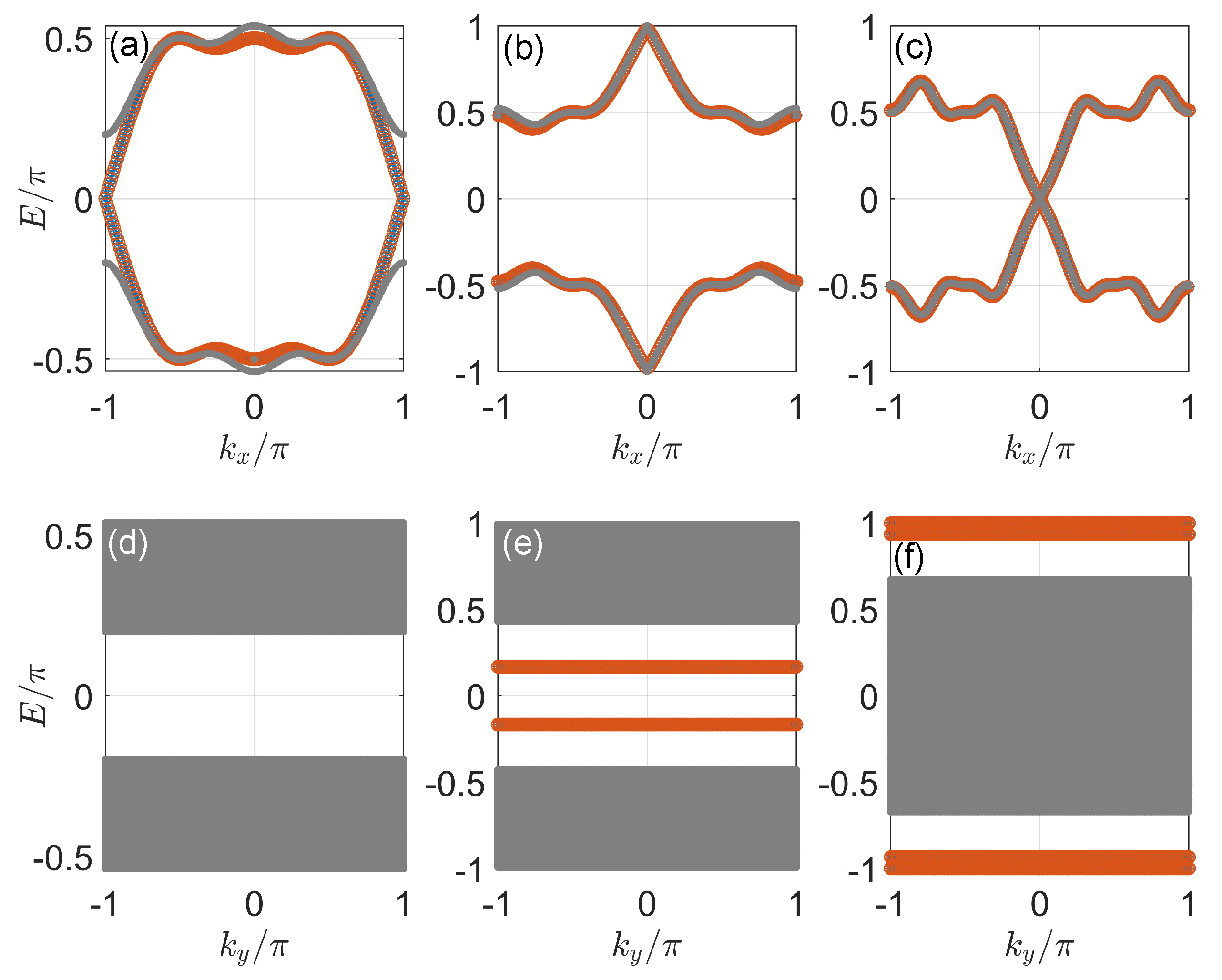
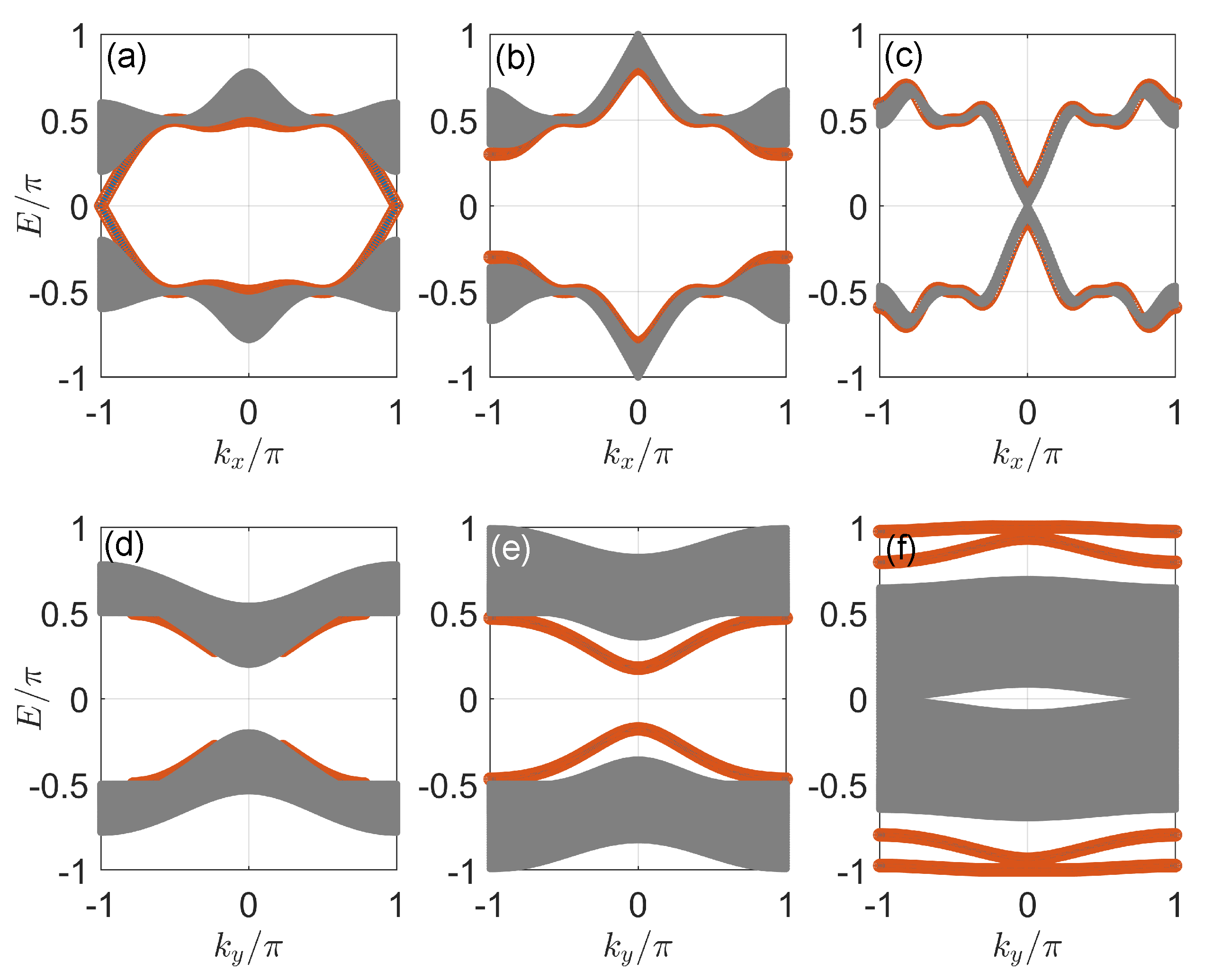
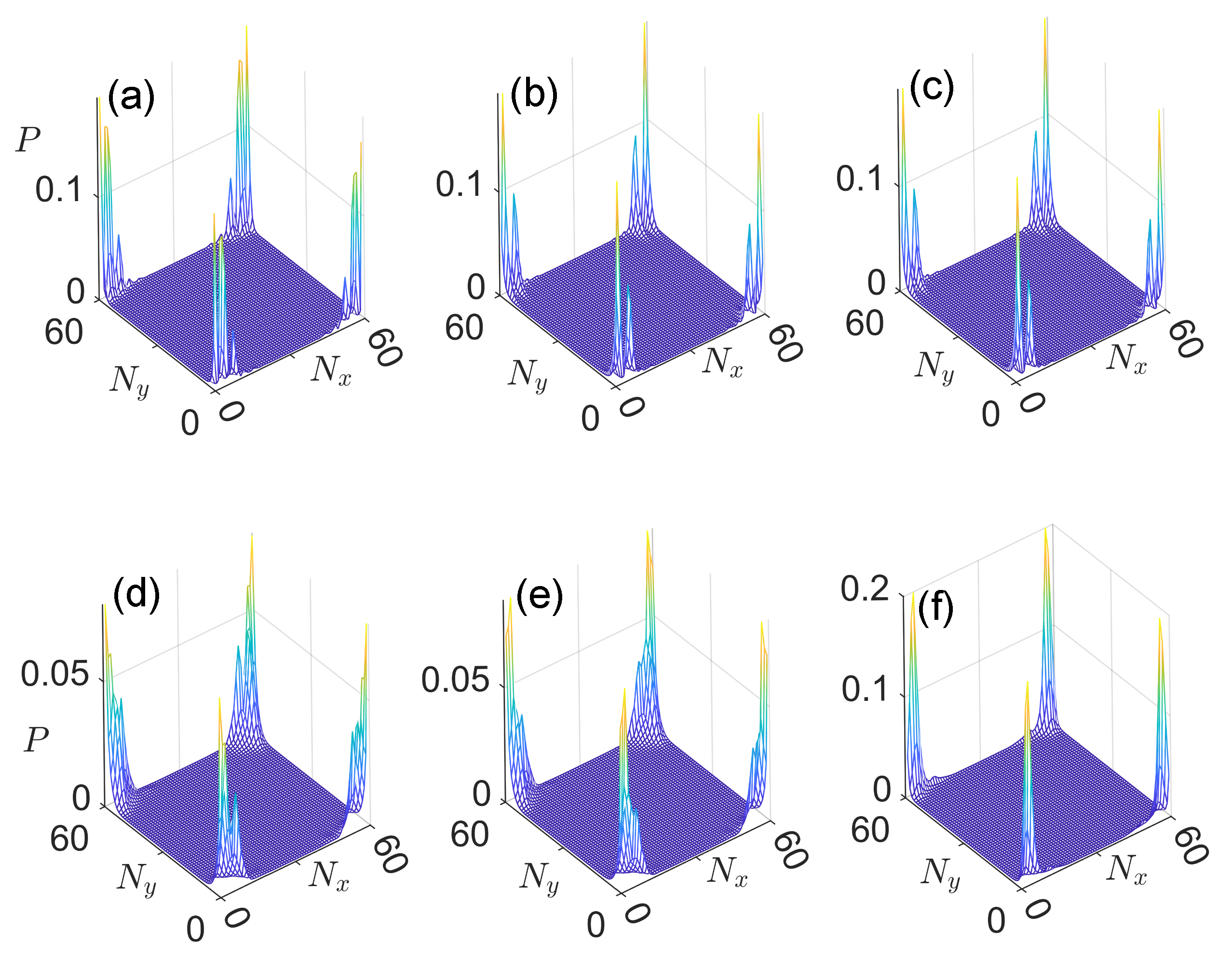
3.1. Case 1:
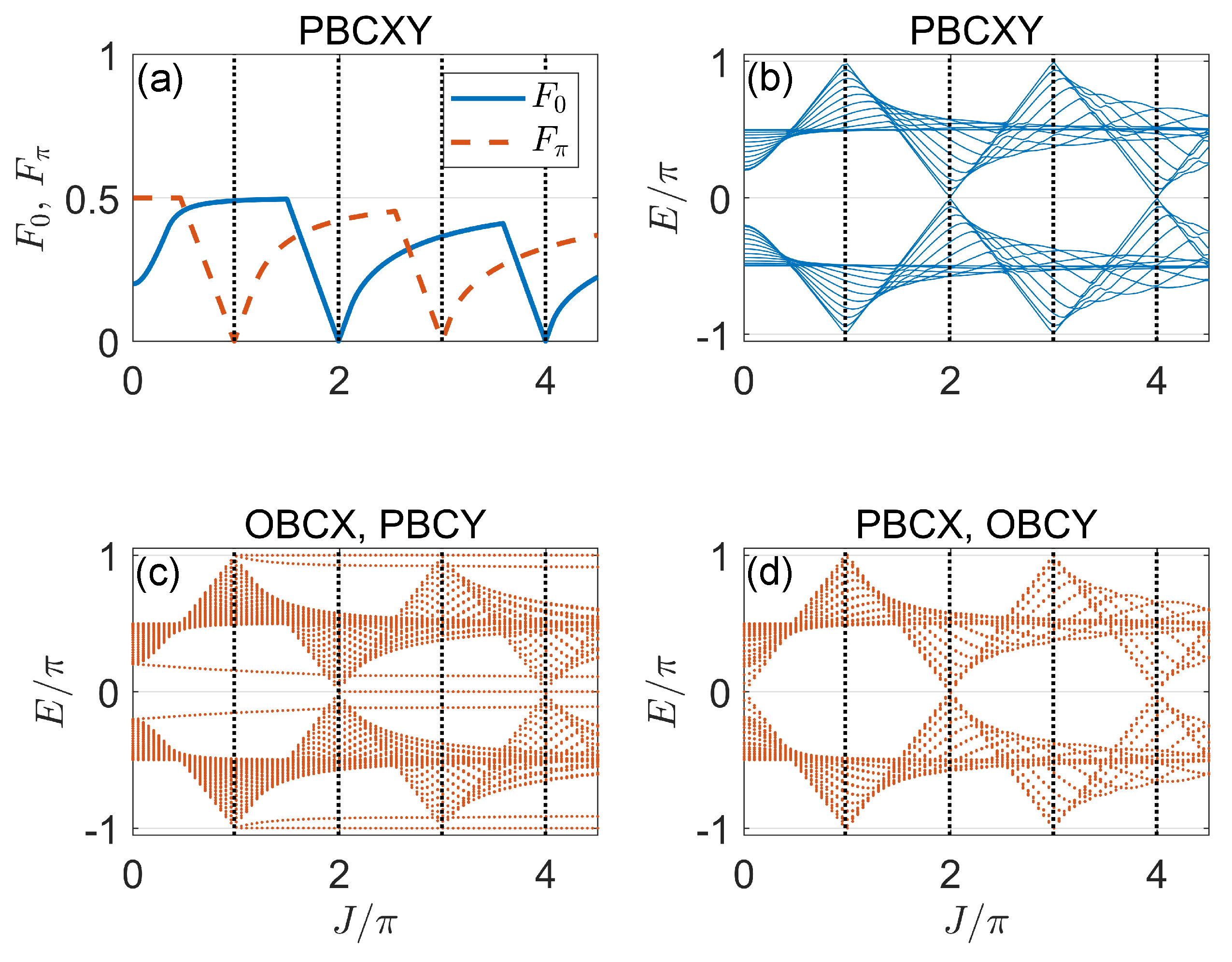
3.2. Case 2:
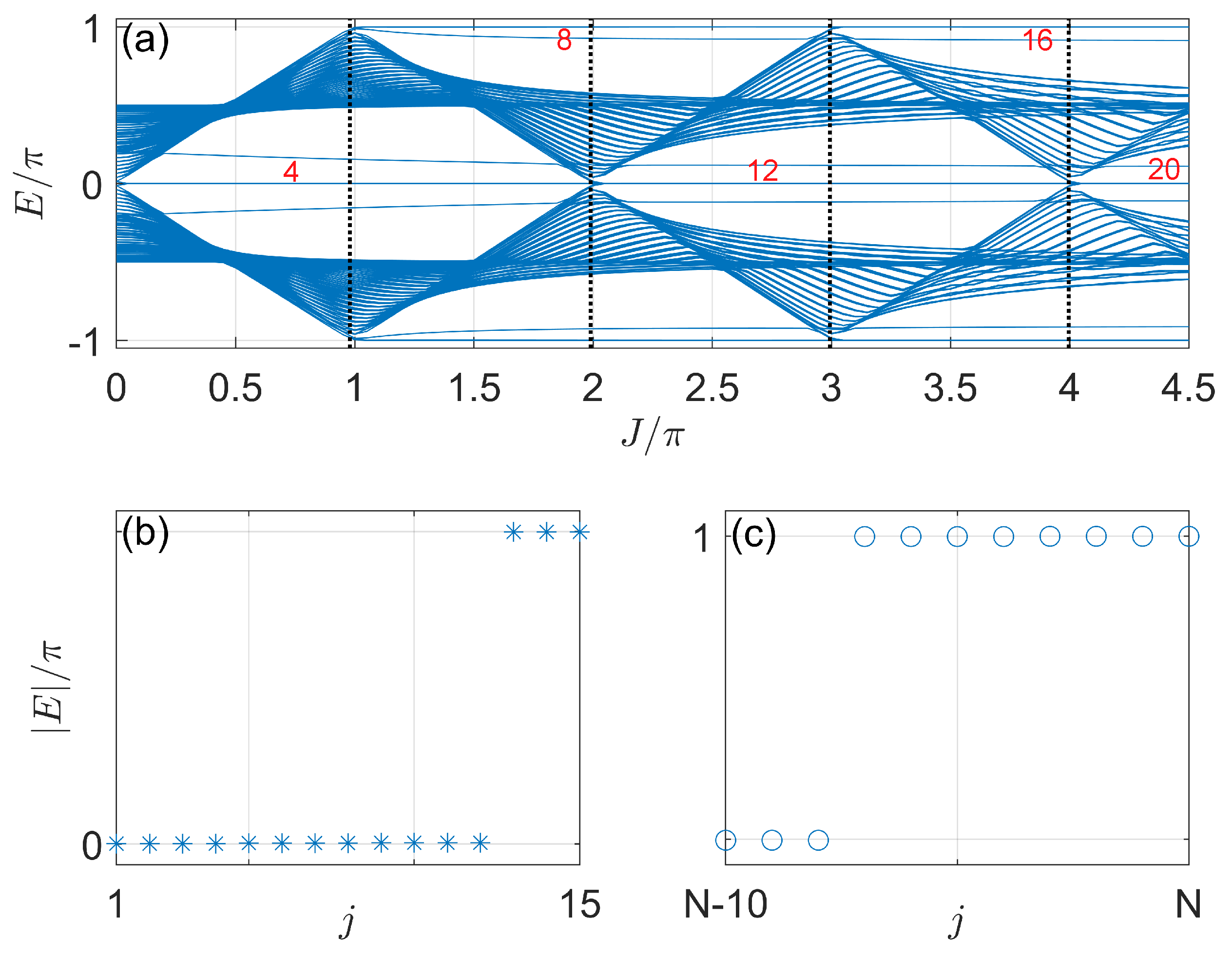
3.3. Case 3:
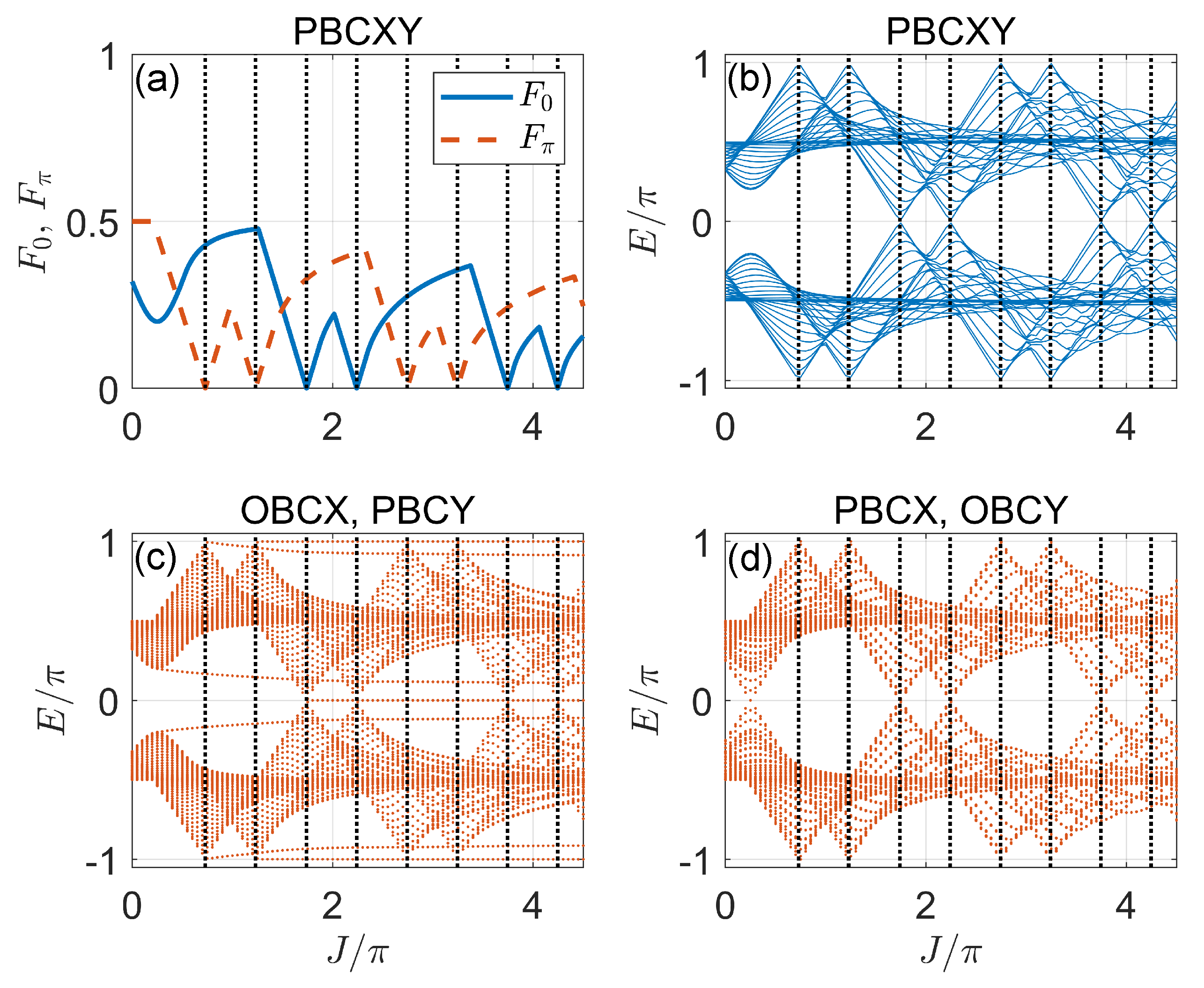
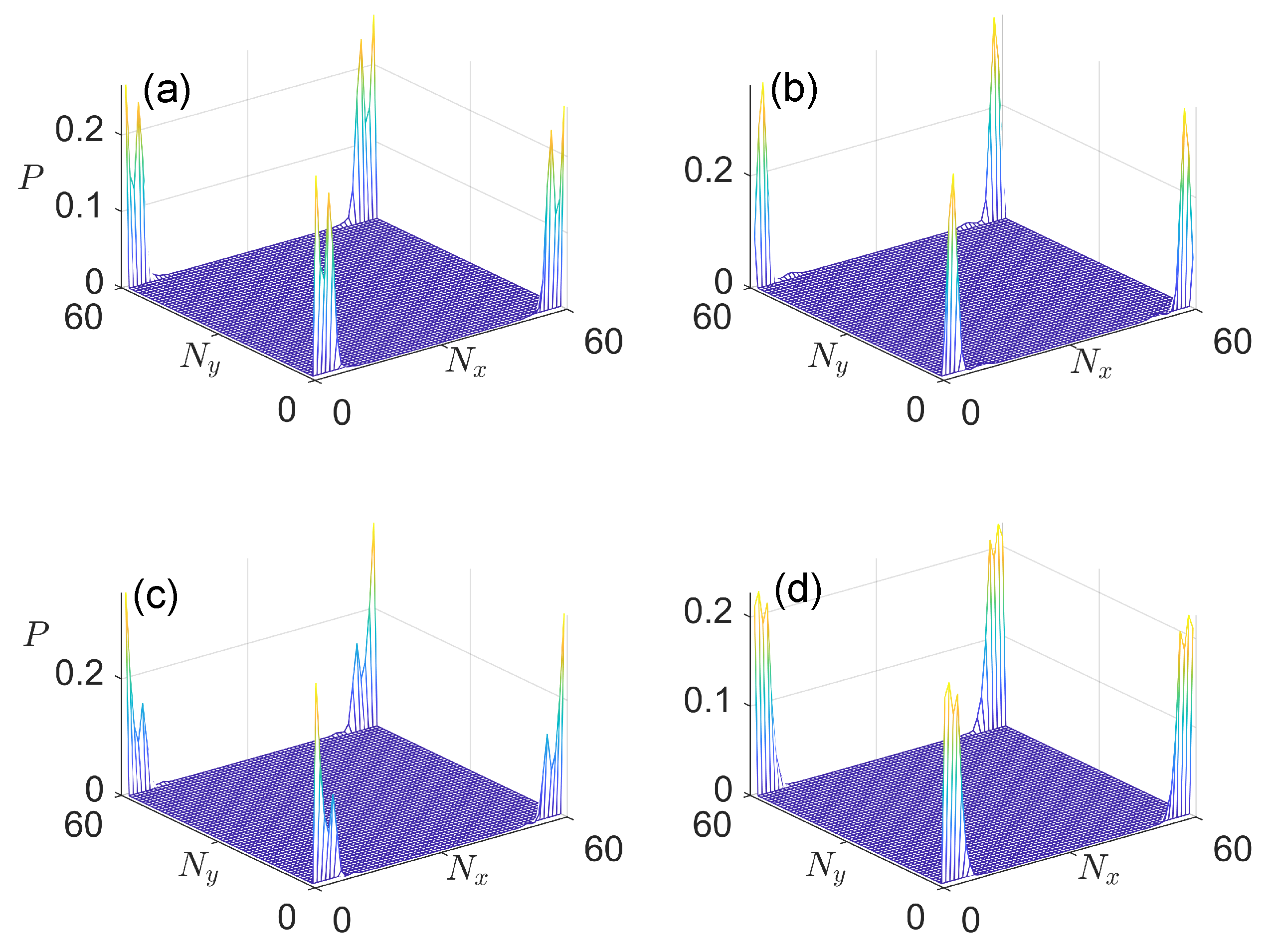
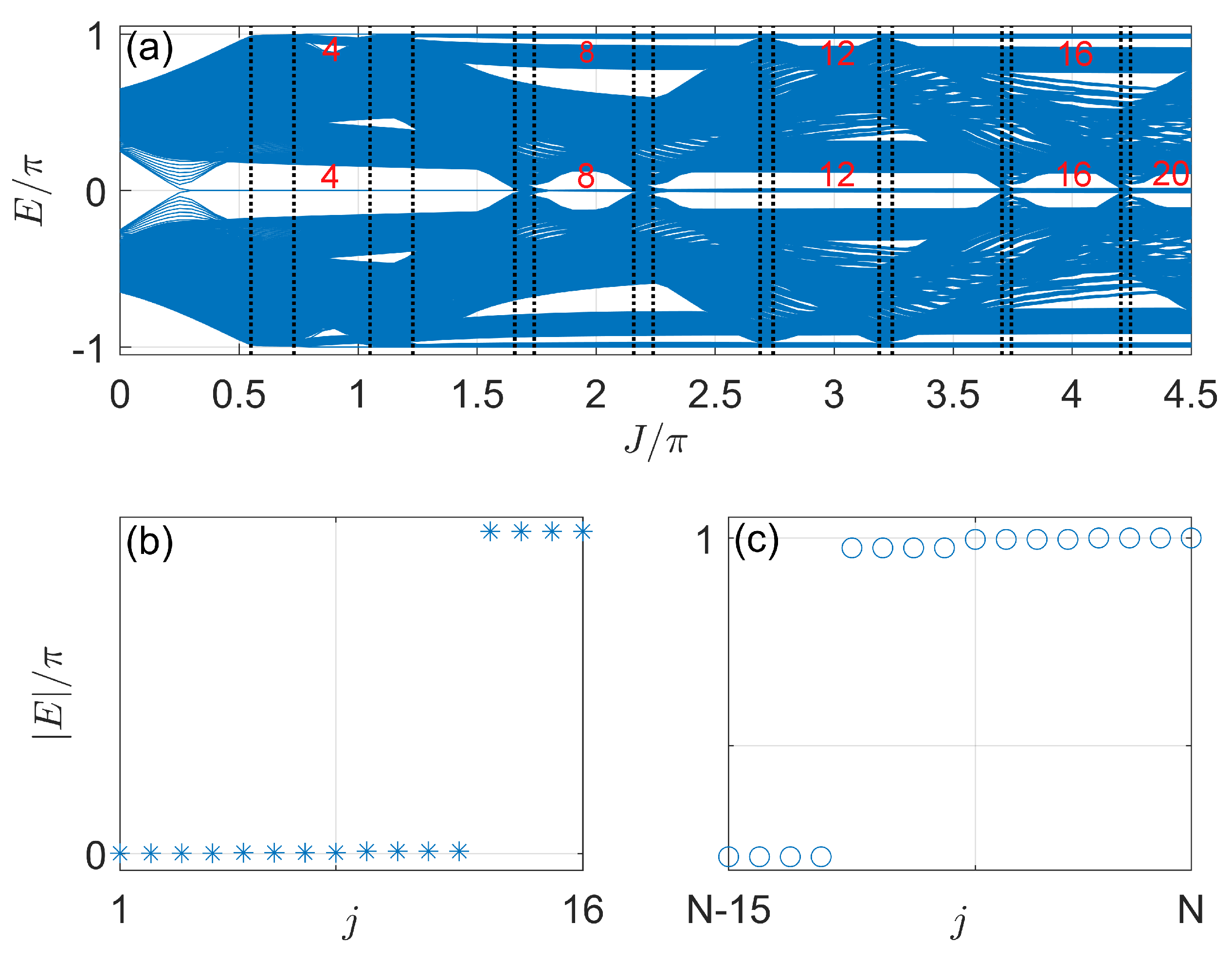
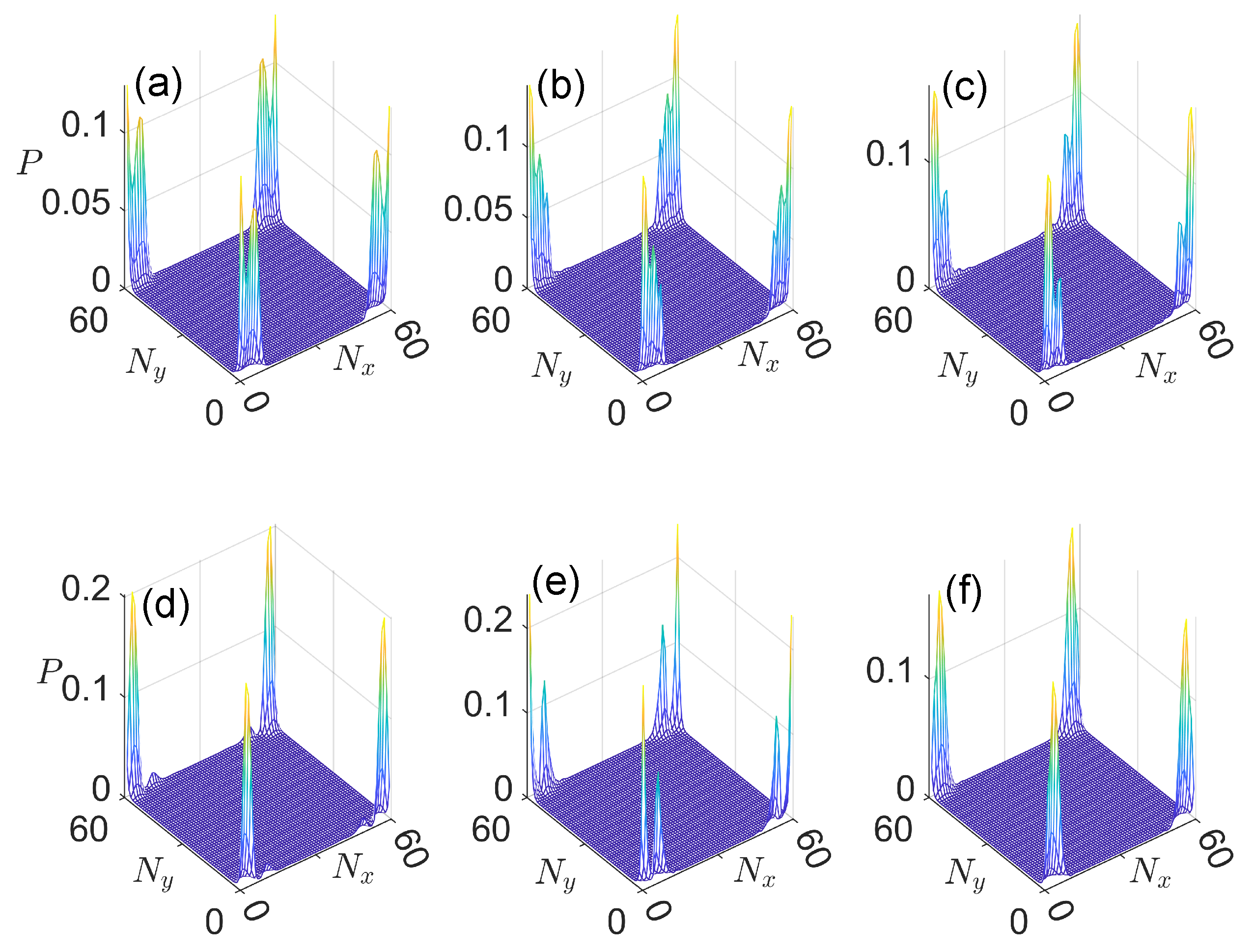
3.4. Case 4: General Situation
4. Discussion and Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cayssol, J.; Dóra, B.; Simon, F.; Moessner, R. Floquet topological insulators. Phys. Status Solidi RRL 2013, 7, 101. [Google Scholar] [CrossRef] [Green Version]
- Eckardt, A. Colloquium: Atomic quantum gases in periodically driven optical lattices. Rev. Mod. Phys. 2017, 89, 011004. [Google Scholar] [CrossRef] [Green Version]
- Harper, F.; Roy, R.; Rudner, M.S.; Sondhi, S. Topology and Broken Symmetry in Floquet Systems. Annu. Rev. Condens. Matter Phys. 2020, 11, 345. [Google Scholar] [CrossRef] [Green Version]
- Rudner, M.; Lindner, N. Band structure engineering and non-equilibrium dynamics in Floquet topological insulators. Nat. Rev. Phys. 2020, 2, 229. [Google Scholar] [CrossRef]
- Nathan, F.; Rudner, M.S. Topological singularities and the general classification of Floquet-Bloch systems. New J. Phys. 2015, 17, 125014. [Google Scholar] [CrossRef] [Green Version]
- Potter, A.C.; Morimoto, T.; Vishwanath, A. Classification of Interacting Topological Floquet Phases in One Dimension. Phys. Rev. X 2016, 6, 041001. [Google Scholar] [CrossRef] [Green Version]
- Roy, R.; Harper, F. Periodic table for Floquet topological insulators. Phys. Rev. B 2017, 96, 155118. [Google Scholar] [CrossRef] [Green Version]
- Yu, J.; Zhang, R.-X.; Song, Z.-D. Dynamical symmetry indicators for Floquet crystals. Nat. Commun. 2021, 12, 5985. [Google Scholar] [CrossRef] [PubMed]
- Rudner, M.S.; Lindner, N.H.; Berg, E.; Levin, M. Anomalous Edge States and the Bulk-Edge Correspondence for Periodically Driven Two-Dimensional Systems. Phys. Rev. X 2013, 3, 031005. [Google Scholar] [CrossRef] [Green Version]
- Titum, P.; Berg, E.; Rudner, M.S.; Refael, G.; Lindner, N. Anomalous Floquet-Anderson Insulator as a Nonadiabatic Quantized Charge Pump. Phys. Rev. X 2016, 6, 021013. [Google Scholar] [CrossRef]
- Zhou, L.; Gong, J. Recipe for creating an arbitrary number of Floquet chiral edge states. Phys. Rev. B 2018, 97, 245430. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Delplace, P.; Fleury, R. Superior robustness of anomalous non-reciprocal topological edge states. Nature 2021, 598, 293–297. [Google Scholar] [CrossRef] [PubMed]
- Ho, D.Y.H.; Gong, J. Quantized Adiabatic Transport In Momentum Space. Phys. Rev. Lett. 2012, 109, 010601. [Google Scholar] [CrossRef] [Green Version]
- Tong, Q.-J.; An, J.-H.; Gong, J.; Luo, H.-G.; Oh, C.H. Generating many Majorana modes via periodic driving: A superconductor model. Phys. Rev. B 2013, 87, 201109. [Google Scholar] [CrossRef] [Green Version]
- Zhou, L.; Wang, H.; Ho, D.Y.H.; Gong, J. Aspects of Floquet bands and topological phase transitions in a continuously driven superlattice. Eur. Phys. J. B 2014, 87, 204. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.-Z.; Lam, C.-H.; You, J.Q. Floquet engineering of long-range p-wave superconductivity: Beyond the high-frequency limit. Phys. Rev. B 2017, 96, 155438. [Google Scholar] [CrossRef] [Green Version]
- Zhou, L.; Gong, J. Floquet topological phases in a spin-1/2 double kicked rotor. Phys. Rev. A 2018, 97, 063603. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.H.; Steinberg, H.; Jarillo-Herrero, P.; Gedik, N. Observation of Floquet-Bloch States on the Surface of a Topological Insulator. Science 2013, 342, 453–457. [Google Scholar] [CrossRef] [Green Version]
- Yang, K.; Zhou, L.; Ma, W.; Kong, X.; Wang, P.; Qin, X.; Rong, X.; Wang, Y.; Shi, F.; Gong, J.; et al. Floquet dynamical quantum phase transitions. Phys. Rev. B 2019, 100, 085308. [Google Scholar] [CrossRef] [Green Version]
- McIver, J.W.; Schulte, B.; Stein, F.-U.; Matsuyama, T.; Jotzu, G.; Meier, G.; Cavalleri, A. Light-induced anomalous Hall effect in graphene. Nat. Phys. 2020, 16, 38–41. [Google Scholar] [CrossRef]
- Chen, B.; Li, S.; Hou, X.; Ge, F.; Zhou, F.; Qian, P.; Mei, F.; Jia, S.; Xu, N.; Shen, H. Digital quantum simulation of Floquet topological phases with a solid-state quantum simulator. Photon. Res. 2021, 9, 81–87. [Google Scholar] [CrossRef]
- Jotzu, G.; Messer, M.; Desbuquois, R.; Lebrat, M.; Uehlinger, T.; Greif, D.; Esslinger, T. Experimental realization of the topological Haldane model with ultracold fermions. Nature 2014, 515, 237–240. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fläschner, N.; Rem, B.S.; Tarnowski, M.; Vogel, D.; Lühmann, K.; Sengstock, K.; Weitenberg, C. Experimental reconstruction of the Berry curvature in a Floquet Bloch band. Science 2016, 352, 1091–1094. [Google Scholar] [CrossRef] [Green Version]
- Asteria, L.; Tran, D.T.; Ozawa, T.; Tarnowski, M.; Rem, B.S.; Fläschner, N.; Sengstock, K.; Goldman, N.; Weitenberg, C. Measuring quantized circular dichroism in ultracold topological matter. Nat. Phys. 2019, 15, 449–454. [Google Scholar] [CrossRef] [Green Version]
- Wintersperger, K.; Braun, C.; Ünal, F.N.; Eckardt, A.; Liberto, M.D.; Goldman, N.; Bloch, I.; Aidelsburger, M. Realization of an anomalous Floquet topological system with ultracold atoms. Nat. Phys. 2020, 16, 1058–1063. [Google Scholar] [CrossRef]
- Kitagawa, T.; Broome, M.A.; Fedrizzi, A.; Rudner, M.S.; Berg, E.; Kassal, I.; Aspuru-Guzik, A.; Demler, E.; White, A.G. Observation of topologically protected bound states in photonic quantum walks. Nat. Commun. 2012, 3, 882. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rechtsman, M.C.; Zeuner, J.M.; Plotnik, Y.; Lumer, Y.; Podolsky, D.; Dreisow, F.; Nolte, S.; Segev, M.; Szameit, A. Photonic Floquet topological insulators. Nature 2013, 496, 196–200. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hu, W.; Pillay, J.C.; Wu, K.; Pasek, M.; Shum, P.P.; Chong, Y.D. Measurement of a Topological Edge Invariant in a Microwave Network. Phys. Rev. X 2015, 5, 011012. [Google Scholar] [CrossRef] [Green Version]
- Mukherjee, S.; Spracklen, A.; Valiente, M.; Andersson, E.; Öhberg, P.; Goldman, N.; Thomson, R.R. Experimental observation of anomalous topological edge modes in a slowly driven photonic lattice. Nat. Commun. 2017, 8, 13918. [Google Scholar] [CrossRef] [Green Version]
- Oka, T.; Kitamura, S. Floquet Engineering of Quantum Materials. Annu. Rev. Condens. Matter Phys. 2019, 10, 387–408. [Google Scholar] [CrossRef]
- Bomantara, R.W.; Gong, J. Simulation of Non-Abelian Braiding in Majorana Time Crystals. Phys. Rev. Lett. 2018, 120, 230405. [Google Scholar] [CrossRef] [Green Version]
- Sitte, M.; Rosch, A.; Altman, E.; Fritz, L. Topological Insulators in Magnetic Fields: Quantum Hall Effect and Edge Channels with a Nonquantized θ Term. Phys. Rev. Lett. 2012, 108, 126807. [Google Scholar] [CrossRef] [Green Version]
- Zhang, F.; Kane, C.L.; Mele, E.J. Surface State Magnetization and Chiral Edge States on Topological Insulators. Phys. Rev. Lett. 2013, 110, 046404. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Slager, R.-J.; Rademaker, L.; Zaanen, J.; Balents, L. Impurity-bound states and Green’s function zeros as local signatures of topology. Phys. Rev. B 2015, 92, 085126. [Google Scholar] [CrossRef] [Green Version]
- Benalcazar, W.A.; Bernevig, B.A.; Hughes, T.L. Quantized electric multipole insulators. Science 2017, 357, 61–66. [Google Scholar] [CrossRef] [Green Version]
- Benalcazar, W.A.; Bernevig, B.A.; Hughes, T.L. Electric multipole moments, topological multipole moment pumping, and chiral hinge states in crystalline insulators. Phys. Rev. B 2017, 96, 245115. [Google Scholar] [CrossRef] [Green Version]
- Langbehn, J.; Peng, Y.; Trifunovic, L.; von Oppen, F.; Brouwer, P.W. Reflection-symmetric second-order topological insulators and superconductors. Phys. Rev. Lett. 2017, 119, 246401. [Google Scholar] [CrossRef] [Green Version]
- Song, Z.; Fang, Z.; Fang, C. (d − 2)-Dimensional edge states of rotation symmetry protected topological states. Phys. Rev. Lett. 2017, 119, 246402. [Google Scholar] [CrossRef] [Green Version]
- Schindler, F.; Cook, A.M.; Vergniory, M.G.; Wang, Z.; Parkin, S.S.P.; Bernevig, B.A.; Neupert, T. Higher-order topological insulators. Sci. Adv. 2018, 4, eaat0346. [Google Scholar] [CrossRef] [Green Version]
- Geier, M.; Trifunovic, L.; Hoskam, M.; Brouwer, P.W. Second-order topological insulators and superconductors with an order-two crystalline symmetry. Phys. Rev. B 2018, 97, 205135. [Google Scholar] [CrossRef]
- Kim, M.; Jacob, Z.; Rho, J. Recent advances in 2D, 3D and higher-order topological photonics. Light Sci. Appl. 2020, 9, 130. [Google Scholar] [CrossRef]
- Schindler, F. Dirac equation perspective on higher-order topological insulators. J. Appl. Phys. 2020, 128, 221102. [Google Scholar] [CrossRef]
- Trifunovic, L.; Brouwer, P.W. Higher-Order Topological Band Structures. Phys. Status Solidi B 2021, 258, 2000090. [Google Scholar] [CrossRef]
- Xie, B.; Wang, H.-X.; Zhang, X.; Zhan, P.; Jiang, J.-H.; Lu, M.; Chen, Y. Higher-order band topology. Nat. Rev. Phys. 2021, 3, 520–532. [Google Scholar] [CrossRef]
- Bomantara, R.W.; Zhou, L.; Pan, J.; Gong, J. Coupled-wire construction of static and Floquet second-order topological insulators. Phys. Rev. B 2019, 99, 045441. [Google Scholar] [CrossRef] [Green Version]
- Seshadri, R.; Dutta, A.; Sen, D. Generating a second-order topological insulator with multiple corner states by periodic driving. Phys. Rev. B 2019, 100, 115403. [Google Scholar] [CrossRef] [Green Version]
- Peng, Y.; Refael, G. Floquet Second-Order Topological Insulators from Nonsymmorphic Space-Time Symmetries. Phys. Rev. Lett. 2019, 123, 016806. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rodriguez-Vega, M.; Kumar, A.; Seradjeh, B. Higher-order Floquet topological phases with corner and bulk bound states. Phys. Rev. B 2019, 100, 085138. [Google Scholar] [CrossRef] [Green Version]
- Nag, T.; Juričić, V.; Roy, B. Out of equilibrium higher-order topological insulator: Floquet engineering and quench dynamics. Phys. Rev. Res. 2019, 1, 032045. [Google Scholar] [CrossRef] [Green Version]
- Huang, B.; Liu, W.V. Floquet Higher-Order Topological Insulators with Anomalous Dynamical Polarization. Phys. Rev. Lett. 2020, 124, 216601. [Google Scholar] [CrossRef] [PubMed]
- Hu, H.; Huang, B.; Zhao, E.; Liu, W.V. Dynamical Singularities of Floquet Higher-Order Topological Insulators. Phys. Rev. Lett. 2020, 124, 057001. [Google Scholar] [CrossRef] [Green Version]
- Pan, J.; Zhou, L. Non-Hermitian Floquet second order topological insulators in periodically quenched lattices. Phys. Rev. B 2020, 102, 094305. [Google Scholar] [CrossRef]
- Ghosh, A.K.; Paul, G.C.; Saha, A. Higher order topological insulator via periodic driving. Phys. Rev. B 2020, 101, 235403. [Google Scholar] [CrossRef]
- Meng, Y.; Chen, G.; Jia, S. Second-order topological insulator in a coinless discrete-time quantum walk. Phys. Rev. A 2020, 102, 012203. [Google Scholar] [CrossRef]
- Zhu, W.; Chong, Y.D.; Gong, J. Floquet higher-order topological insulator in a periodically driven bipartite lattice. Phys. Rev. B 2021, 103, L041402. [Google Scholar] [CrossRef]
- Bhat, R.V.; Bera, S. Out of equilibrium chiral higher order topological insulator on a π-flux square lattice. J. Phys. Condens. Matter 2021, 33, 164005. [Google Scholar] [CrossRef]
- Franca, S.; Hassler, F.; Fulga, I.C. Simulating Floquet topological phases in static systems. SciPost Phys. Core 2021, 4, 007. [Google Scholar] [CrossRef]
- Zhang, R.-X.; Yang, Z.-C. Tunable fragile topology in Floquet systems. Phys. Rev. B 2021, 103, L121115. [Google Scholar] [CrossRef]
- Zhu, W.; Chong, Y.D.; Gong, J. Symmetry analysis of anomalous Floquet topological phases. Phys. Rev. B 2021, 104, L020302. [Google Scholar] [CrossRef]
- Zhou, L. Floquet Second-Order Topological Phases in Momentum Space. Nanomaterials 2021, 11, 1170. [Google Scholar] [CrossRef]
- Zhu, W.; Xue, H.; Gong, J.; Chong, Y.; Zhang, B. Time-periodic corner states from Floquet higher-order topology. Nat. Commun. 2022, 13, 11. [Google Scholar] [CrossRef] [PubMed]
- Jin, J.; He, L.; Lu, J.; Mele, E.J.; Zhen, B. Floquet Quadrupole Photonic Crystals Protected by Space-Time Symmetry. Phys. Rev. Lett. 2022, 129, 063902. [Google Scholar] [CrossRef]
- Franca, S.; Hassler, F.; Fulga, I.C. Topological reflection matrix. Phys. Rev. B 2022, 105, 155121. [Google Scholar] [CrossRef]
- Ghosh, A.K.; Nag, T.; Saha, A. Systematic generation of the cascade of anomalous dynamical first- and higher-order modes in Floquet topological insulators. Phys. Rev. B 2022, 105, 115418. [Google Scholar] [CrossRef]
- Ning, Z.; Fu, B.; Xu, D.-H.; Wang, R. Tailoring quadrupole topological insulators with periodic driving and disorder. Phys. Rev. B 2022, 105, L201114. [Google Scholar] [CrossRef]
- Lei, Y.; Luo, X.-W.; Zhang, S. Second-order topological insulator in periodically driven optical lattices. Opt. Express 2022, 30, 24048–24061. [Google Scholar] [CrossRef]
- Huang, B.; Novičenko, V.; Eckardt, A.; Juzeliūnas, G. Floquet chiral hinge modes and their interplay with Weyl physics in a three-dimensional lattice. Phys. Rev. B 2021, 104, 104312. [Google Scholar] [CrossRef]
- Wang, B.-Q.; Wu, H.; An, J.-H. Engineering exotic second-order topological semimetals by periodic driving. Phys. Rev. B 2021, 104, 205117. [Google Scholar] [CrossRef]
- Zhu, W.; Umer, M.; Gong, J. Floquet higher-order Weyl and nexus semimetals. Phys. Rev. Res. 2021, 3, L032026. [Google Scholar] [CrossRef]
- Ghosh, S.; Saha, K.; Sengupta, K. Hinge-mode dynamics of periodically driven higher-order Weyl semimetals. Phys. Rev. B 2022, 105, 224312. [Google Scholar] [CrossRef]
- Du, X.-L.; Chen, R.; Wang, R.; Xu, D.-H. Weyl nodes with higher-order topology in an optically driven nodal-line semimetal. Phys. Rev. B 2022, 105, L081102. [Google Scholar] [CrossRef]
- Plekhanov, K.; Thakurathi, M.; Loss, D.; Klinovaja, J. Floquet second-order topological superconductor driven via ferromagnetic resonance. Phys. Rev. Res. 2019, 1, 032013. [Google Scholar] [CrossRef] [Green Version]
- Bomantara, R.W.; Gong, J. Measurement-only quantum computation with Floquet Majorana corner modes. Phys. Rev. B 2020, 101, 085401. [Google Scholar] [CrossRef] [Green Version]
- Bomantara, R.W. Time-induced second-order topological superconductors. Phys. Rev. Res. 2020, 2, 033495. [Google Scholar] [CrossRef]
- Peng, Y. Floquet higher-order topological insulators and superconductors with space-time symmetries. Phys. Rev. Res. 2020, 2, 013124. [Google Scholar] [CrossRef] [Green Version]
- Chaudhary, S.; Haim, A.; Peng, Y.; Refael, G. Phonon-induced Floquet topological phases protected by space-time symmetries. Phys. Rev. Res. 2020, 2, 043431. [Google Scholar] [CrossRef]
- Vu, D.; Zhang, R.-X.; Yang, Z.-C.; Sarma, S.D. Superconductors with anomalous Floquet higher-order topology. Phys. Rev. B 2021, 104, L140502. [Google Scholar] [CrossRef]
- Ghosh, A.K.; Nag, T.; Saha, A. Floquet generation of a second-order topological superconductor. Phys. Rev. B 2021, 103, 045424. [Google Scholar] [CrossRef]
- Ghosh, A.K.; Nag, T.; Saha, A. Floquet second order topological superconductor based on unconventional pairing. Phys. Rev. B 2021, 103, 085413. [Google Scholar] [CrossRef]
- Ghosh, A.K.; Nag, T.; Saha, A. Dynamical construction of quadrupolar and octupolar topological superconductors. Phys. Rev. B 2022, 105, 155406. [Google Scholar] [CrossRef]
- Liu, F.; Wakabayashi, K. Novel Topological Phase with a Zero Berry Curvature. Phys. Rev. Lett. 2017, 118, 076803. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, Y.-B.; Li, K.; Duan, L.-M.; Xu, Y. Type-II quadrupole topological insulators. Phys. Rev. Res. 2020, 2, 033029. [Google Scholar] [CrossRef]
- Ezawa, M. Edge-corner correspondence: Boundary-obstructed topological phases with chiral symmetry. Phys. Rev. B 2020, 102, 121405. [Google Scholar] [CrossRef]
- Asaga, K.; Fukui, T. Boundary-obstructed topological phases of a massive Dirac fermion in a magnetic field. Phys. Rev. B 2020, 102, 155102. [Google Scholar] [CrossRef]
- Li, C.-A.; Fu, B.; Hu, Z.-A.; Li, J.; Shen, S.-Q. Topological Phase Transitions in Disordered Electric Quadrupole Insulators. Phys. Rev. Lett. 2020, 125, 166801. [Google Scholar] [CrossRef]
- Khalaf, E.; Benalcazar, W.A.; Hughes, T.L.; Queiroz, R. Boundary-obstructed topological phases. Phys. Rev. Res. 2021, 3, 013239. [Google Scholar] [CrossRef]
- Jia, W.; Zhou, X.-C.; Zhang, L.; Zhang, L.; Liu, X.-J. Unified characterization for higher-order topological phase transitions. arXiv 2022, arXiv:2209.10394. [Google Scholar]
- Zhou, L. Non-Hermitian Floquet topological superconductors with multiple Majorana edge modes. Phys. Rev. B 2020, 101, 014306. [Google Scholar] [CrossRef] [Green Version]
- Asbóth, J.K.; Obuse, H. Bulk-boundary correspondence for chiral symmetric quantum walks. Phys. Rev. B 2013, 88, 121406. [Google Scholar] [CrossRef] [Green Version]
- Asbóth, J.K.; Tarasinski, B.; Delplace, P. Chiral symmetry and bulk-boundary correspondence in periodically driven one-dimensional systems. Phys. Rev. B 2014, 90, 125143. [Google Scholar] [CrossRef] [Green Version]
- Ho, D.Y.H.; Gong, J. Topological effects in chiral symmetric driven systems. Phys. Rev. B 2014, 90, 195419. [Google Scholar] [CrossRef]
- Zhou, L.; Du, Q. Floquet topological phases with fourfold-degenerate edge modes in a driven spin-1/2 Creutz ladder. Phys. Rev. A 2020, 101, 033607. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Tan, S.; Wang, Q.-h.; Zhou, L.; Gong, J. Floquet band engineering with Bloch oscillations. arXiv 2022, arXiv:2208.05260. [Google Scholar]
- Roy, D.; Prosen, T. Random matrix spectral form factor in kicked interacting fermionic chains. Phys. Rev. E 2020, 102, 060202. [Google Scholar] [CrossRef]
- Kells, G.; Meidan, D.; Brouwer, P.W. Near-zero-energy end states in topologically trivial spin-orbit coupled superconducting nanowires with a smooth confinement. Phys. Rev. B 2012, 86, 100503. [Google Scholar] [CrossRef] [Green Version]
- Roy, D.; Bondyopadhaya, N.; Tewari, S. Topologically trivial zero-bias conductance peak in semiconductor Majorana wires from boundary effects. Phys. Rev. B 2013, 88, 020502. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, L. Generating Many Majorana Corner Modes and Multiple Phase Transitions in Floquet Second-Order Topological Superconductors. Symmetry 2022, 14, 2546. https://doi.org/10.3390/sym14122546
Zhou L. Generating Many Majorana Corner Modes and Multiple Phase Transitions in Floquet Second-Order Topological Superconductors. Symmetry. 2022; 14(12):2546. https://doi.org/10.3390/sym14122546
Chicago/Turabian StyleZhou, Longwen. 2022. "Generating Many Majorana Corner Modes and Multiple Phase Transitions in Floquet Second-Order Topological Superconductors" Symmetry 14, no. 12: 2546. https://doi.org/10.3390/sym14122546
APA StyleZhou, L. (2022). Generating Many Majorana Corner Modes and Multiple Phase Transitions in Floquet Second-Order Topological Superconductors. Symmetry, 14(12), 2546. https://doi.org/10.3390/sym14122546




